2. 国家测绘地理信息局卫星测绘应用中心, 北京 100048
2. Satellite Surveying and Mapping Application Center, NASG, Beijing 100048, China
地球重力场和静态海洋环流探测卫星(gravity field and steady-state ocean circulation explorer, GOCE)是欧空局发射的地球重力场探测卫星,其上搭载的静电重力梯度仪由6个单独的加速度计呈Aguirre结构排列而成,可直接测定地球重力位的二阶导数[1-5],实现重力梯度观测值的高精度获取。GOCE重力梯度仪具有高精度、高灵敏度特点,它的稳定运行对外界环境有着严苛要求。GOCE重力梯度仪的校准一般可分为3个阶段:地面校准、在轨校准和外部校准。地面校准是在卫星发射前,在实验室完成。在轨校准是在卫星发射后,于在轨测试期间完成。经过地面校准和在轨校准后,静电重力梯度仪会达到较好的工作状态。但由于空间环境和卫星状态的变化,静电重力梯度仪的工作状态和校准参数会发生相应的变化。在卫星的实际运行过程中,由重力梯度仪非完美运行状态引起的系统误差通常表现为加速度计偏差和加速度计尺度因子不匹配。重力梯度观测数据在应用于科学数据处理前,特别是用于地球重力场恢复等研究之前,需尽可能地消除这些系统误差,需要对重力梯度观测值进行外部校准。
静电重力梯度仪常用的外部校准方法包括基于先验地球重力场模型校准、利用卫星跟踪卫星(satellite to satellite tracking, SST)观测数据校准以及利用地面重力数据校准等[6-12]。文献[13]利用模拟的GOCE SST数据和重力梯度观测数据,确定了主对角分量的尺度因子,其精度达到4×10-3。文献[14]对GOCE level 1b重力梯度观测值进行了外部校准研究,确定的尺度因子精度在10-3量级。文献[15]研究了利用GOCE level-2重力梯度观测数据计算外部校准参数的方法,并对校准结果进行了质量评估,其精度达到了10-4量级。文献[16]提出了将GOCE重力梯度数据从时域转换到频域的方法,这样有利于消除测量值中的有色噪声,进而进行外部校准。文献[17]利用EGM96、EIGEN-2模型求定了CHAMP卫星加速度计修正参数,验证了利用先验模型方法解算校准参数的有效性。文献[18]利用局部地面重力数据对GOCE模拟数据进行了校准分析,发现在平缓且地面重力点分布密度较大的区域,尺度因子可达到10-2水平,在地面重力点分布稀疏的区域,精度在10-1水平。文献[19]利用EGM2008、EIGEN-5C模型计算了主对角线分量的尺度因子,对比了两个重力场模型的校准结果,发现校准后的观测值差异小于10-4E,远小于观测误差。本文利用多种先验重力场模型,对GOCE重力梯度Level-1b产品进行了外部校准分析,确定了GOCE重力梯度观测数据的外部校准参数,对不同模型的校准结果进行了精度评价分析。
1 基于先验重力场的外部校准方法利用先验地球重力场模型开展重力梯度数据的校准是通过GOCE重力梯度观测值与先验重力场模型计算的重力梯度模型值之间的比对进行的,通常采用如下的校准模型[15, 20]
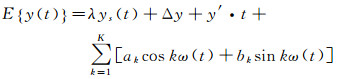 (1)
(1)
式中,E是期望算子;y是真实的重力梯度值,这里可以用先验重力场模型值ym代替;λ是尺度因子;ys是GOCE重力梯度观测值;Δy是偏差;y′为趋势;ω=2πt/T;t为时间;T为平均轨道周期;ak、bk是傅里叶系数。未知数个数有3+2k个,即尺度因子、偏差、趋势和2k个傅里叶系数。
考虑到重力梯度值的在轨变化特性,本文将对重力梯度观测值及模型值进行滤波,滤波后观测值尺度因子与趋势项及傅里叶系数会存在严重的相关性,导致估计结果不准确[1]。只考虑尺度因子和偏差项,重力梯度观测值的观测方程可写为
 (2)
(2)
误差方程可写为
 (3)
(3)
式中,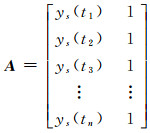

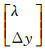
利用最小二乘估计可得
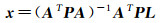 (4)
(4)
求出的外部校准参数x,即为尺度因子和偏差。
GOCE重力梯度观测值是在重力梯度仪参考框架(gradiometer reference frame, GRF)下,而利用重力场模型计算的重力梯度观测值一般是在局部指北坐标系(local north oriented frame, LNOF)下,因此在校准过程中需要进行框架转换。从局部指北坐标系转换至重力梯度仪参考框架,需要经历以下几个坐标旋转步骤:局部指北坐标系→地固坐标系→惯性坐标系→重力梯度仪参考框架
框架转换的函数模型如下
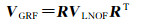 (5)
(5)
GOCE重力梯度数据的预处理包括时变信号改正、粗差探测和外部校准3个过程。在进行重力梯度数据的外部校准前,需要对重力梯度观测数据进行时变改正和粗差探测。本文所采用的GOCE数据自2011年2月11日-2011年6月23日,采样率为1s,观测值总数为11 265 086,观测值在4月和6月有部分缺失,校准周期为7 d。
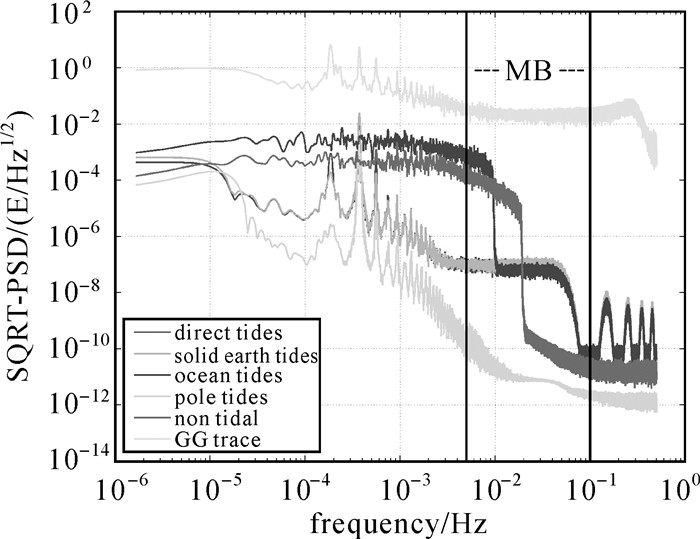
2.1 卫星重力梯度数据时变改正GOCE重力梯度观测值中包含与地球表面和内部有关的时变信号,时变部分反映到大地水准面上可以达到几个毫米甚至厘米级。因此,在进行实际的梯度数据处理过程中,必须探究时变信号的影响。时变改正分为潮汐改正和非潮汐改正两部分。其中潮汐改正主要包括:天文潮汐、固体潮、海潮、极潮和大气潮。非潮汐改正主要考虑高频信号中的大气、海洋质量的季节性变化以及陆地水、冰雪质量变化等[23]。本文对ESA公布的重力梯度观测数据时变改正信号进行了分析。图 1给出了2月18日至2月24日重力梯度观测数据的迹和Vzz分量各种时变信号的功率谱密度。从图中可以看出,在测量带宽0.005~0.1 Hz内,卫星重力梯度时变信号中,海潮的影响最大,达到mE(1 mE=10-12/s2)量级,与梯度仪的精度水平相当,陆地水等非潮汐信号的影响略小于海潮,在10-4 E左右,二者对GOCE重力梯度观测值外部校准的精度影响较大,在实际处理中,要重点考虑。天文潮汐和固体潮的影响量级在10-7 E左右,极潮的影响最小,小于10-10 E,在实际处理中,可不予考虑。
|
| 图 1 重力梯度Vzz观测值中时变信号的功率谱密度 Fig. 1 The power spectral density of the temporal signals in the Vzz observation |
2.2 粗差探测
GOCE重力梯度观测值中粗差的存在对于求解重力场模型有着较大影响,观测值粗差会影响法方程的态性,导致求解过程不稳定。因此GOCE数据处理时必须要对GOCE重力梯度观测值进行粗差的探测、标记及修复。
重力梯度观测值粗差探测一般遵循3个准则[2, 24-25]:
(1) 迹为零准则。重力梯度在地球外部空间满足Laplace方程,即重力梯度张量的迹为零。该准则能够在GOCE重力梯度观测值中不存在粗差和系统偏差,且各分量之间不存在相关性的前提下,检验重力梯度观测值对角线分量是否存在粗差,但无法定位具体分量。
(2) 残差重力梯度为零准则。GOCE重力梯度观测值与利用先验重力场模型计算的梯度值之差理论上应为零。该准则可以定位每个分量的粗差,但是探测效果会受到重力场模型截断误差的影响。
(3) 连续性准则。重力位的二阶导数在地球外部空间是连续的,相邻历元的重力梯度观测值之间不存在跃变。该准则可以定位每个分量的粗差,但前提是忽略内插误差的影响。
本文采取的是连续性准则,其中重力梯度内插值依据三次样条插值法计算得到。结合阈值法,实现粗差探测。
本文对研究所用的GOCE重力梯度观测值的粗差进行了统计分析(如表 1所示)。可以看出,各分量重力梯度观测值的粗差比例均大于0.2%,其中Vxx分量最大,达到0.39%,这会对GOCE重力梯度数据的校准产生较大影响,需要进行剔除处理。
| 分量 | Vxx | Vyy | Vzz | Vxy | Vxz | Vyz |
| 粗差数目 | 43 800 | 29 401 | 26 600 | 26 445 | 30 459 | 27 962 |
| 粗差在数据中的比例/(%) | 0.39 | 0.26 | 0.23 | 0.23 | 0.27 | 0.24 |
2.3 外部校准处理与分析
在完成梯度观测值的时变改正和粗差剔除后,利用EGM96[26]、EGM2008[27]、GIF48[28]、GGM05S[29]、EIGEN-6C4[30]、GO_CONS_GCF_2_SPW_R5[31](简称SPW5)、SGG-UGM-1[32]等不同的先验重力场模型对GOCE重力梯度观测值进行了外部校准处理,所有模型均截断至180阶。
由于重力梯度仪的测量带宽限制,在测量带宽以下重力梯度观测噪声大,因此在校准前对重力梯度观测值与模型值进行了巴特沃斯高通滤波,抑制重力梯度观测值与模型值低频信号的影响。滤波器阶数为2,通带截止频率为0.003 Hz。利用7种模型进行外部校准得到的尺度因子和偏差如图 2、图 3所示。

|
| 图 2 不同重力场模型计算的尺度因子 Fig. 2 The scale factors calculated by different gravity field models |
|
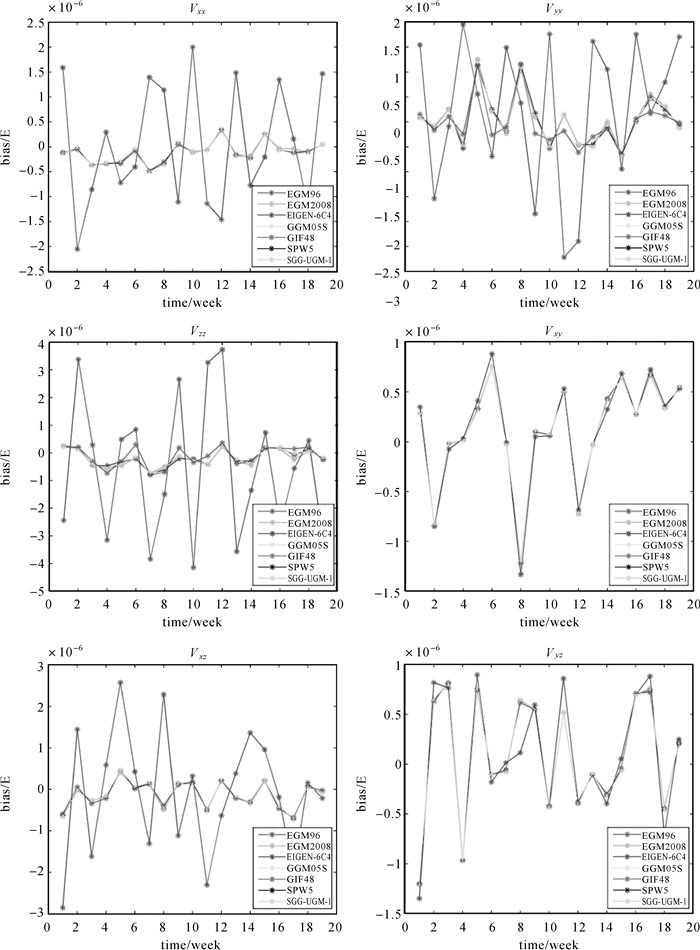
| 图 3 不同重力场模型计算的偏差值 Fig. 3 The biases calculated by different gravity field models |
从图 2可以看出,EGM96模型校准的尺度因子明显偏小,其他6种模型校准得到的尺度因子更接近于1,而且差异较小,这主要是由于EGM96模型精度较差引起的。对GOCE重力梯度分量而言,Vxx、Vyy、Vzz、Vxz分量上尺度因子的变化范围要小于Vxy、Vyz分量。此外,利用GGM05S模型校准时,Vyy分量上的尺度因子相比其他模型的结果偏小。GGM05S模型是利用GRACE卫星数据得到的,GRACE卫星采用高-低卫星跟踪卫星和低-低卫星跟踪卫星观测模式,其观测量分别对应卫星沿轨方向和径向方向,而法线方向的观测值不敏感,这可能是GGM05S模型校准结果出现差异的原因。从图 3可以看出,Vxx、Vyy、Vzz、Vxz分量观测值校准偏差在10-6量级,Vxy、Vyz分量观测值校准偏差达到10-5量级,这与GOCE重力梯度仪的Aguirre结构特性一致。对不同重力场模型而言,EGM96模型校准偏差与其他模型存在较大差异。
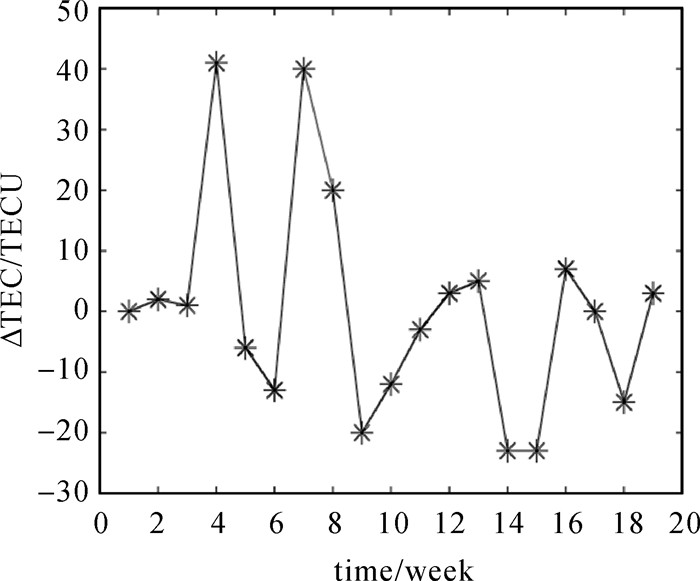
此外,除EGM96外的其余6种模型校准的主对角线分量Vxx、Vyy、Vzz尺度因子在第9、14个校准周期中发生了异常变化。在此期间,GOCE卫星并未开展飞行控制等轨道调整工作,初步判断可能是外部飞行环境变化或重力场异常带来的影响。电离层电子含量变化能够反映出太阳活动和地磁场的变化,利用IGS提供的全球电离层格网数据,计算了相邻两个校准周期内的电子含量变化情况,如图 4所示。可以看出在第9、14个校准周期中电子含量衰减最大,这可能是导致重力梯度观测值主对角线分量尺度因子异常变化的原因之一。
|
| 图 4 校准周期内电离层电子含量变化 Fig. 4 The TEC changes during the calibration period |
2.4 校准精度验证
GOCE重力梯度观测值具有无迹特性,即Vxx(ti)+Vyy(ti)+Vzz(ti)=0,以此对校准结果的有效性进行评价。对校准后梯度观测值的迹进行了统计分析,如表 2所示。
| mE | |||||||
| 时间/周 | EGM96 | EGM2008 | GIF48 | EIGEN-6C4 | GGM05S | SPW5 | SGG-UGM-1 |
| 1 | 19.472 1 | 19.224 3 | 19.223 3 | 19.222 8 | 19.230 4 | 19.223 0 | 19.223 1 |
| 2 | 19.388 1 | 19.117 3 | 19.115 1 | 19.114 8 | 19.123 1 | 19.115 4 | 19.115 5 |
| 3 | 19.470 5 | 19.147 0 | 19.150 0 | 19.149 2 | 19.157 8 | 19.150 2 | 19.150 0 |
| 4 | 19.279 8 | 19.005 6 | 19.003 7 | 19.003 8 | 19.012 6 | 19.003 9 | 19.003 9 |
| 5 | 19.482 8 | 19.198 5 | 19.196 9 | 19.196 2 | 19.204 5 | 19.196 8 | 19.196 9 |
| 6 | 19.015 8 | 18.712 3 | 18.714 3 | 18.713 3 | 18.720 8 | 18.714 1 | 18.714 0 |
| 7 | 19.282 3 | 19.014 3 | 19.011 7 | 19.012 0 | 19.020 4 | 19.012 4 | 19.012 1 |
| 8 | 21.561 2 | 21.224 0 | 21.225 3 | 21.225 4 | 21.237 2 | 21.226 0 | 21.225 7 |
| 9 | 23.532 0 | 23.167 6 | 23.168 5 | 23.167 3 | 23.181 6 | 23.168 3 | 23.167 9 |
| 10 | 19.199 1 | 18.928 0 | 18.924 7 | 18.924 7 | 18.932 1 | 18.925 1 | 18.924 7 |
| 11 | 19.166 4 | 18.911 0 | 18.911 7 | 18.911 5 | 18.920 6 | 18.912 0 | 18.912 3 |
| 12 | 19.937 1 | 19.649 1 | 19.650 5 | 19.649 5 | 19.660 0 | 19.650 2 | 19.650 0 |
| 13 | 18.755 0 | 18.468 2 | 18.465 3 | 18.465 2 | 18.473 0 | 18.465 7 | 18.465 3 |
| 14 | 20.958 3 | 20.665 3 | 20.665 0 | 20.664 6 | 20.673 4 | 20.665 2 | 20.665 5 |
| 15 | 18.751 0 | 18.488 3 | 18.491 0 | 18.490 3 | 18.498 6 | 18.491 0 | 18.490 9 |
| 16 | 19.397 4 | 19.074 9 | 19.072 2 | 19.072 1 | 19.081 0 | 19.072 5 | 19.072 2 |
| 17 | 20.116 5 | 19.814 5 | 19.810 5 | 19.809 5 | 19.816 5 | 19.810 4 | 19.810 9 |
| 18 | 18.866 6 | 18.614 8 | 18.617 6 | 18.617 2 | 18.625 6 | 18.617 8 | 18.617 6 |
| 19 | 18.708 8 | 18.403 8 | 18.401 7 | 18.401 5 | 18.409 6 | 18.401 9 | 18.401 8 |
| 平均值 | 19.702 2 | 19.412 0 | 19.411 5 | 19.411 1 | 19.419 9 | 19.411 7 | 19.411 6 |
从表 2中可以看出,采用7种重力场模型校准后,观测值的迹的均方根平均值均优于20 mE,其中第8周、9周、14周迹的均方根值略大,这与前面得到的尺度因子异常变化的发生时间一致;EGM96模型校准后观测值的迹的均方根较大,其余6种重力场模型的校准结果比较接近。
除了精度较低的EGM96模型外,EIGEN-6C4模型校准后观测值的迹的均方根平均值最小,GGM05S模型的均方根平均值最大。EIGEN-6C4模型解算中采用了卫星测高数据、地面重力数据以及卫星重力数据(GOCE+GRACE+Lageos)等多源数据,GGM05S则仅仅采用了GRACE卫星数据。EGM2008与GIF48重力场模型采用了卫星测高、地面重力和卫星重力数据,且卫星重力数据仅采用GRACE卫星。SPW5模型则是仅由GOCE卫星实测数据反演的重力场模型。SGG_UGM_1模型是联合了EGM2008重力异常数据和GOCE卫星数据的综合类模型。考虑到梯度观测值校准的独立性,以及GRACE卫星在地球重力场频谱贡献上的局限性,在利用先验重力场模型进行外部校准时,采用EGM2008或GIF48等非GOCE多源重力数据模型更合理。表 3统计的是利用7种重力场模型计算得到的尺度因子的标准差。
| 模型 | 分量 | |||||
| Vxx | Vyy | Vzz | Vxy | Vxz | Vyz | |
| EGM96 | 1.110 7×10-3 | 1.316 7×10-3 | 1.997 0×10-3 | 8.426 6×10-2 | 1.412 3×10-4 | 8.93 67×10-4 |
| EGM2008 | 3.966 7×10-5 | 8.148 7×10-4 | 1.467 3×10-4 | 1.504 2×10-2 | 7.637 4×10-6 | 4.632 3×10-4 |
| EIGEN-6C4 | 1.270 1×10-4 | 8.809 3×10-4 | 2.200 9×10-4 | 1.516 9×10-2 | 2.406 1×10-5 | 4.633 5×10-4 |
| GGM05S | 1.336 0×10-4 | 8.322 3×10-4 | 2.074 6×10-4 | 1.523 0×10-2 | 2.649 5×10-5 | 5.085 4×10-4 |
| GIF48 | 1.246 4×10-4 | 9.130 7×10-4 | 2.328 8×10-4 | 1.516 1×10-2 | 2.460 2×10-5 | 4.678 0×10-4 |
| SPW5 | 1.308 3×10-4 | 8.993 0×10-4 | 2.292 9×10-4 | 1.513 4×10-2 | 2.460 6×10-5 | 4.692 5×10-4 |
| SGG-UGM-1 | 1.563 3×10-4 | 8.721 5×10-4 | 2.363 4×10-4 | 1.516 8×10-2 | 2.912 9×10-5 | 4.620 5×10-4 |
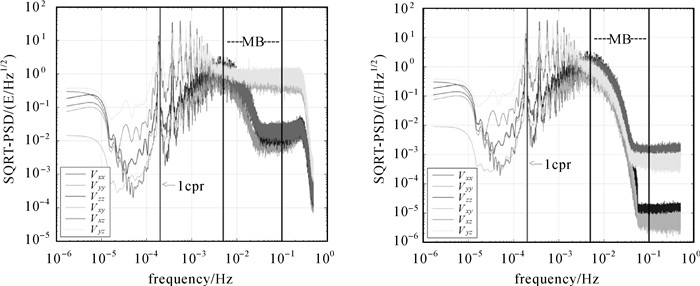
由表 3可以看出,对不同重力场模型而言,利用EGM96模型校准后尺度因子的稳定性较差,其余模型校准后尺度因子的稳定性相对较高,且差异较小,这与表 2中重力梯度观测值迹的特征是一致的;除EGM96模型外的其他模型校准结果表明,Vxx、Vzz、Vxz分量的稳定性要优于其余分量,这与GOCE静电重力梯度仪的Aguirre结构和GOCE卫星飞行姿态有关。此外,尺度因子的稳定性还可能与各分量观测值的误差水平有关,图 5给出了2月18日至2月24日校准周期内的滤波后观测值与GIF48模型值的功率谱密度。
|
| 图 5 GOCE重力梯度观测值与GIF48模型值滤波后的功率谱密度 Fig. 5 The power spectral density of gravity gradient observations and those calculated with GIF48 |
从图 5中可以看出,在GOCE测量带宽内:当频率在0.005~0.03 Hz时,重力梯度观测值Vxx、Vyy、Vzz及Vxz分量的功率谱密度迅速减小,Vxy、Vyz分量则保持不变,大约为1E,而模型值在6个分量的功率谱密度均迅速减小;当频率在0.03~0.1 Hz时,重力梯度观测值Vxx、Vyy、Vzz及Vxz分量的功率谱密度趋于稳定,大约为10~20 mE,Vxy、Vyz分量仍为1E,而模型值在Vxy、Vyz这两个分量上的功率谱密度值不再变化,约为1 mE,其余分量仍继续减小。如果将模型值看作重力梯度真实值,在测量带宽内,Vxy分量观测值与真实值差异最大,其噪声水平最高,因而其校准结果稳定性最低。这与GOCE重力梯度仪的设计特性也是一致的。
3 结论本文首先分析了GOCE重力梯度观测值中时变信号的影响以及粗差的分布特点,然后采用EGM96、EGM2008、GIF48、EIGEN-6C4、GGM05S、SPW5、SGG-UGM-1共7种重力场模型计算了梯度各分量的校准参数,对校准结果进行了精度评价。主要结论如下:
(1) 在重力梯度仪测量带宽内,重力梯度时变信号中,海潮的影响最大,达到mE量级,与重力梯度仪的精度水平相当,陆地水等非潮汐信号的影响在10-4 E左右。在实际处理中,二者要重点考虑。
(2) 除了精度较低的EGM96模型外,其他重力场模型的校准精度水平较为一致。考虑到梯度观测值校准的独立性,以及GRACE卫星在地球重力场频谱贡献上的局限性,在利用先验重力场模型进行外部校准时,采用EGM2008或GIF48等非GOCE多源重力数据模型较为合理。
(3) 除EGM96模型外,其余模型对GOCE梯度仪进行校准后,Vxx、Vyy、Vzz、Vyz分量上尺度因子的稳定性均在10-4量级,Vxz分量能达到10-5量级,Vxy分量为10-2量级,这与重力梯度观测值各分量的精度水平密切相关,Vxy分量在测量带宽内,噪声要大于其他分量。
| [1] | BOUMAN J, RISPENS S, GRUBER T, et al. Preprocessing of gravity gradients at the GOCE high-level processing facility[J]. Journal of Geodesy, 2009, 83(7): 659–678. DOI:10.1007/s00190-008-0279-9 |
| [2] |
罗志才, 吴云龙, 钟波, 等.
GOCE卫星重力梯度测量数据的预处理[J]. 武汉大学学报(信息科学版), 2009, 34(10): 1163–1167.
LUO Zhicai, WU Yunlong, ZHONG Bo, et al. Pre-processing of the GOCE satellite gravity gradiometry data[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10): 1163–1167. |
| [3] |
苏勇, 范东明, 游为.
利用GOCE卫星数据确定全球重力场模型[J]. 物理学报, 2014, 63(9): 099101.
SU Yong, FAN Dongming, YOU Wei. Gravity field model calculated by using the GOCE data[J]. Acta Physica Sinica, 2014, 63(9): 099101. |
| [4] | RUMMEL R, YI Weiyong, STUMMER C. GOCE gravitational gradiometry[J]. Journal of Geodesy, 2011, 85(11): 777–790. DOI:10.1007/s00190-011-0500-0 |
| [5] |
朱广彬.卫星重力梯度测量技术确定地球重力场的理论方法研究[D].武汉: 武汉大学, 2010. ZHU Guangbin. Research on the theory and methodology for the Earth's gravity field determination using satellite gravity gradiometry measurement[D]. Wuhan: Wuhan University, 2010. |
| [6] | ARABELOS D, TSCHERNING C C. Calibration of satellite gradiometer data aided by ground gravity data[J]. Journal of Geodesy, 1998, 72(11): 617–625. DOI:10.1007/s001900050201 |
| [7] | BOUMAN J, KOOP R, TSCHERNING C C, et al. Calibration of GOCE SGG data using high-low SST, terrestrial gravity data and global gravity field models[J]. Journal of Geodesy, 2004, 78(1-2): 124–137. |
| [8] | ARABELOS D N, TSCHERNING C C. A comparison of recent earth gravitational models with emphasis on their contribution in refining the gravity and geoid at continental or regional scale[J]. Journal of Geodesy, 2010, 84(11): 643–660. DOI:10.1007/s00190-010-0397-z |
| [9] | SIEMES C, HAAGMANS R, KERN M, et al. Monitoring GOCE gradiometer calibration parameters using accelerometer and star sensor data:methodology and first results[J]. Journal of Geodesy, 2012, 86(8): 629–645. DOI:10.1007/s00190-012-0545-8 |
| [10] | PAIL R. Local gravity field continuation for the purpose of in-orbit calibration of GOCE SGG observations[J]. Advances in Geosciences, 2013, 1: 11–18. |
| [11] | VISSER P N A M, VAN DEN IJSSEL J A A. Calibration and validation of individual GOCE accelerometers by precise orbit determination[J]. Journal of Geodesy, 2016, 90(1): 1–13. DOI:10.1007/s00190-015-0850-0 |
| [12] | BOUMAN J, FIOROT S, FUCHS M, et al. GOCE level 2 gravity gradients[C]//Proceedings of the 4th International Goce User Workshop. Munchen, Germany: ESA, 2011: 1-4. |
| [13] | VISSER P N A M. GOCE gradiometer validation by GPS[J]. Advances in Space Research, 2007, 39(10): 1630–1637. DOI:10.1016/j.asr.2006.09.014 |
| [14] | FROMMKNECHT B, LAMARRE D, MELONI M, et al. GOCE level 1B data processing[J]. Journal of Geodesy, 2011, 85(11): 759–775. DOI:10.1007/s00190-011-0497-4 |
| [15] | BOUMAN J, FIOROT S, FUCHS M, et al. GOCE gravitational gradients along the orbit[J]. Journal of Geodesy, 2011, 85(11): 791–805. DOI:10.1007/s00190-011-0464-0 |
| [16] | RISPENS S M, BOUMAN J. External calibration of GOCE accelerations to improve derived gravitational gradients[J]. Journal of Geodetic Science, 2011, 1(2): 114–126. |
| [17] |
徐天河, 杨元喜.
利用现有重力场模型求定CHAMP卫星加速度计修正参数[J]. 测绘学报, 2004, 33(3): 200–204.
XU Tianhe, YANG Yuanxi. Calibration for CHAMP accelerometry data based on known earth gravity field model[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 200–204. DOI:10.3321/j.issn:1001-1595.2004.03.003 |
| [18] | WU Yunlong, LI Hui, ZOU Zhengbo, et al. External calibration of GOCE data using regional terrestrial gravity data[J]. Geodesy and Geodynamics, 2012, 3(3): 34–39. DOI:10.3724/SP.J.1246.2012.00034.2 |
| [19] |
徐新禹, 赵永奇, 魏辉, 等.
利用先验重力场模型对GOCE卫星重力梯度观测值进行校准分析[J]. 测绘学报, 2015, 44(11): 1196–1201.
XU Xinyu, ZHAO Yongqi, WEI Hui, et al. Calibration and analysis of SGG observations of GOCE based on prior gravity models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1196–1201. DOI:10.13203/j.whugis20140861 |
| [20] |
吴云龙. GOCE卫星重力梯度测量数据的预处理研究[D].武汉: 武汉大学, 2010. WU Yunlong. Study on pre-processing of GOCE satellite gravity gradiometry data[D]. Wuhan: Wuhan University, 2010. |
| [21] | FUCHS M J, BOUMAN J. Rotation of GOCE gravity gradients to local frames[J]. Geophysical Journal International, 2011, 187(2): 743–753. DOI:10.1111/gji.2011.187.issue-2 |
| [22] |
苏勇, 范东明, 黄强.
GOCE梯度数据坐标系转换及误差分析[J]. 大地测量与地球动力学, 2014, 34(3): 151–154.
SU Yong, FAN Dongming, HUANG Qiang. Coordinate system conversion of GOCE gradients data and error analysis[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 151–154. |
| [23] |
邓文彬, 许闯, 阿力甫·努尔买买提.
卫星重力梯度观测数据的时变信号影响分析[J]. 武汉大学学报(信息科学版), 2016, 41(1): 72–78.
DENG Wenbin, XU Chuang, ALLFU·NURMMAMAT. Effect of time-varying gravity signal on satellite gravity gradient observations[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 72–78. |
| [24] | KERN M, PREIMESBERGER T, ALLESCH M, et al. Outlier detection algorithms and their performance in GOCE gravity field processing[J]. Journal of Geodesy, 2005, 78(9): 509–519. DOI:10.1007/s00190-004-0419-9 |
| [25] |
罗志才, 周波阳, 钟波, 等.
卫星重力梯度测量数据的粗差探测[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1392–1396.
LUO Zhicai, ZHOU Boyang, ZHONG Bo, et al. Outlier detection of satellite gravity gradiometry data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1392–1396. |
| [26] | LEMOINE F G, KENYON S C, FACTOR J K, et al. The development of the joint NASA GSFC and the National Imagery and Mapping Agency (nima) geopotential model EGM96[R]. Greenbelt, MD: NASA Goddard Space Flight Center, 1998: 103-115. |
| [27] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the earth gravitational model 2008(EGM2008)[J]. Journal of Geophysical Research, 2012, 117(B4): B04406. |
| [28] | RIES J C, BETTADPUR S, POOLE S, et al. Mean background gravity fields for grace processing[C]//Proceedings of GRACE Science Team Meeting. Austin, TX: [s.n.], 2011. |
| [29] | TAPLEY B D, FLECHTNER F, BETTADPUR S V, et al. The status and future prospect for GRACE after the first decade[C]//Proceedings of AGU Fall Meeting.[S.l.]: AGU, 2013. |
| [30] | FÖRSTE C, BRUINSMA S L, ABRIKOSOV O, et al. EIGEN-6C4: The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ potsdam and GRGS toulouse[R]. Berlin: GFZ, 2014. |
| [31] | GATTIA, REGUZZONI M. GOCE gravity field model by means of the space-wise approach (release r5)[R]. Berlin: GFZ, 2017. |
| [32] |
梁伟, 徐新禹, 李建成, 等.
联合EGM2008模型重力异常和GOCE观测数据构建超高阶地球重力场模型SGG-UGM-1[J]. 测绘学报, 2018, 47(4): 425–434.
LIANG Wei, XU Xinyu, LI Jiancheng, et al. The determination of an ultra-high gravity field model SGG-ugm-1 by combining EGM2008 gravity anomaly and GOCE observation data[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(4): 425–434. DOI:10.11947/j.AGCS.2018.20170269 |




