2. 武汉大学, 湖北 武汉 430072
2. Wuhan University, Wuhan 430072, China
北斗卫星导航系统取得了长足进展[1-2],在北斗实验验证系统(BDS-1)的基础上,2012年底建成了北斗区域卫星导航系统(BDS-2)[3],目前正在建设北斗全球卫星导航系统。但是,无论是卫星制造商还是用户,一直未给出北斗导航卫星的光压摄动模型。
星历精度是衡量卫星导航系统性能的重要指标之一,其中光压摄动是影响导航卫星定轨、定位精度的重要因素[4-6]。自20世纪80年代,传统固定面质比的光压模型[7-8]不能满足高精度定轨要求起,围绕导航卫星不同光压模型相继出现。按照建模原理不同,光压模型一般分为解析(分析)模型和经验模型。典型的解析模型有GPS卫星制造商Rockwell和IBM联合开发的ROCK模型[9-10]、T10/20/30系列解析模型[11-12],经验模型包括Colombo模型[13]、CODE模型[14-16]及GSPM模型[17-19]。
不同于其他保守和非保守摄动力,光压辐射与卫星本身参数状态密切相关,具有明显的差异。北斗卫星物理参数与GPS卫星不同,特别是,姿态控制模式存在连续动偏和零偏两种。因此,北斗卫星的光压摄动模型与其他模型(GPS模型)相比具有差异性。北斗区域系统运行之初,由于动零转换期间定轨精度发散严重,相关研究人员尝试过分段线性光压解算、脉冲经验力等方法提高定轨精度,对动零转换期间的定轨结果有较为明显的改善。目前,关于北斗卫星定轨研究多是基于经验型模型,系统性地进行综合解析建模的研究较少。
本文基于光压辐射的物理机理、北斗卫星物理参数和姿态控制模式,建立具有明确物理意义的光压辐射综合解析模型,以国际激光测距服务中心公布的激光测距数据和重叠弧段内符合两种方式,通过精密定轨对综合解析模型精度作了验证;在综合解析模型的基础上,基于卫星角动量守恒定理和在轨遥测参数的变化,提出了综合解析模型结合经验修正项Da、Ya改善精密定轨精度的方法,可实现厘米级的精密定轨精度,显著改善了卫星精密定轨效果。
1 光压摄动解析建模符合广义光压辐射机理的摄动源,除了直接太阳光外,还有自身热辐射、地球反照、大功率天线电磁辐射[20]。
1.1 光压辐射理论基础光压摄动,是光子撞击卫星星体和太阳帆板后被反射或被吸收后的能量转化。爱因斯坦狭义相对论给出了能量、质量、动量之间的关系,此为计算单位面元光压辐射力的物理基础
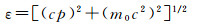 (1)
(1)
式中,ε为辐射能量;c为光速;p为动量;m0为光子质量。
文献[21-22]对光子撞击物体表面产生光压辐射力的物理机理作了详细的分析,本文不再进行分析,式(2)、式(3)给出了一束光照在物体表面产生的法向和切向光压力
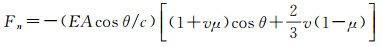 (2)
(2)
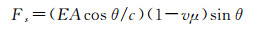 (3)
(3)
式中,Fn和Fs分别为法向和切向力;E=1350 W/m2为太阳辐射常数;A为被照射面元面积;θ为入射角;c为光速;v为反射率;μ为镜面系数。
其中,地球反照光与太阳光类似,二者辐射强度不同。地球反照光辐射分为红外辐射和光学辐射两部分,红外辐射与轨道高度相关,地球同步卫星轨道高度的红外辐射强度约为21~49 W/m2,光学辐射只存在被太阳照亮的半球。
热辐射是卫星与空间环境的热交换方式,航天器通过把热负荷散发到外部环境,与宇宙热辐射背景保持热平衡[23]。热辐射能在卫星与环境之间交换是建立热辐射模型的基础[24],斯特藩-玻尔兹曼定律给出了辐射能量公式[25]
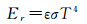 (4)
(4)
式中,Er是热辐射能;ε是材料发射率;σ=5.669 9×10-8 W/(m2·K)4是斯特藩-玻尔兹曼常数;T为表面材料温度。
热辐射引起的热辐射力为
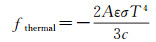 (5)
(5)
式中,fthermal是热辐射力,其他参数含义同上。
导航天线90%以上的功率集中在天线辐射方向,电磁辐射力由有效全向辐射功率EIRP决定。
1.2 综合解析建模方法卫星本体系作为综合解析建模的基准坐标系,其原点与卫星几何中心重合,Z轴平行于天线视场中心轴,Y轴沿某个太阳帆板展开,X轴与Y、Z轴满足右手旋转准则。在星本体系中,综合考虑直接太阳光、卫星自身热辐射、地球反照光、天线电磁辐射的影响,对4种因素进行统一综合建模。
对直接太阳光压、地球反照光解析建模,要考虑的卫星工程参数包括卫星表面部件安装信息、形状尺寸、表面材料反射率、镜面系数、卫星姿态控制规律、卫星质量等。对卫星自身热辐射进行解析建模,涉及卫星表面三维构型、表面材料红外半球发射率及表面部件的外表面温度。天线电磁辐射与天线功率相关。光压摄动解析建模方法[6]在不同文章中均有介绍,本文不再赘述。
以北斗倾斜地球同步轨道(IGSO)卫星和中圆轨道(MEO)卫星为例,表面部件包括平面、圆柱面、圆锥面、抛物面等,涉及十多种表面材料。安装信息和尺寸面积取工程测量值,表面光学特性参数由地面标定。表 1给出了其中部分主要表面部件的参数信息。
| 表面部件 | 安装形状 | 尺寸面积/m2 | 材料 | 反射率 | 镜面系数 |
| +X面 | 固定平面 | 3.784 | 星表多层 | 初期0.64~末期0.35 | 0 |
| -X面 | 固定平面、圆锥形 | 3.784 | 星表多层 | 初期0.64~末期0.35 | 0 |
| +Y面 | 固定平面 | 4.4OSR:2.223其他为多层 | OSR | 初期0.865~末期0.715/0.75 | 1 |
| -Y面 | 固定平面 | 4.4OSR:2.18其他为多层 | OSR | 初期0.865~末期0.715/0.75 | 1 |
| +Z面 | 固定平面 | 3.44白漆:1.039其他为多层 | ACR-1防静电白漆 | 初期0.77~末期0.45 | 0 |
| -Z面 | 固定平面 | 3.44 | 星表多层 | 初期0.64~末期0.35 | 0 |
| 南北帆板 | 绕Y轴旋转 | 6×3.78 | 硅光电太阳电池片 | 0.28 | 0.85 |
卫星姿态控制模式和部件的运动规律决定了表面部件每个面元受照射或遮挡情况以及是否存在二次照射。北斗IGSO/MEO卫星存在两种姿态控制模式,一种是正常情况下的连续动态偏航控制,导航天线视场中心(即星本体的+Z面)对准地心,便于传送导航信号,卫星绕本体系+Z轴偏航旋转,使得太阳矢量在星本体系XOZ面内且+X轴指向太阳,太阳帆板绕Y轴转动,垂直于太阳光线以获得足够的能量;还有一种是当太阳矢量与轨道面夹角<4°且偏航角速度小于5°/s时,卫星绕+Z轴的旋转为0°,太阳帆板垂直于太阳矢量在轨道面内的投影,此时由于太阳与轨道面夹角较小,帆板没有完全垂直跟踪太阳仍能保证足够的能源供应,记为零偏航。北斗GEO卫星只有零偏航一种姿态控制模式。
利用光路跟踪解析建模法计算北斗3类卫星光压摄动加速度,并进行数学建模,分别针对连续动态偏航和零偏航两种姿控模式建立光压摄动综合解析模型,动偏期间取太阳矢量与星本体系+Z轴之间的夹角为自变量,记作θeps∈(0,180°)。零偏期间,取太阳矢量在本体系XOZ面的投影与星本体系+Z轴之间的夹角为自变量,同样记作θeps∈[0,360°]。
利用式(6)所示傅里叶多项式分别针对卫星本体系中XYZ 3方向光压摄动加速度的仿真结果进行数学建模。基于半年时间的仿真结果,傅里叶多项式的系数利用最小二乘拟合残差最小的方式获得,兼顾拟合精度和工程实际应用的便利性,综合解析模型的数学结果用3阶,即式(7)
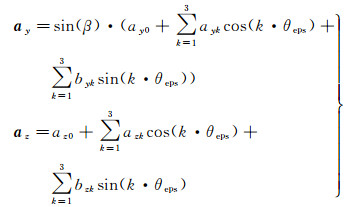 (7)
(7)
仿真结果表明,由热辐射引起的摄动加速度约为直接太阳光压摄动加速度的8%~9%。地球反照光压辐射的作用主要体现在Z轴方向,最大为直接太阳光压辐射的4%~5%,X向为直接太阳光压辐射的1%左右。经计算,天线辐射产生的摄动加速度相对更小,本文忽略不计。
2 综合解析模型的验证与优化为验证综合解析模型用于定轨计算的精度,本节通过SLR检核和重叠弧段来评估模型精度,即比较精密定轨计算结果与作为基准的标称轨道之间残差的均方根RMS评估模型精度。
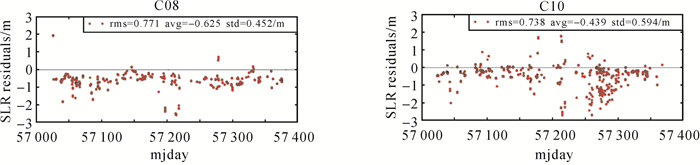
2.1 精密轨道确定验证分析卫星轨道动力学模型中光压摄动模型采用仿真所得的综合解析模型,地球引力场模型采用70×70的Joint Gravity Model 3[26],日、月引力通过初始星历计算日月位置。测试时间为2015年全年,即年积日1-365 d,全球测站数目约70个。每15 min计算一组轨道,计算其与标称轨道残差,全年每天输出一个残差统计值的均方根。定轨计算中,除光压模型参数外,还对卫星初始位置、速度进行估算。图 1为以C08、C10卫星为例,SLR检核残差均方根在2015年全年的分布情况,动态偏航期间全年轨道残差均方根的统计值分别为0.771和0.738 m,残差大于1.5 m作为异常值予以剔除。其中,零偏弧段精度稍差,C08和C10星零偏期间均方根的统计值分别为1.169、1.142 m,残差大于2.5 m作为异常值予以剔除。
|
| 图 1 综合解析模型用于精密定轨残差rms分布 Fig. 1 Residual distribution of precise orbit determination using comprehensive analysis model |
对于综合解析模型亚米级的SLR检核精度,认为误差源于两方面,一是解析建模的输入参数均为理论输入与实际在轨状态间不可避免地存在偏差,二是其他微小干扰项对精密轨道的影响没有被模型化。
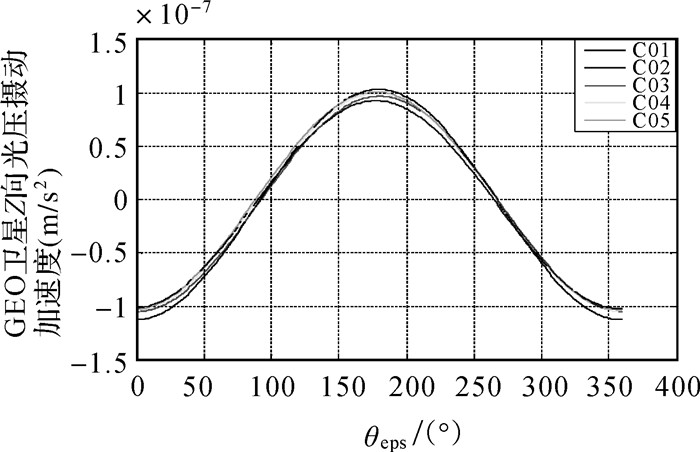
对此,根据事后精密星历反向估计与其相适应的综合解析模型(1阶)的最佳系数,计算结果表明,物理参数、轨道类型均相同的卫星,最佳光压模型系数仍存在一定差异。对于IGSO和MEO卫星中,同一轨道面内卫星间最佳估计系数接近一致,不同轨道面的系数间存在差异,说明光压摄动存在长周期项没有被模型化。同样的,不同GEO卫星间最佳估计参数也有所差异,图 2为5颗GEO卫星最佳估计系数的Z向摄动加速度。
|
| 图 2 北斗GEO卫星最佳估计系数的Z向光压加速度 Fig. 2 Optimal estimation of Z weight of SRP acceleration for GEO satellite |
2.2 经验项对光压模型的改进验证
为研究综合分析模型与在轨实际光压辐射之间的偏差,本节通过卫星姿态、反作用轮转速、磁场强度、推力器累积喷气时间等在轨遥测参数变化计算所受干扰力矩的变化,进而推算等效干扰力。假定卫星为一刚体,根据式(5)所示动量守恒定理,可求卫星等效干扰力矩
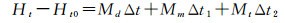 (5)
(5)
式中,Ht为t时刻整星角动量;Ht0为t0时刻整星角动量;Md为等效干扰力矩;Mm为磁力矩;Mt为推力器力矩;Δt=t-t0;Δt1为磁力矩器累积工作时间; Δt2为推力器累积工作时间。
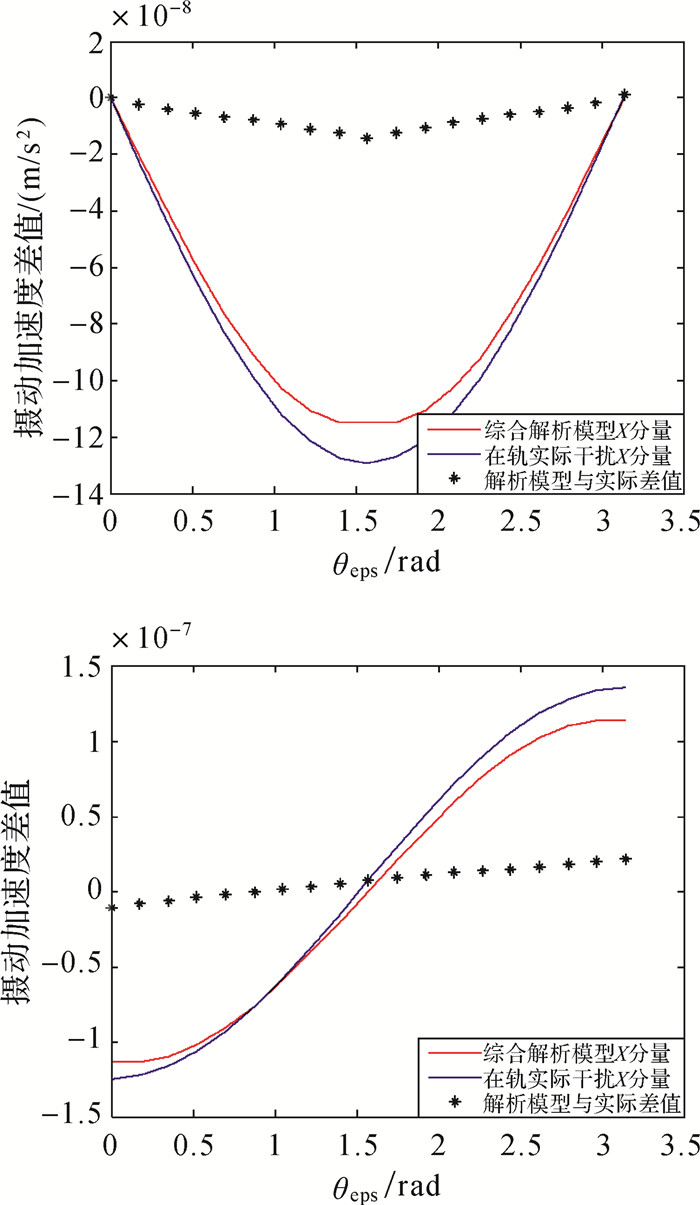
根据在轨遥测每5 min可求解一组绕星本体系XYZ 3方向的平均等效干扰力矩,假定此干扰力矩是由作用在星体表面的干扰力引起的,则可计算作用在卫星的干扰力与光压摄动综合分析模型间的差值。由此推得在星本体系中,在轨卫星所受干扰力除综合解析模型外,还存在一个X向和Z向残差,与θeps相关,可由卫星至太阳的D向常数表示,如图 3所示为一天内的差异分布。此外,Y向分量动偏期间仍存在。
|
| 图 3 综合解析模型与在轨遥测差 Fig. 3 The difference between comprehensive analysis model and in-orbit telemetry data |
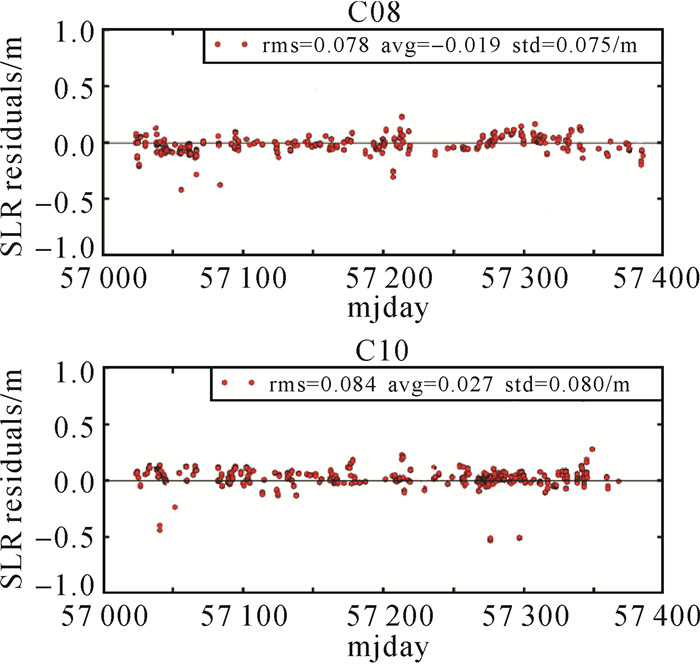
经验证计算,式(7)中3阶综合解析模型降为1阶傅里叶多项式(k=1),并增加Da和Ya两个常值经验修正项进行精密定轨计算,可以获得厘米级的SLR检核精度。图 4为以不同轨道面的C08、C10为代表,C08星和C10星精密定轨校验结果的rms值分别为0.078和0.084 m,残差大于0.5 m作为异常值予以剔除,相比综合解析模型定轨结果有非常明显的改善。此外,与C08星和C10星利用CODE经验模型的定轨残差rms值0.099、0.129 m相比,分别有0.021、0.045 m的改善。同样的方法对国际激光测距服务中心跟踪的北斗C01、C13卫星作精密定轨计算,rms值分别为0.26、0.05 m。
|
| 图 4 综合仿真模型+经验项精密定轨,SLR校核结果 Fig. 4 SLR verification of precise orbit determination using comprehensive analysis model and experiential parameters |
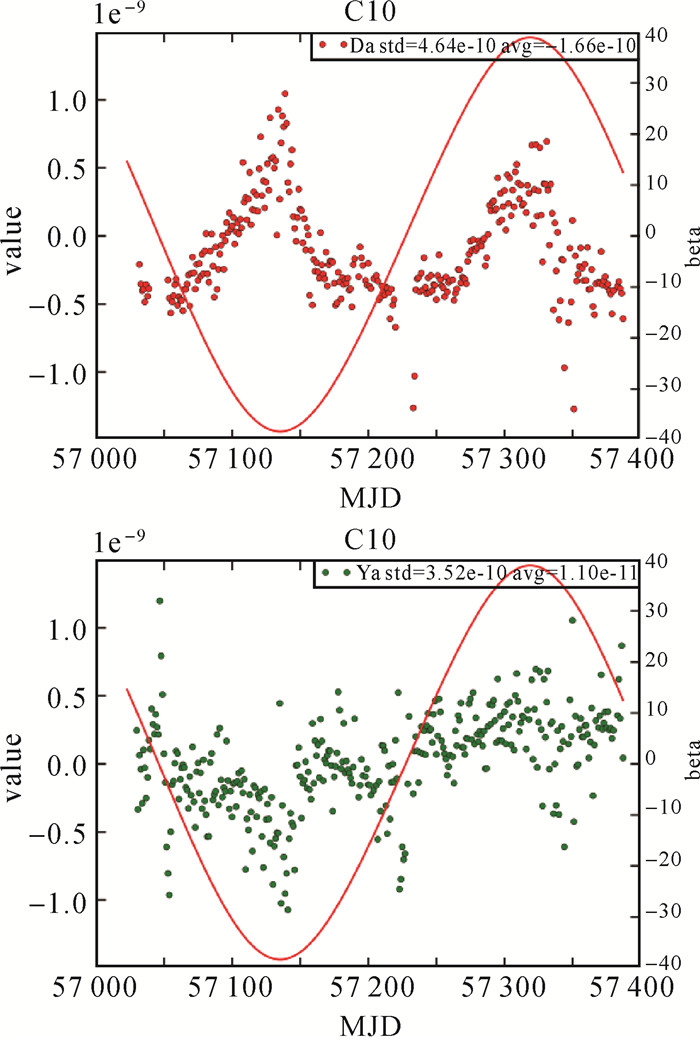
图 5为估计C10星Da、Ya在一年的变化。谱分析结果表明,经验修正项Da与太阳高度角β的-sin(β)呈现较强的相关性,修正项Ya一年内随机分布,没有特别的规律性。
|
| 图 5 C10星经验修正项Da、Ya一年内的变化 Fig. 5 Curve of empirical correction of Da and Ya for one year |
同样是利用综合解析模型加经验项修正项的方式对卫星进行定轨计算,在不考虑钟差的情况下,通过比较重叠弧段法向、切向、径向内符合精度评估模型定轨精度,北斗各卫星的重叠弧段等效URE精度见表 2。其中,GEO卫星精度为0.3 m左右,IGSO卫星为0.15 m左右,MEO卫星为厘米级。
| m | ||
| 卫星号 | 等效URE | 均值 |
| C01 | 0.439 | 0.344 |
| C02 | 0.218 | |
| C03 | 0.325 | |
| C04 | 0.408 | |
| C05 | 0.332 | |
| C06 | 0.193 | 0.179 |
| C07 | 0.172 | |
| C08 | 0.171 | |
| C09 | 0.204 | |
| C10 | 0.154 | |
| C11 | 0.040 | 0.043 |
| C12 | 0.042 | |
| C14 | 0.047 | |
3 结论
本文以北斗卫星为例,基于光压辐射的物理机理、卫星物理参数、姿态控制模式等卫星相关状态信息,建立了光压摄动综合解析模型,并用于精密定轨计算。定轨结果,通过与激光测距数据比较和重叠弧段自校两种评估方式,证明了综合解析模型可支撑分米级的定轨精度。
基于卫星角动量守恒定理和在轨遥测参数变化,推导计算了综合解析模型和实际在轨干扰力差异,提出了在综合解析模型基础上增加Da和Ya经验修正项进行精密定轨的方法。SLR检核结果表明,C08和C10星轨道残差的rms值分别为0.078和0.084 m,事后精密定轨精度可以达到厘米级,相比于CODE经验模型精度分别提高0.021、0.045 m,改善效果显著,全星座重叠弧段定轨精度在0.3 m以内。
| [1] |
杨元喜.
北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6.
YANG Yuanxi. Progress, contribution and challenges of Compass/Beidou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] |
杨元喜, 李金龙, 徐君毅, 等.
中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1734–1740.
YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass satellite navigation system to global PNT Users[J]. Chinese Science Bulletin, 2011, 56(21): 1734–1740. |
| [3] |
杨元喜, 李金龙, 王爱兵, 等.
北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81.
YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary assessment of the navigation and positioning performance of Beidou regional navigation satellite syste9m[J]. Science China Earth Sciences, 2014, 44(1): 72–81. |
| [4] |
刘林, 王海红, 胡松杰.
卫星定轨综述[J]. 飞行器测控学报, 2005, 24(2): 28–34.
LIU Lin, WANG Haihong, HU Songjie. Summary on satellite orbit determination[J]. Journal of Spacecraft TT&C Technology, 2005, 24(2): 28–34. |
| [5] |
李济生.
人造卫星精密轨道确定[M]. 北京: 解放军出版社, 1995: 1-5.
LI Jisheng. Satellite precision orbit determination[M]. Beijing: The People's Liberation Army Press, 1995: 1-5. |
| [6] |
陈秋丽, 陈忠贵, 王海红.基于导航卫星姿态控制规律的光压摄动建模方法[C]//第四届中国卫星导航学术年会论文集: (S3).武汉: [s.n.], 2013: 1-5. CHEN Qiuli, CHEN Zhonggui, WANG Haihong. Method of modeling solar radiation pressure based on attitude control law of navigation satellites[C]//The proceedings of CSNC2013. Wuhan: [s.n.], 2013: 1-5. |
| [7] |
许尤楠.
GPS卫星的精密定轨:模型、软件和测轨网布设研究[M]. 北京: 解放军出版社, 1989: 2-8.
XU Younan. Precise orbit determination of GPS satellite[M]. Beijing: The People's Liberation Army Press, 1989: 2-8. |
| [8] |
许其凤.
GPS卫星导航与精密定位[M]. 北京: 解放军出版社, 1994: 2-11.
XU Qifeng. Navigation and precise positioning of GPS satellite[M]. Beijing: The People's Liberation Army Press, 1994: 2-11. |
| [9] | BAR-SEVER Y E. A new model for GPS yaw attitude[J]. Journal of Geodesy, 1996, 70(11): 714–723. DOI:10.1007/BF00867149 |
| [10] |
陈俊平, 王解先.
GPS定轨中的太阳辐射压模型[J]. 天文学报, 2006, 47(3): 310–319.
CHEN Junping, WANG Jiexian. Solar radiation pressure models for the GPS satellites[J]. Acta Astronomica Sinica, 2006, 47(3): 310–319. DOI:10.3321/j.issn:0001-5245.2006.03.009 |
| [11] | FLIEGEL H F, GALLINI T E, SWIFT E R. Global positioning system radiation force model for geodetic applications[J]. Journal of Geophysical Research, 1992, 97(B1): 559–568. DOI:10.1029/91JB02564 |
| [12] |
赵庆海, 楼楠. T20光压模型及偏导数的推导[C/CD]//第二届中国卫星导航学术年会电子文集.上海: [s.n.], 2011: 1-4. ZHAO Qinghai, LOU Nan. The derive of partial derivative for solar radiation perturbation model of T20[C/CD]//The Proceedings of CSNC2011. Shanghai: [s.n.], 2011: 1-4. |
| [13] | RODRIGUEZ-SOLANO C J, HUGENTOBLER U, STEIGEN-BERGER P. Adjustable box-wing model for solar radiation pressure impacting GPS satellites[J]. Advances in Space Research, 2012, 49(7): 1113–1128. DOI:10.1016/j.asr.2012.01.016 |
| [14] | SPRINGER T A, BEUTLER G, ROTHACHER M. A new solar radiation pressure model for the GPS satellites in CODE IGS analysis center technical report[J]. Advances in Space Research, 1999(23): 673–676. |
| [15] | FLIEGEL H F, GALLINI T E. Solar force modeling of block ⅡR global positioning system satellites[J]. Journal of Spacecraft and Rockets, 1996, 33(6): 863–866. DOI:10.2514/3.26851 |
| [16] |
宋小勇, 毛悦, 贾小林.
BERNESE光压模型参数的统计分析[J]. 测绘科学, 2009, 34(3): 25–27.
SONG Xiaoyong, MAO Yue, JIA Xiaolin. Analysis of the parameter of BERNESE radiation force model by statistic method[J]. Science of Surveying and Mapping, 2009, 34(3): 25–27. |
| [17] | BAR-SEVER Y E. New and improved solar radiation pressure models for GPS satellites based on flight data[R]. Pasadena, CA: Jet Propulsion Laboratory, 1997: 1-33. |
| [18] | BAR-SEVER Y, KUANG D. New empirically derived solar radiation pressure model for global positioning system satellites[R]. Pasadena, CA: Jet Propulsion Laboratory, 2004: 42-159. |
| [19] | BAR-SEVER Y, KUANG D. New empirically derived solar radiation pressure model for global positioning system satellites during eclipse seasons[R]. Pasadena, CA: Jet Propulsion Laboratory, 2005: 42-160. |
| [20] | ZIEBART M, ADHYA S, SIBTHORPE A, et al. Combined radiation pressure and thermal modelling of complex satellites:algorithms and on-orbit tests[J]. Advances in Space Research, 2005, 36(3): 424–430. DOI:10.1016/j.asr.2005.01.014 |
| [21] |
胜照宇.太阳帆航天器的有限元仿真[D].合肥: 中国科学技术大学, 2008: 8-15. SHENG Zhaoyu. Analysis about solar sail[D]. Hefei: University of Science and Technology of China, 2008: 8-15. |
| [22] | ZIEBART M. Generalized analytical solar radiation pressure modeling algorithm for spacecraft of complex shape[J]. Journal of Spacecraft and Rockets, 2004, 41(5): 840–848. DOI:10.2514/1.13097 |
| [23] | VIGUE Y, SCHUTZ B E, ABUSALI P A M. Thermal force modeling for global positioning system satellites using the finite element method[J]. Journal of Spacecraft and Rockets, 1994, 31(5): 855–859. DOI:10.2514/3.26523 |
| [24] | VIGUE Y, SCHUTZ R E, ABUSALI P A M. Improved thermal force modeling for GPS satellites[R].[S.l.]: STI, 1993: 32-34. |
| [25] | TSAI J R. Overview of satellite thermal analytical model[J]. Journal of Spacecraft and Rockets, 2004, 41(1): 120–125. DOI:10.2514/1.9273 |
| [26] | TAPLEY B D, WATKINS M M, RIES J C, et al. The joint gravity model 3[J]. Journal of Geophysical Research, 1996, 101(B12): 28029–28049. DOI:10.1029/96JB01645 |


