2. 西安测绘研究所, 陕西 西安 710054;
3. 地理信息工程国家重点实验室, 陕西 西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
似大地水准面是正常高高程系统的基准面,其与参考椭球面之间的距离为高程异常,与地面点间的距离为正常高。我国使用正常高系统,高精度地确定似大地水准面是国家基础测绘中的一项重要工程[1-4]。目前解算(似)大地水准面的理论方法主要有Stokes理论和Molodensky理论两类。Stokes理论要求边界面外不存在地形质量,为了满足这一条件,可使用Helmert第二压缩法将边界面外的地形压缩成覆盖在边界面上的质量薄膜,使用Helmert第二压缩法的Stokes理论简称为Stokes-Helmert理论[5-6]。美国和加拿大分别基于Stokes-Helmert理论构建了重力大地水准面USGG2009[7]、CGG2010[8]。我国基于Stokes-Helmert理论构建的重力似大地水准面为CNGG2011[9]。
Stokes理论和Molodensky理论均属于第三边值理论,其使用的高程系统分别为正高和正常高。进入空间大地测量时代以来,以前不可直接测量的大地高成了可观测量,这为以重力扰动和大地高为输入量的第二大地边值问题的研究和应用提供了可能。第二边值理论使用Hotine积分进行边值解算,因此第二边值理论也称为Hotine理论。Hotine理论同样要求边界面外不存在地形质量,为此,可使用Helmert第二压缩法进行地形归算。类似于Stokes-Helmert理论的定义,使用Helmert第二压缩法的Hotine理论简称为Hotine-Helmert理论。目前国内外对Hotine-Helmert边值理论的研究与应用较少,尽管Stokes-Helmert边值理论成果为Hotine-Helmert理论提供了很好的借鉴,但不能简单地照搬Stokes-Helmert理论方法,否则忽视了这两种边值问题本身存在的差异。
在第二边值理论方面,文献[10]提出重力扰动较重力异常更易于重力场计算,由于GPS边值属于固定边值问题,因而Runge和Walsh逼近理论更加严格有效。文献[11-13]研究了以地球自然表面为边界面的GPS/重力边值问题并给出了求解高程异常的实用计算公式。文献[14]详细地阐述了以地心参考椭球面为边界面的第二大地边值问题,并提出了将Helmert第二压缩法引入第二边值问题的思路。本文的研究和试验是在文献[14]的基础上展开的。
地形直接、间接影响的计算是Hotine-Helmert边值理论的关键步骤。直接影响可将重力扰动转化为Helmert重力扰动,而间接影响能够将Helmert(似)大地水准面恢复为真实的(似)大地水准面。本文首先介绍了直接、间接影响定义及算法,然后推导了Hotine-Helmert边值解算模型的计算公式,指出了Hotine-Helmert边值理论与Stokes-Helmert边值理论的不同之处。此外,为了控制传统截断核函数的远区截断误差在截断阶附近波动较大的现象(Gibbs现象),文中引入了一种低阶修正的截断Hotine核函数。最后为了证明Hotine-Helmert边值解算模型的有效性,本文根据Hotine-Helmert解算模型求解了试验区重力似大地水准面。
1 地形直接、间接影响地形直接、间接影响的计算是基于Helmert第二压缩法的边值理论(Stokes-Helmert理论和Hotine-Helmert理论)区别于其他边值理论的关键技术环节,因此下文首先介绍地形直接、间接影响的定义及算法。在Hotine-Helmert与Stokes-Helmert边值问题中地形影响的算法是相同的,区别在于使用的高程数据分别为大地高和正高。
将边界面(Stokes-Helmert边值问题的边界面为大地水准面,而Hotine-Helmert边值问题的边界面为参考椭球面)外真实地形质量产生的引力位记为Vt,其计算公式为
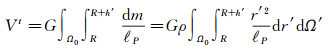 (1)
(1)
式中,G为牛顿引力常数;dm为质量单元;Ω0代表全球域;ρ为地形密度;R为地球平均半径;h′为积分流动点的高程;r′为积分流动点的地心向径;ℓP的计算公式为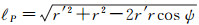
利用Helmert第二压缩法将边界面外的地形压缩成覆盖在边界面上的质量薄层时,需依据一定的压缩准则,本文以质量守恒原则为例进行说明。当遵循质量守恒原则时,压缩面密度σ′为[5]
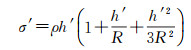 (2)
(2)
此时边界面外压缩地形产生的引力位Vc的计算公式为
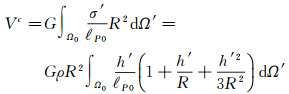 (3)
(3)
式中,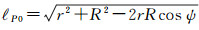
地形压缩时,地形质量的移动使地表重力值发生的变化称为地形压缩对重力的直接影响δA,使大地水准面/似大地水准面发生的变化称为地形压缩对大地水准面高/高程异常的间接影响,其中对高程异常的间接影响记为δζ。根据直接、间接影响与残余地形位的关系,可得出δA、δζ的传统积分算法为[5, 15-16]
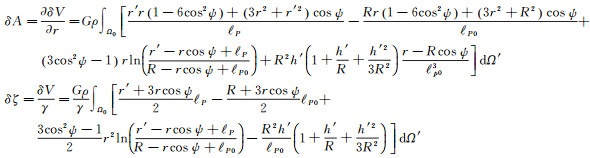 (4)
(4)
式中, γ是地面点的正常重力。式(4)中地形影响为非解析的二重积分形式,可类似于地形改正的棱柱模型算法[17-20],使用棱柱模型计算近区直接、间接影响[21],具体为
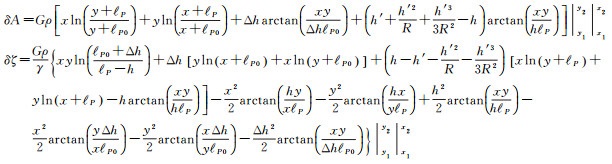 (5)
(5)
式中,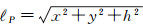
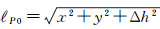
扰动位T为重力位W与正常重力位U之差
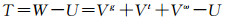 (6)
(6)
式中,Vω为地球离心位;Vg为边界面内质量产生的引力位;Vt的含义同式(1)。地形压缩后扰动位转化为Helmert扰动位TH,则有
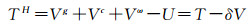 (7)
(7)
根据扰动位与重力扰动δg的关系式δg=-∂T/∂r,可得出Helmert重力扰动δgH
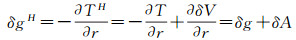 (8)
(8)
由式(8)可看出,Helmert重力扰动实际上是重力扰动与直接影响之和,因此直接影响起到将重力扰动转化为Helmert重力扰动的作用,该过程即为重力扰动的“Hermert化”。在Stokes-Helmert边值理论中,重力异常的“Helmert化”算法为
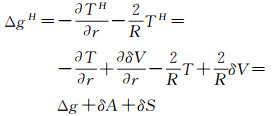 (9)
(9)
式中, δS=2δV/R为地形压缩对重力的次要间接地形影响。对比式(8)、式(9)可知,Hotine-Helmert理论中重力扰动的“Helmert化”与Stokes-Helmert理论中重力异常的“Helmert化”相比,无须计算地形压缩对重力的次要间接地形影响,因此Hotine-Helmert理论模型比Stokes-Helmert理论模型更加简单。
式(8)中Helmert重力扰动与Helmert扰动位的关系式δgH=-∂TH/∂r即为第二边值问题在Helmert空间的边值条件。由于地形压缩使地面与边界面之间已不存在地形质量,即压缩后的Helmert空间是调和的,因此可进行Hotine积分。根据第二边值理论,对Helmert重力扰动应用Hotine积分即可得到Helmert高程异常ζH
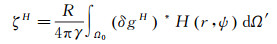 (10)
(10)
式中, (δgH)*表示参考椭球面上的Helmert重力扰动,通过对地面Helmert重力扰动进行向下延拓[22-25]得到。H(r, ψ)为扩展Hotine积分核函数[26-27]
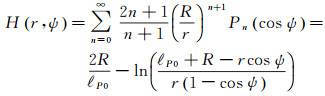 (11)
(11)
式中, 球心距ℓP0的含义同式(3),Pn为勒让德函数。Helmert高程异常与真实空间的高程异常ζ的关系式为
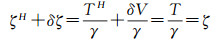 (12)
(12)
从式(12)可看出,间接影响δζ能够将Helmert高程异常ζH恢复为真实空间的高程异常ζ,该过程为高程异常的“去Helmert化”。综合式(8)、式(12)可得出,直接、间接影响的作用可理解为“空间转换”:直接影响将重力扰动从真实空间转换为Helmert空间,而间接影响将解算的高程异常从Helmert空间恢复到真实空间。式中,Hotine积分理论上要求全球积分。为了避免全球积分,实际计算时通常采用移去恢复技术。在移去恢复模式下,确定似大地水准面的Hotine-Helmert边值解算模型为
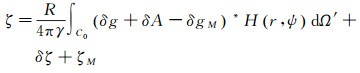 (13)
(13)
式中,C0为Hotine积分的近区积分范围;δgM为模型重力扰动;ζM为模型高程异常。移去恢复模式下,Hotine积分核通常采用下列截断形式
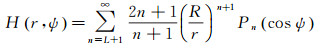 (14)
(14)
Hotine截断积分核是从标准Hotine积分核中除去一定的低阶勒让德级数序列得到的,式(14)中L为除去的勒让德级数的最高阶数。同Stokes截断积分核一样,Hotine截断积分核在截断阶处存在谱泄露现象(Gibbs现象)[28],影响了边值解算的精度。为了改善这一现象,加拿大重力大地水准面模型CGG2010[8]中采用了一种修正形式的Stokes截断核函数。由于Hotine积分核与Stokes积分核的频谱特性相近,且阶数n越大,二者的各阶球谐项差异越小,因此完全可以将Stokes截断核函数的修正方法应用于Hotine截断核函数。低阶修正的Hotine截断核函数的定义为[21]
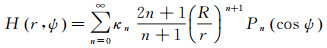 (15)
(15)
式中,κn是一种平滑因子(或称为修正因子),可由不同形式的函数构造(与模型重力数据与实测重力数据的相对精度有关),其中余弦函数构造的平滑因子为
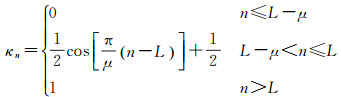 (16)
(16)
式中,μ为低阶修正带宽(阶数)。
3 试验与分析下面根据本文构建的Hotine-Helmert边值解算模型求解试验区重力似大地水准面。试验区地形采用SRTM数据,其高程基准为EGM96大地水准面,通过将SRTM数据与EGM96大地水准面高相加将其转化为大地高数据。试验区重力点范围103.5°-118.5°E、23.5°-36.5°N,共计147 025个(为了比较不同Hotine积分半径的边值解算精度,本试验收集的离散重力点范围稍大。实际上最终使用的离散重力点范围为105.5°-116.5°E,25.5°-34.5°N,共计70 379个)。首先将实测重力离散点格网化为104°-118°E、24°-36°N范围(Hotine积分半径为1°时相应的格网化范围为106°-116°E、26°-34°N)、30″×30″分辨率的重力扰动数据,然后将其平均为1.5′×1.5′分辨率的格网重力扰动。解算的重力似大地水准面范围为108°-114°E、28°-32°N,该区域位于我国中部,区域地形起伏较为明显,因此具有一定的代表性。
为了说明本文构建的Hotine-Helmert边值解算模型的实际应用效果,本试验首先利用试验区GPS水准点数据对目前既有的几种重力场模型进行精度检核,然后基于选定的参考重力场模型进行Hotine-Helmert边值解算试验,最后利用GPS水准点对解算的重力似大地水准面进行精度检核。
3.1 试验区重力场模型的精度课题组搜集了108°-114°E、28°-32°N范围的GPS水准检核点,共计68个。利用此68个GPS水准点对EIGEN-GL04C、EGM2008、EIGEN-6C4等重力场模型进行精度检核,其结果如表 1所示。
| m | ||||||
| 模型 | 阶数 | 最小值 | 最大值 | 平均值 | 均方根 | 标准差 |
| EIGEN-GL04C | 360 | -1.277 | 1.398 | 0.124 | 0.431 | 0.416 |
| EGM2008 | 360 | -1.649 | 0.350 | -0.304 | 0.422 | 0.295 |
| EIGEN-6C4 | 360 | -1.027 | 0.869 | 0.102 | 0.298 | 0.282 |
| EGM2008 | 2190 | -0.703 | -0.115 | -0.300 | 0.318 | 0.106 |
| EIGEN-6C4 | 2190 | -0.109 | 0.300 | 0.106 | 0.132 | 0.078 |
表 1中EIGEN-GL04C模型在试验区的精度最差,EGM2008模型精度不及EIGEN-6C4模型精度高。2190阶的EIGEN-6C4模型是目前精度最高的重力场模型:均方根±13.2 cm、标准差±7.8 cm。由于2190阶的EIGEN-6C4模型已达到较高的精度,若基于该模型计算似大地水准面,较难反映实测数据和算法本身的应用效果。为此,本文移去恢复采用的参考模型为EIGEN-6C4模型的前360阶,其均方根为±29.8 cm,而标准差为±28.2 cm。
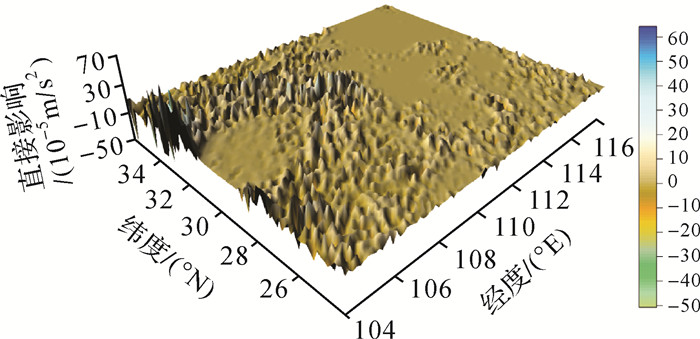
3.2 直接、间接影响的计算下面计算地形直接、间接影响,两种地形影响的积分半径均取1°。直接影响的区域范围为104°-118°E、24°-36°N(当Hotine积分半径为1°时实际使用的直接影响范围为106°-116°E、26°-34°N),与格网重力扰动范围一致。而间接影响的区域范围为108°-114°E、28°-32°N,与求解的高程异常范围一致。为了频谱一致,先计算30″×30″分辨率的格网直接、间接影响,然后将其平均为1.5′×1.5′分辨率。图 2、图 3所示为直接影响区域范围的地形分布及其量值。
|
| 图 2 直接影响 Fig. 2 The direct effect |
|
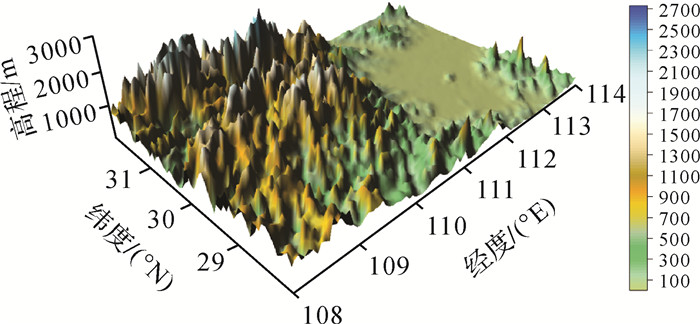
| 图 3 间接影响区域地形分布 Fig. 3 Terrain distribution of the indirect effect |
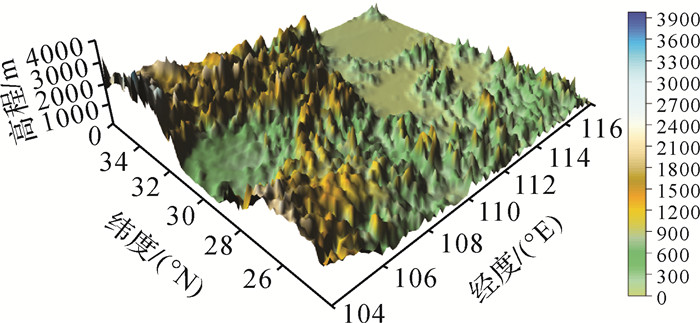
图 1中直接影响区域海拔最高4154 m、平均599 m,该区域直接影响最小-71×10-5 m/s2、最大91×10-5 m/s2、平均0.65×10-5 m/s2。对比图 1、图 2可看出,直接影响的分布与高程具有一定相关性,海拔较低处直接影响起伏的量级较小,而海拔较高处起伏的量级较大。图 3、图 4分别为间接影响计算区域的地形分布及其量值。
|
| 图 1 直接影响区域地形分布 Fig. 1 Terrain distribution of the direct effect |
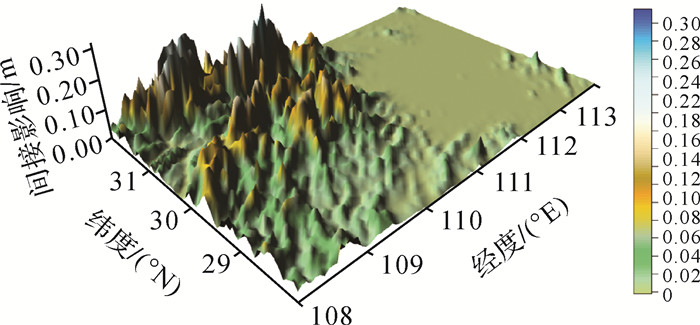
|
| 图 4 间接影响 Fig. 4 The indirect effect |
图 3中,间接影响区域海拔最高2724 m、平均506 m,该区域间接影响最小-0.003 m、最大0.32 m、平均0.026 m。对比图 3、图 4可看出,间接影响与地形具有较强的相关性,间接影响的起伏与地形起伏基本一致,且间接影响的量值基本为正值。
3.3 基于低阶修正的Hotine截断核函数的边值解算试验在上文直接、间接影响计算结果的基础上,下面使用不同修正带宽的低阶修正Hotine核函数展开边值解算的试验,并利用GPS水准点对求解的似大地水准面进行精度检核。精度指标包括均方根和标准差两项,其中均方根包含系统误差,而标准差指标除去了系统偏差。似大地水准面的分辨率为1.5′×1.5′。表 2统计了Hotine积分半径取1°时不同低阶修正带宽求解的似大地水准面精度(计算过程中向下延拓半径为1°),其中Hotine截断核函数的参数L(移去的最高勒让德阶数)设为360。
| m | |||||
| 修正带宽 | 最小值 | 最大值 | 平均值 | 均方根 | 标准差 |
| 0 | -0.069 | 0.351 | 0.122 | 0.147 | 0.083 |
| 180 | -0.007 | 0.313 | 0.143 | 0.158 | 0.066 |
| 270 | 0.005 | 0.266 | 0.141 | 0.153 | 0.059 |
| 360 | -0.021 | 0.197 | 0.104 | 0.115 | 0.048 |
从表 2可看出,采用不同修正带宽计算的似大地水准面精度存在一定的差异。当使用传统的截断核函数(即低阶修正带宽为0)时,似大地水准面精度为±14.7 cm(均方根)、±8.3 cm(标准差)。当低阶修正带宽为360阶时解算的似大地水准面精度最高,其精度为±11.5 cm(均方根)、±4.8 cm(标准差)。
表 3统计了Hotine积分半径为3°时不同低阶修正带宽计算的似大地水准面精度。
| m | |||||
| 修正带宽 | 最小值 | 最大值 | 平均值 | 均方根 | 标准差 |
| 0 | -0.028 | 0.340 | 0.130 | 0.150 | 0.076 |
| 180 | -0.021 | 0.264 | 0.130 | 0.144 | 0.064 |
| 270 | -0.013 | 0.243 | 0.128 | 0.140 | 0.057 |
| 360 | 0.001 | 0.212 | 0.119 | 0.128 | 0.049 |
对比表 2、表 3可看出,使用传统的截断核函数(即低阶修正带宽为0)时,3°Hotine积分半径较1°半径计算的似大地水准面的精度有一定的改善;但使用低阶修正的核函数时,3°与1°Hotine积分半径计算的似大地水准面精度的改善程度不明显。由于积分半径越大,实测重力数据的使用率越低,因此本文选择1°Hotine积分半径解算似大地水准面。
在上述试验的基础上,本文以2190阶EIGEN-6C4模型为参考场解算似大地水准面。表 4统计了不同低阶修正带宽下解算的似大地水准面精度,Hotine积分半径取1°,本试验将Hotine截断核函数的参数L取为2190。
| m | |||||
| 修正带宽 | 最小值 | 最大值 | 平均值 | 均方根 | 标准差 |
| 0 | -0.049 | 0.316 | 0.120 | 0.139 | 0.071 |
| 180 | -0.011 | 0.294 | 0.142 | 0.156 | 0.064 |
| 270 | 0.002 | 0.258 | 0.141 | 0.152 | 0.057 |
| 360 | -0.016 | 0.191 | 0.104 | 0.114 | 0.047 |
| 540 | -0.230 | 0.124 | -0.022 | 0.076 | 0.073 |
从表 4中可看出,当采用2190阶EIGEN-6C4模型作为参考场时,低阶修正的Hotine截断核函数的修正带宽取360阶时解算的似大地水准面精度最高。对比表 2、表 4可知,使用传统截断核函数(即低阶修正带宽为0)时,以2190阶EIGEN-6C4模型作为参考模型时似大地水准面精度(±7.1 cm)较360阶EIGEN-6C4模型作为参考模型时似大地水准面精度(±8.3 cm)有一定的改善;但使用360阶修正带宽的低阶修正核函数时,使用两种参考场解算的似大地水准面精度相差不大(分别±4.7 cm与±4.8 cm)。这是由于传统截断核函数在截断阶附近存在Gibbs现象使其附近阶的高程异常精度较低,当L取2190时,Gibbs现象出现在2190阶附近,其对精度的影响远小于L取360的情形(高程异常低频信息多、高频信息少);而当使用低阶修正的核函数时,Gibbs现象得到有效的控制,此时L取2190或360对边值解算精度的影响不大。
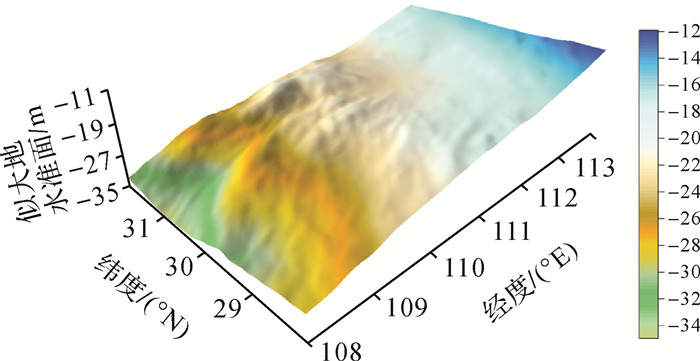
根据以上分析,本文以Hotine积分半径取1°、参考模型为EIGEN-6C4模型的前360阶、核函数低阶修正带宽为360阶条件下计算的重力似大地水准面为最终确定的重力似大地水准面,图 5为其示意图。
|
| 图 5 重力似大地水准面 Fig. 5 The gravimetric quasi-geoid |
本文根据Hotine-Helmert边值解算模型,基于精度为±28.2 cm的参考重力场得到了我国中部6°×4°区域范围内±4.8 cm精度的似大地水准面,明显优于试验区目前重力场模型的最高精度(±7.8 cm),说明本文构建的Hotine-Helmert边值解算模型是比较有效的。
4 结论本文首先介绍了地形直接、间接影响的定义与算法,在此基础上构建了Hotine-Helmert边值问题的解算模型,然后引入了一种低阶修正的截断Hotine核函数以控制传统截断核函数的Gibbs现象。基于本文构建的Hotine-Helmert边值解算模型,本文以EIGEN-6C4重力场模型前360阶作为参考模型(其精度为±28.2 cm),构建了我国中部地区精度为±4.8 cm的1.5′×1.5′分辨率的重力似大地水准面,优于试验区目前的最高重力场模型精度(±7.8 cm),证明了本文提出的Hotine-Helmert边值解算模型的应用效果较好。本试验的大地高数据是由SRTM数据与EGM96模型大地水准面高组合而成的,随着GPS大地高测量精度的提高和应用的普及,Hotine-Helmert边值解算模型将有更加广阔的应用前景。
| [1] |
管泽霖, 管铮, 黄谟涛, 等.
局部重力场逼近理论和方法[M]. 北京: 测绘出版社, 1997.
GUAN Zelin, GUAN Zheng, HUANG Motao, et al. Theory and method of regional gravity field approximation[M]. Beijing: Surveying and Mapping Press, 1997. |
| [2] |
许厚泽.
关于高程系统的思考[J]. 地理空间信息, 2016, 14(1): 1–3.
XU Houze. Consideration on the height system[J]. Geospatial Information, 2016, 14(1): 1–3. DOI:10.3969/j.issn.1672-4623.2016.01.001 |
| [3] |
吴晓平.
似大地水准面的定义及在空中测量中涉及的问题[J]. 测绘科学, 2006, 31(6): 24–25.
WU Xiaoping. Title definition of quasi-geoid and some questions encountered in airborne gravimetry[J]. Science of Surveying and Mapping, 2006, 31(6): 24–25. DOI:10.3771/j.issn.1009-2307.2006.06.004 |
| [4] |
李建成.
我国现代高程测定关键技术若干问题的研究及进展[J]. 武汉大学学报(信息科学版), 2007, 32(11): 980–987.
LI Jiancheng. Study and progress in theories and crucial techniques of modern height measurement in China[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11): 980–987. |
| [5] | MARTINEC Z. Boundary-value problems for gravimetric determination of a precise geoid[M]. Berlin: Springer, 1998. |
| [6] |
荣敏. Stokes-Helmert方法确定大地水准面的理论与实践[D].郑州: 信息工程大学, 2015. RONG Min. Stokes-Helmert method for geoid determination[D]. Zhengzhou: Information Engineering University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-90005-1016058463.htm |
| [7] | WANG Y M, SALEH J, LI X, et al. The US gravimetric geoid of 2009(USGG2009):model development and evaluation[J]. Journal of Geodesy, 2012, 86(3): 165–180. DOI:10.1007/s00190-011-0506-7 |
| [8] | HUANG J L, VÉRONNEAU M. Canadian gravimetric geoid model 2010[J]. Journal of Geodesy, 2013, 87(8): 771–790. DOI:10.1007/s00190-013-0645-0 |
| [9] |
李建成.
最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651–660, 669.
LI Jiancheng. The recent Chinese terrestrial digital height datum model:gravimetric quasi-geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651–660, 669. |
| [10] |
吴晓平, 李姗姗, 张传定.
扰动重力边值问题与实际数据处理的研究[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 73–78.
WU Xiaoping, LI Shanshan, ZHANG Chuanding. Problem of the boundary value of disturbing gravity and practical data processing[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 73–78. |
| [11] |
李斐, 陈武, 岳建利.
GPS在物理大地测量中的应用及GPS边值问题[J]. 测绘学报, 2003, 32(3): 198–203.
LI Fei, CHEN Wu, YUE Jianli. Physical geodesy with GPS[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 198–203. DOI:10.3321/j.issn:1001-1595.2003.03.003 |
| [12] |
李斐, 陈武, 岳建利.
GPS/重力边值问题的求解及应用[J]. 地球物理学报, 2003, 46(5): 595–599.
LI Fei, CHEN Wu, YUE Jianli. On solution and application of GPS/gravity boundary value problem[J]. Chinese Journal of Geophysics, 2003, 46(5): 595–599. DOI:10.3321/j.issn:0001-5733.2003.05.004 |
| [13] |
李斐, 岳建利, 张利明.
应用GPS/重力数据确定(似)大地水准面[J]. 地球物理学报, 2005, 48(2): 294–298.
LI Fei, YUE Jianli, ZHANG Liming. Determination of geoid by GPS/gravity data[J]. Chinese Journal of Geophysics, 2005, 48(2): 294–298. DOI:10.3321/j.issn:0001-5733.2005.02.009 |
| [14] |
魏子卿.
以地心参考椭球面为边界面的第二大地边值问题引论[J]. 测绘科学与工程, 2015, 35(1): 1–6.
WEI Ziqing. Introduction to the second geodetic boundary-value problem with the geocentric reference ellipsoidal surface as the boundary[J]. Geomatics Science and Engineering, 2015, 35(1): 1–6. |
| [15] | SJÖBERG L E. Topographic effects by the Stokes-Helmert method of geoid and quasi-geoid determinations[J]. Journal of Geodesy, 2000, 74(2): 255–268. DOI:10.1007/s001900050284 |
| [16] | WANG Y. Precise computation of the direct and indirect topographic effects of Helmert's second method of condensation using SRTM30 digital elevation model[J]. Journal of Geodetic Science, 2011, 1(4): 305–312. |
| [17] |
郭春喜, 王惠民, 王斌.
全国高分辨率格网地形和均衡改正的确定[J]. 测绘学报, 2002, 31(3): 201–205.
GUO Chunxi, WANG Huimin, WANG Bin. Determination of high resolution grid terrain and isostatic corrections in all China area[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 201–205. DOI:10.3321/j.issn:1001-1595.2002.03.004 |
| [18] |
罗志才, 陈永奇, 宁津生.
地形对确定高精度局部大地水准面的影响[J]. 武汉大学学报(信息科学版), 2003, 28(3): 340–344.
LUO Zhicai, CHEN Yongqi, NING Jinsheng. Effect of terrain on the determination of high precise local gravimetric geoid[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3): 340–344. |
| [19] | FORSBERG R. A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modeling[R]. Columbus(Ohio): Ohio State University, 1984. |
| [20] |
马健, 魏子卿, 沈忱, 等.
地形改正与地形直接影响的转化关系[J]. 测绘科学技术学报, 2017, 34(3): 245–250.
MA Jian, WEI Ziqing, SHEN Chen, et al. Transformation relation between the topographic correction and the direct topographic effect[J]. Journal of Geomatics Science and Technology, 2017, 34(3): 245–250. |
| [21] |
马健. Hotine-Helmert边值问题确定似大地水准面的理论与方法[D].郑州: 信息工程大学, 2018. MA Jian. Theory and methods of the Hotine-Helmert boundary value problem for the determination of the quasi-geoid[D]. Zhengzhou: Information Engineering University, 2018. |
| [22] |
刘敏, 黄谟涛, 欧阳永忠, 等.
顾及地形效应的重力向下延拓模型分析与检验[J]. 测绘学报, 2016, 45(5): 521–530.
LIU Min, HUANG Motao, OUYANG Yongzhong, et al. Test and analysis of downward continuation models for airborne gravity data with regard to the effect of topographic height[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 521–530. DOI:10.11947/j.AGCS.2016.20150453 |
| [23] |
翟振和, 王兴涛, 李迎春.
解析延拓高阶解的推导方法与比较分析[J]. 武汉大学学报(信息科学版), 2015, 40(1): 134–138.
ZHAI Zhenhe, WANG Xingtao, LI Yingchun. Solution and comparison of high order term of analytical continuation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 134–138. |
| [24] | WEI Ziqing. High-order radial derivatives of harmonic function and gravity anomaly[J]. Journal of Physical Science and Application, 2014, 4(7): 454–467. |
| [25] |
马健, 魏子卿, 任红飞, 等.
顾及远区影响的向下延拓实用算法[J]. 地球物理学进展, 2018, 33(2): 498–502.
MA Jian, WEI Ziqing, REN Hongfei, et al. Practical algorithm of the downward continuation considering the far-zone effect[J]. Progress in Geophysics, 2018, 33(2): 498–502. |
| [26] |
李建成, 晁定波.
利用Poisson积分推导Hotine函数及Hotine公式应用问题[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 55–57.
LI Jiancheng, CHAO Dingbo. Derivation of Hotine function using poisson integral and application of Hotine formula[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 55–57. |
| [27] |
程芦颖.
不同扰动位泛函间的积分变换广义核函数[J]. 测绘学报, 2013, 42(2): 203–210.
CHENG Luying. General kernel functions based on integral transformation among different disturbing potential elements[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 203–210. |
| [28] | VANÍČEK P, FEATHERSTONE W E. Performance of three types of Stokes's kernel in the combined solution for the geoid[J]. Journal of Geodesy, 1998, 72(12): 684–697. DOI:10.1007/s001900050209 |


