2. 中国电子科技集团公司航天信息应用技术重点实验室, 河北 石家庄 050081
2. CETC Key Laboratory of Aerospace Information Applications, Shijiazhuang 050081, China
天线组阵技术随着人类探索外层空间而逐步发展起来,是未来深空通信的重要发展方向之一[1-2]。深空通信等技术的发展对天线的性能提出了更高的要求,尤其是要求天线的等效口径越来越大,而大天线结构和重量庞大,伺服驱动非常困难,天线组阵技术便应运而生[3]。天线组阵技术利用多台天线接收来自同一个深空探测器的下行信号或者向同一个深空探测器发射上行信号,通过信号合成提高信噪比,实现数据的上下行高速传输[4]。相比单台天线,天线组阵具有提升系统性能、增强可操作性、降低系统成本等明显优势[5]。
上行组阵是利用地面上分布的多个发射天线组成发射阵列,对同一目标发射信号,并调整各信号的时延、相位,使其在目标处实现同相合成,从而增强深空探测器接收信号的信噪比。为了实现各发射信号在目标处的同相合成,需要对上行天线阵进行精确标校[6]。
天线精确标校主要包括高精度测定天线旋转中心、相位中心等的位置及其实际运动规律。天线旋转中心[7]是指天线方位轴与俯仰轴的交点,如图 1(a)所示。天线相位中心是天线辐射电磁波等效的辐射源中心[8],从旋转中心沿天线指向(又称电轴或机械轴)移动固定距离即可得到相位中心,如图 1(b)所示。

|
| 图 1 天线旋转中心与相位中心 Fig. 1 Sketch map of antenna rotation center and phase center |
天线相位中心受到多种因素的影响而变化[9-11]。对于同一天线,由于自重变形和加工装配等原因,导致不同方位、俯仰角下的相位中心与旋转中心的几何关系发生变化。对于不同天线,同一方位、俯仰角引入的相位滞后也会不同。天线的机械和温度特性的差异以及其他环境因素也会造成相位误差。这些因素导致了相位中心随着方位、俯仰角的变化呈现出复杂的运动规律。
许多学者对天线精确标校问题进行了研究。关于天线旋转中心的标校,2006年,文献[12]采用旋转天线的观测方法,运用最小二乘曲线拟合得到旋转中心,外符合精度达到1 cm。2008年,文献[13]在上海天文台ϕ25 m射电天线归心测量中,对天线绕轴旋转时靶标运动的圆弧轨迹进行测量,然后通过圆拟合得到方位轴和俯仰轴,并取俯仰轴所在平面与方位轴交点为旋转中心,精度达到0.7 mm。文献[14-17]对并置站的本地连接测量提出了观测方法和精度要求。以上文献仅对旋转中心的测量方法进行了介绍,没有进一步描述相位中心与旋转中心的关系,难以为上行阵天线的相位改正提供参考。关于天线相位中心的标校,2008年,文献[18]以天线相位方向图实测数据为基础,通过改变参考点来精确测定相位中心,建立了相位偏差与相位中心位置偏差的关系,利用最小二乘法估算相位中心偏差,测量精度优于1 mm。2011年,文献[19]提出了一种根据相位测量值校准阵列天线相位中心的方法,运用最小二乘法计算出相位中心的精确值。2012年,文献[20]采用球面近场的相位中心测量方法,给出了相位中心的修正方法。上述方法都是基于天线近场或远场辐射理论来测定相位中心,而且得到的皆为单台天线之相位中心,无法利用这些方法标定多台天线相位中心之间的关系。
为精确标校上行阵天线相位中心及其相对位置关系以提升效能,本文提出一种新标校思路:综合应用空间大地测量技术和精密工程测量技术[21],统一各天线测量坐标系;顾及天线阵的工作场景,连续、均匀地选取特定的姿态并获取其实际的机械轴指向;利用多条机械轴计算旋转中心,采用反角度加权插值法推估任意姿态之相位中心,以补偿天线自重变形、机械安装等复杂规律误差的影响,可实现相位中心精确标校,希冀能满足电信号合成的需求。
1 标校原理相位中心不能直接测得,需要根据测量数据推估得到。利用工业摄影测量技术获取规划姿态下天线面板上均匀分布的大量目标点坐标,通过型面拟合获取机械轴,依据点到各机械轴距离平方和最小的原则计算旋转中心,根据机械轴随方位角、俯仰角变化的实际规律,建立推估模型来计算任意姿态下的相位中心。
1.1 测量数据准备为描述天线与深空探测器的位置关系,需要相位中心的地心大地坐标。同一天线不同姿态以及不同天线的摄影测量坐标系相对独立,需要统一,故通过GPS测量引入大地坐标和大地方位角,采用全站仪测量内部网形,建立三维控制网,然后联合利用工业摄影测量系统和全站仪测量系统获取不同方位、俯仰姿态下天线上公共点的坐标,实现从摄影测量坐标系到工程坐标系的转换。
1.2 天线旋转中心的获取采用工业摄影测量获取目标点的坐标,通过CAD面型转换法[22]恢复出天线的设计坐标系,其Z轴即为天线的机械轴、坐标原点为天线的顶点,如图 2(a)所示。将各设计坐标系下的机械轴转换到工程坐标系下,求解各台天线所对应的多条机械轴之交点作为旋转中心,如图 2(b)所示。
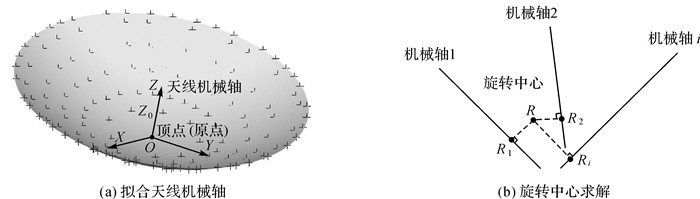
|
| 图 2 天线机械轴与旋转中心 Fig. 2 Antenna mechanical axes and rotation center |
假设在k个姿态下对天线上的目标点进行测量,拟合得到k条机械轴。在理想情况下,这些机械轴在空间内应该交于一点,但是由于自重变形、加工精度、天线的机械和温度特性、测量误差等因素的影响,导致这些机械轴并不相交于一点。可以依据最小二乘准则,求出距k条机械轴距离平方和最小的点,将其作为旋转中心。本文采用文献[23]提出的矩阵法求解旋转中心。
设k条机械轴为l1, l2, …, lk,R(x, y, z)为旋转中心,已知li的顶点为pi=[x0i y0i z0i],方向为ui=[uxi uyi uzi],则li可表示为
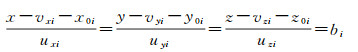 (1)
(1)
式中,R′i(x-vxi, y-vyi, z-vzi)表示旋转中心R在机械轴li上的投影点;bi为比例参数,其绝对值表示R′i到pi的距离。
根据式(1)可列误差方程
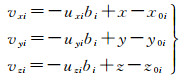 (2)
(2)
将式(2)整理得
 (3)
(3)
以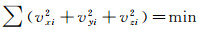
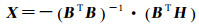 (4)
(4)
参数X的前3个分量(x, y, z)即为旋转中心坐标,根据(x, y, z)和(vxi, vyi, vzi)可求出R′i的坐标。
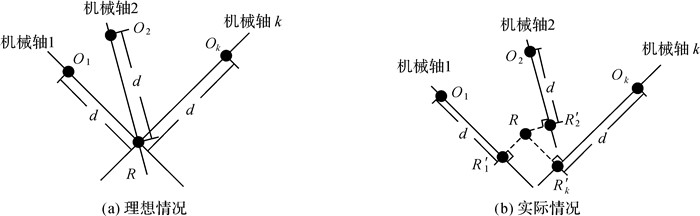
1.3 天线相位中心的推估如图 3(a)所示,依据理想情况下天线的结构设计和工作原理,机械轴过旋转中心R,R到相位中心Oi的距离d由设计给定,机械轴的指向用方位角与俯仰角表示。因此,在获知R、d、机械轴指向的情况下就能确定Oi。
|
| 图 3 天线旋转中心、投影中心与相位中心的关系 Fig. 3 Relation among antenna rotation center, projective center and phase center |
实际情况下,受到自重变形、加工及安装等复杂规律误差的影响,天线各姿态对应的机械轴一般不过R,如图 3(b)所示。此时,将R投影至各机械轴得到投影中心R′i,从R′i沿机械轴延伸d即可获得相位中心Oi。
通过实测得到了k个已知矢量R′iOi(i=1, 2, …, k),借鉴反距离加权插值的思路[24],设计反角度加权插值法来计算任意姿态(α, β)下的矢量R′O(α, β)。
任意姿态(α, β)到已测第i个姿态(αi, βi)的权因子Si(i=1, 2, …, k)为
 (5)
(5)
式中,αi、βi分别为已测第i个姿态所对应的方位角和俯仰角。为避免权无穷大,在分母上加上一个小量常数。
对所有姿态下的权因子求和
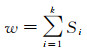 (6)
(6)
则第i个姿态的矢量R′iOi在计算R′O(α, β)时所占的权重为
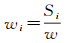 (7)
(7)
故
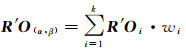 (8)
(8)
然后根据
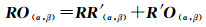 (9)
(9)
来推估相位中心O(α, β)。
2 试验与分析以某试验场地3台ϕ3 m的上行阵天线为试验对象,应用空间大地测量技术和精密工程测量技术获取了试验数据,根据上述方法精确标校相位中心,并通过电信号实测验证本文方法的可行性。
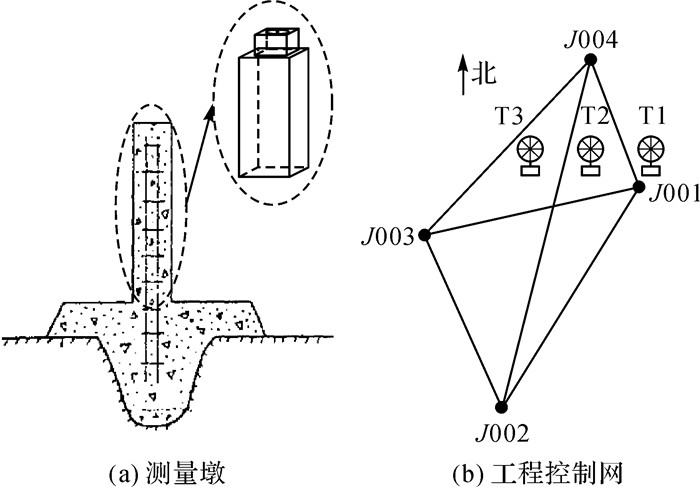
2.1 观测及数据处理过程 2.1.1 基准数据获取根据工程的需求,结合试验场地3台ϕ3 m天线(T1-T3)的分布,修建了J001-J004共4个带有强制对中装置的测量墩,见图 4(a),组成的工程控制网如图 4(b)所示。
|
| 图 4 测量墩和工程控制网 Fig. 4 Observation pillar and engineering control network |
为引入地心大地坐标系,采用3套GPS接收设备,分别对J001-J002-J004和J002-J003-J004进行观测,每个同步环连续观测4 h以上,长基线J002-J004连续观测12 h以上。处理GPS观测数据时,以BJFS、SHAO、LHAZ 3个IGS基准站的GPS观测数据及其大地坐标和运动速度计算J004点的大地坐标[25],然后以J004点的计算结果为控制网基准数据进行局域网平差,进而获得方位基准和其他各点的坐标。
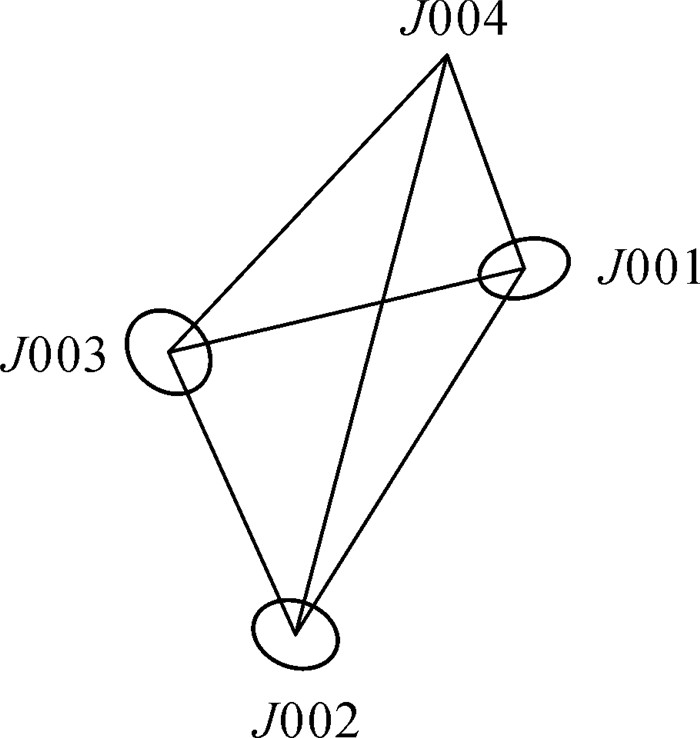
为构建高精度的工程控制网,参照《国家三角测量规范》(GB/T 17942)、《精密工程测量规范》(GB/T 15314),按照三等控制网测量技术要求,采用MS50全站仪配合精密棱镜进行控制测量,分别对平面网和高程网进行平差处理。平面控制网的点位精度如表 1所示,平面误差椭圆如图 5所示。
| mm | ||||
| 点名 | J001 | J002 | J003 | J004 |
| 点位精度 | 0.11 | 0.12 | 0.13 | 0.00 |
|
| 图 5 控制点的平面误差椭圆 Fig. 5 Plane error ellipse of control points |
2.1.2 旋转中心的计算
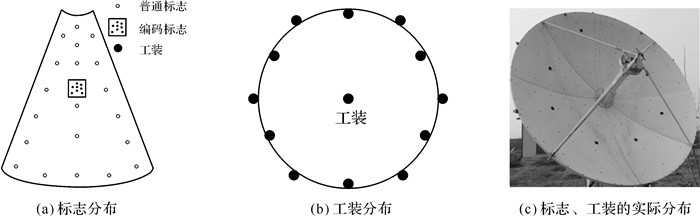
利用工业摄影测量系统采集目标点坐标。在天线面板上布设摄影测量专用标志,如图 6(a)所示。为了实现摄影测量坐标系与工程坐标系的转换,需要一定数量的公共点,公共点处安装有特制的靶座,既可安放球棱镜配合全站仪测量,又可安放摄影测量工装,且通过精密加工来保证摄影测量工装与球棱镜的同心,工装的分布如图 6(b)所示。实际分布如图 6(c)所示。
|
| 图 6 摄影测量标志及工装分布 Fig. 6 Distribution of photogrammetric markers and fixtures |
对每台天线在方位为60°、180°和300°的位置,俯仰从10°至80°每隔10°进行测量,获得了24个姿态下的数据。通过天线面板上目标点与天线设计模型的比对,得到了每个姿态下的机械轴。选取T2天线某姿态(方位角60°、俯仰角50°)的模型比对结果,展示于表 2中。
| mm | ||||
| 精度 | X | Y | Z | 点位 |
| 最大偏差 | 0.98 | 1.46 | 0.56 | 2.12 |
| 最小偏差 | -1.06 | -1.73 | -0.83 | -1.81 |
| 偏差范围 | 2.04 | 3.19 | 1.39 | 3.94 |
| RMS | 0.32 | 0.67 | 0.29 | 0.79 |
从表 2可以看出,目标点与模型比对的精度达到了亚毫米级,确保了机械轴的复现精度。
将矩阵法求得的机械轴交点作为旋转中心,各旋转中心在工程坐标系下的坐标及精度如表 3所示。
| mm | ||||
| 天线编号 | X | Y | Z | RMS |
| T1 | -13 667.50 | -11 217.88 | 973.17 | 2.42 |
| T2 | -12 747.29 | -1 918.03 | 997.41 | 1.84 |
| T3 | -13 336.91 | 7 205.06 | 982.94 | 4.21 |
从表 3可以看出,机械轴相交法得到的旋转中心精度只达到了毫米量级,这恰恰反映出了自重变形、机械加工、安装等复杂规律误差对机械轴指向的影响。由于这些复杂规律误差难以预先构建模型予以消除,依据实测数据,按照本文发明方法来推估相位中心,可以与上述复杂因素导致的运动规律相适应,提高了相位中心的现势性。此外,3台天线旋转中心的精度不等,原因在于通视条件的不足,致使不同天线可观测到的公共点数目及分布情况各异,影响了机械轴的精度,进而导致旋转中心精度略有差别。
2.1.3 相位中心的计算ϕ3 m天线旋转中心到相位中心的设计距离为1000 mm,根据测量结果建立了估计模型,可以计算任意姿态下的相位中心。表 4列出了某姿态(方位角104°、俯仰角53°)下的相位中心在工程坐标系中的坐标。
| mm | |||
| 天线编号 | X | Y | Z |
| T1 | -12 797.71 | -10 920.64 | 1 368.99 |
| T2 | -11 878.52 | -1 622.57 | 1 390.74 |
| T3 | -12 468.55 | 7 500.76 | 1 376.98 |
2.2 电信号的测试与验证
为验证校准方法的有效性,进行了电信号合成测试。测试时,3台天线发射Ku频段微波信号,距离发射天线约1 km处放置一台接收天线,接收天线相对于发射天线的姿态为方位角61.5°、俯仰角11.2°,接收天线连接频谱仪,读取接收到的信号幅度。分别对3台天线单独发射和同时发射等情况进行测试,在同时发射时又对校准前后两种状态进行了测试,结果如表 5所示。
| 情况 | 状态 | 接收信号幅度/dBm | 合成效率/(%) |
| 1 | 单独T1发射 | -77.1 | |
| 2 | 单独T2发射 | -76.5 | |
| 3 | 单独T3发射 | -76.9 | |
| 4 | 未经校准的合成信号 | -72.4 | 27.9 |
| 5 | 经校准的合成信号 | -68.2 | 88.4 |
从表 5可知,试验中所采用的3台天线,未经校准时的合成信号只增加约4 dB,与理论值9.54 dB相差较大,合成效率低,其原因是未校准时3个信号的相位差不准确。经相位中心校准后,合成信号幅度增加了约9 dB,非常接近理论值,合成效率较高。
天线阵相位合成效率的估算式[26]为
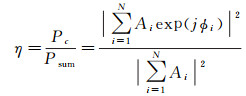 (10)
(10)
式中,Psum为阵列天线单元信号全部同相合成时的天线阵功率;Pc为阵列天线单元信号不同相时的天线阵功率;ϕi为第i个单元的相位;Ai为第i个单元的幅度;j为虚数单位。
此天线工作频率为12 GHz,工作波长为25 mm,设校准误差为l,则l引起的相位差为
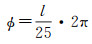 (11)
(11)
实际应用对天线初始相位误差的要求在30°以内。由η=88.4%结合式(10),取Ai(i=1, 2, 3)=1,以T1天线的相位为基准,假定T2、T3与T1相位差的绝对值相等,即|ϕ12|=|ϕ13|,可计算得l12=l23≈±1.7 mm。由式(11)可知l引起的初始相位误差约为24.5°,满足天线相位合成初始相位误差的要求。
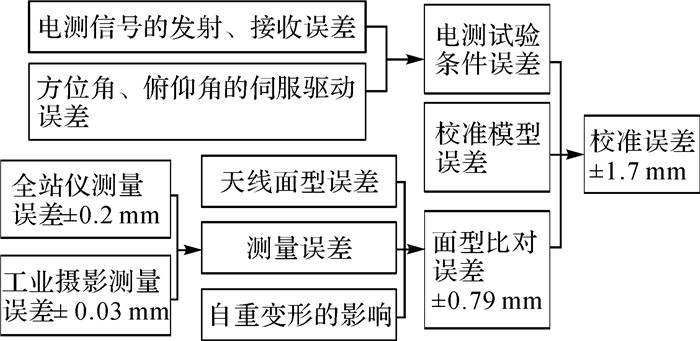
对校准误差的组成进行分析,如图 7所示。
|
| 图 7 校准误差的组成分析 Fig. 7 Composition analysis of calibration error |
由图 7可知,在进一步减小天线面型误差、自重变形、伺服驱动误差、电测信号发射、接收误差的基础上,预期可以获得更优的合成信号。
3 结论本文提出的上行天线阵相位中心精确标校方法,综合应用空间大地测量技术和精密工程测量技术获取了丰富的测量信息,通过顾及天线的现势指向,得到了可靠的机械轴和旋转中心,利用相位中心推估模型,有效地削弱了天线自重变形、机械加工等因素的影响,提高了相位中心的现势性,为天线阵的信号合成提供了精准可靠的数据支持。以3台ϕ3 m上行天线阵为试验对象,采用本文方法所得相位中心用于电信号合成,合成信号幅度增加了约9 dB,合成效率高达88.4%,非常接近于理论值,效果良好。
限于试验条件之简陋,导致各姿态下的公共点数量不等、分布不均匀,这些因素影响了机械轴的精度;另外电测试验也不充分,对相位中心确定方法回馈不足。需要对试验条件、测量方案、校准模型等进行深入细致的优化,以期得到更好的结果。
| [1] |
李海涛, 李宇华, 匡乃雪.
深空探测中的天线组阵技术[J]. 飞行器测控学报, 2004, 23(4): 57–60.
LI Haitao, LI Yuhua, KUANG Naixue. Antenna array forming technology in deep space exploration[J]. Journal of Spacecraft TT&C Technology, 2004, 23(4): 57–60. |
| [2] |
卢满宏, 周三文, 谌明, 等.
深空测控通信技术专题研究[J]. 遥测遥控, 2007, 28(S1): 11–16.
LU Manhong, ZHOU Sanwen, CHEN Ming, et al. Research on deep space TT&C and communication[J]. Journal of Telemetry, Tracking and Command, 2007, 28(S1): 11–16. |
| [3] |
姚飞, 匡麟玲, 詹亚锋, 等.
深空通信天线组阵关键技术及其发展趋势[J]. 宇航学报, 2010, 31(10): 2231–2238.
YAO Fei, KUANG Linling, ZHAN Yafeng, et al. Key techniques and development trend of antenna arraying for deep space communication[J]. Journal of Astronautics, 2010, 31(10): 2231–2238. DOI:10.3873/j.issn.1000-1328.2010.10.001 |
| [4] |
钟晓玲, 周三文, 李海涛, 等.
天线组阵信号合成技术的研究[J]. 遥测遥控, 2007, 28(S1): 43–48.
ZHONG Xiaoling, ZHOU Sanwen, LI Haitao, et al. Research on the antenna arraying signal combining technique[J]. Journal of Telemetry, Tracking and Command, 2007, 28(S1): 43–48. |
| [5] |
周三文, 卢满宏, 黄建国.
天线组阵全频谱合成效率分析[J]. 遥测遥控, 2009, 30(2): 46–52.
ZHOU Sanwen, LU Manhong, HUANG Jianguo. Analysis on combining efficiency of full-spectrum combining[J]. Journal of Telemetry, Tracking and Command, 2009, 30(2): 46–52. DOI:10.3969/j.issn.2095-1000.2009.02.009 |
| [6] |
何国龙, 李国民.
上行天线组阵载波相位并行标校方法研究[J]. 飞行器测控学报, 2012, 31(1): 19–22.
HE Guolong, LI Guomin. A parallel carrier phase calibration method for uplink antenna arrays[J]. Journal of Spacecraft TT#38;C Technology, 2012, 31(1): 19–22. |
| [7] |
马下平, 沈云中, 王解先, 等.
卫星激光测距与甚长基线干涉测量的天线旋转中心的直接解法[J]. 测绘学报, 2014, 43(3): 257–262.
MA Xiaping, SHEN Yunzhong, WANG Jiexian, et al. Direct solution of SLR and VLBI antenna rotation center[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 257–262. DOI:10.13485/j.cnki.11-2089.2014.0037 |
| [8] |
柯炳清, 丁克乾.
天线相位中心的推算及标定[J]. 遥测遥控, 2009, 30(6): 66–69.
KE Bingqing, DING Keqian. Calculation and measurement of antenna phase center[J]. Journal of Telemetry, Tracking and Command, 2009, 30(6): 66–69. DOI:10.3969/j.issn.2095-1000.2009.06.014 |
| [9] |
周命端, 郭际明, 郑勇波, 等.
卫星天线相位中心偏移对GPS精密单点定位精度的影响研究[J]. 测绘通报, 2008(10): 8–9, 13.
ZHOU Mingduan, GUO Jiming, ZHENG Yongbo, et al. A study of the impact of satellite antenna phase center offsets on GPS precise point positioning accuracy[J]. Bulletin of Surveying and Mapping, 2008(10): 8–9, 13. |
| [10] |
胡志刚, 赵齐乐, 郭靖, 等.
GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(S1): 34–38.
HU Zhigang, ZHAO Qile, GUO Jing, et al. Research on impact of GPS phase center variation on precise orbit determination of low earth orbit satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 34–38. |
| [11] |
郭际明, 史俊波, 汪伟.
天线相位中心偏移和变化对高精度GPS数据处理的影响[J]. 武汉大学学报(信息科学版), 2007, 32(12): 1143–1146.
GUO Jiming, SHI Junbo, WANG Wei. Impact of antenna phase center offset and variation for high precision GPS data processing[J]. Geomatics and Information Science of Wuhan University, 2007, 32(12): 1143–1146. |
| [12] |
沈云中, 陈廷武.
上海天文台并址站的空间归心测量[J]. 同济大学学报(自然科学版), 2006, 34(2): 217–220.
SHEN Yunzhong, CHEN Tingwu. Determination of space coordinate differences of co-location sites in Shanghai Observatory[J]. Journal of Tongji University (Natural Science), 2006, 34(2): 217–220. DOI:10.3321/j.issn:0253-374X.2006.02.015 |
| [13] |
李金岭, 乔书波, 刘鹂, 等.
2008年佘山25 m射电天线归心测量[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1387–1391.
LI Jinling, QIAO Shubo, LIU Li, et al. Site survey at Sheshan 25 m radio telescope in 2008[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1387–1391. |
| [14] |
孙中苗, 范昊鹏.
VLBI全球观测系统(VGOS)研究进展[J]. 测绘学报, 2017, 46(10): 1346–1353.
SUN Zhongmiao, FAN Haopeng. Research progress of VLBI Global Observing System (VGOS)[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1346–1353. DOI:10.11947/j.AGCS.2017.20170326 |
| [15] |
李金岭, 张津维, 郭丽.
甚长基线干涉测量天线参考点和轴线偏差监测方法探讨[J]. 测绘科学, 2014, 39(11): 10–14.
LI Jinling, ZHANG Jinwei, GUO Li. Discussion on monitoring method of reference point and axis offset of VLBI antenna[J]. Science of Surveying and Mapping, 2014, 39(11): 10–14. |
| [16] | HYUK G K, JIN S H, HONG S Y, et al. A comparative analysis of 3D circle fitting algorithms for determination of VLBI antenna reference point[J]. Journal of the Korean Society of Surveying, Geodesy, Photogrammetry and Cartography, 2015, 33(4): 231–244. DOI:10.7848/ksgpc.2015.33.4.231 |
| [17] |
马下平.
ITRF中GNSS/SLR并址站归心基线的"一步解"[J]. 测绘学报, 2018, 47(1): 64–70.
MA Xiaping. One step solution to the local tie vectors of GNSS/SLR in ITRF[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(1): 64–70. DOI:10.11947/j.AGCS.2018.20170066 |
| [18] |
尚军平, 傅德民, 邓颖波.
天线相位中心的精确测量方法研究[J]. 西安电子科技大学学报(自然科学版), 2008, 35(4): 673–677.
SHANG Junping, FU Demin, DENG Yingbo. Research on the accurate measurement method for the antenna phase center[J]. Journal of Xidian University (natural science), 2008, 35(4): 673–677. DOI:10.3969/j.issn.1001-2400.2008.04.018 |
| [19] |
陈曦, 傅光, 龚书喜, 等.
阵列天线相位中心的校准方法及误差分析[J]. 西安电子科技大学学报(自然科学版), 2011, 38(3): 145–149.
CHEN Xi, FU Guang, GONG Shuxi, et al. Study of calibration of the phase center of array antennas and its error analysis[J]. Journal of Xidian University, 2011, 38(3): 145–149. DOI:10.3969/j.issn.1001-2400.2011.03.023 |
| [20] |
李颖, 王志雄, 谭伟.
天线相位中心的测量和校准方法研究[J]. 微波学报, 2012(S3): 135–138.
LI Ying, WANG Zhixiong, TAN Wei. Research on measure and calibration of antenna phase center[J]. Journal of Microwaves, 2012(S3): 135–138. |
| [21] |
李广云, 范百兴.
精密工程测量技术及其发展[J]. 测绘学报, 2017, 46(10): 1742–1751.
LI Guangyun, FAN Baixing. The development of precise engineering surveying technology[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1742–1751. DOI:10.11947/j.AGCS.2017.20170313 |
| [22] |
李宗春, 李广云.
天线几何量测量理论及其应用[M]. 北京: 测绘出版社, 2009.
LI Zongchun, LI Guangyun. Measuring theory, technique and application of antenna[M]. Beijing: Surveying and Mapping Press, 2009. |
| [23] | HAN Lejia, BANCROFT J C. Nearest approaches to multiple lines in n-dimensional space[R]. Calgary: University of Calgary, 2010. |
| [24] |
樊子德, 李佳霖, 邓敏.
顾及多因素影响的自适应反距离加权插值方法[J]. 武汉大学学报(信息科学版), 2016, 41(6): 842–847.
FAN Zide, LI Jialin, DENG Min. An adaptive inverse-distance weighting spatial interpolation method with the consideration of multiple factors[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 842–847. |
| [25] |
陈俊勇.
中国现代大地基准——中国大地坐标系统2000(CGCS 2000)及其框架[J]. 测绘学报, 2008, 37(3): 269–271.
CHEN Junyong. Chinese modern geodetic datum-Chinese Geodetic Coordinate System 2000(CGCS 2000) and its frame[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 269–271. DOI:10.3321/j.issn:1001-1595.2008.03.001 |
| [26] | ROGSTAD DH, MILEANT A, PHAM T T. Antenna arraying techniques in the deep space network[M]. Hoboken, New Jersey: John Wiley & Sons, Inc., 2003. |


