2. 香港大学建筑学院, 香港;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
4. 中南大学地球科学与信息物理学院, 湖南 长沙 410083;
5. 中国科学院测量与地球物理研究所, 湖北 武汉 430077;
6. 江苏海洋大学测绘与海洋信息学院, 江苏 连云港 222005
2. Faculty of Architecture, the University of Hong Kong, Hongkong, China;
3. GNSS Research Center of Wuhan University, Wuhan 430079, China;
4. School of Geosciences and Info-physics, Central South University, Changsha 410083, China;
5. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
6. School of Geomatics and Marine Information, Jiangsu Ocean University, Lianyungang 222005, China
合成孔径雷达卫星在向前运动过程中周期性地发射和接收脉冲信号,传感器与目标相对位置的变化所引发的回波数据的多普勒频移构成了合成孔径处理的基础,最终所有目标被压缩至零多普勒时刻,确保卫星姿态几乎不对像素定位产生影响[1]。雷达回波零多普勒聚焦方法虽然巧妙地简化了SAR影像几何,但多普勒中心的变化导致不同模式SAR影像所需配准精度出现显著差异。配准精度需求的多样化使得相关配准方法受到挑战:以TerraSAR-X为代表的高分辨率影像采用低阶多项式拟合配准偏移量时,发现其结果极易受到地形干扰[2-5];SAR影像时序处理时,为了确保相干性较差的影像对满足所要求的配准精度,经常采用复杂的配准传递算法,计算量大,效率低[6]。这些不利因素已影响了InSAR技术的工程化应用。
为了有效解决SAR影像干涉配准问题,几何配准被引入SAR影像时序处理中。该方法类似于光学摄影测量中物方影像匹配方法,根据DEM和卫星轨道基于零多普勒几何定位原理计算影像间的相对偏移量[7]。早期SAR卫星轨道精度较低,几何配准通常作为相关配准的辅助手段以消除地形起伏对影像配准偏移量的干扰[8]。随着GNSS定轨技术的成熟,卫星轨道定位精度已达到厘米级。与此同时,SAR影像聚焦理论也由原来的“一步一停”聚焦模型发展为与卫星运动状态相符的“持续运动”模型,使聚焦影像几何模型更为严格。目前TerraSAR-X等卫星影像绝对定位精度已达到亚米级,几何配准已可以满足条带模式影像的干涉配准要求。与相关配准方法相比,几何配准不受影像大小、相干性的影响,可靠性较高[9-12]。
与几何配准相对应的是基于SAR影像信息的配准方法,即根据影像信息确定同名像点,主要包括相干系数法、相关系数法、最大干涉频谱法、相位差影像平均波动函数法、单点最小二乘匹配法及这些算法的各种改进形式[13-20]。当几何配准精度不足时,基于SAR影像信息的配准方法可用于改正几何配准误差。这些配准方法总体上可分为相关性、谱分集、点目标3大类,文献[21-24]逐步完成配准精度的理论推导,指出配准精度主要受到相干性,分辨率单元数量等参数的影响,目前SAR影像配准已形成以几何配准为基础,依托影像信息辅助配准的理论体系。这一理论不但指导了干涉配准方案设计,还影响着卫星系统设计[21—24]。SAR卫星采用严格回归轨道设计,重复轨道近似平行,几何配准利用公开DEM即可有效估计出地形起伏引起的偏移量局部变化,确保影像相干性不会受到配准误差影响,而且配准误差具有系统误差特性,残余偏移量易于估计和改正,即当几何配准精度不足时,也能确保有足够的影像信息估计其残余偏移量,最终满足影像配准精度的要求[25];TerraSAR-X和Sentinel-1卫星系统设计时根据配准理论对方位向重叠度和上下频带多普勒基线参数进行权衡,以确保几何配准后残余偏移量估计精度和可靠性达到最优[26]。
鉴于SAR影像配准是干涉处理中最重要的一步,本文基于SAR影像配准理论首先讨论不同成像模式所需方位向配准精度和卫星轨道精度,然后进行条带模式和聚束模式的干涉配准方案论证和试验验证,最后利用Sentinel-1卫星TOPS影像进行不同轨道和DEM条件下几何配准试验,分析轨道和DEM对几何配准精度的影响。
1 SAR成像模式与配准精度需求SAR影像距离向为基带信号,理论上距离向配准精度达到0.1像素时即可确保影像相干性不受配准误差影响,而方位向所需配准精度却因成像模式的不同而有所差异[27]。雷达回波聚焦时方位向匹配滤波器为多普勒历程时间反褶后的复共轭,非零多普勒中心在聚焦影像方位向引入了线性相位[28-29],所以聚焦影像方位向受到SAR成像模式和聚焦方式的影响成为频带信号或调频信号,干涉处理时需顾及到由配准误差和多普勒中心引起的干涉相位相对误差。本文仅讨论方位向配准精度,其中干涉图整体相对相位偏差δϕ、多普勒中心fηc与方位向配准偏移量误差δaz之间的关系如式(1)所示[30]
 (1)
(1)
式中,配准偏移量误差δaz以像素为单位;fηcmax、fηcmin分别为聚焦影像多普勒中心的最大值和最小值;Faz为聚焦影像方位向采样率。由式(1)可知,聚焦影像中的多普勒中心变化幅度和方位向采样频率决定了干涉所需的配准精度。干涉测量通常要求干涉相位偏差δϕ不超过3°,也就是
| 成像模式 | 方位向采样频率/Hz | 多普勒带宽/Hz | 方位向多普勒中心变化范围/Hz | 方位向所需配准精度/像素 | 所需轨道切向精度/cm |
| HS (high resolutionspotlight mode) |
~8200 | ~7400 | [~+3000, ~-3000] | ~0.012 | < 0.75 |
| SL (spotlight mode) |
~3900 | ~3400 | [~+1200, ~-1200] | ~0.015 | < 1.50 |
| SM (stripmap mode) |
~3400 | ~2765 | ~0 | ~0.1 | < 15 |
| SC (scanSAR mode) |
~1000 | ~460 | [~-1070, ~+1070] | ~0.004 | < 2.50 |
| ST (staring spotlight) |
~42 000 | ~38 000 | [~-1000, ~+1000] | ~0.1 | < 1.20 |
| TOPS | ~650 | ~425 | [~+4100, ~-4100] | ~0.000 65 | < 0.50 |
星载合成孔径雷达成像模式主要包括条带模式(stripmap)、scanSAR模式、TOPS模式、滑动聚束模式(sliding spotlight)、凝视聚束模式(staring spotlight),其中条带模式是最基本的成像模式。图 1为条带模式零多普勒影像聚焦原理,其中横轴为方位线时间,纵轴为多普勒频率,虚线表示方位向上不同目标的多普勒历程,虚线斜率代表着雷达回波方位向调频率FM。条带模式下方位向上每个目标的多普勒历程是一致的,聚焦时直接将回波数据压缩至零多普勒位置,多普勒中心保持不变。TerraSAR-X卫星提供的精密星历显示在10 s内其影像多普勒中心变化一般小于10 Hz,与之相对应的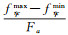

|
| 图 1 条带模式聚焦原理 Fig. 1 Time frequency diagram of raw and focused signals for stripmap mode |
条带模式影像测绘带宽受到距离模糊、方位模糊等制约不能任意扩大。为进一步扩大影像覆盖范围,ScanSAR模式通过在距离向周期性的调整波束方向以实现测绘带宽的增大[32]。图 2为该模式同一方位线多个目标的多普勒历程,尽管其方位向波束方向图Gaap与条带模式一样在成像过程中是不变的,但Burst只接收部分时间段内的回波数据。如果每个Burst单独聚焦处理,其聚焦影像调频率

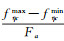

|
| 图 2 ScanSAR模式原始回波与聚焦Burst多普勒频谱的变化 Fig. 2 Time frequency diagram in the ScanSAR mode for two consecutive raw and focused Bursts |
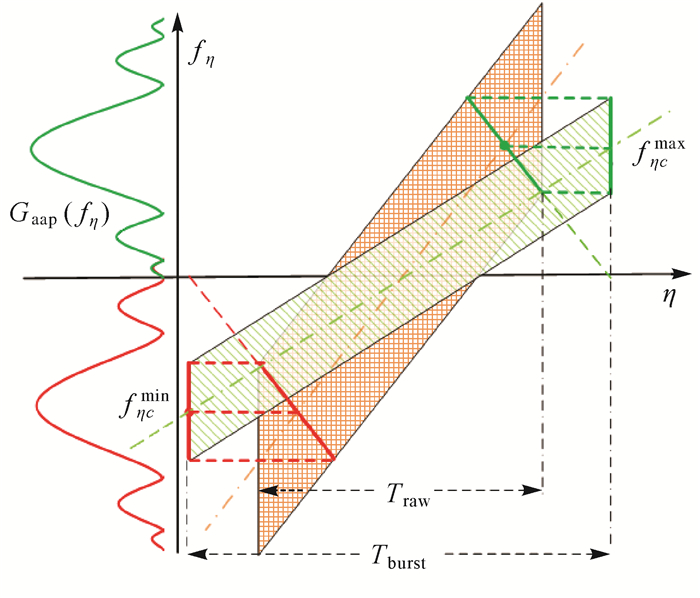
TOPS模式也是通过Burst成像方式获得更大范围的成像区域,如图 3所示,雷达天线波束沿着方位向从后向前扫描导致其回波多普勒中心在方位向上近似于线性变化[37]。尽管每个目标在聚焦前后其多普勒中心并未发生改变,但是零多普勒时间与回波时间的转换导致零多普勒影像持续时间TBurst大于回波持续时间Traw。另外, 为了方便不同子测绘带的拼接,Burst聚焦影像通常进行了方位向降采样处理,使得
|
| 图 3 TOPS模式原始回波与聚焦后多普勒频谱的变化 Fig. 3 Time frequency diagram in the TOPS mode for raw and focused Burst |
聚束模式与TOPS模式成像方式类似,其区别是聚束模式雷达天线波束是通过正向旋转提高方位向分辨率,TerraSAR-X卫星同时提供滑动聚束模式(sliding spotlight)和凝视聚束模式(staring spotlight)两种产品[38-39]。图 4为滑动聚束模式原始回波信号与聚焦后的多普勒频谱,可以看出滑动聚束模式影像在聚焦时通过转换原始回波时间和零多普勒时间,使得回波持续时间Traw大于聚焦影像持续时间Tfocused,其



|
| 图 4 滑动聚束模式原始回波与聚焦影像多普勒频谱变化 Fig. 4 Time frequency diagram of raw data and focused signals for sliding spotlight mode |

|
| 图 5 凝视聚束模式原始回波与聚焦影像多普勒频谱变化 Fig. 5 Time frequency diagram of raw data and focused signals for staring spotlight mode |
综上所述,除了条带模式影像和凝视聚束模式外,TerraSAR-X卫星其他模式影像在干涉处理时所需配准精度均高于0.1像素,如表 1所示。鉴于不同成像模式配准精度需求的差异,目前以几何配准为基础,依托影像信息进行辅助配准的方案因其严格的理论模型和较高的精度成为干涉处理的首选[40]。
2 基于几何配准的SAR影像干涉配准方案随着SAR成像模式的多样化及配准精度需求的差异,以几何配准为基础,依托影像信息进行残余偏移量估计是目前干涉处理中精度和可靠性最高的配准方案。几何配准不仅不受相干性影响,而且配准误差具有一致性,不存在影像局部配准误差突变的情况。当几何配准精度无法满足影像干涉要求时,可以尽量扩大影像中残余偏移量估计窗口依托影像信息估计残余偏移量,提高偏移量估计精度。如聚束模式采用谱分集进行偏移量估计时窗口为整景影像,Burst模式影像采用增强谱分集估计偏移量时其估计窗口为整个Burst[41-44]。
2.1 几何配准精度理论分析目前SAR卫星传感器同步到GPS时间,影像零多普勒时间精确到10-6 s,几何配准依据SAR影像零多普勒几何获取主辅影像间的全局偏移量,其精度主要受到DEM和卫星轨道的影响,其中卫星轨道是以基线误差的形式呈现。距离向几何配准误差δ(Δi)如式(2)所示[45]
 (2)
(2)
式中,Δr为距离向像素采样间隔(pixel spacing);Δi为主辅影像距离向偏移量;B⊥为干涉对垂直基线;δB‖为干涉对平行基线;εh为DEM高程误差;r0为影像零多普勒斜距;θ为影像侧视角。现代雷达卫星均对重复轨道基线进行了严格控制,如TerraSAR-X卫星轨道基线控制在250 m以内,Sentinel-1卫星控制在150 m以内,垂直基线远小于影像零多普勒斜距,由式(5)可知,DEM误差对距离向配准的影响可以忽略不计[46];目前雷达卫星精密轨道精度一般在厘米级,其轨道水平基线误差远小于影像像元空间,充分满足距离向0.1像素的配准精度要求[47]。
如果对影像干涉对基线进行三维分解,除竖直基线和水平基线外,还存在与主影像轨道切向平行的切向基线[48-49]。在几何配准中方位向配准误差δ(Δj)与切向基线密切相关,如式(3)所示[50]
 (3)
(3)
式中,Δaz为方位向像素采样间隔;Δj为主辅影像方位向偏移量;Ba为切向基线;δBa为轨道切向误差;如果干涉对只采用几何配准,δ(Δj)即为式(1)中的δaz。受益于SAR卫星的轨道设计,切向基线通常被控制到50 m以内,重复轨道近似平行,方位向偏移量对地形起伏并不敏感,与距离向配准相比,DEM高程误差对方位向几何配准精度的影响更是微乎其微,切向基线误差δBa是方位向几何配准的主要误差源[51-52]。本文假定卫星轨道完全平行,DEM对方位向配准结果不产生任何影响,依据式(3)可得到TerraSAR-X卫星每种成像模式所需的卫星轨道切向精度,如表 1所示。TerraSAR-X卫星轨道精度为3~5 cm,目前该卫星精密轨道(science orbits)仅可满足条带模式影像采用几何配准进行干涉处理,其他模式影像需利用影像信息配准结果进一步对几何配准结果进行校正[53]。
2.2 条带模式影像几何配准条带模式影像由于多普勒中心几乎不发生变化,方位向配准精度只要求达到0.1像素,以确保配准误差不影响干涉影像对的相干性。TerraSAR-X与Sentinel-1卫星均采用GNSS定轨技术,轨道精度达到3~5 cm,依据式(3)可以得到其条带模式影像几何配准理论精度分别为0.05和0.018像素[54]。ASAR卫星尽管未采用GNSS定轨技术,但是DORIS系统定轨精度也达到了5~10 cm,特别是卫星轨道于2007年进行了调整,轨道基线被控制在250 m以内,方位向几何配准理论精度达到0.025像素[55-56]。上述卫星几何配准精度可直接满足条带模式影像干涉处理的要求,已无必要依托影像信息再次进行优化配准。
为验证几何配准的精度和优势,本文将对比分析同一干涉对的几何配准和相关配准结果。鉴于相关配准结果易受到干涉对相干性的影响,试验对象选择以时间基线为11 d,相干性较高覆盖深圳地区的TerraSAR-X卫星影像干涉对(20090212_20090223),其几何配准、相关配准相应的差分干涉图如图 6(a)和图 6(b)所示。由于两差分干涉图差异难以通过视觉辨别,本文进一步对其相干系数进行比较,发现几何配准相干系数总体上大于相关配准,说明在该试验中几何配准精度优于相关配准。

|
| 图 6 TerraSAR-X卫星几何配准与相关配准差分干涉图(深圳) Fig. 6 TerraSAR-X differential interferogram got by geometrical coregistration and cross correlation |
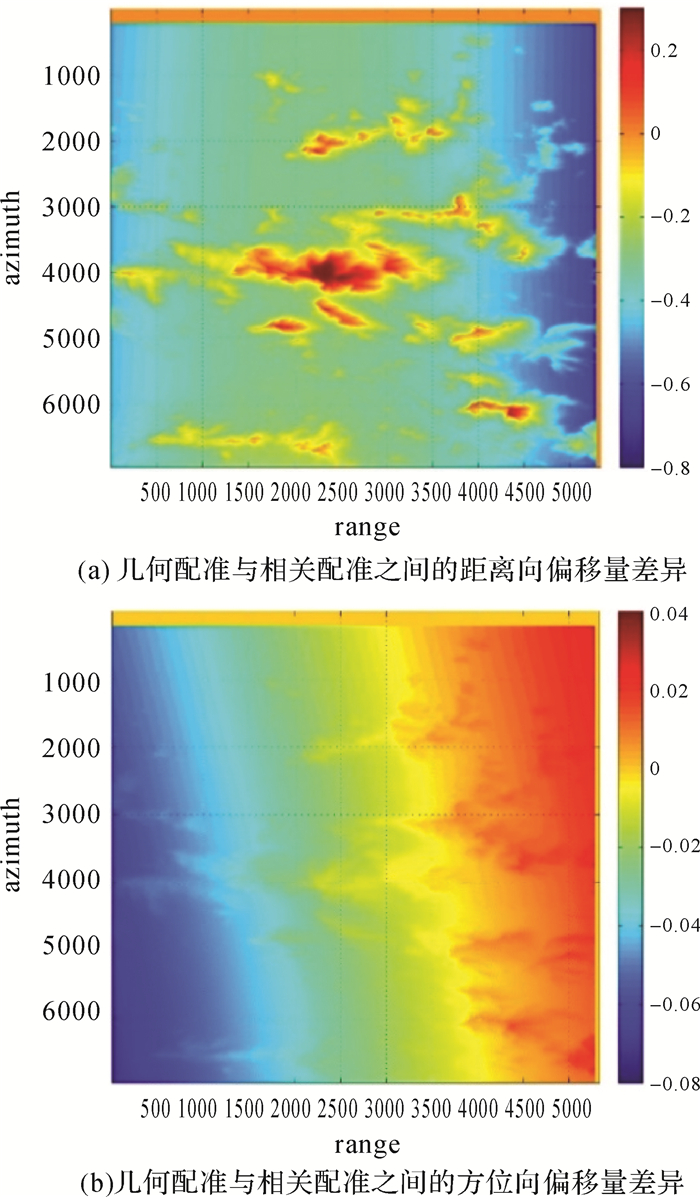
为了进一步分析其原因,本文将几何配准、相关配准相对应的相干系数和偏移量进行相减,其差异空间分布如图 7和图 8所示所示,可以明显看出地形起伏较大的地区相干系数和偏移量差异均比较明显,特别是图 8(a)中的距离向偏移量差异明显与地形相关。这表明虽然几何配准对应的垂直基线为285 m,处于该卫星的极端基线条件,但几何配准依然可以准确估计出地形起伏对影像全局偏移量的影响,而相关配准尽管在高相干条件下每个窗口匹配精度和可靠性足够高,但依靠多项式仍然无法准确拟合出地形起伏引起的影像偏移量局部变化,导致几何配准精度高于相关配准。图 8(b)中的方位向偏移量差异主要沿着影像距离向分布,与地形起伏关系较弱,由式(3)可知卫星轨道在近似平行的条件下,方位向偏移量基本上不受地形信息的影响,可以推断出其偏移量差异主要是由多项式拟合误差引起。因此上述试验也表明了相关配准中的多项式拟合方法配准精度未必低于几何配准,但多项式阶数、配准窗口数量及其空间分布尚未有严格的理论指导,多项式拟合结果存在不确定性。

|
| 图 7 几何配准与相关配准相干系数差异 Fig. 7 The difference of coherence between geometrical coregistration and cross correlation |
|
| 图 8 几何配准与相关配准之间的偏移量差异 Fig. 8 Relative pixel offset between master and slave in range direction and azimuth direction |
几何配准精度不仅可以克服地形起伏对影像干涉对局部偏移量的影响,满足条带模式影像干涉处理的要求,而且偏移量估计误差具有一致性。聚束模式和Burst模式影像干涉配准则是利用几何配准这一特点,依托影像信息对几何配准精度进行优化,以满足干涉处理的要求。当然条带模式影像也可以利用该方法对几何配准结果进行优化,但优化配准后的干涉图相干系数比几何配准相干系数提高不到1%,对条带模式影像干涉图的改善可忽略不计,通常情况下没有必要使用。
2.3 联合几何配准和影像信息的聚束模式影像干涉配准TerraSAR-X聚束模式影像依然为零多普勒投影,其几何配准方法与条带模式一样,但因该模式影像分辨率较高,目前几何配准精度尚不能满足其干涉要求,见表 1,因此聚束模式影像干涉配准需要在几何配准的基础上依托影像信息采用实相关(incoherent cross correlation)或谱分集(spectral diversity)进行残余偏移量估计和校正,否则干涉图相位将出现系统性相位偏差[57]。
图 9为TerraSAR-X滑动聚束模式影像不同配准方案下的干涉图和局部放大图,其中9(a)为仅采用几何配准得到的干涉图,其局部放大图中出现明显的周期性条纹,图 9(b)为几何配准后再次采用谱分集进行残余偏移量改正后得到的干涉图,局部放大图未见异常信号。上述试验表明尽管聚束影像没有出现类似Burst模式影像干涉图拼接时的相位跳变现象,但依然无法忽略几何配准误差带来的干涉图相位相对偏移。为了准确估计和消除几何配准后的聚束模式影像残余偏移量,本文将根据SAR影像配准理论讨论如何合理选择配准方法。其中雷达影像谱分集和相关配准精度Cramer-Rao下限分别如式(4)、式(5)所示[58-59]
 (4)
(4)
 (5)
(5)

|
| 图 9 不同配准精度的滑动聚束模式影像干涉图 Fig. 9 Sliding spotlight interferometric phase for different absolute azimuth coregistration error |
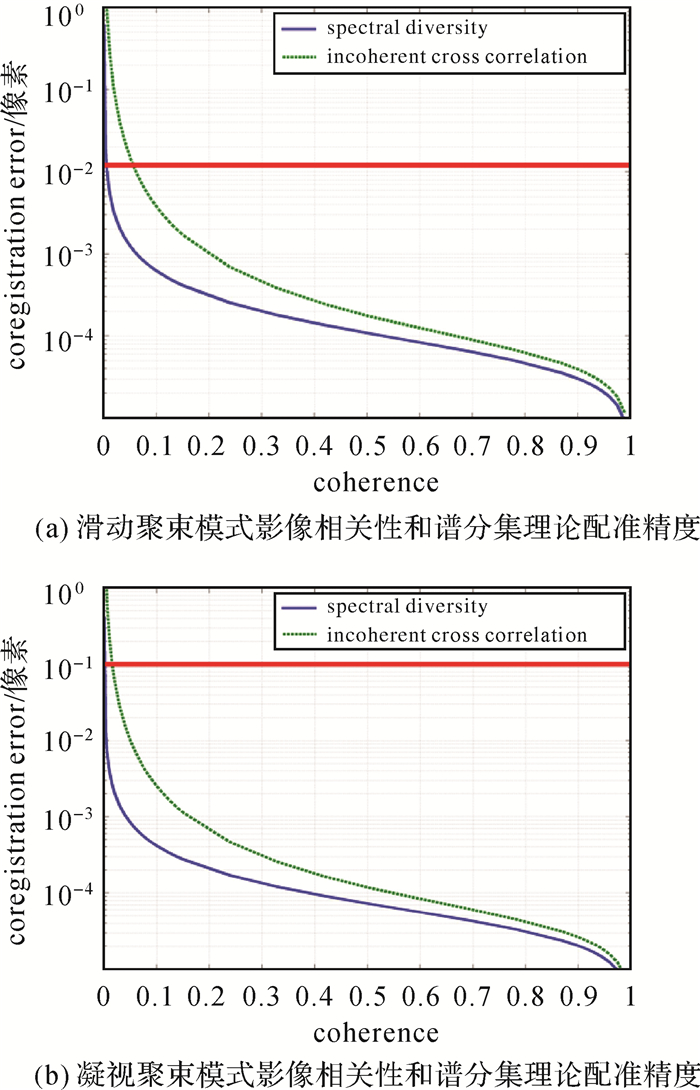
式中,γ为影像相干系数;N为分辨率单元数量;σICC、σSD分别为相关配准和谱分集的标准差,谱分集是按照多普勒带宽三等分进行处理的。由于聚束模式影像持续时间不到1 s,几何配准后残余偏移量被认为是恒定值,影像实相关、谱分集处理窗口即为整景影像,因此聚束模式影像分辨率单元数量N可根据影像像素数量和过采样系数进行计算,凝视聚束模式影像大小为10 912×6185像素,方位向过采样率约为1.12,距离向过采样率约为1.10;滑动聚束模式影像大小为18 221×7946像素,方位向过采样率约为1.11,距离向过采样率约为1.10。根据式(4)和式(5)可得到残余偏移量估计精度Cramer-Rao下限如图 10所示。图中横轴为影像相干系数,纵轴表示配准误差的标准差,红色横线为影像所需要求精度。图 10(a)表明当滑动聚束模式影像相干系数大于0.1时,实相关配准才能满足0.012个像素的精度要求,而谱分集在任何相干条件下均满足精度要求,因此干涉处理时应尽量选用谱分集配准方法。图 10(b)表明凝视聚束模式影像谱分集和实相关配准在任何相干条件下均满足配准精度要求。因此滑动聚束模式影像干涉应采用几何配准与谱分集相结合的方法,凝视聚束模式影像可在几何配准的基础上可任意选择谱分集或相关配准进行偏移量估计和改正。为进一步提高残余偏移量估计的精度和可靠性,本文建议在进行聚束模式影像偏移量估计时引入影像中的点目标,联合谱分集或者相关配准进行干涉处理。
|
| 图 10 聚束模式影像相关性与谱分集理论配准精度 Fig. 10 Theoretical accuray for the estimated misregistration using ICC and SD |
3 几何配准精度影响因素
Burst模式影像干涉处理通常需要极高的方位向配准精度,如Sentinel-1卫星TOPS模式影像需达到0.001像素,TerraSAR-X卫星TOPS模式影像需达到0.000 65像素[60-62]。目前精密轨道条件下的几何配准尚无法满足如此高精度的配准要求,需要利用Burst重叠区域采用增强谱分集技术估计和改正几何配准后的残余偏移量[63-64]。Burst模式影像干涉已被其他文献详细研究,此处不再赘述[65-66]。鉴于Sentinel-1卫星提供两种类型精密轨道,本节则以该卫星TOPS模式作为研究对象,着重研究不同类型DEM和轨道对几何配准精度的影响。
目前用于几何配准和差分干涉处理的数字高程模型主要包括采样间隔为30 m的SRTM v4.1、AW3D,以及采样间隔为90 m的SRTM v2.1,他们均以EGM96重力场模型作为高程基准,其高程精度理论上均满足Sentinel-1几何配准的需要[67-68]。为了测试不同DEM对几何配准的影响,本文选取Sentinel-1卫星142轨道的126个Burst进行干涉处理,并采用增强谱分集估计几何配准的残余偏移量。影像自南向北跨越9省,覆盖山地、平原、丘陵、高原等多种地貌(图 11),SRTM v4.1对应的残余偏移量估计结果如图 12所示。从中可以看出尽管这种超长条带影像是卫星沿着同一轨道进行拍摄的,但其残余偏移量依然会发生明显变化。理论上残余偏移量主要是由轨道和DEM误差引起的,本文将进一步分析两者对几何配准误差的影响程度。

|
| 图 11 Sentinel-1卫星142轨道覆盖我国东部区域地形图 Fig. 11 The topographic map covered by Sentinel-1 image from ascending track 142 over Eastern China |

|
| 图 12 几何配准后增强谱分集估计的方位向偏移量分布 Fig. 12 Azimuth offset estimated by enhance spectral diversity |
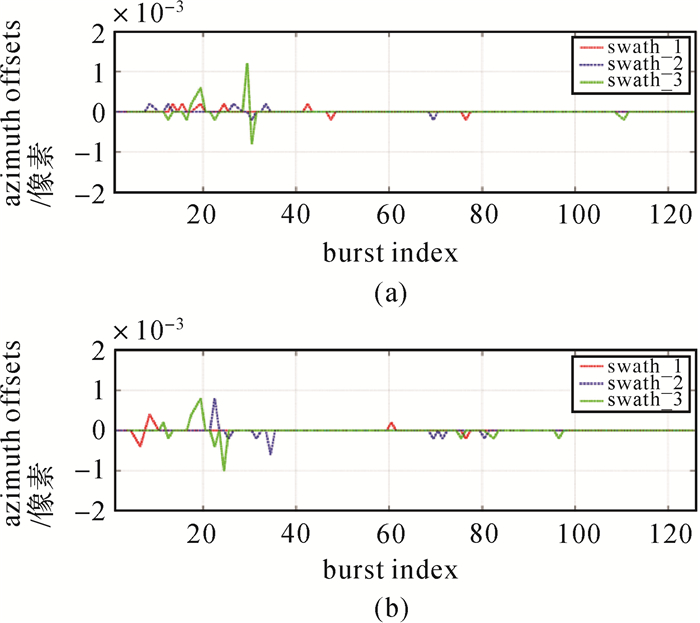
本文进一步以SRTM v4.1对应的增强谱分集估计结果为参考,图 13(a)为SRTM_2.1对应增强谱分集与参考增强谱分集的差分结果,图 13(b)为AW3D对应增强谱分集和参考增强谱分集之间的增强谱分集差分结果,除了覆盖武夷山脉的Burst_5—Burst_35对应结果存在明显跳变,其他Burst未发生明显变化,可认为在相同轨道条件下不同DEM几何配准后残余偏移量基本上是一致的。覆盖武夷山区的增强谱分集估计结果之所以出现较大的变化,是因为武夷山脉地区地形起伏较大(图 11(b)),植被覆盖率较高,影像相干系数较低,本文引用周期图方法估计残余偏移量,增强谱分集干涉相位细微差异则可能导致偏移量估计值发生较大的变化[69-70]。另外增强谱分集估计结果均需要进行多项式拟合,图中跳变值上下波动,无明显系统误差,不会影响最终的偏移量计算结果。因此目前常用的SRTM、AW3D均满足Sentinel-1影像配准的要求,其几何配准差异在0.001像素以内,干涉处理时可任意选择不同类型DEM对Sentinel-1影像进行配准。
|
| 图 13 SRTM30/90、AW3D对应的增强谱分集估计结果之间的差异 Fig. 13 Comparison of azimuth offset estimated by enhance spectral diversity based on free digital elevation data sets(SRTM 30/90, AW3D) |
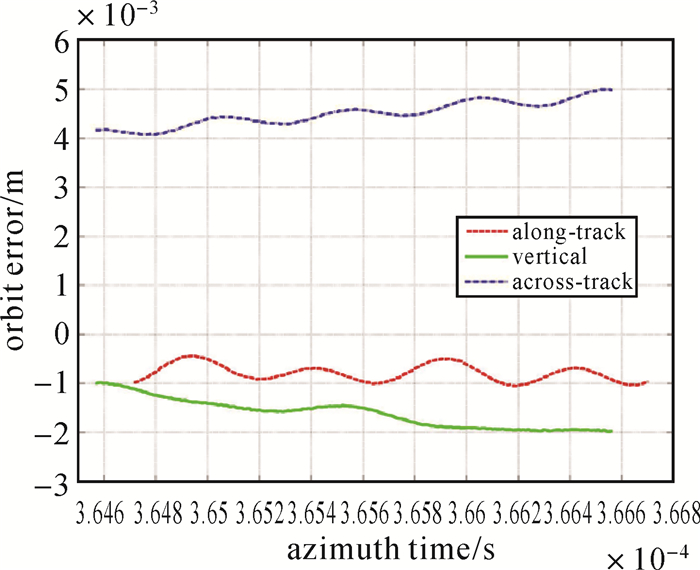
欧空局还提供了Sentinel-1卫星近实时精密轨道(restituted orbit),其精度(约为10 cm)低于精密轨道。如图 14所示,试验影像所对应两种类型轨道位置差异在0.5 cm以内,切向差异在0.1 cm以内。尽管两种类型轨道差异并不大,但干涉处理时两种卫星轨道所对应的增强谱分集差异为0.000 2像素(图 15)。试验表明几何配准误差主要是由卫星轨道误差引起的,特别是切向误差,增强谱分集估计的影像偏移量主要反映了卫星轨道切向基线误差变化情况,这与式(3)的结论是一致的DEM。图 12中所有Burst几何配准后的残余偏移量均小于0.01像素,根据上述结论可以推导出影像对应的轨道切向误差优于10 cm。
|
| 图 14 不同类型精密轨道差异 Fig. 14 The Difference between RES obits and POE orbits |

|
| 图 15 分别采用POE和RES精密轨道的残余偏移量差异 Fig. 15 The difference of residual offset estimated by enhanced spectral diversity between RES and POE orbits |
4 结论
几何配准理论严格,配准精度不受影像相干性和地形影响。未来发射的SAR卫星精密轨道将普遍使用GNSS定规技术,定规精度达到厘米级,几何配准将普遍适用于未来的卫星影像干涉处理中。TerraSAR-X、Sentinel-1等高精度轨道卫星几何配准已可用于条带模式影像干涉配准,但尚无法满足Burst模式、聚束模式的干涉配准精度要求。聚束模式影像干涉配准需要在几何配准的基础上采用相关配准或者谱分集进行残余偏移量校正,Burst模式则需要利用增强谱分集进行残余偏移量校正。由于几何配准精度由卫星轨道和DEM决定,本文进一步利用Sentinel-1卫星影像评估不同轨道和DEM条件下对几何配准的影响,结果表明卫星轨道是几何配准误差的主要来源,常用的DEM(如SRTM、AW3D)几何配准差异远小于0.001像素,理论上均可进行Senitnel-1影像干涉配准处理。
致谢: 感谢香港理工大学吴松波、梁鸿俞、张泽宇,武汉大学温扬茂、胡纪元,西安电子科技大学纪晓楠,安徽大学张鹏飞,首都师范大学陈蜜在本文创作过程中给予的帮助和支持。
| [1] | CURLANDER J C, MCDONOUGH R N. Synthetic aperture radar:systems and signal processing[M]. Hoboken: Wiley-Interscience, 1991. |
| [2] | ARIKAN M, VAN LEIJEN F, GUANG Liu, et al. Improved image alignment under the influence of elevation[C]//Proceedings of Fringe 2007 Workshop. Frascati, Italy: ESA, 2007. |
| [3] | ADAM N, EINEDER M, SCHÄTTLER B, et al. First TerraSAR-X interferometry evaluation[C]//Proceedings of Fringe 2007. Frascati, Italy: ESA, 2007. |
| [4] | FRITZ T, BREIT H, EINEDER M, et al. Interferometric SAR processing: from TerraSAR-X to TanDEM-X[C]//Proceedings of EUSAR 20018, European Conference on Synthetic Aperture Radar. Friedrichshafen, Germany: VDE, 2008: 1-4. |
| [5] | EINEDER M, ADAM N, BRCIC R, et al. High bandwidth spotlight SAR interferometry with TerraSAR-X[C]//Proceedings of IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium. Boston, MA: IEEE, 2008. |
| [6] | HOOPER A J. Persistent scatterer radar interferometry for crustal deformation studies and modeling of volcanic deformation[D]. Stanford: Stanford University, 2006. |
| [7] | HUANYIN Yue, HANSSEN R, KIANICKA J, et al. Sensitivity of topography on INSAR data coregistration[C]//Proceedings of 2004 Envisat & ERS Symposium (ESA SP-572). Salzburg, Austria: ESA, 2005. |
| [8] | NITTI D O, HANSSEN R F, REFICE A, et al. Impact of DEM-assisted coregistration on high-resolution SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(3): 1127–1143. |
| [9] | SCHUBERT A, MIRANDA N, GEUDTNER D, et al. Sentinel-1A/B combined product geolocation accuracy[J]. Remote Sensing, 2017, 9(6): 607. DOI:10.3390/rs9060607 |
| [10] | WEYDAHL D J, ELDHUSET K. Sub-meter geoposition accuracy of image pixels in TerraSAR-X data[C]//Proceedings of ESA Living Planet Symposium. Bergen, Norway: ESA, 2010. |
| [11] | NONAKA T, ISHIZUKA Y, YAMANE N, et al. Evaluation of the geometric accuracy of TerraSAR-X[C]//Proceedings of ISPRS, Beijing: Elsevier BV, 2008: 135-140. |
| [12] | ADAM N, KAMPES B, EINEDER M, et al. The development of a scientific permanent scatterer system[C]//Proceedings of ISPRS Workshop High Resolution Mapping from Space. Hannover, Germany: ISPRS, 2003: 6-8. |
| [13] | YAGUE-MARTINEZ N, EINEDER M, BRCIC R, et al. TanDEM-X mission: SAR image coregistration aspects[C]//Proceedings of the 8th European Conference on Synthetic Aperture Radar. Aachen, Germany: VDE, 2010: 1-4. |
| [14] |
廖明生, 王腾.
时间序列InSAR技术与应用[M]. 北京: 科学出版社, 2014.
LIAO Mingsheng, WANG Teng. Time series InSAR technology and application[M]. Beijing: Science Press, 2014. |
| [15] |
王邦松, 张继贤, 卢丽君, 等.
利用Voronoi图辅助星载干涉雷达配准[J]. 武汉大学学报(信息科学版), 2016, 41(10): 1339–1343.
WANG Bangsong, ZHANG Jixian, LU Lijun, et al. A space-borne InSAR image registration by aided by a Voronoi diagram[J]. Geomatics and Information Science of Wuhan University, 2016, 41(10): 1339–1343. |
| [16] |
赵志伟, 杨汝良, 祁海明.
一种改进的星载干涉SAR复图像最大频谱配准算法[J]. 测绘学报, 2008, 37(1): 64–69.
ZHAO Zhiwei, YANG Ruliang, QI Haiming. An improved maximum spectrum peak co-registration algorithm for space-borne InSAR complex data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 64–69. DOI:10.3321/j.issn:1001-1595.2008.01.012 |
| [17] |
王青松, 瞿继双, 黄海风, 等.
联合实、复相关函数的干涉SAR图像配准方法[J]. 测绘学报, 2012, 41(4): 563–569.
WANG Qingsong, QU Jishuang, HUANG Haifeng, et al. A method based on integrating real and complex correlation function for InSAR image coregistration[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 563–569. |
| [18] |
赵志伟.星载扫描干涉合成孔径雷达系统及信号处理技术[D].北京: 中国科学院研究生院, 2007. ZHAO Zhiwei. The techniques for space-borne scan interferometric synthetic aperture radar system and signal processing[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2007. |
| [19] | 张登荣, 俞乐. 一种高精度的干涉雷达复数影像配准方法[J]. 遥感学报, 2007, 11(4): 563–567. |
| [20] |
彭曙蓉, 王耀南, 刘国才.
基于边缘提取和改进型整体松弛匹配算法的InSAR复图像配准方法[J]. 测绘学报, 2007, 36(1): 62–66, 77.
PENG Shurong, WANG Yaonan, LIU Guocai. A method improving registration accuracy progressively for InSAR complex image[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 62–66, 77. DOI:10.3321/j.issn:1001-1595.2007.01.011 |
| [21] | BAMLER R, EINEDER M. Split band interferometry versus absolute ranging with wideband SAR systems[C]//Proceedings of IGARSS 2004, 2004 IEEE International Geoscience and Remote Sensing Symposium. Anchorage, Alaska: IEEE, 2004: 980-984. |
| [22] | DE ZAN F. Coherent shift estimation for stacks of SAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1095–1099. |
| [23] | DE ZAN F, PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M. On the dependence of delta-k efficiency on multilooking[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1745–1749. DOI:10.1109/LGRS.2015.2424272 |
| [24] | DE ZAN F, PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M. The theoretical performance of different algorithms for shift estimation between SAR images[C]//Proceedings of EUSAR 2018, European Conference on Synthetic Aperture Radar. Aachen, Germany: VDE, 2018. |
| [25] | PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M, DEKKER P L, et al. Considerations of the orbital tube for interferometric applications[C]//Proceedings of ESA Fringe Workshop. Fringe, Frascati, Italy: ESA, 2015: 1-4. |
| [26] | PRATS-IRAOLA P, SCHEIBER R, MAROTTI L, et al. TOPS interferometry with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3179–3188. |
| [27] | HANSSEN R, BAMLER R. Evaluation of interpolation kernels for SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 318–321. |
| [28] | CAFFORIO C, GUCCIONE P, GUARNIERI A M. Doppler centroid estimation for ScanSAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(1): 14–23. |
| [29] | BREIT H, FRITZ T, BALSS U, et al. TerraSAR-X SAR processing and products[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 727–740. |
| [30] | YAGUE-MARTINEZ N, RODRIGUEZ-GONZALEZ F R, BALSS U, et al. TerraSAR-X TOPS, ScanSAR and WideScanSAR interferometric processing[C]//Proceedings of EUSAR 2014, European Conference on Synthetic Aperture Radar. Berlin, Germany: VDE, 2014: 1-4. |
| [31] | BOERNER E, BALSS U, EINEDER M. Simulation of distributed spotlight raw data from X-SAR/SRTM stripmap data[C]//Proceedings of IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium. Anchorage, Alaska: IEEE, 2004. |
| [32] | BAMLER R, HOLZNER J. ScanSAR interferometry for Radarsat-2 and Radarsat-3[J]. Canadian Journal of Remote Sensing, 2004, 30(3): 437–447. |
| [33] | HOLZNER J. Signal theory and processing for burst-mode and ScanSAR interferometry[D]. Edinburgh, UK: University of Edinburgh, 2002. |
| [34] | GUCCIONE P. Interferometry with ENVISAT wide swath ScanSAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 377–381. |
| [35] | HOLZNER J, BAMLER R. Burst-mode and ScanSAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 1917–1934. DOI:10.1109/TGRS.2002.803848 |
| [36] | GUARNIERI A M, PRATI C. ScanSAR focusing and interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(4): 1029–1038. DOI:10.1109/36.508420 |
| [37] | EINEDER M, FRITZ T, MITTERMAYER J, et al. TerraSAR-X ground segment, basic product specification[EB/OL].[2008-02-24]. https://www.dlr.de/Portaldata/1/Resources/raumfahrt/weltraum/TX-GS-DD-3302_Basic-Product-Specification-Document_1.5.pdf. |
| [38] | MITTERMAYER J, KRAUS T, LÓPEZ-DEKKER P, et al. Wrapped staring spotlight SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 5745–5764. |
| [39] |
吴文豪, 王明洲, 李沙, 等.
滑动聚束模式SAR影像干涉处理方法[J]. 武汉大学学报(信息科学版), 2015, 40(12): 1588–1593.
WU Wenhao, WANG Mingzhou, LI Sha, et al. Analysis of sliding spotlight SAR interferometry[J]. Geomatics and Information Science of Wuhan University, 2015, 40(12): 1588–1593. |
| [40] | SCHEIBER R, JÄGER M, PRATS-IRAOLA P, et al. Speckle tracking and interferometric processing of TerraSAR-X TOPS data for mapping nonstationary scenarios[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(4): 1709–1720. DOI:10.1109/JSTARS.2014.2360237 |
| [41] |
吴文豪, 周志伟, 李陶, 等.
精密轨道支持下的哨兵卫星TOPS模式干涉处理[J]. 测绘学报, 2017, 46(9): 1156–1164.
WU Wenhao, ZHOU Zhiwei, LI Tao, et al. A study of Sentinel-1 TOPS mode Co-registration[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1156–1164. DOI:10.11947/j.AGCS.2017.20160352 |
| [42] |
吴文豪.哨兵雷达卫星TOPS模式干涉处理研究[D].武汉: 武汉大学, 2016. WU Wenhao. TOPS interferometry with Sentinel-1[D]. Wuhan: Wuhan University, 2016. |
| [43] | PRATS P, MAROTTI L, WOLLSTADT S, et al. TOPS Interferometry with TerraSAR-X[C]//8th European Conference on Synthetic Aperture Radar. Aachen, Germany: VDE, 2010: 1-4. |
| [44] | YAGVE-MARTÍNEZ N, PRATS-IRAOLA P, GONZÁLEZ F R, et al. Interferometric processing of sentinel-1 TOPS data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2220–2234. |
| [45] | SANSOSTI E, BERARDINO P, MANUNTA M, et al. Geometrical SAR image registration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2681–2870. |
| [46] | KAHLE R, D'AMICO S. The TerraSAR-X precise orbit control-concept and flight results[C]//Proceedings of International Symposium on Space Flight Dynamics (ISSFD). Laurel, MD: DLR, 2014. |
| [47] | FERNANDEZ C. Sentinels POD Team, sentinels POD service file format specifications[EB/OL]. ESA, Paris, France, Tech. Rep. GMESGSEG-EOPG-FS-10-0075, [2018-01-18]. https://sentinel.esa.int/documents/247904/351187/GMES_Sentinels_POD_Service_File_Format_Specification. |
| [48] | D'ERRICO. Distributed space missions for earth system monitoring[M]. New York: Springer-Verlag, 2013. |
| [49] | BÄHR H. Orbital effects in spaceborne synthetic aperture radar interferometry[M]. Karlsruhe, Germany: KIT Scientific, 2013. |
| [50] | PRATS-IRAOLA P, RODRIGUEZ-CASSOLA M, DE ZAN F, et al. Role of the orbital tube in interferometric spaceborne SAR missions[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(7): 1486–1490. DOI:10.1109/LGRS.2015.2409885 |
| [51] | KRAUS T, SCHRANK D, RIZZOLI P, et al. In-orbit performance of TerraSAR-X and TanDEM-X satellites[C]//Proceedings of URSI Commission F-triennial Open Symposium on Radio Wave Propagation and Remote Sensing. Garmisch-Partenkirchen, Germany: IEEE, 2011: 1-6. |
| [52] | PRATS-IRAOLA P, NANNINI M, SCHEIBER R, et al. Interferometric investigations with the Sentinel-1 constellation[C]//Proceedings of ESA FRINGE Workshop. Helsinki, Finland: ESA Publication. 2017: 5537-5540. |
| [53] | HACKEL S, MONTENBRUCK O, STEIGENBERGER P, et al. Model improvements and validation of TerraSAR-X precise orbit determination[J]. Journal of Geodesy, 2017, 91(5): 547–562. |
| [54] | PETER H, JÄGGI A, FERNÁNDEZ J, et al. Sentinel-1A-first precise orbit determination results[J]. Advances in Space Research, 2017, 60(5): 879–892. |
| [55] | DOORNBOS E, SCHARROO R, KLINKRAD H, et al. Improved modelling of surface forces in the orbit determination of ERS and Envisat[J]. Canadian Journal of Remote Sensing, 2002, 28(4): 535–543. DOI:10.5589/m02-055 |
| [56] | KUIJPER D. Envisat ASAR interferometry baseline results of the current Envisat orbit maintenance strategy[C]//Proceedings of SpaceOps 2008 Conference. Heidelberg, Germany: AIAA Space Operations, 2013. |
| [57] | EINEDER M, ADAM N, BAMLER R, et al. Spaceborne spotlight SAR interferometry with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(5): 1524–1535. |
| [58] | BAMLER R, EINEDER M. Accuracy of differential shift estimation by correlation and split-width interferometry for wideband and delta-k SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 151–155. |
| [59] | DE ZAN F. Accuracy of incoherent speckle tracking for circular Gaussian signals[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 264–267. DOI:10.1109/LGRS.2013.2255259 |
| [60] | FERNANDO R G, BRCIC R, YAGUE-MARTINEZ N, et al. Demonstration of TerraSAR-X ScanSAR persistent scatterer interferometry[C]//Proceedings of ESA Fringe Workshop (SP-731). Fringe, Frascati, Italy: ESA Publication, 2015. |
| [61] | DE ZAN F, PRATS-IRAOLA P, SCHEIBER R, et al. Interferometry with TOPS: Coregistration and azimuth shifts[C]//Proceedings of European Conference on Synthetic Aperture Radar (EUSAR). Berlin Offenbach, Germany: VDE, 2014: 1-4. |
| [62] | FATTAHI H, AGRAM P, SIMONS M. A network-based enhanced spectral diversity approach for TOPS time-series analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 777–786. |
| [63] | BAMLER R, EINEDER M, MONTI G A, et al. Session summaries: InSAR theory session[C]//Proceedings of the ESA FRINGE Workshop. Fringe, Frascati, Italy: ESA Publication, 2015. |
| [64] | PRATS P, MAROTTI L, WOLLSTADT S, et al. Investigations on TOPS interferometry with TerraSAR-X[C]//Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium. Honolulu, HI: IEEE, 2010. |
| [65] | XU Bing, LI Zhiwei, FENG Guangcai, et al. Continent-wide 2-D co-seismic deformation of the 2015Mw 8.3 Illapel, Chile earthquake derived from Sentinel-1a data:correction of azimuth co-registration error[J]. Remote Sensing, 2016, 8(5): 376. |
| [66] | GRANDIN R. Interferometric processing of SLC Sentinel-1 TOPS data[C]//Proceedings of Fringe2015: Advances in the Science and Applications of SAR Interferometry and Sentinel-1 InSAR Workshop. Frascati, Italy: ESA Publication, 2015. |
| [67] | HU Zhihua, PENG Jianwei, HOU Yaolin, et al. Evaluation of recently released open global digital elevation models of Hubei, China[J]. Remote Sensing, 2017, 9(3): 262. |
| [68] | GROHMANN C H. Evaluation of TanDEM-X DEMs on selected Brazilian sites:comparison with SRTM, ASTER GDEM and ALOS AW3D30[J]. Remote Sensing of Environment, 2018(212): 121–133. |
| [69] | SAKAR N, BRCIC R, GONZALEZ F R, et al. An advanced co-registration method for TOPSAR interferometry[C]//Proceedings of 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Milan, Italy: IEEE, 2015. |
| [70] | YAGUE-MARTINEZ N, DE ZAN F, PRATS-IRAOLA P. Coregistration of interferometric stacks of Sentinel-1 TOPS data[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(7): 1002–1006. |



