2. 高速铁路运营安全空间信息技术国家地方联合工程实验室, 四川 成都 610031;
3. 高速铁路线路工程教育部重点实验室, 四川 成都 610031
2. State-province Joint Engineering Laboratory of Spatial Information Technology of High-Speed Railway Safety, Chengdu 610031, China;
3. Key Laboratory of High-speed Railway Engineering, Ministry of Education, Chengdu 610031, China
观测值中含有粗差时,采用最小二乘法求得的参数估值会严重偏离其真值,消除或削弱粗差的影响是获取精确、可靠参数估值的必要前提。以最小二乘估计为基础的粗差探测方法,无论是均值漂移模型[1-3]中统计检验量的建立,还是方差膨胀模型[4-7]中等价权的构造,都依赖最小二乘残差或单位权中误差。然而对最小二乘估计,粗差只能部分地反映在相应的观测值残差上,甚至含有粗差的观测值不一定对应着大的改正数[8-9],因此容易导致粗差的误判。实际上,对线性最小二乘估计,最小二乘残差是各个观测值的线性函数,在数值上与各观测值组成的条件方程闭合差相等但符号相反[10]。当观测值含有粗差时,在相应的条件方程闭合差中,L1范数估计较LS估计更能集中反映粗差,因此探测粗差的能力更强。对L1范数估计在测量数据处理中的应用,国内外学者作了大量的研究工作。文献[11]根据Bahadur型线性表达式导出了L1范数估计的方差-协方差矩阵,在此基础上,文献[12]导出了L1范数估计的巴尔达统计量并讨论了其可靠性。文献[13]采用线性规划的单纯形法进行摄影测量中相对定向的粗差检测。文献[14]采用单纯形法讨论了L1范数估计在测量控制网观测值粗差探测中的应用。文献[15]研究了秩亏高斯马尔可夫模型下的L1范数估计单纯形算法。文献[16]研究了线性平差模型的L1范数估计的递归算法。文献[17]通过对相关观测值进行去相关化处理,将单纯形法用于GNSS基线网的粗差探测。
L1范数估计在测量领域受到广泛的关注和研究,正是因为它具有良好的抗差性质,不仅求得的未知参数估值少受甚至不受粗差观测值的影响,而且粗差能够集中反映在相应的闭合差中,从而有助于粗差的发现与定位。然而,在采用L1范数估计解决粗差探测问题的过程中发现,存在一类观测值,虽然具有粗差发现和定位能力,但其含有的粗差无论是多大量级都不能准确定位。若测量系统存在L1抗差性失效点(robustness failpoint in L1-norm estimation, RFP-L1),由于其在平差系统中的位置及是否含有粗差等情况都是未知的,因此无法确保基于L1范数的粗差探测结果的准确性和可靠性,因为只有当RFP-L1不含粗差时结果才会是可靠的,而这无疑会使得粗差定位结果带有不确定性。对此,RFP-L1的识别及其粗差的探测将是解决该问题的关键[18],因为只有确定测量系统中不存在RFP-L1,或存在时能够准确识别其位置并对其是否含有粗差作出准确判断,这种不确定性才能得以消除。考虑到最小二乘的选权迭代法(iteratively reweighed least squares, IRLS)和线性规划的单纯形法等两种L1范数估计的求解方法中,IRLS方法要依赖最小二乘残差确定初始迭代权,当初始值偏离真值较大时最终的估计结果将会极不可靠[8, 16],从而会引入新的不确定性因素。单纯形法求解过程不需要进行最小二乘运算。因此,本文从观测方程出发,结合单纯形法L1范数平差算法,探索研究测量系统中RFP-L1观测值的一般特征和识别方法。
1 条件方程与影响系数平差问题的函数模型为
 (1)
(1)
式中,L为观测值向量;B为设计矩阵;X为未知参数向量;d为常数向量。
由式(1),经矩阵初等变换运算或采用单纯形法,可导出条件方程[19-20]
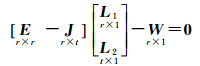 (2)
(2)
式中,[L1 L2]T为观测值向量;E为L1对应的系数矩阵且为单位矩阵;-J为L2对应的系数矩阵;W为闭合差向量。
实际上,式(2)中的J为粗差判断方程的判断矩阵。令A=E-J,A即为条件方程的系数矩阵。A矩阵中第j列向量Aj元素绝对值和ζj为
 (3)
(3)
观测值Lj中若含有大小为Δg的粗差,其对闭合差向量带来的影响ΔWg为
 (4)
(4)
从式(4)可以看出,向量Aj实质上就是Lj中粗差在闭合差向量中的投影向量。
设r个条件方程闭合差的绝对值和为Z,则由式(3)、式(4)可知,Lj中的粗差Δg反映在Z上的大小决定于ζj,当式(2)中Lj在L1时,ζj=1,粗差等量反映在Z中;当Lj在L2中时,ζj不一定为1,粗差会被放大或缩小后反映在Z中。ζj反映的是粗差Δg对函数Z影响程度的大小,为叙述方便,本文称ζj为观测值Lj的粗差对闭合差绝对值和(Z)的影响系数,简称影响系数。
若以残差绝对值和最小为准则,采用单纯形法对测量系统的观测方程进行求解[14],根据其解的结构可知,在单纯形解中,有t个未知参数和r个观测值残差为基变量,剩余的t个观测值残差为取值为零的非基变量。这就说明,t个未知参数是由t个非基变量决定的[10],可以由非基变量对应的观测方程组求得,而余下的r个多余观测值残差可以通过t个未知参数计算得到,目标函数等于r个作为基变量的观测值残差的绝对值和[21]。由此可知,采用单纯形法可以得到形如式(2)的条件方程,而此时各条件方程闭合差的绝对值和Z实质上就是采用单纯形法取得最优解时的目标函数,对于给定的测量系统,要使得Z取得最小值,在偶然误差服从正态分布时,不考虑粗差相互抵消的情况,Lj中的粗差对Z的贡献应达到最小,即观测值Lj的影响系数ζj取各种可能取值中的最小值ζjMIN。
2 最小影响系数与RFP-L1为方便进一步分析最小影响系数与RFP-L1间的关系,结合式(2)引入RFP-L1,即具有粗差发现与定位能力的观测值L′,无论其含有多大量级的粗差,单纯形法求得的式(2)中,其始终位于L2,粗差无法被准确定位[19]。
下面就非RFP-L1和RFP-L1最小影响系数ζMIN的可能取值情况进行分析。
对观测值Lj为非RFP-L1的情况,当Lj中的粗差足够大时,单纯形解中,其以多余观测值的形式出现,从而粗差可以被准确发现和定位。由单纯形解构造的条件方程中,Lj在L1中,其影响系数ζj取得最小值,且ζjMIN=1。
对观测值Lj为RFP-L1的情况,显然,单纯形法得到的条件方程中,Lj必然位于L2。由式(2)构造适用于粗差探测问题的线性规划的标准型[10]。
(1) 目标函数
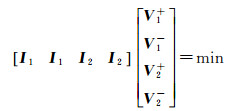 (5)
(5)
(2) 约束条件
 (6)
(6)
式中,V1、V2分别为r维L1残差向量和t维L2残差向量,其中,V1=V1+-V1-,V2=V2+-V2-,V1+、V1-、V2+和V2-的所有元素均为非负,且有V1+与V1-、V2+与V2-相互之间对应的非负元素不同时为非零;I1为r维元素全为1的行向量;I2为t维元素全为1的行向量;l=W-(L1-JL2)。
采取以下的原则选取初始基变量。
(1) 选取的基变量V′i(i=1, 2, …, r)来自V1。
(2) 若li≥0,取V′i=V1i+,若li < 0,取V′i=V1i-。其中,V1i为V1中第i个元素,V1i=V1i+-V1i-,V1i+和V1i-均为非负且不同时为非零。容易理解,如此选取的初始基变量V′实际上就是单纯形法的最优解形式。
在单纯形法求解过程中,检验数r为[13]
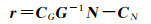 (7)
(7)
式中,CG=[1, 1, …, 1]和CN=[1, 1, …, 1]分别为基变量和非基变量对应的目标函数式(5)中的1×r和1×(2n-r)系数向量;G为r×r基变量系数矩阵,由式(6)中E和-E的列向量组成;N为r×(2n-r)非基变量系数矩阵,由式(6)中E、-E、J和-J的列向量组成。
在取得最优解时,式(7)中非基变量的检验数均不大于0,而当非基变量的检验数等于0时,表明单纯形最优解有无穷多组[22-23],该非基变量在最终的单纯形解中也可以基变量的形式出现。因此,对于RFP-L1粗差观测值Lj的残差Vj+、Vj-,在采用单纯形法取得最优解时始终均位于非基变量中,其对应检验数应严格小于0。即
 (8)
(8)
式中,Nj为Lj的残差Vj+在N中的对应列向量;Cj为Lj的残差Vj+和Vj-在目标函数系数向量CN中对应的列。
因Lj中含有粗差,如果其足够大,那么式(6)的闭合差l中,来自粗差的影响相比偶然误差占有绝对的优势,l向量的正负与式(6)中Vj+对应的系数列向量Nj完全同号,并且l向量中的第i个元素li始终与基变量系数矩阵G的第i行i列元素Gii同号。又目标函数系数向量CG、CN中的元素均等于1,G为对角线元素为1或-1的对角阵,其逆矩阵G-1即为其本身,因此式(8)中的,始终成立,对rj+有
 (9)
(9)
由式(9)可得,Vj+在线性规划标准型中对应的系数矩阵列向量Nj满足
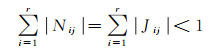 (10)
(10)
式中,Jj为单纯形法求得的条件方程式(2)系数矩阵中粗差观测值Lj对应的列向量。
由于粗差观测值Lj的影响系数ζj在由单纯形解构造的条件方程中取得最小值ζjMIN,结合式(10)可知,RFP-L1观测值Lj的最小影响系数
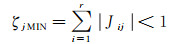 (11)
(11)
由以上分析可得,非RFP-L1和RFP-L1的最小影响系数分别具有以下特征:
(1) 非RFP-L1观测值Lj的影响系数在其为多余观测值时可取得最小值,最小影响系数ζjMIN=1。
(2) RFP-L1观测值Lj的影响系数在其为必要观测值时可取得最小值,最小影响系数ζjMIN < 1。
在常见的测量问题中,高程控制网的函数模型(观测方程)是线性的,其设计矩阵中仅含有±1和0,设计矩阵只与控制点个数、构网形式有关,而与控制点高程和空间位置无关[24]。然而,对测边网、测角(或测方向)网、边角网等平面控制网或三维控制网,其函数模型是非线性的,通常采用给定未知参数概略值线性化得到函数模型,其设计矩阵除了与控制点个数、网形结构有关外,还与控制点的空间位置有关。此外,对线性回归、坐标转换等问题的函数模型虽然是线性的,但其设计矩阵也同样与样本点的个数、空间分布及位置有关,以上这两类测量系统的线性化(或线性)函数模型中未知参数前的系数不会再仅含有±1和0。由线性代数理论可知,对设计矩阵中仅含有±1、0的函数模型,经过矩阵初等变换得到的判断矩阵J[20]中也仅会含有±1和0值,由此可以推断,对具有粗差发现和定位能力的观测值(判断矩阵J中其对应列向量非零元素个数不小于2的观测值),其位于条件方程式(2)的L2时,该观测值对应的列向量元素绝对值和始终不小于2,只有位于条件方程式(2)的L1时可取得影响系数的最小值。
综合以上分析可以得出:
(1) 对观测值具有粗差发现和定位能力且设计矩阵仅含±1和0的测量系统,所有观测值的最小影响系数均等于1,观测值中不存在RFP-L1。
(2) 对设计矩阵除含有±1和0(或不含±1和0)外还含有其他元素的测量系统,观测值中可能会存在RFP-L1,观测值Lj(j=1, 2, …, n)的最小影响系数ζjMIN < 1时,Lj为RFP-L1。
3 RFP-L1的识别根据函数模型设计矩阵的数值特点不难判断出测量系统是否会存在RFP-L1。对一个可能存在RFP-L1的测量系统,由于非RFP-L1和RFP-L1的最小影响系数呈现出明显的差异性,据此也不难判断观测值是否为RFP-L1,而其中最为关键的是计算观测值的最小影响系数ζMIN。粗差观测值Lj的影响系数在利用单纯形法得到的条件方程下可以取得最小值,考虑到间接平差函数模型的计算机自动建立过程比较简便[24],给出一种从观测方程出发计算每个观测值ζMIN的算法。
结合式(1),设计的算法为:
(1) 对观测值具有粗差发现和定位能力的测量系统,式(1)中设计矩阵B,如果其仅含有±1和0值,则所有观测值的最小影响系数等于1,算法结束,否则执行步骤(2)。
(2) 根据式(1)构造线性规划标准型,取目标函数为残差绝对值和最小,采用单纯形法求解条件方程,得到多余观测值向量L1和必要观测值向量L2,令i=1。
(3) 往L2中第i个观测值L2i对应的约束条件常数项l2i中添加一个大粗差Δg(如1000倍观测中误差)。
(4) 采用单纯形法得到条件方程,并根据式(3)计算观测值L2i的最小影响系数ζiMIN。
(5) 如果i=t,算法结束,否则剔除在步骤(3)加入l2i的粗差,令s=i+1,并令i=s,执行步骤(3)。
通过以上步骤,可以求得必要观测值向量L2中各个观测值的最小影响系数,由此即可判断L2中的观测值L2i(i=1, 2,…,t)是否为RFP-L1,若ζiMIN=1,观测值为非RFP-L1;若ζjMIN < 1,观测值为RFP-L1。由于RFP-L1不会出现在单纯形解的多余观测中,因此多余观测向量L1中的观测值不会是RFP-L1、最小影响系数均等于1。
观测值最小影响系数的计算步骤和RFP-L1判别方法,首先进行单纯形求解,将观测值分为L1和L2两部分,然后逐个地把L2中的每一个观测值作为研究对象,从局部来逐一考察并判别每一个观测值是否为RFP-L1。为阐述方便,称为局部分析识别法(local analysis identification method, LAIM)。
需要说明的是,前文的公式推导视观测值为独立且等权,虽然如此,相关结论及RFP-L1识别算法同样适用于观测值独立但不等权的情况,只是在求解时目标函数采用加权残差绝对值和最小。对于相关观测的情况,可以首先采用Cholesky分解法[25]将相关观测等价地转换为独立观测,然后再利用LAIM进行求解。尽管本文的讨论是基于单个粗差假设,不考虑粗差相互抵消的情况,相关结论同样适用于多维粗差情形。此外,对于有t个必要观测的测量系统,LAIM共需进行(t+1)次单纯形法运算,计算效率主要决定于单纯形算法的执行效率。
4 算例分析为验证设计矩阵中仅含“±1”和“0”的测量系统观测值最小影响系数的数值特点,设计了水准网仿真试验;为了进一步检验最小影响系数与RFP-L1观测值的判别关系,并对LAIM方法的有效性进行评价,采用线性回归测量数据进行仿真试验。
4.1 水准网如图 1所示为一水准网,B点高程已知,其余9个点高程待求,全网共计高差观测值18个。
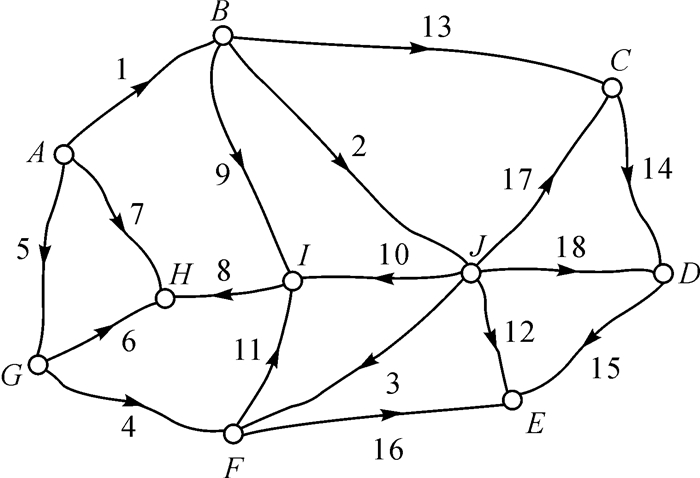
|
| 图 1 水准网 Fig. 1 Leveling network |
观测量对应的观测方程为
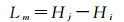 (12)
(12)
式中,Lm为第m个高差观测值(m=1, 2, …, 18);下标i、j为水准点点名(A~J); H为水准点高程参数值或已知高程。
由式(12)可以看出,水准网的每个观测方程中,未知参数的系数为常数1、-1或0,与各水准路线两端水准点高程无关。以L1、L4、L5、L6、L9、L12、L14、L16、L17为必要观测值,得到水准网的判断矩阵J,列于表 1。
| 多余观测值 | 必要观测值 | ||||||||
| L1 | L4 | L5 | L6 | L9 | L12 | L14 | L16 | L17 | |
| L2 | -1 | 1 | 1 | 0 | 0 | -1 | 0 | 1 | 0 |
| L3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | 0 |
| L7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| L8 | -1 | 0 | 1 | 1 | -1 | 0 | 0 | 0 | 0 |
| L10 | 1 | -1 | -1 | 0 | 1 | 1 | 0 | -1 | 0 |
| L11 | 1 | -1 | -1 | 0 | 1 | 0 | 0 | 0 | 0 |
| L13 | -1 | 1 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
| L15 | 0 | 0 | 0 | 0 | 0 | 1 | -1 | 0 | -1 |
| L18 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
由表 1可以看出,水准网的判断矩阵J中仅包含1、-1和0,并且每个必要观测值对应的列向量中非零元素个数至少为2,结合图 1的网形特点,每个水准点的自由度均不小于3,容易得出,水准网中的每个观测值都有粗差发现和定位能力,各种必要观测、多余观测组合形式的判断矩阵J中必要观测值对应列向量非零元素个数始终≥2。由判断矩阵J容易得到水准网的条件方程,可以发现,各个条件方程实质上就是独立闭合环或附合路线,不难理解,对该水准网的各种L1、L2组合形式的条件方程,均反映的是高差观测值之间简单的图形条件关系,在每个条件方程中,观测值的系数为1、-1或0。因此,这类测量系统中,若观测值Lm(m=1, 2, …, n)具有粗差定位能力,且位于条件方程的L2中,则对应的系数列向量非零元素绝对值和必然≥2,即影响系数ζm≥2;如果位于L1中,则对应的系数列向量非零元素绝对值和恒等于1,即影响系数ζm=1。综合这两种情况可知,对水准网中具有粗差定位能力的观测值Lm,最小影响系数ζmMIN=1。
4.2 线性回归表 2为线性回归y=2x+6的模拟数据,其中在y中添加了服从正态分布N(0, 0.52)的随机误差。
| 坐标 | 观测值 | ||||||||
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | |
| x | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 50 |
| y | 35.67 | 38.46 | 39.90 | 41.83 | 44.04 | 45.46 | 48.22 | 49.61 | 105.81 |
对以上的线性回归,有斜率a、截距b两个待求参数。要确定a和b,至少在9组观测值中选择任意两组来构成观测方程进行解算。
采用LAIM方法求取各个观测值的最小影响系数,列于表 3。其中,ζmin为观测值最小影响系数。
| 最小影响系数 | 观测值 | ||||||||
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | |
| ζmin | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 |
从表 3可以看出,L1—L8等8个观测值的最小影响系数均等于1,而L9的最小影响系数小于1,由此不难判断,L9为RFP-L1,而其他观测值不是。为了验证这一结论,设计随机粗差试验:选择Lm(m=1, 2,…,9)中的一个添加粗差,粗差大小介于5~20倍测量中误差之间(2.5~10),粗差的正负号随机,遍历所有观测值,每个观测值添加粗差的试验进行100次,每次试验采用以残差绝对值和最小为目标函数的单纯形法进行求解。分别统计各个观测值的100次随机粗差试验中,单纯形解中其作为多余观测值、必要观测值出现的次数,列于表 4。
| 结果统计 | 观测值 | ||||||||
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | |
| 多余观测次数/次 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 0 |
| 必要观测次数/次 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
从表 4可以看出,L1—L8中的每个观测值在添加粗差时,单纯形解中,粗差观测值都出现在多余观测值中,从而粗差可以完全反映在相应的观测值残差上,粗差均可以定位;L9中无论添加小粗差还是大粗差,单纯形解中都以必要观测值出现,这样粗差就被分配在7个多余观测值残差中,从而粗差无法准确定位。由此可以得出,L1—L9中L9为RFP-L1。为了检验传统粗差处理方法是否能够解决RFP-L1的粗差探测问题,进行以上试验时,同时采用数据探测法和抗差最小二乘法分别进行粗差检核和抗差估计,结果表明,对L1—L8,两种方法可以识别到绝大多数的粗差,但对L9,对介于5~20倍中误差的粗差,两种方法均无法发现粗差。进一步地,往L9中加入更大量级的粗差进行试验,结果表明,当粗差足够大时,数据探测法可以探测到L9中的粗差,抗差最小二乘法也能够识别L9中的粗差。虽然两种传统的粗差处理方法可以处理L9中较大量级的粗差,但均无法有效解决大小为5~20倍中误差的粗差探测问题,而这样量级的粗差却是粗差探测中更为关注的。
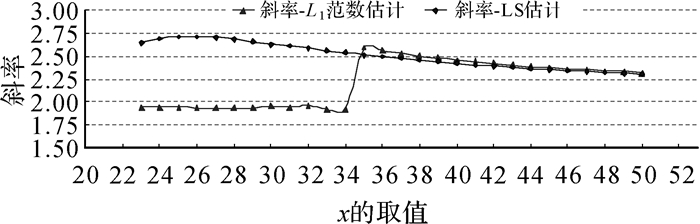
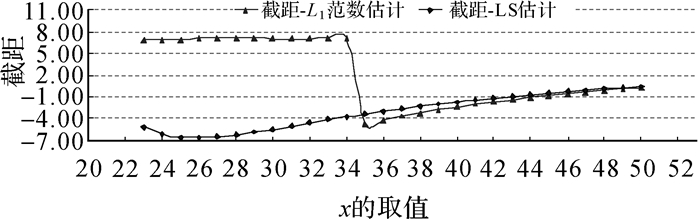
为了进一步分析线性回归算例中L1—L8为非RFP-L1,而L9为RFP-L1的现象,保持L1—L8各观测值中的x和y不变,L9中的x依次取值23~49,对应y值取2x+6,并在y中加入服从N(0, 0.52)的随机误差。采用LAIM方法计算各观测值的最小影响系数,统计发现对L9的各种取值情况,L1—L8的最小影响系数均为1,L9中x取值与其对应的最小影响系数如图 2所示。同时,对L9的各种取值情况,均往L9的y中添加大小为10的粗差,并采用L1范数估计和LS估计方法求得线性回归的斜率a和截距b,结果分别如图 3、图 4所示。
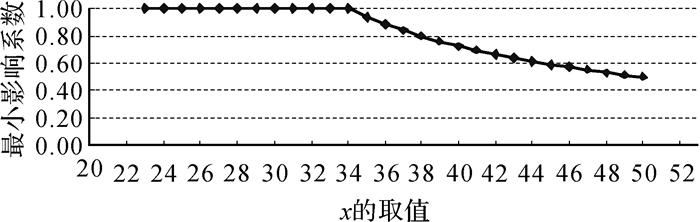
|
| 图 2 L9位置变化时其对应的最小影响系数 Fig. 2 Least influence coefficient corresponding to different positions of L9 |
|
| 图 3 L9位置变化时的斜率 Fig. 3 Slope corresponding to different positions of L9 |
|
| 图 4 L9位置变化时的截距 Fig. 4 Intercept corresponding to different positions of L9 |
由图 2可以看出,L9中x的取值较小时,L9距离其他样本点较近,样本点的空间分布相对均匀,所有观测值的最小影响系数均为1,测量系统中不存在RFP-L1。随着L9中x取值的增大,L9远离其他样本点,其最小影响系数小于1,并逐渐减小,此时单纯形解中,L9中的粗差将被缩放后分配在7个多余观测值残差中,粗差无法正确定位。而且当L9距离其他样本点足够远时,对多余观测值残差进行假设检验甚至可能无法发现粗差。从图 3、图 4可以发现,L9中含有粗差,无论L9中x如何取值,LS估计求得的斜率a和截距b均严重偏离真实值;当L9不为RFP-L1时,L1范数估计求得的斜率a和截距b不受L9中粗差的影响,但随着L9中x取值增大而变为RFP-L1,求得的斜率a和截距b严重偏离真实值。由此可见,对线性回归问题,测量系统存在RFP-L1且含有粗差时,无论是LS估计还是L1范数估计,求得的未知参数均会受到粗差的较大影响;样本点的空间分布是测量系统是否存在RFP-L1的重要影响因素,在采用L1范数估计进行粗差探测分析前,若没进行RFP-L1的识别分析,粗差探测的结果是不可靠的。
综合以上两个算例的试验分析结果可以得出,观测值粗差是否能完全反映在条件方程闭合差函数Z中,与L1、L2的组合形式有关,L1范数估计的目标函数对取得最优解时L1、L2的组合形式起到了约束作用,而最小影响系数ζMIN刻画了观测值粗差投影到L1范数估计目标函数时变化程度的大小;若观测值的最小影响系数小于1,则其为RFP-L1;LAIM可以有效识别出测量系统中的RFP-L1;对函数模型的设计矩阵仅含有1、-1和0的测量系统,不存在RFP-L1观测值。
5 结论针对采用L1范数估计进行粗差探测分析时,存在有一类观测值粗差始终无法准确定位的问题。本文由条件方程,推导出观测值的影响系数计算式,得到最小影响系数大小与RFP-L1观测值的关系,根据矩阵初等变换理论,获得从设计矩阵判断存在RFP-L1观测值的一般性规律。通过算例验证基于最小影响系数识别RFP-L1方法的有效性,并得到如下结论:
(1) 采用L1范数估计探测粗差时,若存在RFP-L1观测值,则粗差会被分配到其他观测值的残差中,粗差将不能准确定位。因此,利用L1范数估计进行粗差检验时应先进行观测值的RFP-L1识别,否则粗差探测的结果将会是错误的。
(2) 最小影响系数直观地描述了观测值粗差对L1范数估计目标函数的影响关系,在残差绝对值和最小的准则下,非RFP-L1的最小影响系数为1,RFP-L1的最小影响系数小于1。
(3) 设计矩阵中仅含有±1和0的测量系统,具有粗差发现和定位能力的观测值,最小影响系数均等于1,不存在RFP-L1问题。
篇幅所限,有关RFP-L1问题解决方法的研究将另文介绍。
| [1] | BAARDA W. A testing procedure for use in geodetic networks[M]. Delft: Netherlands Geodetic Commission, 1968: 27-55. |
| [2] |
於宗俦, 李明峰.
多维粗差的同时定位与定值[J]. 武汉测绘科技大学学报, 1996, 21(4): 323–329.
YU Zongchou, LI Mingfeng. Simultaneous location and evaluation of multidimensional gross errors[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996, 21(4): 323–329. |
| [3] |
欧吉坤.
粗差的拟准检定法(QUAD法)[J]. 测绘学报, 1999, 28(1): 15–20.
OU Jikun. Quasi-accurate detection of gross errors (QUAD)[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 15–20. DOI:10.3321/j.issn:1001-1595.1999.01.004 |
| [4] |
李德仁.
利用选择权迭代法进行粗差定位[J]. 武汉测绘科技大学学报, 1984, 9(1): 46–68.
LI Deren. Gross error location by means of the iteration method with variable weights[J]. Geomatics and Information Science of Wuhan University, 1984, 9(1): 46–68. |
| [5] | RANGELOVA E, FOTOPOULOS G, SIDERIS M G. On the use of iterative re-weighting least-squares and outlier detection for empirically modelling rates of vertical displacement[J]. Journal of Geodesy, 2009, 83(6): 523–535. DOI:10.1007/s00190-008-0261-6 |
| [6] | YANG Y, SONG L, XU T. Robust estimator for correlated observations based on bifactor equivalent weights[J]. Journal of Geodesy, 2002, 76(6-7): 353–358. DOI:10.1007/s00190-002-0256-7 |
| [7] |
杨元喜.
抗差估计理论及其应用[M]. 北京: 解放军出版社, 1993.
YANG Yuanxi. Robust estimation theory and its applications[M]. Beijing: PLA Press, 1993. |
| [8] | BASELGA S. Global optimization solution of robust estimation[J]. Journal of Surveying Engineering, 2007, 133(3): 123–128. DOI:10.1061/(ASCE)0733-9453(2007)133:3(123) |
| [9] | GAO Yang, KRAKIWSKY E J, CZOMPO J. Robust testing procedure for detection of multiple blunders[J]. Journal of Surveying Engineering, 1992, 118(1): 11–23. DOI:10.1061/(ASCE)0733-9453(1992)118:1(11) |
| [10] |
岑敏仪.平差前粗差的发现和定位及其若干规律[D].成都: 西南交通大学, 1999. CEN Minyi. Gross errors detection and location before adjustment of observed values as well as some theorems for judging gross errors[D]. Chengdu: Southwest Jiaotong University, 1999. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y322680 |
| [11] |
彭军还, 陶本藻, 黄珹, 等.
Lq估计的渐近方差-协方差矩阵及其特点[J]. 测绘学报, 2004, 33(4): 293–298.
PENG Junhuan, TAO Benzao, HUANG Cheng, et al. The asymptotic variance-covariance matrix in Lq-norm estimate and its characteristic[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 293–298. DOI:10.3321/j.issn:1001-1595.2004.04.003 |
| [12] |
彭军还.
L1范数估计的巴尔达型检验及其可靠性[J]. 测绘学报, 2005, 34(3): 208–212.
PENG Junhuan. Baarda test and its reliability in L1-norm estimation[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 208–212. DOI:10.3321/j.issn:1001-1595.2005.03.004 |
| [13] |
郑肇葆.
线性规划在摄影测量粗差检测中应用的尝试[J]. 测绘学报, 1985, 14(4): 241–252.
ZHENG Zhaobao. Application of linear programming in the detection of blunders in photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 1985, 14(4): 241–252. DOI:10.3321/j.issn:1001-1595.1985.04.001 |
| [14] | MARSHALL J, BETHEL J. Basic concepts of L1 norm minimization for surveying applications[J]. Journal of Surveying Engineering, 1996, 122(4): 168–179. DOI:10.1061/(ASCE)0733-9453(1996)122:4(168) |
| [15] | AMIRI-SIMKOOEI A. Formulation of L1 norm minimization in Gauss-Markov models[J]. Journal of Surveying Engineering, 2003, 129(1): 37–43. DOI:10.1061/(ASCE)0733-9453(2003)129:1(37) |
| [16] | KHODABANDEH A, AMIRI-SIMKOOEI A R. Recursive algorithm for L1 norm estimation in linear models[J]. Journal of Surveying Engineering, 2011, 137(1): 1–8. DOI:10.1061/(ASCE)SU.1943-5428.0000031 |
| [17] | YETKIN M, INAL C. L1 norm minimization in GPS networks[J]. Survey Review, 2011, 43(323): 523–532. DOI:10.1179/003962611X13117748892038 |
| [18] | ROUSSEUW P J, LEROY A M. Robust regression and outlier detection[M]. New York: Wiley, 1987. |
| [19] | CEN M, LI Z, DING Xiaoli, et al. Gross error diagnostics before least squares adjustment of observations[J]. Journal of Geodesy, 2003, 77(9): 503–513. DOI:10.1007/s00190-003-0343-4 |
| [20] |
岑敏仪, 卓健成, 李志林, 等.
判断观测值粗差能否发现和定位的一种验前方法[J]. 测绘学报, 2003, 32(2): 134–138.
CEN Minyi, ZHUO Jiancheng, LI Zhilin, et al. A method of judging whether gross errors detectable and locatable in observations before least squares adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2): 134–138. DOI:10.3321/j.issn:1001-1595.2003.02.008 |
| [21] |
郑肇葆.
数学规划在测绘学中应用[M]. 北京: 测绘出版社, 2003.
ZHENG Zhaobao. Application of mathematical programming in surveying and mapping[M]. Beijing: Surveying and Mapping Press, 2003. |
| [22] |
束金龙, 闻人凯.
线性规划理论与模型应用[M]. 北京: 科学出版社, 2003.
SHU Jinlong, WEN Renkai. Linear programming theory and model applications[M]. Beijing: Science Press, 2003. |
| [23] | LUENBERGER D G, YE Yinyu. Linear and nonlinear programming[M]. Berlin: Springer, 2008. |
| [24] |
范东明.任意平面网坐标自动解算的非线性最小二乘平差算法[D].成都: 西南交大通大学, 2000. FAN Dongming. The algorithm of nonlinear least squares adjustment of any plane networks with coordinates computed automatically[D]. Chengdu: Southwest Jiaotong University, 2000. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y391917 |
| [25] |
黄维彬.
近代平差理论及其应用[M]. 北京: 解放军出版社, 1992.
HUANG Weibin. Modern adjustment theory and its application[M]. Beijing: PLA Press, 1992. |



