2. 南京师范大学虚拟地理环境教育部重点实验室, 江苏 南京 210023;
3. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023
2. Key Laboratory of Virtual Geographic Environment(Nanjing Normal University), Ministry of Education, Nanjing 210023, China;
3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
坡向(aspect)是重要的地形因子之一,决定着地表接收的太阳能量强度与地表径流方向,对于山地生态具有重要的作用[1-3]。坡向的变化也代表了地表接收能量的改变和坡面形态的转换。坡向变率(slope of aspect, SOA)的概念即由此提出,指坡面指向的变化程度[4]。坡向变率在地学中具有极其重要的科学与实践意义。从地貌学角度来看,坡面指向的转折映射着不同坡面形态的转换,并据此产生众多地貌特征线,如山脊线,山谷线等[5-6]。从生态学角度来看,坡面指向的变化表征着地面接收太阳辐射能量的转换与地表植被的变化,即阴阳坡产生的植被生态变化[7]。此外,风积过程中迎风坡与背风坡的差异也体现出坡面指向的变化[8]。可见,科学准确地计算坡向变率是地貌学、生态学等众多学科相关研究的重要内容。
20世纪以来,数字高程模型(DEM)与数字地形分析(DTA)的提出与应用,为传统的地学分析方法带来革命性的变化[9-13]。现阶段,基于DEM数据,一阶地形因子能够较为方便地计算[14]。但是,坡向变率为二阶地形因子,其计算方法更为复杂[15]。起初,坡向变率的计算是参考坡度的计算方法(对高程数值矩阵求偏导),也就是对坡向数值矩阵求取偏导数,即计算坡向的坡度。据此,随着对坡向变化理解的深入,前人依次提出直接法、正反DEM法、六分法实现了标量条件的坡向变率求解,并取得了广泛的应用[16-19]。可见,前人对坡向变率的计算作了初步的研究,取得了一定的研究成果。但是,坡向变率的计算是一个基于坡向数据基础二阶地形因子的提取[20-21]。该坡向数值矩阵与原始的高程数值矩阵存在本质的不同,即高程数值在很大程度上被看成是一个没有方向特征的常规数学标量,标量值只有大小关系,而无须考虑方向属性。此时对其进行一阶求偏导可直接进行高程求差,即一阶地形因子。而相对二阶地形因子坡向变率而言,坡向数值矩阵的每个像元都代表着其独有的坡面指向,这种指向代表着其特有的方向性[22]。因此,坡向数值矩阵不是一个标量矩阵,简单数学标量的代数运算方式用在坡向数值矩阵上不可避免地违背了数学运算机制。
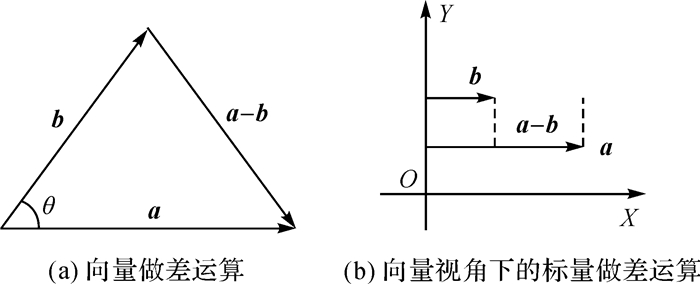
从数学上看,标量运算法则针对的是没有方向属性数据的简单数值计算,而向量运算法则恰好是针对带有方向属性数据的数学向量计算。向量既有大小,也有方向,其运算法则遵循向量运算法则,运算结果是一个向量(图 1(a)),而不是一个标量。因此,坡向变率的计算应该遵循向量运算法则而不是标量运算法则。针对该思路,本文提出基于数学向量几何的坡向变率计算方法。该方法首先以DEM数据为基础提取坡向矩阵数据。其次,对坡向矩阵数据进行数学向量表达。最后,依据该向量化的坡向矩阵来计算坡向变率。并将结果与传统方法进行对比,以期更为科学准确地认识坡向以及计算坡向变率。
|
| 图 1 数学视角下两种不同作差运算 Fig. 1 Two different operations from perspective of mathematics |
1 研究方法 1.1 坡向变率计算基础
坡向变率,即坡向的变化率。变化率在DEM上应用最广泛的是坡度的概念,即求一阶偏导。坡向变率的计算即采用坡向矩阵代替高程矩阵,求取地表某一个点在邻域内的坡向变化率。以高程矩阵为基础的DEM数据,高程变化率提取算法众多。其中,由于三阶反距离平方权差分算法相对合理准确,在研究中已被广泛采用[23]。将此方法借鉴到坡向变率计算过程中,可以得到坡向变率的计算公式
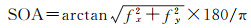 (1)
(1)
式中,fx与fy分别是地表某一个点的坡向在邻域内东西和南北方向上的变化率。在三阶反距离平方权差分算法中,邻域栅格单元内格网数值的代数做差运算是很重要的部分。由于传统方法进行差分运算使用的是未经向量化转换的坡向数值数据,运算法则使用的是标量之间的代数运算法则,忽略了方向对运算的影响,其实质是一维运算(图 1(b))。在本文研究中,对坡向隐式表达的坡向数值矩阵数据进行向量化表达。坡向矩阵中每个坡向值都有其方向。此时,坡向做差运算不是一维运算,而是符合坡向定义的二维向量运算(图 1(a))。
1.2 坡向矩阵向量化表达坡向变率向量计算方法的核心问题是对隐式的坡向方向特征进行向量表达以及向量运算。本文对坡向数据进行向量化表达的方法具体为以下步骤:
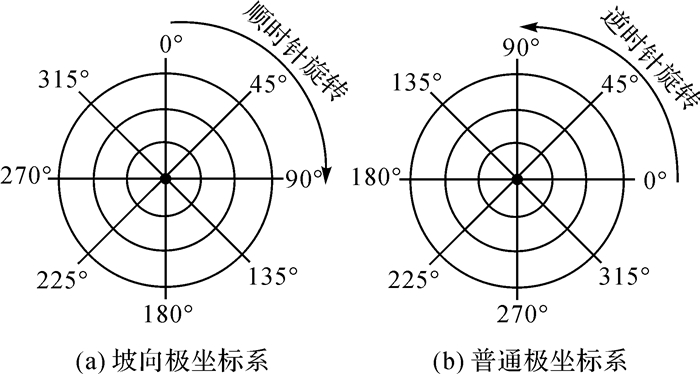
(1) 坡向在坡向极坐标系下的向量表达。坡向向量可以认为处在一个以正北方向为起始方向,顺时针为旋转方向的特殊极坐标系下。本文称之为坡向极坐标系,如图 2(a)所示。坡向值应当首先在坡向极坐标系下表达为向量。其表示为
|
| 图 2 两种不同的极坐标系 Fig. 2 Two different polar coordinate systems |
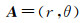 (2)
(2)
式中,r是长度,这里是栅格单元的大小;θ是旋转角度,这里是坡向值;A是坡向在坡向极坐标系下的表示。
(2) 坡向在普通极坐标系下的向量表达。如图 2(b)所示,普通极坐标系是较为常用的一种坐标系,并且可以与平面直角坐标系进行快速转换。坡向极坐标转为普通极坐标的方法如下
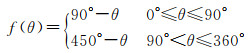 (3)
(3)
式中,θ是坡向值。转换完成之后,每一个地面点的坡向向量在普通极坐标系下表示为
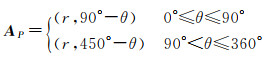 (4)
(4)
式中,r是栅格单元大小;θ是坡向值;AP是坡向在普通极坐标系下的表示。
(3) 坡向在平面直角坐标系下的向量表达。平面直角坐标系更适合于向量之间的运算,因此需要将极坐标系下的坡向向量转换到平面直角坐标系下进行表达。转换公式如下
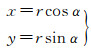 (5)
(5)
式中,r是栅格单元大小;α是AP的旋转角度。坡向向量最终在平面直角坐标系下表示为AR=(x, y)。
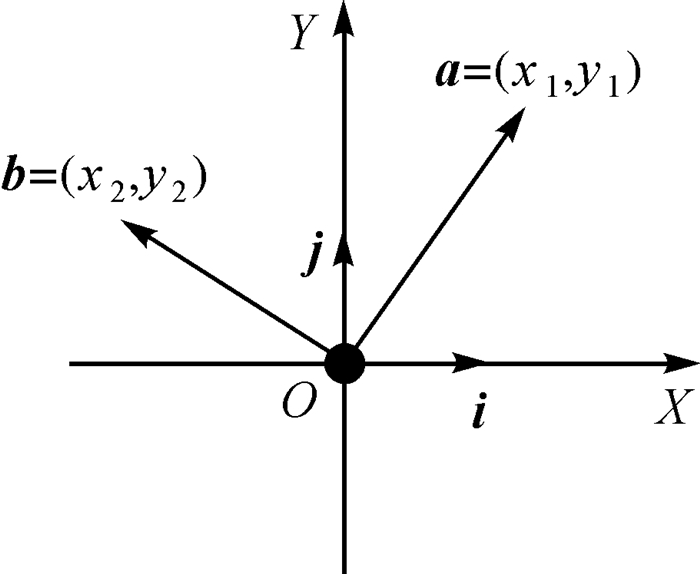
(4) 向量在平面直角坐标系下的坐标表示。分别取与X轴、Y轴方向相同的两个单位向量i、j作为基底向量。任作一个向量a,由平面向量基本定理可知,有且只有一对实数x、y,可以使得等式a=xi+yj成立,于是将(x, y)叫作向量a的直角坐标表示,记作a=(x, y),如图 3所示。
|
| 图 3 平面直角坐标系下向量表示特征 Fig. 3 Vector representation method of plane Cartesian coordinate system |
1.3 坡向变率向量计算
在平面直角坐标系下,平面向量间的运算法则如下:
(1) 已知a=(x1, y1), b=(x2, y2),则a+b=(x1+x1, y2+y2)。
(2) 已知a=(x1, y1), b=(x2, y2),则a-b=(x1-x2, y2-y2)。
(3) 已知a=(x, y)和实数λ, 则λa=(λx, λy)。
(4) 已知a=(x, y), 则a的模长是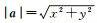
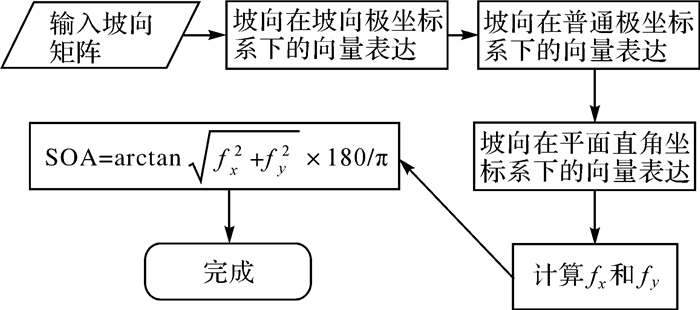
通过以上向量之间的4个运算法则,研究中可完整、准确地将三阶反距离平方权差分算法采用向量运算法则进行求解,并应用于坡向变率的计算。图 4为基于向量几何法计算坡向变率的完整技术流程。
|
| 图 4 基于向量几何法的地表坡向变率提取算法流程 Fig. 4 Flow chart of slope of aspect extraction algorithm based on vector geometry |
2 试验样区与数据
本文采用数学高斯曲面和陕北黄土高原3种典型地貌塬、墚、峁所在地区为研究样区,用于测试基于向量几何法计算坡向变率。其中,高斯曲面为模拟数学地形曲面,高斯合成曲面参数方程的定义如式(6)所示[22]
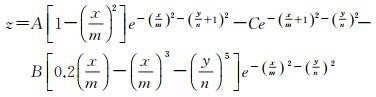 (6)
(6)
式中,A、B、C为地势起伏参数;m、n为范围控制参数。使用基于数学公式建立起来的DEM数据具有无误差的优点,并且可以根据公式直接求取x和y方向上的偏导数fx和fy。结合式(7)有利于求取坡向,为下一步坡向变率的求取奠定基础
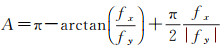 (7)
(7)
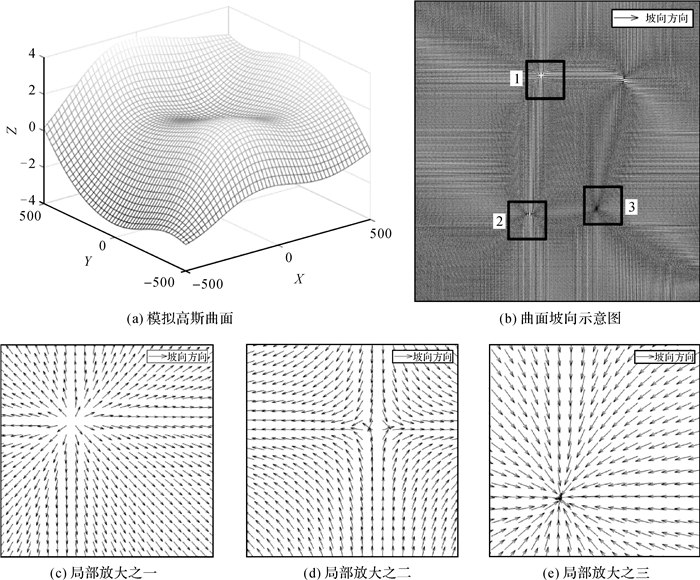
取A=3,B=10,C=1/3,m=500,n=500,标准差为1.326 0,均值为0.624 7,格网分辨率为5×5构建地形曲面如图 5(a)所示。针对高斯数学曲面分别求取偏导fx和fy,再根据式(7)求得坡向结果作为原始坡向数值矩阵。将此坡向数值矩阵按照2.2节向量化后的坡向矢量场图如图 5(b)所示,图 5(c)、(d)、(e)为局部放大图。
|
| 图 5 模拟高斯曲面及曲面坡向 Fig. 5 Simulated Gaussian surface and its aspect |
真实地形所选择的3个样区均位于陕北黄土高原区,其位置如图 6(a)所示,从南至北依次为宜君样区(图 6(d))、吴起样区(图 6(c))和绥德样区(图 6(b))。宜君样区位于陕西省宜君县城东北部,沟谷溯源侵蚀强烈,重力侵蚀活跃[24]。但是其本身属于残塬地貌,因此又具有部分黄土塬地貌特征。吴起样区位于陕西省吴起县北部,区内以黄土墚状丘陵为主,墚坡上面蚀、细沟和切沟侵蚀处于加速阶段,墚地间的冲沟,河沟下切加深[25]。绥德样区位于绥德县无定河中游,区内丘陵起伏,沟壑纵横,土壤侵蚀极为剧烈[26]。表 1为3个样区的基本信息。本试验分别采用3个样区5 m分辨率的DEM数据作为原始数据,设计相关算法展开地表坡向变率计算试验。

|
| 图 6 试验样区位置及其地貌晕眩 Fig. 6 Locations of study areas and the hill shade in sample areas |
| 样区 | 高程/m | 平均坡度/(°) | 地貌类型 |
| 绥德 | 814~1188 | 29.28 | 黄土峁 |
| 吴起 | 1329~1721 | 28.42 | 黄土墚 |
| 宜君 | 768~1158 | 19.23 | 黄土塬 |
3 试验结果与分析 3.1 高斯曲面坡向变率计算结果与分析
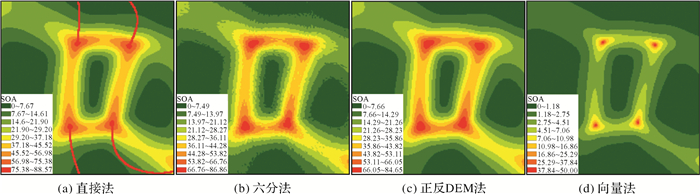
针对高斯曲面,将其坡向矩阵分别采用前人提出方法和本文方法求取坡向变率,即采用直接法、正反DEM法、六分法和向量法求取坡向变率,结果如图 7所示。结果表明,直接法结果出现了明显的“北坡误差”(图 7(a)),而正反DEM法出现了光滑曲面支离破碎以及锯齿状的现象(图 7(b)),六分法得到的结果曲面相比于正反DEM法的结果更加光滑(图 7(c))。
|
| 图 7 不同方法基于高斯曲面的坡向变率计算结果s Fig. 7 SOA results with different methods by using Gaussian surface |
本文所提向量法计算得到的结果与以上3种方法得到的结果截然不同(图 7(d))。一般而言,地表地形特征是由渐变、突变和不变的地表形态组成。这种形态结构也造成了坡向变化在地表空间上的渐变、突变和不变的统一,而渐变和不变的地形表面在地表空间中占据了大部分区域,突变的区域又以地形特征骨架为代表(即山脊,山谷,山顶等),造成了地形在地表空间上的高频信息。因此,该特征相对有利于提取坡面突变的区域。此外,本研究采用各方法的结果频率分布曲线对不同算法的特点进行进一步论述。
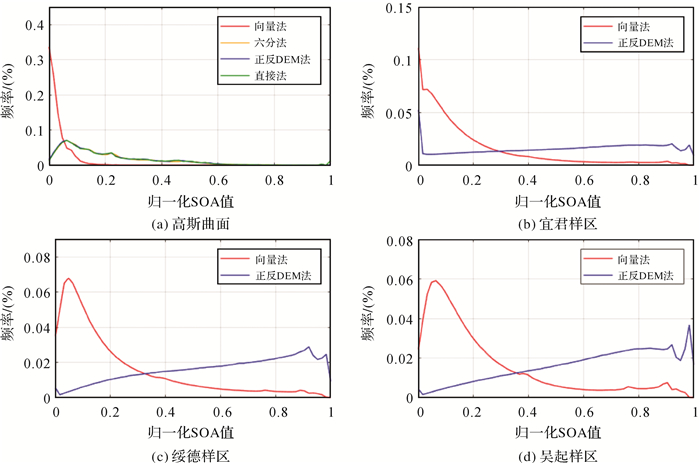
图 8(a)为直接法、六分法、正反DEM法和向量法计算结果的坡向变率频率分布图。为了更加明显地展现每种方法各自的趋势,将4种方法得到的坡向变率结果进行归一化处理。结果可得,直接法、六分法和正反DEM法等标量法的频率分布结果类似(几乎重合,仅少量高值区存在差异),与向量法频率分布结果差异较大。
|
| 图 8 4个样区不同方法坡向变率计算结果频率分布 Fig. 8 Probability distribution of SOA results with different methods in the four sample areas |
3.2 不同样区坡向变率计算结果与分析
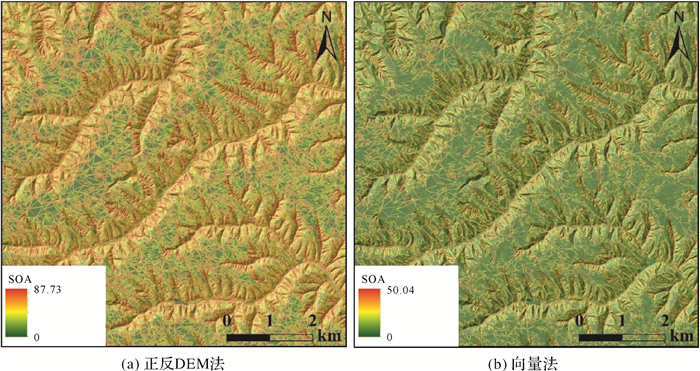
由高斯曲面结果可得,3种标量方法在坡向变率值较小处计算结果差异较小。因此,针对3个真实样区,研究中采用广泛应用的正反DEM法和向量法计算坡向变率,并对所计算结果进行定量分析。图 9、10、11分别是宜君样区、吴起样区、绥德样区在5 m分辨率DEM下使用这两种方法的计算结果。
|
| 图 9 宜君样区坡向变率不同方法的计算结果 Fig. 9 SOA results by different methods in Yijun area |

|
| 图 10 吴起样区坡向变率不同方法的计算结果 Fig. 10 SOA results by different methods in Wuqi area |
|
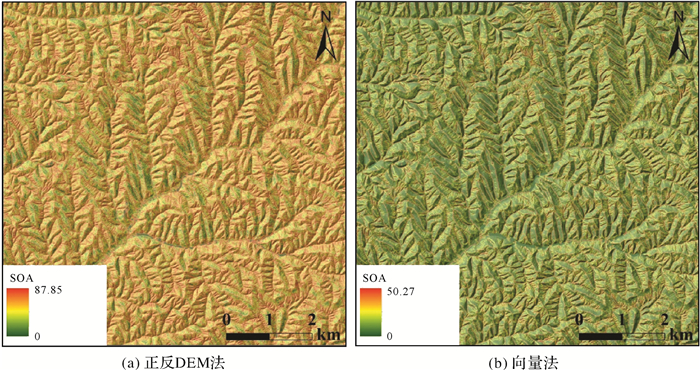
| 图 11 绥德样区坡向变率不同方法的计算结果 Fig. 11 SOA results by different methods in Suide area |
由3个样区计算结果可以看出,类似于高斯曲面计算结果,本文所提向量法得到的结果明显不同于传统的标量计算方式结果。具体表现为,坡向变率值较高的区域呈现出较强的空间结构特征,而坡向变化平缓区域的坡向变率值较小(图 9(b)、图 10(b)、图 11(b))。可以看出,在不考虑坡向存在方向特征时,传统的基于数学标量规则的坡向变率计算方法在相当程度上夸大了地表面的坡向变化特征,使得地表空间中的不变和渐变的地形特征所表现出来的坡向变化难以得到合理的表达。
在高斯曲面试验中,高斯曲面是数学函数拟合DEM数据。因此,所拟合地形表面相对光滑,坡向变化结果以缓和为主,较少出现坡向突变的区域。而实地样区的试验中,样区为地表粗糙的黄土高原丘陵沟壑区,在5 m分辨率的DEM数据基础上,众多表面细节信息能够得到有效的表达,其中包括一定数量的坡面转折信息。图 8(b)、图 8(c)和图 8(d)分别为宜君样区、吴起样区和绥德样区采用正反DEM法和向量法计算得到的坡向变率频率分布结果。图 8(b)为宜君样区的频率分布结果,可以看到坡向变率值为0区域频率很高,这很好地反映了宜君样区的残塬地貌。图 8(d)为绥德样区的频率分布结果,坡向变率高值区域频率明显高于其他两个样区,这与该样区的黄土峁丘陵沟壑地貌类型是相符的。图 8(c)为吴起样区的频率分布结果,而吴起样区本身位于黄土墚状丘陵沟壑区,其地形复杂度高于宜君样区而低于绥德样区。这样的复杂度对比能够较为容易地从图 8(b)、(c)、(d)的3个频率分布结果中得到。
综合图 8(b)、(c)、(d)、图 9—图 11可知,对于黄土地貌类型区域,山脊、山谷、山顶等地形特征部位在样区中表现为地形骨架信息,处于量少而又重要的地位。这些地形特征部位坡向变化较大,属于地表空间地形变化的突变区域。因此,相应的坡向变率计算结果较大。而黄土地貌类型区域地形中大部分仍然是坡向转折较小、坡面形态改变相对平缓的区域。因此,地形特征仍属于渐变区域,相应的坡向变率计算结果较小。向量法得到的坡向变率结果在相当程度上更好地符合黄土地貌坡向变化的认知,坡向变率低值区域占大部分,坡向变率高值区域占小部分。而基于标量运算的正反DEM法恰恰相反,高坡向变率值栅格频率远高于低坡向变率值栅格频率,在相当程度上夸大了地表坡面转变的信息。
通过图 8(b)、(c)、(d)3个样区的向量法结果频率分布情况,结合向量法坡向变率的取值范围,设置区间[0, 5)、[5, 10)、[10, 15)、[15, 20)、[20, 25)、[25, 30)、[30, 35)、[35, 40)、[40, 45)、[45, 50)、[50, 55)对结果进行统计分析。P(d)为不同区间内坡向变率计算结果栅格数占总栅格数目的百分比,E为区间内坡向变率的均值。3个样区的统计结果如表 2所示。可以看出,宜君、吴起和绥德样区在区间[0, 15)内的栅格占总栅格数的百分比分别达到80.67%、74.12%和72.56%。该结果较好地反映了向量法能够较为真实地计算坡向变化结果,符合地表空间中地形在不变、渐变与突变的分布关系。
| 样区 | 统计量 | [0, 5) | [5, 10) | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) | [40, 45) | [45, 50) | [50, 55) |
| 宜君 | P(d)/(%) | 46.15 | 23.01 | 11.51 | 6.44 | 3.99 | 2.52 | 1.83 | 1.74 | 1.80 | 0.90 | 0.000 08 |
| E | 2.156 | 7.204 | 12.23 | 17.31 | 22.28 | 27.33 | 32.41 | 37.55 | 42.69 | 46.55 | 50.03 | |
| 吴起 | P(d)/(%) | 36.20 | 24.87 | 13.05 | 8.07 | 5.52 | 3.71 | 2.70 | 2.38 | 2.25 | 1.15 | 0.001 3 |
| E | 2.674 | 7.212 | 12.27 | 17.35 | 22.31 | 27.34 | 32.40 | 37.51 | 42.63 | 46.70 | 50.11 | |
| 绥德 | P(d)/(%) | 31.06 | 26.82 | 14.68 | 8.56 | 5.19 | 3.07 | 2.41 | 2.85 | 3.45 | 1.82 | 0.001 |
| E | 2.810 | 7.263 | 12.25 | 17.35 | 22.23 | 27.34 | 32.48 | 37.63 | 42.82 | 46.57 | 50.11 |
3.3 不同分辨率向量法坡向变率计算结果分析
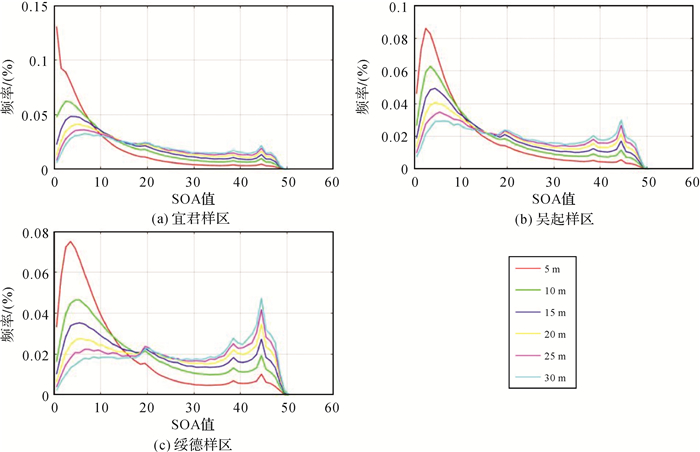
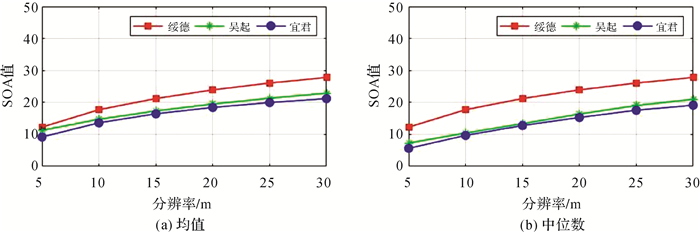
本文对3个样区的5 m分辨率DEM数据,在ArcGIS软件中,使用最邻近点法进行了重采样处理,分别得到10、15、20、25和30 m的DEM数据。对这些数据使用向量法进行坡向变率的求解,以期分析向量法的稳定性。图 12为3个样区不同DEM分辨率下向量法计算结果频率分布。可以看出,3个样区在5 m分辨率下地形信息最为丰富,诸多细节信息得到保留,地表的不变、渐变特征在较高的分辨率下能够较好地表达。随着分辨率的降低,产生削峰填谷现象,部分低等级沟谷和山脊信息得到综合。但高等级沟谷和山脊信息仍然相对突出,因而表现出坡向变率值较高区域占比增大。向量法得到的计算结果在不同样区、不同分辨率的高值区域,其频率分布曲线形状基本保持稳定。图 13是基于不同DEM分辨率的3个样区向量法计算均值(图 13(a))和中位数(图 13(b))结果。可以看出,随着分辨率的降低,基于向量几何的坡向变率计算方法在不同分辨率的DEM下表现出了较好的稳定性。
|
| 图 12 基于不同分辨率的三样区DEM数据的向量法计算结果频率分布 Fig. 12 Probability distribution of SOA results based different resolutions using vector methods in the three sample areas |
|
| 图 13 基于不同分辨率的三样区DEM数据向量法计算结果统计 Fig. 13 Statistic result based on different resolution DEMs using vector method in the three sample areas |
4 结论
本文基于数学中的向量几何方法,考虑到坡向因子的方向属性,提出了基于向量方法来求解数字地形分析中的坡向变率地形因子的计算方法。该方法将坡向数值矩阵进行坐标转换、向量还原、向量运算,最终求解出更加合理的坡向变率结果。本文所提出的基于向量几何的坡向变率方法为精准数字地形分析提供参考。向量几何在数字地形分析中的应用,对于涉及具有方向属性的地形因子计算的科学研究具有重要的借鉴意义。从新的数学向量角度理解数字地形分析相关算法,也是借鉴数学向量几何的方法解决数字地形分析问题的重要实践。
本文分别采用高斯合成曲面的离散化数据和陕北宜君样区、吴起样区和绥德样区的5 m分辨率DEM数据进行试验,得出以下具体结论:①基于向量几何的DEM地表坡向变率计算方法有效地将坡向的方向属性用于计算,避免了传统标量方法无视方向属性造成坡向变率计算结果夸大的误差;②坡向变率计算结果分布特征更加符合地表空间中坡面转折的渐变、突变以及不变的地貌形态分布的基本认知,即不变及渐变的地形区域占据主要地位;③基于向量几何的坡向变率计算方法具有较好的稳定性,适用于多种分辨率DEM数据。
当今数字地形分析理论中,诸多的地形因子在概念的提出是以向量方式进行描述,带有重要的方向属性,这也符合真实的地貌形态描述方式。然而,在对地形因子进行计算与表达时,受制于数据模型、数据结构,无法将其完整含义充分展现,使得绝大多数地形属性计算与特征提取采用标量的形式进行求解,造成了数字地形分析中解译算法的不确定性问题。本文立足于数学向量几何,从一个小的侧面——坡向变率的求解,将向量的思想引入到数字地形分析中。可以看出,向量几何在数字地形分析中具有巨大的发展潜力。今后的研究将针对地形因子,在数学上寻找一种更加抽象的表达方式,更加合理的运算方法,来满足今后数字地形分析走向地貌研究,走向地形演变的过程与机理研究。
| [1] | CARTER B J, CIOLKOSZ E J. Slope gradient and aspect effects on soils developed from sandstone in Pennsylvania[J]. Geoderma, 1991, 49(3-4): 199–213. DOI:10.1016/0016-7061(91)90076-6 |
| [2] | YANG Xin, TANG Guoan, XIAO Chenchao, et al. Terrain revised model for air temperature in mountainous area based on DEMs[J]. Journal of Geographical Sciences, 2007, 17(4): 399–408. |
| [3] |
夏誉玲, 李小娟, 王涛.
基于数字高程模型的混合流向算法[J]. 测绘学报, 2018, 47(5): 683–691.
XIA Yuling, LI Xiaojuan, WANG Tao. A hybrid flow direction algorithm for water routing on DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(5): 683–691. DOI:10.11947/j.AGCS.2018.20170614 |
| [4] |
汤国安, 李发源, 刘学军.
数字高程模型教程[M]. 2版. 北京: 科学出版社, 2010.
TANG Guoan, LI Fayuan, LIU Xuejun. Digital elevation model tutorial[M]. 2nd ed. Beijing: Science Press, 2010. |
| [5] |
朱庆, 田一翔, 张叶廷.
从规则格网DEM自动提取汇水区域及其子区域的方法[J]. 测绘学报, 2005, 34(2): 129–133.
ZHU Qing, TIAN Yixiang, ZHANG Yeting. The extraction of catchment and subcatchment from regular grid DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 129–133. DOI:10.3321/j.issn:1001-1595.2005.02.007 |
| [6] |
程维明, 周成虎, 申元村, 等.
中国近40年来地貌学研究的回顾与展望[J]. 地理学报, 2017, 72(5): 755–775.
CHENG Weiming, ZHOU Chenghu, SHEN Yuancun, et al. Retrospect and perspective of geomorphology researches in China over the past 40 years[J]. Acta Geographica Sinica, 2017, 72(5): 755–775. |
| [7] |
朱秋莲, 邢肖毅, 张宏, 等.
黄土丘陵沟壑区不同植被区土壤生态化学计量特征[J]. 生态学报, 2013, 33(15): 4674–4682.
ZHU Qiulian, XING Xiaoyi, ZHANG Hong, et al. Soil ecological stoichiometry under different vegetation area on loess hilly gully region[J]. Acta Ecologica Sinica, 2013, 33(15): 4674–4682. |
| [8] | XIONG Liyang, TANG Guoan, LI Fayuan, et al. Modeling the evolution of loess-covered landforms in the Loess Plateau of China using a DEM of underground bedrock surface[J]. Geomorphology, 2014, 209: 18–26. DOI:10.1016/j.geomorph.2013.12.009 |
| [9] | LÜ Guonian, XIONG Liyang, CHEN Min, et al. Chinese progress in geomorphometry[J]. Journal of Geographical Sciences, 2017, 27(11): 1389–1412. |
| [10] |
汤国安, 那嘉明, 程维明.
我国区域地貌数字地形分析研究进展[J]. 测绘学报, 2017, 46(10): 1570–1591.
TANG Guoan, NA Jiaming, CHENG Weiming. Progress of digital terrain analysis on regional geomorphology in China[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1570–1591. DOI:10.11947/j.AGCS.2017.20170388 |
| [11] |
朱庆, 赵杰, 钟正, 等.
基于规则格网DEM的地形特征提取算法[J]. 测绘学报, 2004, 33(1): 77–82.
ZHU Qing, ZHAO Jie, ZHONG Zheng, et al. The extraction of topographic patterns based on regular grid DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 77–82. DOI:10.3321/j.issn:1001-1595.2004.01.014 |
| [12] | QIN C, ZHU A X, PEI T, et al. An adaptive approach to selecting a flow-partition exponent for a multiple-flow-direction algorithm[J]. International Journal of Geographical Information Science, 2007, 21(4): 443–458. |
| [13] | CHEN Yumin, ZHOU Qiming, LI Sheng, et al. The simulation of surface flow dynamics using a flow-path network model[J]. International Journal of Geographical Information Science, 2014, 28(11): 2242–2260. |
| [14] | JONES K H. A comparison of algorithms used to compute hill slope as a property of the DEM[J]. Computers & Geosciences, 1998, 24(4): 315–323. |
| [15] | MINÁR J, EVANS I S. Elementary forms for land surface segmentation:the theoretical basis of terrain analysis and geomorphological mapping[J]. Geomorphology, 2008, 95(3-4): 236–259. DOI:10.1016/j.geomorph.2007.06.003 |
| [16] | CHENG Guo, LIU Lu, JING Ning, et al. General-purpose optimization methods for parallelization of digital terrain analysis based on cellular automata[J]. Computers & Geosciences, 2012, 45(1): 57–67. |
| [17] |
褚永彬, 朱利东, 唐斌, 等.
疏勒河上游流域地面坡谱特征[J]. 干旱区地理, 2015, 38(2): 345–350.
CHU Yongbin, ZHU Lidong, TANG Bin, et al. Slope spectrum characteristics of the Shule River's upstream basin[J]. Arid Land Geography, 2015, 38(2): 345–350. |
| [18] |
焦贝贝, 石培基, 刘春芳, 等.
黄土高原低山丘陵区农村居民点分布与地形因子关系研究——以兰州市七里河区为例[J]. 资源科学, 2013, 35(8): 1719–1727.
JIAO Beibei, SHI Peiji, LIU Chunfang, et al. The distribution of rural settlements in relation to land form factors in low hilly land on the Loess Plateau[J]. Resources Science, 2013, 35(8): 1719–1727. |
| [19] |
谢轶群, 汤国安, 江岭.
DEM提取坡向变率中的误差特征与消除方法[J]. 地理与地理信息科学, 2013, 29(2): 49–53.
XIE Yiqun, TANG Guoan, JIANG Ling. Characteristics and correcting methods of errors in extraction of SOA based on DEMs[J]. Geography and Geo-Information Science, 2013, 29(2): 49–53. |
| [20] | FLORINSKY I V. Computation of the third-order partial derivatives from a digital elevation model[J]. International Journal of Geographical Information Science, 2009, 23(2): 213–231. DOI:10.1080/13658810802527499 |
| [21] | MINÁR J, JENČO M, EVANS I S, et al. Third-order geomorphometric variables (derivatives):definition, computation and utilization of changes of curvatures[J]. International Journal of Geographical Information Science, 2013, 27(7): 1381–1402. |
| [22] |
李润超, 袁林旺, 李硕, 等.
DEM坡向提取的向量场模板匹配方法[J]. 测绘学报, 2013, 42(6): 922–928.
LI Runchao, YUAN Linwang, LI Shuo, et al. A vector field template matching method of DEM slope extraction[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 922–928. |
| [23] |
刘学军, 龚健雅, 周启鸣, 等.
基于DEM坡度坡向算法精度的分析研究[J]. 测绘学报, 2004, 33(3): 258–263.
LIU Xuejun, GONG Jianya, ZHOU Qiming, et al. A study of accuracy and algorithms for calculating slope and aspect based on grid digital elevation model (DEM)[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 258–263. DOI:10.3321/j.issn:1001-1595.2004.03.014 |
| [24] | JIANG Sheng, TANG Guoan, LIU Kai. A new extraction method of loess shoulder-line based on Marr-Hildreth operator and terrain mask[J]. PLoS One, 2015, 10(4): e0123804. DOI:10.1371/journal.pone.0123804 |
| [25] |
李登科.
陕北吴起县退耕还林(草)成效的遥感监测分析[J]. 中国沙漠, 2009, 29(1): 125–201.
LI Dengke. Remote sensing analysis on effect of tillage reverting to woodland or grassland in Wuqi, Shaanxi Province[J]. Journal of Desert Research, 2009, 29(1): 125–201. |
| [26] | XIONG Liyang, TANG Guoan, YAN Shijiang, et al. Landform-oriented flow-routing algorithm for the dual-structure loess terrain based on digital elevation models[J]. Hydrological Processes, 2014, 28(4): 1756–1766. DOI:10.1002/hyp.9719 |



