2. 地理信息工程国家重点实验室, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
轨迹数据由定位设备实时记录并上传产生,描述移动对象的时空位置信息。随着网络及定位技术的普及,多种途径汇集形成的众源轨迹数据成为地理大数据的重要部分。这种众源轨迹数据具有来源广泛、时效性强、隐含特征丰富等特点,对交通流量分析[1]、出行模式挖掘[2]、智能位置推荐[3]等具有重要价值。在地理数据更新领域,大量的车辆轨迹数据背后蕴含了道路分布、交通条件(如车流量、通行限制)、设施兴趣点(如加油站、停车场)等最新信息,提取上述隐含信息并实施数据建库与一致性更新,对于解决当前基础测绘数据更新维护面临的技术手段单一、效率低、成本高等问题有积极意义。
利用车辆轨迹数据提取道路分布信息是当前的研究热点,存在两种不同的解决思路。第1种是采用栅格化思想[4-7],对轨迹点分布空间进行剖分形成密度图,利用核密度估计等方法提取道路分布的平面区域,然后通过形态分析操作(如骨架化)获得道路结构线。该类方法优点在于可以充分利用图像处理领域积累的成熟技术。然而,受栅格单元大小、轨迹点分布密度不均衡等因素影响,局部区域提取的道路线容易出现连接破碎,需要后期进行一致性维护补救。第2种是矢量化处理策略,以轨迹点(或轨迹线段)为基本单元,通过统计聚类方法探测道路分布特征。例如,文献[8—11]利用k-means方法结合距离、航向指标对轨迹点进行聚类,在此基础上通过不同的聚类簇处理策略生成道路弧段。文献[12]采用Douglas-Peucker算法[13]探测关键轨迹点,然后采用DBSCAN方法对关键轨迹点进行迭代式聚类提取道路交叉口。文献[14—15]设计了力学模型剔除异常轨迹点,然后利用局部G统计热点分析方法提取道路网结构。文献[16]考虑角度变化、时长间隔提取转向点对,在空间聚类方法支持下获得转向点对簇,继而获得道路网交叉口结构信息。文献[17]引入约束Delaunay三角网探测轨迹点空间集聚性,通过轨迹点的空间剖分面积以及相邻轨迹点距离实现道路边界的精确提取。为提高道路生成过程效率,相关学者还提出增量式的处理策略。例如,文献[18]通过建立轨迹数据与参考路网间的位置、语义关系渐进式地生成道路信息。文献[19]将空间认知规律引入到轨迹线提取路网过程中,基于Delaunay三角网构建轨迹线融合处理模型,通过不断修正细化获得完整的道路网信息。与第1种思路相比较,上述方法不仅利用车辆轨迹的空间分布特征,而且能够获得移动方向、速度等隐含的动力学特征支持。
从图论角度看,道路网由道路交叉口和连接交叉口的道路弧段构成。其中,交叉口的识别与提取是道路网生成的关键步骤。车辆移动过程中,道路交叉口区域产生的轨迹路径在形态结构、转向幅度、速度变化、停留时长方面与其他区域存在显著差异。然而,已有方法大多将轨迹点作为基本分析单元,对局部轨迹路径体现的形态及动力特征变化的缺乏有效考虑,同时如何集成不同类型参量进行综合决策也是面临的难题。基于上述观察以及研究现状分析,本文提出了一种利用车辆轨迹提取道路交叉口特征的方法。首先,分析交叉口的变道轨迹片段与常规非变道轨迹片段间的差异,并定义曲直比、转向角度、行驶速度三个描述参量;然后,利用决策树方法构建多因子决策的轨迹片段分类模型,并结合移动开窗式的轨迹线剖分模型建立交叉口区域变道轨迹片段提取方法;最后,基于相似性原则对交叉口区域轨迹片段实施聚类,并提取轨迹片段簇中心线获得交叉口结构信息。利用多个城市的车辆轨迹数据作为试验测试数据,通过对比式评估验证本文方法的有效性,并对方法的不足之处进行了深入分析。
1 决策树支持下的交叉口识别为了准确描述本文所提出的方法,首先给出以下定义:
定义1 轨迹线(T):由一系列按时间次序排列的点集构成,即T={p1, p2, …, pn}(n≥2)。其中,pi=(xi, yi, ti),xi和yi为轨迹点pi的空间坐标,ti表示pi产生的时间信息。
定义2 轨迹片段(TS):由轨迹线T上部分连续轨迹点构成,如TS(pl, pm)={pl, pl+1, …, pm}(1≤l < m≤n)。
定义3 轨迹直线段(e):由相邻轨迹点组成的直线段,例如ei表示轨迹点由pi和pi+1连接而成的直线段。
特别地,根据轨迹点和直线段的关系,上文中轨迹线T和轨迹片段TS也可对应表示为{e1, e2, …, en-1}和{el, el+1, …, em-1}(1≤l < m≤n)。
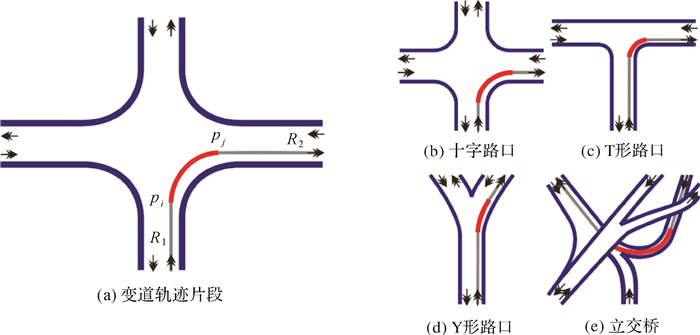
1.1 道路交叉口车辆变道轨迹片段分析道路交叉口是两条或两条以上道路实体交汇衔接处,如图 1(b)-(e)列出的几种典型道路交叉口结构。道路交叉口在整个交通运输过程扮演重要角色,是车辆实现汇集、疏散、行驶道路变更转换的关键区域。在道路实体建模与表达中,交叉口对应道路网络中连接不同道路弧段的结点。本研究将车辆在交叉口区域变道过程产生的轨迹片段称为变道轨迹片段。如图 1(a)所示,车辆从pi点开始进入交叉路口至pj点驶出,完成了从道路R1至R2的变道转换,pi、pj两点间的轨迹片段即称为变道轨迹片段(记为LC_TS(pi, pj))。受道路物理结构和车辆交汇影响,道路交叉口发生的变道行为使得车辆运行状态产生变化。这种变化直接反映在变道轨迹片段的几何形态、隐含动力学特征上。具体地,本文定义以下几个参量描述变道轨迹片段与非变道轨迹片段间的差异性。
|
| 图 1 道路交叉口与变道轨迹片段(红色)示例 Fig. 1 Samples of road intersection and lane-changing trajectory segment |
1.1.1 直曲比
与同一道路上行驶产生的轨迹片段相比较,变道轨迹片段最直观的差异表现在几何形态上,即车辆通过交叉口时行驶轨迹弯曲程度明显增大。这种弯曲程度可通过直曲比进行描述。轨迹片段TS(pl, pm)的直曲比定义如下
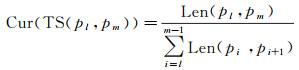 (1)
(1)
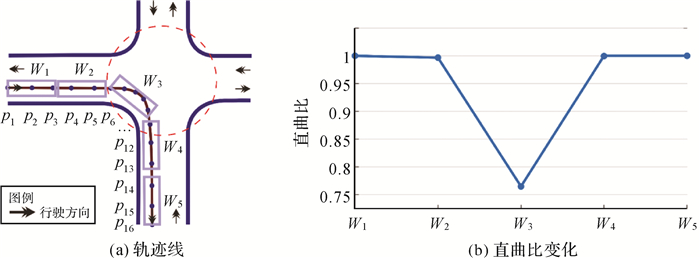
式中,Len(pi, pj)表示轨迹点pi和pj间的直线段长度。以图 2(a)所示某车辆产生的轨迹线为例,从p1开始分析移动窗口内轨迹片段的直曲比(图 2(b)),可以发现同一路段行驶时轨迹片段直曲比接近1,而在道路交叉口变道阶段的轨迹片段直曲比出现异常波动。除少数特殊结构道路和交通状况外(如车辆非正常转向),轨迹片段直曲比越小,所在区域为道路交叉口的可能性越大。
|
| 图 2 轨迹片段直曲比分析 Fig. 2 Curvature analysis of trajectory segments |
1.1.2 转向角度
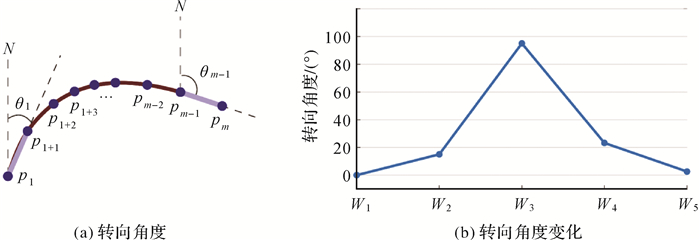
车辆在道路交叉口完成变道行为时伴随行驶方向的显著变化。这种变化可以通过轨迹片段起点与终点间的转向角度进行度量。如图 3(a)所示,轨迹片段TS(pl, pm)在起始点pl处的航向角度为θl,终止点pm处用其前一个点pm-1的航向角度近似代替,即θm-1,则TS(pl, pm)的转向角度计算如下
|
| 图 3 轨迹片段转向角度分析 Fig. 3 Turning angle analysis of trajectory segment |
 (2)
(2)
式中,pi处航向角度定义为正北方向与车辆行驶方向间沿顺时针的夹角。图 3(b)展示了图 3(a)所示移动窗口包含轨迹片段的转向角度。可以发现,同一道路上行驶时轨迹片段转向角度较小(≤30°),而在交叉口区域轨迹片段转向角度较大(≥60°)。
1.1.3 行驶速度道路交叉口衔接路段呈显著弯曲结构,车辆需要降低行驶速度,同时,不同方向车辆需要交互完成变道行为,导致车辆低速甚至短暂停止移动。因此,轨迹片段隐含的速度特征可以作为区分变道轨迹片段与非变道轨迹片段的又一有效指标。假设相邻轨迹点间车辆运动速度均匀,轨迹片段TS(pl, pm)隐含的速度计算如下
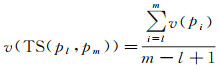 (3)
(3)
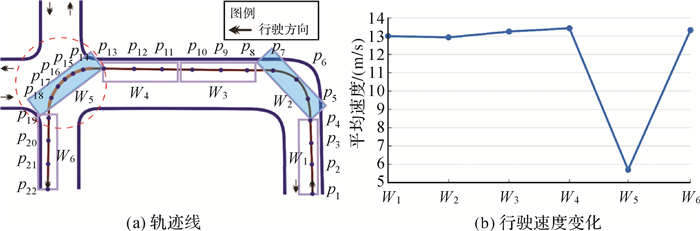
式中,v(pi)表示车辆经过pi时的速度,可由pi与pi+1间的距离和时间间隔计算得到。如图 4(a)所示,车辆经过W2和W5区域时均发生大幅度转向变化,仅通过直曲比、转向角度难以区分变道转向和非变道转向。从图 4(b)所示的速度变化看,W2处行驶速度较大,而道路交叉口的W5处行驶速度出现谷值。
|
| 图 4 行驶速度分析 Fig. 4 Speed analysis of trajectory segments |
1.2 基于CART决策树的变道轨迹片段识别模型
变道轨迹片段识别面临两个难点问题。一方面,单一指标难以准确区分变道轨迹片段与非变道轨迹片段,需要集成几何形态、转向幅度、速度变化进行综合判断。例如,受交通堵塞等因素影响,非道路交叉口区域车辆也可能以较低速度行驶;局部道路呈现弯曲形态分布,导致轨迹片段转向角度较大。另一方面,作为完整轨迹线的一部分,变道轨迹片段准确识别需要专门的轨迹线剖分模型进行支撑。针对上述问题,本研究设计了一种移动开窗策略与决策树学习分类相结合的变道轨迹片段识别模型。
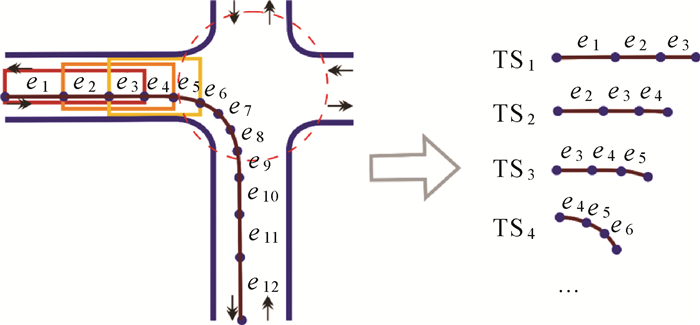
1.2.1 基于移动开窗的轨迹线剖分模型以轨迹线起始点为锚点,创建大小为s的窗口w,以步长μ移动窗口,直至完整遍历该轨迹线。其中,s定义为窗口包含的轨迹直线段数量,μ定义为窗口移动前与移动后锚点间的轨迹直线段数量。在窗口移动过程中,记录每一位置状态下窗口包含的轨迹片段,作为后续变道轨迹片段识别的基本单元。图 5中轨迹线T={e1, e2, …, e12},设置大小s为3、移动步长μ为1的移动窗口,则产生轨迹片段TS1={e1, e2, e3}、TS2={e2, e3, e4}、…、TS10={e10, e11, e12}。窗口尺寸设置需考虑道路交叉口区域大小及通行条件。假设轨迹点采样间隔为1 s,常规条件下交叉口车辆完成变道过程耗时约为5 s,则窗口尺寸可设置为5。窗口移动步长越小,则变道轨迹片段位置识别的准确性越高。
|
| 图 5 基于移动开窗策略的轨迹线剖分处理 Fig. 5 Trajectory subdivision using a sliding window method |
1.2.2 基于决策树学习的轨迹片段分类模型
如前文所述,区分变道轨迹片段与非变道轨迹片段需要综合考虑多重特征,可采用机器学习方法构建分类模型。决策树学习是机器学习领域应用最为广泛的分类学习方法之一[20],其本质是通过归纳推理构建树状结构的分类规则组合。树结构从根节点到叶节点的每一条路径代表一条分类规则,路径内部结点对应某个特征的测试,叶节点对应规则的分类结果。与神经网络等其他监督学习方法构建的分类器相比较,决策树具有分类速度快、效率高、无须对输入数据进行标准化处理的优点。同时,决策树表达的分类规则视觉直观、解译性强易于移植(如转换为If-Then形式)。在地理信息领域,决策树方法已广泛应用于道路网结构识别[21]、地图数据变化探测与更新[22]、空间数据匹配融合[23]等问题。决策树构建可采用算法包括ID3、C4.5、CART,其中CART算法具有准确率高、计算量小、操作简单灵活,能够从复杂样本数据抽象出清晰易解译的分类规则。CART决策树模型构建包括生成和剪枝两个步骤:①根据训练数据广延地生长决策树;②基于最小复杂性代价准则[24]对已生成的决策树实施剪枝,并使用测试数据验证,选择最优子树。
本文采用决策树CART算法构建道路交叉口变道轨迹片段和非变道轨迹片段的分类模型。CART决策树属于监督分类方法,需要提供训练样本进行模型构建与评价。针对轨迹线T包含的某一轨迹片段TS(i),按1.1节定义的参量(即直曲比、转向角度、行驶速度)构建如下数组
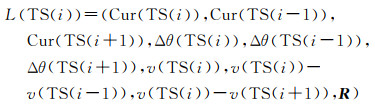
式中,TS(i-1)和TS(i+1)分别表示与TS(i)相邻的前、后轨迹片段;R为标签向量,表示轨迹片段类别(标识为“Y”(属于变道轨迹片段)或者“N”(属于非变道轨迹片段))。表 1所示为归一化后的样本数据组织格式。
| 序号 | Cur (TS(i)) |
Cur (TS(i-1)) |
Cur (TS(i+1)) |
Δθ (TS(i)) |
Δθ (TS(i-1)) |
Δθ (TS(i+1)) |
v (TS(i)) |
v(TS(i))-v(TS(i-1)) | v(TS(i))-v(TS(i+1)) | R |
| 1 | 0.999 9 | null | 0.934 3 | 0.015 0 | null | 0.530 5 | 0.772 3 | null | 0.910 3 | N |
| 2 | 0.934 3 | 0.999 9 | 0.881 3 | 0.530 5 | 0.015 0 | 0.538 4 | 0.677 1 | 0.089 7 | 0.838 5 | Y |
| 3 | 0.881 3 | 0.934 3 | 0.736 3 | 0.538 4 | 0.530 5 | 0.962 5 | 0.600 7 | 0.161 5 | 0.777 1 | Y |
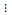 |
1.2.3 变道轨迹片段提取过程
基于移动开窗剖分模型和样本数据训练得到的决策树分类器,从完整轨迹线提取变道轨迹片段的过程设计如下:
(1) 针对移动窗口产生的每一条轨迹片段,计算当前轨迹片段以及其前、后窗口内轨迹片段的直曲比、转向角度、行驶速度参量值(若为起/止轨迹片段,则将其前/后窗口内轨迹片段参量值置空),输入分类器进行类型识别。进一步将分类结果作为属性标注到该轨迹片段包含的每一条轨迹直线段上。如图 6(b)所示,轨迹直线段e1、e2、e3构成的轨迹片段判定为“N”(即非变道轨迹片段),则e1、e2、e3各自增加一个“N”的类型标识。
|
| 图 6 变道轨迹片段提取过程 Fig. 6 The process of lane-changing trajectory segment extraction |
(2) 依次遍历轨迹线包含的所有轨迹直线段,对于每条轨迹直线段统计其记录的所有类型标识。若“Y”数量大于等于“N”数量,则将该轨迹直线段最终标识为“Y”;否则,该轨迹直线段最终标识为“N”。如图 6(c)中e4的属性标识为(“Y”,“N”,“N”),则最终标识为“N”;e5的属性标识为(“Y”,“Y”,“N”),则最终标识为“Y”。
(3) 将相邻且标识为“Y”的轨迹直线段进行连接组织,最终输出变道轨迹片段。如图 6(d)所示一个变道轨迹片段LC_TS={e5, e6, …, e9}。
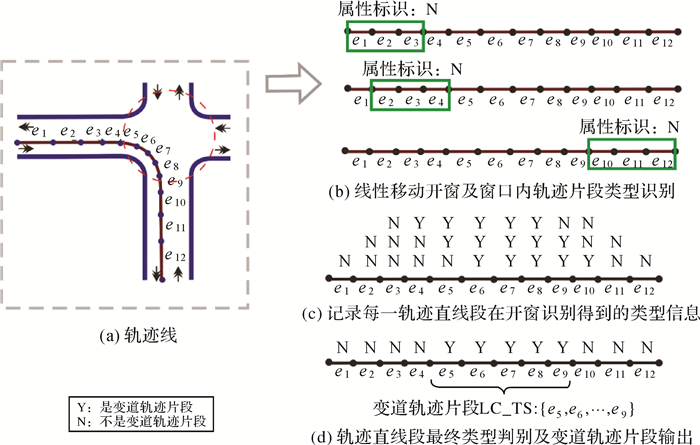
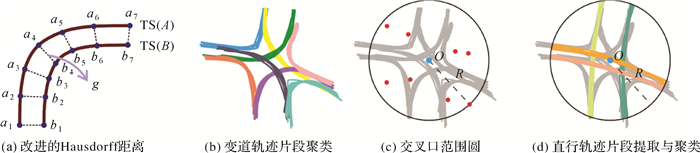
2 交叉口区域轨迹片段聚类与道路结构线生成 2.1 轨迹片段聚类进一步,对交叉口区域的轨迹片段实施相似性聚类形成轨迹片段簇,并提取同一组轨迹片段的中心线作为道路结构线。轨迹片段间相似性由包含轨迹点间的位置关系决定。Hausdorff距离是描述两组点集相似程度的一种度量指标,但集合中的元素是无序的,忽略了轨迹点在时间维上的有序性。文献[25]提出了改进Hausdorff距离,一方面利用平移常量消除了轨迹片段间的公共偏差;另一方面依据时间顺序进行轨迹点间的比较,符合轨迹的时序特征。如图 7(a)所示,轨迹片段TS(A)和TS(B)间Hausdorff距离计算如下
|
| 图 7 道路交叉口区域轨迹片段聚类 Fig. 7 Clustering of trajectory segments in an area of road intersection |
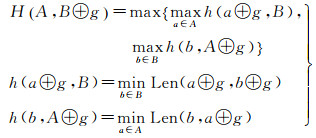 (4)
(4)
式中,H表示Hausdorff距离;⊕是一个集合运算符号(A⊕g={a+g|a∈A});函数Len计算轨迹点间的距离;平移常量g定义为两条轨迹片段间时间同步轨迹点距离的平均值。当两条轨迹片段间Hausdorff距离小于设定阈值,则判定两者属于同一轨迹片段簇。
提取完整的道路交叉口结构,需要得到两个不同层面的轨迹片段聚类结果。一是与道路线相对应的轨迹片段簇,包括变道轨迹片段簇和未发生变道行为的直行轨迹片段簇;二是属于不同交叉口区域的轨迹片段簇的集合。依据变道轨迹片段识别结果,获得上述两个层面聚类结果步骤如下:
(1) 基于Hausdorff距离h对变道轨迹片段进行聚类,得到变道轨迹片段簇。聚类结果如图 7(b)所示,同一种颜色表示的轨迹片段属同一簇。
(2) 针对每一变道轨迹片段簇,取所有轨迹片段两侧端点坐标的平均值作为定位点;然后,依据欧氏距离阈值h′对定位点进行聚类分组,获得属于同一交叉口的变道轨迹片段簇。
(3) 对于每一个道路交叉口,取所有轨迹片段簇定位点的中心位置作为交叉口的中心点O,按交叉口范围取大不取小原则[16],选取定位点与O距离最大值作为交叉口范围半径R(如图 7(c)所示);利用交叉口范围圆裁切经过该区域的非变道轨迹片段,依据Hausdorff距离h聚类成簇(如图 7(d)所示),最终得到该交叉口区域所有的变道轨迹片段簇和非变道轨迹片段簇。
2.2 道路结构线生成针对每一组轨迹片段簇,通过一种迭代式策略提取中心线作为道路弧段[26],从而获得交叉口道路结构特征。假设轨迹片段簇C={TS1, TS2, …, TSm}(m>1), 中心线提取方法如下:
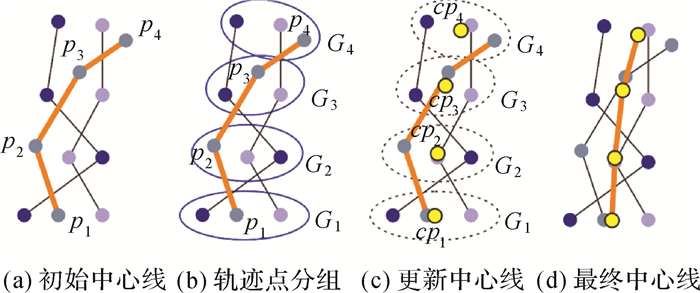
(1) 随机选择轨迹片段簇C中一条轨迹片段作为初步的中心线CL。如图 8(a)所示,C={TS1, TS2, TS3},CL=TS={p1, p2, p3, p4}。
|
| 图 8 轨迹片段簇中心线提取方法 Fig. 8 Extracting center line of a cluster of trajectory segments |
(2) 以CL包含轨迹点为分组种子点,其他轨迹片段的轨迹点按照距离最近原则分别匹配到不同种子点,形成轨迹点分组并按种子点时间次序排列。如图 8(b)所示,按次序形成轨迹点分组G1、G2、G3、G4。
(3) 计算每一分组轨迹点的中心位置点(图 8(c)),按次序连接成线后更新原来中心线CL。如图 8(d),更新后CL={cp1, cp2, cp3, cp4}。
(4) 重复步骤(2)和(3),直至CL更新前后不再发生变化。最后,输出CL作为轨迹片段簇的中心线。
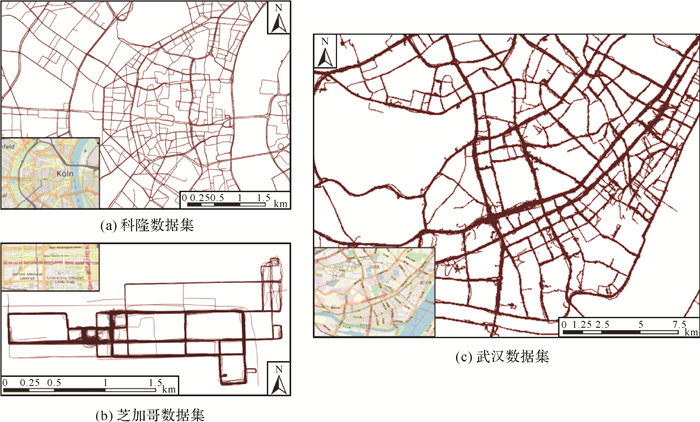
3 试验分析与评价 3.1 试验数据与环境设置如图 9所示,试验数据包括德国科隆市城区车辆移动轨迹数据集[27]、芝加哥校园巴士轨迹数据集和武汉市部分出租车的轨迹数据集。原始轨迹数据实施如下预处理:①按车辆组织轨迹点,依据时间次序连接形成轨迹线; ②当相邻轨迹点时间间隔大于30 s时(如在高层建筑、隧道等区域),对轨迹线实施打断处理;③过滤速度异常(大于200 km/h)的轨迹点。表 2描述了上述预处理工作后的车辆轨迹数据情况。相比较而言,来自科隆和芝加哥的轨迹数据定位误差小,道路上轨迹点分布密度高、车辆行驶速度相对均匀;武汉市出租车轨迹数据定位误差较大,且存在大量低速行驶点以及停留点。考虑到不同数据集间车辆行驶速度、轨迹点采样频率存在差异,变道轨迹片段提取时对轨迹线进行线性加密[28],加密间距dl=10 m。
|
| 图 9 试验轨迹数据集 Fig. 9 Experimental trajectory datasets |
| 试验数据 | 采样频率 /s |
定位误差 /m |
轨迹点数量 /个 |
平均速度 /(m/s) |
| 科隆数据集 | 1 | ≤10 | 170 615 | 10.97 |
| 芝加哥数据集 | 2~3 | 10~15 | 358 144 | 9.13 |
| 武汉数据集 | 2~6 | ≥30 | 527 702 | 4.24 |
建立ArcGIS与Matlab相结合的试验软件平台。其中,ArcGIS平台负责轨迹数据预处理、轨迹片段参量计算、轨迹簇生成及中心线提取等工作,利用Matlab提供的决策树学习模块建立变道轨迹片段识别模型。试验参数设置如下:①综合考虑车辆行驶速度、道路交叉口范围大小、相邻轨迹点时间间隔等,经过多次试验反馈,设置移动窗口大小s=9,窗口移动步长μ=1;②设置轨迹片段聚类的Hausdorff距离阈值h=10 m,轨迹片段簇定位点聚类的欧氏距离h′=80 m。
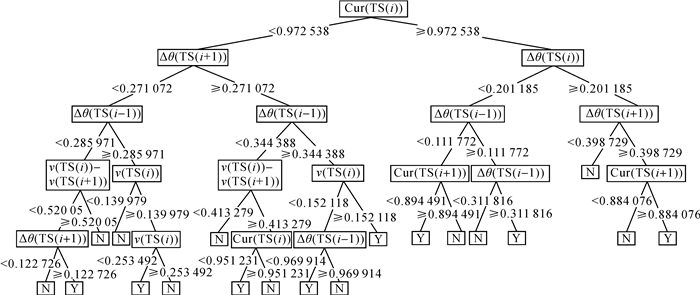
3.2 结果分析在构建轨迹片段决策树分类模型时,以人工标注方式叠加OpenStreetMap道路数据构建样本数据。综合考虑3种不同轨迹数据集的数据规模、采样精度,以及分类模型交叉验证的需要,从科隆数据集提取数量为1500的样本数据。其中,变道轨迹片段与非变道轨迹片段数量比例约1:3,涵盖各种典型的道路交叉口以及非交叉路口区域。对样本数据进行归一化处理后,按照80%和20%的比例划分为训练数据集和测试数据集。图 10是基于训练数据学习得到的轨迹片段决策树分类模型,包括6个层级,19个叶节点。利用测试数据进行验证,该模型对轨迹片段分类的准确率达到96.1%。
|
| 图 10 构建的轨迹片段分类决策树模型 Fig. 10 Decision tree model constructed for trajectory segment classification |
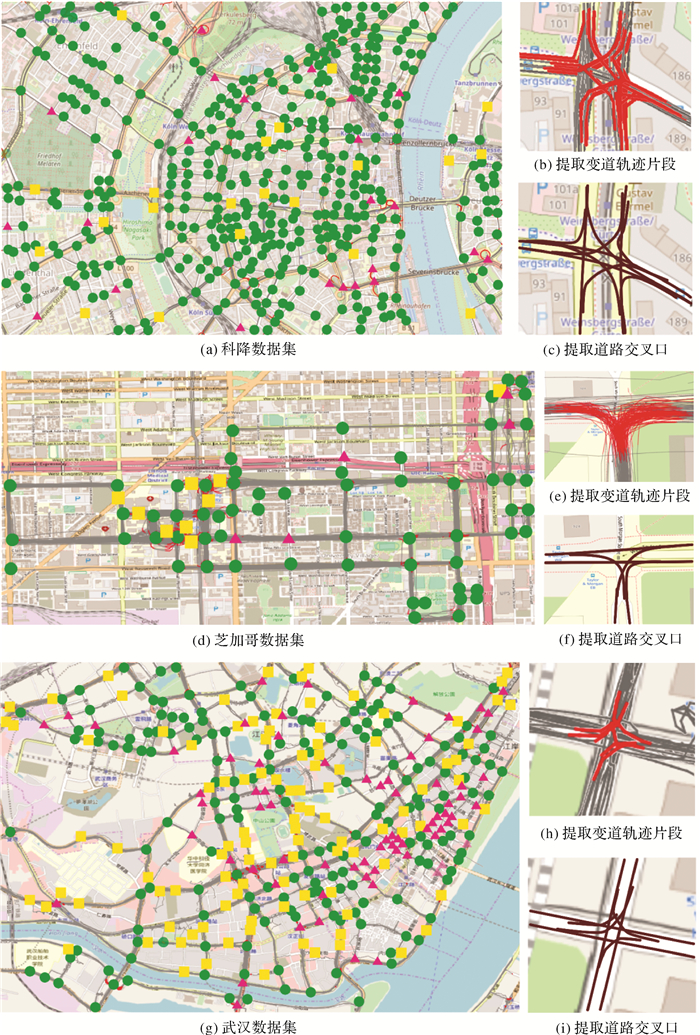
图 11展示了不同轨迹数据集通过分类器提取的变道轨迹片段及道路交叉口结果。图中绿色圈形表示变道轨迹片段识别较为完备的交叉口区域(TruePositive)、黄色矩形表示非道路交叉口但存在识别为变道轨迹片段的区域(FalsePositive)、红色三角形表示变道轨迹片段识别与实际不符的交叉口区域(FalseNegative)。图 11右侧分别为3个轨迹数据集识别得到的变道轨迹片段和交叉口结构示例。定义精确率(precision)和召回率(recall)对交叉口识别提取结果进行量化分析,precision和recall计算公式如下
|
| 图 11 变道轨迹片段识别与交叉口结果提取 Fig. 11 Lane-changing segments recognition and intersection structure extraction |
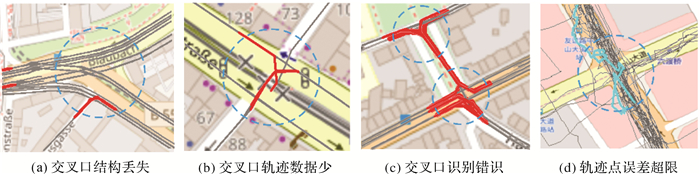
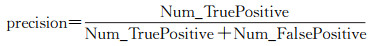 (5)
(5)
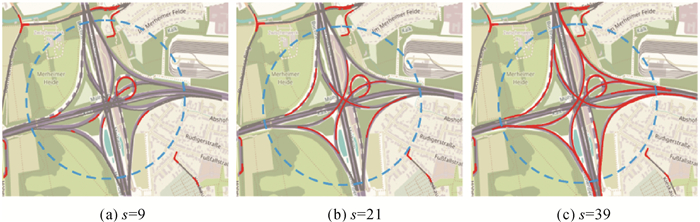
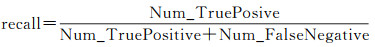 (6)
(6)
式中,Num_TruePositive、Num_FalseNegative和Num_FalsePositive分别表示识别结果为TruePositive、FalseNegative和FalsePositive的数量。将本文方法与转向点对法[16]和局部G统计法[14]进行对比评价。其中,转向点对法转向角阈值取45°,完成一次转向最大时间间隔设为20 s,转向点对相似度聚类阈值取0.75,局部点连通性聚类邻域半径取35 m;局部G统计法中交叉口候选轨迹点G*阈值取1.95。表 3统计了3种方法应用到不同轨迹数据集的交叉口识别结果。从中可以发现:
| 精确率 | 召回率 | ||
| 科隆数据集 | 本文方法 | 93.2 | 92.8 |
| 转向点对法 | 92.4 | 92.2 | |
| 局部G统计法 | 91.7 | 88.1 | |
| 芝加哥数据集 | 本文方法 | 87.1 | 92.4 |
| 转向点对法 | 85.9 | 92.4 | |
| 局部G统计法 | 85.7 | 84.4 | |
| 武汉数据集 | 本文方法 | 62.7 | 70.6 |
| 转向点对法 | 52.8 | 68.7 | |
| 局部G统计法 | 39.2 | 55.3 |
(1) 本文建立的交叉口提取模型对科隆和芝加哥数据集识别结果较好,精确率和召回率接近(或超过)90%,而应用到武汉数据集的交叉口识别精确率和召回率分别为62.7%和70.6%。分析原因:一方面武汉数据的定位精度较低,车辆变道产生的轨迹路径与实际位置偏移较大,导致出现大量轨迹点在一定范围内“抖动”的情况,对变道轨迹片段识别及道路线提取产生干扰;另一方面,决策树学习的样本数据来自科隆数据,构建的分类模型对于科隆数据以及质量特征(如轨迹点定位精度、采样频率)相似的芝加哥数据效果较好,而武汉数据由于样本学习不足导致分类器识别效果不佳。
(2) 面对采样频率高、定位精度较好、同时轨迹点分布密集的轨迹数据(如科隆和芝加哥数据集),3种方法均能取得较高的精确率和召回率;而应用到采样频率较低、定位精度不佳,有效轨迹点分布相对稀疏的情形(如武汉数据集),本文方法相比较转向点对法和局部G统计法有较大提升。局部G统计法通过挖掘轨迹点转向角的局部相关性,找到大转向角轨迹点分布密集的热点范围作为交叉口候选区域,对轨迹分布密集的交叉口有较好的识别效果,但易漏识别轨迹分布稀疏的交叉口。转向点对法通过提取车辆变道过程产生的完整转向特征进行分析,面对低精度轨迹数据时具有一定的抗干扰性,从而提升交叉口识别效果。本文方法除考虑转向特征外,进一步增加几何形态和速度变化指标,并且利用移动开窗策略对轨迹剖分片段进行连续式分析,对局部轨迹点存在的误差起到平滑过滤效果,从而能够更加准确地探测道路交叉口变道轨迹特征,得到相对较高的交叉口识别精确率与召回率。
本文方法产生的错误实例,主要包括两种不同的情形。
(1) 漏识别,即交叉口结构整体或部分丢失。该类问题常见于Y型交叉口(图 12(a))和大型立交桥区域。该类区域车辆行驶产生的转向及速度变化不显著,难以准确提取变道轨迹片段。此外,部分交叉口区域轨迹数据分布稀疏(图 12(b)),虽能从中获得少量变道轨迹片段,但其数量不足以形成有效的变道轨迹片段簇,从而导致交叉口特征未被完整识别。
|
| 图 12 交叉口识别错误示例 Fig. 12 Samples of incorrect extracted road intersections |
(2) 结构不准确,即交叉口识别结果与实际分布状态间存在不一致。如图 12(c)所示,对于交叉口分布密集且间距较小情况,当移动窗口尺寸设置偏大时,本文方法难以准确提取个体交叉口结构。此外,图 12(d)所示区域轨迹点定位误差较大时,导致轨迹片段直曲比、转向角和行驶速度计算结果失真,从而引起变道轨迹片段的错判以及对后续交叉口结构提取产生负面影响。
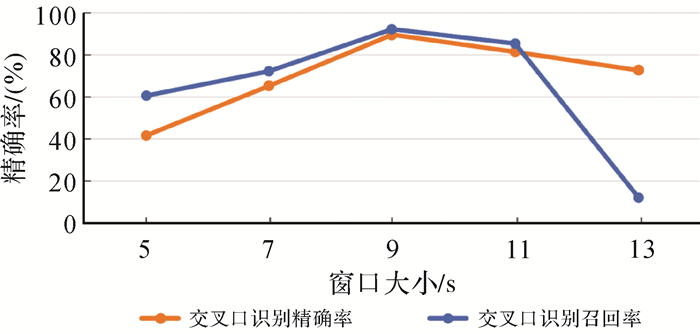
总结错误识别案例发生的缘由,包括两个方面:一是与轨迹数据本身质量相关,如局部轨迹线分布稀疏、轨迹点定位误差大等;二是与方法本身相关,如轨迹线剖分模型中移动窗口的大小对交叉口提取结果有重要影响。窗口太小,导致大型交叉口结构提取不完整;窗口太大,容易丢失小型道路交叉口。以科隆市Merheimer Heide公园旁的大型交叉口为例,图 13对比了3种不同大小窗口下的变道轨迹片段的识别结果。当窗口尺寸参数s=9时(图 13(a)),仅获得局部少量变道轨迹片段;增大窗口尺寸至s=39时(图 13(c)),则可以有效提高变道轨迹片段识别完整性。因此,合理的窗口大小设置十分关键。当轨迹线加密间距为10 m时,图 14统计了科隆数据集在窗口尺寸参数s不同取值下的交叉口识别结果。可以发现,当s=9(窗口内轨迹片段长度约90 m)时交叉口提取结果的精确率和召回率综合表现最好。另一方面,统计该区域所有交叉口的范围大小,发现80%以上范围圆直径处于60~130 m之间。因此,窗口大小设置可参考区域多数交叉口范围圆的直径分布区间。
|
| 图 13 不同大小窗口下变道轨迹片段识别结果 Fig. 13 Results of extracted lane-changing segments under different sizes of opening windows |
|
| 图 14 不同窗口尺寸下的识别结果分析 Fig. 14 Analysis of results with different window sizes |
4 结论
利用车辆轨迹数据提取道路交叉口特征,已有方法主要采用基于轨迹点的统计聚类策略。本文方法将轨迹片段作为基本分析单元,综合几何形态、转向幅度、速度变化指标识别道路交叉口的变道轨迹片段,然后通过轨迹片段的相似性聚类与中心线提取方法获得道路交叉口结构特征。围绕上述思路,设计了移动开窗式的轨迹线分段剖分模型,并引入机器学习领域的决策树学习方法建立轨迹片段分类模型。试验结果表明,本文方法相比传统方法在交叉口特征提取的准确率与召回率上具有优势,特别对采集频率低、分布相对稀疏的轨迹数据提取道路交叉口效果有较大提升。
本文方法还有不足之处有待改进提升。首先,需要建立更加完备的变道轨迹片段样本数据。试验中的样本数据来自科隆数据集,将训练学习得到的分类器应用到武汉数据集,交叉口识别准确率与召回率明显低于科隆数据集识别结果。主要原因是两种轨迹数据采样间隔、定位精度,以及背后的道路格局、交通拥堵状况存在差异,导致变道轨迹片段表现出不同的几何形态与动力学特征。因此,变道轨迹片段样本数据需要结合区域交通特点、轨迹数据质量状况进行补充完善。其次,需要发展窗口大小自适应调整机制,满足不同尺寸变道轨迹片段识别需求,从而实现对不同大小等级交叉口特征的准确提取。
| [1] | ANDRIENKO G, ANDRIENKO N. Spatio-temporal aggregation for visual analysis of movements[C]//Proceedings of2008 IEEE Symposium on Visual Analytics Science and Technology. Columbus, OH: IEEE, 2008: 51-58. |
| [2] |
龙瀛, 张宇, 崔承印.
利用公交刷卡数据分析北京职住关系和通勤出行[J]. 地理学报, 2012, 67(10): 1339–1352.
LONG Ying, ZHANG Yu, CUI Chengyin. Identifying commuting pattern of Beijing using bus smart card data[J]. Acta Geographica Sinica, 2012, 67(10): 1339–1352. |
| [3] | LIU Yaqiong, SEAH H S. Points of interest recommendation from GPS trajectories[J]. International Journal of Geographical Information Science, 2015, 29(6): 953–979. |
| [4] | DAVIES J J, BERESFORD A R, HOPPER A. Scalable, distributed, real-time map generation[J]. IEEE Pervasive Computing, 2006, 5(4): 47–54. |
| [5] | LIU Xuemei, BIAGIONI J, ERIKSSON J, et al. Mining large-scale, sparse GPS traces for map inference: comparison of approaches[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China: ACM, 2012: 669-677. |
| [6] | BIAGIONI J, ERIKSSON J. Inferring road maps from global positioning system traces:survey and comparative evaluation[J]. Transportation Research Record:Journal of the Transportation Research Board, 2012, 2291(1): 61–71. |
| [7] | KUNTZSCH C, SESTER M, BRENNER C. Generative models for road network reconstruction[J]. International Journal of Geographical Information Science, 2016, 30(5): 1012–1039. |
| [8] | EDELKAMP S, SCHRÖDL S. Route planning and map inference with global positioning traces[M]//KLEIN R, SIX H W, WEGNER L. Computer Science in Perspective: Essays Dedicated to Thomas Ottmann.Berlin, Heidelberg: Springer, 2003: 128-151. |
| [9] | SCHROEDL S, WAGSTAFF K, ROGERS S, et al. Mining GPS traces for map refinement[J]. Data Mining andKnowledge Discovery, 2004, 9(1): 59–87. |
| [10] | GUO Tao, IWAMURA K, KOGA M. Towards high accuracy road maps generation from massive GPS Traces data[C]//Proceedings of 2007 IEEE International Geoscience and Remote Sensing Symposium.Barcelona, Spain: IEEE, 2007. |
| [11] | AGAMENNONI G, NIETO J I, NEBOT E M. Robust inference of principal road paths for intelligent transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(1): 298–308. DOI:10.1109/TITS.2010.2069097 |
| [12] | EZZAT M, SAKR M, ELGOHARY R, et al. Building road segments and detecting turns from GPS tracks[J]. Journal of Computational Science, 2018, 29(11): 81–93. |
| [13] | PEUCKER T. A theory of the cartographic line[J]. International Yearbook of Cartography, 1976, 16(1): 134–143. |
| [14] | WANG Jing, RUI Xiaoping, SONG Xianfeng, et al. A novel approach for generating routable road maps from vehicle GPS traces[J]. International Journal of Geographical Information Science, 2015, 29(1): 69–91. |
| [15] | CAO Lili, KRUMM J. From GPS traces to a routable road map[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle, Washington: ACM, 2009: 3-12. |
| [16] |
唐炉亮, 牛乐, 杨雪, 等.
利用轨迹大数据进行城市道路交叉口识别及结构提取[J]. 测绘学报, 2017, 46(6): 770–779.
TANG Luliang, NIU Le, YANG Xue, et al. Urban intersection recognition and construction based on big trace data[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 770–779. DOI:10.11947/j.AGCS.2017.20160614 |
| [17] |
杨伟, 艾廷华.
运用约束Delaunay三角网从众源轨迹线提取道路边界[J]. 测绘学报, 2017, 46(2): 237–245.
YANG Wei, AI Tinghua. The extraction of road boundary from crowdsourcing trajectory using constrained delaunaytriangulation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 237–245. DOI:10.11947/j.AGCS.2017.20160233 |
| [18] | LI Jun, QIN Qiming, XIE Chao, et al. Integrated use of spatial and semantic relationships for extracting road networks from floating car data[J]. International Journal of Applied Earth Observation and Geoinformation, 2012, 19(10): 238–247. |
| [19] |
唐炉亮, 刘章, 杨雪, 等.
符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271–1276.
TANG Luliang, LIU Zhang, YANG Xue, et al. A method of spatio-temporal trajectory fusion and road network generation based on cognitive law[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1271–1276. |
| [20] | RUTKOWSKI L, JAWORSKI M, PIETRUCZUK L, et al. The CART decision tree for mining data streams[J]. Information Sciences, 2014, 266(5): 1–15. |
| [21] |
田晶, 艾廷华, 丁绍军.
基于C4.5算法的道路网网格模式识别[J]. 测绘学报, 2012, 41(1): 121–126.
TIAN Jing, AI Tinghua, DING Shaojun. Grid pattern recognition in road networks based on C4.5 algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 121–126. |
| [22] |
陈利燕, 张新长, 林鸿, 等.
跨比例尺新旧居民地目标变化分析与决策树识别[J]. 测绘学报, 2018, 47(3): 403–412.
CHEN Liyan, ZHANG Xinchang, LIN Hong, et al. Change analysis and decision tree based detection model for residential objects across multiple scales[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 403–412. DOI:10.11947/j.AGCS.2018.20170373 |
| [23] | KIM I H, FENG C C, WANG Yichen. A simplified linear feature matching method using decision tree analysis, weighted linear directional mean, and topological relationships[J]. International Journal of Geographical Information Science, 2017, 31(5): 1042–1060. |
| [24] |
李春鑫, 李天伟.
基于决策树改进CART算法的决策支持与分析技术[J]. 计算机科学, 2004, 31(9A): 44–46.
LI Chunxin, LI Tianwei. Decision support and analysis technique based on improved CART arithmetic of decision trees[J]. Computer Science, 2004, 31(9A): 44–46. |
| [25] |
陈锦阳, 宋加涛, 刘良旭, 等.
基于改进Hausdorff距离的轨迹聚类算法[J]. 计算机工程, 2012, 38(17): 157–161.
CHEN Jinyang, SONG Jiatao, LIU Liangxu, et al. Trajectory clustering algorithm based on improved Hausdorffdistance[J]. Computer Engineering, 2012, 38(17): 157–161. |
| [26] | ETIENNE L, DEVOGELE T, BUCHIN M, et al. Trajectory box plot:a new pattern to summarize movements[J]. International Journal of Geographical Information Science, 2016, 30(5): 835–853. |
| [27] | UDUWARAGODA ERIAC M, PERERA AS, DIAS SAD. Generating lane level road data from vehicle trajectories using kernel density estimation[C]//Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems. ZThe Hague, Netherlands: IEEE, 2014: 384-391. |
| [28] | DENG Min, HUANG Jincai, ZHANG Yunfei, et al. Generating urban road intersection models from low-frequency GPS trajectory data[J]. International Journal of Geographical Information Science, 2018, 32(12): 2337–2361. |



