时空索引是时空数据存储和管理的关键技术之一[1-2]。在分布式NoSQL数据库环境下,时空索引的研究可分为两大类:一类是基于传统的空间索引(QuadTree、R-Tree、Grid索引等)进行分布式改进或扩展的索引方法[3-9];另一类是基于空间填充曲线(space filling curve,SFC)的索引方法(Z-Order,Hilbert, Google S2等)。SFC由于具有良好的集聚特性,可以更好地描述时空数据的空间连续特征[10-11],近年来被广泛应用于时空索引领域。
文献[12]提出了以GeoHash字符串标识空间信息,并与时间属性字符串交织编码构成索引键值的时空索引结构;文献[13]提出了基于R-Tree与Geohash编码的空间索引机制;Google公司于2011年提出了一种四叉树与Hlibert曲线相结合的S2空间数据索引方法[14-15],可以实现多层级的空间要素的表达;关注度较高的开源项目GeoMesa[16]提出了XZ-Ordering[17-18]时空索引方法(以下简称XZ3),其基本思想是将四叉树与Z-Order曲线相结合,将空间信息的GeoHash字符串与时间信息字符串交错来实现时空信息的编码,并以一个随机的二进制编号作为行索引键,从而实现任意分辨率下空间信息的表达,并且查询性能不会随分辨率的提高而出现退化。
对等网络(peer to peer,P2P)是一种去中心化架构,具有高扩展性、高可用性、大吞吐量等特性。Apache Cassandra数据库[19-20]作为一种P2P网络下的NoSQL数据库,显现出了对于动态增长的海量数据管理方面的较大优势,然而基于Cassandra进行时空数据管理特别是对矢量数据管理的研究较少[21-22]。S2空间索引相对于XZ3索引可以更好地实现全球范围内矢量要素的多层级表达及对非点要素的连续性描述,然而现有索引方法应用于P2P网络时,仍存在以下难点问题需要解决:①时空信息联合索引问题,现有索引多侧重于空间索引的研究,如何兼顾时间查询与空间查询的效率是一个难点;②非点要素的合理表达问题,对于线、面状要素,其覆盖的空间范围差异大,查询时既要考虑小范围内的精确快速查询,也要兼顾大范围的全覆盖扫描,如何对非点要素进行合理表达是第2个难点;③最优时空层级确定问题,时间粒度与分层级别直接影响到查询的效率和准确度,如何根据地理要素自身特征确定合理的索引级别(时空分辨率)是第3个难点。
综上所述,本文在“去中心化”的对等网络下,基于S2索引,提出一种自适应层级的时空索引构建方法,实现对时空数据的时空联合查询、合理表达以及高效检索。
1 自适应层级的时空索引原理NoSQL数据库中的时空索引本质上是一种在Row Key中编码时空信息的方式。本文基于S2空间索引,构建一种自适应层级时空索引方法。基本思路为:首先采用分粒度、分层级的方法对时空信息进行联合编码;其次,依据地理要素空间分布方式对点及非点要素进行时空表达;最后,提出时空最优层级确定算法,并基于多层级时空索引树构建MLS3(multi-level sphere 3)时空索引。
1.1 时空信息联合编码 1.1.1 时间信息编码时间信息按照数据更新周期或者采样频率划分为6级,时间粒度在“秒”与“年”之间逐级分布,标记为gi(i=0, 1, …,5),如表 1所示。
| 时间粒度 | 分区键 | 分区键时间格式 | 排序键 | 排序键时间格式 |
| 00 | 年 | yyyy | 月-日时-分-秒 | MM dd hh:mm:ss |
| 01 | 年-月 | yyyyMM | 日时-分-秒 | dd hh:mm:ss |
| 02 | 年-月-日 | yyyyMMdd | 时-分-秒 | hh:mm:ss |
| 03 | 年-月-日时 | yyyyMMdd hh | 分-秒 | mm:ss |
| 04 | 年-月-日时-分 | yyyyMMdd hh:mm | 秒 | ss |
| 05 | 年-月-日时-分-秒 | yyyyMMdd hh:mm:ss | — | — |
定义Tbase为起算基点,Tcurrent为当前时间至Tbase的毫秒数,即Tcurrent=T(g5)-Tbase,则以当前时间对应时间粒度gi的整数部分作为分区键,记为Tpartition(gi),而排序键Tsort(gi)=Tcurrent-Tpartition(gi),得到时间信息在Row Key中编码如图 1所示。

|
| 图 1 Row Key中时间信息的表示 Fig. 1 Time information part in Row Key |
1.1.2 空间信息编码
依据S2索引思想,各个层级中的空间要素均可由对其形成包络的一个和多个格网进行标识。如图 2所示,线要素(灰色粗实线)在第1层级L1的包络Cell集合为(0, 2, 3),在第2层级L2的包络Cell集合为(00, 02, 03, 22, 23, 30, 31),在第3层级L3的包络Cell集合为(001, 002, 020, 022, 023, 031, 220, 231, 232, 303, 310, 311)。
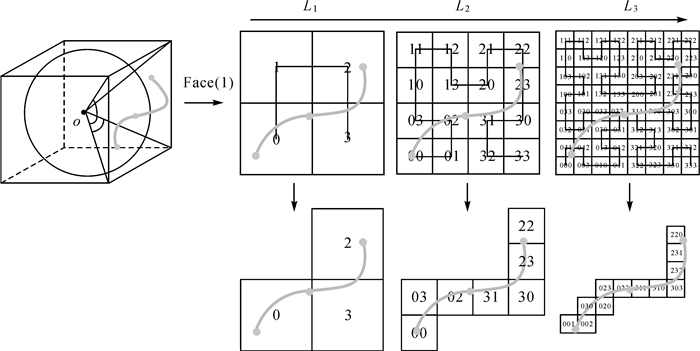
|
| 图 2 空间信息编码 Fig. 2 Spatial information coding |
本文对S2空间索引进行扩展,根据各个格网内的地理要素空间分布疏密情况,对格网作进一步剖分,从而将矢量数据空间信息表示为多层级的Hilbert编码。假设某个要素所在层级为Lm-Ln(0≤m < n≤30),则分区键为空间信息在较低层级m级上的编码,分区内排序键为空间信息在较高层级n级上的编码,如图 3所示。

|
| 图 3 Row Key中空间信息的表示 Fig. 3 Spatial information part in Row Key |
1.1.3 唯一标识信息编码
采用要素唯一标识(feature identification,FID)对同一格网内的多个要素进行区分,基本思路为采用Twitter的SnowFlake算法,按照ID生成的时间自增排序。FID编码包括5部分:标识位位于最高位,表示符号位;时间戳为第2部分,精确到毫秒级;对等网路中节点集群标识(cluster identification,CID)和集群中节点标识(node identification,NID)分别为第3和第4部分;最后部分由12位的计数顺序号构成,支持每个机器节点每毫秒产生4096个ID序号,如图 4所示。

|
| 图 4 Row Key中FID的表示 Fig. 4 FID in Row Key |
1.1.4 Row Key编码组织方式
整合上述时间、空间和唯一标识信息编码,形成时空信息联合编码的Row Key值。组织方式为:①分区键采用“较大时间粒度+父级空间网格标识”联合确定,以保证时空中具有相邻关系的要素分布在同一个或相邻的逻辑分区;②排序键组织方式同分区键类似,采用“较小时间粒度+子级空间网格标识+唯一标识”进行表示。假设时间粒度为i级,在第j层级的要素,空间网格的父级定为m级,n级为其进一步剖分后的子一级,则其时空编码如图 5所示。

|
| 图 5 Row Key内编码组织方式 Fig. 5 Design of Row Key |
1.2 索引编码 1.2.1 点要素的时空表达
对于点要素,本文采用其所在某一级网格的中心点近似表示。假设其分区键为Lm(0≤m < 30),排序键为Ln(m≤n < 30),按照上文所述Row Key设计原则,其分区键由在时间粒度g(i)下的时间值以及空间网格在m级涵盖该点的编码表示,分区内排序键由时间信息中去除分区键时间值的部分、空间信息在第Ln级的编码以及要素唯一标识表示。
以某收费站POI兴趣点为例,假设其更新时间粒度为月份,图层空间范围所在层级为9~10级,则该POI的分区键由月时间粒度“2016-02”和空间信息在9级的Cell ID(35f0ec)组成;分区内排序键由时间戳(01 13:00:00)、空间信息在10级的Cell ID(35f0eb0)以及要素唯一ID组成,如图 6所示。

|
| 图 6 点要素的Row Key表示 Fig. 6 Row Key of point element |
1.2.2 非点要素的时空表达
对于非点要素(线要素和面要素),一个要素的空间信息可能由多个空间网格表示,即一个要素对应多个键值。分区键及分区内排序键组织形式同点要素一致。
以道路线要素为例,假设其更新时间粒度为月份,图层空间范围所在层级为4~7级,则该道路的分区键由月时间粒度“2008-02”和空间信息在4级的Cell ID(35b)组成;分区内排序键由时间戳(01 12:00:00)、空间信息在6至7级的Cell ID(35acc、35ac9b、35accf等)以及要素唯一ID组成,如图 7所示。
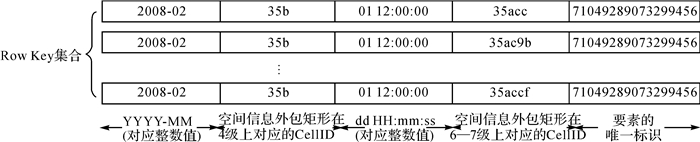
|
| 图 7 一个线要素的Row Key表示 Fig. 7 Row Key of an line element |
2 时空索引构建算法
对于矢量数据时空索引,根据其时空特征自适应确定最优索引级别一直是难点所在。本文构建MLS3索引,通过地理实体时间划分间隔及空间密度特征确定最优索引层级。基本思想为:①最优时间层级。若T时间内,在指定的采样间隔下多个数据获取源产生的数据量为P2P网络下数据库内最优分区数据块大小,则表 1中涵盖时间范围T的最小时间粒度为最优时间层级。②最优空间层级。设定一个初始格网划分数量阈值,若在第N层级上,图层范围内的地物被近似该阈值的格网全覆盖,则N为空间最优初始层级,进而根据N级上每个格网内的要素稀疏程度对格网做多层级剖分,获取该图层的最优空间层级。
2.1 时间粒度确定对于静态离散的时空数据,采用数据的更新周期作为分区键的时间粒度,比如年份或月份;对于动态连续的时空数据,其时间粒度根据其采样频率及数据大小设定。以Cassandra数据库为例,Cassandra数据库单个分区数据块超过100 MB后,在进行压缩、集群扩容等操作时会对Cassandra带来较大的Garbage Collection(GC)压力,数据库性能下降,为此本文以数据库内最优分区数据块大小作为约束计算最优时间粒度。定义时间间隔(时间粒度)总长度为T(ms),采样间隔为I(ms),传感器个数为N(个),存储单条记录所需的空间大小为S(MB),则满足式(1)的时间间隔T为最优时间粒度
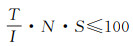 (1)
(1)
最优空间格网层级的确定需要顾及要素的分布、存储代价以及查询时间代价。假设Ecell表示一个单元格(cell)中所包含或相交的要素集合,Equery表示查询范围内所包含或相交的要素集合。
定义1:有效查询单元格:是指与查询范围相交或包含在查询范围内的Cell并且其满足Ecell∩Equery≠Ø。
定义2:无效查询单元格:是指与查询范围相交的Cell并且其满足Ecell∩Equery=Ø。
第k次空间查询所需的查询时间Tk主要由查询m个有效单元格和n个无效查询单元格的耗时组成。由于NoSQL数据库查询某一区域数据耗时主要由数据量决定,因此,可近似认为查询某个cell耗时由其内要素个数和查询单要素耗时决定;进一步假设在同一层级l查询单个要素所需时间相同,表示为ΔTl,则查询时间Tk可表达为式(2)
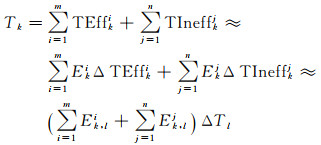 (2)
(2)
式中, TEffki、TIneffkj分别表示查询第i个有效单查询元格和第j个无效查询单元格所需时间;Eki、Ekj分别表示第i个有效查询cell和第j个无效查询cell内要素的数量;ΔTEffki、ΔTIneffkj分别查询单个要素所用时间。
则最小化K次查询所需要的总耗时可以表示为式(3)
 (3)
(3)
假设某一地理范围的空间索引层级集合为L,且在L中各cell内要素数量不超过某一阈值,则查询单个cell的时间与其内要素数量呈线性关系,式(3)可进一步表示为
 (4)
(4)
式中,Nkl表示第k次查询l级cell的数量;ΔEl表示第l级平均每个cell中含有的要素数量(小于一定阈值时近似认为每个cell中要素数量相同); ΔE和ΔT分别表示L集合中各cell要素的平均数量和查询单个要素的平均时间,其乘积为遍历一个cell中所有要素所需平均时间,与第1层级划分的cell数量N1相关,S为要素总数量,λ为线性相关系数,而式(4)中的各项参数又满足式(5)约束
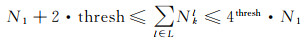 (5)
(5)
则最优空间索引层级确定问题简化为选取合适的初始层级N1和层级数量thresh,以尽可能遍历最少的cell数量达到查询的覆盖范围,从而确保总查询时间最少。
2.3 多层级时空索引树根据上述最优时空索引层级确定策略,本文建立多层级时空索引树(multi-level tree),如图 8所示,其中1级节点为粒度较大的时间信息节点,对应Row Key中分区键中的时间信息编码,由Ti节点表示;2级节点为cell级别,对应分区键中的空间信息编码,由Ci节点表示;第3级节点为粒度较小的时间节点,对应分区排序键的时间信息编码,由Ti+1节点表示。此3级为初始划分,其他层级可根据数据时空分布特征自适应划分,由Ci+1,2,…节点表示,对应分区排序键的空间信息编码。
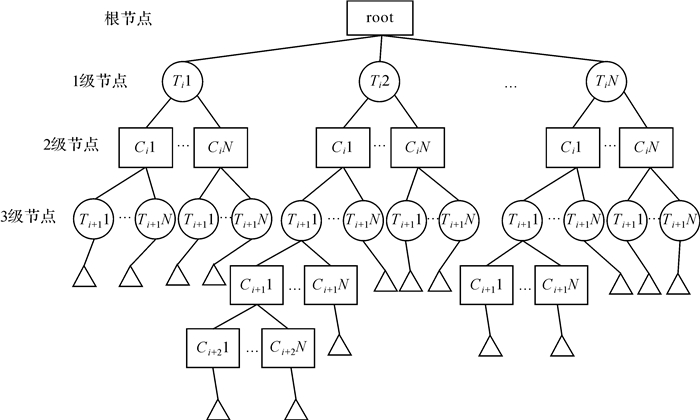
|
| 图 8 多层级时空索引树 Fig. 8 Multi-level temporal-spatial tree |
基于时空层级确定算法及多层级时空索引树的组织方式,本文构建MLS3索引,流程如图 9所示。
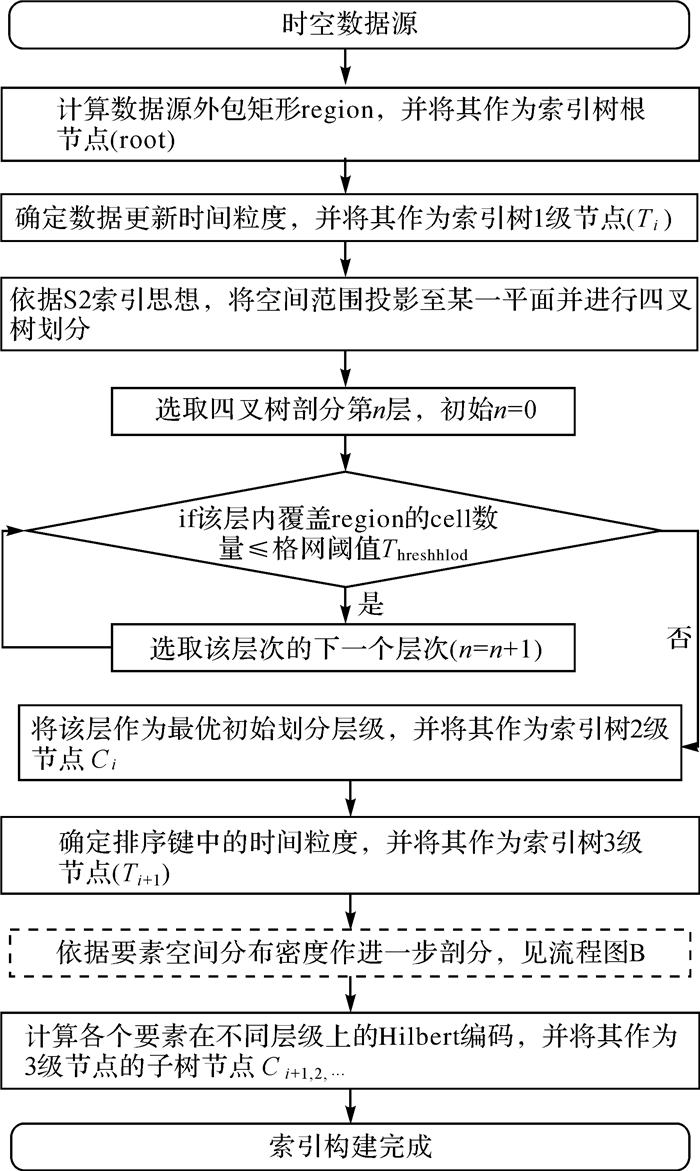
|
| 图 9 多层级时空索引树构建流程 Fig. 9 Flowchart of multi-level temporal-spatial tree construction |
在MLS3算法构建multi-level tree的过程中,节点的剖分操作仅允许在叶子节点发生,流程如图 10所示。
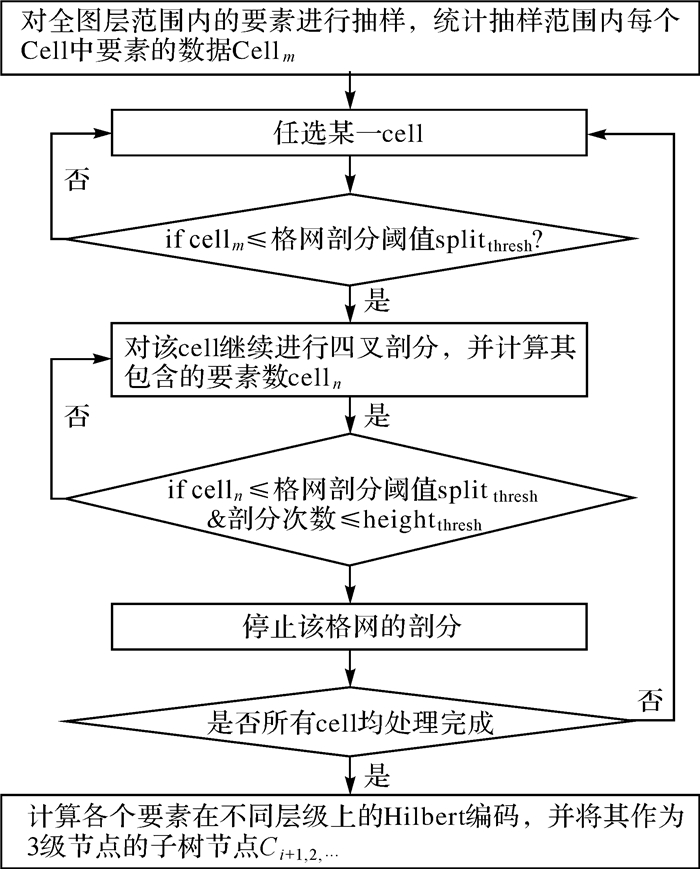
|
| 图 10 叶结点剖分流程(流程B) Fig. 10 Flowchart of leaf node splitting |
该树作为索引策略存储在相应的元数据中,用于查询时进行查询范围划分为若干cell区域查询的依据。遍历查找时间复杂度O(n),n为查询范围内cell数量。
3 试验与分析 3.1 试验数据与试验环境为了验证本文所提时空索引算法MLS3的有效性和合理性,将本文索引算法与XZ3时空索引算法在相同数据集、相同测试环境下进行比较。模拟实际生产环境搭建Cassandra集群,采用P2P架构,共5个数据库节点,冗余备份因子为2,单节点的性能为:IBM X3850服务器,内存大小16 GB、CPU共16核,主频为2.294 GHz,存储空间120 GB。试验数据集采用微软亚洲研究院提供的2008年2月2日至2月8日北京市10 357辆出租车的GPS轨迹(点要素)数据(TDrive Dataset)[23-24],约1500万条数据,里程约900×106 km,以及Open Street Map(OSM)提供的北京市2017年11月至2018年3月共5个月份的数据,包括建筑物(面要素)227 258条、公路(线要素)309 314条(OSM DataSet)[25-26]。
为了测试不同并发访问的应用场景,本文对上述两个数据集分别生成时空查询窗口:①TDrive数据集。随机选择2008年2月2日至2008年2月8日早7时至晚9时时间段内的200个时间种子点,时间窗口大小限制为≤2 h,空间查询窗口为北京市行政区划内随机生成的200个矩形窗口,时间窗口及空间矩形随机组合构成200个时空查询窗口。②OSM数据集。时空查询窗口生成方式与TDrive数据集类似,不再赘述。时空查询窗口如图 11所示。

|
| 图 11 200个时空查询窗口 Fig. 11 200 query windows:TDrive and OSM data set spatio-temporal query windows |
3.2 层级划分合理性验证
为验证层级划分算法的合理性,本文选取TDrive Dateset进行试验验证。对1500多万条GPS数据进行随机采样,采样率为20%,cell剖分阈值splitthresh设为样本的30%。由MLS3算法得到该数据集最适宜初始划分层级为9级,树深度阈值为2,即多层级的划分范围为9~11级。
为验证上述索引层级的合理性,本文在同一数据集下,设置6、7、8、9、10、11、12等7个不同层级作为初始层级,并以200次时空查询平均耗时最低的层级作为7个层次中的最优层次划分。试验结果如图 12所示,可以发现随着索初始层级的增加,查询平均耗时先降后升,从6级到9级平均耗时逐步降低,在9级时达到最低耗时117.17 ms;但是从9级到12级,平均耗时逐步上升,在12级时达到了3520 ms。
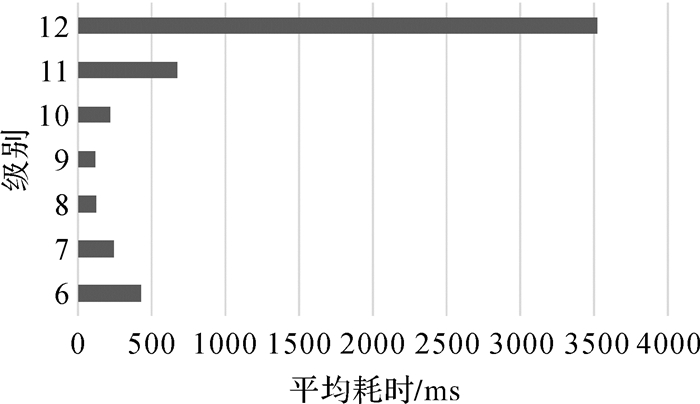
|
| 图 12 不同划分层级参数平均耗时 Fig. 12 Average time-consuming at different levels |
统计本文方法在确定GPS轨迹数据、公路数据及建筑物数据最优索引层级的耗时,分别为1601 ms、314 ms和182 ms,各占索引构建总时间的11%、13%和9%。此外,目前该算法已经应用到智慧临沂、智慧淄博等时空信息云平台建设项目中,经大量实际生产数据验证,一级cell的数据量阈值设定为200个为宜,由此得到国家级图层(如中国范围)最适宜划分层级为4~5级,省级范围图层(如山东省范围)最适宜划分层级为7~8级,市级范围图层(如北京市范围)最适宜划分层级为9~10级。
3.3 索引性能对比分析因S2索引不包含时间索引,故选择XZ3时空索引算法作为对比算法,从索引查询效率、构建效率和空间利用率3个维度检验本文算法的性能。
3.3.1 查询效率XZ3时空索引默认采用单线程、page size为1,故本文首先对默认参数条件下两种算法的性能进行比较。试验数据为TDrive DataSet和OSM DataSet两个数据集,设置1、5、10、15、20、25、30、35和40等多组并发查询访问粒度。试验结果如表 2所示。
| 任务并发数/个 | 1 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | ||
| 平均耗时/ms | TDrive taxi(点) | XZ3 | 1623 | 1628 | 2165 | 2285 | 2317 | 2401 | 2245 | 2606 | 2373 |
| MLS3 | 526 | 625 | 642 | 788 | 676 | 981 | 1011 | 1461 | 1216 | ||
| OSM roads(线) | XZ3 | 2213 | 1931 | 2632 | 4177 | 4948 | 5106 | 5422 | 4036 | 5729 | |
| MLS3 | 520 | 626 | 694 | 836 | 872 | 1953 | 2861 | 3365 | 3958 | ||
| OSM buildings(面) | XZ3 | 2215 | 1869 | 2365 | 3239 | 3662 | 4477 | 4270 | 4417 | 4430 | |
| MLS3 | 374 | 446 | 459 | 521 | 523 | 622 | 595 | 993 | 969 | ||
从整体上看,随着并发查询访问任务的增加,MLS3算法与XZ3索引算法查询耗时均有所增加,但MLS3算法的耗时均低于XZ3算法。如表 2所示,对于GPS轨迹点数据,XZ3算法的查询耗时为本文算法查询耗时的1.7~3.4倍;对于线、面等非点要素,MLS3算法查询效率提升更为明显,XZ3算法的查询耗时分别为本文算法查询耗时的1.2~5.0倍和4~7倍。总体来说,在相同试验参数设置下,本文算法耗时约为XZ3算法的1/7~1/2,表明本文提出的顾及数据分布特征的MLS3算法能够保证查询范围尽可能限定在有效的cell区域内,有效缓解了高并发条件下的复杂时空查询操作的压力。
同时,调优本文索引方法参数与XZ3作进一步对比分析。MLS3采用5线程,page size为1024,XZ3采用GeoMesa提供的默认参数,其试验效果如图 13—图 15所示。可以看出,对于点、线、面3种类型的数据,XZ3查询耗时均有较大浮动,其原因不仅与查询条件所涵盖的数据量有关,同时也与索引算法所采用的SFC有关。XZ3索引基于Z-Order曲线构建,该曲线存在编码相邻的数据其空间关系会发生跳变的特点,而本文索引算法采用Hilbert曲线进行空间信息编码表示,可以保证空间相邻的要素其编码也是连续的,从而确保查询区域中数据最大程度的位于相同分区,减少了分区扫描时无效数据的查询和比较,缩短了查询时间。对于GPS轨迹点数据,XZ3算法在20~10 134 ms间浮动,而MLS3算法在2000 ms以内浮动(图 13);对于路网数据,XZ3算法在1201~3079 ms间浮动,而MLS3算法在630 ms以内浮动(图 14);对于建筑物面数据,XZ3算法在1000~3500 ms间浮动,而MLS3算法在500 ms以内浮动(图 15)。总体来看,MLS3算法在采用多线程和适当page size情况下,性能有大幅度提升,查询效率提升4~7倍左右,并且查询耗时稳定,更适合应用于实际场景。
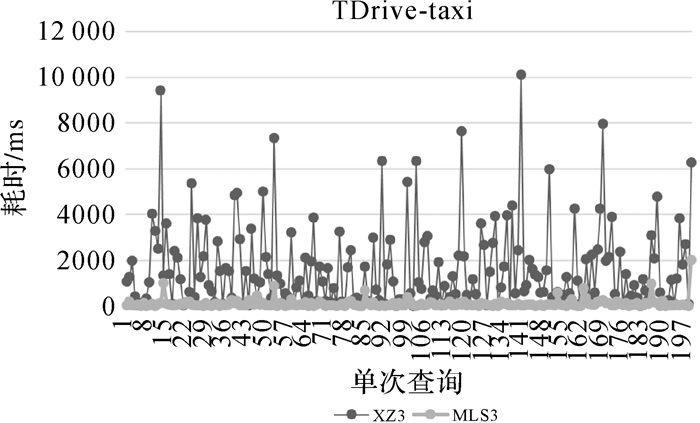
|
| 图 13 TDrive Data Set GPS点图层单次查询耗时对比 Fig. 13 Query time-consuming comparison of GPS points in TDrive data set |
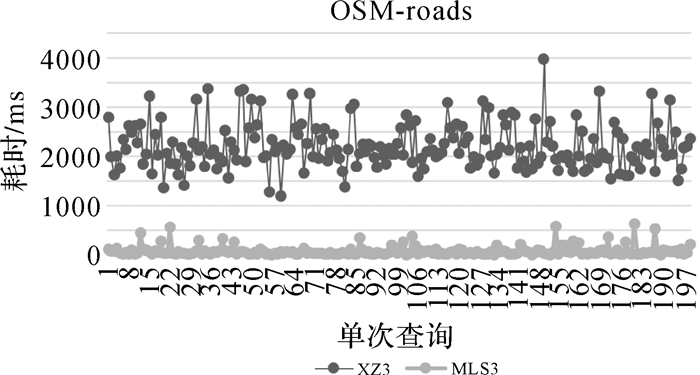
|
| 图 14 OSM Data Set建筑物图层单次查询耗时对比 Fig. 14 Query time-consuming comparison of road layer in OSM data set |
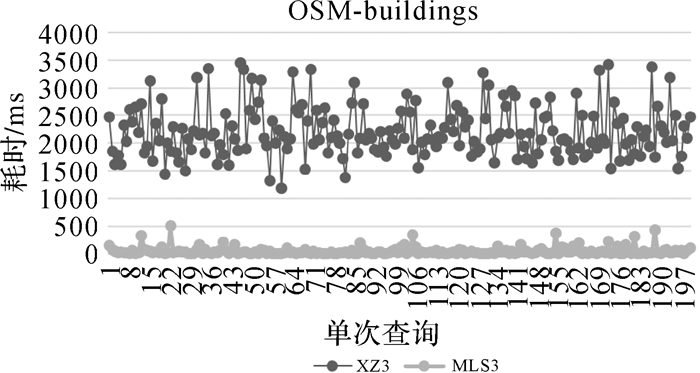
|
| 图 15 OSM Data Set建筑物图层单次查询耗时对比 Fig. 15 Query time-consuming comparison of building layer in OSM data set |
3.3.2 索引构建效率和空间利用率
以索引生成时间作为构建效率,以索引数据量大小占其对应矢量数据大小的比例作为空间利用率,对两种索引方法的性能作进一步比较,各项指标值如表 3所示。可以发现,对于点、线、面3种要素,两种索引方法的空间利用率基本一致,本文方法所占存储比例略高,较XZ3索引分别增加了7.49%、1.54%和3.02%。然而两种索引方法的数据量大小均占总存储空间的0.5%左右,相较于现有硬件存储环境,空间利用率在可接受范围。此外,在索引构建效率方面,本文方法构建耗时相对高于XZ3,增加的时间与数据要素数量呈正相关关系。这是因为XZ3仅仅计算Row Key值,而MLS3需要构建多层级索引树,同时进行索引级别的自动划分和选择,然而,两种索引方法构建过程所需时间不超过数据导入总时间的1/10。
| 指标 | 索引方法 | TDrive taxi (点) |
OSM roads (线) |
OSM buildings (面) |
| 空间利用率 /(%) |
XZ3 | 31.14 | 7.37 | 10.68 |
| MLS3 | 38.63 | 8.91 | 13.70 | |
| 构建效率/s | XZ3 | 63 | 3 | 2 |
| MLS3 | 147 | 23 | 19 |
4 结束语
针对传统时空索引存在的时间、空间查询难以同时顾及, 以及非点要素无法有效表达且最优索引层级难以确定等问题,本文通过地理实体时间粒度及空间密度等特征确定最优索引层级,并构建了时空索引MLS3。大量实际数据验证表明,在查询效率方面,MLS3索引的查询效率可提升4~7倍。此外,以Hilbert填充曲线为核心的MLS3索引相较于以Z-Order填充曲线为核心的XZ3索引能够更好地描述时空数据的连续性,表现出了更加稳定的查询性能,对于海量多尺度数据的分布式存储管理具有较强的适用性。然而为了提高查询效率及稳定性,本文牺牲了部分构建时间及空间利用率,但相较于现有硬件存储环境,增加程度在可接受范围。下一步将优化构建效率及空间利用率,并研究扩展该算法至主从架构的分布式NoSQL数据库中。
| [1] |
覃雄派, 王会举, 李芙蓉, 等.
数据管理技术的新格局[J]. 软件学报, 2013, 24(2): 175–197.
QIN Xiongpai, WANG Huiju, LI Furong, et al. New landscape of data management technologies[J]. Journal of Software, 2013, 24(2): 175–197. |
| [2] |
申德荣, 于戈, 王习特, 等.
支持大数据管理的NoSQL系统研究综述[J]. 软件学报, 2013, 24(8): 1786–1803.
SHEN Derong, YU Ge, WANG Xite, et al. Survey on NoSQL for management of big data[J]. Journal of Software, 2013, 24(8): 1786–1803. |
| [3] | CARY A, SUN Zhengguo, HRISTIDIS V, et al. Experiences on processing spatial data with MapReduce[C]//Proceedings of the 21st International Conference on Scientific and Statistical Database Management. New Orleans, LA: ACM, 2009: 302-319. |
| [4] | WU Sai, JIANG Dawei, OOI B C, et al. Efficient B-tree based indexing for cloud data processing[J]. Proceedings of the VLDB Endowment, 2010, 3(1-2): 1207–1218. |
| [5] | AGUILERA M K, GOLAB W, SHAH M A. A practical scalable distributed B-tree[J]. Proceedings of the VLDB Endowment, 2008, 1(1): 598–609. |
| [6] | AJI A, WANG Fusheng, VO H, et al. Hadoop GIS:a high performance spatial data warehousing system over mapreduce[J]. Proceedings of the VLDB Endowment, 2013, 6(11): 1009–1020. |
| [7] | HJALTASON G R, SAMET H. Speeding up construction of PMR quadtree-based spatial indexes[J]. The VLDB Journal, 2002, 11(2): 109–137. |
| [8] | TANIN E, HARWOOD A, SAMET H. Using a distributed quadtree index in peer-to-peer networks[J]. The VLDB Journal, 2007, 16(2): 165–178. |
| [9] | DU MOUZA C, LITWIN W, RIGAUX P. Large-scale indexing of spatial data in distributed repositories:the SD-Rtree[J]. The VLDB Journal, 2009, 18(4): 933–958. DOI:10.1007/s00778-009-0135-4 |
| [10] | ELDAWY A. SpatialHadoop: towards flexible and scalable spatial processing using mapreduce[C]//Proceedings of the 2014 SIGMOD PHD Symposium. Snowbird, UT: ACM, 2014: 46-50. |
| [11] | WHITMAN R T, PARK M B, AMBROSE S M, et al. Spatial indexing and analytics on Hadoop[C]//Proceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Dallas, TX: ACM, 2014: 73-82. |
| [12] | FOX A, EICHELBERGER C, HUGHES J, et al. Spatio-temporal indexing in non-relational distributed databases[C]//Proceedings of 2013 IEEE International Conference on Big Data. Silicon Valley, CA: IEEE, 2013: 291-299. |
| [13] | LE HONG VAN, TAKASU A. An efficient distributed index for geospatial databases[C]//Proceedings of the 26th International Conference on Database and Expert Systems Applications. Valencia, Spain: Springer, 2015: 28-42. |
| [14] | OCTAVIAN P. Geometry on the sphere: Google's S2 Library[EB/OL].[2011-01-13]. https://docs.google.com/presentation/d/1Hl4KapfAENAOf4gv-pSngKwvS_jwNVHRPZTTDzXXn6Q/view#slide=id.i22. |
| [15] | Google Corporation. S2 geometry library[EB/OL].[2015-08-15]. http://s2geometry.io/. |
| [16] | HUGHES J N, ANNEX A, EICHELBERGER C N, et al. GeoMesa: a distributed architecture for spatio-temporal fusion[C]//Proceedings of SPIE 9473, Geospatial Informatics, Fusion, and Motion Video Analytics V. Baltimore, MD: ACM, 2015. |
| [17] | BÖHM C, KLUMP G, KRIEGE H P. XZ-ordering: a space-filling curve for objects with spatial extension[C]//Proceedings of the 6th International Symposium on Large Spatial Databases. Hong Kong, China: [s.n.], 1999. |
| [18] | HULBERT A, KUNICKI T, HUGHES J N, et al. An experimental study of big spatial data systems[C]//Proceedings of 2016 IEEE International Conference on Big Data (Big Data). Washington, DC: IEEE, 2016. |
| [19] | LAKSHMAN A, MALIK P. Cassandra:a decentralized structured storage system[J]. ACM SIGOPS Operating Systems Review, 2010, 44(2): 35–40. |
| [20] | LAKSHMAN A, MALIK P. Cassandra: a structured storage system on a P2P network[C]//Proceedings of the 21st Annual Symposium on Parallelism in Algorithms and Architectures. Calgary, AB, Canada: ACM, 2009: 47-47. |
| [21] | CHEBOTKO A, KASHLEV A, LU Shiyong. A big data modeling methodology for Apache Cassandra[C]//Proceedings of 2015 IEEE International Congress on Big Data. New York, NY: IEEE, 2015: 238-245. |
| [22] | BRAHIM M B, DRIRA W, FILALI F, et al. Spatial data extension for Cassandra NoSQL database[J]. Journal of Big Data, 2016, 3(1): 11. DOI:10.1186/s40537-016-0045-4 |
| [23] | YUAN Jing, ZHENG Yu, XIE Xing, et al. Driving with knowledge from the physical world[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego, CA: ACM, 2011. |
| [24] | YUAN Jing, ZHENG Yu, ZHANG Chengyang, et al. T-drive: driving directions based on taxi trajectories[C]//Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems. San Jose, CA: ACM, 2010. |
| [25] | HAKLAY M, WEBER P. OpenStreetMap:user-generated street maps[J]. IEEE Pervasive Computing, 2008, 7(4): 12–18. |
| [26] | CURRAN K, CRUMLISH J, FISHER G. OpenStreetMap[J]. International Journal of Interactive Communication Systems and Technologies, 2012, 2(1): 69–78. |



