2. 北京四维图新科技股份有限公司, 北京 100094;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079
2. NavInfo Co., Ltd., Beijing 100049, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
随着高精度导航地图的推广应用,直接从该数据集中自动生产出较低精度的导航地图是当前亟待解决的问题,其中就涉及导航道路图形化简。已有的线图形简化算法很多,国内外学者在这方面已取得丰硕的研究成果,主要分为全域性算法和局域性算法。全域性算法以经典的Douglas-Peucker算法为代表[1],随后有些学者对此方法进行了改进[2-3]。为了使线的简化达到最优化效果,文献[4-7]提出了线简化的最优化算法和智能化方法。局域性算法将线图形划分为一定数量的基本组成单元,然后分别对每个组成单元进行化简[7-10],如文献[10]提出了用斜拉式弯曲划分的曲线化简方法。在线的简化过程中可能会引起空间关系的破坏,因此有些学者就研究了解决这些空间关系冲突的方法[11-12],如文献[11]研究了采用弯曲进行道路化简冲突避免的方法。线在不同尺度下需要保留必要的特征点,线的这些特征点识别方法很多[13-16],如文献[14]提出了曲线形态的结构化表达方法,文献[15]提出了基于拐点和极值点等局部特征点的线弯曲识别方法,文献[16]研究了基于曲率法的曲线特征点选取方法。
对于导航道路数据而言,其图形简化需要考虑导航需求和地图制图规则的约束。当前,在导航空间定位数据中,高精度导航地图的数据要求必须保留到小数点7位数。为了从7位数的导航道路数据中自动提取5位数的导航道路数据,本文采用网格模型表达导航地图数据,试图提出一种渐进式的道路图形化简方法,并协同处理导航道路网上的导航方向信息和可视化效果。
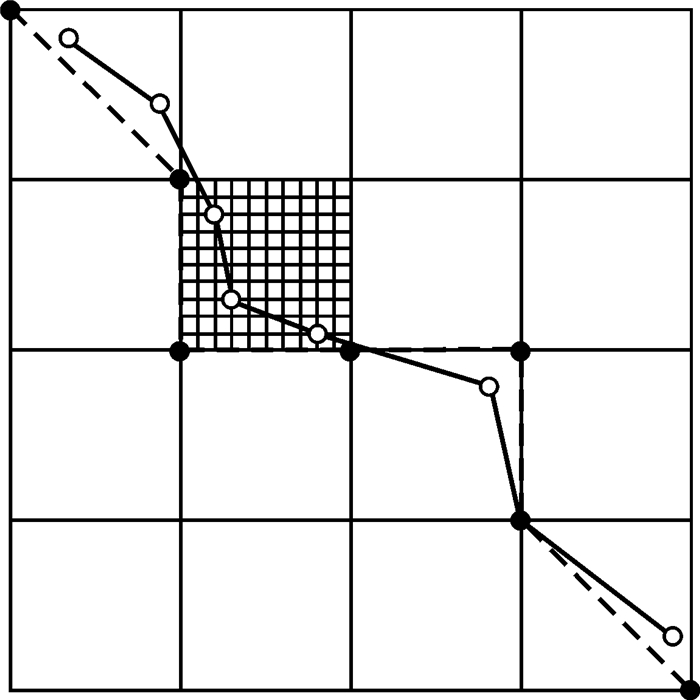
1 导航道路数据表达与需求导航道路网是一个图结构,图由节点和边组成,其中道路为边,道路交叉口为节点。一条道路可以用一串坐标进行描述,例如P={(x1, y1), …, (xi, yi), …, (xn, yn)},其中,(x1, y1)和(xn, yn)为首末点,(xi, yi)(i≠1, i≠n)表示顶点,因此,设道路的内域为P°,道路的首末点为∂P。本文采用网格模型[17]表示化简前后的导航数据。如图 1所示,实线为7位精度的道路,而同一条道路在5位精度下是图中的虚线。
|
| 图 1 不同层次网格模型上的道路 Fig. 1 Roads mesh models with different levels |
基于网格模型的导航道路图形化简的约束条件如下:
(1) 位置精度约束:道路立体交叉点和首末点在导航道路图形化简中不能删除, 只能移动,而顶点则可以删除或移动,点移动距离应该小于导航数据精度。
(2) 距离约束:导航道路上任意两个相邻顶点之间的距离不得超过用户设定的距离阈值范围。因此距离约束条件为:u≤|Vi-Vi+1|≤
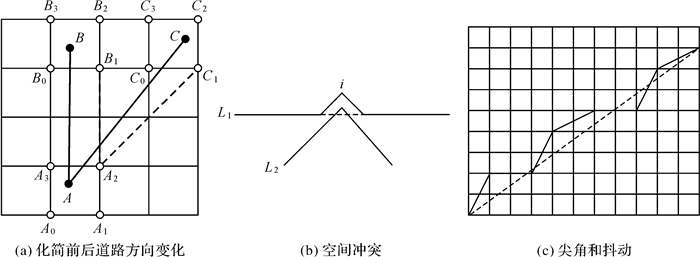
(3) 空间方向关系约束:导航道路图形化简前后要保持道路走向的相似性。如图 2(a)所示,化简前的道路上的3个顶点A、B、C,在化简后每个顶点的可选择位置为其所在的网格单元的4个角点之一,无论选择哪一个点,化简后的道路图形走向都可能发生变化,但是,化简前后道路(图 2(a)中虚线为化简后的道路)走向应当尽量相似。因此,当A∈P°时,A点处转角变化最小;当A∈∂P时,与A点关联的所有道路的方位角变化之和最小。
|
| 图 2 约束条件示意图 Fig. 2 Sketch map of constraint conditions |
(4) 空间拓扑关系约束:导航道路化简前后的空间拓扑关系不能被破坏。如图 2(b)所示,若线L1上删除i点,则会导致L1与L2相交,破坏了这两条线间的空间拓扑关系。因此,道路网中任意两直线段之间的拓扑关系在综合前后应该保持一致。
(5) 视觉光滑程度约束:导航中要考虑化简后道路的可视化效果。如图 2(c)所示,虚线转为5位精度的道路实线后,可能会产生一些急拐弯和抖动现象,针对这种情况就需要进行光滑处理。
2 道路顶点渐进式删除的算法 2.1 基本思想在导航道路化简过程中,需要维护道路空间方向关系和空间拓扑关系,同时还要顾及导航时的可视化效果,因此,本文采用渐进式图形综合的思想[18-19]对道路图形进行简化。这种渐进式思想主要体现在:对道路上的每一个顶点依据约束按顺序决策能否被删除,如果遇到不满足约束的顶点,则不立即处理该点,而是先将该点标记为问题点,然后顺序处理剩下的顶点,直到所有顶点都处理完毕,并同时更新所有被影响的顶点形状特征。然后逐个处理问题点,此时,可能这些顶点的形状特征发生改变,而不必再处理,需要按此过程对单条道路和整个道路网进行迭代处理。若一次迭代处理过程中仍然存在问题点,则需要继续迭代处理这些问题点,直到所有问题点全部处理完毕。
2.2 道路顶点的删除方法为了能够保持化简前后道路的局部形状特征,需要对道路的局部形状特征进行描述,本文采用道路上相邻顶点之间的距离和顶点处的转向角来描述该点的几何形状特征。如图 3(a)所示,Vi为当前的顶点,Vi-1和Vi+1分别为前后顶点,θi为顶点Vi处的转向角,D[i-1, i]和D[i, i+1]分别表示Vi与Vi-1和Vi+1之间的距离。在道路图形化简过程中也需要顾及道路的语义特征,以便在顶点删除过程中根据不同的语义特征进行处理。线的语义特征识别方法有很多[13-15],如文献[13]采用弯曲作为线的基本单元构建二叉树表达线结构的语义特征。对导航道路而言,直线型道路是一个比较重要的特征,因此,本文在计算局部几何特征的基础上将道路线结构的语义特征分为直线段和弯曲段两大类。若转向角小于一个很小的角度,且顶点偏移量小于一个很小的距离值,则提取道路中较长的直线段,将直线段外的部分都看作曲线型道路段。如图 3(b)所示,其中从1号点到3号点之间为直线型道路段;4号点处为右拐,6号点处为左拐,依据这些特征也可以划分出弯曲[15]。另外,在顶点删除过程中不能破坏线之间的空间关系,如同3(c)所示,可以通过栅格索引计算当前顶点与前后两顶点构成的三角形内是否包含其他顶点来判断顶点的删除是否会破坏空间关系。

|
| 图 3 顶点删除的约束 Fig. 3 Constraints on vertex deletion |
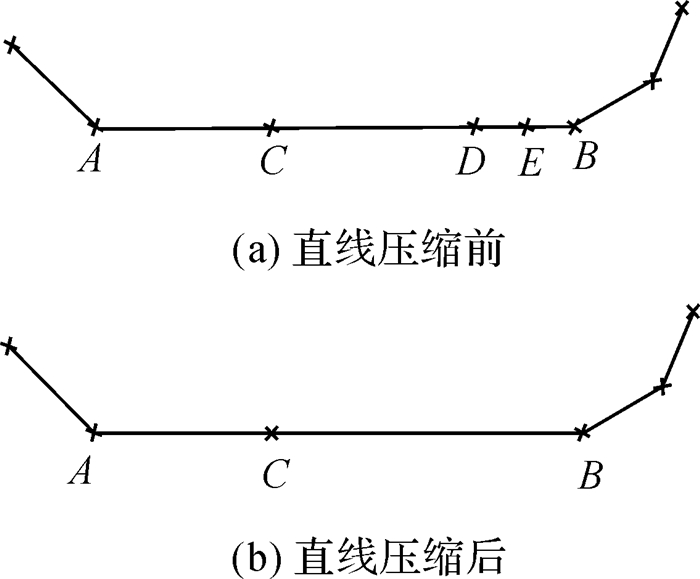
在提取了道路几何特征和语义信息基础后,可对道路顶点进行删除。设β为距离阈值。对于直线型道路段,如图 4(a)所示,其两端的顶点(A和B)不能删除。对于位于直线型道路段内部的点,若D[i-1, i]>β且D[i, i+1]>β,则按照导航要求保留该顶点,如图 4(b)中的C点,否则就删除,如图 4(a)中的D点和E点。对于曲线型道路段部分上的顶点,在顶点删除过程中需要考虑其周围的空间环境,处理方法如下:
|
| 图 4 直线型道路顶点压缩 Fig. 4 Compression of vertices on linear roads |
(1) 当D[i, i-1] < β时,如图 5(a)所示,可以直接删除Vi点;若在删除Vi点后会破坏线之间的空间关系,如图 5(b)所示,则不能删除Vi点,此时应将Vi点标记为“问题点”,正常处理完所有道路之后进行迭代处理。

|
| 图 5 弯曲型道路顶点删除 Fig. 5 Deletion of vertices on curved roads |
(2) 当D[i, i-1]>β且D[i, i+1] < β时,需要在Vi和Vi+1两个点内删除一个点。计算Vi+1点后段直线段的长度D[i+1, i+2],若D[i+1, i+2]>β,则比较Vi点和Vi+1点处的转向角的大小,如图 5(c)所示。当在Vi点处的转向角θi小于Vi+1点处的转向角θi+1时,删除Vi点,否则如图 5(d)所示,暂不删除Vi点,将Vi点标记为问题点,待迭代时再进行判断。若D[i+1, i+2] < β时,在两种情况下可以删除Vi点,如图 5(e)所示。当Vi点处的转向角θi小于导航规定的阈值,即Vi点与前后两个顶点近似在一条直线上时,可以删除Vi点;当Vi+1点处的转向角θi+1大于定义的阈值时,如图 5(f)所示,可以删除Vi点。其他情况下均不能删除Vi点,需将Vi点标记为问题点,待迭代时再进行判别。
对于已标记的所有问题点,需要迭代处理,重新对上一轮处理时不满足约束条件,且暂时没有处理的顶点进行判断。根据约束条件,迭代处理所有问题点,直至满足约束条件。在迭代时需要重新对问题点Vi计算其特征信息,根据问题点不同的空间环境进行处理,处理方法如下:
(1) 若问题点满足条件:D[i, i-1]>β且D[i, i+1]>β,就不再删除该点,取消Vi的问题标记。否则,仍按照弯曲部分的处理方式进行处理。
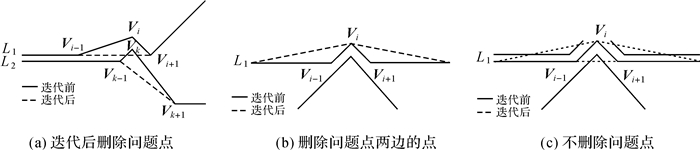
(2) 对于Vi点,如图 6(a)所示,D[i, i-1]>β且D[i, i+1] < β,并且删除Vi点后不再破坏道路之间的空间拓扑关系,删除Vi点。
|
| 图 6 迭代处理 Fig. 6 Iterative processing |
(3) 若删除Vi点后会破坏道路之间的空间拓扑关系,如图 6(b)所示,则删除Vi点两侧的点;但是,若Vi点两侧的点中也不满足删除条件,如图 6(c)所示,则不删除Vi点两侧的点,并将Vi点标记为问题点, 留待移位或人工编辑处理。
2.3 道路局部空间方向关系维护当7位精度的导航数据转换为5位精度时,道路空间方向关系可能会发生变化,如图 1所示,因此需要对化简后的道路进行空间方向关系维护[20]。对空间方向关系的描述方法有很多[21-24],本文采用顶点处的转向角来描述线在该点处的局部空间方向关系。转向角的大小表示道路转向变化的程度,转向角有正负之分,正值为右拐,负值为左拐;对于与道路起点和终点连接的顶点,为了维护交点处道路之间的空间方向关系,采用直线段的方位角来描述。
在5位精度下,原始7位精度的一个点的可选位置有4个。道路内部空间方向关系的维护就是在这4个位置中选择最优的位置,使维护后的线同原始精度下的线在空间方向关系上最相似。本文采用导航数据精度降低前后的顶点转向角偏差或节点(道路交叉点)关联的直线段方位角偏差和点的位置偏差作为局部空间方向关系相似程度的评价指标。
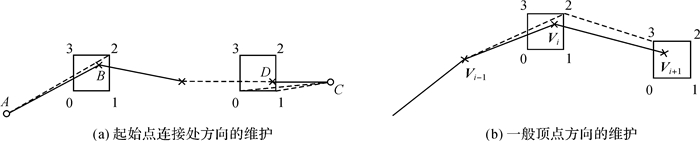
如图 7(a)所示,与起点和终点相连接的点在5位精度条件下的可能位置有4个。设点A和C已是5位精度的点,对B点和D点4个可能位置,计算AB和CD的7位精度与5位精度之间的方位角偏差,选择偏差最小时的B点和D点5位精度位置。若存在与最小方位角偏差相近的位置时,如7(a)中的D点,则选择位置偏差最小的5位精度位置。
|
| 图 7 道路局部空间方向关系维护 Fig. 7 Maintenance of local spatial directional relations of roads |
对于一般顶点Vi,如图 7(b)所示,按照顶点编号顺序进行处理。设Vi-1点的5位精度位置已经确定,则当前顶点Vi的空间方向关系受Vi-1和Vi+1的5位精度位置影响。首先,对Vi点的4个可能的5位精度位置,计算对应的Vi-1点处的转向角偏差Δθi-1,选取其中满足约束条件的位置作为可选的一个或多个位置。然后,对于每个可选的位置,再与Vi+1点的4个可能5位精度位置相连接,计算每个连接在Vi点处转向角的7位精度与5位精度之间的转向角偏差Δθi,选择其中偏差最小的位置作为调整后的位置。同理,若有多个转向角偏差都与最小偏差相当,则选择在5位精度下点位置偏差最小的点作为调整后的优选位置。
另外,在道路局部空间方向关系调整的过程中,可能会出现与原始点处的道路转向相反,这不符合约束条件。但是,若原始点在近似一条直线上,调整前后的转向角偏差Δθi很小,即使道路转向相反,也认为符合约束条件,其中,转向角偏差Δθi的阈值为一个大于0的很小的值。若Δθi大于阈值,就按照前文所提到的方法处理。道路局部空间方向关系维护的目标函数和约束条件见式(1)
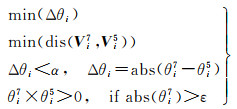 (1)
(1)
式中,abs是取绝对值函数;dis是两点之间的距离函数;θi7表示7位数据精度的Vi点处的转向角;θi5表示5位数据精度下的Vi点处的转向角;Δθi表示Vi点7位精度与5位精度之间的转向角偏差;Vi7表示7位精度下Vi点的坐标;Vi5表示5位精度下Vi点的坐标;α为导航需求的转向角偏差阈值;ε为直线型道路段转向角变化阈值。
2.4 道路局部的视觉光滑当导航道路数据的精度降低时,在道路局部可能存在尖角点和抖动点,在导航道路数据可视化时就需要进行光滑处理。已有许多曲线光滑算法,其中比较常见的方法是用拟合的曲线逼近原始曲线[25-26],但是在网格模型中由于受到网格精度的限制,新生成的5位精度曲线无法实现数学意义上的光滑。本文从道路视觉光滑的角度,提出了一种顾及道路局部视觉认知规律的光滑算法。
首先,需要提取5位精度下道路的尖角点和抖动点,在Vi点处为尖角点的判定条件为:|θi|>β,其中,β为转向角阈值。当与Vi点相邻的顶点的转向角方向同时变化时,则认为在该点处发生了抖动,Vi点为抖动点。但是,从道路可视化上看,若Vi点两侧直线段的长度都比较长,则该点就不是抖动点。抖动点的条件见式(2)
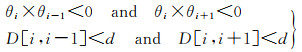 (2)
(2)
式中,θi为i点处的转向角;D[i, i-1]和D[i, i+1]为当前点Vi前后两条直线段的长度;d为长度阈值。
尖角点处的光滑插值方法如图 8(a)所示。设∠COD为需要光滑的尖角,O点处的道路转向角为θi,A和B为待插入的点,|OA|和|OB|为插入线段的长度,β2和β3分别为插入线段OA和OB与直线L2的夹角,L1为∠COD的角平分线,L2垂直于L1, 并相交于O点。下面以A点的位置计算为例,说明插入A点的过程:

|
| 图 8 道路视觉光滑的计算方法 Fig. 8 Calculation method on visual smoothing of roads |
(1) 计算OA与OC向量的夹角,β5=90°-β1/2-β2。
(2) 将O设为坐标原点,以OC为X轴的正方向构建临时坐标系,则可用式(3)计算点A在该临时坐标系中的坐标
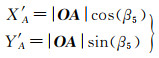 (3)
(3)
(3) 将临时坐标系下的坐标转换为原始坐标系下的坐标,见式(4)
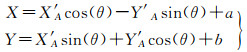 (4)
(4)
式中,X、Y为原始坐标系下点的坐标;θ为临时坐标系下向量OC与原始X轴正方向的夹角;a、b为临时坐标系原点O平移到原坐标系原点在X、Y轴方向上的平移距离。
(4) 计算所得的点为7位精度,需要转换为5位精度,并从4个可能位置中选择最优的位置,条件是:①OA的长度大于导航需求中的距离阈值;②OA与OC之间夹角最小;③插入点A后, β6应反映局部形状特征,即β6×θi>0;对于B点而言,则是β7×θi>0。
抖动点的处理如图 8(b)所示。设长度阈值为dis;Vi点前后两条直线段的长度分别为D[i, i-1]和D[i, i+1]。抖动点处理方法是:若D[i, i-1]dis,且D[i, i+1]dis,则不处理,如图 8(b)的第4号点;否则,用短直线段的中点代替原始的顶点,如图 8(b)中带圆圈的第1、2、3、5、6号点分别代替原始的第1、2、3、5、6号点。
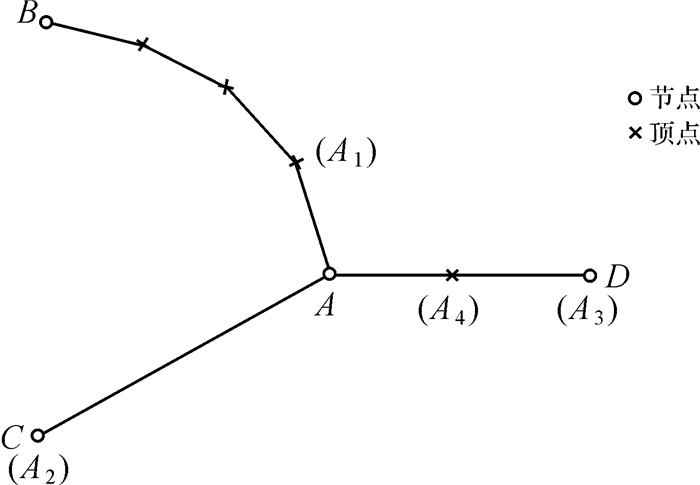
3 节点处空间方向关系维护导航中道路网节点处的道路走向十分重要。如图 9所示,道路节点A与3条道路线相关联,当导航道路数据从7位精度降为5位精度时,需要保持节点A处3条道路之间的空间方向关系。这种空间方向关系,本文用各条道路绕节点A的空间方位间接表达,并只考虑与节点A直接关联的直线段(AA1、AA2、AA3)的空间方位。从图 9可以看出,这里之所以用AA3,而不是AA4,是因为需要考虑到道路段AD是一条直线,这是一个非常重要的导航信息。
|
| 图 9 道路网节点处的空间场景 Fig. 9 Spatial scene at the junction of a road network |
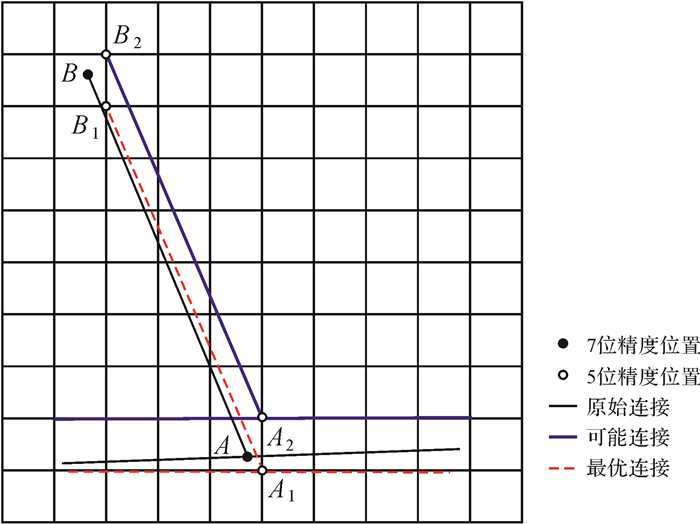
如图 10所示,道路网节点A与点B关联,A点和B点在5位精度下的可能位置均为4个,因此A点和B点的可能连接方式共有4×4=16个。计算所有连接方式的方位角,将所得的16个方位角同原始的7位精度下AB的方位角进行比较,优选偏差最小的连接。当有多个可能的连接都与原始直线段AB的空间方向关系非常相似时,则比较这些连接与原始直线段AB之间的位置偏差。这里的位置偏差定义为节点A的可能位置同原始精度位置之间的距离。同理,对于B点的5位精度位置也是按照这种条件判断,从而间接控制线段AB的长度偏差尽量小。如图 10所示,蓝色的A2B2连接和红色的A1B1连接都与原始直线段AB的空间方向关系非常相似,但是,A1离A更近,因此选择A1B1连接方式。
|
| 图 10 道路网节点处空间方向关系维护 Fig. 10 Maintenance of spatial direction relations at the junction of road network |
当道路网节点关联多个点时,就需要考虑与道路网节点A关联的所有直线段与原始直线段之间空间方向关系的整体相似程度。设节点A与M条直线段相关联,这些原始直线段的方位角为AZ(i),其中,i=1, 2, …, M;5位精度下可能形成的直线段方位角为AZP(i,k, j),其中,i=1, 2, …, M;k为节点A的可能位置,k=0, 1, 2, 3;j为与节点A相邻的点(i=1, 2, …, M)的可能位置,j=0, 1, 2, 3。当数据精度降低时,在节点A处空间场景中具有空间方向关系最相似程度的优选点位置的计算方法见式(5)
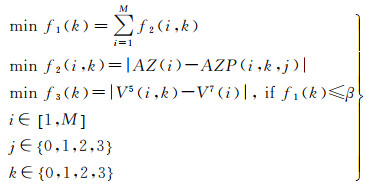 (5)
(5)
式中,f1(k)为点A在k位置下与M条直线段方位角偏差之和;f2(i,k)为点A在k位置下与第i条直线段的方位角偏差;f3(k)为点A在k位置下7位精度与5位精度的距离偏差,V5(i, k)为点A在k位置下5位精度的坐标,V7(i)为点A在7位精度下的坐标;β为角度阈值,当f1(k)≤β时,即当方位角偏差之和变化都比较小时,优选点A位置偏差最小的位置。
为了使得整个道路网所有节点处的空间方向关系整体上尽量保证与原始精度时的空间方向关系最相似,本文先对节点的连接度进行排序,然后优先处理连接度较大的节点。另外,在数据处理的过程中,由于当前处理的节点可能关联了已经处理的节点或被动处理的交叉点,因此对于已经处理过的节点位置就不再调整。算法流程如下:
(1) 扫描所有道路节点,获取与每个节点相连接的所有道路直线段。
(2) 根据节点所关联的道路直线段的数量(节点连接度),对节点进行排序。
(3) 按顺序选取要处理的节点。
(4) 计算当前节点与关联点在精度降低时的所有可能连接方式,对每种连接方式计算方位角偏差,利用式(5)判断当前节点的最优位置。
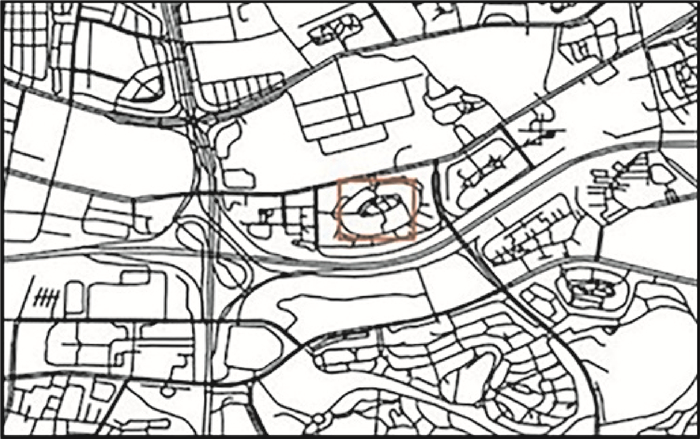
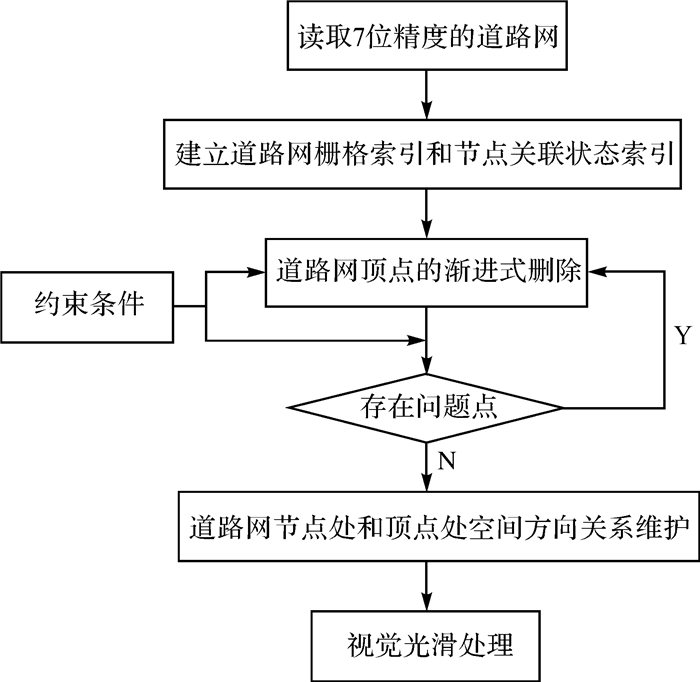
4 生产试验与分析笔者采用C#开发了用于导航道路数据综合(从7位精度转为5位精度)的算法试验软件,已用于多个城市的5位精度导航数据试生产。本文选取重庆市主城区7位精度的导航道路网数据用于算法分析。该数据集共包含道路53 525条和233 584个点,其中,道路网节点有8514个。图 11为生产试验中的部分数据,整个数据处理流程见图 12。
|
| 图 11 高精度的道路网数据 Fig. 11 Road network data with high precision |
|
| 图 12 导航道路图形化简的流程 Fig. 12 Flow chart of graphic simplification for navigation roads |
为了满足导航道路数据从7位精度降为5位精度的需要,在生产试验中设置了相应的参数和阈值,设判定直线的转向角阈值为2°;点之间的最小距离阈值为2 m;最大距离阈值设为5 m;转向角偏差阈值为6°;判定“尖角”的角度阈值为30°;7位精度下插入线段的长度为2.5 m。图 13是图 11中方框区域的试验结果,黑色表示7位精度的目标,绿色表示5位精度的目标。

|
| 图 13 导航道路图形化简的结果 Fig. 13 The result of graphic simplification for navigation roads |
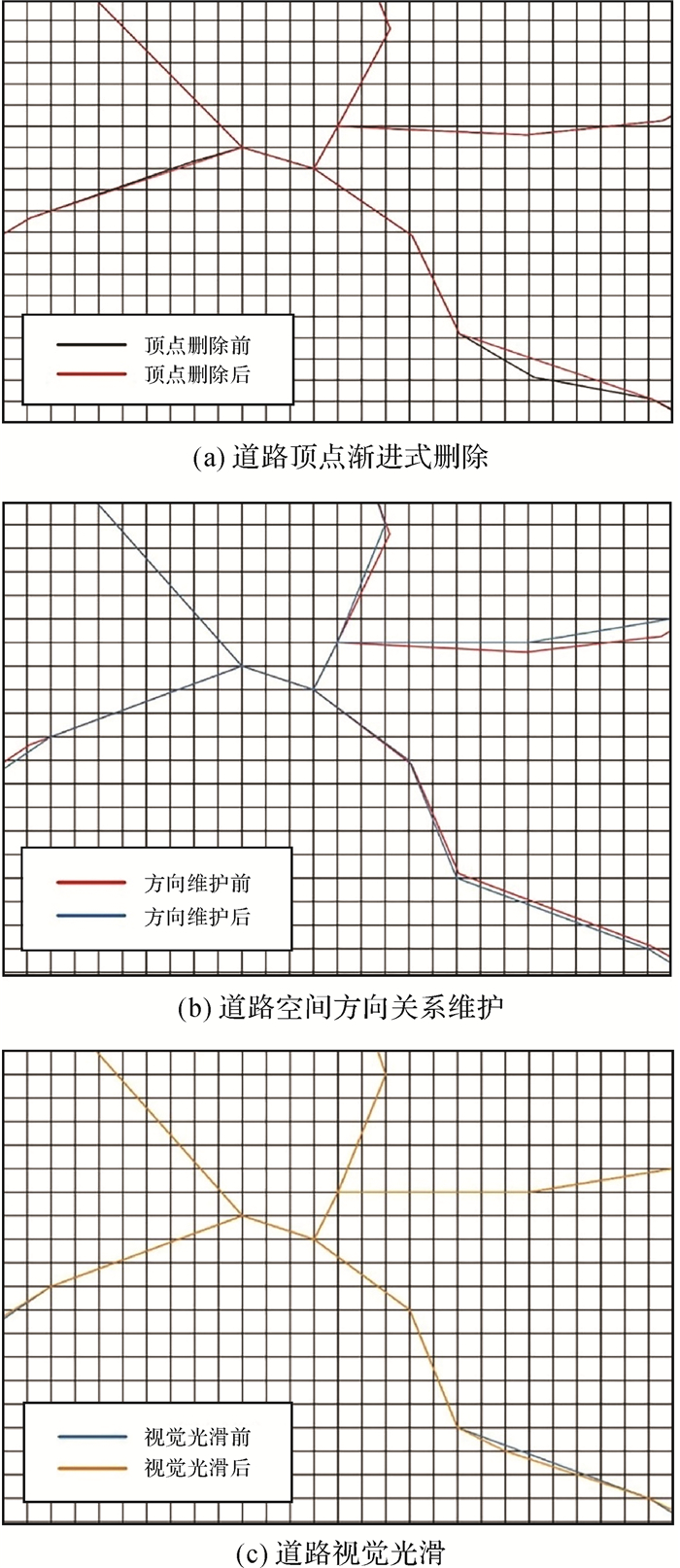
图 14为图 13中红色方框区域的放大图。图 14(a)为道路顶点渐进式删除的结果,红色表示综合后的目标;图 14(b)为道路空间方向维护的结果,蓝色表示空间方向关系维护后的目标;图 14(c)为道路视觉光滑后的结果,黄色表示光滑后的目标。
|
| 图 14 综合过程中各阶段的指定局部放大图 Fig. 14 Enlarged maps of the given local region in each stage of generalization |
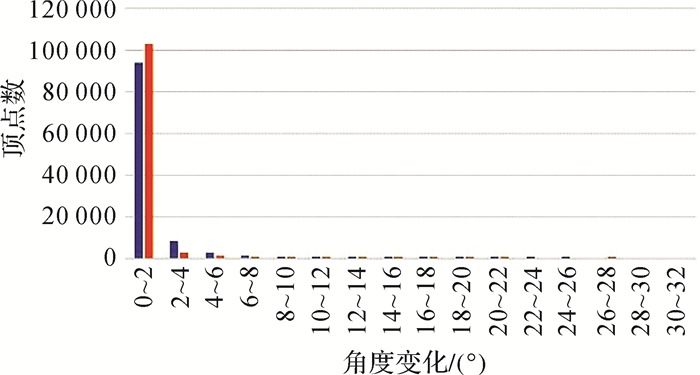
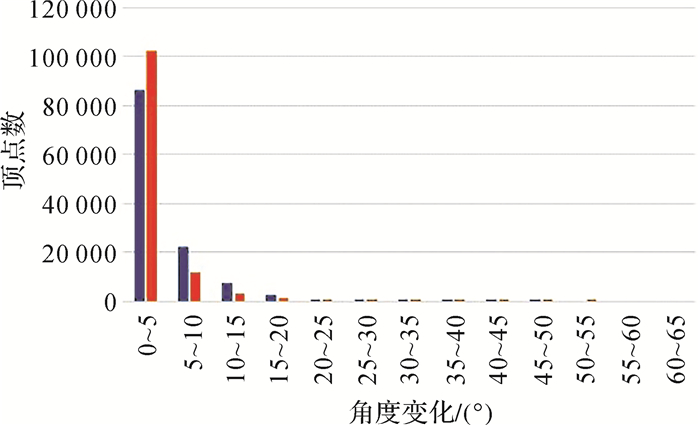
在道路图形简化过程中,空间方向关系维护是非常重要的一个环节,在点之间的最小距离阈值为2 m的情况下,本文分别统计了试验结果中道路网节点和道路顶点处的空间方向关系维护效果。图 15是道路网节点处空间方向关系维护结果的统计图,横轴表示与节点连接的道路直线段方位角在空间方向关系维护前后的角度变化区间;纵轴表示在角度变化区间内的直线段统计数量;蓝色表示调整前;橘黄色表示调整后。图 16是道路顶点处空间方向关系维护结果的统计图,横轴表示道路顶点处转向角在空间方向关系维护前后的角度变化区间;纵轴表示在角度变化区间内的顶点统计数量;蓝色表示调整前;橘黄色表示调整后。从统计图表中可以看出,本文的空间方向关系维护算法使得道路网节点处和道路顶点处的空间方向变化比直接使用四舍五入转换方法的空间方向变化明显减少。
|
| 图 15 节点处空间方向关系维护结果的统计 Fig. 15 Statistics of results at nodes after maintaining spatial directional relations |
|
| 图 16 道路顶点处空间方向关系维护结果的统计 Fig. 16 Statistics of results at vertices after maintaining spatial directional relations |
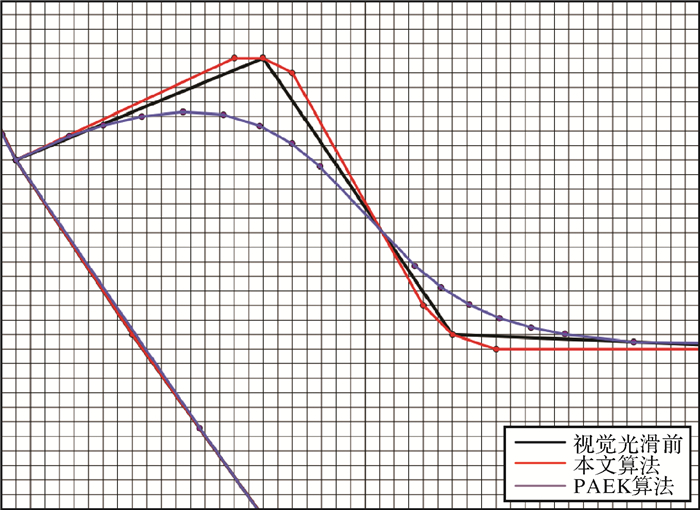
当最小距离阈值为2 m时,本试验结果中没有出现拓扑关系方面的问题点。当设置最小距离阈值为5 m时,就出现了拓扑关系方面的问题点。如图 17所示(7位精度的线为绿色;5位精度的线为棕色),问题点A不满足最小距离阈值条件,但是若删除该点,在点C2处就会出现拓扑关系错误。图 17中蓝色线表示删除A点后出现的拓扑关系破坏情况,从B1到B14是不可以删除的道路立体交叉点,C1和C2是导航地图模型中定义的不可删除点。在5位精度的导航地图数据生产中,点之间的距离有严格规定,若道路简化后存在点之间的距离小于设置的距离阈值,就标识这些点为问题点,以便有针对性地进行人工数据编辑。当导航地图数据可视化时,若道路顶点处转弯很急,符号化后的道路图形就显得不光滑,本文所提出的视觉光滑算法能很好地解决这个问题。将本文方法与ArcGIS中常用的PAEK光滑算法进行对比,结果如图 18所示。

|
| 图 17 存在拓扑关系错误的问题点 Fig. 17 Points with questions about topological errors |
|
| 图 18 两种光滑结果的对比 Fig. 18 Comparison between two kinds of smoothing results |
5位精度的导航地图数据生产有严格的要求,相关的导航需求是:点之间的距离大于2 m;道路网节点处关联的道路之间的空间方向关系变形最小;道路顶点处的转向角变化最小;所有点的位置误差小于1.42 m;空间目标之间的拓扑关系应该与7位精度的导航地图原始数据一致;简化后的道路不能出现抖动和急转弯情况;点之间的距离也需要小于5 m(用户定义的最大距离阈值)。这些要求在整个道路网图形简化过程中都需要进行判断,若存在不满足要求的点,笔者所开发的软件就自动进行标记,说明是问题点。
在试验中也使用ArcGIS10.2的两种线化简方法(点删除方法和弯曲化简方法)对同样的数据集进行了处理。以四维图新导航地图的需求为标准,对比分析了ArcGIS的处理结果和本文算法软件试生产的结果。
试验用的计算机配置条件是:Intel(R) Core(TM)i7-4790 CPU@3.60 GHz, RAM: 8 GB, windows10, 64位。ArcGIS的弯曲化简方法在无选项,阈值为5 m的条件下,耗时60 s;ArcGIS的点删除方法在无选项、阈值为2 m的条件下,耗时54 s;本文的化简算法耗时172.39 s,空间方向关系维护耗时238.13 s,空间拓扑关系维护耗时25.97 s,视觉光滑耗时17.07 s。由此可以看出,本文算法耗时比较多。主要原因是本文算法在化简阶段需要判断和维护空间拓扑关系,为了满足导航需求,还需要维护空间方向关系和视觉光滑效果。而ArcGIS的这两种方法都没有考虑这些空间关系的维护。
在原始试验数据(重庆市主城区)中道路有233 584个点,用本文算法简化后,保留了119 938个点,光滑后有129 884个点。按照本文描述的5位精度下的导航要求,检查了这3个试验结果,产生差异的原因是:点删除方法只考虑了点的偏移量,弯曲化简方法只考虑了弯曲的大小,它们都没有考虑保留点之间的距离应该在导航规定的距离阈值范围内。图 19是这3种方法所得结果的局部放大图,可以直观地了解它们之间的差异。在图形化简算法的对比试验中,ArcGIS的两个线图形化简工具无法直接表达导航道路数据生产的要求,本文依据5位数据精度导航道路数据生产对点之间距离的要求,设置了近似的阈值。

|
| 图 19 3种方法所得结果的局部放大图 Fig. 19 Enlarged maps of partial results of three kinds of methods |
在生产试验中,道路图形化简算法和空间拓扑关系维护算法的参数是按照四维图新5位数据精度导航地图生产的具体要求设置;空间方向关系维护算法和视觉光滑算法的有关角度的阈值是按照生产单位对导航道路数据的要求在进行了多次试验和调整后确定,是经验值。
在试验中所使用的渐进式道路图形简化方法充分利用了道路顶点渐进式删除、空间方向关系维护和视觉光滑等操作。这里的“渐进式”主要体现在:当道路顶点删除时,必须保证满足道路图形简化的约束条件;若无法满足这些约束条件,就需要临时标记该顶点为问题点,并记录其位置,然后在空间上下文关系发生变化后再回头来处理这些问题点,该过程是一个迭代过程。当需要从7位精度的道路数据综合为5位精度的道路数据时,在试验中并不是先综合为6位精度的道路数据,再综合为5位精度的道路数据。
5 总结本文基于网格模型有效表达了高精度导航数据向低精度导航数据的转换过程,详细说明了5位数据精度导航道路数据生产的特殊要求,将道路图形化简、导航地图要素之间空间拓扑关系维护、道路本身和道路网交叉点处空间方向关系维护以及道路数据可视化的视觉光滑等算法协同在一起,提出了一种基于网格模型的导航道路图形渐进式协同化简方法。在该方法中,网格模型体现了导航数据的表达需求;在道路图形化简过程中强调了渐进式质量控制;协同了空间关系维护和视觉光滑;在点删除过程中综合考虑了点之间的距离、点的语义特征和点附近的空间关系;依据导航数据网格模型表达的特征和视觉认知规律,设计了道路的视觉光滑方法。从试验结果看,本文所提出的方法顾及了导航需求,能够维护好道路网在数据精度降低时的空间方向关系,图形的可视化效果好。但是,本文所提出的方法在导航道路网向更低精度转换时如何与道路选取相结合还有待进一步的研究。该方法是针对5位精度的导航道路数据生产特点所提出的,制图综合的约束主要是点之间的最小距离、原始点的最大偏移距离、道路转弯方向和大小、道路连接关系、视觉光滑程度等,道路图形简化的主要任务是在保留道路(网)的导航所需要信息条件下删除多余的道路顶点。因此本文所提出的方法并不直接适用于制图约束条件性质不同的线图形简化任务。
| [1] | DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica, 1973, 10(2): 112–122. DOI:10.3138/FM57-6770-U75U-7727 |
| [2] | HERSHBERGER J, SNOEYINK J. Speeding up the Douglas-Peucker line-simplification algorithm[C]//Proceedings of the 5th International Symposium on Spatial Data Handling. Charleston, South Carolina: [s.n.], 1992: 134-143. |
| [3] | SAALFELD A. Topologically consistent line simplification with the Douglas-Peucker algorithm[J]. Cartography and Geographic Information Science, 1999, 26(1): 7–18. DOI:10.1559/152304099782424901 |
| [4] | CROMLEY R G, CAMPBELL G M. Integrating quantitative and qualitative aspects of digital line simplification[J]. The Cartographic Journal, 1992, 29(1): 25–30. DOI:10.1179/caj.1992.29.1.25 |
| [5] | JIANG Bin, NAKOS B. Line simplification using self-organizing maps[C]//Proceedings of ISPRS Workshop on Spatial Analysis and Decision Making. Hong Kong, China: ISPRS, 2003. |
| [6] |
武芳, 邓红艳.
基于遗传算法的线要素自动化简模型[J]. 测绘学报, 2003, 32(4): 349–355.
WU Fang, DENG Hongyan. Using genetic algorithms for solving problems in automated line simplification[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 349–355. DOI:10.3321/j.issn:1001-1595.2003.04.013 |
| [7] |
郑春燕, 郭庆胜, 胡华科.
基于蚁群优化算法的线状目标简化模型[J]. 测绘学报, 2011, 40(5): 635–638.
ZHENG Chunyan, GUO Qingsheng, HU Huake. The simplification model of linear objects based on ant colony optimization algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 635–638. |
| [8] | WANG Zeshen, MÜLLER J C. Line generalization based on analysis of shape characteristics[J]. Cartography and Geographic Information Systems, 1998, 25(1): 3–15. DOI:10.1559/152304098782441750 |
| [9] | GÖKGÖZ T, SEN A, MEMDUHOGLU A, et al. A new algorithm for cartographic simplification of streams and lakes using deviation angles and error bands[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2185–2204. DOI:10.3390/ijgi4042185 |
| [10] |
钱海忠, 武芳, 陈波, 等.
采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报, 2007, 36(4): 443–449, 456.
QIAN Haizhong, WU Fang, CHEN Bo, et al. Simplifying line with oblique dividing curve method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 443–449, 456. DOI:10.3321/j.issn:1001-1595.2007.04.014 |
| [11] |
何海威, 钱海忠, 王骁, 等.
采用弯曲进行道路化简冲突避免的方法[J]. 测绘学报, 2016, 45(3): 354–361.
HE Haiwei, QIAN Haizhong, WANG Xiao, et al. Avoiding special conflicts in road simplification by using road bends[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 354–361. DOI:10.11947/j.AGCS.2016.20140576 |
| [12] |
李成名, 郭沛沛, 殷勇, 等.
一种顾及空间关系约束的线化简算法[J]. 测绘学报, 2017, 46(4): 498–506.
LI Chengming, GUO Peipei, YIN Yong, et al. A line simplification algorithm considering spatial relations between two lines[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 498–506. DOI:10.11947/j.AGCS.2017.20160546 |
| [13] |
艾廷华, 郭仁忠, 刘耀林.
曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001, 30(4): 343–348.
AI Tinghua, GUO Renzhong, LIU Yaolin. A binary tree representation of curve hierarchical structure in depth[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 343–348. DOI:10.3321/j.issn:1001-1595.2001.04.013 |
| [14] |
翟仁健, 武芳, 朱丽, 等.
曲线形态的结构化表达[J]. 测绘学报, 2009, 38(2): 175–182.
ZHAI Renjian, WU Fang, ZHU Li, et al. Structured representation of curve shape[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 175–182. DOI:10.3321/j.issn:1001-1595.2009.02.014 |
| [15] |
郭庆胜, 黄远林, 章莉萍.
曲线的弯曲识别方法研究[J]. 武汉大学学报(信息科学版), 2008, 33(6): 596–599.
GUO Qingsheng, HUANG Yuanlin, ZHANG Liping. The method of curve bend recognition[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6): 596–599. |
| [16] |
张栋海, 黄丽娜, 费立凡, 等.
一种基于曲率法的曲线特征点选取方法[J]. 测绘科学, 2013, 38(3): 151–153.
ZHANG Donghai, HUANG Lina, FEI Lifan, et al. An algorithm of extracting feature points in curve based on the curvature[J]. Science of Surveying and Mapping, 2013, 38(3): 151–153. |
| [17] | RAPOSO P. Scale-specific automated line simplification by vertex clustering on a hexagonal tessellation[J]. Cartography & Geographic Information Science, 2013, 40(5): 427–443. DOI:10.1080/15230406.2013.803707 |
| [18] |
郭庆胜.
线状要素图形综合的渐进方法研究[J]. 武汉测绘科技大学学报, 1998, 23(1): 52–56.
GUO Qingsheng. Study on progressive approach to graphic generalization of linear feature[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 52–56. |
| [19] |
杜佳威, 武芳, 李靖涵, 等.
一种河口湾海岸线渐进化简方法[J]. 测绘学报, 2018, 47(4): 547–556.
DU Jiawei, WU Fang, LI Jinghan, et al. A progressive simplification method for the estuary coastline[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(4): 547–556. DOI:10.11947/j.AGCS.2018.20170440 |
| [20] |
遆鹏, 贾洪果, 徐柱, 等.
面向道路网络地图示意化的线形简化方法[J]. 测绘学报, 2014, 43(12): 1280–1284, 1292.
TI Peng, JIA Hongguo, XU Zhu, et al. A line-shape-simplification method for schematization of road network map[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1280–1284, 1292. DOI:10.13485/j.cnki.11-2089.2014.0190 |
| [21] |
蔡剑红, 李德仁.
多尺度下的不确定性空间方向锥形模型研究[J]. 武汉大学学报(信息科学版), 2007, 32(8): 735–739.
CAI Jianhong, LI Deren. Research on cone-shaped models of cardinal direction relations considering positional uncertainty of multiple spatial-scale data[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 735–739. |
| [22] |
闫浩文, 郭仁忠.
空间方向关系形式化描述模型研究[J]. 测绘学报, 2003, 32(1): 42–46.
YAN Haowen, GUO Renzhong. Research on formal description model of directional relationships[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 42–46. DOI:10.3321/j.issn:1001-1595.2003.01.009 |
| [23] | DENG Min, LI Zhilin. A statistical model for directional relations between spatial objects[J]. GeoInformatica, 2008, 12(2): 193–217. DOI:10.1007/s10707-007-0031-2 |
| [24] | YAN Haowen, CHU Yandong, LI Zhilin, et al. A quantitative description model for direction relations based on direction groups[J]. GeoInformatica, 2006, 10(2): 177–196. DOI:10.1007/s10707-006-7578-1 |
| [25] |
潘正风, 罗年学, 黄全义.
近似斜轴抛物线加权平均插值法曲线光滑[J]. 测绘学报, 1991, 20(1): 60–65.
PAN Zhengfeng, LUO Nianxue, HUANG Quanyi. Approximate interpolation by weighted average on skew axial parabola[J]. Acta Geodaetica et Cartographica Sinica, 1991, 20(1): 60–65. |
| [26] |
李伟, 郭沛沛, 武鹏达, 等.
地图综合中曲线局部尖锐凸角的光滑方法[J]. 测绘科学, 2018, 43(10): 112–116.
LI Wei, GUO Peipei, WU Pengda, et al. Smooth method of local convex sharp angle in cartographic generalization[J]. Science of Surveying and Mapping, 2018, 43(10): 112–116. |


