测地线是指曲面上测地曲率处处为零的曲线,也是曲面上任意两点之间距离最短的曲线[1],因其具有短程性而广泛用于大地测量、航海导航等领域。将地球看成球体的情况下,参考球面上的大圆线即为测地线,相关参数可以方便求出;而地球实际上是一个近似的旋转椭球体,针对地球椭球面上的测地线方程或弧长却很难计算[2],又由于地球椭球面上的大椭圆与大地线在距离上非常接近,15 000 km的远程距离只有几米之差,因此在航海导航应用过程中,一般用大椭圆线代替测地线作为最短航线,以实现经济高效航行[3]。
针对大椭圆航线及其相关应用问题,国内外学者进行了深入的研究并取得丰硕的成果[4-21]。文献[4—8]分别推导了大椭圆地理坐标解算公式,探讨了大椭圆航线与等角航线的关系并比较了二者在远洋航行中优劣,分析了大椭圆航法与大圆航法的航程计算误差,并结合地图投影理论,研究了大椭圆表象为直线的日晷投影以及墨卡托海图上大地线曲率问题;文献[9—12]采用位置矢量的方法,研究了大椭圆航线航程、方位角和正反解问题;文献[13—15]则采用单位速度矢量的方法,研究了大椭圆航线航程、方位角和正反解问题;文献[16—17]借助计算机代数系统Mathematica,研究了大椭圆航行方法及其相关的导航参数计算,并导出了大椭圆航法航程符号形式的计算公式;文献[18—19]研究了基于大椭圆航线的RNAV航路规划问题;文献[20]在总结前人成果的基础上,采用空间矢量代数方法直接求解大椭圆顶点,提出了基于Newton-Raphson(N-R)的等距离航线设计算法。
总结上述研究成果,大多围绕大椭圆航线的地理坐标、航程和方位角等参数的解算,基于大椭圆航线的航路规划与算法设计等问题展开,针对不同类型投影平面下大椭圆航线的描写,及其曲率和代曲直距问题缺乏系统的研究。而在航线规划与航海导航应用中,大椭圆航线的曲率和代曲直距问题关乎作图的精确性、便捷性和航行的安全性、经济性,因此本文分别针对4种常用投影(墨卡托投影、高斯投影、极球面投影和日晷投影)平面下大椭圆航线的表象、曲率和代曲直距进行分析研究,以解决航线绘制过程中的“以直代曲”问题,为航海人员进行大椭圆航线的量测、设计和绘制提供理论与计算分析依据。
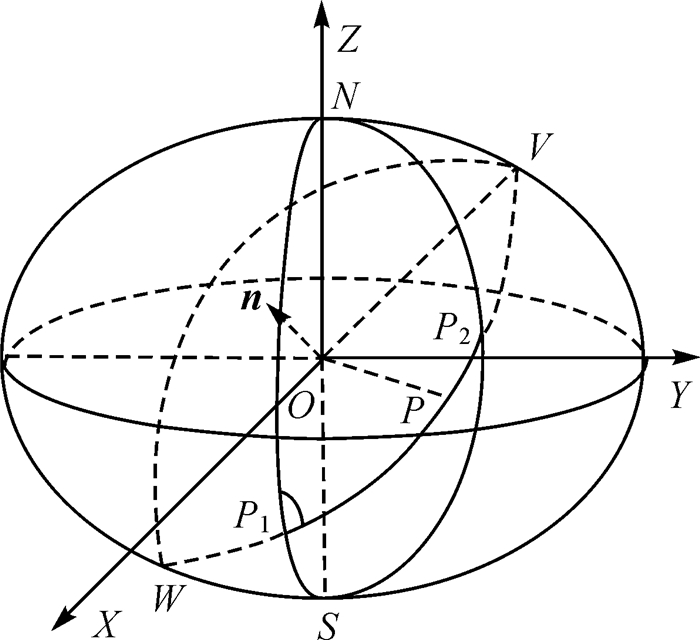
1 常用投影平面上的大椭圆航线参数方程以旋转椭球体球心为原点,建立空间直角坐标系如图 1所示。i、j、k为X、Y、Z坐标轴单位向量。过椭球面上两点P1(B1, l1)、P2(B2, l2)的球心截面OP1P2与椭球面的交线上两点之间的劣弧即为大椭圆航线,记为P1P2。根据文献[20]中的推导,截面椭圆OP1P2所在平面的法向量n的矢量表达式为
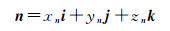 (1)
(1)
|
| 图 1 大椭圆航线示意图 Fig. 1 Sketch of great ellipse route |
式中
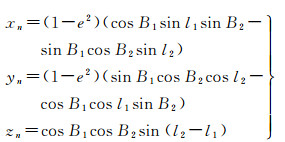 (2)
(2)
设点P1(B1, l1)到P2(B2, l2)间的大椭圆航线上的任意一点为P(B, l),根据大地坐标与空间直角坐标的关系可得P点的坐标矢量P=Ncos Bcos l·i+Ncos Bsin l·j+N(1-e2)sin B·k。由于P是截面椭圆OP1P2与椭球面交线上的点,因此向量n与P垂直,即n·P=0,据此可得P点坐标方程,亦即大椭圆P1P2的方程为
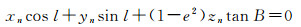 (3)
(3)
即
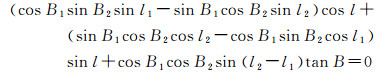 (4)
(4)
等价于
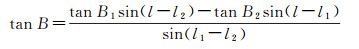 (5)
(5)
式(4)说明,大椭圆航线上任意一点大地坐标与椭球参数(长短半轴、偏心率)无关,只与起止点大地坐标有关。将式(5)大椭圆航线方程写成B(l)=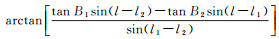
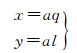 (6)
(6)
式中,a为椭球长半轴;q为等量纬度,其表达式为
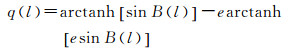 (7)
(7)
 (8)
(8)
式中,系数αi见文献[23];u、v为中间变量,表达式为
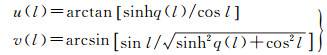 (9)
(9)
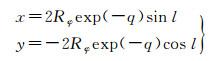 (10)
(10)
式中,Rφ为等角球半径,表达式为Rφ=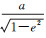

 (11)
(11)
式中,B0为椭球面与地心纬度球面切点处纬度,相应的地心纬度为φ0,表达式为φ0=arctan[(1-e2)tan B0];Rg为切点处的椭球动径,表达式为Rg=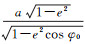
由大椭圆航线方程式(5),求得大地纬度B对经差l的一阶、二阶导数为
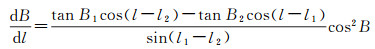 (12)
(12)
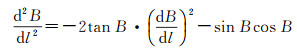 (13)
(13)
由式(7)求得等量纬度q对大地纬度B的一阶导数为
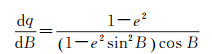 (14)
(14)
进而得到等量纬度q对经差l的一阶、二阶导数为
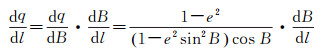 (15)
(15)
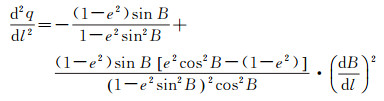 (16)
(16)
联系椭球面墨卡托投影公式(6),可得大椭圆航线平面坐标的一阶、二阶导数
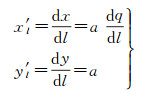 (17)
(17)
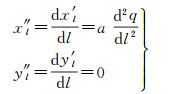 (18)
(18)
最终得到大椭圆航线在墨卡托投影平面上的曲率公式为
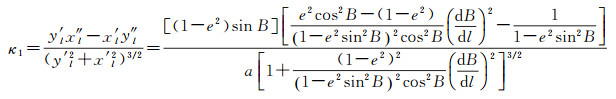 (19)
(19)
曲率半径为M1=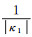
由式(9)首先得到中间变量u、v对经差l的一阶、二阶导数为
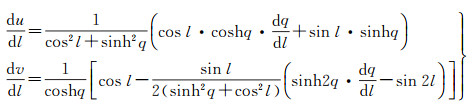 (20)
(20)
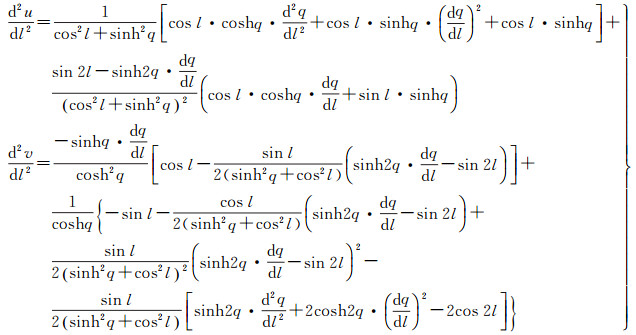 (21)
(21)
然后由式(8)得到投影平面坐标对经差l的一阶、二阶导数为
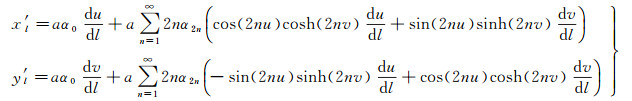 (22)
(22)
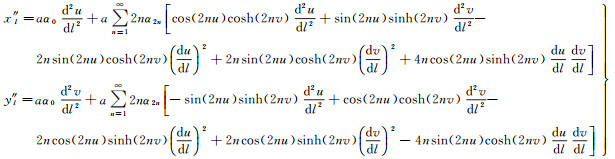 (23)
(23)
最终求得曲率κ2=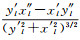
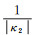
大椭圆航线与经线重合时,大椭圆航线方程与l无关,此时航线的表象就是经线的表象,可令经度为定值,以纬度为曲线参数进行类似的计算。设此时的大椭圆航线l≡lGE,以等量纬度为曲线参数,由式(9)得中间变量u、v对等量纬度q的一阶导数和二阶导数为
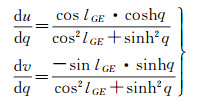 (24)
(24)
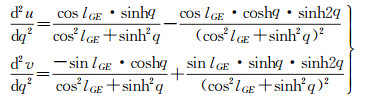 (25)
(25)
然后只需把式(20)—式(23)中的经度参数改为等量纬度参数,即以
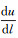
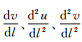
联系椭球面极球面投影方程式(10),可得一阶、二阶导数为
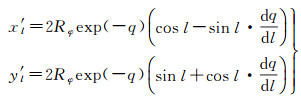 (26)
(26)
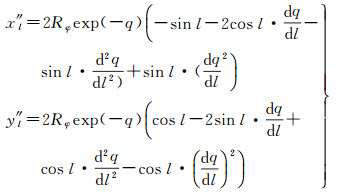 (27)
(27)
最终得到大椭圆航线在极球面投影平面上的曲率公式为(极球面投影平面y为纵坐标,x为横坐标)
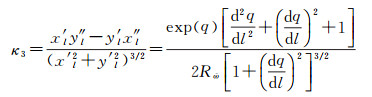 (28)
(28)
曲率半径为M3=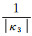
联系椭球面日晷投影公式(11),得到大椭圆航线上任意一点P(B, l)与起始点P1(B1, l1)的日晷投影坐标差为
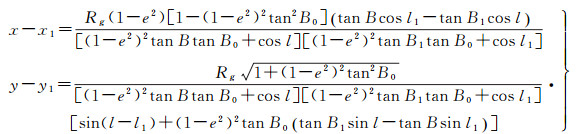 (29)
(29)
由式(5)有
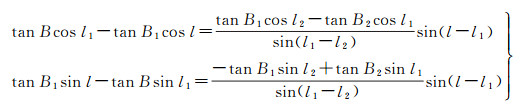 (30)
(30)
因此,有
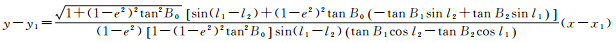 (31)
(31)
由式(31)可知,大椭圆在日晷投影平面上表象为一直线,曲率为0,曲率半径为无穷大。与经线重合的大椭圆航线在日晷投影平面上显然也表现为直线,曲率也为0。
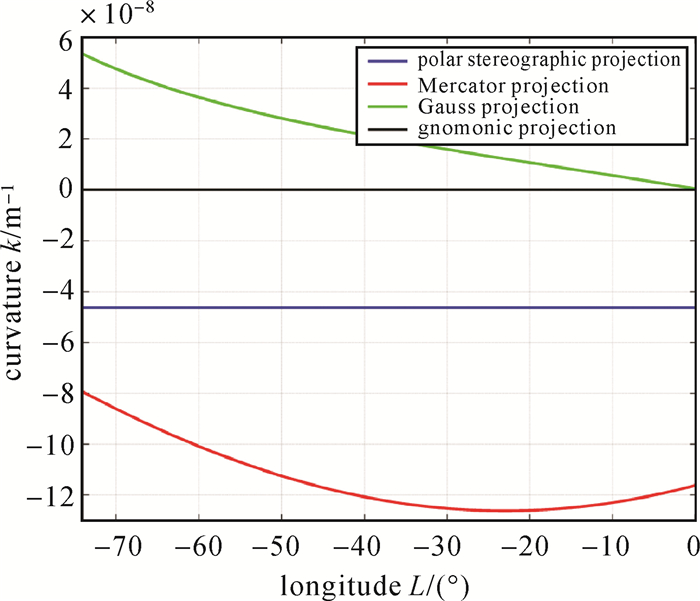
3 算例分析选取纽约(40°43′N, 74°00′W)至伦敦(51°30′N, 00°05′E)的大椭圆航线为例,取WGS 84参考椭球参数,a=6 378 137 m,e=0.081 819 190 843,根据曲率与曲率半径公式,分别绘出墨卡托投影、高斯投影、极球面投影和日晷投影平面上的曲率随大椭圆航线经度变化的曲线如图 2所示,曲率半径变化曲线如图 3所示。
|
| 图 2 常用投影平面上大椭圆航线曲率变化曲线 Fig. 2 Curves of curvature of great ellipse routes on common projection planes |
|
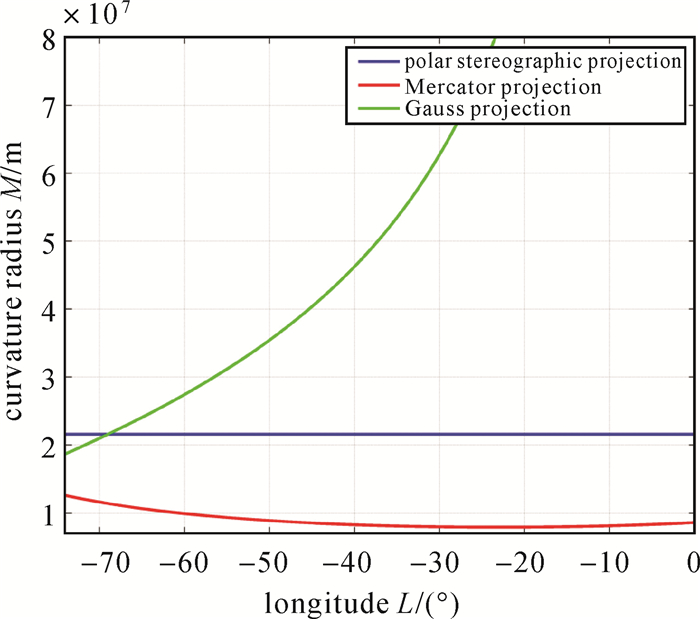
| 图 3 常用投影平面上大椭圆航线曲率半径变化曲线 Fig. 3 Curves of curvature radius of great ellipse routes on common projection planes |
结合图 2、图 3分析:随着经度变化,日晷投影平面上的大椭圆航线曲率恒为零,说明该投影平面上的大椭圆航线确实为一条直线,而其他3种投影平面上大椭圆航线曲率不为零,说明其投影平面上大椭圆航线的表象为曲线。其中,极球面和高斯投影平面上大椭圆航线的曲率数量级为10-8,而墨卡托投影平面上数量级为10-7,说明墨卡托投影平面上大椭圆航线弯曲更明显,这是由于墨卡托投影在中高纬度地区的变形相对较大导致的。同时还可以看出,极球面投影平面上大椭圆航线的曲率变化非常小(看起来为一条直线,但将坐标尺度变小后发现仍为一条曲线),说明大椭圆航线在该投影平面上的表象近似为一圆弧(半径足够大)。综上,在日晷投影平面上进行大椭圆航线的量测和绘算最为方便,而在墨卡托投影平面上针对中高纬度地区大椭圆航线的量测误差较大。
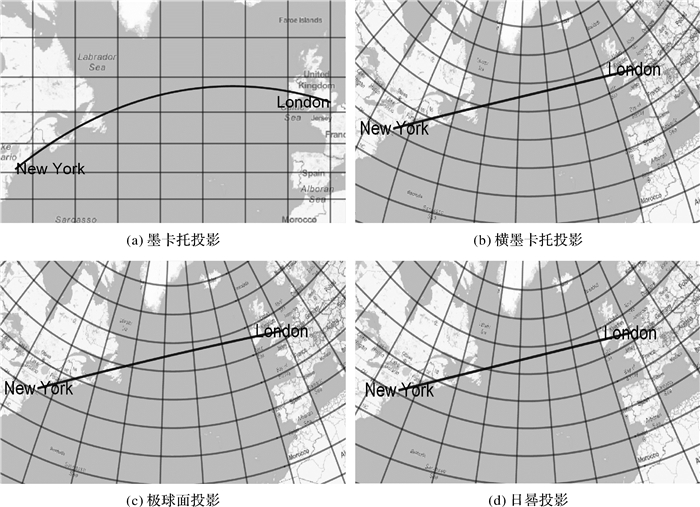
借助计算机代数系统Mathematica,采用GeoGraphics绘图命令,绘出4种常用投影平面上纽约至伦敦的大椭圆航线如图 4所示(其中图 4(b)用横墨卡托投影来代替高斯投影)。由图 4可看出大椭圆航线在日晷投影平面上为一条直线,在墨卡托投影平面上为一条弯曲较为明显的曲线,这充分验证了上述分析结论的准确性,也验证了前文推导公式的正确性。
|
| 图 4 常用投影平面上的大椭圆航线 Fig. 4 Great ellipse route on common projection plane |
通过上述分析可知,大椭圆航线在海图上绘制时,一般都为曲线,难以直接精确绘制,因此可将海图上的大椭圆航线进行分段处理,相邻两点用直线连接,“以直代曲”,绘制精度满足《中国航海图编绘规范》中规定的位置偏差(“以直代曲”时的拱高)不大于制图允许误差Δ=0.01 cm即可。根据文献[8, 26],海图投影平面上一般曲线的代曲直距满足如下不等式
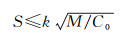 (32)
(32)
式中,k=89.44;S以厘米为单位(图上距离),若以实地距离计算,为SC0/100=0.894 4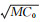
以墨卡托投影平面上纽约至伦敦的大椭圆航线为例,通过计算得到在经度l=-23°1.5′处,曲率绝对值达到极大值点,相应的曲率为κ=-1.262 4×10-7 m-1,在该处曲率半径达到极小值点,其值为M=7.921 4×106 m。因此,在1:500 000墨卡托航海图上,大椭圆航线代曲直距为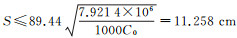
| 投影方式 | 经度l | 曲率绝对值极大值κmax/m-1 | 曲率半径极小值Mmin/m | 比例尺 | 最大代曲直距Smax/cm |
| 墨卡托投影 | -23°1.5′ | 1.262 4×10-7 | 7.921 4×106 | 1:500 000 | 11.258 |
| 高斯投影 | -74° | 5.342 7×10-8 | 1.871 7×107 | 1:500 000 | 17.305 |
| 极球面投影 | -74° | 4.664 6×10-8 | 2.143 9×107 | 1:500 000 | 18.520 |
| 日晷投影 | — | 0 | ∞ | — | ∞ |
由于日晷投影平面上大椭圆航线为曲率处处为0的直线,因此代曲直距可取任意值,这是日晷投影最重要的优点,为航线量测提供了方便。
4 结论本文围绕墨卡托投影、高斯投影、极球面投影和日晷投影4种常用海图投影平面上的大椭圆航线的表象和曲率进行研究,推导出了不同投影平面上的大椭圆航线参数方程、曲率和曲率半径公式,并根据上述方程,绘制了不同投影面上纽约至伦敦大椭圆航线的曲率和曲率半径变化曲线。结果表明,大椭圆航线在日晷投影平面上的表象为一条直线,在其他3种投影面上为曲率较小但曲率不断变化的曲线,其中相比高斯投影和极球面投影,墨卡托投影平面上的大椭圆航线曲率和曲率变化率较大。因大椭圆航线的经济性及其在日晷投影海图上量测和绘算的便利性,使得日晷投影在舰船远洋航行中具有重要应用价值。但由于大椭圆航线在其他常用海图上绘制时一般都为曲率不断变化的曲线,难以直接精确绘制,因此一般将海图上的大椭圆航线进行分段处理,“以直代曲”。利用本文推导的公式可以方便地计算相应航线的曲率半径,进而计算大椭圆航线上任意位置的代曲直距,以解决航线绘制过程中的“以直代曲”问题。本文的研究工作可为航海人员进行大椭圆航线的量测、设计和绘制提供便利参考。
| [1] |
梅向明, 黄敬之.
微分几何[M]. 4版. 北京: 高等教育出版社, 2008.
MEI Xiangming, HUANG Jingzhi. Differential geometry[M]. 4th ed. Beijing: Higher Education Press, 2008. |
| [2] |
熊介.
椭球大地测量学[M]. 北京: 解放军出版社, 1988.
XIONG Jie. Ellipsoidal geodesy[M]. Beijing: PLA Press, 1988. |
| [3] | WILLIAMS R. The great ellipse on the surface of the spheroid[J]. The Journal of Navigation, 1996, 49(2): 229–234. DOI:10.1017/S0373463300013333 |
| [4] |
丁佳波.
大椭圆地理坐标的解算公式[J]. 天津航海, 1993(2): 41–43.
DING Jiabo. Analytical formula of great ellipse in geographic coordinate[J]. Tianjin Hanghai, 1993(2): 41–43. |
| [5] |
丁佳波.
论等角航线和大椭圆之间的关系[J]. 天津航海, 1994(2): 28–29.
DING Jiabo. Study on the relationship between rhumb line and great ellipse[J]. Tianjin Hanghai, 1994(2): 28–29. |
| [6] |
丁佳波.
大圆航法与大椭圆航法的航程计算误差[J]. 天津航海, 1996(3): 3–4.
DING Jiabo. Distance calculation error between great circle sailing and great ellipse sailing[J]. Tianjin Hanghai, 1996(3): 3–4. |
| [7] |
丁佳波.
大椭圆表象为直线的日晷投影[J]. 测绘通报, 1987(4): 34–36.
DING Jiabo. Sundial projection with the large elliptical image as a straight line[J]. Bulletin of Surveying and Mapping, 1987(4): 34–36. |
| [8] |
丁佳波.
墨卡托海图上大地线表象的曲率及其应用[J]. 测绘学报, 1994, 23(2): 155–158.
DING Jiabo. Curvature of large ground line on Mercator chart and its application[J]. Acta Geodaetica et Cartographica Sinica, 1994, 23(2): 155–158. DOI:10.3321/j.issn:1001-1595.1994.02.011 |
| [9] | EARLE M A. A vector solution for navigation on a great ellipse[J]. The Journal of Navigation, 2000, 53(3): 473–481. DOI:10.1017/S0373463300008948 |
| [10] | EARLE M A. Sphere to spheroid comparisons[J]. The Journal of Navigation, 2006, 59(3): 491–496. DOI:10.1017/S0373463306003845 |
| [11] | EARLE M A. Vector solutions for azimuth[J]. The Journal of Navigation, 2008, 61(3): 537–545. DOI:10.1017/S037346330800475X |
| [12] | EARLE M A. Accurate harmonic series for inverse and direct solutions for the great ellipse[J]. The Journal of Navigation, 2011, 64(3): 557–570. DOI:10.1017/S037346331100004X |
| [13] | TSENG W K, LEE H S. Navigation on a great ellipse[J]. Journal of Marine Science and Technology, 2010, 18(3): 369–375. |
| [14] | TSENG W K, GUO J L, LIU C P. A comparison of great circle, great ellipse, and geodesic sailing[J]. Journal of Marine Science and Technology, 2013, 21(3): 287–299. |
| [15] | SJÖBERG L E. Solutions to the direct and inverse navigation problems on the great ellipse[J]. Journal of Geodetic Science, 2012, 2(3): 200–205. |
| [16] |
李厚朴, 王瑞.
大椭圆航法及其导航参数计算[J]. 海军工程大学学报, 2009, 21(4): 7–12.
LI Houpu, WANG Rui. Great ellipse nautical method and its navigation parameters calculation[J]. Journal of Naval University of Engineering, 2009, 21(4): 7–12. |
| [17] |
王瑞, 李厚朴.
基于地球椭球模型的符号形式的航迹计算法[J]. 测绘学报, 2010, 39(2): 151–155.
WANG Rui, LI Houpu. Symbolic expressions of the track calculation methods based on the ellipsoidal model[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 151–155. |
| [18] |
方学东, 黄润秋, 魏光兴.
基于椭球模型的FANS航线算法[J]. 西南交通大学学报, 2006, 41(4): 512–516.
FANG Xuedong, HUANG Runqiu, WEI Guangxing. Calculation method of FANS route based on ellipsoid model[J]. Journal of Southwest Jiaotong University, 2006, 41(4): 512–516. DOI:10.3969/j.issn.0258-2724.2006.04.022 |
| [19] |
方学东.
考虑地球扁率的RNAV航路规划[J]. 测绘科学, 2008, 33(6): 149–150, 129.
FANG Xuedong. RNAV route planning with regard to earth ellipticity[J]. Science of Surveying and Mapping, 2008, 33(6): 149–150, 129. DOI:10.3771/j.issn.1009-2307.2008.06.052 |
| [20] |
刘文超, 卞鸿巍, 王荣颖, 等.
大椭圆航线设计的空间矢量方法[J]. 测绘学报, 2015, 44(7): 741–746.
LIU Wenchao, BIAN Hongwei, WANG Rongying, et al. Great ellipse route planning based on space vector[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 741–746. DOI:10.11947/j.AGCS.2015.20130799 |
| [21] |
边少锋, 李厚朴, 李忠美.
地图投影计算机代数分析研究进展[J]. 测绘学报, 2017, 46(10): 1557–1569.
BIAN Shaofeng, LI Houpu, LI Zhongmei. Research progress in mathematical analysis of map projection by computer algebra[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1557–1569. DOI:10.11947/j.AGCS.2017.20170396 |
| [22] |
刘强.海图投影理论及其在航海导航中的应用[D].武汉: 海军工程大学, 2016. LIU Qiang. Chart projection theory and its application in navigation[D]. Wuhan: Naval University of Engineering, 2016. |
| [23] |
李厚朴, 边少锋, 钟斌.
地理坐标系计算机代数精密分析理论[M]. 北京: 国防工业出版社, 2015.
LI Houpu, BIAN Shaofeng, ZHONG Bin. The theory of computer algebra precision analysis in geographic coordinate system[M]. Beijing: National Defense Industry Press, 2015. |
| [24] |
边少锋, 李忠美, 李厚朴.
极区非奇异高斯投影复变函数表示[J]. 测绘学报, 2014, 43(4): 348–352, 359.
BIAN Shaofeng, LI Zhongmei, LI Houpu. The non-singular formula of gauss projection in polar regions by complex numbers[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 348–352, 359. DOI:10.13485/j.cnki.11-2089.2014.0052 |
| [25] |
李忠美, 边少锋, 金立新, 等.
极区不分带高斯投影的正反解表达式[J]. 测绘学报, 2017, 46(6): 780–788.
LI Zhongmei, BIAN Shaofeng, JIN Lixin, et al. Forward and inverse expressions of polar gauss projection without zoning limitations[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 780–788. DOI:10.11947/j.AGCS.2017.20170009 |
| [26] |
张志衡, 彭认灿, 董箭, 等.
极地海区等距离正圆柱投影平面上等角航线的展绘方法[J]. 测绘科学技术学报, 2015, 32(5): 535–538, 544.
ZHANG Zhiheng, PENG Rencan, DONG Jian, et al. The method for describing rhumb line in polar sea on equidistance cylindrical projection plane[J]. Journal of Geomatics Science and Technology, 2015, 32(5): 535–538, 544. DOI:10.3969/j.issn.1673-6338.2015.05.020 |



