2. 中国科学院大学, 北京 100049;
3. 上海市空间导航与定位技术重点实验室, 上海 200030;
4. 宇航动力学国家重点实验室, 陕西 西安 710043
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai Key Laboratory of Space Navigation and Positioning Techniques, Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
4. State Key Laboratory of Aerospace Dynamics, Xi'an 710043, China
SLR(satellite laser ranging,SLR)数据处理开始于20世纪60年代末,发展于80年代,当时的测距精度在20~30 cm,定轨模型误差较大,定轨精度在米级甚至几十米[1]。到20世纪90年代,随着海洋测高卫星对定轨精度的高要求和多种测量技术综合测量及各种系统差和模型误差的模制,定轨精度可达厘米级[2-3]。近10多年来,SLR的几项关键技术取得了进步:超短激光脉冲技术和皮秒计时器的应用提高了测距精度,白天测距增加了观测数据量,高重复频率(千赫兹)测距的实现更使得观测数据量和精度都有了较大提高。目前,有些SLR测站单次测量精度可达或接近毫米级,定轨精度达亚厘米级[4]。随着计算机的大力发展、力学模型和观测模型认识的提高及SLR数据处理技巧的提高,其定轨精度还会有所提高,成为建立和监测毫米级地球参考架、EOP、地壳运动、低阶重力场、卫星轨道确定和微波轨道精度评估及系统差标定、雷达标校等不可缺少的技术手段[5-9]。
国际激光测距服务(International Laser Ranging Service, ILRS)成立于1998年,目的是在全球范围内定期就所采用的数据处理模型、方法和产品的内容、格式及提供的更新频率等进行讨论,形成SLR数据处理规范和观测规范,系统性、高质量、及时地为SLR各类用户提供有关产品,如测站坐标、EOP、卫星轨道等。ILRS各分析中心基本都于2007年前实现了SLR数据处理自动化,随着IERS处理规范和ILRS有关处理模型等的更新,会进行SLR数据重新处理,提供新的SINEX格式SLR周解等产品[10-12]。但在SLR数据处理中,对测站观测的加权通常是很主观的甚至是武断的,通常是采用经验的权重来进行数据处理,这影响了最优化利用有效数据[13]。为此,需要找到一个客观的方式来确定测站数据的权重和剔除标准。文献[14]提出了一种将模糊逻辑(fuzz-logic)技术应用于SLR数据处理。fuzz-logic技术在大地测量和GIS已被证明很有潜力[15],它原来是基于文献[16]的思想由文献[17—18]的工作发展起来的,文献[19]构造了FCM(fuzzy c-means)算法,以后又由文献[20]进行了推广。大多数分析模糊集技术的方法都是由文献[20]的FCM方法推导出来的,但是这个方法又不是基于一个完全可靠的标准来的,有可能没有提供一个希望的解。因此,文献[21]分析了这种可能,重构了FCM算法。文献[14]就利用改进的FCM算法根据当时ILRS对测站评价的准则加权SLR观测来进行最优SLR数据处理。这个准则包括数据数量、数据质量和运行的协议遵守情况3个因素,是1996年Pearlman先生在上海ILRS数据分析工作组会议上提出的高质量的SLR测站标准。根据这个ILRS测站评价准则产生聚类过程就可以对测站进行分类,给出每个测站的权重。这个过程也推出了相对客观的数据剔除标准从而使得定轨精度有5%~20%的提高。我国目前SLR数据处理的权重和剔除标准还是人为给定的[14],通过处理发现结果差,再进行人工干预调整。该方法不利于SLR数据处理的自动化和结果的及时发送。为此本文在中国科学院上海天文台的SHORDE-II SLR数据处理软件包的基础上,引入文献[22]的改进模糊聚类方法,采用全球SLR测站性能报告给出的有关参数,评定这些参数组合对SLR测站分类定权,包括测站标准点总数、标准点RMS值和标准点合格率等,确定改进的模糊聚类中考虑变量的多少和有关组合,建立最优的测站观测数据权重和剔除标准算法和软件,进行分类定权,并测试了该权重确定方法对SLR定轨精度的影响。
1 改进的模糊聚类算法定权的原理和方法模糊聚类算法是用模糊理论对重要数据进行分析和建模的方法。它可以建立样本类属的不确定性描述,能比较客观地反映现实世界,已经有效地应用在大规模数据分析、数据挖掘、矢量量化、图像分割、模式识别等领域,具有重要的理论与实际应用价值。随着应用的深入发展,模糊聚类算法的研究不断丰富。模糊聚类算法繁多,其中模糊c-均值聚类算法(fuzzy c-means algorithm,FCMA或FCM)应用最广泛且较成功[23-24],它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据分类的目的。
本文所采用的改进FCM模糊聚类算法是按照下面的步骤来确定SLR测站权重和剔除标准:
(1) 按照各个测站的多种属性样本X(涉及测站的数据数量、数据质量和测站运行情况等性质的参数),对测站进行模糊分类,事先给定类别数c和一个收敛标准ε,按照式(1)中的各种条件,初始化各个测站的隶属度u(与测站权重有关)。
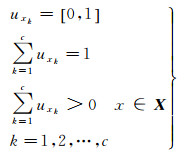 (1)
(1)
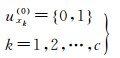 (2)
(2)
(2) 根据初始化后的u以及测站的属性样本集X,按照下式,计算初始聚类中心vk(0)
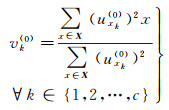 (3)
(3)
(3) 计算得到gvk(0)
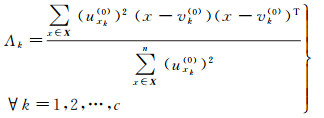 (4)
(4)
令
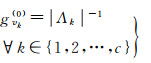 (5)
(5)
(4) 进行迭代,令t=t+1, 重新计算各个测站的隶属度uxk和聚类中心vk
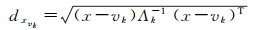 (6)
(6)
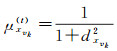 (7)
(7)
 (8)
(8)
 (9)
(9)
(5) 判断是否停止迭代,如果停止迭代,输出权重结果。
当|vk(t)-vk(t-1)|<ε, ∀k∈{1, 2, …, c},认为收敛,停止迭代,否则将隶属度uxk和聚类中心vk代入第(3)步,继续循环,直到收敛。停止迭代后,得到的模糊分类的结果,包括按照事先确定的类别数量c将测站样本集分成的c个模糊类、可以表征相应类别性质的聚类中心vk(c个)和每个测站样本分别属于这c类的隶属度uxk。隶属度uxk越接近于1,表示该测站越是可能属于该模糊类,越接近于0表示该测站越不可能属于此模糊类。然后赋予所分c类不同的权重,那么每一个测站的隶属度uxk最大值对应的类权重即为该测站的权重。至此,利用SLR测站观测情况的各类参数,就可以综合评定给出该测站更为可靠客观的观测权重。
2 测站权重影响主要因素分析在文献[21—22]改进的FCM模糊聚类算法确定SLR测站权重中,本文采用了基于当时SLR测站评价准则,即数据数量、质量和运行的协议遵守情况进行了权重确定。而目前对测站性能的评估有多个参数,如ILRS提供的全球SLR测站性能报告中就列出了测站观测7个特性参数,包括LAGEOS标准点总数、LAGEOS标准点RMS值、LAGEOS标准点合格率、LAGEOS观测圈数、测站长期偏差稳定性、测站短期偏差稳定性和LAGEOS单次测距RMS值。是否这些参数都对SLR观测权重产生影响?为此,本文利用下列5种不同特性参数组合来测试影响测站观测权重的主要因素。表 1中给出了ILRS提供的全球SLR测站性能月报(以2015年6月为例),并以这7项全球SLR测站特性指标进行不同组合,给出了本文所采取的5种组合方案:
| 测站信息 | SLR测站特性指标 | |||||||
| 测站位置 | 测站编号 | 观测圈数 | 标准点总数 | 单次测距RMS/mm | 标准点RMS/mm | 短期偏差稳定性/mm | 长期偏差稳定性/mm | 标准点合格率/(%) |
| Simeiz | 1873 | 207 | 1331 | 10.4 | 17.0 | 27.4 | 12.4 | 92.0 |
| Altay | 1879 | 250 | 1399 | 29.5 | 1.7 | 20.9 | 17.9 | 93.8 |
| Baikonur | 1887 | 379 | 2302 | 31.2 | 6.7 | 20.8 | 6.5 | 95.4 |
| Svetloe | 1888 | 531 | 4523 | 30.7 | 6.0 | 24.7 | 5.9 | 95.2 |
| Zelenchukskya | 1889 | 268 | 2421 | 29.1 | 4.9 | 16.2 | 9.6 | 97.7 |
| Badary | 1890 | 323 | 2064 | 35.8 | 6.4 | 11.9 | 11.9 | 95.8 |
| Katzively | 1893 | 211 | 1256 | 14.1 | 12.4 | 22.8 | 7.2 | 91.1 |
| McDonald | 7080 | 304 | 2522 | 11.6 | 2.3 | 14.3 | 6.2 | 96.2 |
| Yarragadee | 7090 | 2687 | 23 174 | 9.6 | 1.9 | 10.5 | 1.8 | 92.2 |
| Greenbelt | 7105 | 1043 | 9916 | 11.6 | 2.0 | 10.4 | 2.4 | 91.7 |
| Monument_Peak | 7110 | 878 | 7758 | 9.2 | 1.2 | 15.0 | 4.1 | 92.4 |
| Haleakala | 7119 | 392 | 4425 | 12.6 | 2.3 | 19.7 | 4.3 | 90.7 |
| Papeete | 7124 | 220 | 1999 | 9.3 | 2.7 | 12.8 | 15.6 | 97.4 |
| Beijing | 7249 | 261 | 1938 | 18.4 | 5.0 | 19.2 | 10.9 | 92.8 |
| Hartebeesthoek | 7501 | 857 | 8425 | 18.9 | 2.8 | 19.8 | 6.1 | 90.5 |
| Zimmerwald_532 | 7810 | 598 | 7849 | 11.4 | 1.7 | 13.3 | 20.0 | 95.3 |
| Mount_Stromlo_2 | 7825 | 1575 | 15 672 | 8.6 | 1.8 | 10.5 | 2.6 | 95.4 |
| Simosato | 7838 | 231 | 3646 | 14.4 | 2.8 | 12.8 | 4.8 | 93.7 |
| Graz | 7839 | 554 | 3507 | 5.1 | 0.6 | 11.9 | 4.9 | 97.5 |
| Herstmonceux | 7840 | 830 | 7691 | 13.6 | 0.6 | 8.8 | 2.7 | 97.4 |
| Potsdam_3 | 7841 | 290 | 2941 | 11.8 | 2.3 | 13.0 | 5.3 | 95.1 |
| Grasse_MEO | 7845 | 378 | 4900 | 16.6 | 2.5 | 10.4 | 4.9 | 91.5 |
| Matera_MLRO | 7941 | 1418 | 11 488 | 4.1 | 1.2 | 16.1 | 2.6 | 96.1 |
| Wettzell | 8834 | 293 | 1833 | 14.2 | 3.2 | 17.8 | 5.4 | 91.0 |
方案1:考虑LAGEOS标准点总数、LAGEOS标准点RMS值和LAGEOS标准点合格率3个因素来定权。
方案2:考虑LAGEOS观测圈数、LAGEOS标准点RMS值和LAGEOS标准点合格率3个因素来定权。
方案3:考虑LAGEOS标准点总数、LAGEOS标准点RMS值、LAGEOS标准点合格率和测站长期偏差稳定性4个因素来定权。
方案4:考虑LAGEOS标准点总数、LAGEOS标准点RMS值、LAGEOS标准点合格率和测站短期偏差稳定性来定权。
方案5:考虑LAGEOS标准点总数、LAGEOS标准点RMS值、LAGEOS标准点合格率、测站长期偏差稳定性、测站短期偏差稳定性和LAGEOS单次测距RMS值6个因素来定权。
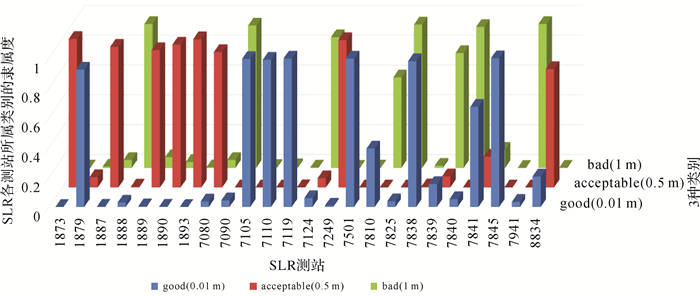
根据ILRS提供的2015年6月的测站性能月报,按照上述5种组合方案分别对测站进行分类定权。分类过程中将涉及的各个质量控制因素都分为好、中、坏3类,然后综合得到各测站对应每一类别的隶属度。以方案1为例,图 1给出了各测站所属类别的隶属度分布情况。将好、中、坏3类分别赋予0.01 m、0.5 m和1.0 m的标准差,将隶属度与对应的标准差相乘并求和,最终得到各个测站所对应的综合标准差,以此来作为SLR测站观测的权重。
|
| 图 1 方案1确定的SLR各测站所属类别隶属度分布情况 Fig. 1 The probability of belonging to each cluster of each SLR station with solution 1 |
3 改进的模糊聚类方法定权结果与定轨精度分析
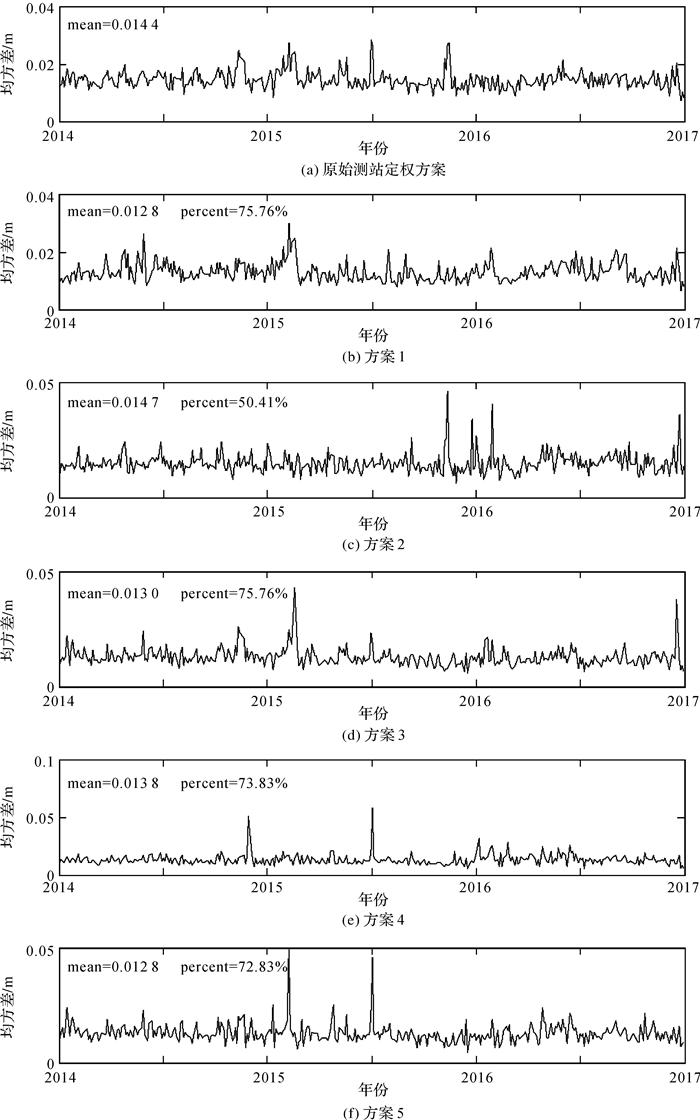
为了验证改进的FCM模糊聚类算法对SLR测站重新定权的效果,利用LAGEOS1卫星2014年1月至2016年12月的全球SLR观测数据进行短弧精密定轨,表 2给出了LAGEOS 1卫星定轨所采用的测量模型和力学模型。然后分别采用原始的测站经验定权方法和改进的FCM定权方法进行精密定轨,图 2给出了原始的定轨精度和采用方案1—5的定轨精度比较。从图中可以看出,方案1给出的测站定权方法,即考虑了LAGEOS标准点总数、LAGEOS标准点RMS值和LAGEOS标准点合格率这3种测站质量因素得到了最好的定轨结果,定轨残差RMS平均为0.012 8 m,比老的定权方法定轨残差RMS平均提高了1.6 mm,且有75.76%的弧段得到了提高;方案2在方案1的基础上将LAGEOS标准点总数更改为LAGEOS观测圈数,定轨精度提高不明显,说明LAGEOS标准点总数比观测圈数更能反映观测数据的质量特性,对定轨影响更显著;方案3、4、5在方案1的基础上分别增加了测站长期偏差稳定性、测站短期偏差稳定性和LAGEOS单次测距RMS值,定轨精度没有明显的提高,分析原因可能是各项测站性能指标之间存在着一定相关性,如测站长期稳定性、短期稳定性和LAGEOS单次测距精度都与方案1所考虑的3个因素有关,当增加这些测站性能指标时,并不能进一步增强这些因素所带来的定权优势。因此认为考虑方案1的LAGEOS标准点总数、LAGEOS标准点RMS值和LAGEOS标准点合格率3个因素已可以刻画测站观测的优劣。
| 模型 | 参数 | |
| 参测考量架模与型 | 地球参考架 | ITRF2014 |
| 岁差模型 | IAU2006 | |
| 章动模型 | IAU2006+IERS章动改正 | |
| 大气折射改正 | Mendes-Pavlis模型 | |
| 质心改正/m | 依测站而定(0.245~0.251) | |
| 力学模型 | 地球重力场/阶 | EGM2008(100×100) |
| 固体潮摄动 | IERS2010 | |
| 海潮摄动 | FES2004 | |
| 行星摄动 | JPL DE421 | |
|
| 图 2 LAGEOS 1卫星采用方案1—5后对测站重新定权后的定轨精度比较 Fig. 2 Comparison of the precision of orbit determination for LAGEOS 1 after reweighting station observations with solution 1—5 |
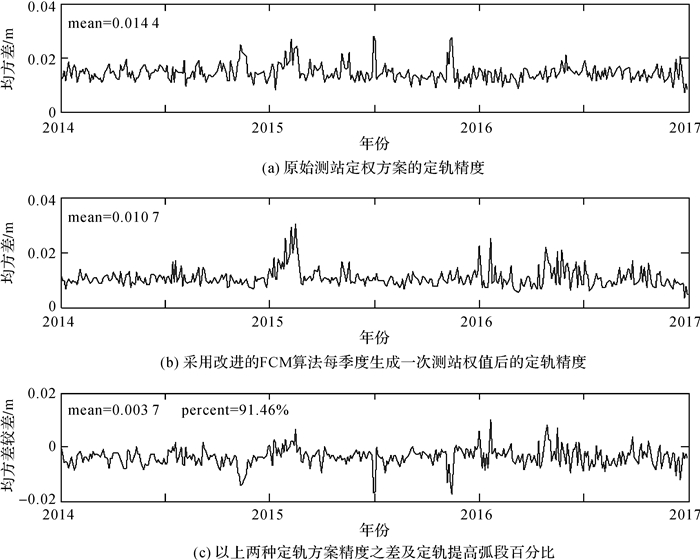
以上的结果是基于2015年6月的全球SLR测站性能月报得到的权值进行2014至2016年的数据处理得到的定轨精度。由于月报只给出了测站2015年6月的性能统计结果,用它所确定出来的测站权值并不适用于处理长时间段的数据,特别是时间与其相差较远的观测弧段。如果能够根据实时发布的测站性能指标实时生成测站权值,将会进一步提高定轨精度。为此,根据ILRS发布的全球SLR测站性能季报,考虑LAGEOS标准点总数、LAGEOS标准点RMS值、LAGEOS标准点合格率3项指标,每季度都重新生成一次测站权值,然后进行精密定轨。图 3给出了LAGEOS 1卫星采用原始测站定权方案和模糊聚类算法定权方案定轨精度的比较。从图中可以看出,该方案在方案1的基础上进一步提高了定轨精度,观测残差均方差平均提高了3.7 mm,且有91.46%的弧段精度得到了提高,并且对于参与计算的各个测站的残差RMS都有所下降。表 3给出了部分参与计算的核心站采用改进的FCM模糊聚类算法对测站定权和原测站定权方法的观测残差比较的统计信息。可以看出大部分测站的残差RMS有所降低,且参与定轨的标准点数也增加了,提高了观测资料的利用率。
|
| 图 3 LAGEOS 1卫星原始测站定权方案与改进的FCM算法定权方案定轨精度比较 Fig. 3 Comparison of orbit determination for LAGEOS 1 with traditional weighting scheme and modified FCM clustering algorithm quarterly |
| 测站编号 | 原测站定权 | 改进的FCM测站定权 | |||
| 标准点个数 | 观测残差RMS值/m | 标准点个数 | 观测残差RMS值/m | ||
| 7080 | 1497 | 0.018 9 | 1500 | 0.017 6 | |
| 7090 | 34 835 | 0.017 6 | 34 919 | 0.017 2 | |
| 7105 | 14 973 | 0.023 5 | 15 116 | 0.015 8 | |
| 7110 | 10 258 | 0.020 4 | 9739 | 0.014 0 | |
| 7501 | 9066 | 0.019 5 | 8862 | 0.017 8 | |
| 7810 | 14 999 | 0.010 8 | 15 016 | 0.009 0 | |
| 7825 | 13 491 | 0.016 9 | 13 983 | 0.012 8 | |
| 7839 | 6466 | 0.012 5 | 6417 | 0.010 7 | |
| 7840 | 12 991 | 0.010 2 | 13 067 | 0.009 8 | |
| 7941 | 13 970 | 0.015 4 | 14 210 | 0.009 5 | |
| 8834 | 4227 | 0.020 8 | 4289 | 0.020 1 | |
4 结论
通过对3年的全球LAGEOS 1卫星SLR观测数据分析,研究了改进的FCM模糊聚类算法对SLR测站重新定权后对精密定轨精度的影响。结果表明,与传统的测站定权方法相比较,改进的FCM模糊聚类算法对测站定权可以系统性地提高定轨精度和数据利用率。特别是所考虑的LAGEOS标准点总数、LAGEOS标准点RMS值、LAGEOS标准点合格率3项测站性能指标随观测时间更新时,以ILRS全球SLR测站性能季报为例,有91.46%的弧段定轨精度得到提高,平均提高精度20%多,幅度达3.7 mm,且观测数据的利用率也得到了明显提升。
| [1] | DEGNAN J J. Satellite laser ranging:current status and future prospects[J]. IEEE Transactions on Geoscience and Remote Sensing, 1985, GE-23(4): 398–413. DOI:10.1109/TGRS.1985.289430 |
| [2] | DEGNAN J J. Millimeter accuracy satellite laser ranging: a review[M]//ESMITH D E, TURCOTTE D L. Contributions of Space Geodesy to Geodynamics: Technology. Washington: AGU, 1993: 133-162. |
| [3] |
冯初刚, 朱元兰, 张飞鹏.
LAGEOS卫星精密定轨及残差分析[J]. 天文学报, 2003, 44(1): 55–64.
FENG Chugang, ZHU Yuanlan, ZHANG Feipeng. Determination of LAGEOS satellite's precise orbits and residual analysis[J]. Acta Astronomica Sinica, 2003, 44(1): 55–64. DOI:10.3321/j.issn:0001-5245.2003.01.009 |
| [4] | PEARLMAN M R. Workshop summary[C]//Proceedings of the 16th International Workshop on Laser Ranging. Poznan: Polish Academy of Science, 2009: 4-8. |
| [5] | SEEBER G. Satellite geodesy[M]. 2nd ed. Berlin: Walter de Gruyter, 2003: 424-436. |
| [6] | GURTNER W, NOOMEN R, PEARLMAN M R. The international laser ranging service:current status and future developments[J]. Advances in Space Research, 2005, 36(3): 327–332. DOI:10.1016/j.asr.2004.12.012 |
| [7] | ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008:an improved solution of the international terrestrial reference frame[J]. Journal of Geodesy, 2011, 85(8): 457–473. DOI:10.1007/s00190-011-0444-4 |
| [8] |
赵罡, 王小亚, 吴斌.
不同测站卫星质心不同改正对卫星激光测距定轨精度的影响分析[J]. 测绘学报, 2012, 41(2): 165–170.
ZHAO Gang, WANG Xiaoya, WU Bin. Effect analysis of system-dependent center-of-mass correction on precision of SLR orbit determination[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 165–170. |
| [9] |
赵春梅, 瞿锋, 程鹏飞, 等.
阿根廷圣胡安激光测距系统的SLR数据质量分析[J]. 测绘学报, 2008, 37(3): 338–341, 348.
ZHAO Chunmei, QU Feng, CHENG Pengfei, et al. Data quality analysis of Argentina San Juan laser ranging system[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 338–341, 348. DOI:10.3321/j.issn:1001-1595.2008.03.012 |
| [10] | PETIT G, LUZUM B. IERS conventions (2010)[R]. IERS Technical Note No.36. Frankfurt: IERS, 2010: 1-95. http://www.mendeley.com/research/iers-conventions-2010/ |
| [11] | PEARLMAN M R, DEGNAN J J, BOSWORTH J M. The international laser ranging service[J]. Advances in Space Research, 2002, 30(2): 135–143. DOI:10.1016/S0273-1177(02)00277-6 |
| [12] | PEARLMAN M, NOLL C, GURTNER W, et al. The international laser ranging service and its support for GGOS[M]//TREGONING P, RIZOS C. Dynamic Planet. Berlin: Springer, 2007: 348-53. |
| [13] |
秦显平, 杨元喜.
抗差方差分量估计在卫星定轨中的应用[J]. 大地测量与地球动力学, 2003, 23(4): 40–43.
QIN Xianping, YANG Yuanxi. Applications of robust variance component estimation to satellite orbit determination[J]. Journal of Geodesy and Geodynamics, 2003, 23(4): 40–43. |
| [14] | SOTO J, AGUIAR M I V, FLORES-SINTAS A. A fuzzy clustering application to precise orbit determination[J]. Journal of Computational and Applied Mathematics, 2007, 204(1): 137–143. DOI:10.1016/j.cam.2006.04.050 |
| [15] | HEINE K. Potential application of fuzzy methods in geodetic fields[C]//Proceedings of the 1st International Symposium on Robust Statistics and Fuzzy Techniques in Geodesy an GIS. Zurich, Switzerland: [s.n.], 2001. |
| [16] | ZADEH L A. Fuzzy sets[C]//ZADEH L A, KLIR G J, YUAN Bo. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems.[S.l.]: World Scientific Publishing Co. Inc., 1996: 394-432. |
| [17] | BELLMAN R, KALABA R, ZADEH L. Abstraction and pattern classification[J]. Journal of Mathematical Analysis and Applications, 1966, 13(1): 1–7. |
| [18] | RUSPINI E H. A new approach to clustering[J]. Information and Control, 1969, 15(1): 22–32. DOI:10.1016/S0019-9958(69)90591-9 |
| [19] | DUNN J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1973, 3(3): 32–57. DOI:10.1080/01969727308546046 |
| [20] | BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[J]. Advanced Applications in Pattern Recognition, 1987, 22(1171): 203–239. |
| [21] | FLORES-SINTAS A, CADENAS J M, MARTIN F. A local geometrical properties application to fuzzy clustering[J]. Fuzzy Sets and Systems, 1998, 100(1-3): 245–256. DOI:10.1016/S0165-0114(97)00038-9 |
| [22] | FLORES-SINTAS A, CADENAS J M, MARTIN F. Partition validity and defuzzification[J]. Fuzzy Sets and Systems, 2000, 112(3): 433–447. DOI:10.1016/S0165-0114(98)00004-9 |
| [23] | HATHAWAY R J, BEZDEK J C. Recent convergence results for the fuzzy c-means clustering algorithms[J]. Journal of Classification, 1988, 5(2): 237–247. DOI:10.1007/BF01897166 |
| [24] | ZHANG Huizhe, CHEN Hong, BAO Lixia. An improved fuzzy c means clustering algorithm and its application in traffic condition recognition[C]//Proceedings of 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery. Yantai: IEEE, 2010: 1608-1612. https://ieeexplore.ieee.org/document/5569360 |
| [25] | OTSUBO T, MÜLLER H, PAVLIS E C, et al. Rapid response quality control service for the laser ranging tracking network[J]. Journal of Geodesy, 2018(10): 1–10. DOI:10.1007/s00190-018-1197-0 |


