2. 北京航天飞行控制中心, 北京 100094;
3. 上海市空间导航与定位技术重点实验室, 上海 200030
2. Beijing Aerospace Control Center, Beijing 100094, China;
3. Shanghai Key Laboratory of Space Navigation and Positioning Techniques, Shanghai 200030, China
我国探月工程分为“绕、落、回”3个阶段。“嫦娥一号”(CE-1)和“嫦娥二号”(CE-2)探测器主要完成绕月飞行及着陆区成像的探测任务。“嫦娥三号”(CE-3)为落月探测器,由着陆器和玉兔号月球车(巡视器)组成,实施了月面勘察任务[1]。“嫦娥五号”(CE-5)探测器于2019年发射,将完成月面取样返回任务,肩负月表自动采样、月面动力上升、采样返回轨道设计、月球轨道交会对接、多目标高精度测控通信、月球样品储存和地面实验室分析等关键任务,为后续载人登月和深空探测工程服务[2]。
CE-5探测器的组成包括轨道器、返回器、着陆器和上升器。在环月并准备着陆阶段,轨道器/返回器组合体(以下简称轨返组合体)将与着陆器/上升器组合体(以下简称着上组合体)执行器间分离操作。器间分离的监测方法通常采用星上搭载的有效载荷,如视觉传感器、测距雷达等进行短距离测量。但在初始分离阶段,上述技术受工作条件限制,均有较长的响应延迟,因而影响了快速可靠的分离状态监视。目前暂未有更好的手段实时监测分离过程的器间相对距离。
同波束干涉测量技术(same-beam interference,SBI)有望提供一种地基的分离过程准实时可靠监测[3-5]。首先,甚长基线干涉测量(very long baseline interferometry,VLBI)是探月飞行任务的常规测定轨手段之一,无须增加探测设备。其次,SBI作为差分VLBI测量技术,能大幅消除或削弱VLBI相对时延测量的系统误差,提高分离过程中相对距离的解算精度[6-8]。
为简便快捷地监测器间分离,本文提出了仅利用单基线SBI的器间分离监测算法。首先,在地心地固系下推导了器间相对距离的SBI观测方程,然后以相对距离的历元解时序构造了监视统计量,基于滑动窗口分别对分离时刻和达到安全距离时刻进行双重分离状态判断。利用CE-3着陆器的实测SBI数据,本算法对着陆器上两天线的静态相对位置的解算平均误差为0.15 m,与参考文献[23]中CE-3巡视器两天线相对位置测量精度(0.16 m)处于同一量级。最后,仿真了CE-5器间分离过程。试验结果表明器间分离的监测响应延迟小于30 s。
1 单基线同波束干涉测量实时监测原理 1.1 同波束干涉测量原理VLBI利用位置已知的上千千米基线两端的地面站接收到的同一深空信号的到达时延,高精度地测量信号源角位置信息[9]。当两个角距接近的信号源可以被地面天线的同一波束内观测到时,可以形成差分干涉测量,称为同波束干涉测量[10-12]。
以CE-5飞行器为例,SBI测量原理如图 1所示,相应的观测几何方程可写为
 (1)
(1)

|
| 图 1 空气动力学学报201905 Fig. 1 SBI principle and coordinate transformation relation |
式中,Δτ为SBI差分时延;τR、τC分别是着上组合体和轨返组合体天线相位中心对应的VLBI时延;ρ3、ρ4和ρ1、ρ2分别为着上组合体和轨返组合体与两地面站间的视向距离;c为光速(c=299 792 458 m/s)。
根据飞行器与地月的几何关系(参见图 2),式(1)中两组视向距离的矢量可进一步表示为
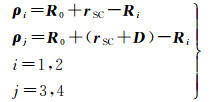 (2)
(2)
|
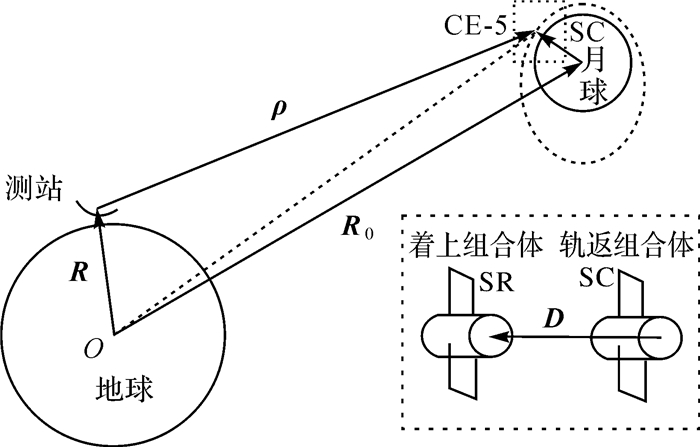
| 图 2 CE-5轨返组合体观测几何示意图与局部放大 Fig. 2 Visual distance of CE-5 orbiter returner assembly diagram and partial enlarged detail |
式中,R0表示月球在地心天球坐标系下的位置矢量;Ri表示测站i的地固系位置矢量;rSC表示嫦娥五号轨返组合体的月心天球坐标系下的位置矢量;D为两器相对位置矢量,也是两器分离的监视参数。以下将各矢量统一在地固系下,给出坐标转换过程。
1.2 坐标系及坐标转换探月飞行器的SBI观测涉及较多的地球和月球坐标系,下面分别给出CE-5环月段和CE-3着陆后的月球坐标系及其坐标转换关系。
1.2.1 CE-5环月段的坐标系转换在分离阶段,CE-5的轨返组合体始终在环月轨道上,其轨道状态可采用月心天球坐标系(又称为月心惯性系)下的位置和速度向量(rSC, 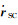
CE-5卫星固连坐标系定义为:原点在轨返组合体与运载火箭对接面的几何中心;X轴沿卫星纵轴,指向卫星运动方向;Z轴垂直于X轴和太阳翻板展开方向,且指向月球方向;Y轴与Z轴和X轴构成右手直角坐标系。
显然,该坐标系与RTN坐标系定义基本类似,只是坐标轴指向不同,基本面为卫星轨道垂面,基本方向为卫星运动方向。
1.2.1.1 固连坐标系与月心天球坐标系已知轨返组合体的位置和速度向量,可以计算固连坐标系转到月心天球坐标系的旋转矩阵ΦMCISF(A, B, C),3个列向量的计算公式为[13]
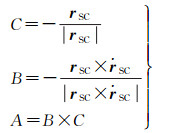 (3)
(3)
两者三轴指向完全一致,坐标原点分别为地心和月心。坐标转换仅有平移参数,可根据DE历表获得R0。
1.2.1.3 地心天球坐标系至地心地固系旋转矩阵ΦECEFECI考虑岁差、章动、地球自转和极移等,具体计算方法可参考文献[14—15]。
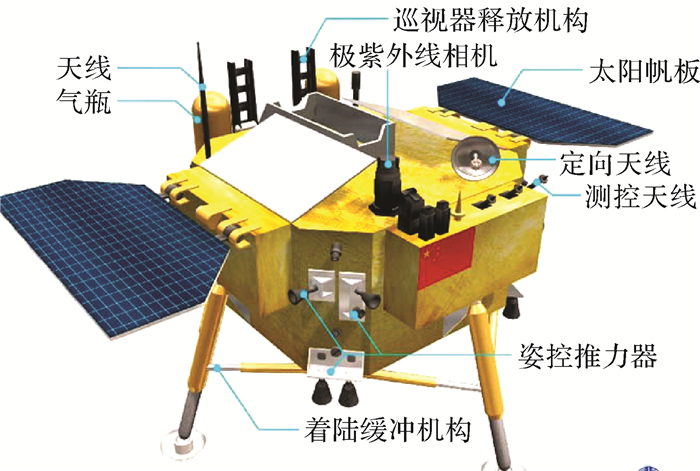
1.2.2 CE-3着陆器的坐标系转换CE-3着陆器上有遥感(全向)、数传(定向)天线,即图 3中的测控、定向天线。利用这两个天线下行信号进行SBI观测时,坐标转换略有不同,即着陆器固连坐标系-月固系-月心天球坐标系-地心天球坐标系-地固系。这里仅介绍前面3个坐标系的转换。
CE-3着陆器的卫星固连坐标系选为着陆器落月点(B、L、H)为原点的东北天坐标系。结合姿态信息可得到CE-3遥感、数传天线在该坐标系下的标称绝对位置和相对位置矢量D0。
1.2.2.1 着陆器固连坐标系和月固系着陆器固连坐标系和月固系与地面点东北天坐标系至地固系的转换方法类似,参见文献[17]。
1.2.2.2 月固系和月心天球坐标系月固系和月心天球坐标系与地固系至地心天球坐标系不同,月球是慢自转天体,月固系旋转至月心天球坐标系由JPL的DE/LE历表提供的3个欧拉角(Λ、i、Ω)给出,即月固系与月心天球坐标系之间的旋转矩阵为[18]
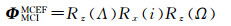 (4)
(4)
由式(1)和式(2)可知,实时解算两器分离的相对位置矢量D需要3条线性不相关的基线。若分离前两器的姿态信息及对应天线的相对位置已知,且令分离方向为轨返组合体的运动方向,则分离体的相对位置变化可表示为
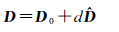 (5)
(5)
式中,D0是两器对应天线初始相对位置;
此时两者的相对位置矢量转化为方向已知一维未知量,即相对距离。因此,仅需要单条基线即可逐历元解算相对位置信息。
1.3.2 分离状态统计量根据两器相对距离的时间序列,基于滑动窗口构造分离监视统计量。滑动窗口的长度为N,对任意历元t,统计量为滑动窗口内的相对距离的加权平均,即
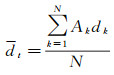 (6)
(6)
式中,dk和Ak分别为窗口内第k个观测距离及其权重。
分离过程中,相对距离不断增加,因此t时刻的真实距离dtreal理论上不小于历元t的加权均值,即dtreal≥dt。
1.3.3 双重阈值设定为了增强监视判断的可靠性,对分离状态统计量设定了两个相对距离阈值dstart和dsafe。因此,双重阈值法对应了两器分离的双重判定参数,即分离时刻t1和达到安全距离时刻t2。
当分离状态统计量dt分别满足
 (7)
(7)
对应的起始历元t1和t2分别判定为起始分离时刻和达到安全距离的时刻。
2 试验结果与分析首先,利用CE-3着陆器上的数传和遥感天线的实测SBI数据,验证了静态监视距离精度为0.3 m,保证了本文推导的相对距离解算的算法可行性。然后,利用该算法仿真CE-5的环月段分离过程,生成两器分离的SBI观测时序,并通过实时分离监测算法对分离时刻及安全距离时刻进行判断。
2.1 CE-3实测数据算法验证 2.1.1 测量数据选取CE-3着陆器遥感(DOR)和数传(data)天线作为信号源,利用佳木斯—喀什基线对其进行SBI观测。连续观测分为两个时段,数据间断较大,共计约3 h,分别为2018-01-28 T09:54:27—T11:51:25,以及2018-01-29 T10:54:27—T12:07:26,每秒采样,对应原始VLBI数据分布如图 4所示。

|
| 图 4 28日与29日VLBI观测时间分布 Fig. 4 VLBI observation time distribution on 28th and 29th |
2.1.2 VLBI信号处理 2.1.2.1 差分时延获取
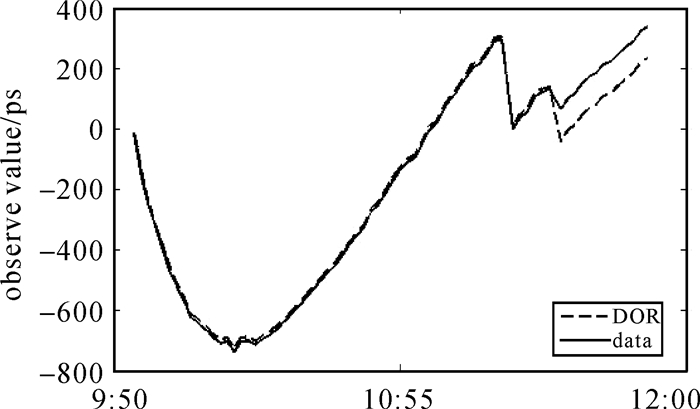
CE-3着陆器数传天线发射频率约为8496 MHz的数传信号(data),遥感天线发送频率约为8470 MHz的遥测信号(DOR),下行遥测信号含有4根DOR点频信号,距离主载波分别为±3.8 MHz、±19 MHz,其中+19 MHz的DOR信号接近数传信号[19-20]。根据干涉测量处理流程[26-27],分别解算DOR信号及数传信号的干涉相位与干涉相时延。图 5给出了28日该基线观测的CE-3两个天线VLBI相位时延(即图 4(a)的观测数据),在28日10时20分和30分时出现跳变是由于观测过程中信号发生中断,缺失约10 s观测数据,再次接收信号时,受测站硬件、信号源等因素影响,造成VLBI观测时延发生整周跳变。
|
| 图 5 28日遥感(DOR)、数传(data)天线时延 Fig. 5 The delay of DOR and data on 28th |
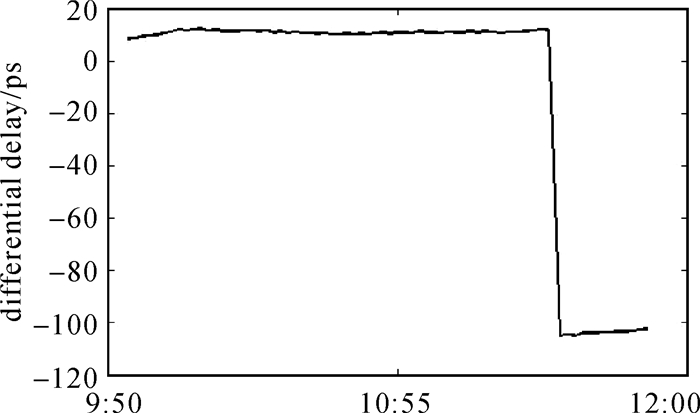
将观测信号差分后即为含模糊度的差分相位时延Δτ,见图 6。随机误差约为0.225 ps(0.07 mm)。该测量精度与文献[24]的SBI测量精度0.588 6 ps及0.196 2 ps、文献[25]的SBI测量精度0.53 ps处于同一量级。
|
| 图 6 含模糊度的差分相位时延 Fig. 6 Differential phase delay with fuzzy degree |
2.1.2.2 模糊度解算
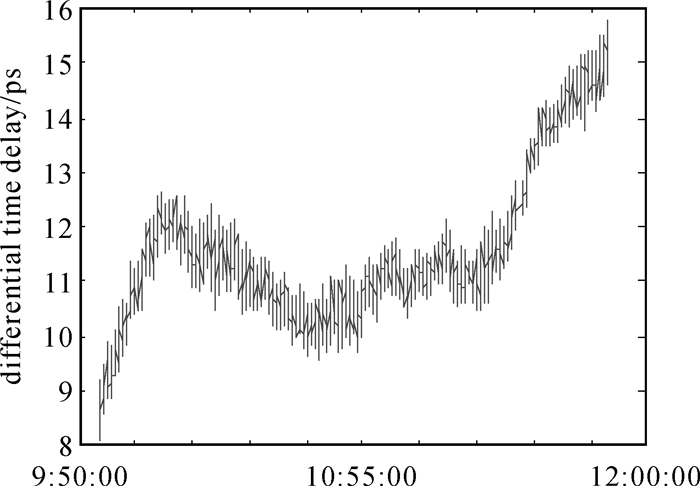
图 7为固定模糊度后的差分时延。接收到的下行信号中心频率约为8496 MHZ,其整周时延约为120 ps。由于两信号源相距很近(约1 m),SBI的差分能够消除和削弱绝大部分系统误差影响,仅利用先验位置和概略姿态信息计算出理论差分时延
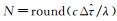
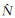
|
| 图 7 28日模糊度固定后的差分时延 Fig. 7 Differential time delay with fixed fuzzy degree on 28th |
2.1.2.3 两天线的静态相对距离解算
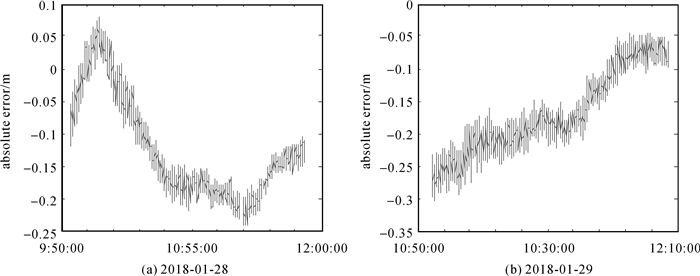
图 8给出了CE-3着陆器遥感和数传天线静态相对距离的解算误差时序。两段数据表明,利用SBI单基线解算的相对距离,整体偏差约为0.15 m,单点精度优于0.3 m。
|
| 图 8 CE-3相对距离解算误差时序 Fig. 8 CE-3 relative distance calculation error |
2.2 CE-5分离监测仿真 2.2.1 仿真条件
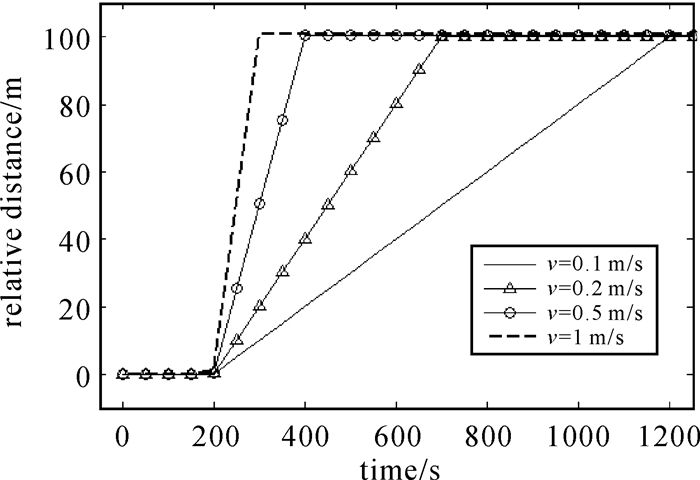
令2018年9月21日9:33分(UTC)的CE-5绕月轨道根数为:轨道倾角80°,近月点高度15 km,远月点高度100 km,其余为0(文献[22])。从第200 s开始分离,分离速度分别取为0.1、0.2、0.5和1 m/s。令分离距离达到80 m时达到安全距离,达到100 m时结束仿真。图 9为分离过程的两器相对距离变化。
|
| 图 9 分离距离随时间的变化 Fig. 9 The variation of separation distance with time in simulation |
分别选取佳木斯—喀什基线和上海—喀什基线对CE-5进行SBI仿真观测,采样率为1 s。
在仿真过程中主要考虑的误差源包括:①轨道误差,取先验位置误差10 km;②卫星姿态误差,令卫星固连坐标系的X轴Y轴各有0.5°方向误差;③SBI观测误差,差分时延观测量取10 ps的白噪声误差。
需要说明的是,CE-3两天线的SBI观测随机误差约为0.3 ps,卫星姿态误差约为0.2°。因此,CE-5的仿真过程中,10 ps的差分时延误差和0.5°的姿态误差,基本涵盖了可能的观测时延误差和实际姿态误差等因素[21]。
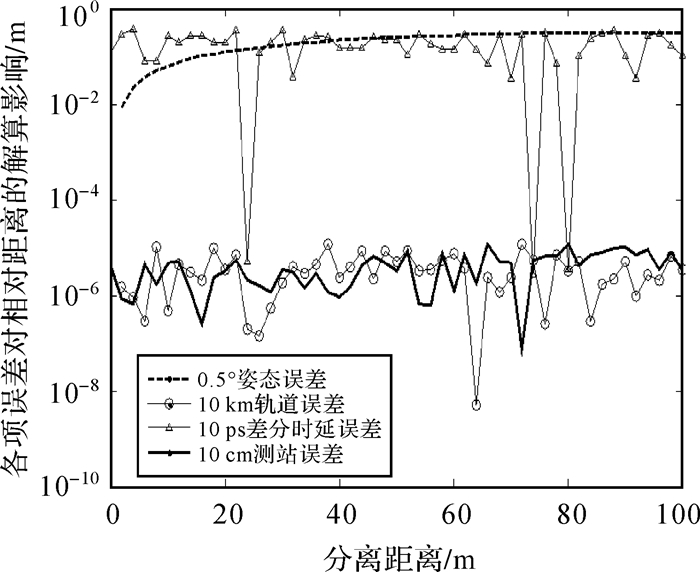
以佳木斯—喀什基线为例,图 10给出了4项误差对SBI相对距离解算的影响。在百米的相对距离之内,该观测弧段的单点解算表明:①0.5°姿态误差和10 ps差分时延误差对相对距离解算值能够引进接近1 m的误差影响;②轨道误差和测站坐标误差对观测结果的影响基本可以忽略,这是因为,在SBI的双差模式下,上述误差影响能够基本消除(双差后误差约为0.1 ps)。
|
| 图 10 各项误差对相对距离解算的影响 Fig. 10 The influence of errors on relative distance calculation |
2.2.2 仿真结果
对分离速度为0.1~1 m/s的分离方案进行仿真。分别以佳木斯—喀什基线和上海—喀什基线的两个单基线SBI进行解算,分离期间两器相对距离的解算精度均优于1 m。
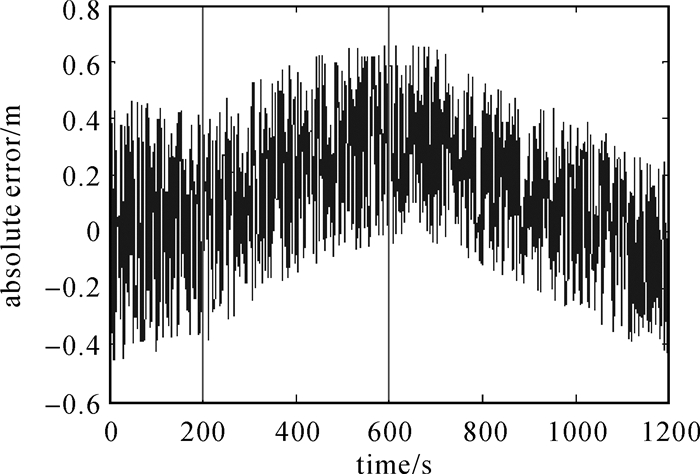
图 11给出了分离速度为0.2 m/s时,佳木斯—喀什单基线的相对距离解算偏差时序。可以看出,分离前(<200 s)相对距离不变,解算结果最稳定;随着分离距离的增加(200~600 s),解算偏差有整体增加的趋势,这是因为距离越大,姿态误差对解算结果影响越明显,绝对误差越大;而在分离完成(>600 s)后,误差大小与卫星位置变化有关,这是因为随着卫星运动,卫星相对于测站的姿态不断改变,导致观测误差发生变化。
|
| 图 11 佳木斯—喀什基线0.2 m/s分离过程解算误差时序 Fig. 11 Absolute error of Hamusi-Kashi line of 0.2 m/s |
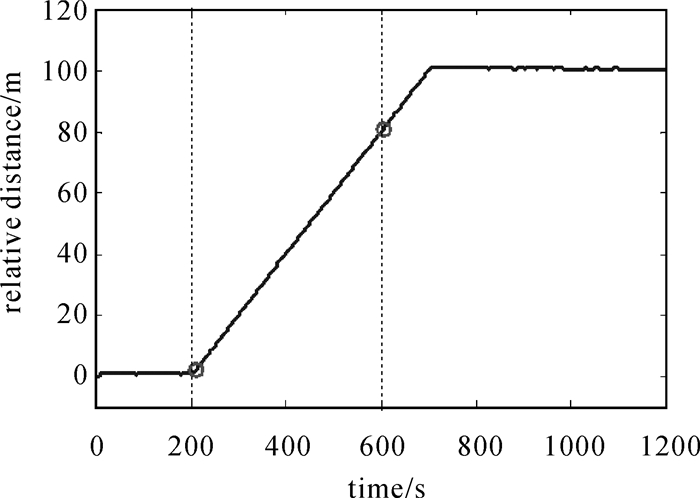
图 12为上述仿真条件下的双重阈值法分离判断结果。统计量滑动窗口宽度取为10,分离时刻与达到安全距离时刻的判断结果分别为212 s和612 s,与理论时刻(200 s和600 s)相比,响应时延均为12 s。
|
| 图 12 佳木斯—喀什基线0.2 m/s分离过程距离的判断 Fig. 12 Judgment of separation distance |
表 1总结了4种分离速度下,两条单基线各自独立解算和判断分离的响应时延。可以看出:
| s | |||||
| 基线 | 分离速度 v/(m/s) |
分离时刻 /s |
响应时延 /s |
安全距离时刻/s | 响应时延 /s |
| 佳木斯—喀什 | 0.1 | 200 | 25 | 1000 | 24 |
| 0.2 | 200 | 12 | 600 | 12 | |
| 0.5 | 200 | 9 | 360 | 10 | |
| 1 | 200 | 6 | 280 | 7 | |
| 上海—喀什 | 0.1 | 200 | 29 | 1000 | 30 |
| 0.2 | 200 | 13 | 600 | 14 | |
| 0.5 | 200 | 11 | 360 | 11 | |
| 1 | 200 | 7 | 280 | 7 | |
(1) 分离监测与安全距离监测时延均小于30 s,基本实现了准实时的器间分离监测。
(2) 分离速度越大,分离与安全距离的响应效果越好。这是因为,速度较大时,数据变化较为明显,解算的相对距离误差减小,缩短判断时间,从而判断更及时准确。当分离速度为1 m/s时,每条基线的响应时延都优于10 s,而分离速度为0.1 m/s时,响应时延超过20 s。
(3) 佳木斯—喀什基线的监测分离优于上海—喀什基线的监测。佳木斯—喀什基线长度更长,SBI观测对CE-5具有更高的角分辨率。特别是分离速度较低时,长基线的监视优势更为显著。当分离速度为0.1 m/s时,佳木斯—喀什基线对分离和安全距离的响应时延不大于25 s,而上海—喀什基线对应的响应时延接近30 s。
3 结论针对CE-5组合体间分离距离实时测量需求,在两个探测器(信号源)相对方向已知的条件下,利用单基线同波束干涉测量的空间距离解算模型,提出了基于两器相对距离单点解算时序的两器分离双阈值判定方法。
(1) 基于CE-3着陆器遥感、数传天线的SBI实测数据,利用佳木斯—喀什基线,单点解算了着陆器两天线的静态相对距离。两天共计约3 h观测试验表明,着陆器两天线的相对距离的均值偏差约为0.15 m,能够满足分离监测的精度要求。
(2) 对CE-5的两器分离过程和单基线SBI观测进行仿真,通过两器分离双阈值判定法表明,顾及10 km卫星轨道误差、10 ps观测噪声以及0.5°卫星姿态误差等影响因素,该方法能在分离距离80 m范围内,实现CE-5器间分离的可靠监测,监测时延小于30 s。
| [1] |
叶培建, 黄江川, 孙泽洲, 等.
中国月球探测器发展历程和经验初探[J]. 中国科学(技术科学), 2014, 44(6): 543–558.
YE Peijian, HUANG Jiangchuan, SUN Zezhou, et al. The process and experience in the development of Chinese lunar probe[J]. Scientia Sinica Technologica, 2014, 44(6): 543–558. |
| [2] |
钱志瀚, 李金岭.
甚长基线干涉测量技术在深空探测中的应用[M]. 北京: 中国科学技术出版社, 2012: 55-57.
QIAN Zhihan, LI Jinling. VLBI techniques for deep space exploration[M]. Beijing: Chinese Science Technology Press, 2012: 55-57. |
| [3] |
杜兰, 郑勇, 李杰.
VLBI在GEO卫星精密定轨中的应用[J]. 测绘科学技术学报, 2006, 23(4): 269–271.
DU Lan, ZHENG Yong, LI Jie. VLBI-augmented orbit determination for geostationary satellites[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(4): 269–271. DOI:10.3969/j.issn.1673-6338.2006.04.010 |
| [4] |
乔书波, 李金岭, 孙付平.
VLBI在探月卫星定位中的应用分析[J]. 测绘学报, 2007, 36(3): 262–268.
QIAO Shubo, LI Jinling, SUN Fuping. Application analysis of lunar exploration satellite positioning by VLBI technique[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 262–268. DOI:10.3321/j.issn:1001-1595.2007.03.004 |
| [5] | ZENSUS J A, DIAMOND P J, NAPIER P J. Very long baseline interferometry and the VLBA[R]. San Francisco: Astronomical Society of the Pacific, 1995. http://adsabs.harvard.edu/abs/1995ASPC...82.....Z |
| [6] |
郑鑫, 刘庆会, 吴亚军, 等.
双月球探测器相对定位的同波束VLBI技术研究[J]. 宇航学报, 2014, 35(9): 1030–1035.
ZHENG Xin, LIU Qinghui, WU Yajun, et al. Research on same-beam VLBI technique for relative position determination of two lunar spacecrafts[J]. Journal of Astronautics, 2014, 35(9): 1030–1035. DOI:10.3873/j.issn.1000-1328.2014.09.007 |
| [7] |
黄勇, 单荃, 李培佳, 等.
基于同波束VLBI测量的月球交会对接轨道确定[J]. 中国科学(物理学力学天文学), 2016, 46(8): 089511.
HUANG Yong, SHAN Quan, LI Peijia, et al. The application of the seam beam VLBI technique for the orbit determination of CE-5 in the rendezvous and docking phase[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2016, 46(8): 089511. |
| [8] | KIKUCHI F, LIU Qinghui, HANADA H, et al. Picosecond accuracy VLBI of the two subsatellites of SELENE (KAGUYA) using multifrequency and same beam methods[J]. Radio Science, 2009, 44(2): RS2008. |
| [9] |
唐歌实, 韩松涛, 陈略, 等.
深空网干涉测量技术在"嫦娥3号"任务中应用分析[J]. 深空探测学报, 2014, 1(2): 146–149.
TANG Geshi, HAN Songtao, CHEN Lue, et al. Analysis on interferometric tracking technology by China deep space network in the Chang'e-3 mission[J]. Journal of Deep Space Exploration, 2014, 1(2): 146–149. |
| [10] |
吴伟仁, 刘庆会, 黄勇, 等.
"嫦娥3号"月面探测器同波束干涉测量系统的设计与实现[J]. 深空探测学报, 2015, 2(1): 34–42.
WU Weiren, LIU Qinghui, HUANG Yong, et al. Design and realization of same-beam interferometry measurement of CE-3[J]. Journal of Deep Space Exploration, 2015, 2(1): 34–42. |
| [11] | ZHOU Huan, LI Haitao, DONG Guangliang. Relative position determination between Chang'E-3 lander and rover using in-beam phase referencing[J]. Science China Information Sciences, 2015, 58(9): 1–10. |
| [12] |
洪晓瑜.
VLBI技术的发展和"嫦娥工程"中的应用[J]. 自然杂志, 2007, 29(5): 297–299.
HONG Xiaoyu. VLBI techniques and application in the Chang'e lunar orbiter[J]. Chinese Journal of Nature, 2007, 29(5): 297–299. DOI:10.3969/j.issn.0253-9608.2007.05.010 |
| [13] |
曹月玲.应用SLR对LAGEOS卫星精密定轨及测定地心运动[D].上海: 同济大学, 2008. CAO Yueling. Precise orbit determination and geocentric movement of LAGEOS satellite's precise orbit based on SLR[D]. Shanghai: Tongji University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1449571 |
| [14] |
杜兰, 张捍卫, 周庆勇, 等.
坐标转换参数之间的相关性解析[J]. 大地测量与地球动力学, 2011, 31(1): 59–62.
DU Lan, ZHANG Hanwei, ZHOU Qingyong, et al. Analysis of correlation of coordinate transformation parameters[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 59–62. |
| [15] |
张捍卫, 郑勇, 马高峰.
GCRS与ITRS之间的坐标转换研究[J]. 大地测量与地球动力学, 2011, 31(1): 63–67.
ZHANG Hanwei, ZHENG Yong, MA Gaofeng. Research on coordinate transformation between GCRS and ITRS[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 63–67. |
| [16] |
李清.嫦娥三号今晚月球软着陆——着陆细节全图解[EB/OL]. (2013-12-14)[2018-01-23]. http://www.xinhuanet.com//photo/2013-12/14/c_125859856.htm. LI Qing. Chang'E-3 will be soft landing tonight: all detail in one picture[EB/OL]. (2013-12-14)[2018-01-23]. http://www.xinhuanet.com//photo/2013-12/14/c_125859856.htm. |
| [17] |
史海锋, 张卫斌.
空间直角坐标与大地坐标转换算法研究[J]. 大地测量与地球动力学, 2012, 32(5): 78–81.
SHI Haifeng, ZHANG Weibin. Study on transformation from Cartesian to geodetic coordinates[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 78–81. |
| [18] | ARCHINAL B A, A'HEARN M F, CONRAD A, et al. Erratum to:reports of the IAU working group on cartographic coordinates and rotational elements:2006& 2009[J]. Celestial Mechanics and Dynamical Astronomy, 2011, 110(4): 401–403. DOI:10.1007/s10569-011-9362-2 |
| [19] |
刘庆会, 陈明, 熊蔚明, 等.
基于超高精度多频点同波束VLBI技术的月球车精密相对定位[J]. 中国科学(物理学力学天文学), 2010, 40(2): 253–260.
LIU Qinghui, CHEN Ming, XIONG Weiming, et al. Relative position determination of a lunar rover using high-accuracy multi-frequency same-beam VLBI[J]. Science China Physics, Mechanics and Astronomy, 2010, 40(2): 253–260. |
| [20] |
陈明, 刘庆会, 陈冠磊, 等.
同波束干涉测量差分相位计算与DOR时延精度验证[J]. 测绘学报, 2013, 42(6): 817–823.
CHEN Ming, LIU Qinghui, CHEN Guanlei, et al. Calculation of differential phases in same-beam VLBI and accuracy verification of DOR delay[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 817–823. |
| [21] |
刘伟平, 郝金明, 李作虎.
由广播星历解算卫星位置、速度及精度分析[J]. 大地测量与地球动力学, 2010, 30(2): 144–147.
LIU Weiping, HAO Jinming, LI Zuohu. Solution method and accuracy analysis of satellite position and velocity from broadcast ephemeris[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 144–147. |
| [22] |
黄勇, 昌胜骐, 李培佳, 等.
"嫦娥三号"月球探测器的轨道确定和月面定位[J]. 科学通报, 2014, 59(23): 2268–2277.
HUANG Yong, CHANG Shengqi, LI Peijia, et al. Orbit determination of Chang'E-3 and positioning of the lander and the rover[J]. Chinese Science Bulletin, 2014, 59(23): 2268–2277. |
| [23] | LIU Qinghui, ZHENG Xin, HUANG Yong, et al. Monitoring motion and measuring relative position of the Chang'E-3 rover[J]. Radio Science, 2014, 49(11): 1080–1086. DOI:10.1002/2014RS005449 |
| [24] |
郑鑫, 刘庆会, 吴亚军, 等.
基于同波束VLBI差分相时延的"玉兔"月球车动作监视分析[J]. 中国科学(物理学力学天文学), 2014, 44(8): 872–878.
ZHENG Xin, LIU Qinghui, WU Yajun, et al. Motion monitoring and analysis of Chang'E-3 rover based on same-beam VLBI differential phase delay[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2014, 44(8): 872–878. |
| [25] |
陈永强, 周欢, 李伟, 等.
深空探测器单基线干涉测量相对定位方法[J]. 宇航学报, 2017, 38(6): 605–611.
CHEN Yongqiang, ZHOU Huan, LI Wei, et al. New VLBI method for relative position determination between deep space probes using single baseline[J]. Journal of Astronautics, 2017, 38(6): 605–611. |
| [26] |
唐歌实.
深空测控无线电测量技术[M]. 北京: 国防工业出版社, 2012.
TANG Geshi. Radiometric measuring techniques for deep space navigation[M]. Beijing: National Defense Industry Press, 2012. |
| [27] |
任天鹏, 唐歌实, 刘景勇, 等.
基于CEI的高精度相位干涉测量试验[J]. 遥测遥控, 2015, 36(6): 8–12.
REN Tianpeng, TANG Geshi, LIU Jingyong, et al. CEI-based high-precision phase interferometry tests[J]. Journal of Telemetry, Tracking and Command, 2015, 36(6): 8–12. DOI:10.3969/j.issn.2095-1000.2015.06.002 |