2. 中国地震局第一监测中心, 天津 300180
2. The First Monitoring and Application Center, China Earthquake Administration, Tianjin 300180, China
水汽(precipitable water vapor,PWV)是大气的主要组成部分之一,其对天气和气候的变化有着重要的影响。PWV分布对于研究中小尺度灾害天气,以及短时天气预报中具有重要的意义[1-4]。PWV时空变化导致雷达信号的延迟,降低了合成孔径雷达差分干涉测量(InSAR)的精度[5-7]。常规PWV获取手段具有局限性,如无线电探测法精度高但时间分辨率较低[8-9]。目前,利用GNSS获取PWV技术以及GNSS PWV应用的研究已经趋于成熟[10-14]。对于GNSS反演的PWV精度,国内外多位学者开展了GNSS PWV与无线电探空、水汽辐射计(WVR)PWV比较,获得了两者偏差为1~2 mm的结论[4, 15-16],因此可认为GNSS反演的PWV精度高,可满足气象应用的精度要求。受测站间距数十千米的限制,GNSS PWV存在空间上不连续呈离散分布的特征。利用MODIS影像反演的PWV在空间上是面状连续的,可对大区域PWV进行分析研究,且MODIS PWV的变化趋势与GNSS PWV接近,MODIS PWV可以弥补GNSS PWV在空间上的不连续性。受降水、云层、地表反射光谱不确定等影响,MODIS PWV的相对误差超过10%,如果可以消除地表反射光谱、温度廓线等的不确定性影响,其相对误差可优于5%,因此认为MODIS PWV的精度较低[17-19]。目前对于GNSS PWV与MODIS PWV的相关研究主要集中于小区域以及短时段[20-24]。
融合GNSS PWV与MODIS PWV各自的优势可用于天气预报和InSAR大气校正。为了推广MODIS PWV产品的应用,需要提高MODIS PWV精度。中国大陆构造环境监测网络(CMONOC)积累了全国260个GNSS站点观测资料,本文拟利用CMONOC观测资料开展中国大陆地区MODIS PWV校正研究。首先开展GNSS PWV与MODIS PWV的相关性比较;然后依据不同气候类型的测站分布,构建基于GNSS的不同气候类型MODIS PWV校正模型;最后进行模型的可靠性分析,并进行精度评定。
1 研究数据本文研究数据包括GNSS PWV和MODIS PWV,研究数据时间为2016年1月—12月。
1.1 GNSS PWV反演GNSS PWV由CMONOC观测数据经高精度定位定轨软件GAMIT计算获得。CMONOC是一个由260个连续观测和2000个不定期观测站点构成的观测网络。GNSS PWV解算方案如下:解算软件为GAMIT10.6,星历为IGS精密星历,Relax解算模式,卫星高度角10°,测站天顶对流层延迟(ZTD)的解算为每两小时估算一个值,ZTD由静力学延迟(ZHD)与对流层湿延迟(ZWD)组成,ZHD采用Saastamoinen模型结合测站纬度、大地高和气压观测数据精确计算获得,ZWD由ZTD减去ZHD获得[4]。ZWD转化为PWV,可采用公式PWV=∏×ZWD计算获得,转换系数∏可由Bevis提出的公式计算获得[25]。对于由GNSS观测和气象数据反演获得的PWV序列,针对PWV明显异常值,认为是粗差,给予删除预处理。GNSS PWV单位为毫米(mm),解算精度为1~2 mm,可满足气象应用的要求。
1.2 MODIS PWV反演MODIS PWV反演方案如下:解算软件为ENVI5,利用MOD05 PWV产品的近红外波段可反演PWV,MODIS PWV单位为mm。MODIS影像可通过NASA网站下载MODIS的MOD05 PWV产品获得论文研究所需MODIS PWV数据(https://ladsweb.modaps.eosdis.nasa.gov/search/)。
GNSS PWV的获取时间分辨率为2 h,而MODIS PWV的时间分辨率为每天2个观测值,为了便于两者比较及计算相关性,本文选择将GNSS PWV的时间分辨率抽稀成每天2个观测值,2次观测值时间与MODIS PWV时间最为接近。
2 MODIS PWV校正利用GNSS PWV进行MODIS PWV,首要任务是确定两者之间的关系,进而选择合适的模型校正方法。本节首先开展GNSS PWV与MODIS PWV的相关性分析,计算两者的偏差;然后选择回归分析方法构建基于GNSS PWV的MODIS PWV校正模型。
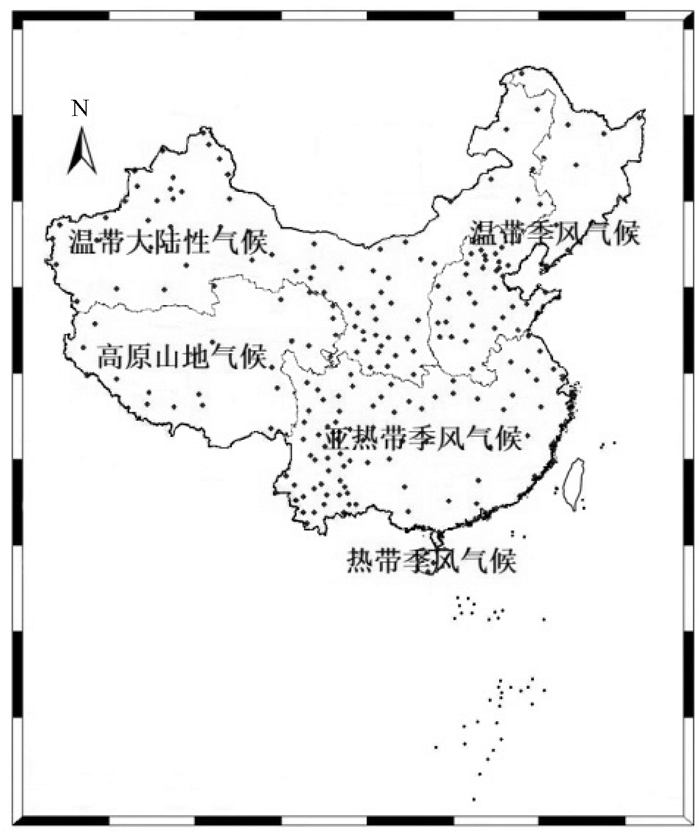
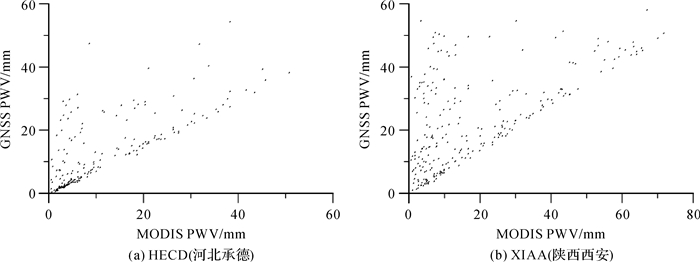
2.1 GNSS PWV与MODIS PWV相关性分析由于CMONOC站点多,若每一个站点都开展GNSS PWV与MODIS PWV的相关性分析和建模工作,模型工作量大且使用也不方便。因此,本文依据中国大陆地区的气候分布类型,将CMONOC站点分别划入到各气候类型(图 1),并依据气候类型分别开展GNSS PWV与MODIS PWV的相关性比较。图 2为随机选择两个站点的MODIS PWV与GNSS PWV对比的散点图。
|
| 图 1 CMONOC站点气候带划分图 Fig. 1 Map of climate zone stations of CMONOC |
|
| 图 2 MODIS PWV与GNSS PWV对比 Fig. 2 Comparison between MODIS PWV and GNSS PWV |
从图 2可以看出MODIS PWV与GNSS PWV之间具有较好的相关性,且两者的演变趋势较为一致,这些特点为利用GNSS PWV对MODIS PWV进行校正提供了基础。
由于我国具有多种气候类型,每种气候类型之间降水差异较大,另外,我国的降水具有明显的季节性,因此,需要对数据进行分类。表 1为按照气候类型以及季节划分之后的MODIS PWV与GNSS PWV的相关性统计,表 2为两者之间的平均偏差和均方根误差统计。表 1中的各气候类型的样本数计算如下:首先统计2016年各站点GNSS PWV与MODIS PWV的对应个数获得站点样本数,然后将各气候类型包含站点的样本数相加获得各气候类型的样本数。对于4个季节的样本数,就是分别求出各季节GNSS PWV与其对应的MODIS PWV序列的对应个数,然后将各气候类型包含站点的季节样本数相加获得各气候类型的季节样本数。
| 数据时间 | 高原山地 | 热带季风 | 温带大陆 | 温带季风 | 亚热带季风 |
| 全年相关性 | 0.654 | 0.143 | 0.662 | 0.776 | 0.530 |
| 样本数 | 5045 | 760 | 21 834 | 11 976 | 15 355 |
| 春季相关性 | 0.373 | 0.366 | 0.452 | 0.672 | 0.402 |
| 样本数 | 1306 | 176 | 5617 | 3034 | 3558 |
| 夏季相关性 | 0.279 | -0.418 | 0.747 | 0.799 | 0.307 |
| 样本数 | 1227 | 203 | 5559 | 3036 | 3808 |
| 秋季相关性 | 0.569 | -0.221 | 0.484 | 0.74 | 0.381 |
| 样本数 | 1340 | 193 | 5585 | 3075 | 4007 |
| 冬季相关性 | 0.512 | 0.168 | 0.176 | 0.240 | 0.316 |
| 样本数 | 1172 | 188 | 5073 | 2831 | 3682 |
| mm | ||||||||||||||
| 数据时间 | 高原山地 | 热带季风 | 温带大陆 | 温带季风 | 亚热带季风 | |||||||||
| 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | |||||
| 全年 | -1.83 | 6.01 | -9.98 | 20.9 | -1.43 | 3.74 | -2.09 | 5.85 | -7.96 | 16.07 | ||||
| 春季 | -1.67 | 3.32 | -5.15 | 17.22 | -0.94 | 2.91 | -2.45 | 3.66 | -7.39 | 12.44 | ||||
| 夏季 | -4.11 | 8.23 | -13.33 | 25.74 | -2.34 | 6.58 | -0.97 | 8.97 | -13.31 | 22.78 | ||||
| 秋季 | -1.41 | 4.74 | -14.13 | 22.81 | -1.41 | 3.44 | -2.25 | 5.06 | -8.39 | 14.66 | ||||
| 冬季 | -0.11 | 1.39 | -6.63 | 13.78 | -0.98 | 1.96 | -2.75 | 2.98 | -2.55 | 6.14 | ||||
由表 1可以看出MODIS PWV与GNSS PWV具有较好的相关性,除热带季风气候区域外,在其他气候区域两者的全年相关性超过了0.5。高原山地全年的相关性优于4个季节的相关性,其原因在于:MODIS PWV与GNSS PWV分季节的相关性低的原因在于短期小起伏不匹配影响了两者的相关性,而全年的相关性更好的原因是短期小起伏不匹配对于一年的时间尺度来说其影响较小,因此两者的全年相关性优于分季节相关性。高原山地气候类型GNSS PWV与MODIS PWV在夏季的相关性明显低于其他3个季节,热带季风气候类型的GNSS PWV与MODIS PWV在夏、秋两个季节的相关性不同于全年和其他两个季节的相关性,相关性为负,这是因为该区域降水主要集中于夏季和秋季,而降水发生前的云层较厚影响了MODIS PWV精度。
由表 2可知,MODIS PWV与GNSS PWV之间存在一些偏差,因高原山地、温带大陆和温带季风气候类型区域的PWV值较小,MODIS PWV与GNSS PWV的偏差与均方根误差相对较小,为10 mm以内。热带季风和亚热带季风区域全年的PWV值较大且波动较大,降水过程多,因此这两个区域MODIS PWV与GNSS PWV的偏差与均方根误差较大,超过10 mm,部分季节超过了20 mm。
通过MODIS PWV与GNSS PWV的误差统计分析,说明MODIS PWV精度不高,有必要进行校正;而MODIS PWV与GNSS PWV的相关性分析,说明可利用GNSS PWV开展MODIS PWV校正研究。
2.2 MODIS PWV校正模型对MODIS PWV校正时,以年、季节两个尺度进行模型构建。其中季节划分是以3—5月为春季;6—8月为夏季;9—11月为秋季;12至次年2月为冬季。模型建立好之后对模型进行精度评定,分别对5个气候类型的MODIS PWV进行两个尺度的校正与建模,模型的一般表达式为
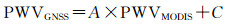 (1)
(1)
式中,PWVGNSS为GNSS PWV;PWVMODIS为MODIS PWV;A为模型系数;C为常数。为了兼顾模型构建所需样本数较多以及检验样本充分,本文选择80%样本数据用于模型构建,20%样本数据用于模型验证,数据选择为随机选取。表 3为MODIS PWV校正模型中各项参数的统计。
| 气候类型 | 季节 | 常数项 | 模型系数 | R2 |
| 高原山地 | 全年 | 4.199 | 0.732 | 0.382 |
| 春季 | 3.25 | 0.484 | 0.135 | |
| 夏季 | 12.934 | 0.243 | 0.060 | |
| 秋季 | 4.583 | 0.619 | 0.225 | |
| 冬季 | 0.797 | 0.683 | 0.309 | |
| 热带季风 | 全年 | 39.773 | 0.089 | 0.020 |
| 春季 | 27.4 | 0.188 | 0.128 | |
| 夏季 | 53.996 | -0.084 | 0.097 | |
| 秋季 | 51.836 | -0.151 | 0.108 | |
| 冬季 | 25.21 | 0.181 | 0.053 | |
| 温带大陆 | 全年 | 2.873 | 0.743 | 0.456 |
| 春季 | 2.570 | 0.393 | 0.133 | |
| 夏季 | 3.439 | 0.797 | 0.550 | |
| 秋季 | 3.821 | 0.536 | 0.244 | |
| 冬季 | 4.098 | 0.141 | 0.039 | |
| 温带季风 | 全年 | 2.599 | 0.752 | 0.612 |
| 春季 | 3.001 | 0.645 | 0.437 | |
| 夏季 | 2.041 | 0.768 | 0.629 | |
| 秋季 | 2.859 | 0.724 | 0.548 | |
| 冬季 | 3.248 | 0.275 | 0.064 | |
| 亚热带季风 | 全年 | 16.266 | 0.549 | 0.300 |
| 春季 | 14.485 | 0.349 | 0.115 | |
| 夏季 | 34.905 | 0.173 | 0.073 | |
| 秋季 | 24.977 | 0.238 | 0.069 | |
| 冬季 | 7.633 | 0.326 | 0.107 |
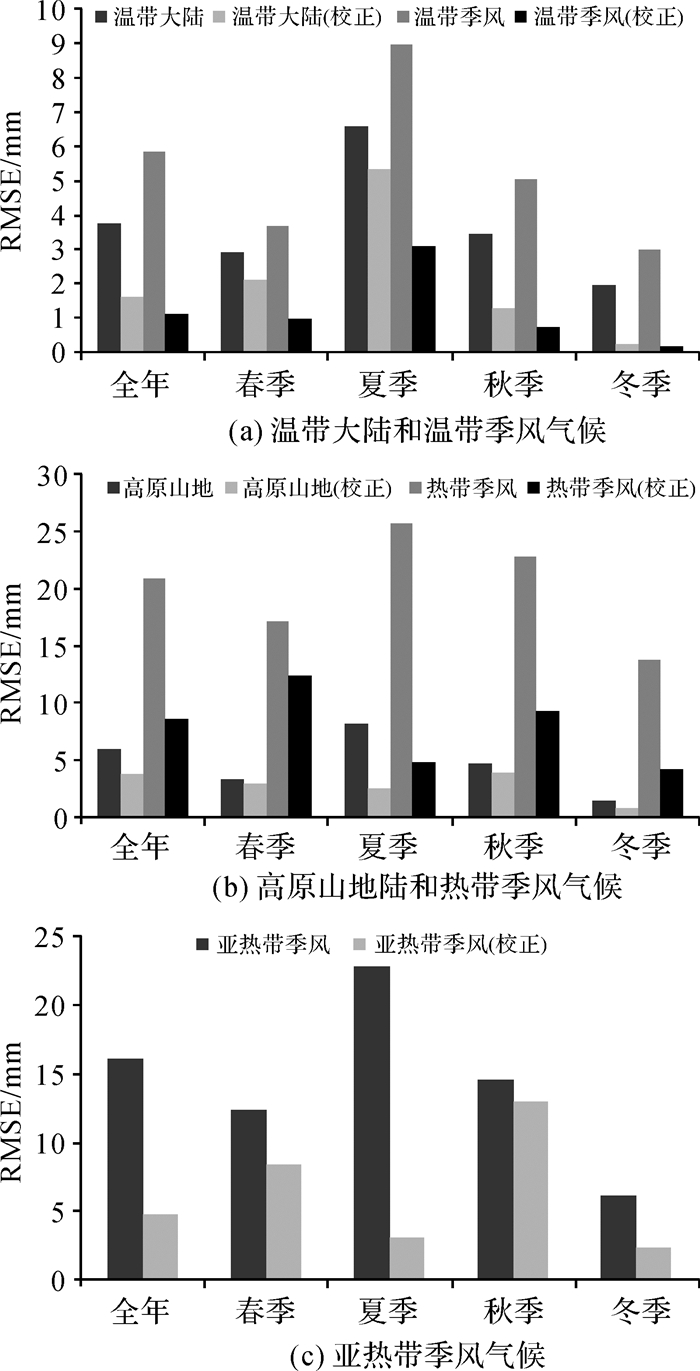
MODIS PWV校正模型构建后需要进行模型的可靠性检验,本文采用预留的20%样本进行模型的可靠性验证。表 4为对模型验证结果的平均偏差和均方根误差的统计。图 3为用直方图绘制的校正前后MODIS PWV与GNSS PWV差值的均方根误差。
| mm | ||||||||||||||
| 数据时间 | 高原山地 | 热带季风 | 温带大陆 | 温带季风 | 亚热带季风 | |||||||||
| 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | 平均偏差 | 均方根误差 | |||||
| 全年/mm | 3.55 | 3.83 | 8.51 | 8.59 | 1.09 | 1.63 | -0.25 | 1.10 | 2.81 | 4.79 | ||||
| 样本数 | 1045 | 61 | 3835 | 2977 | 5356 | |||||||||
| 春季/mm | -2.55 | 2.99 | -11.9 | 12.44 | -1.79 | 2.12 | 0.19 | 0.97 | -8.17 | 8.45 | ||||
| 样本数 | 307 | 77 | 1118 | 535 | 859 | |||||||||
| 夏季/mm | -1.62 | 2.58 | -4.33 | 4.78 | -0.84 | 5.34 | -0.07 | 3.09 | 2.41 | 3.12 | ||||
| 样本数 | 228 | 54 | 1060 | 537 | 809 | |||||||||
| 秋季/mm | 3.76 | 3.93 | 9.16 | 9.42 | 1.07 | 1.29 | 0.01 | 0.72 | 13.06 | 13.07 | ||||
| 样本数 | 341 | 44 | 1086 | 576 | 1008 | |||||||||
| 冬季/mm | -0.06 | 0.87 | -4.23 | 4.25 | -0.06 | 0.25 | -0.04 | 0.17 | -1.76 | 2.32 | ||||
| 样本数 | 173 | 49 | 1074 | 332 | 683 | |||||||||
|
| 图 3 MODIS PWV(校正前后)与GNSS PWV差值的均方根误差 Fig. 3 The RMS of the difference between MODIS PWV and GNSS PWV, and the difference between corrected MODIS PWV and GNSS PWV |
对比表 2、表 4和图 3,可知:无论哪个气候类型,全年模型的精度都低于春季、秋季,以及冬季这3个季节的模型精度,但是优于夏季模型。此外,热带季风区的夏季和秋季MODIS校正模型的模型系数表现为负数。其原因主要是夏季降水多,MODIS影像受降水以及云层影响较大,而GNSS PWV不受季节、降水等天气因素的影响,所以导致夏季的MODIS PWV精度低于其他季节,并且MODIS PWV与GNSS PWV的相关性受这些因素的影响,表现出异常性,也可以说降水的多少对模型精度有影响,降水越少,模型精度越高。此外,由于GNSS PWV的变化具有年周期、半年周期,以及更小尺度的周期,对全年数据进行建模,由于周期性质复杂,所以导致全年模型的精度低于季节模型的精度。另外,对比分析表 2、表 4和图 3,还可知:热带季风气候类型地区的MODIS PWV校正效果优于其他区域,如热带季风气候区域的全年模型均方根误差校正精度由原来的20.9 mm,达到8.59 mm,校正效果明显。
3 模型推广及验证对我国进行分区构建MODIS PWV校正模型,这极大地减少了模型数量,但是区域模型是否就能代替站点模型,还需验证。以下对区域模型用于区域内站点MODIS PWV校正的精度进行验证。如果对所有站点开展单站点模型构建并进行检验,由于CMONOC站点达260个,工作量甚大,本文篇幅限制也不容许把所有站点模型及检验结果列出,本文区域模型的检验随机选择两个站点进行。
3.1 模型推广——区域模型用于单站点检验对以上构建的区域模型进行推广,验证区域模型用于单站点的精度。对各气候类型选择2个站点进行区域模型的检验,检验之前需要构建单站点MODIS PWV校正模型,GNSS站建模的样本数和验证的样本数选取的原则参照与气候类型类似的方法,建模数据约80%,检验数据为20%,模型如表 5所示。
| 气候类型 | 站点 | 常数 | 模型系数 | R2 | 样本数 |
| 高原山地 | LHAS(拉萨) | 4.473 | 0.594 | 0.414 | 260 |
| XNIN(西宁) | 5.482 | 0.614 | 0.386 | 266 | |
| 热带季风 | HIHK(海口) | 38.926 | 0.099 | 0.026 | 230 |
| HISY(三亚) | 40.155 | 0.116 | 0.033 | 201 | |
| 温带季风 | HETS(唐山) | 8.64 | 0.607 | 0.386 | 271 |
| ZHNZ(郑州) | 10.029 | 0.638 | 0.423 | 210 | |
| 温带大陆 | XJFY(富蕴) | 5.754 | 0.541 | 0.316 | 300 |
| XIAA(西安) | 13.705 | 0.494 | 0.358 | 250 | |
| 亚热带季风 | AHBB(蚌埠) | 16.599 | 0.498 | 0.349 | 225 |
| GXNN(南宁) | 31.278 | 0.222 | 0.092 | 229 |
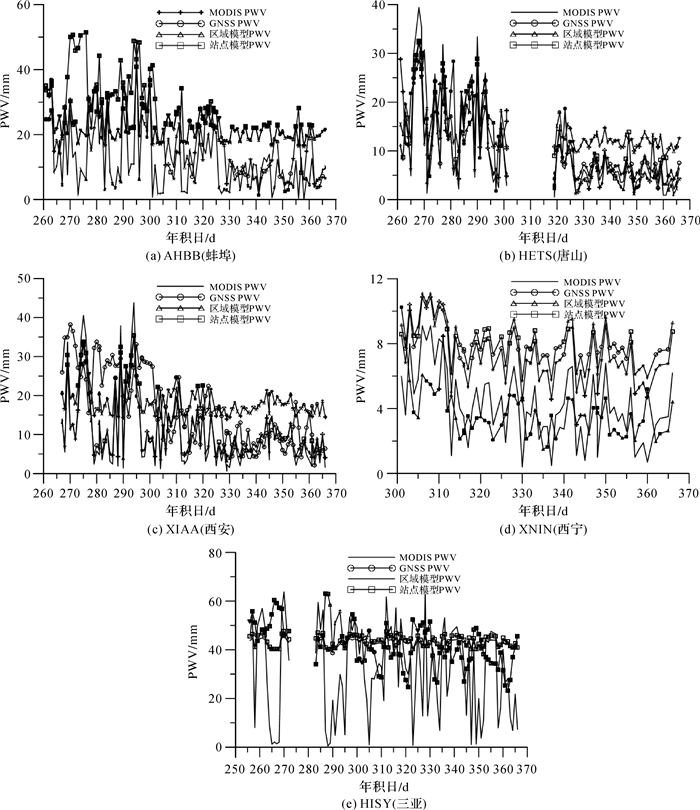
选用单站点检验数据用于单站点模型和区域模型的MODIS PWV校正,并与同时段的GNSS PWV和MODIS PWV相比较,图 4为部分单站点模型和区域模型的MODIS PWV校正值与GNSS PWV、MODIS PWV的比较。统计区域模型用于单站点校正与单站点模型直接校正的平均偏差和均方根误差(表 6)。
|
| 图 4 MODIS PWV、GNSS PWV、区域模型PWV和站点模型PWV的对比 Fig. 4 Comparison among MODIS PWV, GNSS PWV, regional model PWV, and single station model PWV |
| mm | |||||||
| 气候类型 | 站点 | 平均偏差 | 均方根误差 | 样本数 | |||
| 单点模型 | 区域模型 | 单点模型 | 区域模型 | ||||
| 高原山地 | LHAS(拉萨) | 4.75 | 4.89 | 4.62 | 4.95 | 69 | |
| XNIN(西宁) | 4.26 | 3.49 | 3.23 | 4.86 | 67 | ||
| 热带季风 | HIHK(海口) | 4.16 | 5.69 | 5.15 | 5.68 | 72 | |
| HISY(三亚) | 1.50 | 0.28 | 1.48 | 2.26 | 94 | ||
| 温带季风 | HETS(唐山) | 3.82 | -0.76 | 4.13 | 5.34 | 103 | |
| ZHNZ(郑州) | 2.37 | -4.09 | 3.03 | 5.55 | 92 | ||
| 温带大陆 | XJFY(富蕴) | 3.21 | -6.1 | 4.07 | 8.30 | 105 | |
| XIAA(西安) | 1.78 | -0.03 | 2.08 | 2.52 | 135 | ||
| 亚热带季风 | AHBB(蚌埠) | 2.35 | 2.66 | 3.88 | 4.29 | 105 | |
| GXNN(南宁) | 7.91 | 2.57 | 5.87 | 7.72 | 69 | ||
根据表 6和图 4可以得出结论:利用区域模型对单站点MODIS PWV进行校正,其模型精度与单站点模型的精度相差不大,大部分站点区域模型用于单站点MODIS PWV校正的精度可达到毫米级,某些情况下可以用区域模型代替站点模型对MODIS PWV进行校正。当对精度要求不是特别高的时候,以及站点数据不能满足要求时,可以利用区域模型对站点进行MODIS PWV的校正工作。另外,区域模型对区域内MODIS PWV校正,不需要对每个站点都单独进行校正工作,这大大减少了人力与物力。
3.2 MODIS PWV校正模型精度评定MODIS PWV是面状连续的,上文对MODIS PWV的校正是基于点状数据进行的,无法将MODIS PWV面状连续的优点利用起来,而ArcGIS软件能够通过一定的插值方法将点状数据以面状的形式显示出来。
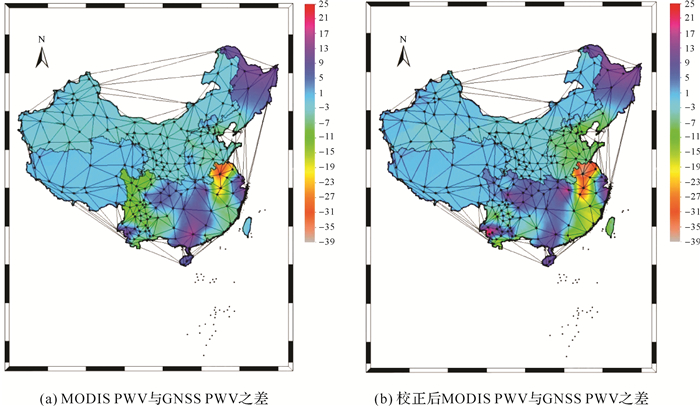
插值方法有多种,中国地形起伏差异较大,直接采用克里金或反距离加权方法插值效果不佳。Delaunay三角网的优点是结构良好,数据结构简单,与不规则的地面特征和谐一致,可表示线性特征和叠加任意形状的区域边界。本文选择区域气候模型在GNSS站点校正,然后通过采用构建Delaunay三角形,再在三角形内进行水汽内插的方式获得中国大陆地区的MODIS PWV插值结果。利用ArcGIS中的空间分析功能对插值后的图像进行作差,这样就可以得到面状的差值图,弥补前面仅对点状数据进行分析的不足,充分利用MODIS PWV的面状优势。图 5为2016年11月24日UTC 03:40时刻的GNSS PWV、MODIS PWV,以及校正后MODIS PWV之间的差值图。
|
| 图 5 GNSS PWV、MODIS PWV,以及校正后MODIS PWV之间的差值 Fig. 5 Difference diagram among GNSS PWV, MODIS PWV and the calibration-PWV of MODIS |
由图 5可知:亚热带季风气候、温带季风气候的MODIS PWV校正后效果优于校正前精度,温带大陆性气候、高原山地气候和热带季风气候校正前后的差异不显著。为了精确获得各类型气候的校正效果,对各气候区所有GNSS站点校正前后的MODIS PWV与GNSS PWV之差,分别统计校正前后的平均偏差和均方根误差(表 7)。
| mm | ||||||
| 高原山地 | 热带季风 | 温带大陆 | 温带季风 | 亚热带季风 | ||
| 均方根误差 | 校正前 | 0.13 | -5.49 | -0.71 | -2.53 | -6.63 |
| 校正后 | 3.55 | 8.51 | 1.09 | -0.25 | 2.81 | |
| 平均偏差 | 校正前 | 3.54 | 11.88 | 2.11 | 3.27 | 11.46 |
| 校正后 | 1.34 | 8.51 | 1.63 | 1.11 | 4.79 | |
由表 7可知:从平均偏差来看,各气候类型校正后的MODIS PWV优于校正前MODIS PWV;就均方根误差而言,对于亚热带季风和温带季风气候类型来说,校正后效果优于校正前,温带大陆气候校正前后相当,高原山地和热带季风气候校正后效果低于校正前。原因分析如下:因选择的数据时间为2016年11月24日,处于秋末冬初季节,高原山地和温带大陆气候区域的水汽值较低,水汽值低于10 mm,水汽变化小,校正效果较差。而温带季风气候和亚热带季风气候水汽值相对较高,因此校正效果明显。热带季风气候水汽值虽高,由于该区域站点较少,改善效果欠佳。
4 结论本文通过对CMONOC的GNSS资料处理、分析,然后利用GNSS PWV对MODIS PWV进行校正,并结合气象学等多学科,开展了MODIS PWV校正研究,得出了以下结论:利用GNSS PWV对MODIS PWV进行校正,区域模型和站点模型的校正后精度均能够达到毫米级,达到了气象业务应用的要求;利用区域模型对单站点MODIS PWV进行校正,其模型精度与单站点模型的精度相差不大,区域模型用于单站点PWV校正时大部分站点的精度可达到毫米级,某些情况下可以用区域模型代替单站点模型对MODIS PWV进行校正;利用Delaunay三角网插值分析,可以将校正后的点状数据扩展为面状数据,插值结果可以对气象预报起到一定的参考作用。
鉴于热带季风气候地区MODIS PWV与GNSS PWV的相关性低,为提高模型精度,可选用其他更合适的函数关系来构建基于GNSS的MODIS PWV校正模型。利用模型校正的MODIS PWV用于获取全国MODIS PWV变化图时,为保证精度,插值需要考虑温度、气压、地形等因素对该地区PWV变化的影响。
致谢: 感谢中国大陆构造环境监测网络中心为本文研究提供GMONOC站点GNSS观测数据和气象数据!
| [1] | DI PIAZZA A, LO CONTI F, NOTO L V, et al. Comparative analysis of different techniques for spatial interpolation of rainfall data to create a serially complete monthly time series of precipitation for Sicily, Italy[J]. International Journal of Applied Earth Observation and Geoinformation, 2011, 13(3): 396–408. DOI:10.1016/j.jag.2011.01.005 |
| [2] | NELSON R R, CRISP D, OTT L E, et al. High-accuracy measurements of total column water vapor from the Orbiting Carbon Observatory-2[J]. Geophysical Research Letters, 2016, 43(23): 12261–12269. DOI:10.1002/2016GL071200 |
| [3] | JI Dabin, SHI Jiancheng, XIONG Chuan, et al. A total precipitable water retrieval method over land using the combination of passive microwave and optical remote sensing[J]. Remote Sensing of Environment, 2017, 191(3): 313–327. |
| [4] |
王勇, 刘严萍.
地基GPS气象学原理与应用研究[M]. 北京: 测绘出版社, 2012.
WANG Yong, LIU Yanping. Theory and application of ground-based GPS meteorology[M]. Beijing: Surveying and Mapping Press, 2012. |
| [5] |
鄢子平, 李振洪.
InSAR大气水汽改正模型的比较应用研究[J]. 武汉大学学报(信息科学版), 2008, 33(7): 723–726.
YAN Ziping, LI Zhenhong. Comparison of atmospheric water vapour correction models for InSAR measurements[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 723–726. |
| [6] |
常亮, 郭立新, 冯贵平.
MODIS红外水汽校正及其在InSAR大气改正中的应用[J]. 大地测量与地球动力学, 2016, 36(1): 47–51.
CHANG Liang, GUO Lixin, FENG Guiping. Calibration of MODIS water vapor product at infrared band and its application to InSAR atmospheric correction[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 47–51. |
| [7] |
王江涛, 邓喀中, 范洪冬, 等.
基于MODIS与GPS的D-InSAR大气延迟改正量提取[J]. 测绘科学技术学报, 2012, 29(4): 271–275.
WANG Jiangtao, DENG Kazhong, FAN Hongdong, et al. Extraction of D-InSAR atmospheric delay correction based on MODIS and GPS[J]. Journal of Geomatics Science and Technology, 2012, 29(4): 271–275. DOI:10.3969/j.issn.1673-6338.2012.04.009 |
| [8] |
陈娇娜, 李国平, 黄文诗.
成都地区秋、冬季GPS可降水量的时空分析[J]. 气象科学, 2009, 29(5): 682–686.
CHEN Jiaona, LI Guoping, HUANG Wenshi. On the spatial-temporal analysis of GPS precipitable water vapor in Autumn and Winter in Chengdu Plain[J]. Scientia Meteorologica Sinica, 2009, 29(5): 682–686. DOI:10.3969/j.issn.1009-0827.2009.05.019 |
| [9] |
王永前, 施建成, 刘志红, 等.
利用微波辐射计AMSR-E的京津冀地区大气水汽反演[J]. 武汉大学学报(信息科学版), 2015, 40(4): 479–486.
WANG Yongqian, SHI Jiancheng, LIU Zhihong, et al. Passive microwave remote sensing of precipitable water vapor over Beijing-Tianjin-Hebei region based on AMSR-E[J]. Geomatics and Information Science of Wuhan University, 2015, 40(4): 479–486. |
| [10] |
许超钤, 史俊波, 郭际明, 等.
联合地基GPS和空基COSMIC掩星的可降水量研究[J]. 武汉大学学报(信息科学版), 2011, 36(4): 467–470.
XU Chaoqian, SHI Junbo, GUO Jiming, et al. Analysis of combining ground-based GPS network and space-based COSMIC occultation observation for precipitable water vapor application[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 467–470. |
| [11] |
姚宜斌, 张顺, 孔建.
GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1408–1420.
YAO Yibin, ZHANG Shun, KONG Jian. Research progress and prospect of GNSS space environment science[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1408–1420. DOI:10.11947/j.AGCS.2017.20170333 |
| [12] |
于胜杰, 柳林涛, 梁星辉.
约束条件对GPS水汽层析解算的影响分析[J]. 测绘学报, 2010, 39(5): 491–496.
YU Shengjie, LIU Lintao, LIANG Xinghui. Influence analysis of constraint conditions on GPS water vapor tomography[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 491–496. |
| [13] | SINGH D, GHOSH J K, KASHYAP D. Precipitable water vapor estimation in India from GPS-derived zenith delays using radiosonde data[J]. Meteorology and Atmospheric Physics, 2014, 123(3-4): 209–220. DOI:10.1007/s00703-013-0293-1 |
| [14] |
李星光, 郑南山.
参数设置对高精度GPS数据解算的影响探讨[J]. 测绘科学, 2015, 40(1): 33–37, 51.
LI Xingguang, ZHENG Nanshan. Discussion on effects of different parameter settings on high-precise GPS data solution[J]. Science of Surveying and Mapping, 2015, 40(1): 33–37, 51. |
| [15] | YAO Yibin, SHAN Lulu, ZHAO Qingzhi. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application[J]. Scientific Reports, 2017, 7(1): 12465. DOI:10.1038/s41598-017-12593-z |
| [16] | WANG Yong, LIU Yanping, LIU Lintao, et al. Retrieval of the change of precipitable water vapor with zenith tropospheric delay in the Chinese Mainland[J]. Advances in Space Research, 2009, 43(1): 82–88. DOI:10.1016/j.asr.2007.07.050 |
| [17] |
张天龙, 韦晶, 甘敬民, 等.
利用MODIS近红外数据反演大气水汽含量研究[J]. 光谱学与光谱分析, 2016, 36(8): 2378–2383.
ZHANG Tianlong, WEI Jing, GAN Jingmin, et al. Precipitable water vapor retrieval with MODIS near infrared data[J]. Spectroscopy and Spectral Analysis, 2016, 36(8): 2378–2383. |
| [18] | GURBUZ G, JIN Shuanggen. Long-time variations of precipitable water vapour estimated from GPS, MODIS and radiosonde observations in Turkey[J]. International Journal of Climatology, 2017, 37(15): 5170–5180. DOI:10.1002/joc.5153 |
| [19] | DE OLIVEIRA G, BRUNSELL N A, MORAES E C, et al. Evaluation of MODIS-based estimates of water-use efficiency in Amazonia[J]. International Journal of Remote Sensing, 2017, 38(19): 5291–5309. DOI:10.1080/01431161.2017.1339924 |
| [20] | GUI Ke, CHE Huizheng, CHEN Quanliang, et al. Evaluation of radiosonde, MODIS-NIR-clear, and AERONET precipitable water vapor using IGS ground-based GPS measurements over China[J]. Atmospheric Research, 2017, 197(11): 461–473. |
| [21] |
方圣辉, 毕创, 乐源, 等.
利用GPS可降水量校正MODIS近红外水汽数据[J]. 测绘科学, 2016, 41(9): 38–41.
FANG Shenghui, BI Chuang, LE Yuan, et al. Calibration of MODIS near infrared vapor products using precipitable water vapor retrieved from GPS data[J]. Science of Surveying and Mapping, 2016, 41(9): 38–41. |
| [22] |
张俊东, 陈秀万, 李颖, 等.
基于GPS数据的MODIS近红外水汽改进反演算法研究[J]. 地理与地理信息科学, 2013, 29(2): 40–44.
ZHANG Jundong, CHEN Xiuwan, LI Ying, et al. Research on improved retrieval algorithm of MODIS near-IR water vapor based on GPS data[J]. Geography and Geo-Information Science, 2013, 29(2): 40–44. |
| [23] |
曹艳丰, 陈宝献, 陈秀万, 等.
基于GPS数据的MODIS大气可降水量反演精度提高模型[J]. 遥感信息, 2014, 29(2): 23–27.
CAO Yanfeng, CHEN Baoxian, CHEN Xiuwan, et al. A real-time accuracy model of MODIS PWV using GPS PWV Data[J]. Remote Sensing Information, 2014, 29(2): 23–27. DOI:10.3969/j.issn.1000-3177.2014.02.004 |
| [24] |
王西地.基于GPS和MODIS数据的大气可降水量算法研究[D].南京: 东南大学, 2017. WANG Xidi. Research on precipitable water vapor based on GPS and MODIS data[D]. Nanjing: Southeast University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10286-1018005753.htm |
| [25] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS meteorology:remote sensing of atmospheric water vapor using the global positioning system[J]. Journal of Geophysical Research, 1992, 97(D14): 15787–15801. DOI:10.1029/92JD01517 |



