2. 中南大学地理信息系, 湖南 长沙 410083
2. Department of Geo-Informatics, Central South University, Changsha 410083, China
现实世界中的地理现象经常表现为伴生关系,例如:生态领域中植被之间的共生关系(如湿地植物群落间生态位的重叠[1])、犯罪地理学中地理环境(或设施)与犯罪间的诱导关系(如酒精售卖点附近高犯罪率问题[2])以及城市规划中不同类型兴趣点之间在产业布局上的依赖关系(如学校与便利店的聚集关系[3])。此类频繁发生在邻近位置的事件集合通常被定义为空间同位模式(本文特指事件间均满足互邻近关系的团型同位模式[4])。发现空间同位模式对于深入理解空间要素间的交互关系具有重要意义,已经广泛应用于生态学、犯罪学、城市规划、交通运输等诸多领域。
当前空间同位模式挖掘方法主要包含两个步骤[5]:①构建空间要素实例的空间邻域关系,生成候选空间同位模式实例;②计算候选空间同位模式的频繁度(如参与指数[5]),并提取频繁度超过给定阈值的空间同位模式及其分布区域。针对步骤①,当前研究主要采用基于距离的策略(给定距离阈值约束下,一个空间要素实例的邻域定义为与其距离小于该阈值的其他空间要素实例的集合)构建邻域关系,并采用实例连接的方法生成候选模式实例。为了提高候选模式实例生成的效率,一些改进实例连接的方法被相继提出,如部分连接[6]、无连接[7]及基于密度的方法[8]等。针对步骤②,一些学者相继针对同位模式频繁度的度量、阈值定义及局部同位模式识别开展研究。例如,为了量化空间同位模式实例间距离对频繁度度量的影响,文献[3]在参与指数基础上考虑距离衰减定义了加权参与指数;为了缓解参与指数阈值设定的困难,文献[9]采取参与指数进行排序的方法选取N个最显著的同位模式;文献[10]假定所有同位模式参与指数服从正态分布,提出一种用迭代方法逐步挖掘相对显著的空间同位模式来缓解距离阈值和参与指数设定的困难;文献[11-12]借助统计检验的方法挖掘显著同位模式,降低了参与指数阈值设定的主观性。为了识别局部空间同位模式,一些基于区域划分[13-15]与实例聚类分析[16-17]的方法被相继提出。从空间同位模式的挖掘流程可以发现,空间要素实例的邻域关系构建起到了基础性的作用,尤其当空间要素的实例分布不均匀时,邻域关系构建的准确性对挖掘结果具有直接影响:
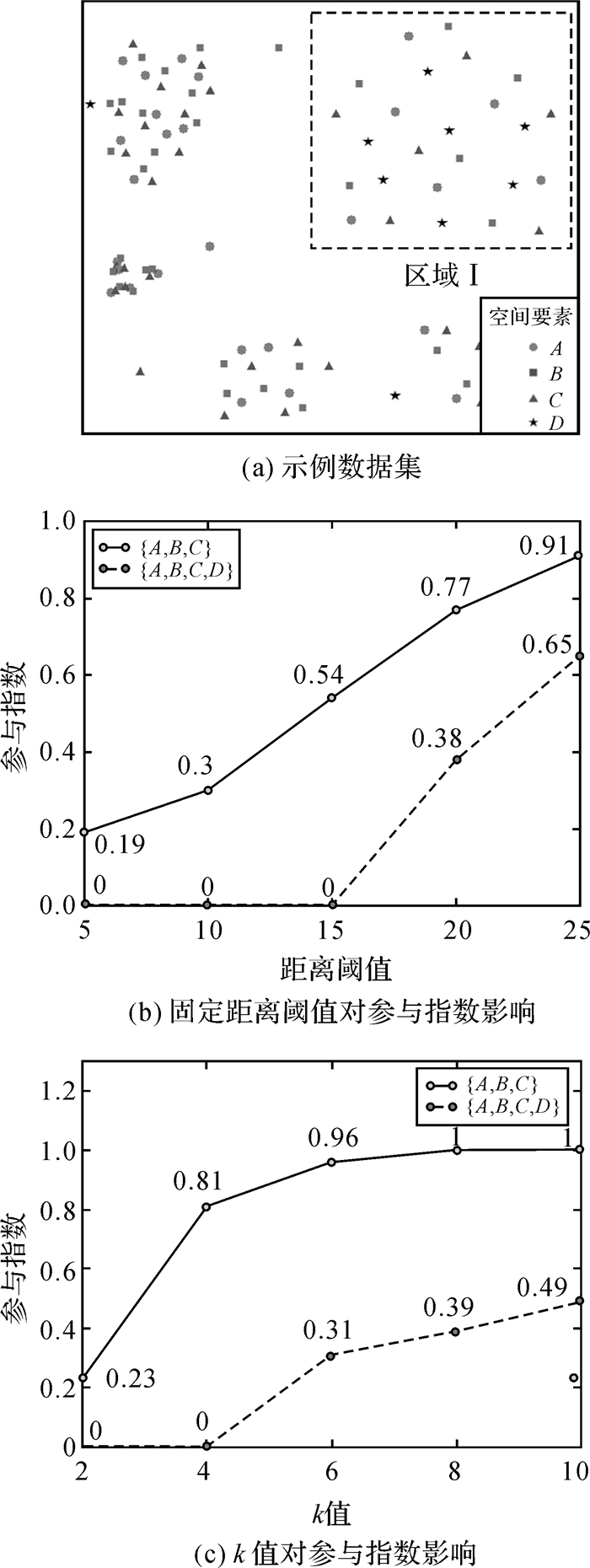
(1) 错误的邻域关系会影响实例生成的准确性(过多或过少的构建实例),进而影响空间同位模式频繁度度量的准确性,最终导致关联模式的误报或遗漏。以图 1(a)为例,一个包含4类空间要素的示例数据集中包含多个密度不一的区域,数据集中预设了一个全局同位模式{A, B, C}和一个局部同位模式{A, B, C, D}(位于区域Ⅰ)。如图 1(b)所示,当距离阈值过小时,低密度区域实例无法生成,导致参与指数偏小({A, B, C}无法发现);当距离阈值过大时,高密度区域生成过多错误实例,导致参与指数过高估计({A, B, C, D}错误识别为全局模式)。
|
| 图 1 示例数据集 Fig. 1 Simulated data set |
(2) 当前局部同位模式提取大多采用对候选实例聚类的策略识别同位模式的分布区域[16],邻域关系构建不准确也会造成局部关联模式的误报或遗漏。例如,采用文献[16-17]方法发现图 1(a)中的局部关联模式时,采用距离阈值过小时,低密度区域的实例无法生成,局部模式{A, B, C, D}无法发现或误报。
为了提高空间要素实例邻域关系构建的准确性,一些学者也开展了一些探索性的工作:
(1) 基于空间统计的方法,即利用某种空间统计的方法(如空间自相关)估计一个全局最优的距离阈值[9]。然而,该方法虽然避免了用户对距离阈值的设定,但是全局统一的距离阈值无法在空间要素分布不均匀时建立正确的空间邻域关系。采用文献[9]中基于空间自相关方法对示例数据集估计的距离阈值为13.02,在此距离阈值下,区域Ⅰ中的实例无法生成,计算模式{A, B, C}参与指数为0.4(低估),同位模式{A, B, C, D}参与指数为0(遗漏)。
(2) 基于k近邻的空间邻域关系构建策略,即一个空间要素实例的邻域是与其最邻近的k个其他类型空间要素实例的集合[10, 13, 18]。然而,k值的变化仍然对同位模式挖掘结果有较大影响,随着k值增大,错误的实例增多(包含了噪声点),导致参与指数被过高估计(图 1(c))。
(3) 基于邻近图的空间邻域关系构建策略,即在所有要素实例构建的邻近图中(如Delaunay三角网),一个空间要素实例的邻域是在邻近图中与其存在邻近关系的其他空间要素实例集合[19-20]。基于邻近图所构建的空间邻域关系往往受限于所选邻域图的特性,例如,空间同位模式中要素实例间需要满足互邻近关系,而基于Delaunay三角网所构建的空间邻域关系中互为邻域的空间要素实例最多为3个,导致了无法挖掘长度超过3的同位模式[19]。此外,邻近图的边界误差也容易导致不同密度区域的实例存在错误的邻域关系。
为了克服邻域关系构建对空间同位模式挖掘准确性和完整性的影响,本文依据数据本身的分布特征自适应地构建空间要素实例间的邻域关系(即自然邻域),并在自然邻域支持下自适应发现由整体到局部的空间同位模式,降低人为设置邻域参数(如邻域距离阈值、邻居数目)与数据实际分布不符合而带来的挖掘误差。
1 研究策略空间同位模式本质上来源于地理现象间自相关结构的互相诱导关系(induced spatial autocorrelation),即某个(些)空间要素的自相关结构是受到其他具有自相关结构要素的影响而产生[21]。空间同位模式的挖掘结果可能有两种形式[22]:①空间要素的空间自相关是由其他空间要素的自相关结构诱发的;②空间要素的空间自相关是由某些未知要素诱导产生的。本文对这两种形式的同位模式不进行区分。采用频繁度度量指标(如参与指数)探测同位模式时,随机分布的空间要素之间或随机分布与聚集分布要素之间的频繁度也会较高,但是这类由于随机分布要素导致的同位模式并没有地理含义,通常被视为虚假的同位模式[12, 23]。基于上述分析,在发现同位模式时首先需要排除随机分布空间要素的干扰,本文采用最邻近指数法[24]识别随机分布的空间要素。
进而,仅针对呈现聚集分布的空间要素挖掘同位模式,分别针对每种候选同位模式建立邻域关系。本文认为空间要素实例间自然的邻近关系需要满足3个基本条件:
(1) 距离邻近性约束:随着两个空间要素实例间的距离增大,两者之间关联紧密性随之降低。因此空间要素实例与其邻域间距离应小于一定范围。
(2) 密度一致性约束:在空间邻域内空间要素实例的密度应尽量保持一致,密度的显著变化预示邻域关系的破坏。
(3) 关系紧密性约束:由社交网络中好友关系的亲密性度量可知,两个关系紧密的空间邻居需要互为邻居且应包含公共邻居。
基于上述分析,自然邻域可以定义为依据空间要素局部分布特征(即距离邻近性、密度一致性与关系紧密性)而构建的空间要素间的邻近关系。自然邻域旨在自适应地构建要素实例间的邻近关系,避免在密度较稀疏区域同位模式实例构建的遗漏,以及在密度较高区域同位模式实例构建的冗余,且降低人为设置邻域参数阈值对模式实例生成的干扰,保证同位模式实例生成的准确性。
针对每种候选同位模式,采用自然邻域构建其模式实例,并采用频繁度度量指标(如参与指数指标)对候选模式进行频繁性度量。对于全局不频繁的候选模式,可以进一步借助邻近图(如Delaunay三角网)描述其模式实例间的连通性,发现局部区域的同位模式。
基于上述研究策略,下面将对空间自然邻域构建与同位模式分布区域自适应提取方法进行具体阐述。
2 空间自然邻域构建依据空间要素实例间自然邻近关系评价的3条原则,本文首先提出了自然邻域的构建方法。
2.1 基于Delaunay三角网的距离邻近性约束估计如上文所述,每一个空间要素实例存在一定的邻域范围,即邻域上限距离,处于该距离范围内的其他空间要素实例构成了当前空间要素实例的潜在邻域。本文首先借助Delaunay三角网对邻域距离上限进行估计。Delaunay三角网可以一定程度上反映要素实例间的邻近关系,其中一些过长的边(如图 2(a)所示,不同密度区域间的边,如实例15和51;噪声实例之间的边,如实例5和90)通常预示着邻近关系的破坏,借助边长的统计规律识别的长边阈值可以用于估计邻域上限距离。给定包含n个空间要素实例的空间数据集SDB,DT表示依据n个空间要素实例的空间位置所构建的Delaunay三角网的边长集合,针对任一的空间要素实例p,其邻域上限距离估计值limitp表达如下
 (1)
(1)

|
| 图 2 距离邻近性约束示例 Fig. 2 Spatial proximity constraint |
式中,mean(DT)表示边长集合DT的均值;SD(DT)表示边长集合DT的标准差。在邻域上限距离约束下,进一步给出候选邻域的定义:
定义1 候选邻域:针对每个空间要素的实例p,在其邻域上限距离内的所有要素实例依据与p的距离大小升序排列,定义为p的候选邻域集合,记为CN(p)。
要素实例p的候选邻域表示了其空间邻域的最大可能范围,对候选邻域内实例按照与p的距离进行排序可以对邻近关系的紧密度进行度量,也决定了后续对候选邻域集合进行筛选的先后次序,即先从与p距离近的要素实例进行搜索。下面以图 1中的示例数据为例,对候选邻域的构建进行阐述。图 2(a)和(b)中分别展示了示例数据集与区域Ⅰ构建的Delaunay三角网,邻域上限距离如图 2(a)中圆所示。实例1(高密度区域)的候选邻域集合为{25, 8, 12, 2, 27, 9, 26, 13, 28, 4, 11, 29, 14, 10, 3, 62},实例7(低密度区域)的候选邻域集合为{23, 22, 20, 75, 6, 17, 21, 74, 16, 15, 19},实例90(噪声)的候选邻域集合为{3, 10, 14, 29, 96, 28, 9, 11, 2}。
2.2 基于局部密度变异的密度一致性约束在每个要素实例p的候选邻域中进一步依据密度一致性原则进行筛选。p依次与其候选邻域内要素实例CNi(p)连接,并统计落入以p和CNi(p)间距离为直径的圆中的其他空间要素实例个数ni。若空间要素实例p与候选邻域集合中实例处于同一密度区域时,则ni应该保持不变或者处于增加的状态,当ni下降时,则可能预示了两种情况[25]:
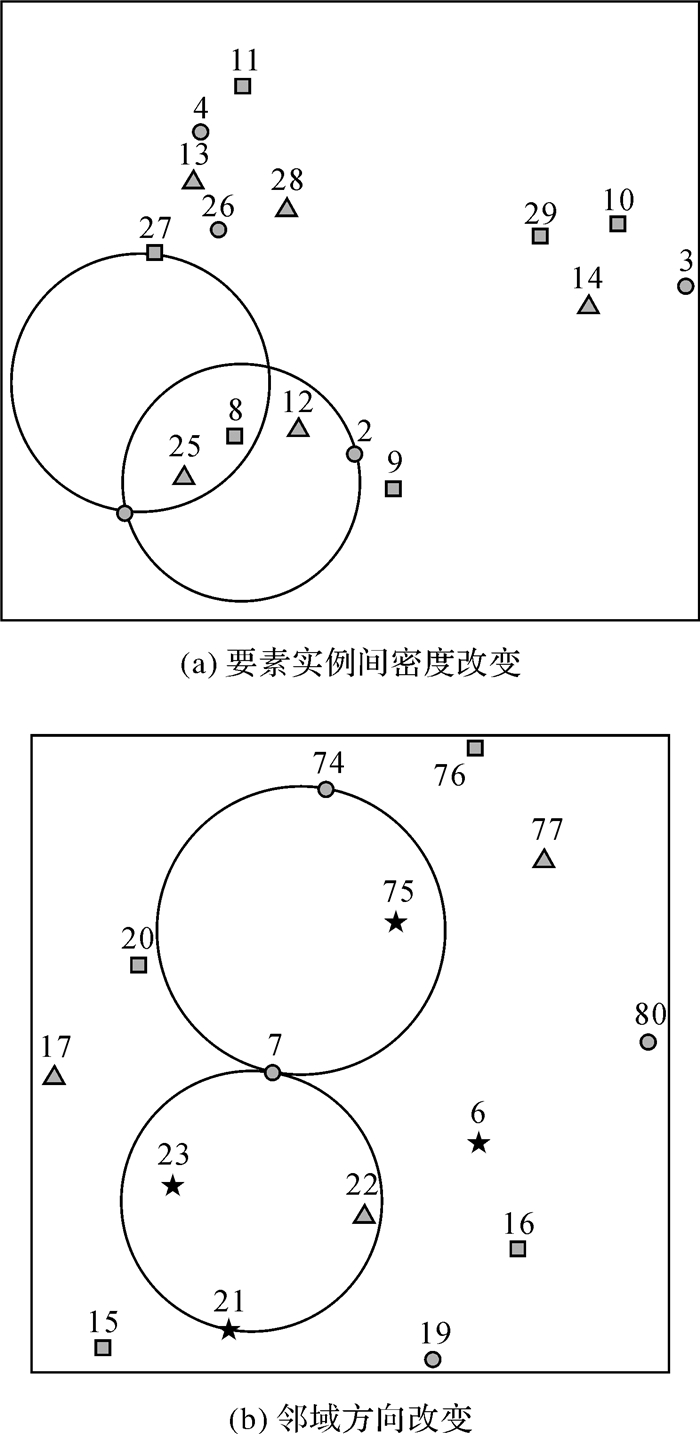
(1) 空间要素实例与其候选邻域集合内实例处于不同的密度区域,如图 3(a)所示。以实例1和2为直径的圆中包含3个实例,而以1和27为直径的圆中包含2个实例,27表示了局部区域密度下降的位置,实例1与实例27处于不同的密度区域;
|
| 图 3 实例间密度变化 Fig. 3 Density between instances |
(2) 空间要素实例与其候选邻域集合内实例处于同一密度区域但邻域方向改变,如图 3(b)所示。以实例7和21为直径的圆中包含2个实例,而以7和74为直径的圆中包含1个实例,虽然圆中包含实例数目下降,但是实例7与实例74处于同一密度区域,实例21和74表示了实例7在不同方向的邻域实体。
本文针对上面第1种情况,将位于局部区域密度下降位置的要素实例定义为密度断点(如实例27为实例1的密度断点)。为了识别密度一致的邻域,在此基础上给出密度邻域和密度一致邻域的定义:
定义2 密度邻域:针对每个空间要素的实例p,识别第1个密度断点前的所有候选邻域集合中的实例,这些实例构成p的密度邻域,记为DN(p)。
定义3 密度一致邻域:针对每个空间要素的实例p,将其密度邻域初始化为密度一致邻域,遍历p的断点,若该断点pbreak与p的密度邻域有重叠(DN(pbreak)∩DN(p)≠Φ,则将该断点与下一断点之前的候选邻域加入p的密度一致邻域中,记为HN(p),否则停止遍历。
以图 2(a)中实例7和图 2(b)中实例1为例对密度邻域与密度一致邻域构建进行阐述。以实例7与CN(7)中各个实例为直径的圆中落入实例的数目依次为{0, 0, 0, 0, 1, 1, 2, 1, 2, 2, 2},密度断点为{74},则DN(7)={23, 22, 20, 75, 6, 17, 21},实例7与实例74(DN(74)={75, 76, 77})密度邻域存在重叠(两者处于相同密度区域),得HN(7)={23, 22, 20, 75, 6, 17, 21, 74, 16, 15, 19}。以实例1与CN(1)中各个要素为直径的圆中落入实例的数目依次为{0, 1, 2, 3, 2, 4, 4, 5, 5, 7, 8, 9, 8, 11, 11, 1},密度断点为{27, 14, 62},得DN(1)={25, 8, 12, 2},由于实例1与实例27(DN(27)={26, 13, 4, 28, 11})密度邻域不重叠(两者处于不同的密度区域),得HN(1)={25, 8, 12, 2}。
2.3 基于共享邻近的关系紧密性约束在密度一致邻域内,进一步对要素实例间的关系紧密性进行约束。本文受到社交网络(如微信)中好友关系的亲密度评价的启发对要素实例间的关系紧密度进行度量。在社交网络中两个关系紧密的用户需要同时满足两个条件:①两人互为好友;②两人具有公共好友。据此,本文定义了判断两个要素实例间关系紧密性的两个约束条件;
(1) 互邻域约束条件:两个要素实例同时包含在二者的密度扩展邻域内;
(2) 共享邻居约束条件:两个要素实例的密度扩展邻域有重叠。
在上述两个约束条件的约束下,进一步给出自然邻域的定义:
定义4 自然邻域:针对每个空间要素的实例p,遍历其密度一致邻域中的要素实例qi,若p与qi互为密度一致邻域且拥有共同密度一致邻域(p∈HN(qi),qi∈HN(p)且HN(p)∩HN(qi)≠Φ),则将qi加入p的自然邻域中,记为NN(p),否则停止遍历。
以图 2(a)中实例7、实例90和图 2(b)中实例1为例对自然邻域的构建进行阐述。空间要素实例1与HN(1)中要素均满足互邻域约束条件和共享邻居约束条件,得NN(1)={25, 8, 12, 2};实例7与实例74(HN(74)={75, 76, 77})不满足互邻域约束条件,得NN(7)={23, 22, 20, 75, 6, 17, 21};实例90与实例3(HN(90)={3, 10, 14, 29},HN(3)={10, 14, 29, 9, 2})不满足互邻域约束条件,得NN(90)=Φ,即实例90为噪声。
3 空间同位模式分布区域自适应提取要素实例间的自然邻域构建后,分别针对每种候选模式生成其实例,采用参与指数[5]对该模式的频繁度进行度量:
空间同位模式参与指数:对于长度为k的候选空间同位模式C={f1, f2, …, fk},其参与指数定义如下
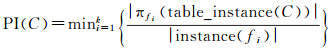 (2)
(2)
式中,|πfi(table_instance(C))|表示参与同位模式C的要素fi的实例数目;|instance(fi)|表示要素fi实例的数目。
若候选同位模式在整个研究区域内的参与指数大于给定阈值,则将该模式识别为全局同位模式。现有研究认为有效的同位模式其参与指数一般应大于0.5,因此本文将参与指数阈值设为0.5(文献[12])。若候选同位模式参与指数小于0.5(即在全局不显著),进一步借助模式实例间Delaunay三角网的连通性对候选同位模式的局部分布区域进行探测:
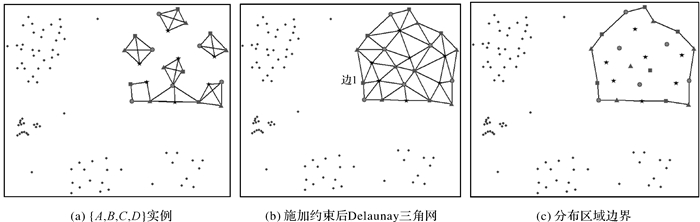
(1) 针对候选同位模式中所有要素实例构建Delaunay三角网,三角网的边可以区分为两种类型:连接候选模式要素实例的边EI(如图 4(a)所示)与连接候选模式实例之间边Eo(如图 4(b)边1所示)。从每个候选模式实例出发,若两个候选模式实例间所有边长均小于统计约束条件SC,则将两个候选模式实例进行连通,直到每个候选模式实例均与满足约束条件候选模式实例连通
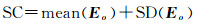 (3)
(3)
|
| 图 4 同位模式分布区域提取 Fig. 4 Discovery of localities of co-location pattern |
式中, mean(Eo)表示候选模式实例之间边长平均值;SD(Eo)表示候选模式实例之间边长的标准差。
(2) 在每个候选模式实例连通后构成的子图中,借助Delaunay三角网中三角形边长共享特性搜索候选同位模式的分布区域边界。若Delaunay三角网中边仅存在于一个唯一的三角形,则该边被识别为边界边,通过连接具有公共顶点的边界边生成候选同位模式的分布区域边界,如图 4(c)所示。
(3) 在每个候选模式分布区域内,若该候选模式的参与指数超过给定阈值且模式实例规模足够多,则将该候选模式识别为一个局部的同位模式。候选模式的实例规模度量指数SI(C)定义如下
 (4)
(4)
式中,|regional_instance(C)|表示C在相应局部区域中的实例个数;|global_instance(C)|表示C在整个研究区域中的实例个数。
4 试验分析 4.1 模拟试验与比较本文首先设计了一组模拟试验对本文方法的有效性进行验证,同时与当前3种空间同位模式RCMNG[16]、RCMKNN[13]和多层次方法[17]进行比较。本文方法需要设置参与指数阈值与实例规模度量指数阈值两个参数。依据现有研究建议,本文将参与指数阈值设为0.5(文献[12]),参考空间聚类领域对簇规模的阈值设定,本文将实例规模度量指数阈值设为0.02(文献[26])。依据文献[16]的试验分析,RCMNG方法中局部参与指数阈值设为0.07,邻域距离根据文献[9]中的L函数进行估计;依据文献[13]建议,RCMKNN方法中距离变化系数阈值设置为0.6,α参数设置为0.01;依据文献[17]建议,多层次方法距离阈值也采用L函数估计。模拟数据生成步骤如下所示:
(1) 将整个研究区域(400×400)均匀地划分为4个100×100的子区域,在每个区域随机生成数目为nseed的种子点,如图 5(a)所示(为了方便说明,仅用一个区域说明模拟数据生成过程)。

|
| 图 5 模拟数据生成 Fig. 5 Experimental setup of synthetic data sets |
(2) 每个区域内,以每个种子点为圆心,以半径rseed画圆,在每个圆内生成数目为ninstance的独立分布的实例点并移除种子点,如图 5(b)所示。
(3) 以每个实例点为圆心,以给定半径rinstance画圆,在每个圆内随机生成数目为nfeature的同位模式要素实例并移除实例点,如图 5(c)所示。
(4) 在整个研究区域内生成数目为nnoise的噪声点(分布随机且空间要素类型随机),如图 5(d)所示。
由上述模拟数据产生过程可以发现,nseed控制同位模式在某个子区域分布区域的数目,rseed控制同位模式分布区域的大小,通过修改rseed和ninstance的值,可以控制不同分布区域要素实例的密度。模拟数据均包含一个全局同位模式(分布于4个区域)和一个局部同位模式(分布于区域2和区域3)。首先将nseed和ninstance固定(区域1:nseed=4,ninstance=10;区域2:nseed=2,ninstance=10;区域3:nseed=2,ninstance=10;区域4:nseed=5,ninstance=10)。进一步分别改变rseed、nfeature和nnoise探索要素实例密度变化、同位模式长度变化及噪声数目变化对本文及对比方法影响。若挖掘结果区域和设定区域相交区域占挖掘结果区域和设定区域面积均大于50%以上时,本文认为挖掘结果是正确的。本文采用召回率和精确率作为评定算法挖掘结果的定量标准。
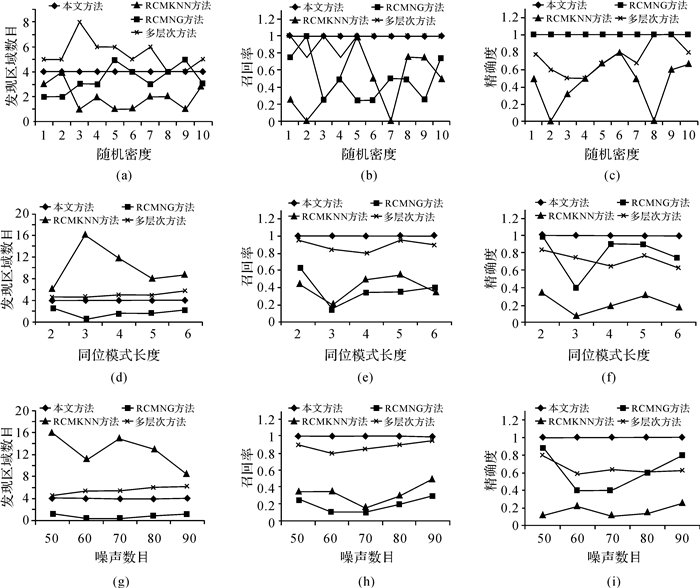
4.1.1 要素实例密度变化对挖掘结果的影响为了评估要素实例密度变化对挖掘结果的影响,首先将nnoise(50)和nfeature(区域1和区域4:nfeature=2,区域2、3:nfeature=3)取值固定,进而4个区域的rseed随机选择10次(区域1和4的rseed取值范围为10~30,区域2和3的rseed取值范围为20~50)。本文方法与对比方法的试验结果如图 6(a)-(c)所示。本文方法可以有效发现整体与局部的同位模式,而其他几种方法的挖掘结果受要素实例密度变化的干扰较大:RCMNG方法计算的局部参与指数是基于局部子图中要素实例个数与全局实例个数的比值,低密度区域或范围较小的局部同位模式的要素实例数目相对较少,导致局部参与指数计算值普遍过小,容易出现遗漏;RCMKNN方法中当要素密度变化时,邻居数目k估计的误差极易导致模式实例生成的错误,进而造成挖掘结果经常出现误判和漏判的情况;多层次方法采用全局统一的距离阈值(估计的距离为30~40,远大于本文预设的阈值(2~5)),在生成候选模式实例时存在较多错误,故挖掘结果经常出现误判。
|
| 图 6 模拟试验对比 Fig. 6 Comparison of three methods |
4.1.2 空间同位模式长度对挖掘结果的影响
为了在要素实例分布不均匀的前提下评估同位模式长度对挖掘结果的影响,首先将nnoise(50)、rseed(区域1和2:rseed=25,区域3:rseed=40,区域4:rseed=20)和rinstance(区域1和2:rinstance=5,区域3:rinstance=8,区域4:rinstance=4)取值固定,进而改变nfeature的取值进行试验。针对每个nfeature随机生成10组数据(共生成50组随机数据),挖掘结果定量评价指标取平均值。试验结果如图 6(d)-(f)所示:本文方法的挖掘结果不受模式长度的影响,均可准确识别预设的同位模式;RCMKNN方法的挖掘结果质量在不同模式长度情况下波动较大,其主要原因在于邻居数目k值的估计策略比较敏感;RCMNG与多层次方法的挖掘结果质量在不同模式长度情况下波动较小,但是RCMNG方法由于局部参与指数估计偏低导致的漏判问题以及多层次方法由于候选模式实例生成误差导致的误判问题总是存在。
4.1.3 噪声数量对挖掘结果的影响为了在要素实例分布不均匀的前提下评估噪声数量对挖掘结果的影响,首先将nfeature(区域1和4:nfeature=2,区域2和3:nfeature=3)、rseed(区域1和2:rseed=25,区域3:rseed=40,区域4:rseed=20)、rinstance(区域1和2:rinstance=5,区域3:rinstance=8,区域4:rinstance=4)取值固定,进而改变nnoise的取值进行试验。针对每个nnoise随机生成10组数据(共生成50组随机数据),挖掘结果定量评价指标取平均值。试验结果如图 6(g)-(h)所示:本文方法对噪声不敏感;RCMKNN方法对噪声最为敏感,主要原因还是在于邻居数目k值估计的不稳定;RCMNG方法和多层次方法在不同噪声情况下的表现相对稳定,但是结果漏判与误判问题依然存在。
通过上述试验可以发现:自然邻域方法在不同密度、不同模式长度及噪声数目情况下均可以可靠地构建空间要素实例间邻近关系,从而保证了同位模式实例生成的准确性,进而可以有效避免同位模式挖掘结果的误判与遗漏问题。
4.2 犯罪同位关联模式挖掘进一步采用本文方法挖掘犯罪事件、城市兴趣点数据集中的空间同位模式。犯罪地理学研究表明,犯罪事件在空间上具有互相诱导关系而且受到城市地理环境的影响,发现犯罪事件间及犯罪与城市兴趣点间的同位模式对于犯罪预防与犯罪管控具有重要价值[27]。本文以美国波特兰市作为研究区域,收集了2014年1-3月伤害罪(740)、抢劫罪(188)和盗窃罪(7143)3种犯罪事件以及餐饮(食品、咖啡和餐馆,共715条记录)、娱乐设施(夜店和酒吧,共131条记录)、车站(公交站点与车站,共1764条记录)和购物场所(购物中心、商店、便利店和杂货店,共715条记录)4类兴趣点。
本文方法挖掘结果共包含9个全局同位模式和36个局部同位模式,部分挖掘结果如表(1)所示。分析挖掘结果,可以发现:
| 空间同位模式 | 层次 | PImin | PImax | PIglobal |
| {娱乐设施,购物设施} | 全局 | 0.80 | 0.80 | 0.80 |
| {伤害罪,抢劫罪} | 全局 | 0.77 | 0.77 | 0.77 |
| {购物设施,抢劫罪} | 全局 | 0.73 | 0.73 | 0.73 |
| {餐饮设施,伤害罪} | 全局 | 0.70 | 0.70 | 0.70 |
| {伤害罪,盗窃罪} | 全局 | 0.68 | 0.68 | 0.68 |
| {购物设施,伤害罪} | 全局 | 0.59 | 0.59 | 0.59 |
| {娱乐设施,抢劫罪} | 全局 | 0.55 | 0.55 | 0.55 |
| {餐饮设施,盗窃罪} | 全局 | 0.51 | 0.51 | 0.51 |
| {车站设施,盗窃罪} | 全局 | 0.51 | 0.51 | 0.51 |
| {抢劫罪,盗窃罪} | 局部 | 0.53 | 0.75 | 0.37 |
| {餐饮设施,购物设施} | 局部 | 0.55 | 1.00 | 0.48 |
| {伤害罪,娱乐设施} | 局部 | 0.82 | 1.00 | 0.46 |
| {伤害罪,车站设施} | 局部 | 0.73 | 1.00 | 0.44 |
| {伤害罪,抢劫罪,盗窃罪} | 局部 | 0.55 | 0.60 | 0.28 |
| {娱乐设施,抢劫罪,购物设施} | 局部 | 0.56 | 1.00 | 0.36 |
| {餐饮设施,车站设施} | 局部 | 0.73 | 0.92 | 0.49 |
| {伤害罪,车站设施,盗窃罪} | 局部 | 0.6 | 0.62 | 0.29 |
| {伤害罪,餐饮设施,抢劫罪} | 局部 | 0.63 | 0.89 | 0.29 |
| {伤害罪,餐饮设施,盗窃罪} | 局部 | 0.56 | 1.00 | 0.29 |
| {伤害罪,餐饮设施,购物设施} | 局部 | 0.65 | 1.00 | 0.26 |
| {餐饮设施,娱乐设施} | 局部 | 0.6 | 1.00 | 0.45 |
| {娱乐设施,盗窃罪} | 局部 | 0.57 | 0.95 | 0.23 |
| {娱乐设施,车站设施} | 局部 | 0.53 | 1.00 | 0.14 |
| {伤害罪,购物设施,车站设施} | 局部 | 0.63 | 1.00 | 0.12 |
| {餐饮设施,车站设施,盗窃罪} | 局部 | 0.56 | 1.00 | 0.23 |
| {伤害罪,娱乐设施,盗窃罪} | 局部 | 0.52 | 0.85 | 0.14 |
| {抢劫罪,车站设施} | 局部 | 0.59 | 1.0 | 0.22 |
| {餐饮设施,抢劫罪,盗窃罪} | 局部 | 0.64 | 1.0 | 0.17 |
| {伤害罪,抢劫罪,车站设施} | 局部 | 0.72 | 1.0 | 0.13 |
| {伤害罪,购物设施,盗窃罪} | 局部 | 0.56 | 0.85 | 0.20 |
| {伤害罪,餐饮设施,车站设施} | 局部 | 0.57 | 1.0 | 0.20 |
| {购物设施,车站设施} | 局部 | 0.82 | 1.00 | 0.22 |
| {餐饮设施,娱乐设施,购物设施} | 局部 | 0.78 | 1.00 | 0.23 |
| {抢劫罪,购物设施,盗窃罪} | 局部 | 0.56 | 1.0 | 0.10 |
| {抢劫罪,车站设施,盗窃罪} | 局部 | 0.57 | 0.64 | 0.12 |
| {伤害罪,娱乐设施,购物设施} | 局部 | 0.61 | 0.76 | 0.18 |
(1) 犯罪与兴趣点、不同犯罪类型之间均存在同位关系,充分说明了犯罪间的诱导关系与环境设施对犯罪事件的影响,可以为犯罪管控提供针对性指导意见。
(2) 某些同位模式在整个波特兰市都是频繁出现的(如{餐饮设施,伤害罪}、{娱乐设施,抢劫罪}和{餐饮设施,盗窃罪}),这表明这些模式是一种普遍模式,而某些同位模式仅发生在局部区域(如图 7所示局部同位模式),这表明同位模式分布具有异质性的特点,本文的挖掘结果可以为差异性犯罪防控提供参考。

|
| 图 7 部分局部同位模式及其分布区域 Fig. 7 Some regional co-location patterns and their localities |
以{娱乐设施,伤害罪}和{车站,伤害罪}两个局部同位模式为例,对本文挖掘结果进行分析。伤害罪分布于整个研究区域且分布不均匀(篇幅所限未进行展示),在研究区域中部的市中心最集中,在研究区域西部最稀疏。娱乐设施兴趣点主要分布在研究区域中部和东南部,车站主要分布在研究区域西部、中部和东部部分区域(篇幅所限未进行展示)。{娱乐设施,伤害罪}局部同位模式(如图 7(c)所示)主要是由于娱乐设施主要集中于市中心,酒吧、夜店等人员来源复杂、流动较大的兴趣点诱发伤害性犯罪机率较大,未来应进一步加强管控;{车站,伤害罪}局部同位模式(如图 7(d)所示)主要出现在车站分布密集的市中心和东部部分区域,这说明人员流动和聚集是诱发伤害性犯罪的重要因素,但是该同位模式并没有在车站最密集的西部区域出现,这间接说明西部区域的犯罪防控是比较有效的。
5 结论与展望本文提出了一种基于自然邻域的空间同位模式自适应挖掘方法,从距离邻近性、密度变化一致性、关系紧密性3个角度建模空间数据的局部分布特征,能够在空间要素实例分布不均情况下准确构建要素实例间邻近关系(即自然邻域),并借助要素实例Delaunay三角网的连通性自适应地发现局部的同位模式。通过模拟试验与实例验证发现:本文方法不需要人为设置参数构建要素实例间的邻近关系;与当前几种代表性方法比较,本文方法在要素实例分布不均匀的复杂情况下能更准确、稳定地发现全局与局部的同位模式,同时挖掘得到的犯罪与兴趣点同位模式分布区域对于犯罪预防与管控具有一定的指导价值。
进一步研究工作将主要集中在3个方面:①本文方法的复杂度约为2O(n2)(创建自然邻域和构建候选同位模式实例)+O(nlogn)(局部同位模式提取),为了适应在大规模数据集中的应用需求需要进一步研究自然邻域的高效构建方法;②本文采用经验阈值的策略设置参与指数阈值在实践中可能存在一定偏差,未来需要进一步研究参与指数的自适应估计;③当前空间要素的记录数据多具有时间属性,需要进一步研究时空自然邻域的构建方法。
| [1] |
王香红, 栾兆擎, 闫丹丹, 等.
洪河沼泽湿地17种植物的生态位[J]. 湿地科学, 2015, 13(1): 49–54.
WANG Xianghong, LUAN Zhaoqing, YAN Dandan, et al. Niche of 17 kinds of plants in marshes in Honghe[J]. Wetland Science, 2015, 13(1): 49–54. |
| [2] | WANG Fahui, HU Yujie, WANG Shuai, et al. Local indicator of colocation quotient with a statistical significance test:examining spatial association of crime and facilities[J]. The Professional Geographer, 2017, 69(1): 22–31. DOI:10.1080/00330124.2016.1157498 |
| [3] | YU Wenhao, AI Tinghua, HE Yakun, et al. Spatial co-location pattern mining of facility points-of-interest improved by network neighborhood and distance decay effects[J]. International Journal of Geographical Information Science, 2017, 31(2): 280–296. DOI:10.1080/13658816.2016.1194423 |
| [4] | WANG Junmei, HSU W, LEE M L. A framework for mining topological patterns in spatio-temporal databases[C]//Proceedings of the 14th ACM International Conference on Information and Knowledge Management. Bremen, Germany: ACM, 2005: 429-436. |
| [5] | HUANG Y, SHEKHAR S, XIONG H. Discovering colocation patterns from spatial data sets:a general approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(12): 1472–1485. DOI:10.1109/TKDE.2004.90 |
| [6] | YOO J S, SHEKHAR S, SMITH J, et al. A partial join approach for mining co-location patterns[C]//Proceedings of the 12th Annual ACM International Workshop on Geographic Information Systems. Washington DC: ACM, 2004: 241-249. |
| [7] | YOO J S, SHEKHAR S. A joinless approach for mining spatial colocation patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(10): 1323–1337. DOI:10.1109/TKDE.2006.150 |
| [8] | XIAO Xiangye, XIE Xing, LUO Qiong, et al. Density based co-location pattern discovery[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Irvine, California: ACM, 2008: 102-114. DOI: 10.1145/1463434.1463471. |
| [9] | YOO J S, BOW M. Mining spatial colocation patterns:a different framework[J]. Data Mining and Knowledge Discovery, 2012, 24(1): 159–194. |
| [10] | QIAN Feng, HE Qinming, CHIEW K, et al. Spatial co-location pattern discovery without thresholds[J]. Knowledge and Information Systems, 2012, 33(2): 419–445. DOI:10.1007/s10115-012-0506-9 |
| [11] | DENG Min, HE Zhanjun, LIU Qiliang, et al. Multi-scale approach to mining significant spatial co-location patterns[J]. Transactions in GIS, 2017, 21(5): 1023–1039. DOI:10.1111/tgis.2017.21.issue-5 |
| [12] | BARUA S, SANDER J. Mining statistically significant co-location and segregation patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1185–1199. DOI:10.1109/TKDE.2013.88 |
| [13] | QIAN Feng, CHIEW K, HE Qinming, et al. Mining regional co-location patterns with kNNG[J]. Journal of Intelligent Information Systems, 2014, 42(3): 485–505. DOI:10.1007/s10844-013-0280-5 |
| [14] | CELIK M, KANG J M, SHEKHAR S. Zonal co-location pattern discovery with dynamic parameters[C]//Proceedings of the 7th IEEE International Conference on Data Mining. Omaha: IEEE, 2007: 433-438. |
| [15] | DING Wei, EICK C F, YUAN Xiaojing, et al. A framework for regional association rule mining and scoping in spatial datasets[J]. Geoinformatica, 2011, 15(1): 1–28. DOI:10.1007/s10707-010-0111-6 |
| [16] | MOHAN P, SHEKHAR S, SHINE J A, et al. A neighborhood graph based approach to regional co-location pattern discovery: a summary of results[C]//Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Chicago, Illinois: ACM, 2011: 122-132. |
| [17] |
蔡建南, 刘启亮, 徐枫, 等.
多层次空间同位模式自适应挖掘方法[J]. 测绘学报, 2016, 45(4): 475–485.
CAI Jiannan, LIU Qiliang, XU Feng, et al. An adaptive method for mining hierarchical spatial co-location patterns[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 475–485. DOI:10.11947/j.AGCS.2016.20150337 |
| [18] |
边馥苓, 万幼.
k-邻近空间关系下的空间同位模式挖掘算法[J]. 武汉大学学报(信息科学版), 2009, 34(3): 331–334.
BIAN Fuling, WAN You. A novel spatial co-location pattern mining algorithm based on k-nearest feature relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 331–334. |
| [19] | BEMBENIK R, RYBIИSKI H. FARICS:A method of mining spatial association rules and collocations using clustering and delaunay diagrams[J]. Journal of Intelligent Information Systems, 2009, 33(1): 41–64. DOI:10.1007/s10844-008-0076-1 |
| [20] | SUNDARAM V M, THNAGAVELU A, PANEER P. Discovering co-location patterns from spatial domain using a delaunay approach[J]. Procedia Engineering, 2012, 38(12): 2832–2845. |
| [21] | FORTIN M J, DALE M R T. Spatial analysis:a guide for ecologists[M]. Cambridge: Cambridge University Press, 2005. |
| [22] | CAI Jiannan, DENG Min, LIU Qiliang, et al. Nonparametric significance test for discovery of network-constrained spatial co-location patterns[J]. Geographical Analysis, 2018, 65(9): 126–137. |
| [23] | BUYONG T. Spatial data analysis for geographic information science[M]. Kuala Lumpur, Malaysia: Penerbit UTM, 2007. |
| [24] | CLARK P J, EVANS F C. Distance to nearest neighbor as a measure of spatial relationships in populations[J]. Ecology, 1954, 35(4): 445–453. DOI:10.2307/1931034 |
| [25] | INKAYA T, KAYALIGIL S, ÖZDEMIREL N E. An adaptive neighbourhood construction algorithm based on density and connectivity[J]. Pattern Recognition Letters, 2015, 52(1): 17–24. |
| [26] | ESTIVILL-CASTRO V, LEE I. Argument free clustering for large spatial point-data sets via boundary extraction from delaunay diagram[J]. Computers, Environment and Urban Systems, 2002, 26(4): 315–334. DOI:10.1016/S0198-9715(01)00044-8 |
| [27] |
龙冬平, 柳林, 冯嘉欣, 等.
社区环境对入室盗窃和室外盗窃影响的对比分析——以ZG市ZH半岛为例[J]. 地理学报, 2017, 72(2): 341–355.
LONG Dongping, LIU Lin, FENG Jiaxin, et al. Comparisons of the community environment effects on burglary and outdoor-theft:a case study of ZH peninsula in ZG city[J]. Acta Geographica Sinica, 2017, 72(2): 341–355. |



