2. 中国测绘科学研究院, 北京 100830;
3. 河南省科学院地理研究所, 河南 郑州 450052
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. Institute of Geographical Sciences, Henan Academy of Sciences, Zhengzhou 450052, China
随着社会经济和城市建设的发展,城市道路网规模逐渐扩大,并逐渐表现出复杂网络的特性。对大规模路网来说,采用经典算法计算精确的最短路径普遍存在时间复杂度过高、存储消耗过大等问题[1-2]。在大部分实际应用中,可以使用良好的近似路径来代替精确路径,同时考虑计算时间和精度间的平衡[3]。多年来,研究学者提出多种预处理技术,包括启发策略[4-5]、分层策略[2, 6]、地标点策略[7-11]等,通过预处理保留网络部分重要信息,达到提高计算效率的目的。
地标点策略被广泛地应用于两节点间的距离估计,通过选择一定数量的中心节点,并预计算所有中心点间的最短路径来提高计算效率,选择的节点也称为landmarks[7-8]、reference nodes[9]、beacons[10]、tracers[11]等。文献[7]提出了满足误差限制条件的基于覆盖和分割的地标选择方法;文献[8]对地标点选择策略进行总结,对比分析了基本策略、限制策略和划分策略在地标点选择上的效率,并结合三角测量原理在社交网络上进行最短路径估计;文献[10]在随机选择参考点的基础上,通过可以进行一定比例调整的距离来保证性能。上述研究表明,最短路径估计可以利用地标点提升计算效率。然而,这些方法不能同时实现地标点的规模控制和均衡分布,当地标点规模较大时,预计算所有地标点间的距离也具有较高的空间复杂度。
地标点可以充分利用节点的重要性提高选取质量。同时,在大规模道路网中,两节点间的最短路径较大可能地经过较为重要的节点,交通发达的地方,节点分布往往比较密集,大部分节点通常经过中心性较大的节点连接在一起。节点重要性对最短路径的计算具有一定的启发性。复杂网络中的节点重要性评价的方法很多,多采用单一指标或多指标的形式[12-13]。度中心性[14]、中介中心性[15]、接近中心性[16]等方法均分别从不同的方面刻画了节点在特定网络中的重要性。但现实道路网结构类型多样,很难用单一指标来说明节点在网络中的重要程度[13]。
本文针对大规模道路网的结构特点,结合地标点策略和层次策略,提出一种顾及节点重要性的最短路径估计方法。该方法应用复杂网络理论和Critic赋权法分析节点的重要性,通过限制参数和节点重要性序列使中心节点均衡的分布于网络中,同时,制定层次网络构建方案将原网络中的部分搜索问题转移到高层网络中,寻找一条实际存在的近似路径作为可能的最短路径,从而提高运算效率并保持较高的有效性。
1 节点重要性评价方法 1.1 评价指标利用复杂网络理论分析道路节点在网络中的几何或属性特性,能够准确地定位网络的重要节点,对网络中重要基础设施和交通枢纽的协调管理,增强城市交通管理和服务质量,提高路径分析和交通拥堵分析的效率具有重要的现实意义。度中心性、集聚系数[17]、接近中心性、中介中心性、特征向量中心性[18]等是当前节点重要性评价中主要的量化指标[19-22]。这些重要性度量指标最初应用在社会网络中,随后被推广到其他类型网络的研究中。在现实道路网中,节点常用来表示道路口、交叉路口、交通枢纽等,节点之间的连边表示实际道路线,边的权重表示该条道路的实际长度、欧氏距离、旅行时间距离等。
(1) 度中心性,是指网络中与节点直接连接的边数[14]
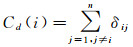 (1)
(1)
式中,δij表示与节点i是否与节点j相交,若相交,则δij=1,否则为0。度中心性是研究节点中心性最直接的度量指标,其值越大,表明节点越重要,连接的道路越多。
(2) 局部集聚系数,是指节点的相邻节点之间的连接数与它们所有可能存在的连接数的比值[17]。无向图中节点i的集聚系数为
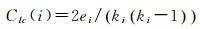 (2)
(2)
式中,ki为i的邻接节点数,i与其邻接节点之间最多可能存在2/(ki(ki-1))条连接,ei为邻接节点间的边的数量。集聚系数表示节点的聚集程度,其值越大,表明节点与邻接节点间存在模块结构的可能性越大。
(3) 接近中心性,是指节点到其他所有节点的最短路径长度之和的倒数[16]
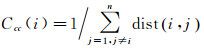 (3)
(3)
式中,dist(v, s)为节点i与j之间的最短路径长度。接近中心性反映道路节点与其他节点之间的接近程度,用来度量节点在网络中是否处于核心位置,其值越大,表明节点越重要,节点的影响及服务范围越广。
(4) 中介中心性,是指经过该节点的最短路径数目与所有最短路径数目的比值[15, 22]
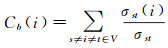 (4)
(4)
式中,σst为任意节点s到t的最短路径数目,σst(i)为节点s到t的最短路径中经过节点i的最短路径数目。中介中心性反映了节点作为“桥梁”的重要程度,其值越大,表明最短路径经过的次数越多,在整个网络中的影响力和控制力越强。
(5) 特征向量中心性,通过邻接节点的重要性来衡量本节点的重要性[18]
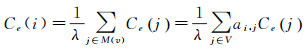 (5)
(5)
式中,A=(ai, j)为邻接矩阵,如果节点i与j相连,则ai, j=1,否则为0;λ为常数,M(i)为节点i的邻接节点。特征向量中心性反映了节点在网络中的价值,相比于接近中心性,其考虑了邻点的重要性。
1.2 基于Critic的多指标集成单一指标仅能从单一层面反映节点的重要性,且节点重要性不仅取决于自身属性,在一定程度上受其相邻节点甚至更远节点的影响[19]。为了综合考虑节点在网络中起到的局部及全局影响,以上述指标综合评价网络节点的重要性,更准确有效地发掘出复杂网络中的重要节点,节点重要性评价模型定义如下
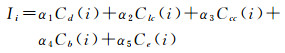 (6)
(6)
式中,Ii为节点i的重要度;α1、α2、…、α5为系数;Cd(i)、Clc(i)、…、Ce(i)分别表示离差标准化后的度中心性、集聚系数、接近中心性、中介中心性和特征向量中心性。
由于指标系数的确定缺少专家经验和可靠的网络信息,本文对指标参数α1、α2、…、α5进行多重共线性分析,采用客观赋权法Critic方法[23]实现模型信息量的最大化。指标Cj, 0 < j≤5所包含的信息量表达如下
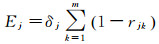 (7)
(7)
式中,δj为第j个指标的标准差,rjk为指标j与k间的相关系数。可以看出,指标j的信息量包含两部分:①单指标内部信息量,即指标标准差δj;②不同指标间的信息量,即指标与其他指标的冲突性rjk,rjk越大,冲突性越低。Ej越大,指标所包含的信息量越大,该指标的相对重要性越强。那么,指标Cj的系数αj表示为
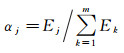 (8)
(8)
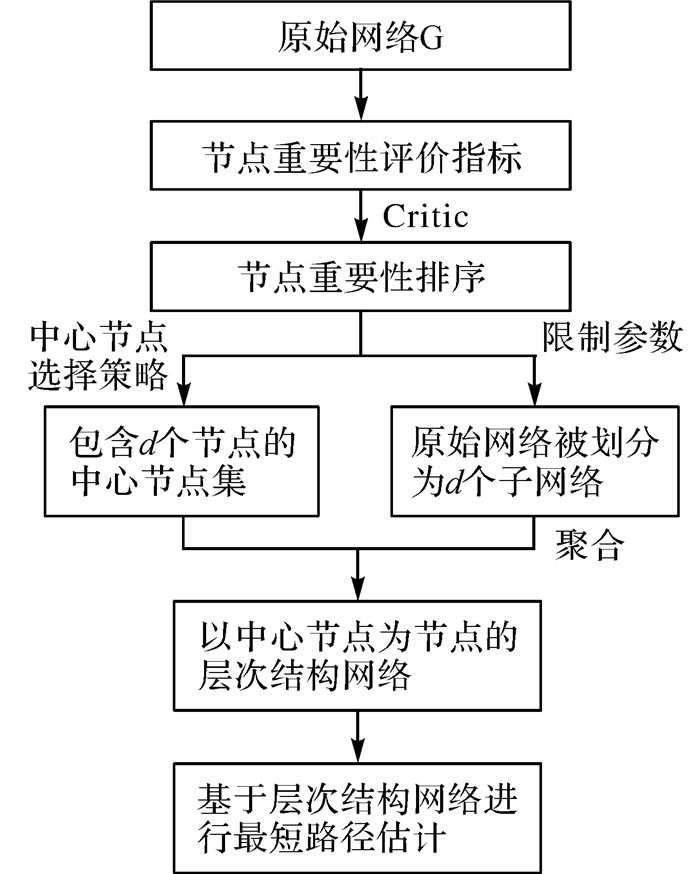
本文的研究思路可概括为:首先,根据原始网络计算单项评价指标,利用Critic方法实现节点重要性的多指标集成;其次,依据节点序列及限制条件,选择中心节点并实现网络划分;然后,根据中心节点集合和中心节点间的连接关系构建层次结构网络;最后,在层次结构网络上实现最短路径值的估计。方法流程如图 1所示,主要步骤描述如下:
|
| 图 1 方法流程 Fig. 1 Analysis process |
(1) 节点重要性评价。从原始网络中提取节点重要性的评价指标,采用客观赋权法Critic方法探究节点重要程度,生成节点重要性序列。
(2) 中心节点选择与网络划分。依据节点重要性序列,以优先重要性强的节点、排除被标记的节点为原则生成中心节点集,通过限制参数将原始网络划分为若干个子网络(见2.2节)。
(3) 层次结构网络构建。中心节点集构成层次结构网络的节点,对具有连接关系的中心节点间进行辅助边构建,构成层次结构网络的边。
(4) 最短路径估计。依据所构建的层次结构网络,实时计算得到任意两个节点间的近似最短路径(见2.3节)。
2.2 网络划分策略影响最短路径计算精度的一个核心因素是网络划分,而中心节点作为子网络的核心,其选择很大程度上影响了划分的效率和划分后网络的拓扑结构。现有研究中提出和使用的中心点选择的基本策略,主要包括随机法与基于度中心性、中介中心性、接近中心性等带有启发思想的度量方法。基本策略以其中某一种方法作为中心节点的选择策略,指定选取数量控制节点规模。但是,基本策略可能会使中心节点分布较为集中,部分中心节点的覆盖贡献较小,因此,本文在此基础上,引入多指标评价模型将网络节点的相对重要性进行量化,通过限制性的网络划分策略,使中心节点较为均匀的分布于整个网络。
不妨假设某一中心节点li的覆盖范围为β,被li所覆盖的节点不纳入选择范围,在能够有效减小中心节点规模的同时,提高算法执行效率。为此,从空间角度引入规模参数m和深度参数h,分别用于调节中心节点的覆盖范围。对于无向图G(V, E, W),网络划分包括以下几个步骤:
(1) 依据节点重要性由高到低排序得到序列T。
(2) 从序列T中依次选取节点s。
(3) 若s未被标记,将s加入到中心点集S,将以s为中心节点的子网络记为Gs,并执行步骤(4),否则执行步骤(2)。
(4) 从节点s开始执行宽度优先遍历,若搜索到的节点t满足覆盖条件β(m, h),则对t进行标记,并划分到子网络Gs中,记录s到t的最短路径。
(5) 循环执行步骤(2)—(4),直到序列T为空。
以上步骤生成了一个包含d个中心节点的集合S,并将原始网络G划分为d个子网络,记为G1、G2、…、Gd。本文以节点数量表示规模参数,以节点到中心节点的最短距离上限表示深度参数,即β(m, h)满足dist(s, t)≤h且num(Vs)≤m,其中,Vs表示Gs的节点集,num(Vs)表示Gs包含的节点数量。
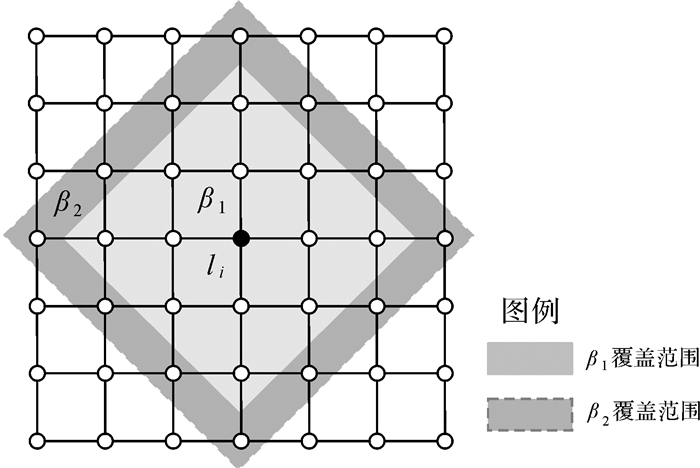
如图 2所示,每两个节点间的距离值为1,β1和β2表示节点li的覆盖条件,其中,浅色阴影部分覆盖的节点满足β1:m=13, h=2,虚线范围内的节点满足的β2:m=25, h=3,被覆盖的节点和边组成以li为中心节点、以β1/β2为限制参数的子网络Gli。
|
| 图 2 中心节点覆盖示意图 Fig. 2 Coverage of the center nodes |
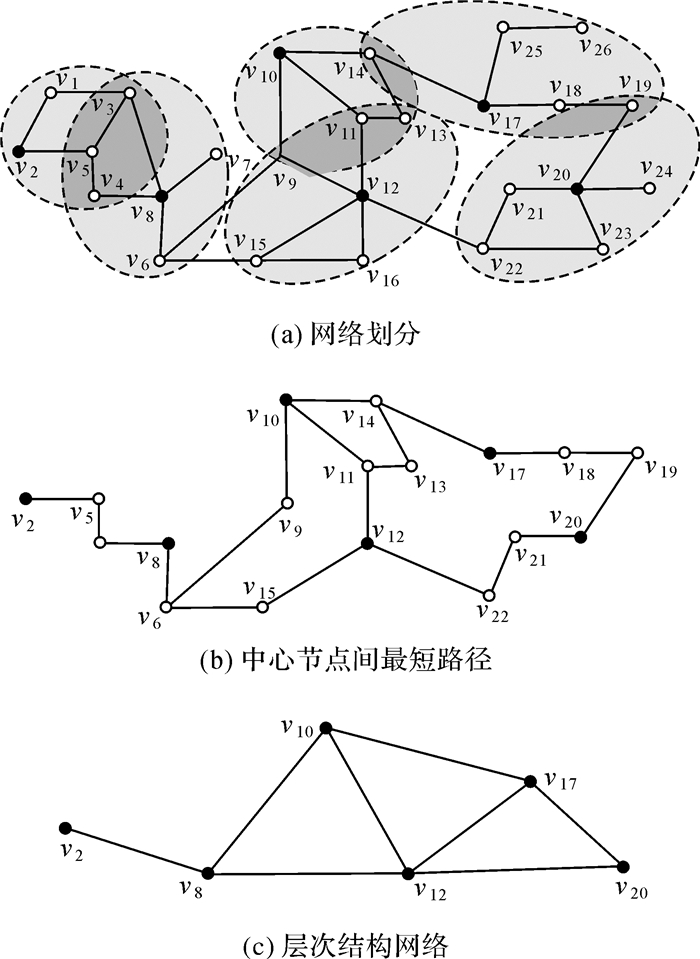
在对网络进行划分后,将中心节点集合抽象为层次结构网络的节点,依据子网络间的连接情况构建辅助边,这些边构成层次结构网络的边。给定无向图G(V, E, W),划分后的子网络为{G1, G2, …, Gd},Gi(Vi, Ei, Wi), 1≤i≤d对应中心节点li,构建思想主要包括两步:节点收缩和辅助边构建。节点收缩:将Gi中所有节点压缩为一个超级节点li;辅助边构建:在存在公共节点或连接边的任意两个子网络Gi, Gj间的超级节点li与lj间添加辅助边lj, k,并计算和保存li与lj的最短路径。因此,层次结构网络Gh为一个包含d个中心点的图,实现了网络规模的收缩。如图 3所示,黑色节点为中心节点,白色节点为普通节点。图 3(a)中灰色椭圆表示网络划分情况;图 3(b)表示具有连接关系的中心节点间的最短路径;图 3(c)表示构建得到的层次结构网络,基于层次结构网络实现最短路径的近似计算。
|
| 图 3 层次结构网络构建示意图 Fig. 3 Network partition |
2.3 最短路径近似估计
为了有效估计两节点间的最短路径,本文以通过中心节点的一条实际存在的路径近似代表节点间的最短路径,分别计算起始点或目标点到与其最近的中心节点间的最短距离,然后在层次网络中进行最短路径计算。因此,对于任意节点对(s, t),其最短路径包含三部分,即s和t分别到所属子网络中距离其最近的中心节点间的最短路径与中心节点间的最短路径之和。最短路径及最短路径的近似值表示为
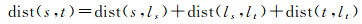 (9)
(9)
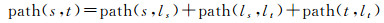 (10)
(10)
式中,ls、lt表示到s、t所属子网络中距离最近的中心节点,path(s, t)表示s到t的近似最短路径,dist(s, t)表示s到t的近似最短路径值。dist(ls, lt)、在Gh中计算得到,为近似值;dist(s, ls)、dist(t, lt)、path(s, ls)与path(t, lt)在网络划分时已经进行计算并存储,为真实值,因此可以直接查询获得。若s为中心节点,则dist(s, ls)、path(s, ls)项为0;同理,若t为中心节点,则dist(t, lt)、path(t, lt)项为0。为了保证路径的真实性,在计算path(ls, lt)的过程中动态读取辅助边计算的中间结果,即具有连接关系的中心节点间的最短路径,最终生成一条实际存在的近似路径。
与常见的随机方法、度中心性等基本策略不同,在最短路径计算时,考虑了大规模道路网中最短路径较大可能经过重要性较大的节点,算法依据网络中的节点重要性来构建中心节点集合、划分区域,充分考虑了网络的拓扑结构。同时,常见的基于地标点的最短路径估计方法,通过预处理所有地标点间的最短路径,以求在查询时可以达到O(1)的时间复杂度,但对于大规模道路网数据,往往需要较高的空间复杂度。本文在充分简化后的层次网络上实时计算最短路径,在满足一定的精度要求情况下,降低了空间复杂度,有效提高了计算效率。
3 试验 3.1 数据集本文使用大规模道路网数据——纽约城市道路网作为测试数据。纽约城市道路网为无向平面图,有264 346个节点和730 100条边,99%的节点度分布在[1, 4]之间。道路交叉口和道路分别抽象为网络的节点和边,边权重为相应的路段的长度。本文采用复杂网络分析软件计算生成节点的度中心性、集聚系数、接近中心性、中介中心性和特征向量中心性,指标的描述性统计信息见表 1。
| 评价指标 | 最小值 | 中位数 | 最大值 | 均值 | 标准差 | 综合权重 |
| 度中心性 | 1.000 0 | 3.000 0 | 8.000 0 | 2.761 9 | 0.978 5 | 0.232 8 |
| 局部集聚系数 | 0.000 0 | 0.000 0 | 1.000 0 | 0.020 8 | 0.086 2 | 0.189 2 |
| 接近中心性 | 0.002 2 | 0.003 8 | 0.005 4 | 0.003 9 | 0.000 6 | 0.368 0 |
| 中介中心性 | 0.000 0 | 0.000 0 | 0.225 0 | 0.001 0 | 0.007 2 | 0.070 7 |
| 特征向量中心性 | 0.013 0 | 0.109 1 | 1.000 0 | 0.127 5 | 0.086 9 | 0.139 3 |
首先,对指标进行标准化,计算各指标的标准差和相关性,根据Critic方法计算各指标的综合权重(见表 1)。从表中可以看出,对于该道路网来说,接近中心性和度中心性在5项指标中具有较大的权值,占总比重的60%,而中介中心性的权值最小,为0.070 7。节点重要性的综合统计结果显示,节点重要值呈正态分布特征。其中,88%的节点的重要性值介于[0.1, 0.4]之间,表明绝大部分节点具有相似的重要性;仅有9%的节点重要性值介于[0.5, 1.0]之间,说明网络中存在少量的占支配地位的节点。
3.2 层次网络构建结果分析为了比较单指标与综合指标计算得到的节点重要性,以及限制条件等因素对层次网络和最短路径计算结果的影响,本文分别采用随机法、度中心性和多指标集成法,基于约束条件进行网络划分与层次结构网络构建,分别记为RANDOM/β、DEGREE/β和SYNTHESIS/β。同时,将上述方法同两种现有选取思想进行比较:①文献[24]中区域中心点的选择策略,考虑复杂网络的无标度特性,依据节点度中心性序列,选取的中心节点集合满足度数之和不大于全部节点度数之和的50%,或数量不超过节点总数的10%,记为DEGREE/CDZ;②文献[7]中带有限制条件的地标点选择策略,通过深度参数h降低覆盖的重叠度,本文以综合节点重要性定义节点序列,记为SYNTHESIS/h。
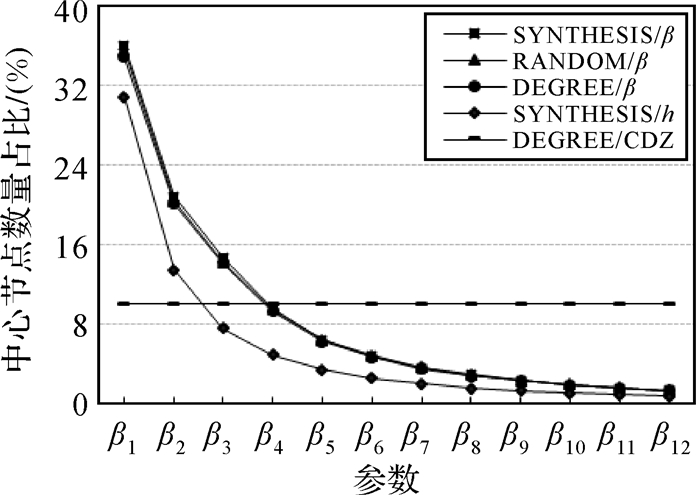
为了进一步探讨限制参数β对层次网络规模的影响,分别设置参数β1(5, 200)、β2(10, 400)、β3(15, 600)、β4(25, 800)、β5(40, 1000)、β6(55, 1200)、β7(75, 1400)、β8(95, 1600)、β9(120, 1800)、β10(150, 2000)、β11(185, 2200)、β12(220, 2400),前者规模参数m以节点数量表示;后者深度参数h表示节点到中心节点的最短距离上限,单位为米。从中心节点的数量占节点总数的比例(见图 4)、辅助边数量与原始网络边总数的比值(见图 5)两个方面来衡量层次网络的规模。
|
| 图 4 不同选取方法下中心节点数量占比 Fig. 4 The percentage of center nodes in different methods |
|
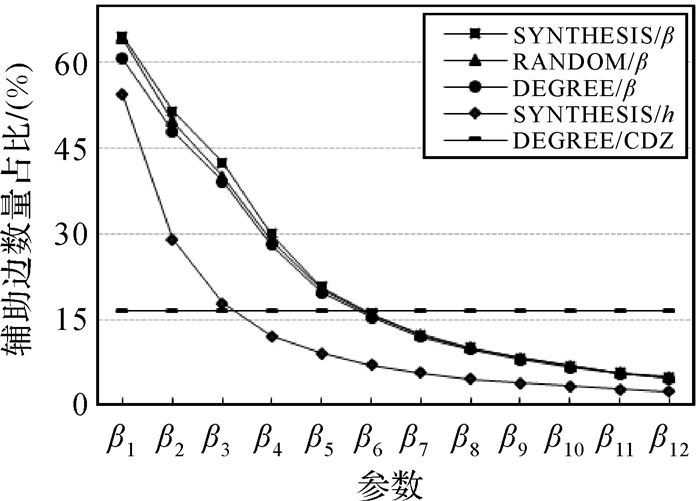
| 图 5 不同选取方法下辅助边数量占比 Fig. 5 The percentage of auxiliary edges in different methods |
图 4和图 5所示:①5种方法均有效降低了原始网络的规模,除DEGREE/CDZ方法指定了中心节点数量外,其他方法得到的中心节点数量和辅助边数量均随参数变化呈指数型降低;②SYNTHESIS/β、DEGREE/β和RANDOM/β方法在数量上没有明显的差异,β1(5, 0.2)时,SYNTHESIS/β方法得到的层次网络规模最大,但其中心节点数量和辅助边数量也仅占原始网络节点数量和边的36%和64%,β12(220, 2.4)时,3种方法的中心节点数量和辅助边数量均仅占原始网络节点和边的1.3%和4.8%;③SYNTHESIS/h方法只采用深度参数h作为限制条件,因此增大了中心节点的覆盖范围,在数量上明显小于上述3种方法。
3.3 最短路径近似结果分析在构建的5种层次结构网络上,本文采用点对点Dijkstra算法[25]近似计算任意两点间的最短路径,使用二叉堆实现优先队列,算法复杂度为O(mlogn)[26]。在大规模网络上估计所有节点的最短路径是非常昂贵的,因此,从原始网络中随机选取500个节点对,根据不同层次网络上最短路径值的平均路径比,测评计算的准确性。路径比是指若干节点对的最短路径近似值与精确值比值,比值越接近1,表示方法的准确率越高。
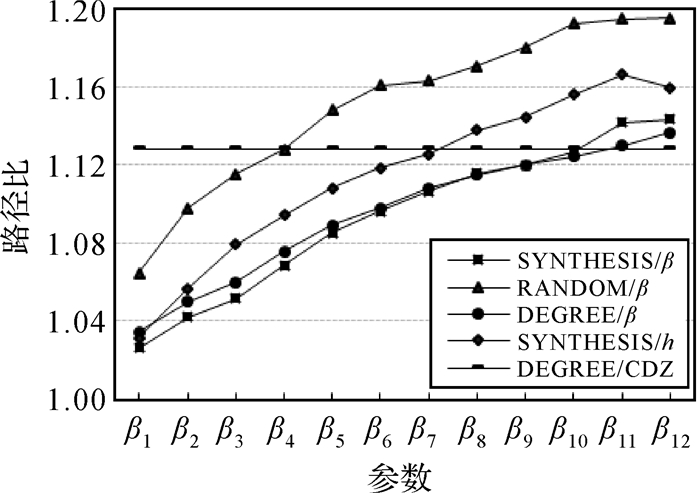
为了比较不同方法构建的层次网络对计算精度的影响,图 6显示了最短路径比与限制参数的变化趋势。结果显示,DEGREE/CDZ方法的平均路径比为1.128,其他方法均随参数的增大而增大;在一定参数范围内,SYNTHESIS/β方法最为精确,β1时路径比达到1.026,DEGREE/β略高于SYNTHESIS/β方法;RANDOM/β方法随机选择中心节点,通用性较好,但是没有考虑网络的拓扑结构特性,准确性最低。SYNTHESIS/β与DEGREE/β方法考虑了网络的中心性特征,优先考虑具有较大重要性的节点,说明重要性越大的节点在最短路径计算中起越重要的作用。
|
| 图 6 不同方法下的平均路径比 Fig. 6 Average path ration in different methods |
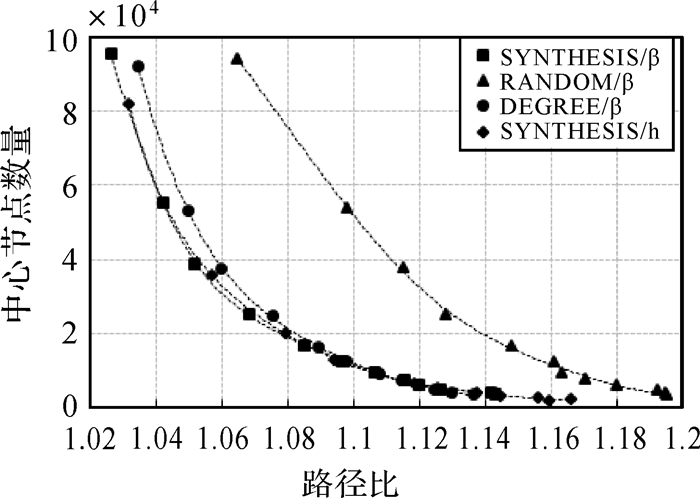
图 7表示中心节点规模同平均路径比的关系,从4种方法的趋势线可以看出,平均路径比随着中心节点数量的降低而增加。对于相同数量的中心节点,SYNTHESIS/β和SYNTHESIS/h方法表现出较高的准确性,且变化趋势基本吻合,而RANDOM/β方法的准确性最低。由本文算法的原理可知,节点重要性评价模型和限制参数的取值直接影响了中心节点的选取结果,并最终影响了最短路径的计算精度。随着限制参数的增大,中心节点的数量也增大,子网络规模越来越大。本文的中心节点选择方法与网络划分方法SYNTHESIS/β与SYNTHESIS/h的试验结果表明,相对于单一指标,对多指标集成方法能够更好地保留重要节点,有效降低了中心节点的数目,且估算结果较为精确,同时满足了距离的性能与准确性的要求。
|
| 图 7 平均路径比与中心节点数量关系 Fig. 7 The relationship between average path ration and number of center nodes |
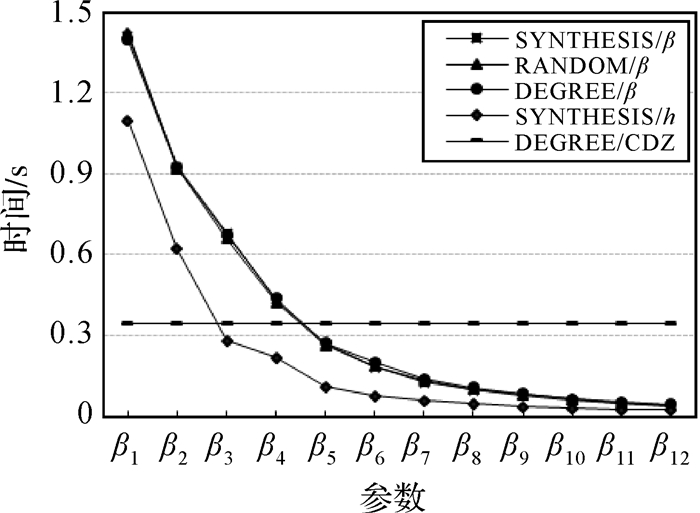
由算法复杂性可知,最短路径的计算时间随网络规模的减小而减小,所以在相同的限制参数下,SYNTHESIS/h计算时间最优,但其计算精度低于SYNTHESIS/β、DEGREE/β。原始网络中最短路径的平均计算时间为3.76 s,图 8可以看出,SYNTHESIS/β、DEGREE/β和RANDOM/β方法在计算时间上基本吻合,对计算精度最为精确的SYNTHESIS/β方法来说,在参数β1到β12,计算时间呈指数型降低,从1.412 s到0.039 s,计算效率提高了2.7到94倍。通过以上分析,SYNTHESIS/β方法不仅能保证较高的计算精度,也能够有效提高最短路径的计算效率。
|
| 图 8 最短路径平均计算时间 Fig. 8 Mean time of shortest paths |
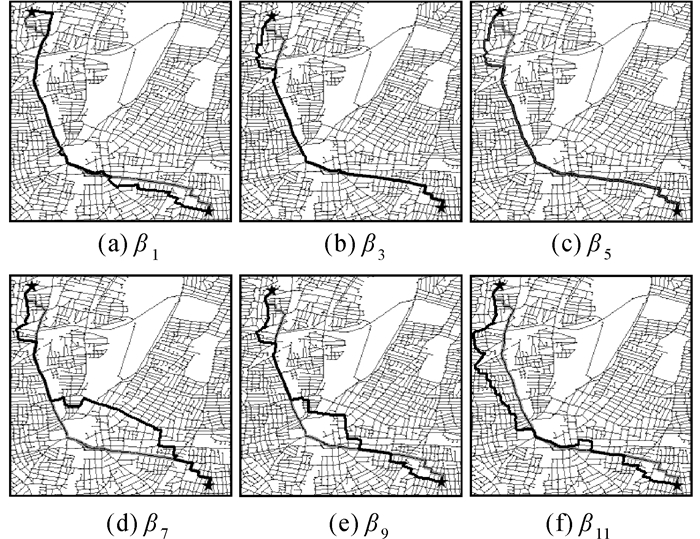
为了更好地显示近似最短路径的估计效果,在不同参数下选取任意节点对进行近似最短路径计算。图 9给出了参数为β1、β3、β5、β7、β9、β11等6种取值下的计算结果,灰色粗线表示节点间的精确路径,黑色粗线表示相应参数下的近似最短路径。可以看出,在不同参数下,β1、β3和β5得到的近似最短路径均能较好地分布于精确路径的周边,随着参数的增大,差距越大。因此,在实际的最短路径计算中,本文方法顾及了节点的重要性和限制范围,降低了网络规模,通过调整选取参数,可以根据误差要求选取一定的参数进行最短路径的近似估计,满足了道路网下最短路径近似计算的基本要求。
|
| 图 9 不同参数下最短路径近似结果 Fig. 9 Approximation results of shortest path in different parameters |
4 结论
本文在分析节点重要性评价指标的基础上,基于Critic方法与复杂网络理论实现节点重要性的综合评价。基于此,提出了顾及节点重要性的最短路径估计方法,引入规模参数和深度参数实现网络划分,制定层次结构网络的构建方案,实现大规模道路网数据的有效化简和最短路径的快速有效估计。本文以大规模道路网数据进行测试,试验结果说明,顾及节点重要性的最短路径估计方法能够更好地均衡划分后子网络的规模,提高最短路径的计算效率的同时保持了较高的计算精度,适用于大规模的道路网的最短路径快速计算。
以复杂网络理论为基础,本文方法能够为面向较大规模的交通运输网络、社会关系网络、通讯网络等现实网络的节点重要性分析、网络简化和最短路径分析等提供思路。本文方法仅从网络本身的拓扑与空间特征出发进行处理,未对道路网的属性特征和城市结构特征等因素进行考虑。后续需要扩展研究的内容有以下3点:①目前试验表明该方法对于单中心特征明显的纽约市数据具有较好的适用性,今后将在不同类型城市道路网(如多中心、放射状、环状道路等)上考察该方法的适用性与应用特点,进行更全面的评估和改进;②节点重要性分析、限制参数的界定与道路网节点的实际辐射范围存在关联,结合现实道路网中节点或边的属性信息,实现不同类型道路网的最短路径特征研究与动态分析;③实际道路网络多为有向图且具有转向限制,基于有向图计算得到评价指标,在计算过程中考虑边的方向性,将该方法拓展到有向交通网络中;结合混合边-节点算法[27]进一步研究具有转向限制的大规模道路网络的最短路径近似计算。
| [1] | BOVY P H L, STERN E. Route choice:wayfinding in transport networks[M]. Alphen, Netherlands: Kluwer Academic Publishers, 2012. |
| [2] |
宋青.大规模网络最短路径的分层优化算法研究[D].上海: 上海交通大学, 2012. SONG Qing. Research on hierarchical shortest path algorithms for large-scale networks[D]. Shanghai: Shanghai Jiao Tong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10248-1012034727.htm |
| [3] | MIHALAK M, ŠRAMEK R, WIDMAYER P. Approximately counting approximately-shortest paths in directed acyclic graphs[J]. Theory of Computing Systems, 2016, 58(1): 45–59. |
| [4] | MAUE J, SANDERS P, MATIJEVIC D. Goal directed shortest path queries using precomputed cluster distances[C]//Proceedings of 2006 International Workshop on Experimental and Efficient Algorithms. Berlin: Springer, 2006: 316-327. |
| [5] | GOLDBERG A V, WERNECK R F. Computing point-to-point shortest paths from external memory[C]//Proceedings of the Seventh Workshop on Algorithm Engineering and Experiments and the Second Workshop on Analytic Algorithmics and Combinatorics. Vancouver: SIAM, 2005, : 26-40. |
| [6] | IDWAN S, ETAIWI W. Computing breadth first search in large graph using hMetis partitioning[J]. European Journal of Scientific Research, 2009, 29(2): 215–221. |
| [7] | QIAO Miao. Query processing in large-scale networks[D]. Hong Kong: The Chinese University of Hong Kong, 2013. |
| [8] | POTAMIAS M, BONCHI F, CASTILLO C, et al. Fast shortest path distance estimation in large networks[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management. Hong Kong, China: ACM, 2009: 867-876. |
| [9] | KRIEGEL H P, KRÖGER P, RENZ M, et al. Hierarchical graph embedding for efficient query processing in very large traffic networks[M]//Scientific and Statistical Database Management. Berlin: Springer, 2008: 150-167. |
| [10] | KLEINBERG J, SLIVKINS A, WEXLER T. Triangulation and embedding using small sets of beacons[C]//Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science. Rome, Italy: IEEE Computer Society, 2004: 444-453. |
| [11] | FRANCIS P, JAMIN S, JIN Cheng, et al. IDMaps:a global internet host distance estimation service[J]. IEEE/ACM Transactions on Networking, 2001, 9(5): 525–540. DOI:10.1109/90.958323 |
| [12] | WANG Shibo, ZHAO Jinlou. Multi-attribute integrated measurement of node importance in complex networks[J]. Chaos, 2015, 25(11): 113105. DOI:10.1063/1.4935285 |
| [13] |
于会, 刘尊, 李勇军.
基于多属性决策的复杂网络节点重要性综合评价方法[J]. 物理学报, 2013, 62(2): 54–62.
YU Hui, LIU Zun, LI Yongjun. Key nodes in complex networks identified by multi-attribute decision-making method[J]. Acta Physica Sinica, 2013, 62(2): 54–62. |
| [14] | FREEMAN L C. Centrality in social networks conceptual clarification[J]. Social Networks, 1978, 1(3): 215–239. DOI:10.1016/0378-8733(78)90021-7 |
| [15] | BRANDES U. A faster algorithm for betweenness centrality[J]. Journal of Mathematical Sociology, 2001, 25(2): 163–177. |
| [16] | BAVELAS A. Communication patterns in task-oriented groups[J]. Journal of the Acoustical Society of America, 1950, 22(6): 725–730. DOI:10.1121/1.1906679 |
| [17] | WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684): 440–442. DOI:10.1038/30918 |
| [18] | BONACICH P. Some unique properties of eigenvector centrality[J]. Social Networks, 2007, 29(4): 555–564. DOI:10.1016/j.socnet.2007.04.002 |
| [19] |
刘刚, 李永树, 杨骏, 等.
对偶图节点重要度的道路网自动选取方法[J]. 测绘学报, 2014, 43(1): 97–104.
LIU Gang, LI Yongshu, YANG Jun, et al. Auto-selection method of road networks based on evaluation of node importance for dual graph[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 97–104. DOI:10.13485/j.cnki.11-2089.2014.0014 |
| [20] | YANG Yunyun, XIE Gang, XIE Jun. Mining important nodes in directed weighted complex networks[J]. Discrete Dynamics in Nature and Society, 2017(5): 1–7. |
| [21] |
栾学晨, 杨必胜, 张云菲.
城市道路复杂网络结构化等级分析[J]. 武汉大学学报(信息科学版), 2012, 37(6): 728–732.
LUAN Xuechen, YANG Bisheng, ZHANG Yunfei. Structural hierarchy analysis of streets based on complex network theory[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 728–732. |
| [22] |
李清泉, 曾喆, 杨必胜, 等.
城市道路网络的中介中心性分析[J]. 武汉大学学报(信息科学版), 2010, 35(1): 37–41.
LI Qingquan, ZENG Zhe, YANG Bisheng, et al. Betweenness centrality analysis for urban road networks[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 37–41. |
| [23] | DIAKOULAKI D, MAVROTAS G, PAPAYANNAKIS L, et al. Determining objective weights in multiple criteria problems:the CRITIC method[J]. Computers & Operations Research, 1995, 22(7): 763–770. |
| [24] |
唐晋韬, 王挺, 王戟.
适合复杂网络分析的最短路径近似算法[J]. 软件学报, 2011, 22(10): 2279–2290.
TANG Jintao, WANG Ting, WANG Ji. Shortest path approximate algorithm for complex network analysis[J]. Journal of Software, 2011, 22(10): 2279–2290. |
| [25] | DIJKSTRA E W. A note on Two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269–271. |
| [26] |
陆锋.
最短路径算法:分类体系与研究进展[J]. 测绘学报, 2001, 30(3): 269–275.
LU Feng. Shortest path algorithms:taxonomy and advance in research[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 269–275. DOI:10.3321/j.issn:1001-1595.2001.03.016 |
| [27] | LI Qingquan, CHEN Biyu, WANG Yafei, et al. A hybrid link-node approach for finding shortest paths in road networks with turn restrictions[J]. Transactions in GIS, 2015, 19(27): 3059–3068. |



