遥感图像分割是将图像域划分成具有不同土地利用和土地覆盖(land use and land cover, LULC)类型区域的过程,是实现遥感图像信息自动提取的关键步骤,具有重要意义[1]。相对于传统中、低分辨率遥感图像,高空间分辨遥感图像(下文简称高分遥感图像)蕴含更加丰富的地物几何、纹理和光谱信息,呈现更多的地物细节信息[2]。高分遥感图像这些特点在地物目标提取方面极具潜力,但也给传统的遥感图像分割方法带来一些新的挑战[3]:①在更精细的空间尺度下,高分遥感图像中同类地物的光谱信息呈现更强的异质性,使得传统分割算法结果存在大量分割噪声;②城市遥感图像中呈现大量的琐碎地物类型,这些地物在分割结果中表现为几何噪声,传统分割算法难以处理这些几何噪声问题;③高分遥感图像中存在大量的“同谱异物”和“同物异谱”现象,分别造成同类地物光谱测度的聚类性降低和同类地物的可区分性降低,使得传统分割算法效果不佳;④数据量呈几何级数增长,呈现明显海量性的特点,使传统分割算法难以处理。
针对高分遥感图像的新特点,大部分学者在构建遥感图像分割模型过程中,将空间信息作为一种重要的约束信息,衍生出大量顾及空间约束的高分遥感图像分割算法,并取得丰硕的研究成果[4-6]。最小生成树(minimum spanning tree, MST)作为图论中的一种经典模型,因其能完备、高效地表达遥感图像中蕴含的空间关联和光谱信息而受到广泛关注[7-14]。MST是无向邻接图(下文简称为图)在全局权和最小约束条件下的最优表达,是一种典型的全局最优化问题。图像的MST表达结果中同质区域表现为空间上的集聚特性,而同质区域间的边界表现为不连通或连通节点间权值较大。视觉上,图像MST呈现边缘不连通的特性,使其对同质区域的不规则边界表达效果较为理想。但是,MST易受图像噪声影响,如在噪声处的权值较大,导致基于阈值的MST划分方法的结果中存在严重过分割现象。
而对于高分遥感图像海量性数据的特点,扩展现有稳健快速的分割方法,是解决海量遥感图像处理的有效途径之一。模糊c均值(fuzzy c-means, FCM)聚类算法作为遥感图像分割的经典算法之一,具有稳健性强、快速、稳定和易于扩展等特点,在遥感图像分割中应用广泛。该类方法包含以区域和像素为基本分割单元的两种方式[15-16],其中基于区域的分割方法因其具备一定的抗噪性和对目标边界不规则性的良好表达能力,且以区域作为决策单元,大大降低了分割决策的复杂性,在图像分割中应用广泛[8]。在基于区域和统计的遥感图像分割方法中,根据区域划分与分割过程之间的关系,可分为动态和静态划分两类。动态划分方法是指在分割过程中根据迭代求解的参数动态调整几何划分参数,该类方法不仅能达到区域划分逼近目标不规则边界的目的,而且能得到分布参数的最优估计。常用的几何划分方法有规则划分[5]、Voronoi划分[17]和泊松划分[18]等。典型的如文献[16]采用Voronoi划分作为基本的几何划分方法,在此基础上构建区域隐马尔可夫随机场(regional hidden Markov random field, RHMRF),并定义基于区域的模糊目标函数,对全色高分辨率遥感图像取得较高的分割精度。虽然该方法对彩色图像或纹理图像中的简单几何边界目标取得较好结果,但它存在迭代收敛慢、计算量大以及对复杂非规则目标边界精细结构表达效果不佳等缺点。另外,动态划分方法需迭代划分图像域,导致该类方法计算时间较长,在一定程度限制了其推广应用。
不同于动态划分方法,静态划分方法只在算法运行初期根据相似性准则对图像域进行一次划分,并在该划分得到的子区域基础上构建图像分割模型。由于在模型求解过程中只需估计模型参数,从而避免了求解过程对图像域的反复划分过程,因此极大地节省了算法运行时间。但该类方法存在分割结果依赖于初始划分结果的问题,因此建立有效表达地物目标边界非规则性的划分模型是该类方法成败的关键。常用的静态划分方法有超像素划分[19]、Mean-Shift划分[20]和MST划分[21-22]等,这些算法大都利用图像的光谱信息作为划分的主要判据,虽然具有一定的抗噪性且能获得局部最优结果,但是对于高分辨率遥感中广泛存在的几何噪声,易造成严重的过分割现象。
针对以上问题,本文试图将MST作为静态划分方法对图像域进行划分,在此基础上构建区域HMRF模型和结合KL散度信息(Kullback-Leibler divergence information)与信息熵正则化项的FCM目标函数;然后采用求偏导的方式对各模型参数进行求解,从而得到全局最优分割结果。其中,MST静态划分包括图像的MST表达和在其基础上的顾及区域形状信息的同质区域划分方法,试图通过引入形状信息抑制划分的几何噪声。同时,本文方法将隐马尔可夫随机场[8](hidden Markov random field, HMRF)从建模像素间邻域关系扩展到建模同质区域间的邻域关系,更方便有效地获取模型参数估计和图像最优分割。
1 算法描述 1.1 图像MST表达与划分令Z={Zs=Z(us, vs); (us, vs)∈P, s∈N}为定义在栅格P(图像域)上的离散随机场,其中,(us, vs)为像素s的平面坐标,s为像素索引,N={1, 2, …, n}为像素索引集,n为像素个数,Zs={Zsb; b=1, 2, …, B}为表征第s个像素光谱测度矢量的随机变量,即定义在P上的连续随机函数Z在(us, vs)上的采样,b为波段索引,B为波段个数。给定遥感图像z={zs=z(us, vs); (us, vs)∈P, s∈N}可视为离散随机场Z的一个实现,Z的所有可能实现构成的光谱矢量特征空间记为ΩZ。将像素映射为节点,并以节点8邻域作为节点间的邻接关系,构建图像的图G=(V, E, W)。其中V={vs=(us, vs, zs); s∈N}为节点集,E={ec=(vs, vs′); c=1, 2,…, C, s∈N, s′∈Np(s)}为边集,C为边的条数,Np(s)为节点s的8邻域,W={wc=w(vs, vs′); c=1, 2, …, C}为边集对应的权值矢量,wc定义了边ec连接的两个节点间光谱矢量的非相似性测度
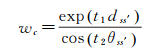 (1)
(1)
式中,dss′和θss′分别为节点vs和vs′之间光谱矢量欧氏距离和夹角;t1和t2∈(0, 1)分别用于调节dss′和θss′在权函数中的作用强度,本文中t1和t2分别取0.1和0.8。
图G的生成树T′=(V, E′)是G中具有树状结构的子图,即E′⊂E,且所有节点具有连通性。MST(T=(V, E′))是T中权重和最小的一棵,即图像的MST表达T去除了图像的图表达中的冗余连接边,且是在全局连接权和最小约束下的全局最优简化。另外,T有如下特性:边的个数|E′|=|V|-1,即边的个数比节点个数少1;T是无环图。因此,图像的MST表达具有如下优点:基于T上的操作时间复杂度为O(|V|),即具有线性复杂度;T的每条边都是割边,即删除或者恢复一条连接边会增加或者减少一个划分区域,极大简化了区域划分操作的复杂度,且每个子区域都对应一个子树;目标的边界表现为沿边生成的特性,有利于表达目标的复杂不规则边界。目前常用的经典MST生成算法有两种:Prim和Kruskal,二者均基于贪心策略[23]。其中Prim算法是一种点驱动的MST生长算法,基于斐波那契堆(Fibonacci heap)和邻接的数据结构下的该算法时间复杂度为O(|E|+|V|log|V|),适用于稠密图;Kruskal算法为边驱动算法,其时间复杂度为O(|E|log|E|),适用于稀疏图。由图像8邻域构建的图G可认为是稀疏图,因此本文基于Kruskal算法构建图像的MST。
为解决高分辨率遥感中大量存在的几何噪声和同质区域内异质性增强的问题,借助最小异质区域划分的思想,在图像MST表达的基础上,将光谱测度相似性和划分区域的形状差异作为区域合并的准则。首先,假设每个节点均为一个同质区域,T的每条边ec∈E′都是割边,因此将其作为区域合并边。然后定义区域合并的准则,即最小异质区域准则:对于ec中连接的两个区域Pi、Pi′,根据判据h(Pi, Pi′)≤S决定是否合并这两个区域。最后,依次遍历每条割边,直至完成所有的区域合并。其中,S为合并阈值,定义了最小均质区域的尺度,合并判据函数h(Pi, Pi′)为区域间光谱测度相似性和形状参数的线性组合,定义为
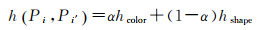 (2)
(2)
式中,α∈[0, 1]为光谱测度相似性权重;光谱测度相似性hcolor定义为
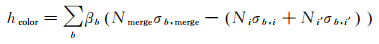 (3)
(3)
式中,σb, merge、σb, i和σb, i′分别为合并后的区域(Pi∪Pi′)、区域i和i′的标准差;Nmerge、Ni和Ni′分别为合并后的区域、区域i和i′的像素个数;βb=1/σb2为波段b的权重;σb2为波段b的方差。形状参数hshape为区域形状紧致度hcompt和平滑度hsmooth的线性组合,即
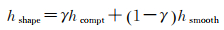 (4)
(4)
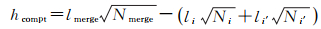 (5)
(5)
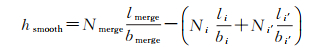 (6)
(6)
式中,γ∈[0, 1]为区域形状紧致度权重;lmerge、li和li′分别为合并后区域、区域i和i′的轮廓线长度;bmerge、bi和bi′分别为合并后区域、区域i和i′的外包矩形周长。MST静态划分过程如图 1所示。其中,图 1(a)为模拟图像,该图像由3个同质区域(区域1、2和3)构成,其中区域1包含区域4(1个像素),用该区域模拟几何噪声;图 1(b)为图 1(a)的无向带权图,邻接关系为8邻域,且为了能清楚地体现边权特性,只标注边权大于20的边,由此图可见在图表达中,边缘像素的连接边具有较大边权值;图 1(c)为生成的图像MST,可见图像MST能清楚地表达边界;图 1(d)为采用MST静态划分得到的划分树,每个子树对应一个均质区域。所以,静态MST划分在较好地表达目标的不规则边界的同时也能有效处理几何噪声。
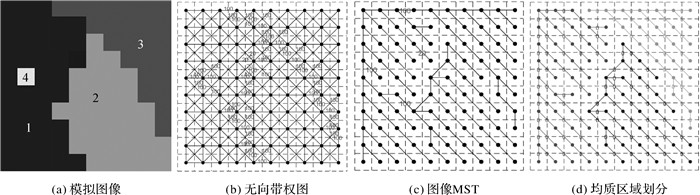
|
| 图 1 MST均质区域划分 Fig. 1 Homogeneous region tessellation by MST |
1.2 区域隐马尔可夫场模型
上述MST划分将图像域划分为若干个子区域,但是这些子区域的划分是局部最优的,而非全局最优的。所以,分割算法一般都需要采用额外聚类算法,以得到全局最优分割结果。为此,本文借助像素HMRF-FCM的图像分割思想,在MST划分的基础上构建RHMRF-FCM算法,以获得全局最优分割结果。
假定图像z的聚类数为q,令Q={1, …, q},且图像z在MST划分下可将图像域P划分为m个子区域,即P={Pi; i∈M},M={1, 2, …, m}。第i个子区域数据zi={za(ua, va); (ua, va)∈Pi, a∈Ni},其中a为子区域像素索引,Ni为其像素个数。每个子区域互不重叠且服从某种光谱测度一致性准则,因此可进一步假设每个子区域内的像素标号均相同,即,可将子区域作为分割决策的基本单元。对于每个子区域索引i∈M,其标号空间Xi={xi; xi∈Q}。则对于子区域标号叉积空间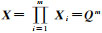
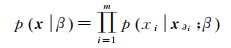 (7)
(7)
式中,β为标号场邻域作用强度
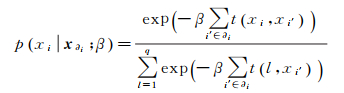 (8)
(8)
在光谱测度空间的随机场p(z)和子区域标号随机场p(x)的基础上,参考基于像素的HMRF模型定义,RMRF定义为
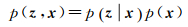 (9)
(9)
式中,p(z|x)采用似然函数方式进行计算,即
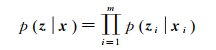 (10)
(10)
根据HMRF定义,p(z)为光谱测度观测量的随机场,而p(x)为非观测状态量(隐变量)的MRF,故将观测量随机场与隐变量MRF构建的模型称为HMRF。假设同标号数据服从同一多值高斯分布,则
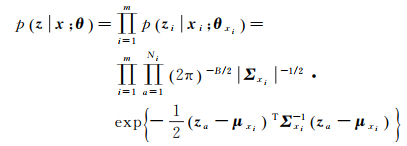 (11)
(11)
式中,μxi和Σxi分别为第xi类多值高斯分布的均值和协方差矩阵;θxi={μxi, Σxi};θ={θ1, θ2, …, θq}。
1.3 模糊目标函数文献[24]提出一种基于像素的改进HMRF-FCM算法。基于该算法思想,定义如下基于区域的HMRF-FCM目标函数
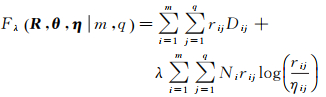 (12)
(12)
式中,第2项为KL散度信息正则化项,用于抑制过分割;λ为模糊度参数;R={rij; i=1, 2, …, m,j=1, 2, …, q}为模糊关系矩阵,rij为模糊关系函数,刻画了第i个区域数据隶属于第j个聚类间的程度;η={ηij; i=1, 2, …, m,j=1, 2, …, q}为标号HMRF先验分布,ηij为区域标号HMRF模型的先验分布,定义为
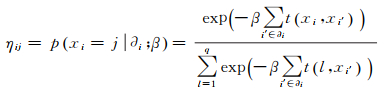 (13)
(13)
Dij为第i个区域数据关于第j类的信息量和,定义为
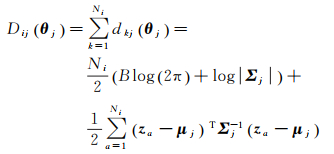 (14)
(14)
基于区域划分的全局最优分割结果即为目标函数式(12)的最小化解。对模糊关系矩阵R的反模糊化就可以得到每个区域的明晰类属性。反模糊化目前一般采用最大化模糊关系的方式进行求解,即
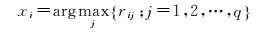 (15)
(15)
目标函数式(12)中的未知参数包括μj、Σj和rij,其中参数μj和Σj为关于目标函数的显式参数,因此分别通过求目标函数关于这两个参数的偏导数进行求解。结果为
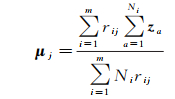 (16)
(16)
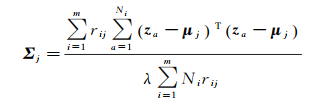 (17)
(17)
模糊关系rij满足约束条件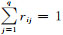
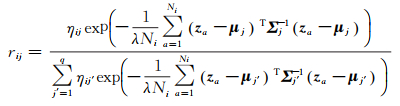 (18)
(18)
综合以上讨论,最优分割算法的流程可总结如下:
(1) 设置循环索引d=0、聚类数q、模糊度参数λ、迭代停止次数T。
(2) 随机初始化模糊关系rij(0)。
(3) 根据式(13)计算标号场的先验分布ηij(d)。
(4) 分别用式(16)、(17)估计聚类分布参数μj(d)和Σj(d)。
(5) 将μj(d)和Σj(d)代入式(18)计算rij(d+1)。
(6) 将rij(d+1)代入式(15)求得xsi(d+1)。
(7) 如果达到停止迭代次数,则退出循环;否则,d=d+1并返回步骤(3)继续迭代。
2 试验与讨论为验证本文图像分割算法的可行性和有效性,在Intel Xeon CPU E5-2670 2.6 GHz/8 G内存/Matlab环境下,对WorldView3 Pan-Sharpen 0.5 m分辨率遥感图像进行了分割试验。如图 2所示,图 2(a)为512×512的待分割图像;图 2(b)为人工判读的分割结果图,包含5个同质区域,分别由灰度值为28(Ⅰ)、75(Ⅱ)、112(Ⅲ)、140(Ⅳ)和255(Ⅴ)5种灰度标识,A其作为标准分割结果,并用于定量评价。首先,为了验证本文算法的有效性和可靠性,设计两个对比试验:①定量分析静态划分算法中尺度参数S、光谱测度参数α和区域形状紧致度权重γ对最终分割结果的影响;②定量分析本文算法和eCognition软件中的多分辨率分割方法以及分水岭算法。其次,为验证本文算法的实用性,对整景WorldView 3遥感图像进行试验。另外,提出本文算法各个参数统一设置如下:FCM停止迭代次数T=30;模糊度参数λ=0.1;标号场邻域作用强度β=0.1。

|
| 图 2 试验数据和标准分割结果 Fig. 2 Experiment image and standard segment |
2.1 静态划分参数对最终分割结果的影响
首先,为了定性和定量评价分割尺度对分割结果的影响,分别对S=40、100、160和220,α=0.9,γ=0.1进行分割试验,试验结果分别如图 3(a1)-(a2)、(b1)-(b2)、(c1)-(c2)和(d1)-(d2)所示。其中,图 3(a1)-(d1)为各静态划分参数下的划分结果。图 3(a2)-(d2)为对应的RHMRF-FCM算法最优分割结果。对比图 3(a1)-(d1)的静态划分结果,随着S的增大,静态划分结果中的过划分现象逐渐减少;对比图 3(a2)-(d2)的最优分割结果,随着尺度参数的增大,分割结果中包含的几何噪声逐渐减少。从视觉上看,图 3(a2)-(d2)中的最优分割结果的复杂地物边界表达较为完整、准确,如图 3黑框部分所示,从而验证了RHMRF-FCM算法的有效性。

|
| 图 3 不同尺度下的分割结果 Fig. 3 Segmentation result from different S |
为了定量评价4个尺度参数S=40、100、160和220的分割精度,采用混淆矩阵[25]作为定量分割精度评价模型,评价结果如表 1所示。由表 1可知,在S为40时,同质区域Ⅲ的用户精度低于0.7。理论上,这是由于在该尺度参数下,初始静态分割结果过分割较为严重,对最优分割过程造成一定程度的扰动;其他尺度参数的各精度指标均在0.7以上,且总精度和Kappa值均优于0.8,说明当尺度参数取[100, 200]时,对分割结果影响较小。另外,在S=100下的各项精度指标总体最优。因此,将S=100作为最优划分尺度,进一步探讨在该尺度参数下,α和γ对静态划分结果和最优分割结果的影响。
| S | 精度指标 | 同质区域 | ||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | ||
| 40 | 用户精度 | 0.92 | 0.90 | 0.68 | 0.99 | 0.81 |
| 产品精度 | 0.85 | 0.80 | 0.87 | 0.96 | 0.85 | |
| 总精度 | 0.87 | |||||
| Kappa值 | 0.84 | |||||
| 100 | 用户精度 | 0.96 | 0.95 | 0.81 | 0.99 | 0.85 |
| 产品精度 | 0.88 | 0.90 | 0.91 | 0.98 | 0.92 | |
| 总精度 | 0.93 | |||||
| Kappa值 | 0.91 | |||||
| 160 | 用户精度 | 0.92 | 0.94 | 0.75 | 0.99 | 0.84 |
| 产品精度 | 0.88 | 0.88 | 0.94 | 0.98 | 0.81 | |
| 总精度 | 0.90 | |||||
| Kappa值 | 0.88 | |||||
| 220 | 用户精度 | 0.88 | 0.94 | 0.72 | 0.99 | 0.81 |
| 产品精度 | 0.85 | 0.87 | 0.91 | 0.97 | 0.76 | |
| 总精度 | 0.88 | |||||
| Kappa值 | 0.86 | |||||
其次,为评价不同α对分割结果的影响,分别对α=0.9、0.8和0.7(S=100,γ=0.1)进行分割试验,试验结果分别如图 3(b1)-(b2)、图 4(a1)-(a2)和(b1)-(b2)所示。其中,图 3(b1)和图 4(a1)-(b1)为各静态划分参数下的划分结果;图 3(b2)和图 4(a2)-(b2)为对应的RHMRF-FCM算法最优分割结果。视觉上,对比各静态划分结果,随着α的减小,静态划分结果的过划分现象略微增加,最优分割结果中的复杂地物边界表达较为完整、准确,如图 3(b1)-(b2)和图 4中的黑框所示。

|
| 图 4 S=100、γ=0.1下不同α的分割结果 Fig. 4 Segmentation result from different α with S=100 and γ=0.1 |
为了定量评价取上述α值所得的分割精度,得到如表 2所示的评价结果。由表 2可知,各α参数的精度指标均在0.8以上,且相互间的差距较小,这说明当α∈[0.7, 0.9]时,本文算法的静态划分结果对最优分割过程影响较小,从而验证算法的稳健性。另外,在α=0.8时的各项精度指标最优。因此,将α=0.8作为最优光谱测度参数,进一步探讨在该参数下,γ对静态划分结果和最优分割结果的影响。
| α | 精度指标 | 同质区域 | ||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | ||
| 0.9 | 用户精度 | 0.94 | 0.94 | 0.80 | 0.99 | 0.84 |
| 产品精度 | 0.89 | 0.89 | 0.89 | 0.98 | 0.91 | |
| 总精度 | 0.91 | |||||
| Kappa值 | 0.90 | |||||
| 0.8 | 用户精度 | 0.96 | 0.95 | 0.83 | 0.99 | 0.85 |
| 产品精度 | 0.88 | 0.90 | 0.92 | 0.98 | 0.92 | |
| 总精度 | 0.93 | |||||
| Kappa值 | 0.91 | |||||
| 0.7 | 用户精度 | 0.95 | 0.93 | 0.82 | 0.99 | 0.93 |
| 产品精度 | 0.95 | 0.90 | 0.89 | 0.98 | 0.91 | |
| 总精度 | 0.92 | |||||
| Kappa值 | 0.90 | |||||
最后,为评价不同区域形状紧致度参数γ对分割结果的影响,分别对γ=0.1、0.2、0.3(S=100,α=0.8)进行分割试验,试验结果如图 4(a1)-(a2)、图 5(a1)-(a2)和(b1)-(b2)所示。其中,图 4(a1)、图 5(a1)-(b1)分别为各静态划分参数下的划分结果。图 4(a2)和图 5(a2)-(b2)分别为对应的RHMRF-FCM算法最优分割结果。视觉上,静态划分结果的过划分现象随着光谱测度参数γ的增大而轻微增大,但对最终的分割结果影响不是很明显。图 5的定量评价结果如表 3所示,表中列出各γ参数的各项精度指标。在γ=0.1时的各项精度指标最优。

|
| 图 5 S=100、α=0.8下不同γ的分割结果 Fig. 5 Segmentation result from different γ with S=100 and α= 0.8 |
| γ | 精度指标 | 同质区域 | ||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | ||
| 0.1 | 用户精度 | 0.96 | 0.95 | 0.83 | 0.99 | 0.85 |
| 产品精度 | 0.88 | 0.90 | 0.92 | 0.98 | 0.92 | |
| 总精度 | 0.93 | |||||
| Kappa值 | 0.91 | |||||
| 0.2 | 用户精度 | 0.86 | 0.91 | 0.89 | 0.98 | 0.92 |
| 产品精度 | 0.95 | 0.93 | 0.81 | 0.99 | 0.85 | |
| 总精度 | 0.92 | |||||
| Kappa值 | 0.90 | |||||
| 0.3 | 用户精度 | 0.86 | 0.89 | 0.87 | 0.98 | 0.90 |
| 产品精度 | 0.95 | 0.93 | 0.77 | 0.99 | 0.82 | |
| 总精度 | 0.91 | |||||
| Kappa值 | 0.89 | |||||
综上所述,初始分割参数中的尺度参数对初始划分结果影响最为明显,而α与γ对初始划分结果影响较小。试验结果表明,S、α和γ分别取[100, 200]、[0.7, 0.9]和[0.1, 0.3]时,尺度参数对最终的分割结果影响较小,从而证明本文算法的稳健性。
2.2 对比试验为验证本文算法的有效性,将本文算法与eCognition 9.0软件中的多分辨率分割方法、分水岭算法结果做定性、定量分析。其中,eCognition软件中的多分辨率分割方法和分水岭算法都是目前高分辨图像分割中常用的方法,但是这两种算法都只包含静态划分部分,并未包含最优分割部分。因此,本试验只用eCognition软件处理得到多分辨率分割方法和分水岭算法的静态划分结果,并导入Matlab中,用本文提出的RHMRF-FCM算法处理得到最优分割结果。算法结果如图 6所示,其中图 6(a1)-(a2)为本文算法在S=100、α=0.8和γ=0.1下处理得到的分割结果;图 6(b1)-(b2)为eCognition软件多分辨率分割算法在相同参数下的分割结果;图 6(c1)-(c2)为eCognition软件分水岭算法在长度因子15下的分割结果。

|
| 图 6 对比算法分割结果 Fig. 6 Segmentation results from comparing algorithms |
从静态划分结果上看,3个算法都能较好地拟合地物的不规则边界;从划分对象的个数上看,多分辨分割算法划分的子区域个数最少,本文算法个数偏多,而分水岭算法的个数太多。但是,对比3个算法的划分结果,依然可以从中发现一些细微的差别。如,本文算法对图像中的地物边缘特征保持得更好,而多分辨率分割方法对于一些弱对比度的边缘保持的效果较差,这是由于本文算法借助图像的MST表达提高了对地物不规则边缘的辨识。而本文算法和多分辨率分割方法均采用顾及光谱测度相似性和形状参数的划分准则,都能较为理想地划分出城市场景中复杂建筑物边缘,而分水岭算法则未考虑形状参数,也在一定程度上使得该算法对大的复杂几何形体划分上呈现过分割的特性。另外,对比3个算法的最优分割结果(图 6(a2)-(c2)),视觉上看复杂地物边界表达较为完整,这也说明了本文提出的最优分割算法的有效性。
3种对比算法的精度评价结果如表 4所示,对比发现本文算法的各项精度指标均优于对比算法,且本文算法的总精度相对于多分辨率分割方法提高了18%,相对于分水岭算法提高了15%。
| 算法名称 | 精度指标 | 同质区域 | ||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | ||
| 本文算法 (100, 0.8, 0.1) |
用户精度 | 0.96 | 0.95 | 0.83 | 0.99 | 0.85 |
| 产品精度 | 0.88 | 0.90 | 0.92 | 0.98 | 0.92 | |
| 总精度 | 0.93 | |||||
| Kappa值 | 0.91 | |||||
| eCognition Multi-Solution分割算法 (100, 0.8, 0.1) |
用户精度 | 0.93 | 0.73 | 0.51 | 0.99 | 0.63 |
| 产品精度 | 0.59 | 0.81 | 0.64 | 0.94 | 0.72 | |
| 总精度 | 0.77 | |||||
| Kappa值 | 0.72 | |||||
| eCognitionWatershet算法 (长度因子15) |
用户精度 | 0.87 | 0.79 | 0.53 | 0.99 | 0.69 |
| 产品精度 | 0.75 | 0.81 | 0.69 | 0.94 | 0.67 | |
| 总精度 | 0.80 | |||||
| Kappa值 | 0.75 | |||||
2.3 整景图像分割试验
为了验证本文算法的实用性,对1景8192×8192的WorldView-3 0.5 m高分遥感图像进行分割试验。分割参数设置为:S=100、α=0.8、γ=0.1和q=6,算法结果如图 7所示。其中,图 7(a1)为原图,黑框区域为局部放大图位置,如图 7(b1)所示;图 7(a2)为原图与划分结果边界叠加图,包含128 587个均质区域;图 7(a3)为最优分割结果;图 7(b2)-(b3)分别为图 7(b1)的分割结果。视觉上看,静态划分结果能较好地划分均质区域,且对复杂地物边界表达较为完整,最优分割结果中各同质区域划分较为合理。算法总体运行时间大约为3 h,对于6千万以上节点规模的MST求解来说,时间上可以接受,从而证明了本文算法的实用性。

|
| 图 7 整景图像分割结果 Fig. 7 Segmentation results of whole scene image |
3 结论
高分辨遥感图像中包含大量的几何噪声,具有地物目标的光谱测度异质性增强等特点,采用传统以像素为基本决策单元的分割方法,容易造成分割结果中包含大量噪声的问题,严重影响分割结果的高层分析应用。为此,本文提出一种结合静态MST划分和区域HMRF-FCM算法的高分辨率遥感图像分割方法。该方法在图像MST表达的基础上,将形状信息引入同质区域的划分中,在有效抑制几何噪声的同时能较好地表达地物目标的不规则边界。在此基础上结合区域HMRF模型构建的模糊目标函数,能够有效克服地物目标光谱测度异质性高的问题。为了验证本文算法的有效性和可行性,以WorldView-3高分遥感图像为试验数据,探讨了静态划分算法中尺度参数、光谱测度参数、区域形状紧致度权重对最终分割结果的影响,以及对比分析了本文算法和eCognition软件中的多分辨率分割方法、分水岭分割方法的分割。试验结果表明,本文算法能有效抑制分割噪声,且能较好地拟合地物的不规则边界,从而自适应、快速有效地分割遥感图像,相对于对比算法,分割精度提高了10%以上。由于该算法较为高效,因此在今后的工作中将该方法应用于大尺度高分辨遥感图像的分割,并设计相应的并行算法,以进一步提高算法的实用性。
| [1] | LI Yu. Remotely sensed data segmentation under a spatial statistics framework[D]. Waterloo: University of Waterloo, 2010. https://uwspace.uwaterloo.ca/handle/10012/4931?show=full |
| [2] |
李德仁, 童庆禧, 李荣兴, 等.
高分辨率对地观测的若干前沿科学问题[J]. 中国科学(地球科学), 2012, 42(6): 805–813.
LI Deren, TONG Qingxi, LI Rongxing, et al. Current issues in high-resolution Earth observation technology[J]. Science China:Earth Sciences, 2012, 42(6): 805–813. |
| [3] |
洪亮.基于对象马尔可夫模型的高分辨率遥感影像分割方法研究[D].武汉: 武汉大学, 2010. HONG Liang. Research on the segmentation of high resolution remote sensing image based on object-oriented Markovian random fields model[D]. Wuhan: Wuhan University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10486-2010166987.htm |
| [4] | ASKARI G, XU Aigong, LI Yu, et al. Automatic determination of number of homogenous regions in SAR images utilizing splitting and merging based on a reversible jump MCMC algorithm[J]. Journal of the Indian Society of Remote Sensing, 2013, 41(3): 509–521. |
| [5] |
王玉, 李玉, 赵泉华.
结合规则划分和M-H算法的SAR图像分割[J]. 武汉大学学报(信息科学版), 2016, 41(11): 1491–1497.
WANG Yu, LI Yu, ZHAO Quanhua. SAR image segmentation combined regular tessellation and M-H algorithm[J]. Geomatics and Information Science of Wuhan University, 2016, 41(11): 1491–1497. |
| [6] |
赵泉华, 李晓丽, 赵雪梅, 等.
结合Voronoi划分HMRF模型的模糊ISODATA图像分割[J]. 信号处理, 2016, 32(10): 1233–1243.
ZHAO Quanhua, LI Xiaoli, ZHAO Xuemei, et al. Fuzzy ISODATA image segmentation integrating Voronoi tessellation HMRF Model[J]. Journal of Signal Processing, 2016, 32(10): 1233–1243. |
| [7] | WANG Ping, WEI Zheng, CUI Weihong, et al. A minimum spanning tree based method for UAV image segmentation[C]//ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences. Prague: [s.n.], 2016: 111-117. http://adsabs.harvard.edu/doi/2016ISPAnIII7..111W |
| [8] |
黎莹, 戴芳, 郝勇, 等.
基于最小生成树的图像分割[J]. 计算机工程与应用, 2013, 49(13): 149–151.
LI Ying, DAI Fang, HAO Yong, et al. Image segmentation based on minimum spanning tree[J]. Computer Engineering and Applications, 2013, 49(13): 149–151. DOI:10.3778/j.issn.1002-8331.1111-0064 |
| [9] | PENG Bo, ZHANG Lei, ZHANG D. A survey of graph theoretical approaches to image segmentation[J]. Pattern Recognition, 2013, 46(3): 1020–1038. DOI:10.1016/j.patcog.2012.09.015 |
| [10] |
巫兆聪, 胡忠文, 张谦, 等.
结合光谱、纹理与形状结构信息的遥感影像分割方法[J]. 测绘学报, 2013, 42(1): 44–50.
WU Zhaocong, HU Zhongwen, ZHANG Qian, et al. On combining spectral, textural and shape features for remote sensing image segmentation[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 44–50. |
| [11] |
李慧, 唐韵玮, 刘庆杰, 等.
一种改进的基于最小生成树的遥感影像多尺度分割方法[J]. 测绘学报, 2015, 44(7): 791–796.
LI Hui, TANG Yunwei, LIU Qingjie, et al. An improved algorithm based on minimum spanning tree for multi-scale segmentation of remote sensing imagery[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 791–796. DOI:10.11947/j.AGCS.2015.20140060 |
| [12] | ZAHN C T. Graph-theoretical methods for detecting and describing gestalt clusters[J]. IEEE Transactions on Computers, 1971, C-20(1): 68–86. |
| [13] |
王平, 魏征, 崔卫红, 等.
一种基于统计学习理论的最小生成树图像分割准则[J]. 武汉大学学报(信息科学版), 2017, 42(7): 877–882.
WANG Ping, WEI Zheng, CUI Weihong, et al. An image segmentation method based on statistics learning theory and minimum spanning tree[J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 877–882. |
| [14] | FELZENSZWALB P F, HUTTENLOCHER D P. Efficient graph-based image segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167–181. |
| [15] |
赵雪梅, 李玉, 赵泉华.
结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割[J]. 电子与信息学报, 2014, 36(11): 2730–2736.
ZHAO Xuemei, LI Yu, ZHAO Quanhua. Image segmentation by fuzzy clustering algorithm combining hidden Markov random field and Gaussian regression model[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2730–2736. |
| [16] |
赵泉华, 李晓丽, 赵雪梅, 等.
结合马氏距离的区域化模糊聚类遥感图像分割[J]. 中国矿业大学学报, 2017, 46(1): 222–228.
ZHAO Quanhua, LI Xiaoli, ZHAO Xuemei, et al. Remote sensing image segmentation algorithm with regional fuzzy cluster and Mahalanobis distance[J]. Journal of China University of Mining & Technology, 2017, 46(1): 222–228. |
| [17] | LUCARINI V. Symmetry-break in Voronoi tessellations[J]. Symmetry, 2009, 1(1): 21–54. |
| [18] | SCHNEIDER R. Weighted faces of Poisson hyperplane tessellations[J]. Advances in Applied Probability, 2009, 41(3): 682–694. DOI:10.1239/aap/1253281060 |
| [19] | ACHANTA R, SHAJI A, SMITH K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274–2282. DOI:10.1109/TPAMI.2012.120 |
| [20] | BANERJEE B, VARMA S, BUDDHIRAJU K M, et al. Unsupervised multi-spectral satellite image segmentation combining modified mean-shift and a new minimum spanning tree based clustering technique[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3): 888–894. DOI:10.1109/JSTARS.2013.2266572 |
| [21] | CUI Weihong, ZHANG Yi. An effective graph-based hierarchy image segmentation[J]. Intelligent Automation & Soft Computing, 2011, 17(7): 969–981. |
| [22] | NARAYAN D, MURTHY S, KUMAR G H. Image segmentation based on graph theoretical approach to improve the quality of image segmentation[J]. Proceedings of World Academy of Science, Engineering and Technology, 2008, 18(1): 35–38. |
| [23] |
杨佳学.大规模图上的最小生成树并行算法研究[D].沈阳: 东北大学, 2013. YANG Jiaxue. Research on the parallel algorithm of the minimum spanning tree on large scale graphs[D]. Shenyang: Northeastern University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10145-1015556214.htm |
| [24] | CHATZIS S P, VARVARIGOU T A. A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation[J]. IEEE Transactions on Fuzzy Systems, 2008, 16(5): 1351–1361. DOI:10.1109/TFUZZ.2008.2005008 |
| [25] | CONGALTON R G, GREEN K. Assessing the accuracy of remotely sensed data:principles and practices[M]. Boca Raton: CRC Press, 2008: 169-190. |



