高光谱遥感影像能够同时提供地物丰富的光谱和空间信息,因此被广泛应用于精细农业、环境监测、城市规划和军事侦察等领域。高光谱影像地物分类则是开展各类应用的重要环节之一,其最终目的是给影像中的每个像元赋予唯一类别标识。然而,高光谱影像的高维和小样本特性使得高光谱影像地物分类仍然面临巨大挑战。为此,支持向量机[1](support vector machine, SVM)、稀疏表达[2]、半监督学习[3]和主动学习[4]等一系列分类方法被用于高光谱影像分类。但在不进行特征提取的情况下,这些分类方法很难在高光谱遥感影像地物分类中取得理想结果。
深度学习方法通过多层的神经网络来提取更加抽象的特征表达,以更好地描述高维数据的复杂结构,进而获得更高的分类和识别精度。卷积神经网络(convolutional neural network, CNN)是深度学习技术中极具代表性的网络模型之一,其能够直接处理高维的二维图像数据,避免了人工设计特征的复杂过程,而是隐式地从训练数据中进行学习,从而降低了分类和识别过程中数据重建的复杂度。由于采用了权值共享机制,使得CNN易于并行实现;此外,CNN对平移、尺度、形状、光照等具有一定程度的不变性。由于具有以上优点,CNN近年来已经被成功用于目标识别、图像理解、机器翻译等不同领域。随着深度学习的快速发展,高光谱研究人员逐渐将深度学习方法用于解决高光谱影像分类问题。堆栈式自编码器[5](stacked autoencoders,SAE)是一种简单有效的深度学习方法,率先被用于高光谱影像分类。随后,一维卷积神经网络[6](1D-CNN)、深度置信网络[7]和循环神经网络[8]也被用于高光谱影像分类。大量的研究成果表明,综合利用光谱和空间特征能够有效提高高光谱遥感影像地物分类的精度。因此,利用二维卷积神经网络[9-13](2D-CNN)提取高光谱影像空间特征,并结合光谱特征,能获得比1D-CNN更好地分类效果。此外,深度学习还与主动学习[14]、半监督分类[15]、迁移学习[16]等方法结合以进一步提高高光谱影像地物分类精度。
近年来,基于深度学习的高光谱遥感影像地物分类方法得到了广泛的研究,并取得了一定进展。但神经网络中通常包含了大量参数,需要大量标注数据对其进行优化。而高光谱遥感影像标注数据费时费力,用于训练的标注数据非常有限。因此无法直接应用大规模的深层网络对高光谱遥感影像地物进行分类。针对此问题,目前主要的研究集中于如何简化网络和减少参数数量,以使深度学习方法适应高光谱遥感影像地物分类小样本的特性。此外,为利用空间特征提高分类精度,现有的深度学习方法一般需要首先使用主成分分析对高光谱影像进行降维预处理,进而采用CNN提取空间特征,最后结合光谱特征进行分类。但降维处理会丢失高光谱数据的细节信息,而这些细节信息很有可能是区别不同地物的判别信息。
针对以上问题,本文通过引入残差学习结构来解决小样本条件下深层网络难以训练的问题,并利用三维卷积来对高光谱影像进行特征提取。三维卷积可直接对高光谱影像进行处理,不需要降维等预处理操作,因此能够更加充分地利用高光谱影像提供的光谱和空间信息。本文构建的深层三维卷积网络能够提取更加抽象的特征表达,且不需要降维预处理,能够提高高光谱遥感影像地物分类精度。在Pavia大学、Indian Pines和Salinas三组高光谱数据集上验证了本文算法的有效性。
1 本文算法 1.1 卷积神经网络CNN最初是受到视觉系统中神经机制的启发,针对二维形状的识别而设计的一种多层感知机。该方法将局部连接、权值共享、空间亚采样三种思想结合起来获得某种程度的平移、尺度、形状不变性,具有对二维图像适应性强的特点。同时,CNN结构的可拓展性很强,它通常由若干卷积层、池化层(下采样层)和全连接层组成,可以采用很深的网络结构。因此,CNN能够处理更复杂的分类和识别问题,并取得较为理想的结果。
卷积层中输出特征图的每个神经元与其输入进行局部连接,并通过对应的连接权值与局部输入进行加权求和再加上偏置,得到该神经元的输出值。在同一个输入特征图和同一个输出特征图中,CNN的权值共享,即使用相同的卷积核。与全连接网络相比,CNN通过局部连接和权值共享,极大地减少了网络中可训练的参数,降低了网络模型复杂度,也降低了过拟合风险,从而获得了更好的泛化能力。具体在第i个卷积层中的第j个特征图中,(x, y)位置的值vijxy根据式(1)计算得到。其中,Pi和Qi为卷积核的大小,m为i-1层特征图个数;v(i-1)k(x+p)(y+p)为i-1层中第k个特征图(x+p, y+q)位置的值;wijkpq为与i-1层第k个特征图相连接的卷积核,bij为偏置;f(·)为激活函数
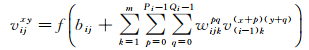 (1)
(1)
池化层完成对卷积层输出特征图的下采样操作,以实现特征对平移、尺度、形状的不变性,同时达到减少训练参数的目的。常见的下采样操作有均值池化和最大池化。卷积神经网络经过若干交替的卷积层和池化层后,将特征输入全连接层和分类器中,并计算损失函数。卷积神经网络的训练目标是使损失函数最小,通常采用反向传播算法进行训练。
1.2 三维卷积CNN最初是针对二维形状的识别而设计,可以直接处理二维图像,建立从底层信号到高层语义的映射关系,并在视觉图像分类和识别中取得了成功。然而,卷积神经网络在对视频等三维数据进行分析时,具有一定局限性。高光谱遥感影像是三维的数据立方体。因此,卷积神经网络在对高光谱遥感影像地物进行分类前需要使用主成分分析等方法进行降维预处理。但降维处理会损失高光谱图像中的细节信息,而这些细节信息往往有助于区分不同地物类别。
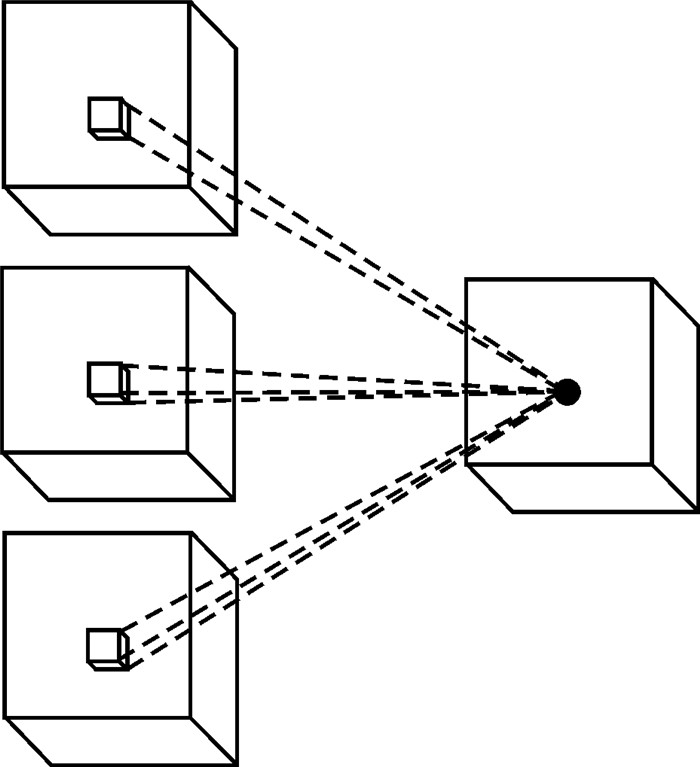
针对二维卷积神经网络对高光谱影像三维结构信息利用不足的问题,本文提出利用三维卷积神经网络对高光谱影像数据立方体进行处理。三维卷积神经网络[17]最早被用于视频分析,该方法通过三维卷积操作可以从不同帧间同时提取空间维和时间维特征,因此能更好地对视频中运动进行分析。三维卷积层与二维卷积层类似,三维卷积操作示意图如图 1所示。在第i个卷积层中的第j个特征图中,(x, y, z)位置的值vijxyz根据式(2)计算得到。其中,Pi、Qi和Ri为三维卷积核的大小,m为i-1层特征图个数;v(i-1)k(x+p)(x+q)(z+r)为i-1层中第k个特征图(x+p, y+q, z+r)位置的值;wijkpqr为与i-1层第k个特征图相连接的卷积核,bi, j为偏置;f(·)为激活函数
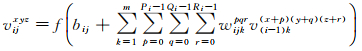 (2)
(2)
|
| 图 1 三维卷积操作示意图 Fig. 1 Illustration of 3D convolution |
1.3 残差学习
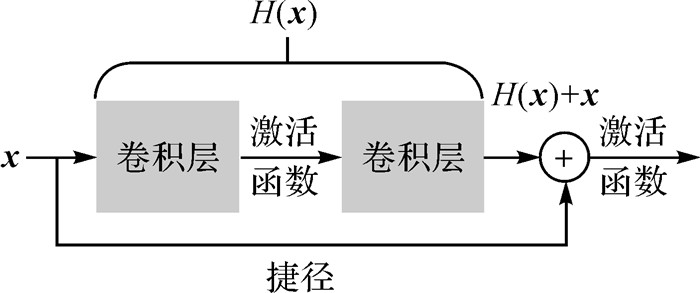
深度学习,即通过卷积等操作,可以将样本在原空间的特征表示变换到新的特征空间,自动地学习得到层次化的特征表示[18]。与传统模式识别方法相比,深层网络具有更多的隐藏层和更复杂的网络结构,因此具有更强的特征学习和特征表达能力。网络的深度对于分类识别任务非常重要,但在有限的训练样本条件下,随着网络深度的增加,神经网络往往存在退化问题,即分类识别的准确率增长的速率会很快达到饱和,甚至下降。文献[19]提出了一种深度残差学习框架来解决网络退化问题。残差学习示意图如图 2所示,假设x为神经网络输入,要拟合的函数映射为F(x),可以定义一个残差映射H(x):=F(x)-x,则原始函数映射F(x)可以表示成H(x)+x。在前馈神经网络中,H(x)+x可以理解为主径H(x)和捷径x的加和,因此并未引入额外参数,不影响原始网络的复杂度,仍然可以利用反向传播算法对网络进行训练。
|
| 图 2 残差学习示意 Fig. 2 Illustration of residual learning |
残差学习的基本思想是在传统网络结构的基础上,引入一条捷径,跳跃绕过一些层的连接与主径相加。引入捷径后,训练过程中的底层误差可以通过捷径向上层传播,缓解了因层数过多而导致的梯度弥散问题,使得深层网络的训练变得容易。
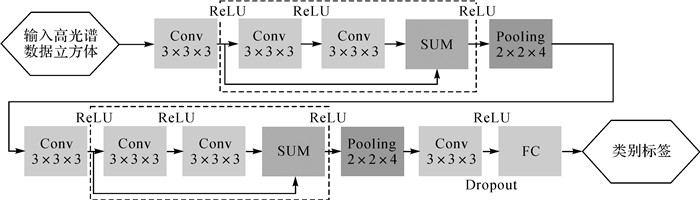
1.4 本文网络结构高光谱遥感影像是典型的三维数据立方体,且标注训练样本费时费力。因此,在应用深层网络对高光谱影像进行分类时,需要面临高维和小样本导致的“维数灾难”问题以及网络退化问题的挑战。为此,本文构建如图 3所示的深层三维卷积网络用于对高光谱遥感影像进行分类。图 3所示的深层三维卷积网络的深度主要体现在具有更多的隐藏层数,该网络由输入层、一个三维卷积层、两个残差学习模块(包含3个三维卷积层)、两个池化层、一个全连接层和输出层组成。表 1给出了常用于高光谱影像分类的深度学习模型包含的隐藏层数和本文网络包含的隐藏层数。由表 1可知,与目前常用于高光谱影像分类的深度学习模型相比,本文网络具有更多的隐藏层数,能够提取和利用更加抽象的深层特征。
|
| 图 3 深度三维卷积网络结构 Fig. 3 Architecture of deep 3D convolution network |
图 3中,Conv表示卷积核大小为3×3×3的三维卷积层,Pooling表示步长2×2×4为池化层,FC表示全连接层。ReLU[20-21](rectified linear units)激活函数相比于传统的Sigmoid和tanh激活函数具有更快的收敛速度。因此,本文所有三维卷积层均采用ReLU激活函数进行非线性映射。ReLU激活函数形式为
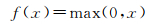 (3)
(3)
图 3中,虚线框内为一个残差学习模块。通常的残差学习模块中包含池化层,这将导致捷径和主径特征维度不同而无法相加,一般的做法是对主径的特征图进行补全或上采用处理。本文对每个三维卷积层的输入进行补全处理,以使得卷积前后的特征图维度相同,且在残差学习模块中不使用池化层,从而实现主径和捷径特征图的相加融合。每个残差学习模块后连接一个步长2×2×4为的池化层,以减少计算量,并对特征进行聚合。高光谱影像通常具有较高的光谱维度,且各波段间存在较强的相关性,即存在大量冗余信息。文献[6]在利用1D-CNN对光谱特征进行分类时,仅使用了一个池化层。因此,使用了较大的池化步长5,以达到快速降低光谱特征维度的目的。鉴于此,本文网络在每个残差模块后连接一个池化层,并将光谱维度池化步长设置为4,而空间维度池化步长均设置为2。然后,将最后一个三维卷积层输出的特征图展成一维向量,与全连接层相连,并在全连接层采用Dropout正则化方法,随机丢弃隐藏层一定比例的节点,以控制过拟合风险。最后,在输出层采用Softmax函数作为激活函数,以完成高光谱影像的多种地物分类任务。Softmax激活函数形式为
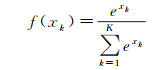 (4)
(4)
本文网络的训练与传统卷积网络训练相同,包含前向网络计算和反向传播两个步骤。首先,将训练样本输入到网络中得到输出的类别标签,并计算相对于已知类别标签的交叉熵损失函数。然后,采用基于反向传播的随机梯度下降法来优化网络参数。
2 试验结果与分析试验的硬件环境为32 G内存、i7-5700Q处理器,GTX970M显卡。试验程序均在Ubuntu16.04系统下,基于谷歌深度学习开源库TensorFlow实现。
2.1 试验数据为验证算法的有效性,使用具有代表性的Pavia大学[22-23]、Indian Pines[24]和Salinas[25]高光谱遥感数据集进行分类试验。
(1) Pavia大学数据集:该数据由ROSIS传感器获得,光谱覆盖范围为430~860 nm,影像大小为610×340像素,空间分辨率为1.3 m,去除受噪声影响的波段后,剩余103个波段可用于分类。该数据集对9种地物进行了标注。地物类别、选取的训练样本数量、确认样本数量以及测试样本数量见表 2。
| 序号 | 地物类别 | 训练样本 | 确认样本 | 测试样本 |
| 1 | 柏油路面 | 180 | 20 | 6631 |
| 2 | 草地 | 180 | 20 | 18 649 |
| 3 | 砖块砂砾 | 180 | 20 | 2099 |
| 4 | 树木 | 180 | 20 | 3064 |
| 5 | 金属板 | 180 | 20 | 1345 |
| 6 | 裸土 | 180 | 20 | 5029 |
| 7 | 沥青屋顶 | 180 | 20 | 1330 |
| 8 | 砖块 | 180 | 20 | 3682 |
| 9 | 阴影 | 180 | 20 | 947 |
| 总数 | 1620 | 180 | 42 776 |
(2) Indian Pines数据集:该数据集由AVIRIS传感器获得,光谱覆盖范围为400~2500,影像大小为145×145像素,空间分辨率为20 m,去除受噪声影响的波段后,剩余200个波段可用于分类。该数据集对16种地物进行了标注。参照文献[24],去除样本数量较少的地物类别,选取样本较多的9种地物进行试验分析。地物类别、选取的训练样本数量、确认样本数量以及测试样本数量见表 3。
| 序号 | 地物类别 | 训练样本 | 确认样本 | 测试样本 |
| 1 | 未耕玉米地 | 180 | 20 | 1428 |
| 2 | 玉米幼苗 | 180 | 20 | 830 |
| 3 | 草地/牧场 | 180 | 20 | 483 |
| 4 | 草地树木 | 180 | 20 | 730 |
| 5 | 干草/料堆 | 180 | 20 | 478 |
| 6 | 未耕大豆地 | 180 | 20 | 972 |
| 7 | 大豆幼苗 | 180 | 20 | 2455 |
| 8 | 整理过的大豆 | 180 | 20 | 593 |
| 9 | 木材 | 180 | 20 | 1265 |
| 总数 | 1620 | 180 | 9234 |
(3) Salinas数据集:该数据集由AVIRIS传感器获得,光谱覆盖范围为430~860,影像大小512×217为像素,空间分辨率为3.7 m,去除受噪声影响的波段后,剩余204个波段可用于分类。该数据集对16种地物进行了标注。地物类别、选取的训练样本数量、确认样本数量以及测试样本数量见表 4。
| 序号 | 地物类别 | 训练样本 | 确认样本 | 测试样本 |
| 1 | 椰菜_绿_野草1 | 180 | 20 | 2009 |
| 2 | 椰菜_绿_野草2 | 180 | 20 | 3726 |
| 3 | 休耕地 | 180 | 20 | 1976 |
| 4 | 粗糙的休耕地 | 180 | 20 | 1394 |
| 5 | 平滑的休耕地 | 180 | 20 | 2678 |
| 6 | 残株 | 180 | 20 | 3959 |
| 7 | 芹菜 | 180 | 20 | 3579 |
| 8 | 未结果实的葡萄 | 180 | 20 | 11 271 |
| 9 | 正在开发的葡萄园土壤 | 180 | 20 | 6203 |
| 10 | 开始衰老的玉米 | 180 | 20 | 3278 |
| 11 | 长叶莴苣4wk | 180 | 20 | 1068 |
| 12 | 长叶莴苣5wk | 180 | 20 | 1927 |
| 13 | 长叶莴苣6wk | 180 | 20 | 916 |
| 14 | 长叶莴苣7wk | 180 | 20 | 1070 |
| 15 | 未结果实的葡萄园 | 180 | 20 | 7268 |
| 16 | 葡萄园小路 | 180 | 20 | 1807 |
| 总数 | 2880 | 320 | 54 129 |
2.2 试验结果与分析
深度三维卷积网络(Res-3D-CNN)结构的设计参考了计算机视觉领域CNN设计的一般经验,即在更高的卷积层,使用更多的卷积核,例如第1个卷积层中使用8个卷积核,在第2个卷积层在使用16个卷积核。在一个残差结构中所有卷积层使用的卷积核数量相同,以确保捷径和主径特征维度相同。表 5给出了不同数据集第一个卷积层使用不同数量的卷积核对应的总体分类精度。表 6给出了不同数据集第一个卷积层使用不同数量的卷积核对应的训练时间。由表 5-6可知,参数数量随着卷积核数量增加而增加,因此使用更多的卷积核需要更多的训练时间;但分类精度在某个数量的卷积核处达到饱和,继续增加卷积核数量,反而会加剧网络退化现象,从而导致分类精度下降。由于不同传感器获取高光谱数据的光谱维度不同,因此,不同传感器高光谱数据的最优卷积核数量也有所不同。根据表 5,对于ROSIS传感器获得的Pavia大学数据最优的卷积核数为32,而对于AVIRIS传感器获得的Indian Pines和Salinas数据最优的卷积核数量为16。
| (%) | |||
| 卷积核数量 | Pavia大学数据集 | Indian Pines数据集 | Salinas数据集 |
| 8 | 93.23 | 89.06 | 94.84 |
| 16 | 94.34 | 93.10 | 95.46 |
| 32 | 96.30 | 90.50 | 93.71 |
| 64 | 92.98 | 84.32 | 92.50 |
| s | |||
| 卷积核数量 | Pavia大学数据集 | Indian Pines数据集 | Salinas数据集 |
| 8 | 649 | 1136 | 2087 |
| 16 | 781 | 1569 | 3411 |
| 32 | 1026 | 3404 | 6208 |
| 64 | 5069 | 9471 | 17 153 |
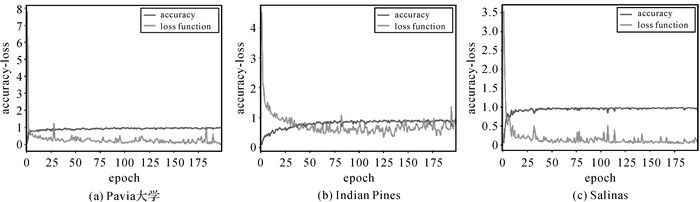
网络结构确定后,利用均值为0、方差为0.1的截断正态分布对卷积层和全连接层的权重进行随机初始化,偏置均初始化为0.1。Dropout参数设置为0.5(即随机关闭隐藏层50%的节点)。采用Adam[26]优化器对网络进行训练,初始学习率设置为0.001。网络训练最大迭代次数为200次,图 4给出了训练过程中损失函数和总体分类精度在确认样本上的变化情况,最后选择在确认样本上分类精度最高的模型对测试数据进行分类。每个样本空间邻域大小参照文献[15]设置为9×9,即输入到网络中的每个样本为9×9×B数据立方体,其中为B波段数。
|
| 图 4 训练过程中损失函数和总体分类精度在确认样本上的变换情况 Fig. 4 The loss function and the overall accuracy on the validating sample during the training procedure |
为验证Res-3D-CNN的有效性,分别与SVM、EMPs[25](Extended morphological profiles)、1D-CNN、去除残差模块的浅层三维卷积网络(S-3D-CNN)、与本文网络结构相同但未加入残差结构的三维卷积网络(3D-CNN)进行对比分析。其中不同分类算法的训练数据、确认数据、测试数据数量均相同,即每个类别地物随机选取200个样本作为训练数据,再从训练数据中随机选取10%作为确认数据集。SVM的核函数为高斯径向基核函数,核函数参数和惩罚系数采用交叉验证的方法在确认数据集上选取最优参数。1D-CNN网络结构与文献[6]中设置相同。EMPs参数设置与文献[25]中设置相同。2D-CNN网络结构与文献[9]中设置相同。1D-CNN、2D-CNN、S-3D-CNN、3D-CNN和Res-3D-CNN均选取在确认数据集上分类精度最高的模型对测试数据进行分类,并与真实地物标记对比评价精度。
表 7-9分别给出了3组数据集对应的分类结果。SVM和1D-CNN仅使用光谱特征进行分类,但由于训练样本数量有限的原因,1D-CNN的分类精度低于SVM。EMPs和2D-CNN均能够综合利用空-谱特征进行分类,因此总体分类精度(overall accuracy, OA)、平均分类精度(average accuracy, AA)和Kappa系数较SVM和1D-CNN有较为明显的提升。这是由于单纯利用光谱特征分类存在“同物异谱, 异物同谱”问题,而综合利用空-谱特征进行分类,加入了空间约束,因此能够改善分类效果。使用2个三维卷积层、2个池化层和一个全连接层的S-3D-CNN在3组数据集上,较EMPs和2D-CNN算法在总体分类精度、平均分类精度和Kappa系数均略有提升,这说明使用三维卷积网络能够更好地利用高光谱影像的三维空-谱特征,但由于训练样本数量较少,精度提升效果不明显。进一步增加三维卷积层数,使用7个三维卷积层、2个池化层和一个全连接层的深层网络(与本文网络层数相同,但未引入残差结构),3D-CNN的网络结构相比于S-3D-CNN更复杂,但分类精度反而下降。这说明在训练样本有限的情况下,用于高光谱影像分类的三维卷积网络也存在退化现象。为克服网络退化现象对分类精度的影响,同时利用深层网络提取更加抽象的特征来改善高光谱影像的整体分类效果,本文在深层网络中引入残差学习,构建了Res-3D-CNN,并在3组数据集上,OA、AA和Kappa系数相比于其他方法均有明显提高,例如Pavia大学数据集,Res-3D-CNN的OA相比SVM、EMPs、1D-CNN和2D-CNN分别提高了7.14%、5.30%、10.13%和4.19%;Indian Pines数据集,Res-3D-CNN的OA相比SVM、EMPs、1D-CNN和2D-CNN分别提高了6.76%、5.87%、10.45%和3.10%;Salinas数据集,Res-3D-CNN的OA相比SVM、EMPs、1D-CNN和2D-CNN分别提高了3.86%、1.92%、7.83%和1.99%。
| (%) | |||||||
| 序号 | SVM | EMPs | 1D-CNN | 2D-CNN | S-3D-CNN | 3D-CNN | Res-3D-CNN |
| 1 | 91.24 | 86.17 | 76.61 | 88.80 | 92.08 | 95.66 | 95.23 |
| 2 | 85.37 | 91.57 | 95.30 | 90.33 | 92.02 | 89.04 | 96.88 |
| 3 | 90.66 | 88.61 | 81.47 | 91.19 | 86.57 | 95.43 | 94.85 |
| 4 | 98.07 | 95.07 | 94.81 | 99.71 | 99.64 | 98.50 | 98.43 |
| 5 | 100.0 | 99.03 | 99.48 | 100.0 | 99.78 | 99.93 | 99.85 |
| 6 | 87.25 | 94.35 | 58.48 | 92.22 | 96.48 | 93.06 | 93.28 |
| 7 | 96.32 | 95.79 | 91.28 | 95.56 | 98.95 | 98.27 | 97.67 |
| 8 | 89.65 | 83.24 | 80.39 | 95.17 | 97.77 | 95.49 | 95.71 |
| 9 | 100.0 | 99.89 | 99.26 | 99.58 | 100.0 | 100.0 | 100.0 |
| OA | 89.16 | 91.00 | 86.17 | 92.11 | 93.96 | 92.96 | 96.30 |
| AA | 93.17 | 92.64 | 86.34 | 94.73 | 95.92 | 96.15 | 96.88 |
| Kappa | 85.96 | 88.24 | 81.56 | 89.72 | 92.12 | 90.83 | 95.11 |
| (%) | |||||||
| 序号 | SVM | EMPs | 1D-CNN | 2D-CNN | S-3D-CNN | 3D-CNN | Res-3D-CNN |
| 1 | 82.49 | 69.75 | 62.89 | 83.75 | 81.93 | 77.52 | 86.55 |
| 2 | 85.54 | 87.71 | 88.31 | 96.14 | 93.25 | 91.45 | 94.58 |
| 3 | 96.89 | 97.93 | 93.79 | 98.96 | 96.69 | 97.10 | 98.96 |
| 4 | 99.59 | 98.77 | 96.85 | 98.77 | 97.26 | 99.18 | 99.86 |
| 5 | 100.0 | 99.79 | 100.0 | 98.74 | 100.0 | 100.0 | 100.0 |
| 6 | 82.82 | 91.87 | 65.84 | 93.93 | 91.05 | 90.95 | 94.75 |
| 7 | 73.93 | 82.57 | 79.96 | 77.72 | 85.74 | 82.77 | 86.97 |
| 8 | 91.74 | 90.56 | 87.86 | 98.65 | 96.29 | 93.93 | 96.46 |
| 9 | 98.66 | 95.10 | 97.94 | 98.02 | 99.92 | 98.74 | 99.84 |
| OA | 86.34 | 87.23 | 82.65 | 90.00 | 91.23 | 89.44 | 93.10 |
| AA | 90.18 | 90.45 | 85.94 | 93.86 | 93.57 | 92.40 | 95.33 |
| Kappa | 84.12 | 85.11 | 79.69 | 88.39 | 89.76 | 87.68 | 91.94 |
| (%) | |||||||
| 序号 | SVM | EMPs | 1D-CNN | 2D-CNN | S-3D-CNN | 3D-CNN | Res-3D-CNN |
| 1 | 99.40 | 99.85 | 97.61 | 98.11 | 100.0 | 100.0 | 99.70 |
| 2 | 99.54 | 99.49 | 99.62 | 99.54 | 98.74 | 99.97 | 100.0 |
| 3 | 99.90 | 100.00 | 99.75 | 98.03 | 99.44 | 97.27 | 98.73 |
| 4 | 99.71 | 99.78 | 100.0 | 100.0 | 100.0 | 99.64 | 99.78 |
| 5 | 97.80 | 97.46 | 72.63 | 98.21 | 99.78 | 99.78 | 99.22 |
| 6 | 99.60 | 99.70 | 99.82 | 100.0 | 100.0 | 99.87 | 100.0 |
| 7 | 99.44 | 98.91 | 99.27 | 97.85 | 99.80 | 99.66 | 99.89 |
| 8 | 79.24 | 81.60 | 92.41 | 87.82 | 85.42 | 78.14 | 89.51 |
| 9 | 99.69 | 98.03 | 99.79 | 96.70 | 98.97 | 99.40 | 99.81 |
| 10 | 94.02 | 97.04 | 90.09 | 96.28 | 97.93 | 97.10 | 97.04 |
| 11 | 99.91 | 98.78 | 98.50 | 98.03 | 100.0 | 99.25 | 98.03 |
| 12 | 99.64 | 100.0 | 99.90 | 99.90 | 100.0 | 99.95 | 100.0 |
| 13 | 98.14 | 99.02 | 99.67 | 100.0 | 100.0 | 99.78 | 99.78 |
| 14 | 99.07 | 99.72 | 94.21 | 99.72 | 100.0 | 99.91 | 99.91 |
| 15 | 75.15 | 85.90 | 37.07 | 79.43 | 79.94 | 90.00 | 85.13 |
| 16 | 98.95 | 99.39 | 99.28 | 94.80 | 99.83 | 99.23 | 99.94 |
| OA | 91.60 | 93.54 | 87.63 | 93.47 | 93.89 | 93.66 | 95.46 |
| AA | 96.20 | 97.17 | 92.48 | 96.53 | 97.49 | 97.43 | 97.90 |
| Kappa | 90.67 | 92.82 | 86.17 | 92.73 | 93.20 | 92.96 | 94.95 |
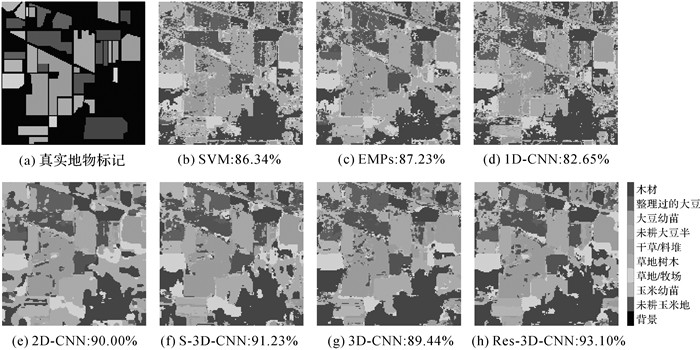
图 5-7给出了不同数据集上不同算法的分类图,Res-3D-CNN分类噪声相比于其他方法更少,获得了最好的分类效果。事实上,图 5-7的结果与表 7-9的结果是一致的。虽然Res-3D-CNN在OA、AA和Kappa系数上相比于其他方法均有明显提高。但对于不同数据集中易于区分的地物类别,Res-3D-CNN分类效果与其他方法相当。如Pavia大学数据集中的第4、5、9类地物,Indian Pines数据集中的4、5、9类地物,Salinas数据集中的除了第8和15类的其他地物类别,这些地物类别的特征与其他地物类别之间区分较为明显,即使使用SVM对光谱特征进行分类也能取得很好的分类效果。Res-3D-CNN对于特征相近容易误分的地物类别的分类精度提升较为明显,因此能改善总体分类效果。

|
| 图 5 各算法在Pavia大学数据集上的分类结果图及其对应的总体分类精度 Fig. 5 Classification maps and overall accuracy with different methods on the University of Pavia dataset |
|
| 图 6 各算法在Indian Pines数据集上的分类结果图及其对应的总体分类精度 Fig. 6 Classification maps and overall accuracy with different methods on the Indian Pines dataset |

|
| 图 7 各算法在Salinas数据集上的分类结果图及其对应的总体分类精度 Fig. 7 Classification maps and overall accuracy with different methods on the Salinas dataset |
2.3 训练样本数量对分类精度的影响
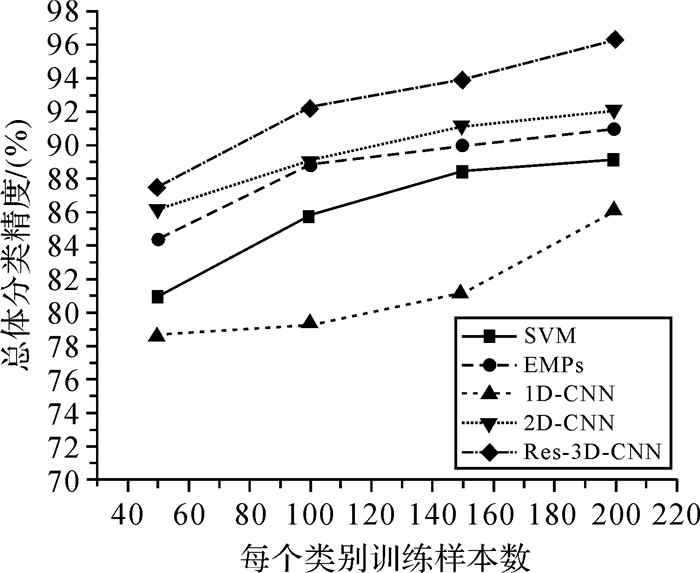
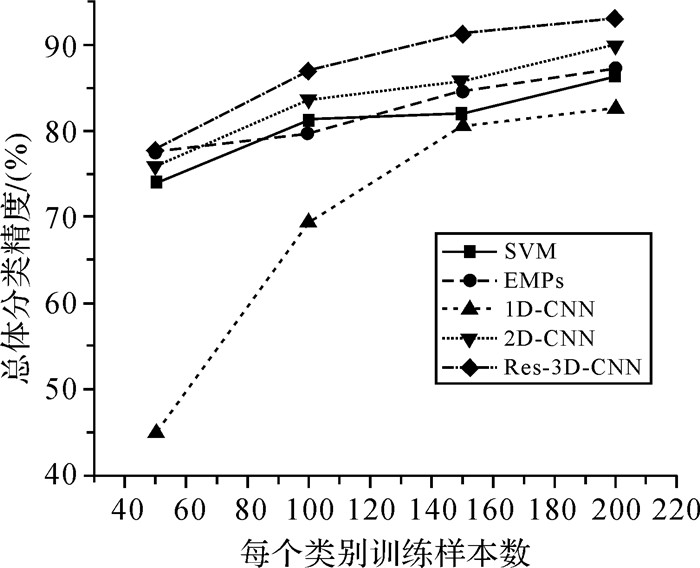
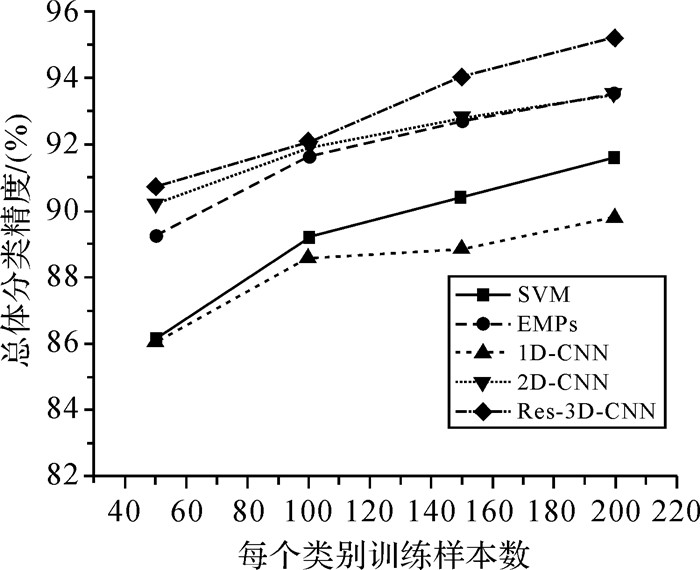
深度网络已经被证明对于大规模数据的分类识别非常有效。但相对于高维的数据结构,高光谱影像通常能够提供的标注样本较少。为分析训练样本数量对本文算法的影响,从每类地物中分别随机选取50、100、150、200个样本作为训练数据(仍然从训练样本中随机选取10%的样本作为确认数据)进行试验。不同分类算法在不同数据集上的总体分类精度如图 8-10所示。由图 8-10可知在进一步减少训练样本数量的情况下,Res-3D-CNN的总体分类精度仍高于SVM、EMPs、1D-CNN和2D-CNN算法。
|
| 图 8 Pavia大学数据集:不同训练样本数目对应的总体分类精度 Fig. 8 Overall accuracy with different number of training samples on the University of Pavia dataset |
|
| 图 9 IndianPines数据集:不同训练样本数目对应的总体分类精度 Fig. 9 Overall accuracy with different number of training samples on the Indian Pines dataset |
|
| 图 10 Salinas数据集:不同训练样本数目对应的总体分类精度 Fig. 10 Overall accuracy with different number of training samples on the Salinas dataset |
为进一步证明Res-3D-CNN在小样本情况下的有效性,从每类地物中随机选取20个样本作为训练数据(仍然从训练样本中随机选取10%的样本作为确认数据)进行试验。表 10给出了不同算法的总体分类精度,Res-3D-CNN仍然能够获得最高的分类精度。这也说明了与SVM和现有的基于深度学习的高光谱影像分类方法相比,本文算法即使在小样本的情况下仍然能够有效提高分类精度。但此时EMP和2D-CNN在Pavia大学数据集和Salinas数据集上的分类精度已经接近Res-3D-CNN的分类精度,进一步减少标记样本数量,则无法保证所设计网络模型的优势。因此,为保证Res-3D-CNN的分类效果,分类时每类地物随机选取的标记样本数量不应少于20个。
| (%) | |||
| Pavia大学数据集 | Indian Pines数据集 | Salinas数据集 | |
| SVM | 68.20 | 66.21 | 85.53 |
| EMP | 77.90 | 66.67 | 86.70 |
| 1D-CNN | 71.41 | 41.24 | 81.33 |
| 2D-CNN | 79.42 | 73.86 | 87.47 |
| Res-3D-CNN | 79.49 | 76.01 | 87.77 |
众所周知,深度学习需要大量的训练样本,Res-3D-CNN主要从3个方面来解决训练样本数量较少时的深度网络训练问题。首先,大量研究表明在高光谱影像分类过程中充分考虑空间信息对最终分类结果的影响,有助于降低分类的不确定性,从而提高分类精度。为此,Res-3D-CNN利用三维卷积网络来充分利用高光谱影像的空-谱信息。然后,深度学习模型通常需要较多的训练样本,且经常面临梯度弥散问题,即采用反向传播算法传播梯度的时候,随着传播深度的增加,梯度的幅度会急剧减小,会导致浅层神经元的权重更新非常缓慢,不能有效学习。为此,Res-3D-CNN在三维卷积网络中引入残差学习结构,来有效缓解梯度弥散问题,使网络的训练变得更加容易。最后,针对训练样本数量较少时,深层网络容易出现的过拟合现象,Res-3D-CNN采用Dropout[27]正则化方法降低过拟合风险。
3 总结与展望本文针对高光谱影像分类高维和小样本的特点,利用三维卷积提取高光谱影像的三维空-谱特征,并利用残差学习模块构建深层网络对高光谱影像进行分类。采用Pavia大学、Indian Pines和Salinas 3组高光谱影像数据集进行试验验证。试验结果表明:①三维卷积网络能够直接以高光谱数据立方体作为输入,不需要事先降维预处理,是一种有效的利用高光谱影像空-谱特征的方法;②在选取较少的训练样本的情况下,残差学习模块能够较好地解决深层网络在高光谱影像地物分类时的退化问题,因此,本文构建的深层三维卷积网络能够有效改善整体分类效果。
虽然本文构建的深层三维卷积网络能够在训练样本有限的情况下改善高光谱遥感影像地物分类精度,但改善效果随着训练样本数量的减少而下降。进一步的研究工作将结合样本增强和半监督学习方法,以期使用更少的训练样本数量,获得更高的分类精度。
| [1] | CAMPS-VALLS G, BRUZZONE L. Kernel-based methods for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(6): 1351–1362. DOI:10.1109/TGRS.2005.846154 |
| [2] |
唐中奇, 付光远, 陈进, 等.
基于多尺度分割的高光谱图像稀疏表示与分类[J]. 光学精密工程, 2015, 23(9): 2708–2714.
TANG Zhongqi, FU Guangyuan, CHEN Jin, et al. Multiscale segmentation-based sparse coding for hyperspectral image classification[J]. Optics and Precision Engineering, 2015, 23(9): 2708–2714. |
| [3] | DÓPIDO I, LI Jun, MARPU P R, et al. Semisupervised self-learning for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7): 4032–4044. DOI:10.1109/TGRS.2012.2228275 |
| [4] |
田彦平, 陶超, 邹峥嵘, 等.
主动学习与图的半监督相结合的高光谱影像分类[J]. 测绘学报, 2015, 44(8): 919–926.
TIAN Yanping, TAO Chao, ZOU Zhengrong, et al. Semi-supervised graph-based hyperspectral image classification with active learning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 919–926. DOI:10.11947/j.AGCS.2015.20140221 |
| [5] | CHEN Yushi, LIN Zhouhan, ZHAO Xing, et al. Deep learning-based classification of hyperspectral data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 2094–2107. DOI:10.1109/JSTARS.2014.2329330 |
| [6] | HU Wei, HUANG Yangyu, LI Wei, et al. Deep convolutional neural networks for hyperspectral image classification[J]. Journal of Sensors, 2015, 2015(7): 220–231. |
| [7] | CHEN Yushi, ZHAO Xing, JIA Xiuping. Spectral-spatial classification of hyperspectral data based on deep belief network[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2381–2392. DOI:10.1109/JSTARS.2015.2388577 |
| [8] | MOU Lichao, GHAMISI P, ZHU Xiaoxiang. Deep recurrent neural networks for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(7): 3639–3655. DOI:10.1109/TGRS.2016.2636241 |
| [9] | YUE Jun, ZHAO Wenzhi, MAO Shanjun, et al. Spectral-spatial classification of hyperspectral images using deep convolutional neural networks[J]. Remote Sensing Letters, 2015, 6(6): 468–477. DOI:10.1080/2150704X.2015.1047045 |
| [10] | YUE Jun, MAO Shanjun, LI Mei. A deep learning framework for hyperspectral image classification using spatial pyramid pooling[J]. Remote Sensing Letters, 2016, 7(9): 875–884. DOI:10.1080/2150704X.2016.1193793 |
| [11] | GHAMISI P, CHEN Yushi, ZHU Xiaoxiang. A self-improving convolution neural network for the classification of hyperspectral data[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(10): 1537–1541. DOI:10.1109/LGRS.2016.2595108 |
| [12] | MEI Shaohui, JI Jingyu, HOU Junhui, et al. Learning sensor-specific spatial-spectral features of hyperspectral images via convolutional neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8): 4520–4533. DOI:10.1109/TGRS.2017.2693346 |
| [13] | LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. Supervised deep feature extraction for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1909–1921. DOI:10.1109/TGRS.2017.2769673 |
| [14] | LIU Peng, ZHANG Hui, EOM K B. Active deep learning for classification of hyperspectral images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(2): 712–724. DOI:10.1109/JSTARS.2016.2598859 |
| [15] | LIU Bing, YU Xuchu, ZHANG Pengqiang, et al. A semi-supervised convolutional neural network for hyperspectral image classification[J]. Remote Sensing Letters, 2017, 8(9): 839–848. DOI:10.1080/2150704X.2017.1331053 |
| [16] | JIAO Licheng, LIANG Miaomiao, CHEN Huan, et al. Deep fully convolutional network-based spatial distribution prediction for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5585–5599. DOI:10.1109/TGRS.2017.2710079 |
| [17] | JI Shuiwang, XU Wei, YANG Ming, et al. 3D convolutional neural networks for human action recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 221–231. DOI:10.1109/TPAMI.2012.59 |
| [18] |
尹宝才, 王文通, 王立春.
深度学习研究综述[J]. 北京工业大学学报, 2015, 41(1): 48–59.
YIN Baocai, WANG Wentong, WANG Lichun. Review of deep learning[J]. Journal of Beijing University of Technology, 2015, 41(1): 48–59. |
| [19] | HE Kaiming, ZHANG Xianyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770-778. http://www.tandfonline.com/servlet/linkout?suffix=CIT0020&dbid=16&doi=10.1080%2F15481603.2018.1426091&key=10.1109%2FCVPR.2016.90 |
| [20] | NAIR V, HINTON G E. Rectified linear units improve restricted Boltzmann machines[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa: Omnipress, 2010: 807-814. https://www.researchgate.net/publication/221345737_Rectified_Linear_Units_Improve_Restricted_Boltzmann_Machines |
| [21] | KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc, 2012: 1097-1105. https://www.researchgate.net/publication/267960550_ImageNe |
| [22] |
黄鸿, 郑新磊.
高光谱影像空-谱协同嵌入的地物分类算法[J]. 测绘学报, 2016, 45(8): 964–972.
HUANG Hong, ZHENG Xinlei. Hyperspectral image land cover classification algorithm based on spatial-spectral coordination embedding[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 964–972. DOI:10.11947/j.AGCS.2016.20150654 |
| [23] |
张春森, 郑艺惟, 黄小兵, 等.
高光谱影像光谱-空间多特征加权概率融合分类[J]. 测绘学报, 2015, 44(8): 909–918.
ZHANG Chunsen, ZHENG Yiwei, HUANG Xiaobing, et al. Hyperspectral image classification based on the weighted probabilistic fusion of multiple spectral-spatial features[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 909–918. DOI:10.11947/j.AGCS.2015.20140544 |
| [24] | LI Wei, WU Guodong, ZHANG Fan, et al. Hyperspectral image classification using deep pixel-pair features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 844–853. DOI:10.1109/TGRS.2016.2616355 |
| [25] | BENEDIKTSSON J A, PALMASON J A, SVEINSSON J R. Classification of hyperspectral data from urban areas based on extended morphological profiles[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 480–491. DOI:10.1109/TGRS.2004.842478 |
| [26] | KINGMA D P, BA J. ADAM: A method for Stochastic optimization[R]. The 3rd International Conference for Learning Representations. San Diego: [s.n.], 2015. |
| [27] | SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout:a simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929–1958. |


