2. 地理国情监测国家测绘地理信息局工程技术研究中心, 陕西 西安 710054
2. Engineering Research Center of National Geographic Conditions Monitoring, National Administration of Surveying, Mapping and Geoinformation, Xi'an 710054, China
合成孔径雷达干涉测量(synthetic aperture radar interferometry,InSAR)已广泛应用于火山、冰川、地面沉降、地震和滑坡等多类地表形变的监测中,成为现代地球学科研究的重要技术之一。InSAR结果的监测精度直接依赖于干涉相位的精度,然而由于热噪声、配准、体散射等失相干因素导致InSAR干涉图往往存在严重噪声,因此需要对干涉图降噪(或称滤波)以获得高精度的测量成果。在干涉图滤波方面,国内外研究大致可分为空间域和频率域两类方法。空间域滤波包括:中值滤波[1]及非局部滤波方法[2]等。频率滤波的方法是针对信号高低频特性进行平滑处理,最常用的有基于傅里叶变换的Goldstein滤波[3]和基于正余弦变换的小波滤波[4],前者应用较为广,且发展出诸多改进算法[5-8]。
这些改进主要集中在Goldstein滤波参数的估计方面,即自适应的滤波参数的确定。文献[5]采用相干值代替了经典的单一滤波参数;文献[6]兼顾了视数和相位标准差对相干值的影响,自适应地估计Goldstein滤波参数;文献[7]以一种不顾及强度信息的伪相干图来确定滤波参数;文献[8]利用同质点计算的无偏相干性并采用稳健估计的非线性滤波参数来进行滤波的。但是在噪声很强的低相干地区,即使最新发展的稳健估计的滤波参数也难以得到令人满意的结果。本文研究从相位时间域信息来进行噪声的滤除。
为克服噪声及失相干的影响,文献[9]提出SqueeSAR算法,分析农田、植被区等分布式目标(distributed scatterers,DS)的统计分布特性,对相位进行优化,通过提高信噪比获取更多的点目标,获取更为完整的形变信息。该方法首先采用KS(Kolmogorov-Smirno)提取的服从同一统计分布的同质像元点,然后采用最大似然估计的方法优化相位值。但是由于SqueeSAR的计算过程不仅要对相干矩阵求逆前进行插入阻尼因子防止负的或过小的特征值,而且需要一个最小的非线性目标函数进行最优化相位的求解,计算比较复杂。文献[10]利用同质点对干涉图进行自适应多视降噪,在非城市区域取得不错的结果。文献[11]首先采用像元分类技术排除水体等非分布式目标,然后采用AD(Anderson-Darling)检验的方法精化同质点,最后采用同质滤波(自适应多视)的方法提高信噪比获取了更多的监测点目标,在煤矿区域获取了更多的形变信息。文献[12]提出了改进的非局部滤波方法,即时空同质滤波。首先采用KS(Kolmogorov-Smirno)检验的方法确定同质点,考虑相位在同质地区具有相关性,然后采用了同质点进行空间的非局部滤波,加权值采用了常规的基于欧氏距离的指数衰减模型来确定。文献[13]提出了CAESAR方法,采用协方差矩阵特征分解的方法对干涉图滤波,其计算效率优于SqueeSAR。但是该方法采用的协方差矩阵分解方法容易受到协方差矩阵的不稳定性影响,从而影响后续的相位解算精度。
本文对干涉图滤波时,首先参考PS与DS方法解算中对每一像元进行时间域协方差矩阵进行稳健估计,然后通过协方差矩阵特征值分解,选取最大特征值对应的特征向量(相位)来代表该像元的相位以进行SAR干涉图的降噪,最后采用真实SAR数据验证了该方法的优越性。
1 协方差矩阵的稳健估计一般认为SAR信号的实部和虚部服从均值为零的复高斯分布,地物目标往往具有空间相关性,服从复高斯分布[9, 14],则任一像元p在N景SAR影像中的观测向量为d(p)=[d1(p)d2(p)…dN(p)]T,其概率密度函数可表示为
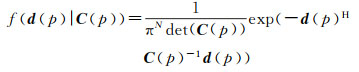 (1)
(1)
式中,C(p)为像元p点SAR数据序列d(p)的协方差矩阵;det(·)表示矩阵行列式运算;H为Hermitian共轭转置。对协方差矩阵C(p)进行极大似然估计可得
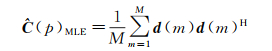 (2)
(2)
式中,M是与任一点p具有相同分布的同质像元个数;m表示p点的同质像元。因此,对于任一像元,识别其同质点是进行协方差矩阵估计的前提。经典的识别同质点方法有基于复观测值本身的散射数据(如强度或者幅度值)进行非参数检验法,如:KS(Kolmogorov-Smirno)检验[9]、AD(Anderson-Darling)检验[15]和BWS(Baumgartner-Weiβ-Schindler)检验[15]等。但由于这类方法选择同质点时计算速度慢,尤其对于大数据集时其效率较差。本文采用基于统计区间估计的方法[16],即
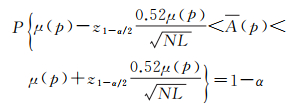 (3)
(3)
式中,μ(p)为p点在N景SAR影像中的幅度值的均值,其估值为A(p)=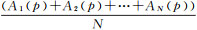
假设待估参数向量X,进行了n次观测,即观测值L=[l1 l2 … lN]T,f是L的概率密度函数,由极大似然估计有
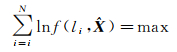 (4)
(4)
胡贝尔将其广义化为
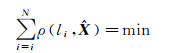 (5)
(5)
同样,联合式(1)和式(2),式(5)可具体化为
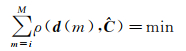 (6)
(6)
则SAR时序观测值d(p)=[d1(p), d2(p), …, dN(p)]T的协方差

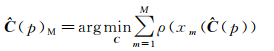 (7)
(7)
式中,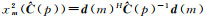

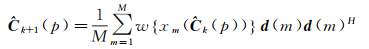 (8)
(8)
式中,w(·)表示等价权函数。一般地,等价权函数w(·)可由式(4)得
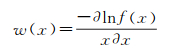 (9)
(9)
在实用中,由于SAR影像中与p点异质的点服从长尾分布,可用复多维t分布表示[17]
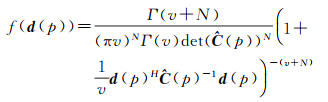 (10)
(10)
式中,v是t分布的自由度;Γ(·)是gamma函数。将式(10)代入式(9),并考虑到复数t分布向实数t分布的变换,可得[18-19]
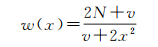 (11)
(11)
为抑制严重的长尾分布的影响,可假设v=0,且有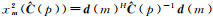
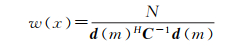 (12)
(12)
式中,C=I·E,I为p点强度的均值,I=A2,E为单位矩阵。则w(x)变为
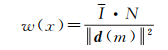 (13)
(13)
最终可得任一点的稳健的协方差矩阵由加权的同质点强度来估计,即
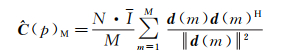 (14)
(14)
该方法又称为符号协方差矩阵,不需迭代也能达到抗差的效果[20]。
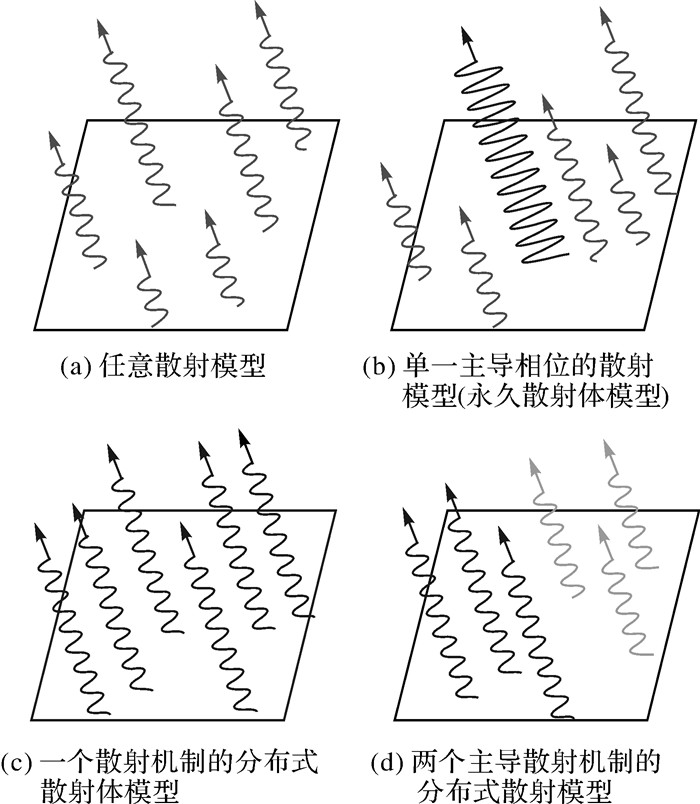
2 协方差矩阵的特征值分解干涉图每一像元的信号矢量中包含多类型的散射信号,图 1所示为SAR像元的不同散射机制模型。图 1(a)表示任意散射机制模型,是SAR影像中常见的散射模型;图 1(b)为永久散射体,即存在单一主导散射机制模型,在强相干区域很常见;图 1(c)为分布式目标的单一主导散射机制模型,主要存在于高分辨率像元内;图 1(d)为分布式目标的多主导散射机制模型,易出现在低分辨率像元内。
由于SAR时间序列数据的像元协方差矩阵的特征值对应不同强度的散射信号,可以通过对每一像元的协方差矩阵进行特征值分解来分离不同散射特征的信号,即
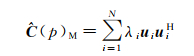 (15)
(15)
式中,λi为非负特征值;(u1, u2, …, uN)为对应的特征向量。不失一般性,令λ1>λ2>…>λN,不同的λi,对应不同的散射相位,λi值越大,其主导的散射相位越占优势,每个λi对应一个独立的散射机制,于是将
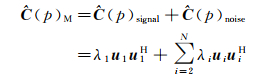 (16)
(16)
因此,对稳健估计的协方差矩阵进行特征值分解后,找出最大的特征值和特征向量,即主导散射体,从而达到对干涉图像元相位降噪的目的。由于本文采用的是高分辨率的TerraSAR-X的Strip模式数据,距离向和方位向的分辨率分别为1.7和0.9 m。分辨率单元内包含了较少的地物目标,所以假设分辨率单元地物类型单一,符合图 1(b)、(c)散射机制模型。因此本文基于稳健估计的协方差矩阵分解的SAR干涉图降噪只考虑单一主导的散射相位。
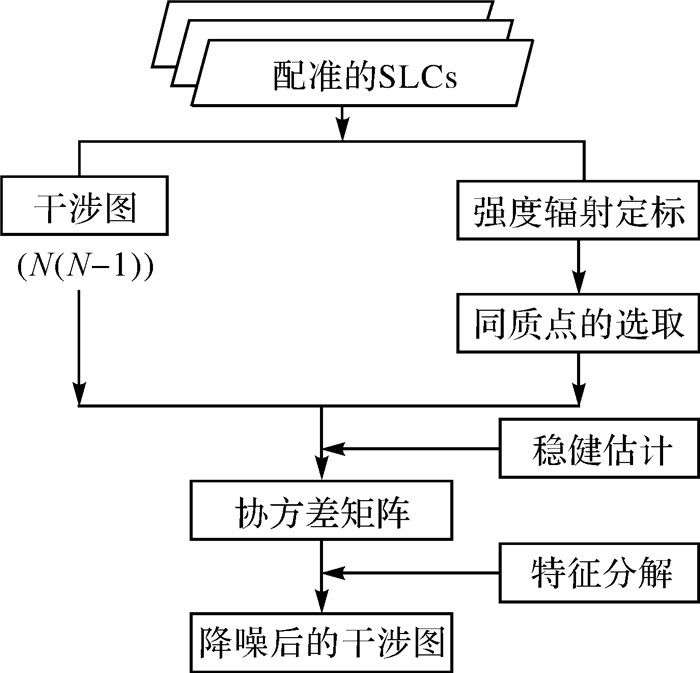
图 2为稳健协方差矩阵分解SAR干涉图降噪流程。该方法首先对多期SAR影像进行配准,并对强度图进行辐射定标;然后基于定标后的SAR强度图根据式(3)逐项元选取同质点;之后采用同质点构建待估像元的稳健协方差矩阵;最后对协方差矩阵进行特征值分解,选取最大特征值对应的特征向量(相位)作为该像元的最终相位值,实现干涉图像元降噪的目的。
|
| 图 2 稳健协方差矩阵分解SAR干涉图降噪流程 Fig. 2 Flowchart of SAR interferogram denoising based on robust covariance matrix decomposition |
3 试验结果与分析 3.1 试验数据
本文采用8景覆盖山西省清徐县地面沉降区域的TerraSAR-X数据进行干涉图去噪试验,其参数列表见表 1,影像中心入射角为23.87°。待去噪干涉图由主影像20151013与从影像20150717组成,时间间隔为88 d,垂直基线为-45.63 m,干涉图大小在SAR坐标系下为4000×4000像素。该区域由于受到地下水开采的影响产生严重的地面沉降和地裂缝等地质灾害等现象[22-24],而地面沉降主要发生在农田等低相干区域。采用常规InSAR滤波方法难以得到有效的形变信息。
| 序号 | 影像获取日期 | 垂直基线/m | 时间基线/d |
| 1 | 2015-07-17 | -45.63 | -88.00 |
| 2 | 2015-08-08 | -118.26 | -66.00 |
| 3 | 2015-08-30 | -38.74 | -44.00 |
| 4 | 2015-10-13* | 0.00 | 0.00 |
| 5 | 2015-11-04 | -79.65 | 22.00 |
| 6 | 2015-12-18 | -1.59 | 66.00 |
| 7 | 2016-01-09 | 15.26 | 88.00 |
| 8 | 2016-02-11 | -198.99 | 121.00 |
| 注:*表示主影像。 | |||
3.2 同质点的选取试验
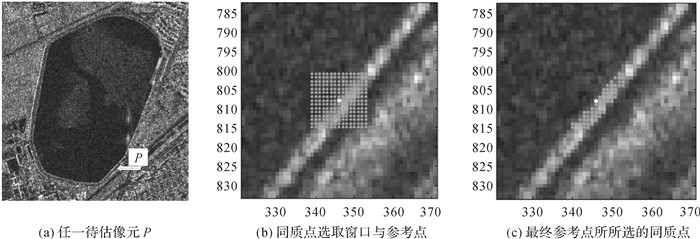
利用式(3)采用8景SAR影像的强度图进行同质点的选取,选取同质点的试验区域如图 3(a)中P点箭头所指示为某一池塘的边缘。图 3(b)中中心白点代表待估计的参考点,本文同质点识别窗口选取15×15个像元,如图 3(b)灰色点阵所示。该窗口对应的实际距离约为30×30 m,充分考虑到形变区域的形变特征(特别是形变梯度)与协方差矩阵的稳定性。图 3(c)为最终确定与该点同质的点。
|
| 图 3 同质点识别示意图 Fig. 3 Sketch map of homogeneous point identification |
图 4(a)为主影像采用同质点进行强度图的降噪图,该图将用于计算协方差矩阵中的强度值,图 4(b)为8景SAR影像的平均强度图,图 4(c)为主影像降噪前的强度图,可见同质点滤波大大抑制了SAR强度图的噪声。

|
| 图 4 强度图噪声滤波前后对比图 Fig. 4 The intensity maps comparison before and after noise filtering |
为比较本文的滤波方法,采用文献[8]提出的非线性滤波参数法(本文称为改进的Goldstein滤波)来进行,即
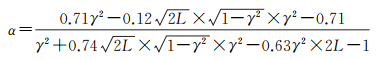 (17)
(17)
式中,γ为无偏估计相干值,位于0~1;L为干涉图视数。
3.3 干涉图降噪对比分析图 5-图 7为原始干涉图、改进的Goldstein滤波和本文方法滤波后的干涉图、相干图及相干直方图。图 5(a)为采用30 m分辨率的外部DEM差分后的原始差分干涉图,图中左上角的条纹为地面沉降信息,但由于失相干的影响,干涉图噪声很严重。由图 5(b)、(c)可以看出干涉图相干性很低,特别在具有形变的农田区域,因此需要进行滤波才能获取有用的地表形变信息。

|
| 图 5 原始干涉图及其质量图 Fig. 5 Original interferogram and its quality map |

|
| 图 6 改进的Goldstein滤波后的干涉图及其质量图 Fig. 6 Filtered interferogram with the improved Goldstein filer and its quality map |

|
| 图 7 本文方法滤波后的干涉图及其质量图 Fig. 7 Denoised interferogram with the proposed method and its quality map |
对比图 5,图 6中改进的Goldstein滤波后的干涉图干涉条纹明显变清晰了,特别在城市等高相干地区。但由于低相干地区相干性改善不明显,干涉条纹仍出现不连续现象。图 6(c)比图 5(c)的整体相干性大大提高,但两个直方图的分布特征类似。如图 7所示,本文方法降噪后的干涉图的条纹变更加清晰,条纹的连续性得到增强,特别是在低相干区域,噪声得到有效的抑制。图 7(c)的相干统计直方图的分布有明显改善,整体相干值显著提升。
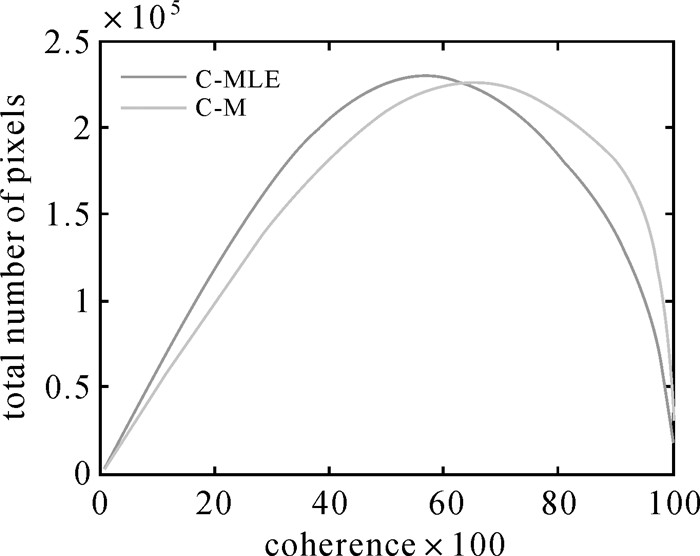
为了对比协方差矩阵稳健估计的效果,对传统协方差矩阵(式(2))分解后的相干值和经过稳健估计的协方差矩阵(式(14))分解后的相干值进行统计,如图 8所示(横轴代表相干性,纵轴代表像元的个数)。由图 8可以看出,经过稳健估计得到的协方差矩阵分解后的干涉图相干性整体有所提升,从8.7e+06提升到9.0e+06。
|
| 图 8 稳健估计(C-M)与传统协方差矩阵(C-MLE)分解后相干性统计图 Fig. 8 Coherent statistical analysis afterdecomposition of robust covariance matrix estimation and traditional covariance matrix estimation |
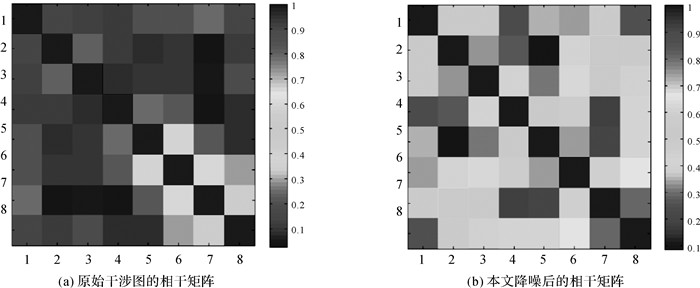
以下选取3个典型的散射点区域,如图 3(a)p1、p2和p3分别对应低相干点(农田)、中等程度的相干点(池塘边)和高相干点(房顶),通过采用本文滤波方法前后相干性矩阵图的变化来展示本文方法降噪的效果,如图 9-图 11所示。图中(a)对应原始干涉图的相干性矩阵,图中(b)对应经过本文降噪后的相干性矩阵,由于本文总共采用8景SAR数据,所以每个点的相干矩阵为8×8。由3个相干性矩阵在滤波前后的对比分析可见,在3类散射区域,本文的降噪方法均能很好地抑制噪声水平,特别对于中低相干区域(见图 9与图 10)。本文算法滤波后,相干性均得到显著提升,这对于增加有效的地表监测点信息至关重要。
为定量分析本文方法的降噪能力,采用相位梯度[25]和相位残差点[9]作为定量评定的指标。相位梯度主要判断相位的平滑程度,利用邻域像元之间的相位差值,计算每个像元八邻域的梯度APD,如式(18)所示,最后计算整个干涉图的梯度和(SPD),如式(19)
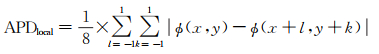 (18)
(18)
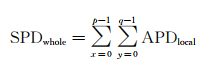 (19)
(19)
式中,ϕ(x, y)代表相位。同样,相位残差点作为评价干涉图的另外一个指标,其利用顺时针计算四邻域的相位闭合差Δk是否为2π的整数倍,即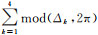
对本文提出的干涉图降噪方法和改进的Goldstein滤波两种方法分别进行了干涉图滤波对比试验,其滤波相位质量统计结果见表 2。首先,相位梯度和(SPD)指标表明,传统的协方差矩阵分解法和改进的Goldstein滤波后的相位梯度和均值分别为0.40 rad和0.53 rad,减少比例比改进的Goldstein滤波方法从15.47%提高到35.27%,而本文具有稳健估计的方法比传统的协方差矩阵分解法从35.27%提高到43.92%,而相位梯度和均值降低至0.35 rad,相比改进的Goldstein滤波,降噪能力提升了2.8倍。其次从相位残差点的统计结果可以看出,本文方法使得干涉图相位残差点由2 635 542个减少到667 200个,减少比例为74.68%,约为改进的Goldstein滤波干涉图的残差点的1/3,可见在低相干区域相位不连续性得到很大的改善。进一步发现稳健估计方法比传统的协方差矩阵分解法的残差点少近1/3,说明稳健的协方差矩阵估计对于干涉图噪声的减弱效果明显。总之,基于协方差矩阵分解的干涉图降噪法比改进的Goldstein滤波在相干性提高与有效目标点的增加方面均有显著效果,特别是在低相干区域的农田等区域。进一步试验发现稳健的协方差矩阵估计法比传统的协方差矩阵分解法的整体相干性又有一定的提高。
| 项目 | 相位梯度和(SPD) | 相位残差点 | |||
| 均值/rad | 减少比例/(%) | 总数 | 减少比例/(%) | ||
| 原始干涉图 | 0.62 | - | 2 635 542 | - | |
| 改进的Goldstein滤波 | 0.53 | 15.47 | 1 797 788 | 31.78 | |
| 传统的协方差矩阵分解 | 0.40 | 35.27 | 923 200 | 64.79 | |
| 本文方法 | 0.35 | 43.92 | 667 200 | 74.68 | |
同样本文采用相位剖线对比原始相位、改进的Goldstein滤波和本文方法,即3种方法的降噪能力及相位精度,如图 7(a)中的P剖线。该条剖线的相位值基本稳定在-1 radian左右,如图 12所示,其中浅色圆点代表原始相位,黑色圆点代表改进的Goldstein滤波,星号点代表本文方法。图 12表明本文方法使得缠绕相位更加平滑,相位噪声得到有效控制,而原始相位基本处于一种随机飘动的状态,改进的Goldstein滤波相位同样噪声表现严重。
4 结论
本文运用基于稳健估计的协方差矩阵分解方法对干涉图进行降噪。该方法基于同质点估计协方差矩阵,对少量引入的异质点采用稳健估计的方法进行处理,理论上保证了协方差矩阵的无偏性;在此基础上对无偏的协方差矩阵进行特征值分解,选取最大特征值对应的特征向量作为单一主导散射体的像元或只含一种散射机制的分布式散射体像元的最终相位,从而达到对干涉图降噪的目的。通过覆盖山西清徐地表形变区域的8景Strip模式的TerraSAR-X数据试验,表明本文降噪方法比改进的Goldstein滤波得到的干涉图条纹更加清晰;定量的相位梯度和与相位残差点对比发现本文提出的降噪方法滤波效果更优,特别在低相干区域的相位相干性得到了明显提高,增加了低相干区域的监测点密度,这对于低相干区域InSAR技术的应用具有重要作用。
| [1] | REES W G, SATCHELL M J F. The effect of median filtering on synthetic aperture radar images[J]. International Journal of Remote Sensing, 1997, 18(13): 2887–2893. DOI:10.1080/014311697217413 |
| [2] | DELEDALLE C A, DENIS L, TUPIN F. NL-InSAR:nonlocal interferogram estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(4): 1441–1452. DOI:10.1109/TGRS.2010.2076376 |
| [3] | GOLDSTEIN R M, WERNER C L. Radar interferogram filtering for geophysical applications[J]. Geophysical Research Letters, 1998, 25(21): 4035–4038. DOI:10.1029/1998GL900033 |
| [4] | LOPEZ-MARTINEZ C, FABREGAS X. Modeling and reduction of SAR interferometric phase noise in the wavelet domain[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(12): 2553–2566. DOI:10.1109/TGRS.2002.806997 |
| [5] | BARAN I, STEWART M P, KAMPES B M, et al. A modification to the Goldstein radar interferogram filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(9): 2114–2118. DOI:10.1109/TGRS.2003.817212 |
| [6] | LI Zhiwei, DING Xiaoli, HUANG C, et al. Improved filtering parameter determination for the Goldstein radar interferogram filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(6): 621–634. DOI:10.1016/j.isprsjprs.2008.03.001 |
| [7] | ZHAO Chaoying, ZHANG Qin, DING Xiaoli, et al. An iterative Goldstein SAR interferogram filter[J]. International Journal of Remote Sensing, 2012, 33(11): 3443–3455. DOI:10.1080/01431161.2010.532171 |
| [8] |
赵文胜, 蒋弥, 何秀凤.
干涉图像第二类统计Goldstein自适应滤波方法[J]. 测绘学报, 2016, 45(10): 1200–1209.
ZHAO Wensheng, JIANG Mi, HE Xiufeng. Improved adaptive Goldstein interferogram filter based on second kind statistics[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1200–1209. DOI:10.11947/j.AGCS.2016.20150457 |
| [9] | FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks:SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460–3470. DOI:10.1109/TGRS.2011.2124465 |
| [10] | GOEL K, ADAM N. An advanced algorithm for deformation estimation in non-urban areas[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 100–110. DOI:10.1016/j.isprsjprs.2012.06.001 |
| [11] | ZHANG Zhengjia, TANG Yixian, ZHANG Hong, et al. Subsidence monitoring in coal area using time-series InSAR combining persistent scatterers and distributed scatterers[C]//Proceedings of 2014 IEEE Geoscience and Remote Sensing Symposium. Quebec City, Canada: IEEE, 2014: 433-436. https://www.sciencedirect.com/science/article/pii/S0303243415000392 |
| [12] |
王明洲, 李陶, 江利明, 等.
地表形变监测的改进相干目标法[J]. 测绘学报, 2016, 45(1): 36–43.
WANG Mingzhou, LI Tao, JIANG Liming, et al. An improved coherent targets technology for monitoring surface deformation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 36–43. |
| [13] | FORNARO G, VERDE S, REALE D, et al. CAESAR:an approach based on covariance matrix decomposition to improve multibaseline-multitemporal interferometric SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2050–2065. DOI:10.1109/TGRS.2014.2352853 |
| [14] | BAMLER R, HARTL P. Synthetic aperture radar interferometry[J]. Inverse Problems, 1998, 14(4): 1–54. DOI:10.1088/0266-5611/14/4/001 |
| [15] | GOEL K, ADAM N. High resolution deformation time series estimation for distributed scatterers using TerraSAR-X data[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012, I-7: 29–34. DOI:10.5194/isprsannals-I-7-29-2012 |
| [16] | JIANG Mi, DING Xiaoli, HANSSEN R F, et al. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1213–1224. DOI:10.1109/TGRS.2014.2336237 |
| [17] | SCHMITT M, SCHÖNBERGER J L, STILLA U. Adaptive covariance matrix estimation for multi-baseline InSAR data stacks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 6807–6817. DOI:10.1109/TGRS.2014.2303516 |
| [18] | WANG Yuanyuan, ZHU Xiaoxiang. Robust estimators for multipass SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 968–980. DOI:10.1109/TGRS.2015.2471303 |
| [19] | OLLILA E, KOIVUNEN V. Influence functions for array covariance matrix estimators[C]//Proceedings of 2003 IEEE Workshop on Statistical Signal Processing. St Louis, MO: IEEE, 2003: 462-465. https://www.researchgate.net/publication/4070522_Influence_functions_for_array_covariance_matrix_estimators |
| [20] | VISURI S, KOIVUNEN V, OJA H. Sign and rank covariance matrices[J]. Journal of Statistical Planning and Inference, 2000, 91(2): 557–575. DOI:10.1016/S0378-3758(00)00199-3 |
| [21] | CAO Ning, LEE H, JUNG H C. A phase-decomposition-based PSInSAR processing method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1074–1090. DOI:10.1109/TGRS.2015.2473818 |
| [22] | ZHANG Qin, ZHU Wu, DING Xiaoli, et al. Two-dimensional deformation monitoring over Qingxu (China) by integrating C-, L-and X-bands SAR images[J]. Remote Sensing Letters, 2014, 5(1): 27–36. DOI:10.1080/2150704X.2013.864789 |
| [23] |
赵超英, 张勤, 张静.
山西清徐地裂缝形变的InSAR监测分析[J]. 工程地质学报, 2011, 19(1): 70–75.
ZHAO Chaoying, ZHANG Qin, ZHANG Jing. Deformation monitoring of ground fissure with SAR interferometry in Qingxu, Shanxi Province[J]. Journal of Engineering Geology, 2011, 19(1): 70–75. DOI:10.3969/j.issn.1004-9665.2011.01.011 |
| [24] |
门玉明, 彭建兵, 李寻昌.
山西清徐县地裂缝灾害现状及类型分析[J]. 工程地质学报, 2007, 15(4): 453–457.
MEN Yuming, PENG Jianbing, LI Xunchang. Present status and classification of ground fissure hazards in Qingxu County Shanxi Province[J]. Journal of Engineering Geology, 2007, 15(4): 453–457. DOI:10.3969/j.issn.1004-9665.2007.04.004 |
| [25] | LI Zhilin, ZOU Weibao, DING Xiaoli, et al. A quantitative measure for the quality of InSAR interferograms based on phase differences[J]. Photogrammetric Engineering & Remote Sensing, 2004, 70(10): 1131–1137. |