2. 海军大连舰艇学院军事海洋与测绘系, 辽宁 大连 116018
2. Department of Military Oceanography and Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China
多波束测深系统实现了从“点”“线”测量到条带式、全覆盖、“面”测量的转变,在精度和效率方面都具有传统单波束测深系统无法比拟的优势[1-2]。作为当前海底地形测量的主流产品,多波束测深系统在获取水深数据的同时,还记录了反向散射强度数据。对于多波束测深数据的处理,经过近30多年的发展已经日趋成熟,形成了较为完善的理论体系和数据处理方法[3-5]。而对于反向散射强度的数据处理及其应用方面,尽管国内外学者进行了相关的研究并取得了一定的研究成果,但由于海底反向散射强度的随机性和复杂性,利用多波束反向散射强度进行海底底质分类仍然是国内外研究的热点问题[6-9]。
海底反向散射强度的研究主要集中在两个方面:一是从能量的观点出发探索海底平均反向散射强度的变化规律;二是采用随机过程的数学方法研究散射强度的统计特性,如分布函数和能量谱等。多波束海底底质分类也是基于这两方面展开的。在平均反向散射强度变化规律分析方面,文献[10]根据声散射在不同角度下的自然特性,将海底反向散射强度随入射角的变化划分为3个区域,并解释了每一个区域海底反向散射强度的主要贡献量。基于文献[10]的工作,文献[11-12]对实测的多波束海底反向散射强度数据进行了处理,提取平均反向散射强度随入射角变化曲线上的显著特征,以此估计海底的底质类型。针对文献[11]方法容差性差的问题,文献[13]提出了综合描述反向散射强度随入射角变化整体信息的参数拟合法。在散射强度统计特性分析方面,主要采用基本统计量、分位数和直方图、功率谱率、灰度共生矩阵和纹理分析等算法从声呐图像上提取特征参数以描述海底底质类型变化[14-18]。这两种方法各有优缺点,第1种方法突出了平均反向散射强度随入射角的变化信息,忽略了反向散射强度的统计特性;第2种方法反映了反向散射强度的统计特性,但没有顾及与入射角的相关性。如果能在一幅图上既能反映平均反向散射强度随入射角的变化信息,又能观察反向散射强度在不同入射角处的统计特性,将增加海底底质分类的特征信息,有望提高海底底质分类的精度和可靠性。
基于此,本文探讨综合反映平均反向散射强度随入射角变化信息及反向散射强度统计信息的强度表示方法,构建反向散射强度随入射角变化的三维概率密度图。针对条带上存在不同海底底质类型时,平均反向散射强度和概率密度极大值会出现系统性偏差或较大波动的情况,提出基于概率密度极大值和次极大值比率的底质边界迭代逼近技术,并通过实例验证分类方法的有效性。
另外,与最新研究成果相比[19-21],本文提出的沿航迹方向的相同入射角的反向散射强度概率密度统计分析方法,通过相同入射角下声强点云的概率曲线分析,规避了海底地形改正模型误差等因素的影响,凸显了海底入射角与反向散射强度的响应关系。该方法更大的优势是可以较为精确地识别不同底质类型的边界,对于海底混合型底质的识别与分类具有重要价值。
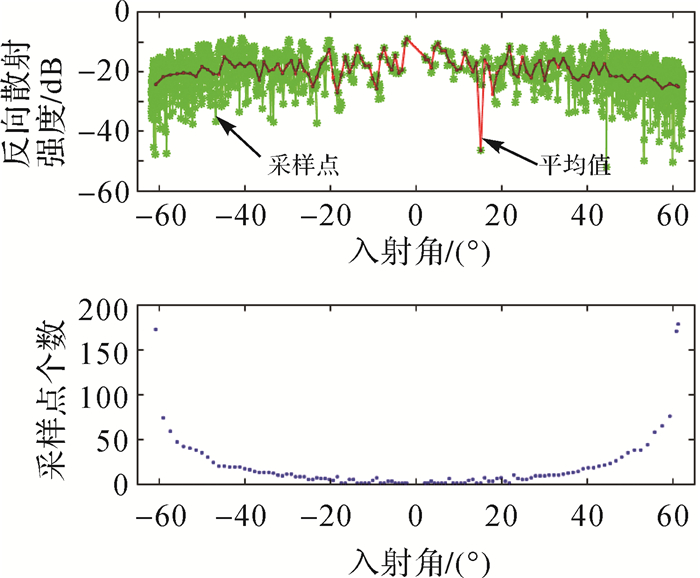
1 反向散射强度随入射角变化的三维概率密度表示一般而言,多波束采用“波束-强度式”记录反向散射强度数据[22],也就是一个波束内记录多个反向散射强度数据。图 1为Simrad EM3000多波束测深系统实测的1 ping反向散射强度数据。随着波束入射角的增加,波束采样点数量增加。由于反向散射强度的随机特性,在相同入射角处,反向散射强度的幅度变化较大,这导致即使将多ping(10 ping)反向散射强度以点云的形式表示(图 2),也很难看出其规律性信息。
|
| 图 1 1 ping数据 Fig. 1 1 ping data |

|
| 图 2 反向散射强度随入射角变化点云数据 Fig. 2 Point cloud data of backscatter strength with incidence angle |
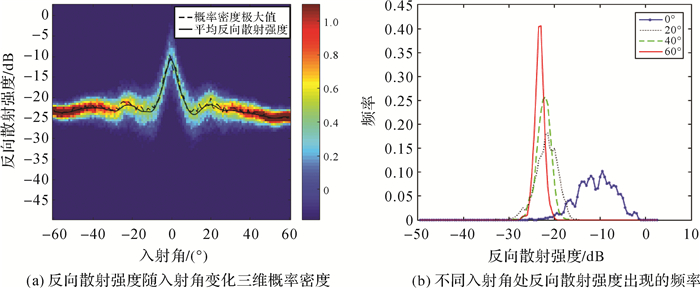
为了直观显示反向散射强度随入射角变化的趋势性信息和分布情况,构建三维概率密度图,如图 3(a)所示。横坐标表示海底入射角,纵坐标表示反向散射强度,在指定入射角处,反向散射强度出现的频率以图右侧的颜色条表示。由图 3(a)既可以直观地看出反向散射强度随入射角变化的趋势性信息,也可以通过不同入射角处反向强度的宽度分析分布特征。图 3(b)分别绘制了入射角为0、20°、40°和60°时不同反向散射强度出现的频率(横坐标为反向散射强度,纵坐标为出现的频率)。由图上可以看出,在指定入射角处,反向散射强度基本呈正态分布,且随着入射角的增加,方差减小。
|
| 图 3 反向散射强度概率密度 Fig. 3 Probability density graph of backscatter strength |
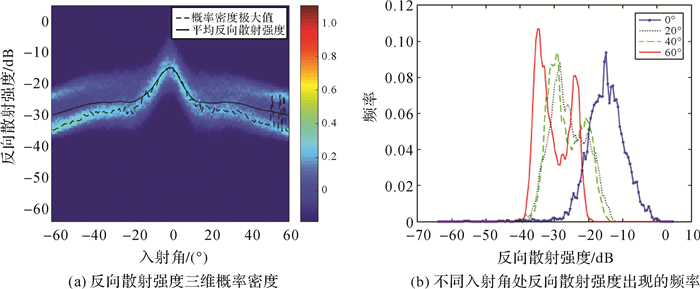
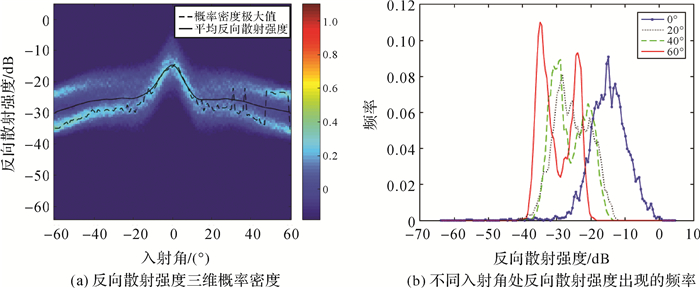
当多波束条带覆盖区域存在不同的海底底质类型时,反向散射强度随入射角变化的趋势性信息和分布都会发生变化,体现在三维概率密度图上,会出现两组趋势性信息,如图 4(a)所示。体现在图 4(b)上,在入射角为20°、40°和60°处,会出现多个峰值,以60°入射角为例,存在主峰fmax主和次峰fmax次。这说明反向散射强度概率密度图能直观反映海底底质类型的变化。
|
| 图 4 不同底质类型反向散射强度的概率密度 Fig. 4 Probability density graph of backscatter strength in different types of substrates |
2 理论模型
反向散射强度随入射角变化的三维概率密度图显示反向散射强度在给定入射角θ处的数量q,用坐标表示为(θ, bs, q)。有研究结果表明[23-25]:在给定入射角处,海底反向散射强度服从K分布,其概率密度函数为
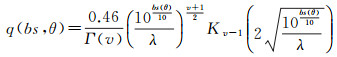 (1)
(1)
式中,Kv-1(·)为第2类v-1阶修正的贝塞尔函数;v为形状参数;λ为尺度参数。
在不同入射角处,反向散射强度的采样率不同,如图 1所示,边缘波束采样率较高(每个波束有上百个采样点),而中央波束采样率较低(有的波束仅采样1个点)。为了在统一尺度上分析反向散射强度随入射角的变化规律,同时简化研究的分布模型,取每个波束的反向散射强度均值作为该波束的反向散射强度值。设每个波束的采样数为N,则均值为
 (2)
(2)
根据中心极限定理,只要母体分布的生矩函数存在,且母体分布偏度不过大,则当N>30时,子样均值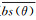
 (3)
(3)
式中,u和σ分别为反向散射强度的均值和方差。假设将多ping反向散射强度以一定间隔划分为M个部分,则在给定入射角θ处,其均值BSmean(θ)和概率密度极大值对应的反向散射强度BSmax(θ)用公式分别表示为
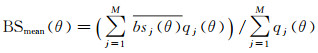 (4)
(4)
 (5)
(5)
由以上分析知,如果多波束条带覆盖区海底底质类型相同,
如果多波束条带覆盖区海底底质类型不同,
由以上分析知,可利用概率密度极大值和反向散射强度的差值Δ(θ)统计信息作为海底底质类型划分的依据
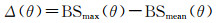 (6)
(6)
如果Δ(θ)随入射角变化呈随机波动且振幅较小,则认为ping覆盖区域为相同的底质类型,如果Δ(θ)呈系统性偏差或波动幅度较大,则认为ping覆盖区域底质类型不同,逐步调整ping范围,以划分海底底质类型边界。
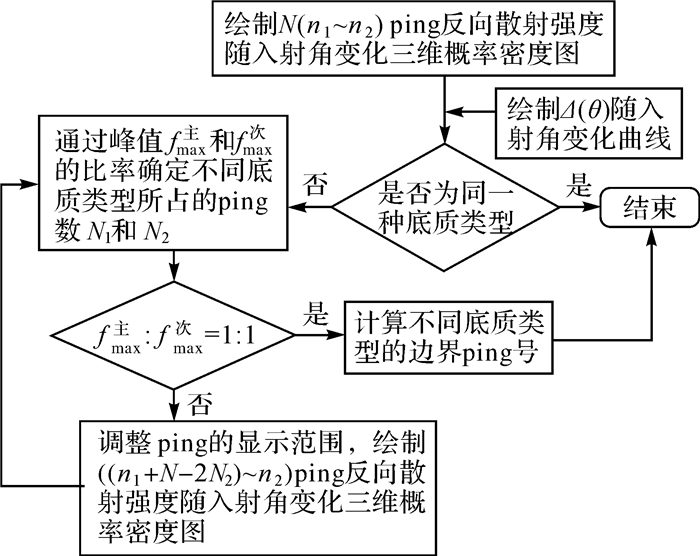
3 海底底质分类的方法流程海底底质分类流程图如图 5所示,具体计算步骤如下:
|
| 图 5 海底底质分类流程 Fig. 5 Flow chart of seafloor classification |
(1) 绘制多ping反向散射强度随入射角变化三维概率密度图,结合Δ(θ),判断ping覆盖海底是否为同一底质类型。
(2) 如果为不同的底质类型,通过在相同入射角θ(一般取40°~60°的某一数值)处的反向散射强度频率峰值fmax主和fmax次的比率确定不同底质类型所占的ping数N1和N2
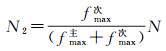 (7)
(7)
式中,N为ping的总数,假设ping的取值为n1~n2,则N=n2-n1。
(3) 以ping数较少的底质类型为基准,即以N2为基准,调整并缩减ping的显示范围,取值为(n1+N-2N2)~n2或n1~(n2-N+2N2)。
(4) 以调整后的ping为基础,重复步骤(1)、(2)、(3),直到fmax主:fmax次=1:1。
(5) 设步骤(4)后,最终显示的ping的总数为N′,显示的ping号为n′1~n′2,则可近似认为底质类型的分界ping号为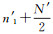
(6) 由于刚开始选取的ping数较多,频率峰值并不能完全反映两种底质类型所占的ping数,因此,以上确定的底质类型分界ping号精度相对较低。为了精确确定底质类型的分界线,需减小显示ping的数量,通常取分界ping号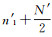
图 4所示数据为EM3000多波束测深系统在青岛胶州湾海域获取的某条带1~3000 ping的数据,将其与海底底质直接采样点数据比较结果为:该覆盖区内海底底质类型为淤泥和粗砂,分界ping号为1820,其中淤泥占1820 ping,粗砂占1180 ping。
选择图 4(b)中60°区域的反向散射强度频率峰值(fmax主=0.107,fmax次=0.081)计算两种底质类型的ping数比,计算结果为N2=1292,根据步骤(3),重新显示416~3000 ping的数据,其三维概率密度图如图 6所示。
|
| 图 6 不同海底底质反向散射强度随入射角变化概率密度(415~3000 ping) Fig. 6 Probability density graph of backscatter strength with incidence angle in different types of substrates(415~3000 ping) |
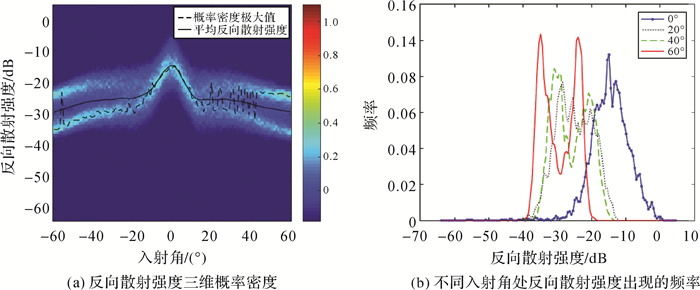
由图 6(b)可以看出,60°倾角处两个峰值频率之间仍存在差值。重复步骤(2)和(3),依据图 6(b)中的频率峰值((fmax主=0.110,fmax次=0.093)),计算得N2=1184,经计算显示ping号为632~3000 ping,三维概率密度图如图 7所示。
|
| 图 7 不同海底底质反向散射强度随入射角变化概率密度(632~3000 ping) Fig. 7 Probability density graph of backscatter strength with incidence angle in different types of substrates(632~3000 ping) |
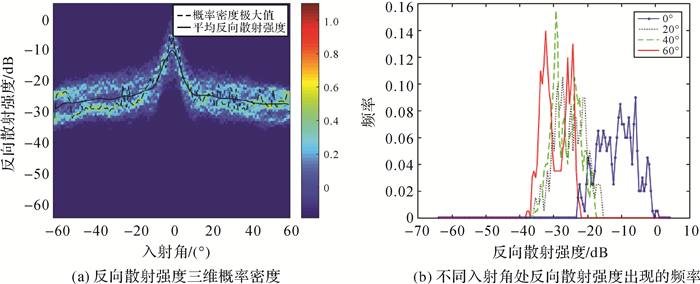
经过以上计算,可概略得到两种底质类型的分界ping号为1816。取1816 ping前后100 ping的数据,生成的概率密度图如图 8所示。依据图 8(b)中的频率峰值((fmax主=0.14,fmax次=0.12)),计算得N2=92,分界ping号为1824。与已知两种海底的分类ping号1820相比,本次分类结果只有4 ping的误差,相当于2 m(本次测量船速为5 m/s,采样率为10 ping/s,4 ping相当于航迹方向上的2 m)的误差。
|
| 图 8 不同海底底质反向散射强度随入射角变化概率密度(1716~1916 ping) Fig. 8 Probability density graph of backscatter strength with incidence angle in different types of substrates(1716~1916 ping) |
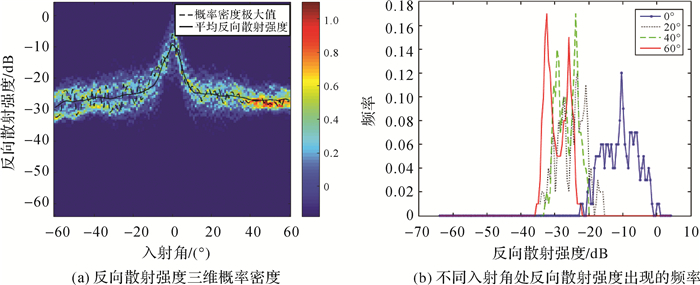
为了进一步说明分类结果的有效性,取分界ping前后50 ping的数据生成概率密度图,如图 9所示。尽管显示的ping数(100 ping),但仍可看出有两个概率密度极大值,证明存在两种底质类型,这也间接说明了该分类方法具有较高的分辨率和精度。由图 9也可以看出,条带左侧与右侧底质类型分界线可能略有不同,因此,也可以将左侧波束和右侧波束分开进行单独讨论。
|
| 图 9 不同海底底质反向散射强度随入射角变化概率密度(1774~1874 ping) Fig. 9 Probability density graph of backscatter strength with incidence angle in different types of substrates(1774~1874 ping) |
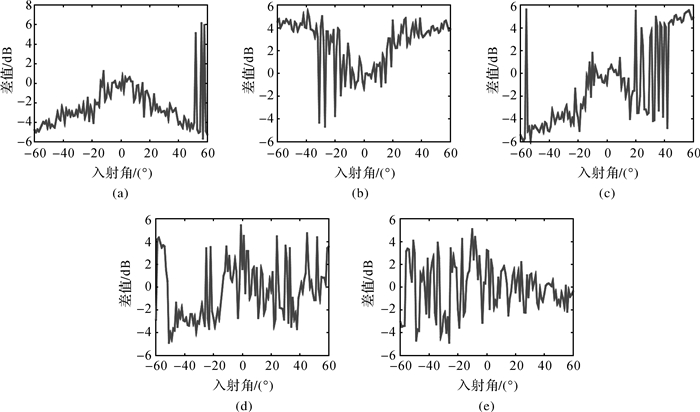
图 10中的(a)-(e)分别为图 4、图 6-图 9显示数据Δ(θ)的变化情况。由图中数据可以看出,随着分界ping的不断优化,Δ(θ)呈现0均值的随机变化。
|
| 图 10 Δ(θ)随入射角变化 Fig. 10 Δ(θ) with incidence angle |
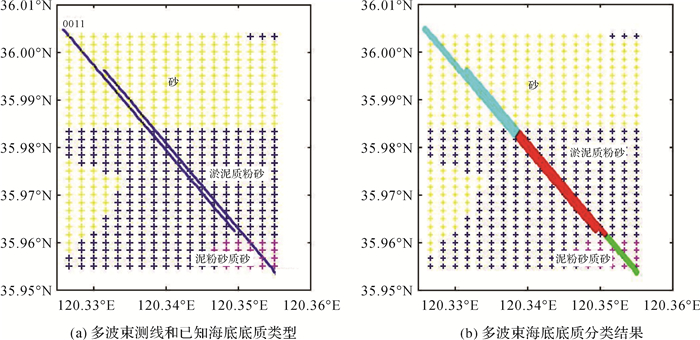
为了进一步说明本文分类方法的有效性,选择已知海底底质类型的区域进行多波束底质分类结果验证。利用离散的海底采样点数据格网化后形成的海底底质类型范围如图 11(a)所示,分别为砂、淤泥质粉砂和泥粉砂质砂。0007和0011为EM3000多波束测量的两条测线,利用本文方法确定海底底质边界线后,分别用红色、绿色、天蓝色表示不同的海底底质类型,如图 11(b)所示。由图 11(b)可以看出,多波束底质分类结果与已知海底类型分布基本一致,这充分说明了本文分类方法的有效性。
|
| 图 11 多波束海底底质分类结果 Fig. 11 Multibeam seafloor substracts classification results |
5 结论
本文构建了多波束反向散射强度随入射角变化的三维概率密度图。该图像既能表达平均反向散射强度随入射角变化的趋势性信息,又能反映反向散射强度的分布特性,可直观表达多波束条带覆盖区内海底底质的种类,便于快速划分海底底质类型数量。对于条带覆盖区内存在多种底质类型的情况,提出了利用给定入射角处反向散射强度频率峰值比率确定不同底质类型ping数的方法,并采用迭代技术,逐步逼近底质类型边界。实例验证结果表明,该方法能有效判别航迹方向上海底底质类型的界线,精度达到10 ping以内。
| [1] |
李家彪, 王小波, 华祖根, 等.
多波束勘测原理技术与方法[M]. 北京: 海洋出版社, 1999.
LI Jiabiao, WANG Xiaobo, HUA Zugen, et al. Multibeam sounding surveying:principle, technology and data processing methods[M]. Beijing: Ocean Press, 1999. |
| [2] |
赵建虎, 刘经南.
多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008.
ZHAO Jianhu, LIU Jingnan. Multibeam bathymetric surveying and image processing[M]. Wuhan: Wuhan University Press, 2008. |
| [3] |
阳凡林, 李家彪, 吴自银, 等.
浅水多波束勘测数据精细处理方法[J]. 测绘学报, 2008, 37(4): 444–450, 457.
YANG Fanlin, LI Jiabiao, WU Ziyin, et al. The methods of high quality post-processing for shallow multibeam data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 444–450, 457. DOI:10.3321/j.issn:1001-1595.2008.04.008 |
| [4] |
王海栋, 柴洪洲, 王敏.
多波束测深数据的抗差Kriging拟合[J]. 测绘学报, 2011, 40(2): 238–242, 248.
WANG Haidong, CHAI Hongzhou, WANG Min. Multibeam bathymetry fitting based on robust Kriging[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 238–242, 248. |
| [5] |
赵荻能, 吴自银, 周洁琼, 等.
声速剖面精简运算的改进D-P算法及其评估[J]. 测绘学报, 2014, 43(7): 681–689.
ZHAO Dineng, WU Ziyin, ZHOU Jieqiong, et al. A method for streamlining and assessing sound velocity profiles based on improved D-P algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 681–689. |
| [6] | SIMMONS S M, PARSONS D R, BEST J L, et al. An evaluation of the use of a multibeam echo-sounder for observations of suspended sediment[J]. Applied Acoustics, 2017, 126(1): 81–90. |
| [7] |
严俊, 张红梅, 赵建虎, 等.
多波束声呐后向散射数据角度响应模型的改进算法[J]. 测绘学报, 2016, 45(11): 1301–1307.
YAN Jun, ZHANG Hongmei, ZHAO Jianhu, et al. Study on improvement of multibeam backscatter angular response model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1301–1307. DOI:10.11947/j.AGCS.2016.20160169 |
| [8] |
何林帮.
基于多波束和浅剖的海底浅表层沉积物分类关键问题研究[J]. 测绘学报, 2016, 45(12): 1498.
HE Linbang. Research on key issues of sediment classification for seabed and sub-bottom based on multi-beam and sub-bottom profile echo intensity[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1498. DOI:10.11947/j.AGCS.2016.20160466 |
| [9] |
金绍华, 翟京生, 刘雁春, 等.
海底入射角对多波束反向散射强度的影响及其改正[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1081–1084.
JIN Shaohua, ZHAI Jingsheng, LIU Yanchun, et al. Influence of seafloor incidence angle on multibeam backscatter intensity and corrected method[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1081–1084. |
| [10] | JACKSON D R, BAIRD A M, Crisp J J, et al. High-frequency bottom backscatter measurements in shallow water[J]. Journal of the Acoustical Society of America, 1986, 80(4): 1188–1199. DOI:10.1121/1.393809 |
| [11] | HUGHES CLARKE J E, DANFORTH B W, VALENTINE P. Areal seabed classification using backscatter angular response at 95kHz[C]//Proceedings of SACLANT Conference on High Frequency Acoustics in Shallow Water. Lerici: NATO SACLANT Undersea Research Centre, 1997. |
| [12] | FONSECA L, MAYER L. Remote estimation of surficial seafloor properties through the application angular range analysis to multibeam sonar data[J]. Marine Geophysical Researches, 2007, 28(2): 119–126. DOI:10.1007/s11001-007-9019-4 |
| [13] |
金绍华, 肖付民, 边刚, 等.
利用多波束反向散射强度角度响应曲线的底质特征参数提取算法[J]. 武汉大学学报(信息科学版), 2014, 39(12): 1493–1498.
JIN Shaohua, XIAO Fumin, BIAN Gang, et al. A method for extracting seabed feature parameters based on the angular response curve of multibeam backscatter strength[J]. Geomatics and Information Science of Wuhan University, 2014, 39(12): 1493–1498. |
| [14] | PACE N G, GAO H. Swathe seabed classification[J]. IEEE Journal of Oceanic Engineering, 1988, 13(2): 83–90. DOI:10.1109/48.559 |
| [15] | AUGUSTIN J M, LE SUAVE R, LURTON X, et al. Contribution of the multibeam acoustic imagery to the exploration of the sea-bottom[J]. Marine Geophysical Researches, 1996, 18(2-4): 459–486. DOI:10.1007/BF00286090 |
| [16] | ENGQUIST B, FREDERICK C, HUYNH Q, et al. Seafloor identification in sonar imagery via simulations of Helmholtz equations and discrete optimization[J]. Journal of Computational Physics, 2017, 338(2): 477–492. |
| [17] | DE MOUSTIER C, MATSUMOTO H. Seafloor acoustic remote sensing with multibeam echo-sounders and bathymetric sidescan sonar systems[J]. Marine Geophysical Researches, 1993, 15(1): 27–42. DOI:10.1007/BF01204150 |
| [18] | PRESTON J. Automated acoustic seabed classification of multibeam images of stanton banks[J]. Applied Acoustics, 2009, 70(10): 1277–1287. DOI:10.1016/j.apacoust.2008.07.011 |
| [19] | COLLIER J S, BROWN C J. Correlation of sidescan backscatter with grain size distribution of surficial seabed sediments[J]. Marine Geology, 2005, 214(4): 431–449. DOI:10.1016/j.margeo.2004.11.011 |
| [20] | MONTEYS X, HUNG P, SCOTT G, et al. The Use of Multibeam backscatter angular response for marine sediment characterisation by comparison with shallow electromagnetic conductivity[J]. Applied Acoustics, 2016, 112(1): 181–191. |
| [21] | HANIOTIS S, CERVENKA P, NEGREIRA C, et al. Seafloor segmentation using angular backscatter responses obtained at sea with a forward-looking sonar system[J]. Applied Acoustics, 2015, 89(2): 306–319. |
| [22] |
金绍华, 翟京生, 刘雁春, 等.
Simrad EM多波束声纳系统回波强度数据的分析与应用[J]. 海洋技术, 2011, 30(1): 48–51.
JIN Shaohua, ZHAI Jingsheng, LIU Yanchun, et al. Analysis and application of echo intensity data in Simrad EM multibeam sonar system[J]. Ocean Technology, 2011, 30(1): 48–51. DOI:10.3969/j.issn.1003-2029.2011.01.012 |
| [23] | HAMILTON L J, PARNUM I. Acoustic seabed segmentation from direct statistical clustering of entire multibeam sonar backscatter curves[J]. Continental Shelf Research, 2011, 31(2): 138–148. DOI:10.1016/j.csr.2010.12.002 |
| [24] | JACKSON D R, BRIGGS K B. High-frequency bottom backscattering:roughness versus sediment volume scattering[J]. Journal of the Acoustical Society of America, 1992, 92(2): 962–977. DOI:10.1121/1.403966 |
| [25] | LE CHENADEC G, BOUCHER J M, LURTON X. Angular dependence of K-distributed sonar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1224–1235. DOI:10.1109/TGRS.2006.888454 |



