2. 中国矿业大学低碳能源研究院, 江苏 徐州 221008
2. Low Carbon Energy Institute, China University of Mining and Technology, Xuzhou 221008, China
基于永久散射体高信噪比、高相干特性,PSInSAR方法能够有效克服传统D-InSAR技术易受失相干、大气效应等因素干扰的难题[1-4]。在探测地表微小形变及长期缓慢形变方面的突出优势使PSInSAR在城区形变监测、滑坡监测、高程修正等方面得到广泛应用[5-7]。楼房、桥梁、道路等人工建筑物作为天然PS点在城区被密集识别,其密度一般高于100个/km2;但在非城区PSInSAR的形变监测能力十分有限,稳定反射物的缺少导致其PS点密度一般不足10个/km2(参见文献[8])。稀疏PS点网络不利于大气相位、线性形变速率和地形残差的精确估计,更无法获取部分关键区的可靠形变信息。为解决这一大难题,国内外学者展开了深入的研究。
目前,主要有两类思路提高非城区PSInSAR适应力:一类是优化外部条件,包括采用TerraSAR-X、Radarsat-2与ALOS-2等高分辨率SAR数据以识别小尺度散射目标,合理布设人工角反射器以提取关键研究区的形变信息等[9-12];另一类是基于经典PSInSAR提出针对性更强的改进算法。第2类算法中,文献[13-14]通过引入空间相干指数筛选PS点,同时改进了地形残差估算模型和解缠模型,提出了斯坦福算法(Stanford method for persistent scatterers, StaMPS);文献[15-16]采用稳定相干指数、振幅离差指数控制其追踪的像元质量,并利用被追踪像元构建Delauney三角网分离线性微分相位和非线性形变(coherent pixels technique, CPT);文献[17-18]通过对距离、方位向上的配准偏移量进行统计、分析,从而提取临时相干点(temporarily coherent point),再通过最小二乘以及粗差探测法解算TCP在时间序列上的线性形变和残余地形信息(TCPInSAR);经典PSInSAR方法创始人Ferretti提出了新的时序干涉算法--SqueeSAR,只要适当地“挤压”每个DS点的相干矩阵以获取优化后DS的相位信息,则DS点可与PS点融入PSInSAR技术框架中进行联合处理[8];文献[19]从放宽限制条件后筛选出的部分相干目标中提取相位信息,显著提高了非城区地表形变监测的空间覆盖率(quasi-PS technique, QPS)。
上述PSInSAR改进算法的不断提出有效增加了有效监测目标在非城区空间分布密度。本文在经典PSInSAR基础上,综合各改进算法的适用性,提出一种改进算法尝试获取试验区靖边县非城区在2014-10-23—2016-05-09期间的可靠形变信息。该算法考虑季节性周期变化,以相干系数作为门槛因子筛选干涉对,其连接图一般不再呈现为放射状特征;利用振幅离差指数、干涉对相干性为双重阈值联合筛选干涉图集中具有稳定散射特性TCT点;构建TCT空间拓扑网解析形变分量和高程修正二维分量,同时引入相关值至迭代计算模型弱化TCT点在相干性较低时的相位贡献,进行差分参数最优解估计;进而利用相邻TCT点大气效应的空间自相关特性分离目标大气延迟相位,反演地形残差和视线方向形变。最终通过与经典PSInSAR对比分析,验证临时相干目标时序分析方法的有效性和可靠性。
1 研究方法 1.1 临时相干目标假设N幅SAR影像覆盖同一范围,在经典PSInSAR中需选择一幅主影像,然后将N-1幅从影像与主影像配准、干涉形成N-1个干涉对,其连接图一般呈现为放射状。放射状干涉组合方式能保证观测期内时序分析的完整性和连通性[20]。SAR影像对中,设主影像为i,从影像为k,那么干涉对(i, k)中某一像元p空间邻近区域内W个像素随机过程平稳,则像元p的相干系数γpi, k可表示为
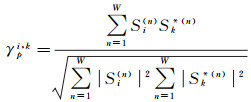 (1)
(1)
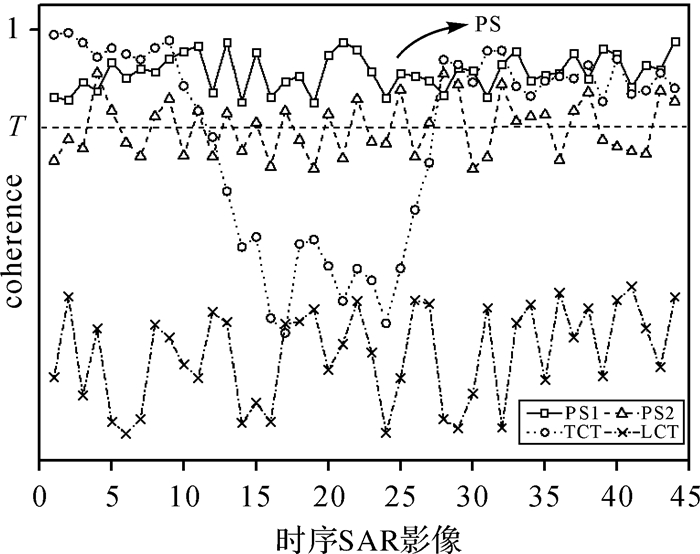
式中,Si(n)、Sk(n)分别表示i、k两个SAR影像的局部像素信息(复数)块;*表示复数共轭算子[1]。以利用相干性选取PS点为例,解释TCT的含义:利用式(1)可算出单个像元在各个观测期内的相干值,同时设PS筛选阈值为T(图 1),可将地表散射体分为4类:①整个观测期内相干性均高于阈值T;②相干值在阈值T上下波动,且
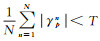
|
| 图 1 地面散射体分类 Fig. 1 Ground scatterer classification |
为利用TCT提取有效形变信息,可通过放宽限制条件同时筛选出TCT与PS,但两者相位稳定性的差别导致PSInSAR方法技术框架不适用于TCT。而本文采用的处理思路是通过放弃单一的超级主影像式SAR影像连接结构,剔除低相干干涉对,以保留TCT信息备后续的识别和利用。同时由于目标约束条件不变,TCT仍具有较高的信噪比和相干质量,因此将TCT融入PSInSAR技术框架进行处理是可行的。
1.2 干涉组合为深度挖掘蕴含在部分时序内高相干点,舍弃了单一放射状时序SAR影像干涉组合方式,采用小基线集(small baseline subset, SBAS)思想,利用相干系数为门槛控制干涉组合质量。与SBAS方法相比,TCT是干涉点目标分析技术,且后者是通过干涉对相干系数控制干涉对质量,而前者采用的是小时空基线方法[21]。
在式(1)的基础上,平均SAR图像内所有像元的相干系数得到干涉对(i, k)的相干值γi, k
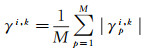 (2)
(2)
式中,M为像元数量。γi, k用于衡量两幅SAR影像干涉相位的质量,相干性越高,则干涉图中蕴含散射特性稳定、相位噪声小的像元越多,有利于临时相干目标识别、大气相位分析及差分参数估计。顾及季节周期性变化,通过相干性筛选干涉对可以一定程度上多选出一些相干性较好的干涉对。
N幅时序SAR数据可以生成CN2对干涉组合。确定门槛值S1的两个约束条件为:①干涉对的相干质量较好;②不同时相SAR影像(i)能作为小基线集的主影像生成至少一组干涉对。本文利用24景时序SAR影像试验,共生产276组干涉对,依据式(2)计算干涉对相干矩阵,结果如图 2所示。干涉对门槛函数可表示为
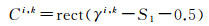 (3)
(3)

|
| 图 2 干涉组合相干值 Fig. 2 Coherence of interferograms |
式中,rect()为矩形函数。当Ci, k=0,表示干涉对被放弃。
根据门槛确定的基本原则,试验中S1取为0.3,干涉对相干矩阵经式(3)计算后结果如图 3(见后文),通过门槛函数的控制,共得到74组干涉对。由图 3可以发现两点:①干涉组合受到试验区气候和季节影响,秋冬季干涉对连接线较为密集说明期间相干质量更好,地物反射特性更稳定;②与不同季节干涉组合相比,同一季节的干涉组合地物反射特性更稳定。可见干涉对相干质量不仅与时空基线相关,也与气候、季节等引起地面目标散射特性变化的因素相关,因此采用相干系数确定干涉组合较SBAS的小基线方法更直接和精确。干涉组合方式通过门槛函数筛选后,干涉对相干质量较高,非城区TCT信息被保留。
|
| 图 3 TCT干涉组合方式 Fig. 3 Interferometric pairs of TCT |
1.3 TCT识别方法
理论上,相干系数和振幅离差指数均能衡量像元相位噪声水平[22]。局部窗口越大,相干系数可靠程度越高,但牺牲了分辨率,导致孤立的TCT难以被提取,因此同时采用振幅离差指数联合筛选干涉图集中TCT。对于SAR复数影像,像元p的振幅值A在标准差σn下服从Rice分布[1, 23]
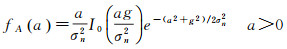 (4)
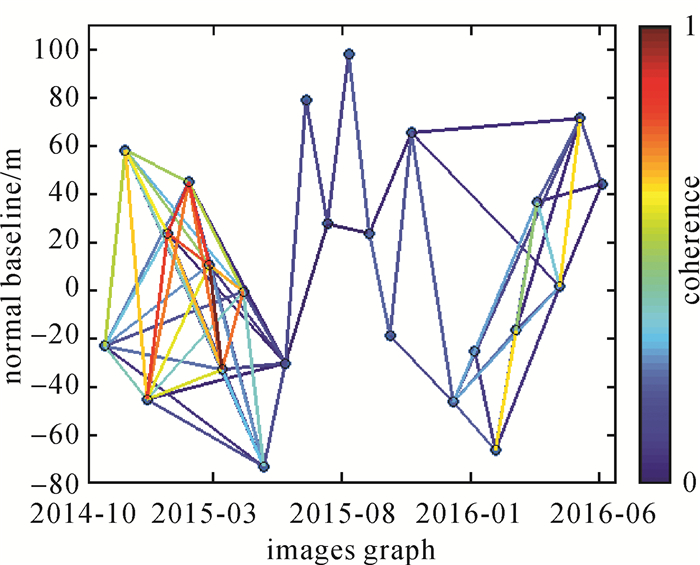
(4)
式中,g为复合反射率;I0为Bessel函数。对于低信噪比(SNR)像元,Rice概率密度函数转换为Rayleigh分布;对于像元(SNR>4),fA(a)趋向于高斯分布。当g≫σn时,则σv=DA,即振幅离差指数DA能够等价衡量相位标准差σv。此时,基于相干系数γpn和振幅离差指数DA双阈值联合筛选法的TCT识别函数模型为
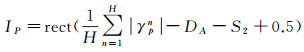 (5)
(5)
式中,rect()为矩形函数;H表示由Ci, k门槛函数筛选后干涉对的总数量;S2为识别阈值。仅当IP=1时,表示像元p被识别为TCT点。
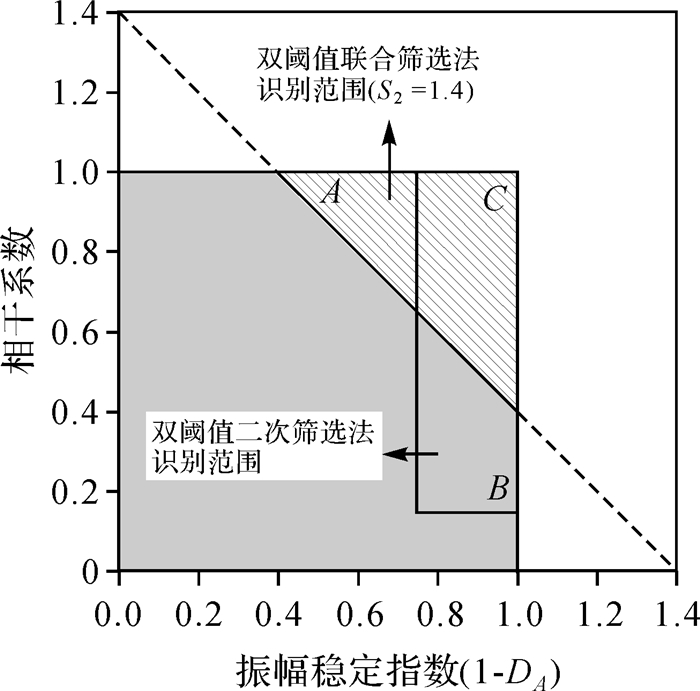
双阈值联合筛选法与双阈值二次筛选法[24]相比,不同之处有二:①目标识别流程简化,相干系数粗筛选和振幅离差指数精筛选的串行流程演变为双阈值并行筛选流程;②目标识别范围异质化。图 4中A、B为双阈值联合筛选和二次筛选的异质区域,C为重叠区域。A对应的振幅稳定指数(1-DA)较小,相干系数较大;而B对应的相干系数较小,振幅稳定指数较大;总体上A区的振幅稳定指数与相干系数和高于B区域。
|
| 图 4 不同双阈值筛选法识别范围 Fig. 4 The distinguished range of different dual-threshold screening methods |
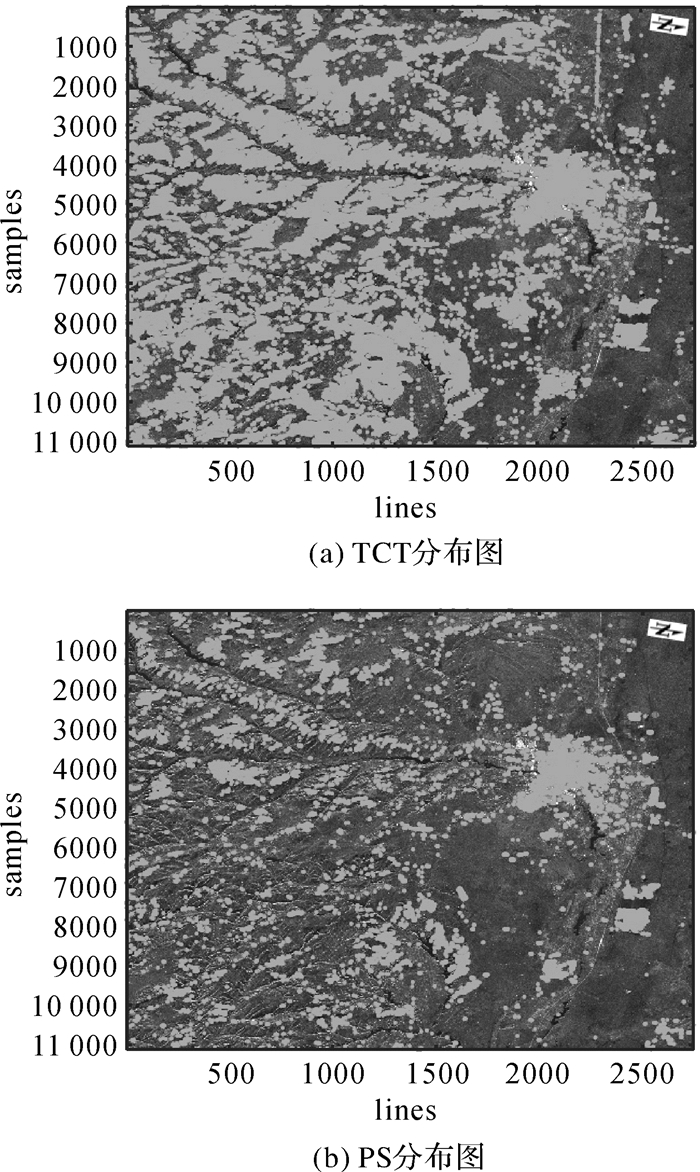
由1.2节中试验干涉组合结果,利用TCT识别函数模型,在74组干涉对里共识别得到119 489个TCT点,其空间分布密度为81个/km2,结果如图 5(a)所示。为对比TCT算法和PSInSAR在非城区形变监测点空间分布,采用相同的识别函数和联合阈值进行PS点探测,结果如图 5(b),经典PSInSAR共识别出25 045个PS点,密度仅为17个/km2。
|
| 图 5 TCT与PS的空间分布 Fig. 5 Spatial distribution of TCTand PS |
1.4 差分参数估计
TCT被有效识别后,需要进一步探讨其干涉相位构成,估计差分参数,分离大气延迟相位,提取地形残差和形变信息。在干涉对(i, k)中某一像元p的初始差分干涉相位ϕpi, k由参考椭球面相位ϕref、地形相位ϕtopo、地表形变相位ϕdef及残余相位ϕres(包含大气延迟、噪声等)构成。利用卫星精密轨道数据以及外部数字高程模型(DEM)去除ϕref、ϕtopo,得
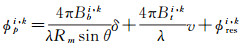 (6)
(6)
式中,Bti, k、Bbi, k表示干涉对(i, k)的时空基线;Rm和θ表示距p点的斜距和雷达波入射角;λ为波长;δ为DEM修正值;v为地表形变速率;ϕresi, k为残余相位。
利用大气空间自相关特性,基于TCT构建Delaunay三角平差网,对连接边上空间邻近的TCT再次进行差分以进一步削弱大气相位影响,进一步说明了稀疏PS点网络不利于大气相位解算和形变信息提取。建立像元p及其连接边上的相邻像元q共H个观测方程,如式(7)
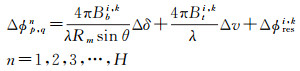 (7)
(7)
由于大气状态在空间尺度上表现出较高自相关特征,且干涉组合中TCT点保持高信噪比,因此可以充分认为|Δϕres| < π。但此时Δϕp, qn仍然是被缠绕的。为求得Δϕp, qn缠绕解除后的值,进而解算ϕpi, k,采用了时序复相干值ξp估计未知参数Δδ和Δv。
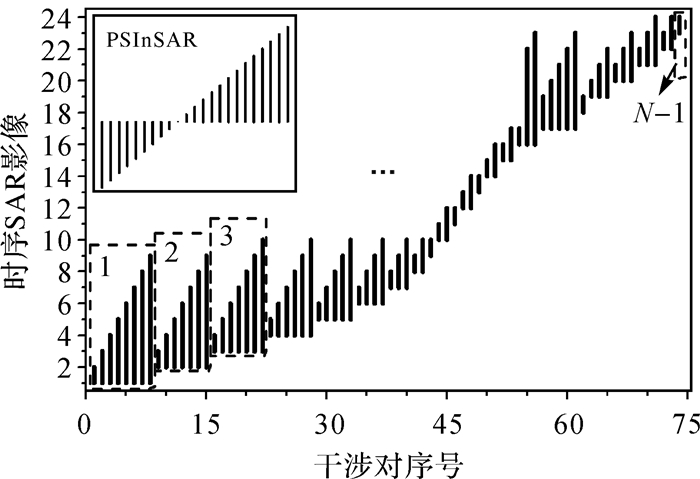
尽管各干涉对中的PS点的相位质量存在波动性,但PS点是通过了整个时序相位稳定性和相干性检验的高质量点,因此PSInSAR对全时序的干涉对相位贡献采用了等权方法解算。双阈值联合筛选出的TCT在所有干涉对中也保持了较高的相位稳定性。仅从时序角度看,TCT点与PS点类似,可采取等权方法进行参数解算。然而TCT方法是考虑季节性变化重建了干涉对连接组合,可能生成以同一SAR影像为主影像的多个干涉对,从而使这些干涉对在共同主影像的时相上对参数解算的贡献难以解析。针对该问题,依据干涉对时相特征将干涉对组合割裂为N-1个小干涉对集,如图 6所示。每个小干涉对集内部采用干涉对相干性衡量不同干涉对对参数解算的贡献程度,并以其为权重弱化低相干干涉对的参数解算贡献,而N-1个小干涉对集采用等权方法。其理由是:①在时间维度上,小干涉对集组块化后可以被视为相对独立的整体,所有小干涉对集的集成维持了全时序的连通性和完整性;②小干涉对集内已采用相干性衡量不同干涉对的参数解算权重;③由双阈值联合法筛选后的TCT在所有干涉对中也是高相干的稳定点,如同PS点。
|
| 图 6 时序SAR影像干涉对时间基线图 Fig. 6 Temporal intervals of the multitemporal SAR image pairs |
因此本文提出了基于TCT的时序复相干值ξp计算模型
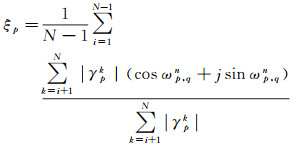 (8)
(8)
式中,ωp, qn为模型残差,表示差分模型相位和观测相位Δϕp, qn的残值,干涉对(i, k)均通过了式(3)门槛,且i < k,j为虚数单位。割裂干涉对组合为小干涉对集进而解算全时序干涉复相干值ξp,既赋予了不同相干性干涉对相位贡献的差异性,也突出了小干涉对集相位贡献的时序意义。当|ξp|取得最大值时,模型与观测相位契合程度最高,其对应的参数Δδ、Δv为最佳估值,即
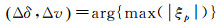 (9)
(9)
最后,利用经典PSInSAR算法,由最佳估值点解缠起始,利用Delaunay网络边对Δδ、Δv进行积分迭代运算得到TCT点线性形变速率和高程修正值,并分离出大气延迟相位和非线性形变相位[1, 25]。
2 试验结果 2.1 试验区及数据概况以陕西榆林市靖边县为试验区域验证基于临时相干目标方法在非城区地表形变监测应用的有效性。该区北部为风沙滩区,南部为丘陵沟壑、梁峁涧区,总面积约为1470 km2。结合图 7和图 5,A为靖边县城建成区,人工建筑的稳定反射特性使其范围内有密集分布的TCT点;B为丘陵沟壑区,蕴藏着丰富的石油资源,并有中国第一个全产业链CO2-EOR试点项目在此开展,CO2封存和石油开采活动可能会引起地表形变,该区域被识别出分布较为密集的TCT;C为风沙滩区,该区被识别的TCT点密度极低,存在大量的低信噪比LCT点。

|
| 图 7 试验区光学影像(Landsat8, 假彩色合成6/5/4) Fig. 7 Optical images of the experimental area (Landsat8, false color composite 6/5/4) |
试验获取的24景C波段Sentinel-1A卫星影像为干涉宽(interferometric wide swath, IW)观测模式的SLC数据,IW模式下影像空间分辨率为5×20 m,其时间跨度为2014-10-23-2016-05-09,入射角约为43°。表 1列出了采用SAR数据的成像日期、时空基线和多普勒质心频率差(以2015年3月28日为基点)。采用ESA提供的精密轨道数据进行配准、参考面相位去除等处理。采用日本宇宙航空研究开发机构(JAXA)发布的AW3D30数字高程模型为参考DEM去除地形相位。该数据由5 m分辨率DSM重采样得到,分辨率、高程精度和时效性突出优势使其更利于后续的地形相位去除、地形残差估值。
| 序号 | 成像日期 | 空间基线/m | 时间基线/d | Dopper质心频率差/Hz |
| 1 | 2014-10-23 | -22.681 | -156 | 0.01 |
| 2 | 2014-11-16 | 58.763 | -132 | 0.003 |
| 3 | 2014-12-10 | -44.801 | -108 | 0.048 |
| 4 | 2015-01-03 | 24.136 | -84 | 0.072 |
| 5 | 2015-01-27 | 45.450 | -60 | 0.074 |
| 6 | 2015-02-20 | 11.153 | -36 | 0.073 |
| 7 | 2015-03-04 | -32.399 | -24 | 0.014 |
| 8 | 2015-03-28 | 0 | 0 | -0.006 |
| 9 | 2015-04-21 | -72.814 | 24 | 0.003 |
| 10 | 2015-05-15 | -29.746 | 48 | 0.05 |
| 11 | 2015-06-08 | 79.644 | 72 | 0.081 |
| 12 | 2015-07-02 | 28.045 | 96 | 0.07 |
| 13 | 2015-07-26 | 98.397 | 120 | 0.024 |
| 14 | 2015-08-19 | 24.157 | 144 | -0.048 |
| 15 | 2015-09-12 | -18.234 | 168 | -0.012 |
| 16 | 2015-10-06 | 65.985 | 192 | -0.002 |
| 17 | 2015-11-23 | -45.986 | 240 | 0.061 |
| 18 | 2015-12-17 | -24.837 | 264 | 0.064 |
| 19 | 2016-01-10 | -65.994 | 288 | 0.05 |
| 20 | 2016-02-03 | -16.020 | 312 | 0.031 |
| 21 | 2016-02-27 | 37.287 | 336 | 0.071 |
| 22 | 2016-03-22 | 2.175 | 360 | -0.057 |
| 23 | 2016-04-15 | 71.927 | 384 | -0.018 |
| 24 | 2016-05-09 | 44.735 | 408 | 0.012 |
2.2 试验结果
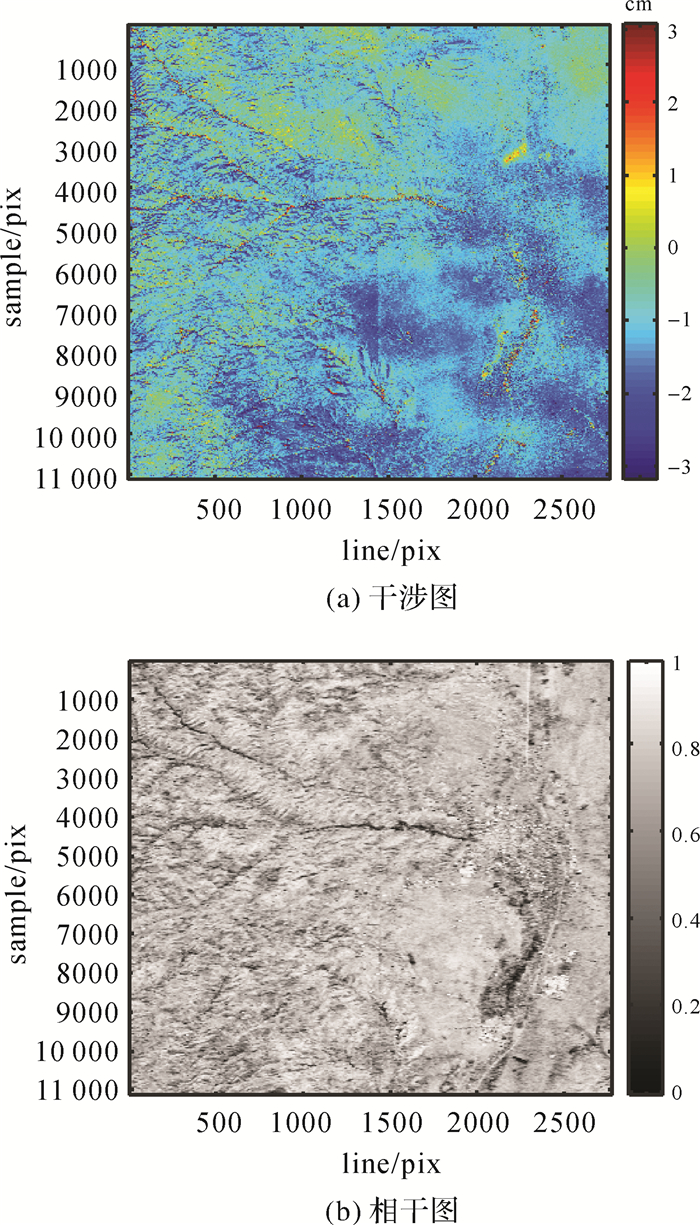
试验干涉组合策略如图 3所示,由于干涉门槛的存在,生成的差分干涉图效果较好,呈现出比较清晰的干涉相位。选择(2, 3)干涉对的差分干涉图及相干图作为示例展示74组干涉结果,如图 8所示。(2, 3)干涉对成像日期分别为2014-11-16和2014-12-10,Bt2, 3为24 d,Bb2, 3为103.564 m,Dopper质心频率差Bdc2, 3为0.045 Hz,γ2, 3为0.57。
|
| 图 8 干涉对(2, 3)干涉图(去平、去地形)及相干图 Fig. 8 Interferogram and coherence map of interferometric pair(2, 3) |
图 8(a)中可以看到干涉对(2, 3)在去除参考面、地形相位贡献后绝大部分区域的干涉效果较好,但也含有较为明显的大气相位。同时由于失相干原因,水域、沟壑等区域受到较严重噪声,这些区域在图 8(b)相干图中颜色较暗。
利用双阈值联合筛选法(S2=1.4)同时探测到TCT和PS点信息如图 5所示。可以发现,人工建筑物既能被识别为TCT,也能被识别为PS,城区TCT、PS点分布密度最高;非城区植被较为稀疏区域能识别出较多的TCT,却由于时间失相干原因存在较少PS点,因此非城区TCT的分布密度显著高于PS点密度;在水域、风沙滩区及植被密集的沟壑区,无论TCT或PS均不能被有效探测,此区域TCT、PS分布密度极低。
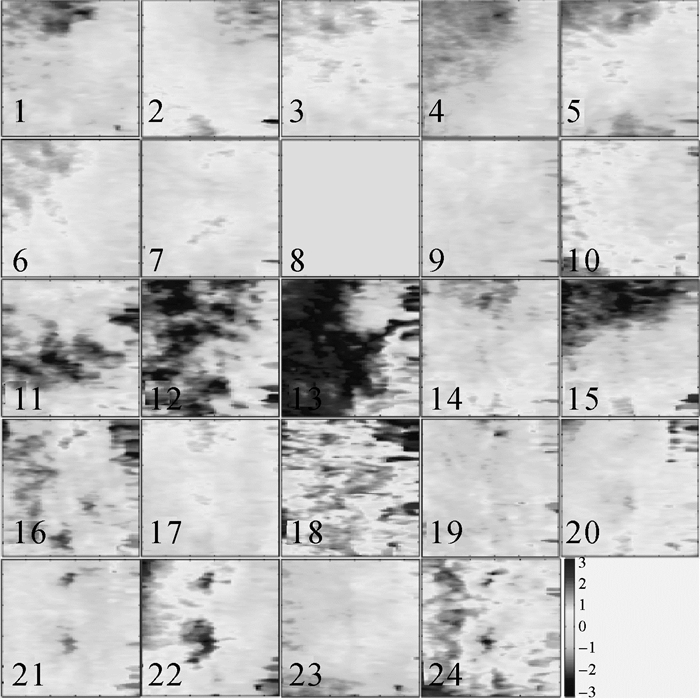
构建基于TCT点的Delaunay差分网络,该网络共含358 405条连接边。通过估计差分参数,迭代计算分离出的大气延迟相位,图 9显示了基于TCT点的大气延迟相位内插生成的大气延迟相位图。干涉相位在去除线性形变、高程误差、大气延迟及非线性形变后的残余相位分布均匀且其绝对值趋近于0,能在一定程度说明TCT时序分析方法的可靠性。图 10统计了TCT在干涉对(2, 3)中的残余相位,绝大部分TCT的|ϕres2, 3|小于1,其均值为0.14 rad,标准差为0.16 rad。
|
| 图 9 大气延迟相位图 Fig. 9 Atmospheric phase map |

|
| 图 10 干涉对(2, 3)残余相位统计 Fig. 10 Phase residuals statistics of interferometric pair (2, 3) |
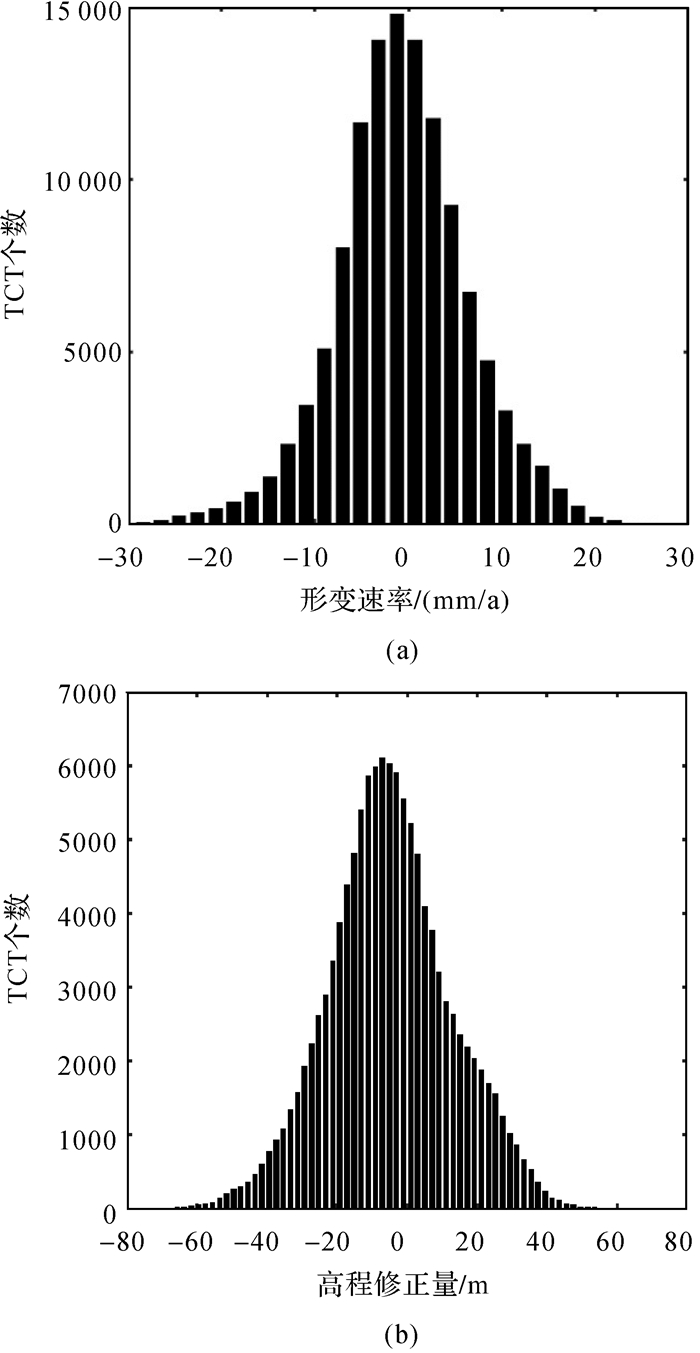
分离残差相位贡献后提取到试验区TCT点的形变速率和高程修正量信息,对其进行统计分析以辅助考察地表形变规律。由表 2、表 3和图 11可以得到以下3点结论:①试验区的TCT点既有抬升,也有沉降,但其值相当微小,83.73%的TCT点形变速率绝对值在10 mm/a以内;②TCT的高程修正量反映了外部DEM的高程精度,试验区域地形复杂多变,119 489个TCT点平均高程修正绝对值小于5 m,一定程度上说明了AW3D数据的可靠性;③TCT形变速率平均值为-0.66 mm/a,且其形变服从高斯分布,说明试验区不存在显著的大形变场。
|
| 图 11 TCT形变速率和高程修正量统计 Fig. 11 Deformation velocity and residual height statistical chart of TCT |
| v/ (mm/a) |
[-∞, -20] | [-20, -10] | [-10, 0] | [0, 10] | [10, 20] | [20, +∞] |
| 个数 | 1258 | 8776 | 53 535 | 46 512 | 8882 | 526 |
| 占比 /(%) |
1.05 | 7.34 | 44.80 | 38.93 | 7.43 | 0.44 |
| average | -0.66 | median | -0.77 | STDEV | 7.29 |
| δ/m | [-∞, -40] | [-40, -20] | [-20, 0] | [0, 20] | [20, 40] | [40, +∞] |
| 个数 | 2809 | 18 810 | 53 943 | 33 150 | 10 163 | 614 |
| 占比 /(%) |
2.35 | 15.74 | 45.14 | 27.74 | 8.51 | 0.51 |
| average | -4.93 | median | -5.53 | STDEV | 17.81 |
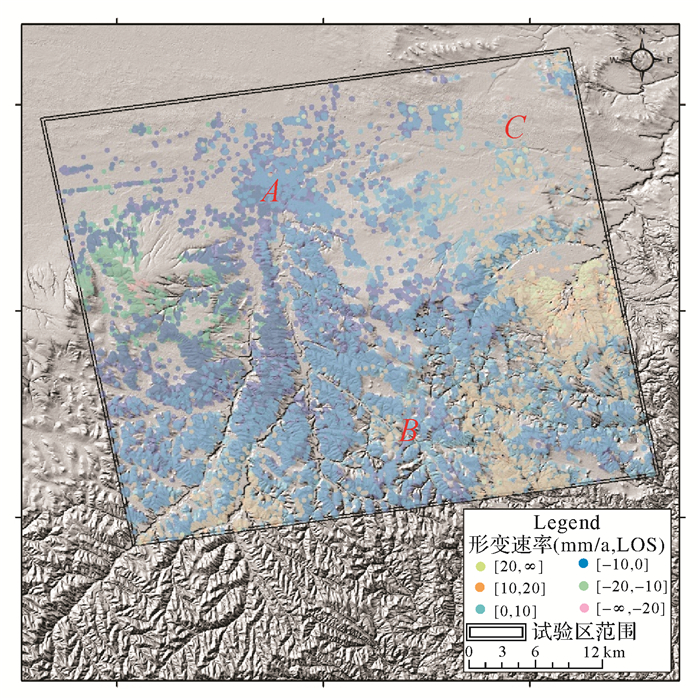
图 12显示了基于临时相干目标干涉测量方法提取到试验区2014-10-23-2016-05-09期间TCT点在雷达视线向形变速率结果。利用Kriging内插法获得整个试验区在观测期间LOS方向地表形变速率场,如图 13所示。可以发现,试验区绝大部分区域地表形变均匀,且形变速率绝对值小于10 mm/a,与统计分析的结论吻合;南部丘陵沟壑区TCT形变场得到有效提取,其形变速率为-10~10 mm/a;北部风沙滩区由于TCT点密度小,其形变场结果存在较大的误差;而利用Kriging内插法时,零星分布的TCT引起的“扩散”现象也会造成形变场结果误差。
|
| 图 12 试验区TCT形变速率(LOS) Fig. 12 TCT deformation velocity of the area(LOS) |

|
| 图 13 试验区形变速率场(LOS) Fig. 13 Deformation velocity field of the area(LOS) |
2.3 验证分析
经典PS-InSAR方法自Ferretti提出就引起国内外广泛响应,十多年的发展使永久散射体干涉测量方法的可靠性得到了充分的验证[1, 26-27]。在缺少现场地表形变监测数据情况下,本文采用相同的SAR、DEM和轨道数据等对试验区进行了同期的PSInSAR形变监测。对比分析临时相干目标干涉测量方法和PSInSAR方法结果,以说明TCT方法的有效性和可靠性。
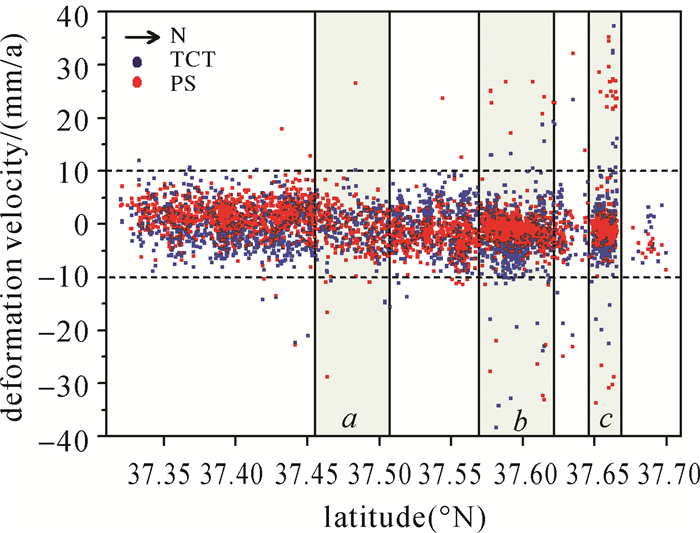
基于PSInSAR方法解算出PS点形变信息后,提取到地理编码后的TCT和PS同名点(经纬度重叠)共7764个。因TCT空间分布密度大于PS点,且多数PS点同被识别为TCT,故同名点空间分布状况与PS分布相似。依据同名点纬度序列,对两种算法获取的形变速率进行一致性和差异性分析,见图 14。由图 14可以发现3点:①整体上,两种算法提取的同名点形变速率保持较高的一致性,且形变速率值趋近于零线,与试验结果相吻合;②同名点形变速率分布方面,其“聚束”效应较为明显,同名点形变速率值集中分布于[-10 mm/a, 10 mm/a],而北部风沙滩区包含孤立存在的同名点,造成纬度相对较高区间抛射出部分形变速率绝对值较大的同名点;③同名点空间分布密度方面,由于试验区土地覆被多样性导致了不同区域提取的同名点空间密度不同。图 14中a区域是南部沟壑区,其提取同名点的密度远低于较高纬度的b区域,因为b区域内包含了同名点分布丰富的靖边县城建成区。c区间对应的是县城东北方向开发的靖边新能源产业园建成区,所以其同名点分布密度也较高。综上,通过对比分析纬度序列上两种算法的形变速率结果,TCT算法结果的有效性得到充分的证明。
|
| 图 14 同名点形变速率分布图 Fig. 14 Deformation velocity distribution of the same point |
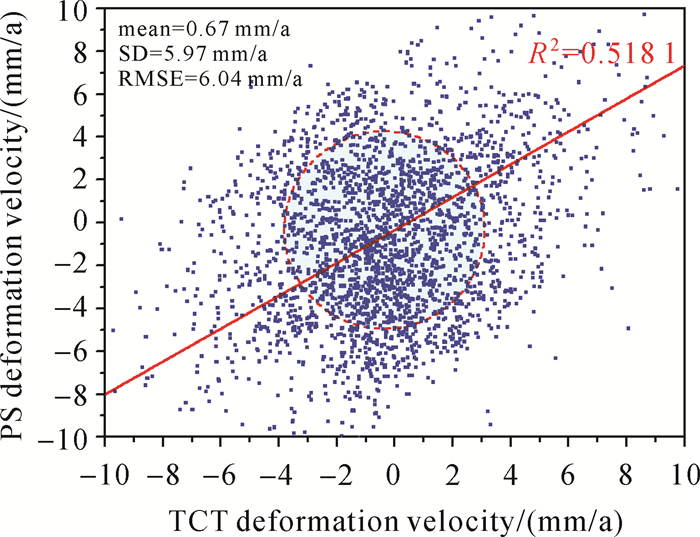
为进一步验证TCT算法的可靠性,构建同名点形变速率散点图(图 15),散点的横纵坐标分别表示TCT和PS解算的形变速率结果。从图 15中,可发现:①散点聚束于趋势线附近,两种算法的形变速率结果的R2值为0.518 1;②散点主要堆积于以(0, 0)为中心的区域内,再次证实了试验区无显著形变场结果。7764个TCT监测结果均方根误差为6.01 mm/a,显示出较好的测量精度;形变速率差标准差为5.97 mm/a,导致该结果的原因可能是TCT方法和PS方法提取的点密度不同造成的时空滤波、相位分解等差异。综上,通过直接对比两种算法形变速率结果并进行差值统计分析,说明了TCT监测结果是比较可靠的。
|
| 图 15 同名点形变速率散点图 Fig. 15 Deformation velocity scatter of the same point |
PSInSAR的单一放射状干涉组合方式使部分时间段相干性较低的TCT相位质量不稳定,造成较大误差。而基于小干涉对集的干涉组合方式改变了TCT的相干性,其在时序上的稳定性需要检验。分别提取建成区、丘陵沟壑区和风沙滩区的同名样点(A、B、C),其区域位置分布如图 12,时序分析结果如图 16。可见两种算法的形变时序结果在A、B两点的趋势较为一致,其差值的绝对均值分别为1.60 mm和1.71 mm;位于C点处的同名点TCT算法结果与PS相比,表现出部分波动性,其差值的绝对均值为2.50 mm,主要还是由风沙滩区地物反射特性不稳定造成的TCT点稀疏引起。总的来看,以PS点为参考,TCT点的形变时间序列稳定性较高。

|
| 图 16 同名点时序形变量 Fig. 16 Time-series deformation of the same point |
3 结论
采矿活动、油气开发、CO2地质封存及滑坡等引起的地表形变过程多发生于永久散射体稀缺的非城区,制约了经典PSInSAR在此类区域的监测应用。本文提出一种基于临时相干点的方法以监测非城区地表形变。该方法利用空间平均相干系数过滤低相干干涉对,融合振幅离差指数和相干性指标以提取TCT点;构建TCT相位分析网络,引入相干系数估计最优差分参数;利用大气空间自相关特性分离延迟相位,反演地表形变信息。利用该算法,采用C波段Sentinel-1A数据,以地形、地貌复杂多变的靖边县为试验区进行了形变监测试验。
非城区监测点密度方面,TCT方法识别到监测目标分布密度为81个/m2,较PSInSAR方法提高376%,非城区目标分布密度改善尤为明显,克服了经典PSInSAR在非城区形变监测的局限性。同时利用TCT方法获取到TCT形变速率和试验区形变速率场,结果表明83.73%的TCT点形变速率绝对值小于10 mm/a。为验证TCT方法形变监测结果的有效性和可靠性,与经典PSInSAR监测结果进行对比分析。提取同名点后分析结果同时显示出试验区无显著形变场;同名点形变速率值集中分布于[-10 mm/a, 10 mm/a],北部风沙滩区形变速率由于孤立目标存在引起形变速率出现“蔓延”现象;由于试验区土地覆被多样性导致了不同区域提取的同名点空间密度不同;TCT和PS解算的形变速率结果匹配程度较好,TCT监测结果均方根误差为6.01 mm/a,形变速率差标准差为5.97 mm/a。
综上所述,本文提出的基于临时相干点的干涉测量方法能够弥补经典PSInSAR在非城区形变监测空间覆盖率低和形变反演相位不可靠的缺点,并且考虑季节性变化的干涉对筛选方法能提取到相干性较好的干涉对。而当地面有大范围、快形变场时,其监测结果与地面实测数据是否保持一致性缺乏进一步论证,这也是后续研究的重点方向。
| [1] | FERRETTI A, PRATI C, ROCCA F. Permanent scatterers in SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8–20. DOI:10.1109/36.898661 |
| [2] | KAMPES B M, HANSSEN R F. Ambiguity resolution for permanent scatterer interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(11): 2446–2453. DOI:10.1109/TGRS.2004.835222 |
| [3] | FERRETTI A, PRATI C, ROCCA F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2202–2212. DOI:10.1109/36.868878 |
| [4] | COLESANTI C, FERRETTI A, NOVALI F, et al. SAR monitoring of progressive and seasonal ground deformation using the permanent scatterers technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(7): 1685–1701. DOI:10.1109/TGRS.2003.813278 |
| [5] |
秦晓琼, 杨梦诗, 王寒梅, 等.
高分辨率PS-InSAR在轨道交通形变特征探测中的应用[J]. 测绘学报, 2016, 45(6): 713–721.
QIN Xiaoqiong, YANG Mengshi, WANG Hanmei, et al. Application of high-resolution PS-InSAR in deformation characteristics probe of urban rail transit[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 713–721. DOI:10.11947/j.AGCS.2016.20150440 |
| [6] |
刘晓龙, 张永红, 宋伟东.
时序PSInSAR研究建筑物高度信息提取[J]. 武汉大学学报(信息科学版), 2017, 42(4): 482–487, 524.
LIU Xiaolong, ZHANG Yonghong, SONG Weidong. Building height information extracting technique based on PSInSAR[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 482–487, 524. |
| [7] | CIAMPALINI A, RASPINI F, LAGOMARSINO D, et al. Landslide susceptibility map refinement using PSInSAR data[J]. Remote Sensing of Environment, 2016, 184(2): 302–315. |
| [8] | FERRETTI A, FUMAGALLI A, NOVALI F, et al. A new algorithm for processing interferometric data-stacks:SqueeSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(9): 3460–3470. DOI:10.1109/TGRS.2011.2124465 |
| [9] | NG H M, GE L L, DU Z Y, et al. Satellite radar interferometry for monitoring subsidence induced by longwall mining activity using Radarsat-2, Sentinel-1 and ALOS-2 data[J]. International Journal of Applied Earth Observation and Geoinformation, 2017, 61(1): 92–103. |
| [10] |
李永生, 张景发, 罗毅, 等.
利用高分辨率聚束模式TerraSAR-X影像的PSInSAR监测地表变形[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1452–1455.
LI Yongsheng, ZHANG Jingfa, LUO Yi, et al. Monitoring land deformation using PSInSAR with TerraSAR-X high resolution spotlight SAR images[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1452–1455. |
| [11] |
邢学敏.
CRInSAR与PSInSAR联合监测矿区时序地表形变研究[J]. 测绘学报, 2014, 43(8): 878.
XING Xuemin. Study on monitoring the time series ground deformation in mining area based on CRInSAR and PSInSAR integration[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 878. DOI:10.13485/j.cnki.11-2089.2014.0081 |
| [12] |
徐小波, 屈春燕, 单新建, 等.
CR-InSAR与PS-InSAR联合解算方法及在西秦岭断裂中段缓慢变形研究中的应用[J]. 地球物理学报, 2016, 59(8): 2796–2805.
XU Xiaobo, QU Chunyan, SHAN Xinjian, et al. Mapping slow deformation of the middle segment of the West Qinling Fault using the combined algorithm of CR-InSAR and PS-InSAR[J]. Chinese Journal of Geophysics, 2016, 59(8): 2796–2805. |
| [13] | HOOPER A, ZEBKER H, SEGALL P, et al. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers[J]. Geophysical Research Letters, 2004, 31(23): 1–5. |
| [14] | HOOPER A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches[J]. Geophysical Research Letters, 2008, 35(16): 96–106. |
| [15] | BLANCO-SÁNCHEZ P, MALLORQUÍ J J, DUQUE S, et al. The coherent pixels technique (CPT):an advanced DInSAR technique for nonlinear deformation monitoring[J]. Pure and Applied Geophysics, 2008, 165(6): 1167–1193. DOI:10.1007/s00024-008-0352-6 |
| [16] | BLANCO P, MALLORQUI J, DUQUE S, et al. Advances on DInSAR with ERS and Envisat data using the coherent pixels technique (CPT)[C]//Proceedings of 2016 IEEE International Symposium on Geoscience and Remote Sensing. Denver, CO: IEEE, 2006: 1898-1901. |
| [17] | ZHANG Lei, LU Zhong, DING Xiaoli, et al. Mapping ground surface deformation using temporarily coherent point SAR interferometry:application to Los Angeles Basin[J]. Remote Sensing of Environment, 2012, 117(1): 429–439. |
| [18] | ZHANG Lei, DING Xiaoli, LU Zhong, et al. A novel multitemporal InSAR model for joint estimation of deformation rates and orbital errors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3529–3540. DOI:10.1109/TGRS.2013.2273374 |
| [19] | PERISSIN D, WANG Teng. Repeat-pass SAR interferometry with partially coherent targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 271–280. DOI:10.1109/TGRS.2011.2160644 |
| [20] |
刘国祥, 陈强, 丁晓利.
基于雷达干涉永久散射体网络探测地表形变的算法与实验结果[J]. 测绘学报, 2007, 36(1): 13–18.
LIU Guoxiang, CHEN Qiang, DING Xiaoli. Detecting ground deformation with permanent-scatterer network in radar interferometry:algorithm and testing results[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 13–18. DOI:10.3321/j.issn:1001-1595.2007.01.003 |
| [21] | BERARDINO P, FORNARO G, LANARI R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375–2383. DOI:10.1109/TGRS.2002.803792 |
| [22] | LIU Guoxiang. Mapping of Earth deformations with satellite SAR interferometry: a study of its accuracy and reliability performances[D]. Hong Kong, China: The Hong Kong Polytechnic University, 2003. |
| [23] | PAPOULIS A. Probability, random variables, and stochastic processes[M]. New York: McGraw-Hill, 1984. |
| [24] |
陈强, 刘国祥, 李永树, 等.
干涉雷达永久散射体自动探测——算法与实验结果[J]. 测绘学报, 2006, 35(2): 112–117.
CHEN Qiang, LIU Guoxiang, LI Yongshu, et al. Automated detection of permanent scatterers in radar interferometry:algorithm and testing results[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 112–117. DOI:10.3321/j.issn:1001-1595.2006.02.004 |
| [25] |
陈强, 刘国祥, 丁晓利, 等.
永久散射体雷达差分干涉应用于区域地表沉降探测[J]. 地球物理学报, 2007, 50(3): 737–743.
CHEN Qiang, LIU Guoxiang, DING Xiaoli, et al. Radar differential interferometry based on permanent scatterers and its application to detecting regional ground subsidence[J]. Chinese Journal of Geophysics, 2007, 50(3): 737–743. DOI:10.3321/j.issn:0001-5733.2007.03.012 |
| [26] |
李德仁, 廖明生, 王艳.
永久散射体雷达干涉测量技术[J]. 武汉大学学报(信息科学版), 2004, 29(8): 664–668.
LI Deren, LIAO Mingsheng, WANG Yan. Progress of permanent scatterer interferometry[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 664–668. |
| [27] |
朱建军, 李志伟, 胡俊.
InSAR变形监测方法与研究进展[J]. 测绘学报, 2017, 46(10): 1717–1733.
ZHU Jianjun, LI Zhiwei, HU Jun. Research progress and methods of InSAR for deformation monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1717–1733. DOI:10.11947/j.AGCS.2017.20170350 |



