空间异常探测是空间数据挖掘的重要手段之一[1-2],能够有效挖掘地理现象的异常空间分布模式,这些异常模式通常蕴含着地理现象或地理过程的特殊发展规律。异常探测最初源自统计学中的粗差探测研究,但在实践中发现有些“粗差”并不一定是错误,往往隐含了某种特殊的规律或性质,具有重要的应用价值。基于此,文献[3]给出异常的本质性定义,即“严重偏离其他对象的观测数据,以至于令人怀疑它是由不同机制产生的”。文献[4]进一步顾及空间数据的特性描述空间异常“专题属性与其空间邻近域内实体的专题属性显著不同的空间实体”。因此,空间异常是与其空间邻近域显著不同,而在整体趋势上差异可能不明显的空间实体。
考虑到空间数据具有空间位置属性和非空间专题属性,可将空间异常模式大致分为两类:①仅顾及空间位置属性的空间异常模式;②同时顾及空间位置属性和非空间专题属性的空间异常模式。其中,第1类模式的实际应用主要是针对空间点事件(例如犯罪、疾病等)的异常模式探测,并且仅考虑空间点事件的发生位置。主要方法包括:基于距离的方法[5]、基于密度的方法[6]、基于聚类的方法[7]、基于图论的方法[8]。第2类模式通常根据空间属性(即位置)确定空间邻近关系,根据专题属性确定异常程度。主要方法包括:基于图的方法[9-10]、基于距离的方法[4, 11]、基于局部度量的方法[12]、基于聚类的方法[13-14]。其中,基于图的方法将空间数据转换为图(如Delaunay三角网[9]、k邻近图[10]等),从图结构中探测空间异常;基于距离的方法采用专题属性值与空间邻近域内实体专题属性均值[4](或中值[11])的差值来度量实体的异常程度,继而统计识别异常实体,该类方法适用于发现全局的异常,而容易忽略局部的异常现象;基于局部度量的方法借助局部密度的概念定义局部异常度,局部异常度较大的空间实体被视为异常,该类方法顾及了空间实体的局部特征,故可以更好地发现局部的异常现象;基于聚类的方法的基本思想是将异常探测过程转换成聚类过程,将空间聚类后获得的孤立点或小簇视为空间异常,其主要目的在于发现空间簇,缺乏对空间异常的准确度量,探测异常的能力有限。
然而,上述两类空间异常探测模式都是针对单一类别实体进行挖掘,没有考虑数据的类型和标签。随着数据类型的越来越丰富,综合考虑多种类别数据间的关系进行挖掘更具实际意义。针对空间异常探测中顾及实体类别的问题,学者们开展了系列研究。如文献[15]提出语义异常(semantic outlier),即“与同类别实体相比具有明显差异,而与其他类别相比正常的实体”;与此相反,文献[16]提出交叉异常(cross-outlier),即“与其他类别实体相比具有明显差异的实体”,通过采样邻域和计数邻域所包含的参考实体的数目采用k倍标准差原则进行异常的统计判别;文献[17]概括了文献[15-16]的研究工作,提出类异常(class outlier)探测模型,并进行客户关系管理的实例分析;文献[18]进一步提出一种基于距离的类异常探测方法;文献[19]提出空间分类数据异常探测的框架,并发展了基于成对相关函数PCF和k近邻的空间分类异常探测方法;文献[20]采用广义t检验检测混合类型数据中的异常;文献[21]借助关联规则处理多种类型数据,提出一种多域空间异常探测方法;文献[22]则通过融合多种类型数据发现城市中的集簇异常;与多类别空间异常探测相关的研究还有空间同位模式[23]、多类别空间聚类[24]等。
分析上述针对顾及数据类别的空间异常探测的研究工作可以发现,不论是单一类别异常探测或多类别异常探测的结果识别依赖于人为设定异常数目,需要较多先验知识,缺乏对异常模式显著性的统计判别。现实世界中许多地理事物或地理现象可以用空间点进行有效表达,如犯罪事件、城市基础设施(如银行、学校、医院)地理位置等,因此,本文针对两种类别的空间点数据(基本数据集和参考数据集),借鉴空间点模式分析,提出一种空间交叉异常显著性判别的非参数检验方法。
1 空间交叉异常显著性判别的非参数检验方法给定存在空间依赖关系的基本数据集和参考数据集,空间交叉异常显著性判别主要分为4个步骤:①针对基本数据集实体采用约束Delaunay三角网表达空间邻近关系,进而构建合理、稳定的空间邻近域;②统计落在基本数据集实体空间参考邻域半径r范围内的参考数据集实体的数目,度量基本数据集实体初始空间交叉异常度;③针对每个基本数据集实体,采用α-Shape法[27]构建其支撑域;④统计落在其支撑域内参考数据集实体的数目,采用蒙特卡洛随机模拟按照均质泊松过程生成m次的空间分布数据,进而对异常的显著性进行判别,并进行评价分析。下面对每个步骤进行详细阐述。
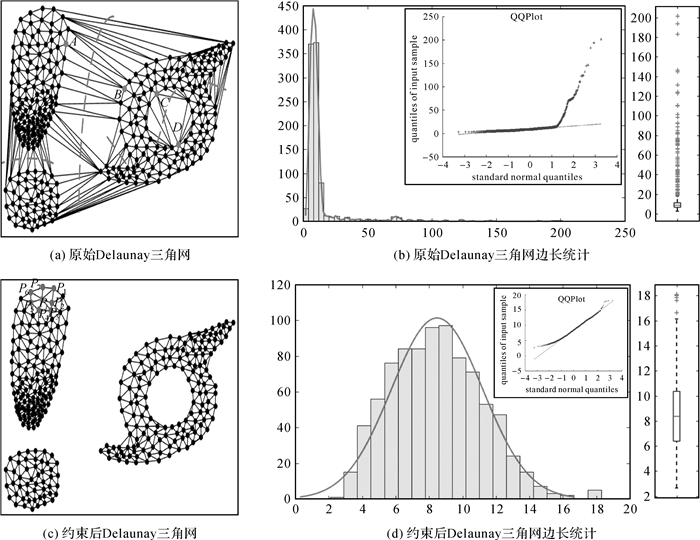
1.1 空间邻近域构建空间邻近域是度量空间异常的基础。由于eps-邻域和k-NN邻域的构建需要引入额外参数(如空间半径eps、最近邻数k),对于空间分布不均匀数据设置较为困难,本文采用约束Delaunay三角网自适应构建空间邻近域。Delaunay三角网是一种满足最大最小角特性、外接圆特性和唯一性的三角剖分,能自然的反映空间实体间的邻接关系[7-8]。但原始Delaunay三角网在边界和空洞处的边长明显偏长,如图 1(a)中实体A与B,C与D空间邻近是不合理的。文献[25]通过试验证明,可以通过删除超过平均边长一定倍数的边来有效移除不合理边。本文针对边长集合呈现的偏态分布特征,采用一种稳健的平均边长来处理不合理的边。
|
| 图 1 空间邻近域构建 Fig. 1 The construction of spatial neighborhood |
定义1 稳健平均边长:给定基本数据集PD,PD中所有实体生成的Delaunay三角网的N条边构成边长集合E,E中所有边长按升序排列,序列中位于上、下四分位数之间所有边长的均值称为稳健平均边长,记为RAE(E)
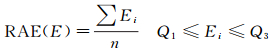 (1)
(1)
式中,Q1为边长下四分位数;Q3为边长上四分位数;n表示上下四分位数之间所有边的数量。
定义2 不合理的边:边长集合E中,与稳健平均边长相比明显偏大的边定义为不合理的边,所有不合理的边构成集合EIC
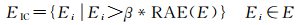 (2)
(2)
式中,β是不合理边判别阈值的调节系数,用于控制实体空间邻域大小。当β取值较大时,不合理边判别阈值相应较大,从而可能吸收更多较远距离的邻近点作为实体的邻近域;当β取值较小时,不合理边的判别阈值较严格,使得空间邻近的实体被割裂,不被纳入邻近域。通过对不同分布密度的模拟数据进行试验分析发现,β取值[2, 4]时,可以获得较理想的空间邻域构建结果。由于空间数据(尤其是点实体)分布的复杂性,当研究区域内实体分布密度差异过大时,β的取值(在[2, 4]之间)可能产生空间邻域的过分割,针对特殊情形,用户可以根据数据特征和应用情景选择更为合适的β取值。
本文基于原始Delauany三角网中不合理边的边长相对较长这一特点,根据Delaunay三角网边长统计分布规律,借鉴箱线图中稳健统计量(即四分位距)[26],给出一种参数β的估值方法,根据三角网边长的最大估计值与边长中位数的比值作为参数β的估计值
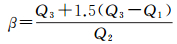 (3)
(3)
式中,Q1、Q2、Q3分别为边长的下四分位数、中位数和上四分位数。最大估计值Q3+1.5(Q3-Q1)为箱线图中的上限,该比值能够反映三角网中长边与边长中位数的偏离程度。
如图 1(c)所示,经打断操作后空洞和边界处的不合理边被有效移除,且约束后边长满足近似正态分布,如图 1(d)所示Q-Q图上的点近似在一条直线附近,据此建立的实体间邻近关系更为合理、稳定。且本文方法能够有效处理数据分布分散,存在异常值的情形。没有隶属于任何簇的实体识别为空间位置孤立点,不参与接下来的检测。
定义3 空间邻域:对于基本数据集任一实体Pi,与打断不合理的边后的Delaunay三角网的边直接相连的空间实体构成Pi的空间邻域SN(Pi),如图 1(c)中实体Pi的空间邻域为{P1, P2, P3, P4, P5, P6, P7}。
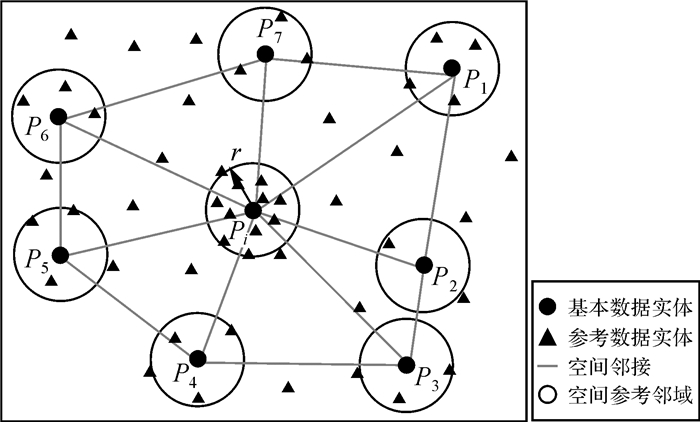
1.2 初始空间异常度度量定义4 空间参考邻域:给定基本数据集实体Pi,落在点Pi为中心,半径为r圆形范围内的参考数据集实体,为实体Pi的空间参考邻域,记为SRN(Pi),如图 2所示。
|
| 图 2 空间邻域及空间参考邻域 Fig. 2 Spatial neighborhood and spatial reference neighborhood |
半径r表达基本数据集实体的影响范围,即空间参考邻域半径,其描述了基本数据集实体与参考数据集实体间的相关关系。本文采用基本数据集实体与最邻近参考数据集实体的距离集合中最小值和最大值为界构成的距离范围定义为空间参考邻域距离域。在此基础上,空间交叉异常度是指基本数据集实体Pi的空间参考邻域数目与其邻近域内空间实体的空间参考邻域数目均值的差异,记为SCOM(Pi)
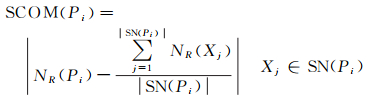 (4)
(4)
式中,NR(Pi)为基本数据集实体Pi的空间参考邻域实体数目;|SN(Pi)|为实体Pi的空间邻域数目。
当空间参考邻域半径选择较小时,参考邻域实体数目较少,交互特征比较弱,异常度量偏小;当空间参考邻域半径选择较大时,参考邻域实体较多,且空间参考邻域范围易出现重叠,导致参考数据实体在不同参考邻域内重复计数,使得空间邻域实体间的差异变小,异常度量偏小,异常不再显著。
1.3 支撑域构建空间交叉异常是指基本数据集实体与其空间邻域实体相比在空间参考邻域上具有明显差异。主要强调在局部范围内对比分析空间参考邻域实体数目的差异,因此,本文以每个基本数据集实体的空间支撑域为研究范围,探究落在基本数据集实体支撑域范围内参考数据集实体的分布特征及差异。
定义5 支撑域:基本数据集实体Pi与其空间邻域SN(Pi)实体的空间参考邻域半径r圆上点,以及落在空间参考邻域半径r圆内的参考数据集实体所构成的点集的空间范围,即为实体Pi的支撑域S。
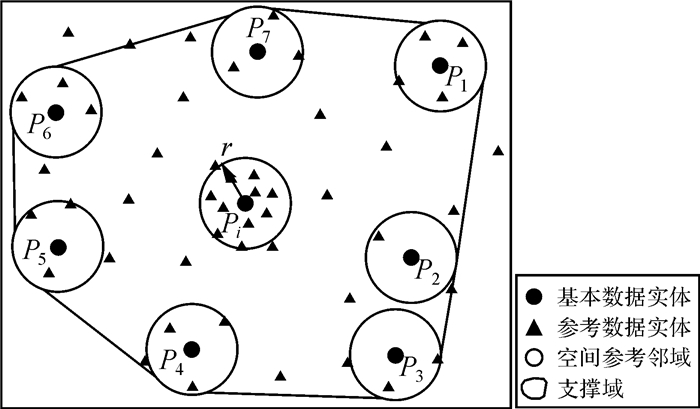
本文采用α-Shape算法[27]构建支撑域。该算法是一种确定性算法,有着严格的数学定义,对于任一有限点集,可直观表示点集的形状,且通过参数α控制多边形生成的精细程度。支撑域如图 3所示。
|
| 图 3 支撑域示意图 Fig. 3 The diagram of support domain |
1.4 显著空间点异常判别
针对基本数据集实体,统计落在其支撑域内参考数据集实体,记为参考数据子集。从随机空间过程的角度出发,给出零假设:基本数据集实体的空间参考邻域数目与其空间邻域实体的空间参考邻域数目没有明显差异。即参考数据子集在支撑域内满足完全空间随机分布(CSR)的零假设,在该假设下事件在支撑域内服从均质泊松分布,这意味着支撑域中的每一个事件是以等概率发生在区域的任意位置上的,并且其发生独立于空间位置和其他的事件[28],如式(5)所示。
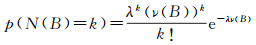 (5)
(5)
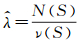 (6)
(6)
式中,N(B)为区域B内参考数据实体的数目,且B⊆S;ν(B)为区域B的面积;λ为强度函数,采用式(6)进行估计;N(S)和ν(S)分别为支撑域S内参考数据实体的数目和面积。
基于该零假设,采用蒙特卡洛随机模拟的方法在支撑域内生成空间随机数据,计算实体异常度的经验概率密度分布,并对异常的显著性进行统计判别,具体步骤如下:
(1) 给定空间基本数据集PD={P1, P2, …, Pn}和空间参考数据集RD={R1, R2, …, Rq},依据式(3)计算基本数据集实体的初始空间异常度SCOM(P10)、SCOM(P20)、…、SCOM(Pn0);
(2) 针对基本数据集实体Pi(i=1, 2, …, n),构建其支撑域。依据零假设,参考数据子集在支撑域内满足均质泊松过程,因此,在支撑域范围内生成相同数目且满足随机分布的点集,并度量空间异常度SCOM(Pik)。通过m次蒙特卡洛模拟构造异常显著性检验统计量的零假设概率密度分布,如图 4所示,由此可以计算出基本数据集实体Pi空间异常显著性p-value(·)
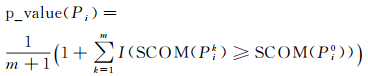 (7)
(7)
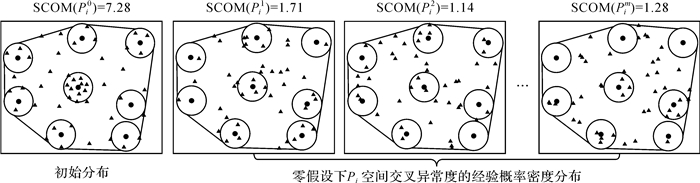
|
| 图 4 随机模拟构造实体空间异常度经验概率密度分布示例 Fig. 4 Construction of the empirical probability density distribution of spatial outlier measure |
式中,I(·)表示指示函数,取值0或1。给定显著性水平α,若p-value(Pi)小于α,则实体Pi为显著空间交叉异常。
1.5 多尺度挖掘结果评价基于单一空间参考邻域半径挖掘得到的异常模式通常不能充分刻画异常实体的分布特征,更有意义的是在多个参考半径下挖掘空间异常模式,即空间交叉异常模式的多尺度挖掘。异常模式的稳定性与视觉的显著性存在明显的对应关系,显著异常模式会在较广范围内被感知。借鉴空间聚类[29-30]、空间同位模式[31]挖掘中对多尺度挖掘结果的评价策略,本文采用生存距离对不同参考邻域半径的挖掘结果进行评价。
定义6 生存距离(living distance, LD):在不同的空间参考邻域半径上分别进行空间异常模式的挖掘,若异常模式O在其中连续的半径距离上均统计显著,则该连续半径即为异常模式O的生存距离。需指出,生存距离度量的是异常模式的稳定性,模式的生存距离越长,表示该模式相对越稳定,可指导异常模式的筛选与评价。本文以基本数据集内实体为基准,计算基本数据内每个实体与参考数据集内所有实体间的距离,取其中的最短距离作为该实体与参考数据集的距离;进而,统计基本数据集内所有实体到参考数据集的距离的最小值(记为minR)和最大值(记为maxR),构成空间参考邻域距离域[minR, maxR],在该范围内等步长进行取值,进行多尺度挖掘分析。且当等分越细时,分析结果越可靠,同时时间花销也越大,因此,在平衡效率与精度的基础上,需选择合适的等分。
2 试验分析与应用为了验证本文方法的有效性,分别采用模拟数据与实际数据进行试验分析,采用精确率和召回率与文献[16](cross-outlier detection, COD)进行定量比较,该方法需要3个输入参数,即空间邻域半径r′,局部性参数α′,显著偏差系数k。试验中蒙特卡洛随机模拟次数m设为999,空间交叉异常的显著性水平设为0.05。
2.1 模拟试验与比较为了验证本文方法在探测显著空间交叉异常的有效性,设置3组模拟数据,分布范围均为10×10的单元。其中模拟数据集SD1中基本数据集PD和参考数据集RD都随机分布在研究区域,设置了9个明显的空间交叉异常;模拟数据集SD2中PD随机分布,RD具有明显的空间自相关,呈聚集分布,设置了8个明显交叉异常;模拟数据集SD3的分布与SD2正好相反,设置了9个明显交叉异常。如图 5所示。
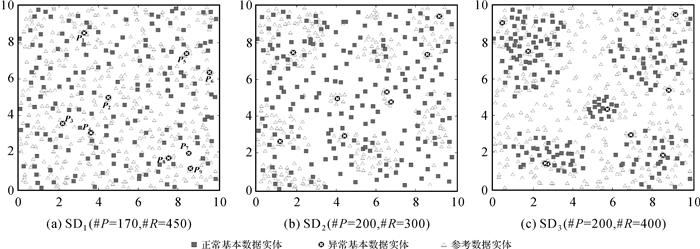
|
| 图 5 模拟数据集 Fig. 5 Simulated datasets |
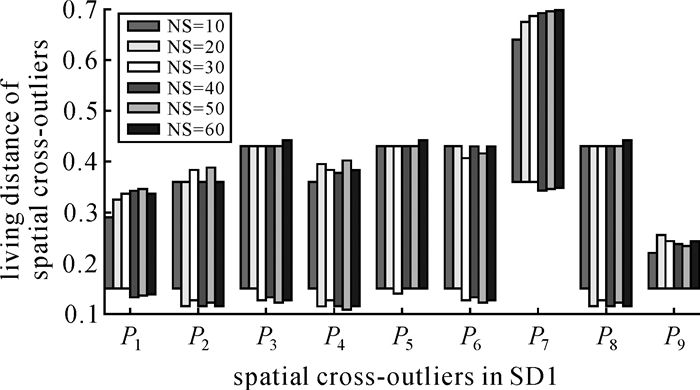
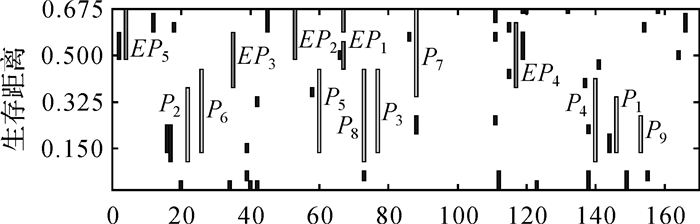
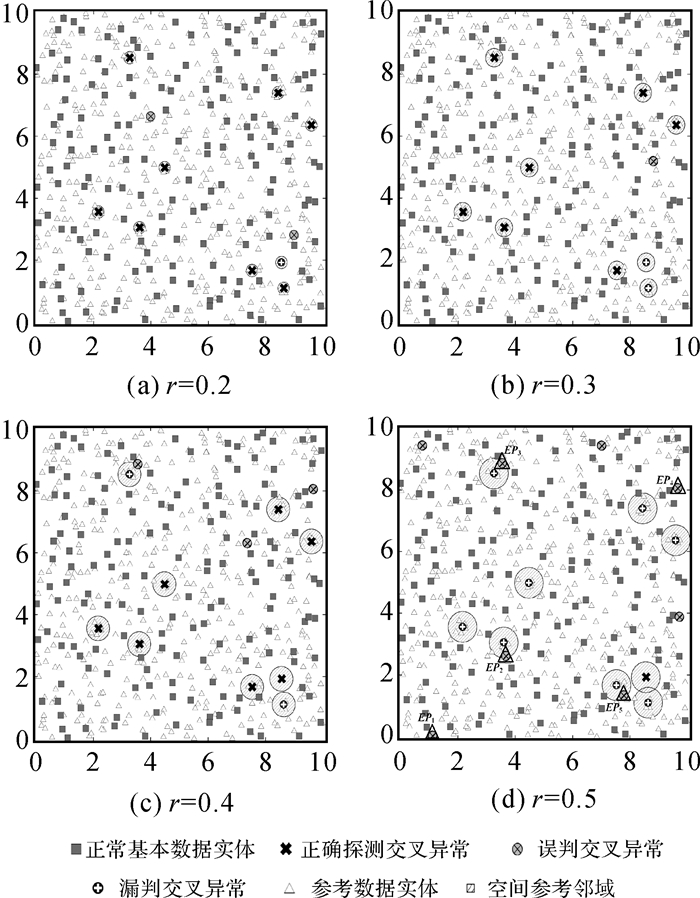
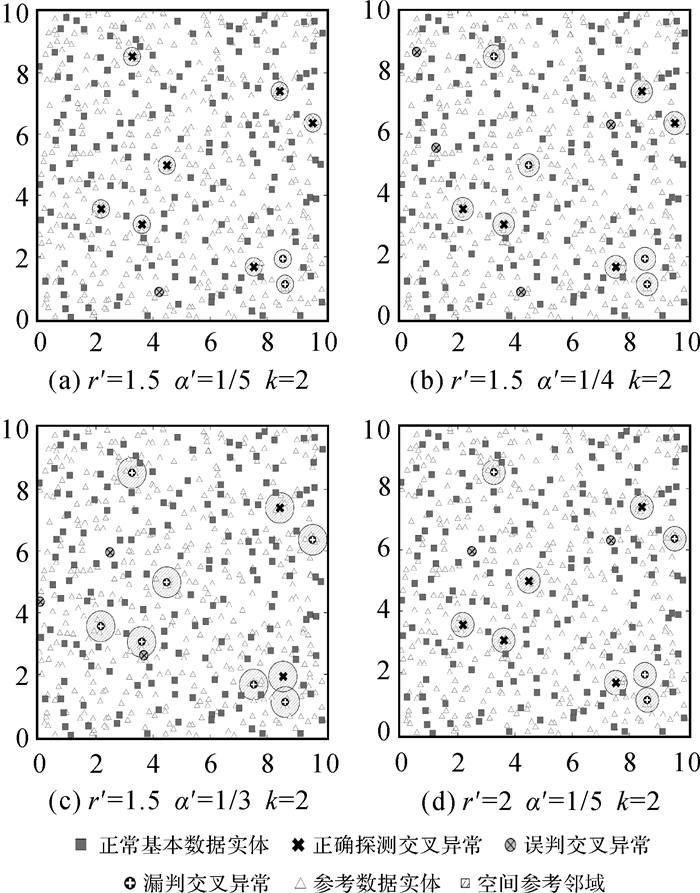
模拟数据SD1,空间参考邻域距离域为[0.01, 0.71],均值为0.23,采用不同等分距离域(10, 20, 30, 40, 50, 60)的预设空间交叉异常生存距离区间如图 6所示。从图中可以发现,当等分大于等于20时,生存距离区间变化微小,因此在综合考虑精度与效率的基础上,选择等分20份,探测结果如图 7所示。其中r=0.2/0.3/0.4/0.5的探测结果如图 8(a)—(d)所示,其精确率和召回率如表 1所示。从试验结果可以发现,预设的明显交叉异常在不同的参考邻域半径下均可有效的探测出来,其中生存距离分别为P1:[0.15, 0.325],P2:[0.115, 0.36],P3、P5、P6:[0.15, 0.43],P4:[0.115, 0.395],P7:[0.36, 0.675],P8:[0.115, 0.43],P9:[0.15, 0.22];当参考邻域半径扩大到0.5时,精确率和召回率均较低,除P7外,其他预设的交叉异常均不再显著,而多分布在预设异常的周围、边界或空洞区域,存在明显的边界效应,如图 8(d)中EP1—EP5。这是因为随着空间参考邻域半径不断扩大,支撑域范围增大,落在支撑域内的参考数据实体增多,且参考邻域范围出现重叠,导致参考数据实体在不同参考邻域内的重复计数,进而使得空间邻域实体间的差异减小,异常不再显著。COD算法的参数采用文章作者推荐的启发式方法进行设置,不同参数探测结果如图 9所示,可以发现:当参数r′=1.5 α′=1/5 k=2时识别了预设明显空间异常中的7个,其他参数下的准确率均较低,且P9在不同参数下均未识别。从F值比较本文方法精度优于COD法。
|
| 图 6 模拟数据集SD1空间交叉异常不同等分下的距离区间 Fig. 6 Distance ranges of spatial cross-outliers on SD1 |
|
| 图 7 模拟数据集SD1空间交叉异常生存距离 Fig. 7 The living distance of spatial cross-outliers on SD1 |
|
| 图 8 模拟数据集SD1不同参考邻域半径探测结果 Fig. 8 Detection results of different reference neighbor radius on simulated dataset SD1 |
|
| 图 9 模拟数据集SD1探测结果—COD Fig. 9 Detection results of simulated dataset SD1—COD |
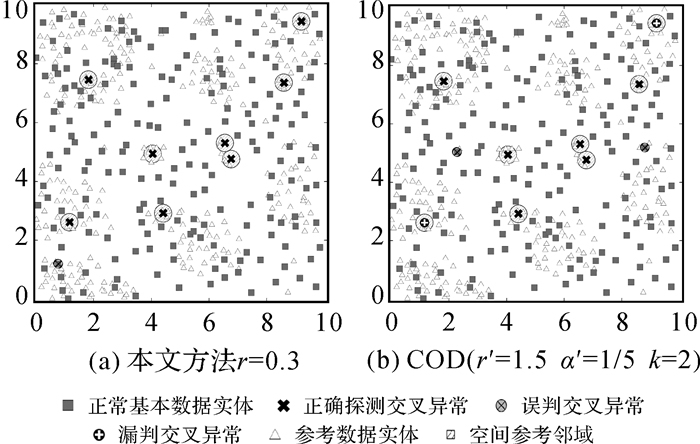
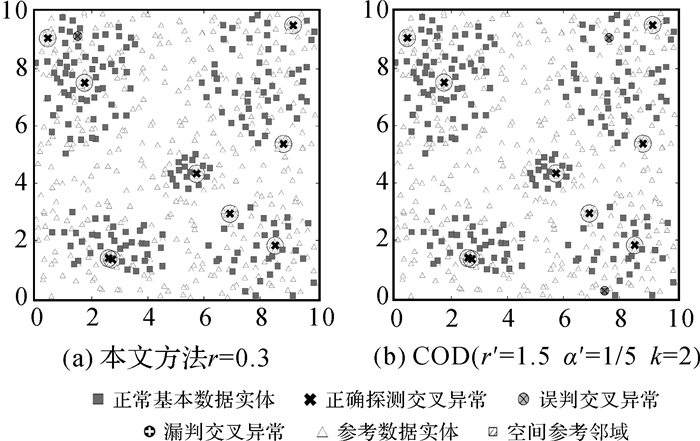
针对模拟数据SD2和SD3,采用启发式策略设定参数,并与预设异常模式相比较优的探测结果分别如图 10、图 11所示。可以发现:针对基本数据集或参考数据集存在空间自相关时本文方法均可有效探测出预设的明显异常,F值均高于COD法;因在每个基本数据实体的支撑域内进行分析,属于局部的研究策略,可更好地探测局部异常。通过试验分析,当两类实体间具有较强的依赖性,呈现出二元聚集分布时,探测效果较好。
|
| 图 10 模拟数据集SD2探测结果 Fig. 10 Detection results of simulated dataset SD2 |
|
| 图 11 模拟数据集SD3探测结果 Fig. 11 Detection results of simulated dataset SD3 |
2.2 实际应用与分析
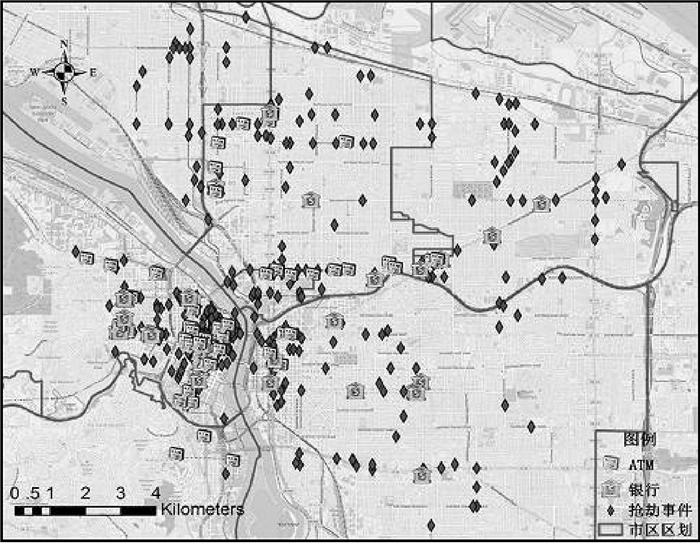
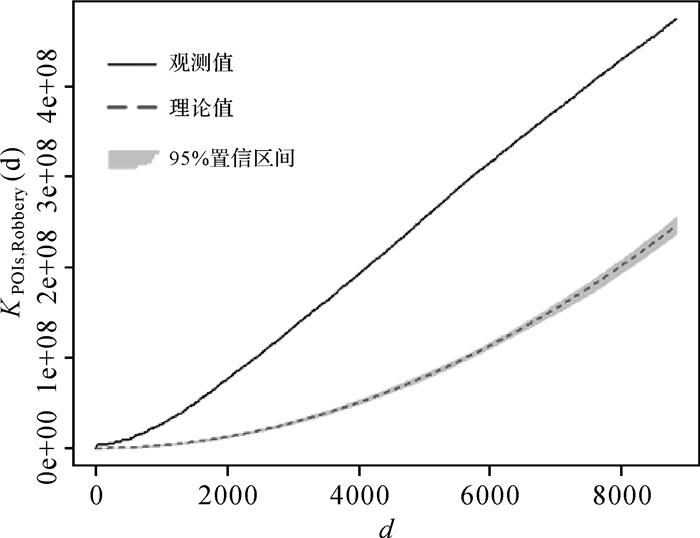
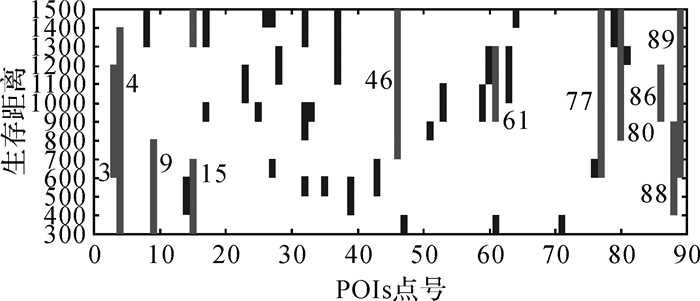
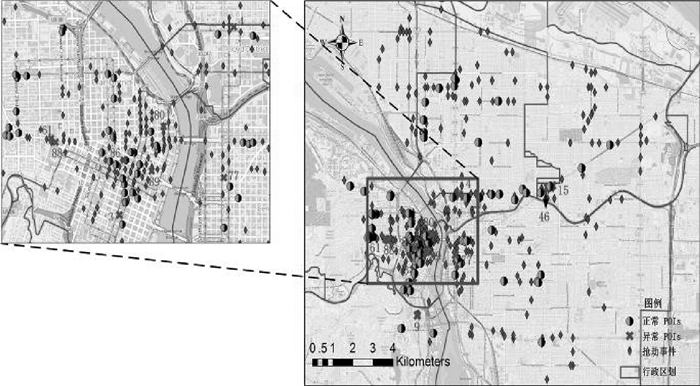
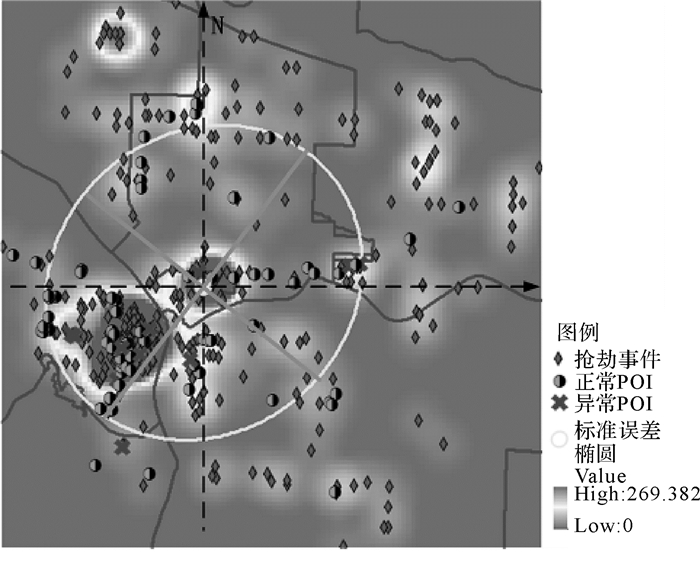
实例采用城市金融设施(银行、ATM)与抢劫犯罪事件进行分析。抢劫案件的社会影响恶劣,严重影响居民安全感,且这类犯罪行为的发生与空间环境存在一定的关系。试验研究区域为美国波特兰市城区,基本数据集采用城市金融设施兴趣点,参考数据集采用抢劫犯罪事件点数据。其中兴趣点POIs共89个(ATM 55个,Bank 34个),抢劫犯罪点数据共426个,时间为2014年,其空间分布如图 12所示,其中兴趣点和抢劫事件在主城区分布比较密集,在其他区域相对比较分散。从图 15中的标准差椭圆可发现抢劫犯罪事件由西南向东北扩散,且图 13的Cross-K函数[32]表明兴趣点与抢劫犯罪事件间存在显著的空间依赖关系。通过分析抢劫犯罪事件在兴趣点POIs周围的分布情况,空间参考邻域半径设为300~1500 ft(1 ft=0.305 m),随机重排次数为999次,显著性水平设为0.05。通过在不同半径水平上的探测结果,并获取空间交叉异常的生存距离,如图 14所示,图 15给出了具有稳定生存距离的空间交叉异常。近一步从空间交叉异常的属性、生存距离的长短及异常周围道路建筑等分布情况进行分析。
|
| 图 12 实际数据集空间分布 Fig. 12 Distribution of real-world dataset |
|
| 图 13 实际数据集的Cross-K函数值 Fig. 13 Cross-K function of real-world dataset |
|
| 图 14 空间交叉异常生存距离 Fig. 14 The living distance of spatial cross-outliers |
|
| 图 15 空间交叉异常探测结果 Fig. 15 The detection results of spatial cross-outliers |
从表 2可以发现,空间交叉异常中Bank有4个,ATM有7个,其中点号4、46、77、80、89具有较长生存距离,且均为ATM;而Bank类异常的生存距离均较短。从图 16可以发现,交叉异常多分布在抢劫事件高发区域边缘。环境犯罪学认为犯罪发生有一些必备要素,如罪犯、被害人、被触犯的法律以及合适的时间和场所,相比盗窃等侵财犯罪,抢劫犯罪在作案后会被立即发现,需要迅速逃逸,所以抢劫罪犯对逃逸方便性的重视胜过其他方面[33],如异常点80、89周边道路交通复杂,且靠近跨江大桥,便于作案后快速逃逸和隐藏。进一步结合波特兰市的市区行政区划,可以发现异常点4、9、15、46发生在城市不同管辖区的交界线附近,这可能与边界警力部署、跨区警力调度难等有关。
| 数据集 | 方法 | TP | FP | FN | TN | 精确率 /(%) |
召回率 /(%) |
F值 /(%) |
| SD1 | 本文方法(r=0.2) | 7 | 3 | 2 | 158 | 70.0 | 77.8 | 73.7 |
| 本文方法(r=0.3) | 7 | 1 | 2 | 160 | 87.5 | 77.8 | 83.3 | |
| 本文方法(r=0.4) | 7 | 3 | 2 | 158 | 70.0 | 77.8 | 73.7 | |
| 本文方法(r=0.5) | 1 | 8 | 8 | 153 | 11.1 | 11.1 | 11.1 | |
| COD(r′=1.5 α′=1/5 k=2) | 7 | 1 | 2 | 160 | 87.5 | 77.8 | 83.3 | |
| COD(r′=1.5 α′=1/4 k=2) | 5 | 4 | 4 | 157 | 55.6 | 55.6 | 55.6 | |
| COD(r′=1.5 α′=1/3 k=2) | 2 | 3 | 7 | 158 | 40.0 | 22.2 | 28.6 | |
| COD(r′=2.0 α′=1/5 k=2) | 5 | 2 | 4 | 159 | 71.4 | 55.6 | 62.5 | |
| SD2 | 本文方法(r=0.3) | 8 | 1 | 1 | 191 | 88.9 | 88.9 | 88.9 |
| COD(r′=1.5 α′=1/5 k=2) | 6 | 2 | 2 | 190 | 75.0 | 75.0 | 75.0 | |
| SD3 | 本文方法(r=0.3) | 9 | 0 | 1 | 191 | 100 | 90.0 | 94.7 |
| COD(r′=1.5 α′=1/5 k=2) | 9 | 0 | 2 | 191 | 100 | 81.8 | 90.0 |
| 点号 | 属性 | 生存距离/ft | 点号 | 属性 | 生存距离/ft |
| 3 | Bank | 600~1200 | 77 | ATM | 600~1500 |
| 4 | ATM | 300~1400 | 80 | ATM | 800~1500 |
| 9 | ATM | 300~800 | 86 | ATM | 900~1200 |
| 15 | Bank | 300~700, 1300~1500 | 88 | Bank | 400~900 |
| 46 | ATM | 700~1500 | 89 | ATM | 600~1500 |
| 61 | Bank | 900~1300 |
|
| 图 16 抢劫事件分布密度及标准差椭圆 Fig. 16 The distribution density and standard deviational ellipse of robbery events |
3 结论与展望
空间异常探测对于揭示地理实体或地理现象的潜在发展规律具有重要价值,已成为空间数据挖掘的重要手段之一。针对现有空间异常探测方法缺乏异常显著性的统计判别以及未同时考虑实体的类别进行异常探测分析,本文提出一种空间交叉异常显著性判别的非参数检验方法,从数据驱动的角度进行建模,不依赖于数据分布的任何假设。通过模拟试验分析和实例应用发现,本文方法具有两方面的优势:划定支撑域从统计显著性的角度判别空间异常,减少了人为设定阈值的依赖;引入生存距离的概念对多尺度挖掘结果进行评价。当研究多个类别间的分布或交互作用关系的异常时,可以分解为多个的二元分布异常探测问题进行解决。本文进一步的研究工作主要集中在:针对数据分布形式发展自适应的距离,进一步提高探测方法的稳健性;方法采用了随机模拟,计算量较大,将研究采用并行计算、数据分块等技术手段提升算法的运行效率,使其可以适用于海量数据的分析处理。
| [1] |
李德仁, 王树良, 李德毅.
空间数据挖掘理论及应用[M]. 2版. 北京: 科学出版社, 2013.
LI Deren, WANG Shuliang, LI Deyi. Spatial Data Mining Theories and Applications[M]. 2nd ed. Beijing: Science Press, 2013. |
| [2] |
刘大有, 陈慧灵, 齐红, 等.
时空数据挖掘研究进展[J]. 计算机研究与发展, 2013, 50(2): 225–239.
LIU Dayou, CHEN Huiling, QI Hong, et al. Advance in Spatiaotemporal Data Mining[J]. Journal of Computer Research and Development, 2013, 50(2): 225–239. |
| [3] | HAWKINS D. Identification of Outliers[M]. London: Chapman and Hall, 1980. |
| [4] | SHEKHAR S, LU C T, ZHANG Pusheng. A Unified Approach to Detecting Spatial Outliers[J]. GeoInformatica, 2003, 7(2): 139–166. DOI:10.1023/A:1023455925009 |
| [5] | KNORR E M, Ng R T. Algorithms for Mining Distance-Based Outliers in Large Datasets[C]//Proceedings of the 24th International Conference on Very Large Data Bases, New York: VLDB Press, 1998: 392-403. |
| [6] | BREUNIG M M, KRIEGEL H P, Ng R T, et al. LOF: Identifying Density-Based Local Outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. Dallas: ACM, 2000: 93-104. |
| [7] |
刘启亮, 邓敏, 石岩, 等.
一种基于多约束的空间聚类方法[J]. 测绘学报, 2011, 40(4): 509–516.
LIU Qiliang, DENG Min, SHI Yan, et al. A Novel Spatial Clustering Method Based on Multi-constraints[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 509–516. |
| [8] | SHI Yan, DENG Min, YANG Xuexi, et al. Adaptive Detection of Spatial Point Event Outliers Using Multilevel Constrained Delaunay Triangulation[J]. Computers, Environment and Urban Systems, 2016, 59: 164–183. DOI:10.1016/j.compenvurbsys.2016.06.001 |
| [9] |
杨学习, 石岩, 邓敏, 等.
一种基于多层次专题属性约束的空间异常探测方法[J]. 武汉大学学报(信息科学版), 2016, 41(6): 810–817.
YANG Xuexi, SHI Yan, DENG Min, et al. A New Method of Spatial Outlier Detection by Considering Multi-level Thematic Attribute Constraints[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 810–817. |
| [10] | LU C T, DOS SANTOS JR R F, LIU Xutong, et al. A Graph-based Approach to Detect Abnormal Spatial Points and Regions[J]. International Journal on Artificial Intelligence Tools, 2011, 20(4): 721–751. DOI:10.1142/S0218213011000309 |
| [11] | CHEN Dechang, LU C T, KOU Yufeng, et al. On Detecting Spatial Outliers[J]. GeoInformatica, 2008, 12(4): 455–475. DOI:10.1007/s10707-007-0038-8 |
| [12] | CHAWLA S, SUN P. SLOM:A New Measure for Local Spatial Outliers[J]. Knowledge and Information Systems, 2006, 9(4): 412–429. DOI:10.1007/s10115-005-0200-2 |
| [13] | DENG Min, LIU Qiliang, LI Guangqiang. Spatial Outlier Detection Method Based on Spatial Clustering[J]. Journal of Remote Sensing, 2010, 14(5): 944–958. |
| [14] |
唐建波, 刘启亮, 邓敏, 等.
空间层次聚类显著性判别的重排检验方法[J]. 测绘学报, 2016, 45(2): 233–240.
TANG Jianbo, LIU Qiliang, DENG Min, et al. A Permutation Test for Identifying Significant Clusters in Spatial Dataset[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 233–240. DOI:10.11947/j.AGCS.2016.20140605 |
| [15] | HE Zengyou, DENG Shengchun, XU Xiaofei. Outlier Detection Integrating Semantic Knowledge[M]//MENG Xiaofeng, SU Jianwen, WANG Yujun. Advances in Web-age Information Management. Berlin, Heidelberg: Springer, 2002: 126-131. |
| [16] | PAPADIMITRIOU S, FALOUTSOS C. Cross-Outlier Detection[M]//MENG Xiaofeng, SU Jianwen, WANG Yujun. Advances in Spatial and Temporal Databases. Berlin, Heidelberg: Springer, 2003: 199-213. |
| [17] | HE Zengyou, XU Xiaofei, HUANG J Z, et al. Mining Class Outliers:Concepts, Algorithms and Applications in CRM[J]. Expert Systems with Applications, 2004, 27(4): 681–697. DOI:10.1016/j.eswa.2004.07.002 |
| [18] | HEWAHI N M, SAAD M K. Class Outliers Mining:Distance-Based Approach[J]. International Journal of Computer and Information Engineering, 2007, 1(9): 2805–2818. |
| [19] | LIU Xutong, CHEN Feng, LU C T. On Detecting Spatial Categorical Outliers[J]. GeoInformatica, 2014, 18(3): 501–536. DOI:10.1007/s10707-013-0188-9 |
| [20] | LU Y C, CHEN Feng, WANG Yating, et al. Discovering Anomalies on Mixed-type Data Using a Generalized Student-t Based Approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(10): 2582–2595. DOI:10.1109/TKDE.2016.2583429 |
| [21] | JANEJA V P, PALANISAMY R. Multi-domain Anomaly Detection in Spatial Datasets[J]. Knowledge and Information Systems, 2013, 36(3): 749–788. DOI:10.1007/s10115-012-0534-5 |
| [22] | ZHENG Yu, ZHANG Huichu, YU Yong. Detecting Collective Anomalies from Multiple Spatio-temporal Datasets Across Different Domains[C]//Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle: ACM, 2015: 2. |
| [23] |
蔡建南, 刘启亮, 徐枫, 等.
多层次空间同位模式自适应挖掘方法[J]. 测绘学报, 2016, 45(4): 475–485.
CAI Jiannan, LIU Qiliang, XU Feng, et al. An Adaptive Method for Mining Hierarchical Spatial Co-location Patterns[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 475–485. DOI:10.11947/j.AGCS.2016.20150337 |
| [24] | PEI Tao, WANG Weiyi, ZHANG Hengcai, et al. Density-based Clustering for Data Containing Two Types of Points[J]. International Journal of Geographical Information Science, 2015, 29(2): 175–193. DOI:10.1080/13658816.2014.955027 |
| [25] | KOLINGEROVÁ I, ŽALIK B. Reconstructing Domain Boundaries within a Given Set of Points, Using Delaunay Triangulation[J]. Computers & Geosciences, 2006, 32(9): 1310–1319. |
| [26] | HUBERT M, VANDERVIEREN E. An Adjusted Boxplot for Skewed Distributions[J]. Computational Statistics & Data Analysis, 2008, 52(12): 5186–5201. |
| [27] | EDELSBRUNNER H, KIRKPATRICK D, SEIDEL R. On the Shape of a Set of Points in the Plane[J]. IEEE Transactions on Information Theory, 1983, 29(4): 551–559. DOI:10.1109/TIT.1983.1056714 |
| [28] |
王远飞, 何洪林.
空间数据分析方法[M]. 北京: 科学出版社, 2007: 60.
WANG Yuanfei, HE Honglin. Spatial Data Analysis Method[M]. Beijing: Science Press, 2007: 60. |
| [29] | LEUNG Y, ZHANG Jiangshe, XU Zongben. Clustering by Scale-space Filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(12): 1396–1410. DOI:10.1109/34.895974 |
| [30] | PEI Tao, ZHU Axing, ZHOU Chenghu, et al. A New Approach to the Nearest-neighbour Method to Discover Cluster Features in Overlaid Spatial Point Processes[J]. International Journal of Geographical Information Science, 2006, 20(2): 153–168. DOI:10.1080/13658810500399654 |
| [31] | DENG Min, HE Zhanjun, LIU Qiliang, et al. Multi-scale Approach to Mining Significant Spatial Co-location Patterns[J]. Transactions in GIS, 2017, 21(5): 1023–1039. DOI:10.1111/tgis.2017.21.issue-5 |
| [32] | RIPLEY B D. The Second-Order Analysis of Stationary Point Processes[J]. Journal of Applied Probability, 1976, 13(2): 255–266. DOI:10.2307/3212829 |
| [33] |
毛媛媛, 丁家骏.
抢劫与抢夺犯罪行为时空分布特征研究——以上海市浦东新区为例[J]. 人文地理, 2014, 29(1): 49–54.
MAO Yuanyuan, DING Jiajun. Study on Spatial-temporal Patterns of Robbery and Snatch:A Case Study of Pudong New Area, Shanghai[J]. Human Geography, 2014, 29(1): 49–54. |



