2. 杭州电子科技大学生命信息与仪器工程学院, 浙江 杭州 310018
2. College of Life Information Science and Instrument Engineering, Hangzhou Dianzi University, Hangzhou 310018, China
高光谱图像具有图谱合一、光谱分辨率高、光谱范围宽、光谱相关性强等特点,使得它在目标侦察、地质勘查、农业生态调查等方面发挥了重要的作用[1]。
高光谱图像较高的光谱维数和光谱分辨率为地物分类带来巨大的机遇,然而在训练样本有限的情况下,高光谱图像分类过程会存在Hughes现象,即小样本数目与高光谱维数之间的矛盾。为解决这一问题,一方面可采用特征提取和波段选择方法对高光谱图像进行降维处理[2-7]。典型的特征提取方法包括主成分分析和流形学习等[3]。波段选择是指按照一定的准则选择具有代表性的波段用于分类,可用的波段选择准则包括波段相关系数、互信息、JM距离和散度等[1]。文献[4]基于场景中的先验知识,采用互信息实现了波段选择。文献[5]采用JM距离和最小估计冗余协方差作为测度,提出了一种改进萤火虫算法的波段选择方法。文献[6]采用互信息等三种测度计算相邻波段间的相关性,然后对波段进行分类与重新分组。文献[7]采用粒子群算法同时进行波段自动选择和支持向量机参数优化,但是由于采用基于封装(wrapper)的波段选择方法,需要已知样本标签来计算优化的目标函数。文献[8]提出了一种结合波段分组特征和形态学特征的高光谱图像分类方法。上述方法虽然能够提取出不相关的有效波段组合,但是算法的复杂度较高。
对分类器进行优化设计是提高高光谱图像分类精度的另一手段。常采用的分类器包括支持向量机[9](support vector machine,SVM)、稀疏表示[10-12](sparse representation,SR)、协作表示[13, 14](collaborative representation,CR)、集成学习法[6, 15],深度学习法[16]等。SVM算法通过核函数将原始特征向量映射到高维空间,通过建立决策面实现分类,由于具有较强的小样本训练分类能力,因而在高光谱图像中得到广泛应用[9]。SR算法本质上是基于多近邻原则把待分类样本表示为字典中各训练样本的稀疏线性组合[11],通常情况下样本数较多时才能达到较高的识别率。当训练样本较少时,基于CR的分类性能优于基于SR的分类性能[13-14]。文献[13]在基于协作表示方法进行高光谱图像分类时,由于设计的算法能够有效结合空谱信息,故分类精度明显高于仅采用谱特征的分类精度。集成学习法通过合并一组弱分类器来提高分类器的性能,训练得到的强分类器性能优于任何一个弱分类器。文献[6]提出了一种基于分类器集成的高光谱遥感图像分类算法。其中波段分组通过波段分类和重新分组两个过程实现,基分类器采用最大似然法,采用基于选择性集成的分类器合成方法。该算法虽然能够取得较好的分类效果,但是存在算法过程复杂,难以实现对高光谱数据的实时处理。随着深度学习在计算机视觉等方面的成功应用,目前正逐步拓展到高光谱图像分类应用[16],但只有在使用较多训练样本的情况下才能取得较好的分类精度。
超限学习机(extreme learning machine,ELM)是具有单个隐藏层的前馈神经网络,由于将输入层与隐藏层间的连接权重随机化处理,通过求解岭回归问题计算隐层与输出层间的连接权重[17],因此ELM算法具有可调参数少、计算速度快和泛化能力好等优点。将超限学习机用于高光谱图像分类时,研究人员对其进行了拓展[15, 18-19]。文献[15]提出了一种集成超限学习机算法对高光谱图像进行分类,由于是通过对训练样本进行重采样方式来训练弱分类器,因此不适用于训练样本较少情况下的分类问题。文献[18]采用差分进化算法对超限学习机的参数进行优化,以提高高光谱图像的分类精度和计算速度。文献[19]提出了两种基于空谱特征复合核的超限学习机算法,其中单一空间特征或谱特征核函数均由激活函数构成的核函数和一般高斯核函数组成。由于采用了空谱联合特征,因而算法分类精度较高。
针对文献[6, 15]提出的算法中存在的波段选择算法复杂度高、采用的集成学习算法不适合小样本情况的问题,考虑到高光谱具有较高的光谱维数,本文采用对高光谱图像谱维进行平均分组和随机抽样的方式进行特征降维,基于集成学习理论设计了一种融合空谱特征和超限学习机的高光谱图像分类方法。提出的算法首先基于每个像素点的邻域信息提取空谱特征,然后对空谱特征的谱维进行平均分组和随机抽样,提取降维后的特征。采用超限学习机学习得到弱分类器,基于多次抽样特征得到的分类结果,基于投票表决法得到最终的分类结果。采用3个典型高光谱数据集进行了算法性能测试,验证了所提出的算法的有效性。
1 超限学习机原理超限学习机是单隐层前馈神经网络,通过对输入层与隐层间的权重进行随机化处理,在目标分类、特征学习等方面具有良好的性能。因不需要迭代更新权重,故具有训练速度快的优势,通过合理地选择随机权重的分布,能够保证分类的精度。对某一类目标进行分类时,ELM的输出模型为[17]
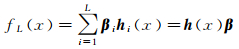 (1)
(1)
式中,hi(x)=G(ai,bi,x)为第i个隐层节点输出映射;G为隐层节点采用的激活函数;x∈Rd,为输入特征向量;ai∈Rd,为输入层与第i个隐层节点的随机连接权重;bi∈R,为第i个隐层节点的偏置;L为隐层节点个数;β=[β1, β2, …, βL]T为隐层节点与输出节点间的连接权重向量。设训练样本数目为N,当目标类别数目B>1时,ELM优化的目标函数为[17]
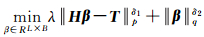 (2)
(2)
式中,δ1>0, δ2>0, p, q=0, 1, 2,…, +∞;λ为正则化参数;H为所有训练样本经过L个隐层节点映射得到的变换矩阵,维数为N×L;由于是对多类别样本进行分类,故β此时拓展为L×B的连接矩阵;T为N×B目标类别矩阵,如式(3)所示,每一行中对应目标类别位置处为1,其余位置为-1。
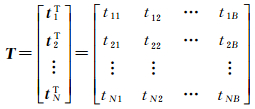 (3)
(3)
当δ1=2, δ2=2, p=2, q=2时,式(2)具有闭环解,具体如式(4)和式(5)所示,I为单位矩阵。
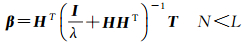 (4)
(4)
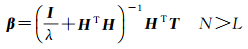 (5)
(5)
集成学习算法通过合并一组弱分类器来提高分类器的性能,训练得到强分类器的分类性能优于其中弱分类器的性能[20]。基于集成学习理论设计分类器时,可以采用样本重采样[21]、特征重采样[22]和样本权重迭代更新[15]等几种方式训练弱分类器。考虑到高光谱图像的训练样本数少、光谱维数高的特点(>100),可以采用对光谱特征进行随机抽样的方式进行降维,在降低高光谱特征维数的同时,为保证分类精度,可通过多次抽样,基于集成学习思想训练得到强分类器。本文算法首先基于空间像素邻域信息的均值提取空谱特征,然后通过对提取的特征向量进行平均分组和随机抽样实现特征降维,通过多次抽样训练得到多个弱分类器,最后采用投票表决法得到强分类器。算法流程如图 1所示。
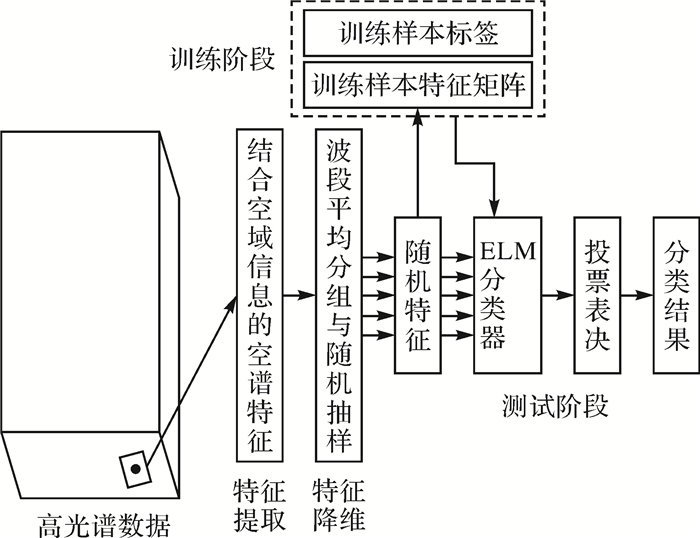
|
| 图 1 融合空谱特征和集成超限学习机的高光谱图像分类流程 Fig. 1 Flowchart of hyperspectral image classification by combination of spatial-spectral features and ensemble extreme learning machines |
2.1 空谱联合特征
试验研究表明,采用空谱联合特征能够提高高光谱图像分类的正确率[10-14, 19]。基于空间像素邻域的光谱特性具有一定相似性,或属于同一类物质的假设,选择空间邻域内一定区域(例如9×9)的样本均值作为空域特征[13, 19]。将空间中某一点(i, j)的谱特征记做f1(i, j),则基于空间邻域Q计算得到的空域特征为
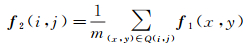 (6)
(6)
式中,m为空间邻域Q内样本总数。空域特征计算结合了空间邻域信息,但在某些情况下,个别地物的样本数目少,空间分布不均匀,故可通过结合谱特征和空域特征来保证分类的精度。故对于高光谱图像中每个像素(i, j)提取的空谱特征为f(i, j)=f1(i, j), f2(i, j)。
2.2 波段平均分组与随机抽样从前面分析知,可通过特征提取和波段选择两种方式降低光谱维数,通过设定合适的优化准则进行波段选择与分组,虽然能够获得有效的特征集合,但是算法计算复杂度较高[5]。考虑到高光谱相邻波段间具有一定的相关性,为保留原始光谱维度所包含的有用信息,可对原始空谱特征向量进行平均分组或基于优化度量的非均匀分组[8],分成若干个区间,然后从每个区间随机选择一定数量的波段进行组合,以达到特征降维的目的。图 2为Indian Pines数据中16类典型地物的归一化光谱曲线,总计光谱维数为200,采用平均分组和非均匀分组两种方式进行波段分组的示意图分别如图 2中的虚线和点划线所示。采用非均匀分组方法虽然能够发现相关系数等发生突变的波段,但是如何从分组后的波段集合中选择有利于目标分类的波段子集,同样是值得深入研究的问题。采用平均分组思想虽然是一种次优选择,但是考虑了地物光谱特性随波段的变化趋势。当采用随机抽样方法获得降维后的波段组合时,带有一定随机性,当光谱维数降低到一定程度时,分类精度同时会有所降低,故本文采用对提取的空谱特征进行多次抽样,基于降维后的特征训练若干分类器,采用集成学习思想训练得到用于高光谱分类的强分类器。设抽样后特征在原特征中的索引记做indexk,k=1, 2, …, C为抽样次数,其中C为采用的弱分类器数目。
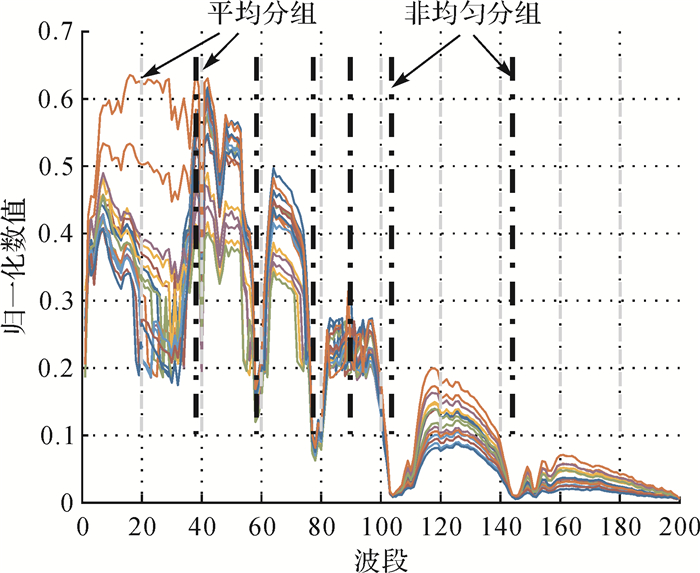
|
| 图 2 典型地物光谱曲线平均分组示意 Fig. 2 Schematic diagram of average grouping for spectral curves of representative ground objects |
2.3 超限学习机参数学习
对所有的训练样本提取空谱特征,记作fm{1, 2},m为样本的标号。以谱特征为例,将样本提取的谱特征按列进行排列,构成特征矩阵F,F=[f1,f2,…,fN],N为样本个数。对于第k个分类器,经过随机抽样后的特征矩阵为F(indexk,:)。采用超限学习机进行训练时,根据式(7)生成输入层与隐层间的权重矩阵Wk,按照式(8)生成偏置向量Biask。
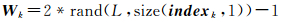 (7)
(7)
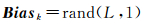 (8)
(8)
式中,rand(m, n)为产生行和列分别为m和n,满足均匀分布且位于区间[0 1]的随机数矩阵,size(v, 1)函数用于获取矩阵或向量的行数。则第k个分类器对应的映射矩阵为
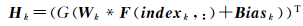 (9)
(9)
根据式(9),利用式(4)或式(5)求得输出权重矩阵βk。经过超限学习机得到的弱分类器classifierk包含{Wk,Biask,indexk,βk,G}等参数。对于谱特征和空域特征分别训练得到一组弱分类器,记作classifierk1和classifierk2,k=1, 2, …, C。
2.4 基于特征加权融合与投票表决的分类器集成Bagging算法[21]通过对样本进行重采样训练得到弱分类器集合,这些弱分类器通过投票表决的方式确定分类标签。通过Bagging算法,能够有效降低分类算法的方差,提高算法的泛化能力。
对于一个测试样本y,设提取的空谱特征向量分别为fy1和fy2,当采用弱分类器classifierk进行分类时,根据式(9)进行特征降维与映射,利用式(1)求解得到一个1×B的向量,基于如式(10)所示的加权模型[23]计算得到属于每一类目标的分类,并得到分向量scorek,其中w为[0 1]之间的权重。然后通过式(11)求得其最大值处对应的索引j,即为目标的类别Label(k)。
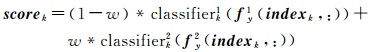 (10)
(10)
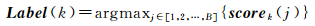 (11)
(11)
根据Bagging算法思想,对所有C个分类器的结果{Label(k)}k=1, 2, …, C统计分类结果直方图得到{bin(j)}j=1, 2, …, B,采用投票表决法确定目标估计测试样本y的类别R(y),如式(12)所示
 (12)
(12)
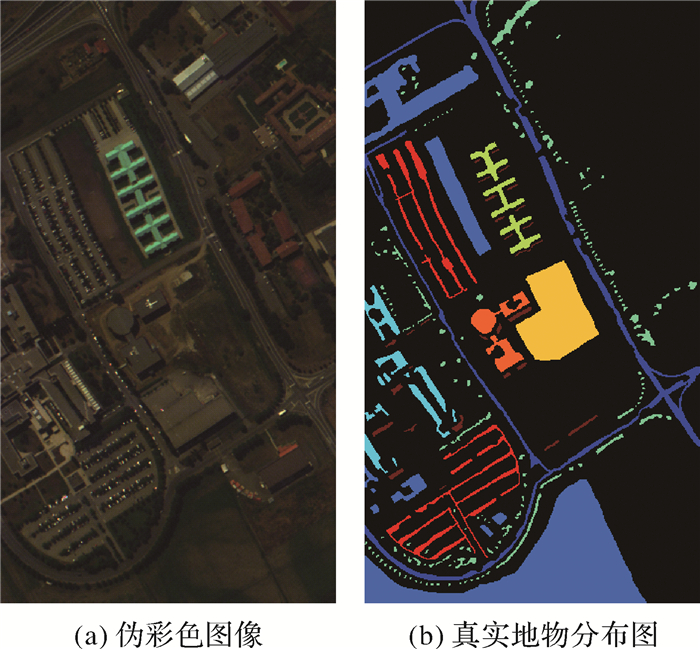
为验证本文提出算法的有效性,将其应用于Indian Pines、Pavia University、Salinas 3个典型高光谱数据的分类。3种高光谱数据的参数描述见表 1[12],相应数据和地物类别真实分布可通过公开网站进行下载(http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scences)。其中Indian Pines选用的数据是高光谱遥感数据AVIRIS92AV3C。该数据是美国印第安纳西北部地区植被影像,图像大小为145×145,波长范围为0.4~2.5 μm,原始波段数为220个,移除水吸收波段(104—108波段、150—163波段、220波段)后的波段数为200个。基于波段50、27和17生成的伪彩色图像如图 3所示。基于Pavia University与Salinas高光谱图像的指定波段生成的伪彩色图像及相应真实地物分布图分别如图 4和图 5所示。
| 数据集 | 尺寸 | 分辨率/m | 光谱范围/μm | 目标类别 | 使用波段 |
| Indian Pines | 145×145×220 | 20 | 0.4~2.5 | 16 | 200 |
| Pavia University | 610×340×115 | 1.5 | 0.43~0.86 | 9 | 103 |
| Salinas | 512×217×224 | 3.7 | 0.4~2.5 | 16 | 204 |

|
| 图 3 Indian Pines伪彩色图像及真实地物类别(使用波段50、27、17) Fig. 3 False color image based on bands 50, 27, 17 and ground-truth map for Indian Pines |
|
| 图 4 Pavia University伪彩色图像及真实地物类别(使用波段60、30、2) Fig. 4 False color image based on bands 60, 30, 2 and ground-truth map for Pavia University |

|
| 图 5 Salinas伪彩色图像及真实地物类别(使用波段50、30、20) Fig. 5 False color image based on bands 50, 30, 20 and ground-truth map for Salinas |
进行分类前,首先对输入的高光谱数据进行归一化,使数值范围位于区间[0 1]。评价指标分别为平均分类精度(AA),总体分类精度(OA)和Kappa系数(κ)[1]。
根据文献[19],本文用于提取空谱特征的邻域范围设定为9×9,从每个波段分组中选择的波段数目设定为5。试验中将波段平均分组数设定为弱分类器数目C,因此在每个波段分组中抽样次数确定的情况下(设定为5),弱分类器数目C影响空谱信息的保留程度。虽然不同类别物质的谱特征在不同波段分组中(或谱窗)的判别能力不同,但是考虑到进行分类器设计时,需综合利用不同波段分组中的联合表示能力,若损失信息过多,必将会降低高光谱的分类精度。对于Indian Pines和Salinas高光谱数据,设定C=20,Pavia University高光谱数据C=10,这样经过随机抽样获得的随机特征保留了原始特征约50%的信息。由于降维后空谱特征维数分别为100、50、100,故当超限学习机隐层节点个数大于100时,就能将特征由低维空间映射到高维空间,从而更有利于分类器设计。试验中,超限学习机隐层节点个数L=500,由于将原始高光谱数据归一化到[0 1],故激活函数G(·)设定为sin(·)函数。
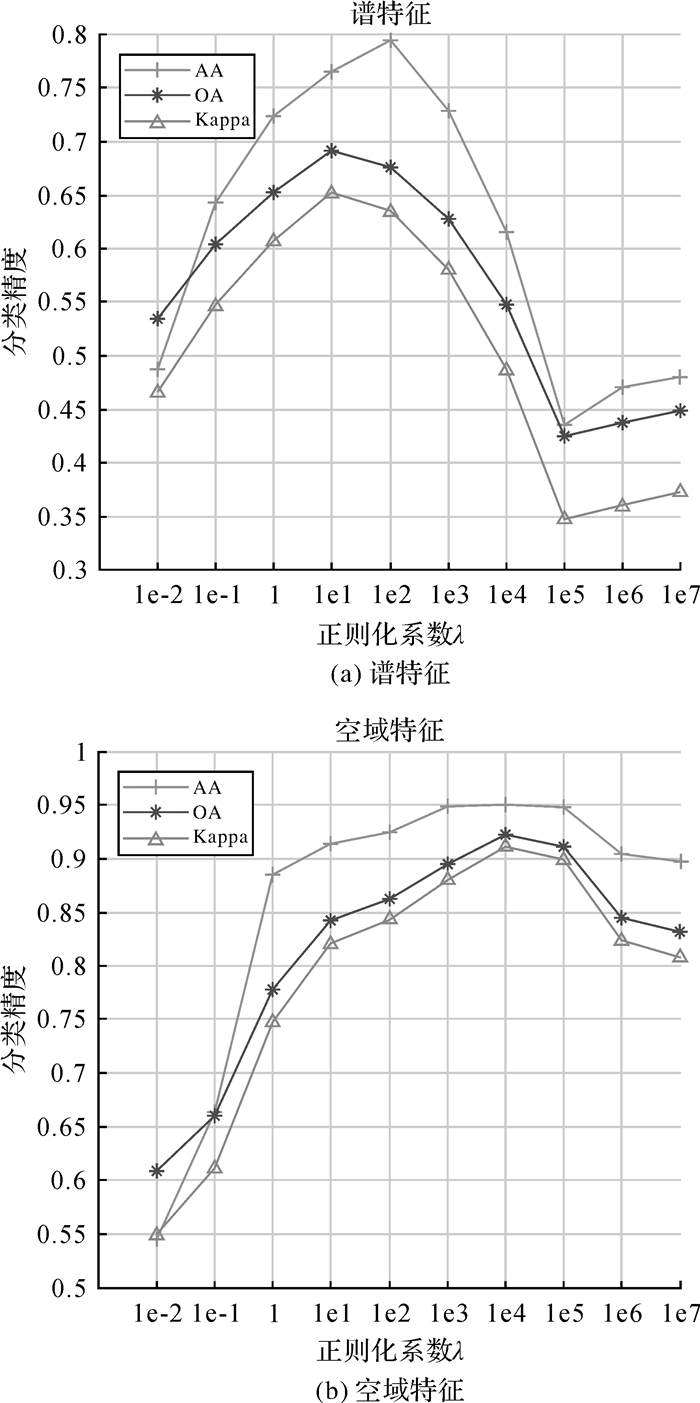
正则化参数λ是影响ELM分类能力的主要因素,故首先通过试验分析了λ对于高光谱分类精度的影响。采用Indian Pines高光谱图像进行测试,训练样本数目设定为40(注:对于Indian Pines数据中样本数较少的几类,若训练样本超过总样本50%时,取训练样本为总样本的50%)。当加权系数设定为w=0.9,试验结果如图 6所示。从图 6中可以看出,对于谱特征和空域特征而言,λ的影响不尽相同,当λ=1e1时,基于谱特征的分类结果最好;对于空域特征,随着λ的增加,分类精度逐步增加,当λ=1e4时,分类精度最优,之后逐步下降。考虑到分类精度与训练样本的抽样分布有关,具有一定的随机性,为保证分类精度,故λ取较大的数值,在后续试验中对于谱特征和空域特征设定λ分别为1e2和1e5。
|
| 图 6 正则化系数对分类精度的影响 Fig. 6 Influence of regularization parameter on classification accuracy |
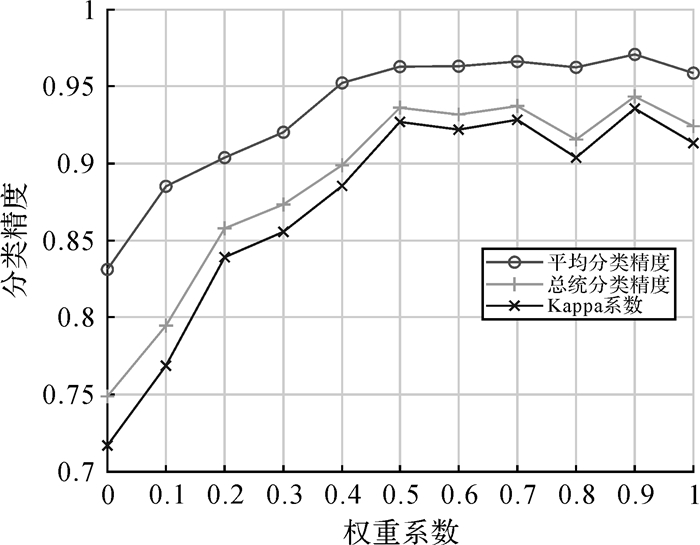
当λ=1e5时,改变权重系数w,对Indian Pines的分类结果如图 7所示。考虑到高光谱图像中相邻像素属于同一类别/物质的概率较高,采用相邻区域内谱特征的均值作为特征向量,起到了低通滤波的作用,能够有效地降低噪声影响。从图 7中可以看出,随着权重系数w的增加,分类精度逐渐提高并趋于平稳,当w=0.9时取得了接近95%的总体分类精度,且仅采用空域特征(w=1.0)的分类性能优于仅采用谱特征(w=0.0)的分类性能。在后续试验中设定空谱特征的权重系数为w=0.9。
|
| 图 7 权重系数对分类精度的影响 Fig. 7 Influence of weighted coefficient on classification accuracy |
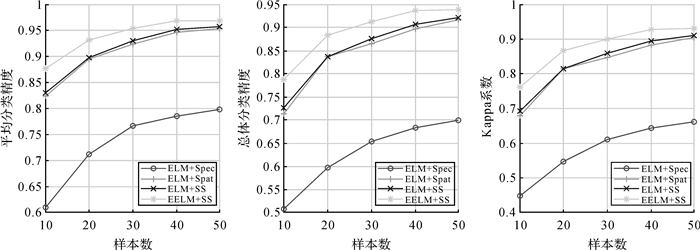
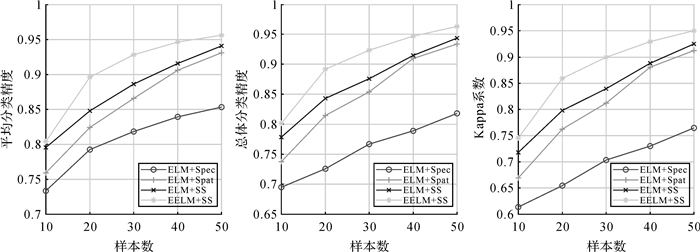
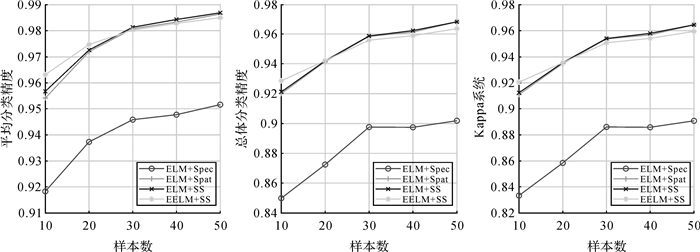
为验证采用的集成学习算法的优势,分别采用谱特征、空域特征、空谱特征,利用ELM算法训练分类器进行分类,与本文分类算法进行比较,试验中采用的训练样本数分别设定为10、20、30、40、50,试验结果如图 8—图 10所示。从图 8和图 9中可以看出,对于Indian Pines和Pavia University高光谱数据,随着样本数的增加,本文算法的分类精度明显优于其他3种方法。当采用ELM训练分类器时,采用空域特征的分类结果与采用空谱特征的分类结果十分接近,这也说明通过结合空间邻域信息,能够有效地提高高光谱图像的分类精度。当采用集成学习思想训练分类器时,对获得的空谱特征进行特征抽样,进一步提高了分类器的分类精度。对于Salinas高光谱数据,当样本数超过30时,采用ELM和空谱特征的分类结果略优于本文算法,这主要是与高光谱图像中各类别样本的分布有关,对于Salinas而言,同一类别的目标分布相对集中,光谱特性相近,故样本的类内方差小,因而采用基于集成学习的超限学习机算法的分类结果并没有提高,而对于Indian Pines和Pavia University,每类目标分布相对广泛,同类目标光谱曲线差异较大,故本文算法充分利用了提取特征光谱维度的差异性,基于特征随机抽样的方式实现特征降维,提高了高光谱数据分类的精度。
|
| 图 8 Indian Pines分类结果 Fig. 8 Classification result for Indian Pines |
|
| 图 9 Pavia University分类结果 Fig. 9 Classification result for Pavia University |
|
| 图 10 Salinas分类结果 Fig. 10 Classification result for Salinas |
将本文算法与支持向量机、稀疏表示算法进行对比试验,将3种算法分别记作EELM、SVM、SR。由前面分析可知,采用空域特征相比于谱特征具有更强分类能力,故其他算法均采用如式(6)所示的空域特征。采用SVM训练分类器时,采用径向基核函数,Gamma和惩罚因子C采用交叉验证方式获得;采用SR进行分类时,基于每类目标的训练样本,采用文献[24]提出的字典学习方法对其进行优化,字典数目与训练样本数目相同,重构算法采用SPAMS工具箱[25]提供的mexLasso(·)函数。总计进行了5次蒙特卡洛模拟试验,当训练样本数目为40时,试验结果分别见表 2、表 3和表 4。文献[19]采用类似文献[9]的复合核方式融合高光谱的空谱特征,采用基于核映射的超限学习机算法用于高光谱分类,对Indian Pines、Pavia University和Salinas 3个高光谱数据的分类结果(AA, OA, Kappa)分别为(96.7±0.58, 93.4±0.99, 92.4±1.13)、(92.7±1.13, 93.5±1.37, 91.4±1.77)、(98.4±0.36, 96.4±0.79, 96.0±0.88)。对比文献[19]和本文算法的分类结果可以看出,本文算法在Indian Pines和Salinas的分类结果与之接近,但对Pavia University的分类结果更优,这说明了通过对高光谱数据进行降维,采用集成学习的方法训练分类器,能够提高高光谱数据分类的精度。
| 序号 | 颜色 | 类别 | 训练样本数 | 测试样本数 | SVM | SR | EELM |
| 1 | Alfalfa | 23 | 23 | 96.52±5.07 | 100.00±0.00 | 100.00±0.00 | |
| 2 | Corn-notill | 40 | 1388 | 68.04±6.15 | 82.29±5.28 | 92.46±2.58 | |
| 3 | Corn-mintill | 40 | 790 | 79.72±6.12 | 87.95±3.82 | 94.58±3.34 | |
| 4 | Corn | 40 | 197 | 95.33±5.42 | 98.38±2.75 | 97.87±3.51 | |
| 5 | Grass-pasture | 40 | 443 | 87.45±6.19 | 94.54±5.09 | 95.03±5.93 | |
| 6 | Grass-trees | 40 | 690 | 96.32±1.04 | 99.25±0.52 | 99.59±0.38 | |
| 7 | Grass-pasture-mowed | 14 | 14 | 100.00±0.00 | 100.00±0.00 | 100.00±0.00 | |
| 8 | Hay-windrowed | 40 | 438 | 99.32±0.68 | 100.00±0.00 | 100.00±0.00 | |
| 9 | Oats | 10 | 10 | 98.00±4.00 | 100.00±0.00 | 100.00±0.00 | |
| 10 | Soybean-notill | 40 | 932 | 79.16±4.47 | 87.62±3.88 | 89.68±2.53 | |
| 11 | Soybean-mintill | 40 | 2415 | 76.20±2.34 | 86.84±1.68 | 88.47±2.54 | |
| 12 | Soybean-clean | 40 | 553 | 82.17±5.36 | 82.17±7.41 | 92.84±1.21 | |
| 13 | Wheat | 40 | 165 | 99.03±1.12 | 99.52±0.59 | 99.88±0.24 | |
| 14 | Woods | 40 | 1225 | 96.18±1.82 | 97.26±2.60 | 98.43±1.39 | |
| 15 | Buildings-grass-trees-drives | 40 | 346 | 90.12±3.62 | 94.86±0.72 | 97.34±1.15 | |
| 16 | Stone-steel-towers | 40 | 53 | 98.87±1.51 | 99.25±1.51 | 99.25±1.51 | |
| AA | 90.15±0.97 | 94.37±1.03 | 96.59±0.61 | ||||
| OA | 82.97±1.12 | 90.11±1.47 | 93.60±0.81 | ||||
| κ | 80.63±1.26 | 88.69±1.68 | 92.69±0.92 | ||||
| time | 14.27±1.01 | 23.47±1.36 | 42.03±2.23 |
| 序号 | 颜色 | 类别 | 训练样本数 | 测试样本数 | SVM | SR | EELM |
| 1 | Asphalt | 40 | 6591 | 82.27±1.87 | 85.87±3.57 | 91.66±2.58 | |
| 2 | Meadows | 40 | 18 609 | 92.40±3.76 | 96.10±1.30 | 95.82±2.24 | |
| 3 | Gravel | 40 | 2059 | 77.82±3.49 | 93.06±1.25 | 90.68±1.86 | |
| 4 | Trees | 40 | 3024 | 92.16±1.88 | 91.75±2.52 | 92.98±2.67 | |
| 5 | Painted metal sheets | 40 | 1305 | 99.68±0.25 | 100.00±0.00 | 99.31±0.37 | |
| 6 | Bare Soil | 40 | 4989 | 94.48±1.21 | 95.25±1.92 | 98.77±0.78 | |
| 7 | Bitumen | 40 | 1290 | 90.12±2.98 | 97.77±2.25 | 98.96±1.26 | |
| 8 | Self-Blocking Bricks | 40 | 3642 | 83.09±9.83 | 72.26±8.30 | 88.58±5.11 | |
| 9 | Shadows | 40 | 907 | 93.34±0.96 | 90.01±2.38 | 97.07±1.84 | |
| AA | 89.49±0.86 | 91.34±1.00 | 94.87±0.65 | ||||
| OA | 89.72±1.61 | 91.95±1.30 | 94.68±1.40 | ||||
| κ | 86.53±2.02 | 89.37±1.69 | 92.99±1.81 | ||||
| time | 29.70±1.56 | 54.65±0.37 | 83.86±3.23 |
| 序号 | 颜色 | 类别 | 训练样本数 | 测试样本数 | SVM | SR | EELM |
| 1 | Brocoli_green_weeds_1 | 40 | 1969 | 99.64±0.25 | 100.00±0.00 | 99.95±0.08 | |
| 2 | Brocoli_green_weeds_2 | 40 | 3686 | 99.27±0.42 | 99.95±0.04 | 99.99±0.02 | |
| 3 | Fallow | 40 | 1936 | 97.21±1.91 | 99.11±0.58 | 100.00±0.00 | |
| 4 | Fallow_rough_plow | 40 | 1354 | 97.05±0.85 | 98.39±0.88 | 98.89±0.50 | |
| 5 | Fallow_smooth | 40 | 2638 | 93.03±5.15 | 96.71±2.93 | 98.54±0.56 | |
| 6 | Stubble | 40 | 3919 | 99.75±0.43 | 99.99±0.01 | 99.97±0.04 | |
| 7 | Celery | 40 | 3539 | 98.84±0.41 | 98.99±0.85 | 99.84±0.22 | |
| 8 | Grapes_untrained | 40 | 11 231 | 75.39±6.67 | 88.56±2.32 | 89.51±1.64 | |
| 9 | Soil_vinyard_develop | 40 | 6163 | 98.52±1.67 | 99.84±0.19 | 100.00±0.01 | |
| 10 | Corn_senesced_green_weeds | 40 | 3238 | 92.52±1.23 | 96.79±1.64 | 98.25±1.09 | |
| 11 | Lettuce_romaine_4wk | 40 | 1028 | 98.25±0.65 | 99.90±0.15 | 100.00±0.00 | |
| 12 | Lettuce_romaine_5wk | 40 | 1887 | 99.43±0.20 | 100.00±0.00 | 99.97±0.03 | |
| 13 | Lettuce_romaine_6wk | 40 | 876 | 99.63±0.36 | 99.47±0.52 | 99.79±0.18 | |
| 14 | Lettuce_romaine_7wk | 40 | 1030 | 99.30±0.91 | 99.65±0.39 | 99.90±0.11 | |
| 15 | Vinyard_untrained | 40 | 7228 | 88.45±2.50 | 88.69±1.50 | 90.89±5.18 | |
| 16 | Vinyard_vertical_trellis | 40 | 1767 | 99.05±0.64 | 99.55±0.16 | 99.47±0.33 | |
| AA | 95.96±0.70 | 97.85±0.32 | 98.44±0.32 | ||||
| OA | 91.87±1.62 | 95.52±0.53 | 96.32±0.57 | ||||
| κ | 90.97±1.79 | 95.01±0.59 | 95.90±0.64 | ||||
| time | 72.77±7.48 | 119.06±2.53 | 238.61±4.27 |
试验中采用的PC机硬件配置如下:CPU为Intel(R) Core(TM) i5-3230M @2.6 GHz,内存为12 GB,显卡为NVIDIA NVS5400M,2 GB独立显存。采用的Matlab版本为Matlab 2017a。SVM和SR算法分别采用LibSVM和SPAMS工具箱实现分类,算法中主要函数均为C语言实现,本文算法仅采用Matlab函数实现。当采用训练样本数目为40时3种算法对3个高光谱数据中所有测试样本进行分类的总计耗时分别由表 2至表 4中的time项给出。SVM算法耗时与分类难度密切相关,计算复杂度由优化后支持向量的个数决定;SR算法与分类的类别总数,及构成每一类的字典元素个数有关,同时受稀疏系数恢复算法影响;本文算法的耗时与采用的弱分类器数目有关,同时受ELM算法中隐层节点个数影响。从表 2—表 4中可以看出,本文算法由于需要多个弱分类器投票表决确定目标类别,故算法耗时明显高于SVM算法的耗时。为提高本文算法的分类速度,一方面可以采用对算法进行优化,并采用C语言进行算法实现,另一方面采用的投票表决方法使得可以采用并行化处理来加速算法的运行速度。本文设计算法的耗时不受训练样本数目的影响,而SVM和SR算法均受训练样本数目影响,训练样本数目越多,算法耗时也同时会增加。
当采用不同数量或比例的训练样本时,进行5次蒙特卡洛模拟试验,本文算法的分类结果见表 5。文献[9]采用多核SVM高光谱数据进行分类,对Indian Pines数据的总体分类结果为90.91%,本文算法的总体分类结果为93.64%,但本文算法采用了更少数目的训练样本。文献[6]也采用了集成学习思想设计分类器,当采用训练样本占总样本比例为50%时,对Indian Pines数据的总体分类精度达到了97.76%,本文算法的分类结果为99.26%,本文算法分类精度高,且无须复杂的优化过程进行波段选择;由于采用对样本重采样的方式训练分类器进行集成,而Indian Pines每类数据较少,故文献[15]并没有给出Indian Pines的分类结果;当训练样本比例为13%时,文献[15]对Salinas的总体分类精度为97.19%,本文算法采用10%的训练样本时的总体分类精度为98.59%,优于文献[15]的结果。
| 数据集 | 评价指标 | 训练样本数量(比例) | ||||
| 50 | 100 | 5% | 10% | 50% | ||
| Indian Pines | AA | 97.16±0.57 | 98.00±0.31 | 91.38±1.91 | 95.62±1.82 | 98.65±0.94 |
| OA | 94.14±0.77 | 95.93±1.06 | 95.11±0.52 | 97.82±0.64 | 99.26±0.20 | |
| κ | 93.31±0.88 | 95.30±1.22 | 94.41±0.60 | 97.52±0.73 | 99.16±0.22 | |
| Pavia University | AA | 95.51±0.41 | 96.57±0.30 | 95.43±0.33 | 95.56±0.37 | 96.10±0.41 |
| OA | 95.57±1.03 | 96.80±0.41 | 97.61±0.13 | 97.70±0.14 | 98.01±0.18 | |
| κ | 94.14±1.33 | 95.74±0.54 | 96.82±0.17 | 96.95±0.19 | 97.36±0.24 | |
| Salinas | AA | 98.37±0.28 | 98.78±0.25 | 99.30±0.04 | 99.29±0.12 | 99.56±0.07 |
| OA | 96.14±0.58 | 97.14±0.52 | 98.62±0.13 | 98.59±0.18 | 99.20±0.06 | |
| κ | 95.70±0.65 | 96.81±0.59 | 98.46±0.15 | 98.43±0.20 | 99.10±0.07 | |
这也说明,基于集成思想设计分类器时,对高光谱的光谱维采用平均分组和特征抽样的方式,在一定程度上优于基于样本重采样的方式,更有利于小样本情况下的高光谱图像分类。文献[12]提出了一种快速轻量级的基于谱信息的稀疏表示分类器,通过结合空间信息提高了高光谱图像分类精度。如表 6所示,当训练样本比例为10%时,文献[12]对Indian Pines的总体分类精度为97.51%,本文算法为97.82%;当训练样本比例为5%时,文献[12]对Pavia University和Salinas的总体分类精度分别为98.59%和98.42%,本文算法分别为97.61%和98.62%。从结果对比来看,本文算法与文献[12]算法通过有效地利用空谱信息,均取得了较高的分类精度,且都具有实现简单、无需复杂优化过程的优点。当采用稀疏表示进行高光谱图像分类时,通过融合多种互补特征能够提高分类精度。文献[26]从高光谱图像中提取谱特征、形状和纹理特征,设计了基于联合稀疏表示的高光谱图像分类算法。当训练样本比例为5%时,文献[26]对Indian Pines的总体分类精度达到96.81%,高于本文分类精度(95.11%)。文献[27]同样采用多特征融合策略,设计了一种自适应稀疏表示高光谱分类算法。当训练样本比例为10%时,文献[27]和文献[10]的总体分类精度分别为97.91%和98.22%,本文算法分类精度为97.82%。本文设计方法仅采用了空谱特征,由于采用了集成学习思想设计分类器,因此容易扩展到多特征情况。
综合以上分析,本文算法基于集成学习设计分类器,通过对提取的空谱特征进行平均分组与特征随机抽样的方式,采用ELM设计弱分类器。试验结果表明,本文算法的分类精度优于文献中部分分类算法的分类精度,但本文算法具有实现简单、无须复杂优化过程、训练速度快等优点,更有利于实际应用。
4 结论针对高光谱图像数据波段多、冗余度大等特点,提出了一种基于空谱特征和集成超限学习机的高光谱图像分类方法。该方法在将ELM算法用于高光谱图像分类时,有效结合了目标空谱特征、波段分组与随机选择和集成学习3种手段,提高了分类模型的泛化能力。试验结果表明该方法具有以下优点:①结合空谱特征能够极大地提高目标的识别准确率;②对原始特征向量进行平均分组与随机抽样实现特征降维,与基于优化的波段选择方法相比降低了算法设计的复杂度;③超限学习机具有可调参数少、计算速度快等优点,采用集成学习思想提高了分类模型的泛化能力。由于采用的空谱特征使用了固定大小的窗口,没有针对待分类数据集进行优化,故当同一地物在连续空间范围样本较少时,提出的方法分类性能会有所下降。故下一步的研究方向是如何设计更加有效的空谱特征,并通过融合纹理、形状等互补特征,进一步提高高光谱数据分类的性能。
| [1] |
童庆禧, 张兵, 郑兰芬.
高光谱遥感-原理、技术与应用[M]. 北京: 高等教育出版社, 2006.
TONG Qingxi, ZHANG Bing, ZHENG Lanfen. Hyperspectral Remote Sensing[M]. Beijing: Higher Education Press, 2006. |
| [2] | PU Hanye, CHEN Zhao, WANG Bin, et al. A Novel Spatial-spectral Similarity Measure for Dimensionality Reduction and Classification of Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7008–7022. DOI:10.1109/TGRS.2014.2306687 |
| [3] |
孙伟伟.
基于流形学习的高光谱影像降维理论与方法研究[J]. 测绘学报, 2014, 43(4): 439.
SUN Weiwei. Theory and Methods of Dimensionality Reduction Using Manifold Learning for Hyperspectral Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 439. DOI:10.13485/j.cnki.11-2089.2014.0066 |
| [4] | GUO B, GUNN S R, DAMPER R I, et al. Band Selection for Hyperspectral Image Classification Using Mutual Information[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 522–526. DOI:10.1109/LGRS.2006.878240 |
| [5] | SU Hongjun, YONG Bin, DU Qian. Hyperspectral Band Selection Using Improved Firefly Algorithm[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(1): 68–72. DOI:10.1109/LGRS.2015.2497085 |
| [6] |
樊利恒, 吕俊伟, 邓江生.
基于分类器集成的高光谱遥感图像分类方法[J]. 光学学报, 2014, 34(9): 0910002.
FAN Liheng, LÜ Junwei, DENG Jiangsheng. Classification of Hyperspectral Remote Sensing Images Based on Bands Grouping and Classification Ensembles[J]. Acta Optica Sinica, 2014, 34(9): 0910002. |
| [7] |
丁胜, 袁修孝, 陈黎.
粒子群优化算法用于高光谱遥感影像分类的自动波段选择[J]. 测绘学报, 2010, 39(3): 257–263.
DING Sheng, YUAN Xiuxiao, CHEN Li. Automatic Band Selection of Hyperspectral Remote Sensing Image Classification Using Particle Swarm Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 257–263. |
| [8] |
张帆, 杜博, 张良培, 等.
一种结合波段分组特征和形态学特征的高光谱图像分类方法[J]. 计算机科学, 2014, 41(12): 275–279.
ZHANG Fan, DU Bo, ZHANG Liangpei, et al. Band Grouping Based Hyperspectral Image Classification Using Mathematical Morphology and Support Vector Machines[J]. Computer Science, 2014, 41(12): 275–279. DOI:10.11896/j.issn.1002-137X.2014.12.059 |
| [9] |
谭熊, 余旭初, 秦进春, 等.
高光谱影像的多核SVM分类[J]. 仪器仪表学报, 2014, 35(2): 405–411.
TAN Xiong, YU Xuchu, QIN Jinchun, et al. Multiple Kernel SVM Classification for Hyperspectral Images[J]. Chinese Journal of Scientific Instrument, 2014, 35(2): 405–411. |
| [10] | GAN Le, XIA Junshi, DU Peijun, et al. Class-oriented Weighted Kernel Sparse Representation With Region-level Kernel for Hyperspectral Imagery Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(4): 1118–1130. DOI:10.1109/JSTARS.2017.2757475 |
| [11] |
杨钊霞, 邹峥嵘, 陶超, 等.
空-谱信息与稀疏表示相结合的高光谱遥感影像分类[J]. 测绘学报, 2015, 44(7): 775–781.
YANG Zhaoxia, ZOU Zhengrong, TAO Chao, et al. Hyperspectral Image Classification Based on the Combination of Spatial-spectral Feature and Sparse Representation[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 775–781. DOI:10.11947/j.AGCS.2015.20140207 |
| [12] | TOKSÖZ M A, ULUSOY İ. Hyperspectral Image Classification via Basic Thresholding Classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 4039–4051. DOI:10.1109/TGRS.2016.2535458 |
| [13] | LI Wei, DU Qian, ZHANG Fan, et al. Collaborative-Representation-based Nearest Neighbor Classifier for Hyperspectral Imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 389–393. DOI:10.1109/LGRS.2014.2343956 |
| [14] | BO Chunjuan, LU Huchuan, WANG Dong. Hyperspectral Image Classification via JCR and SVM Models with Decision Fusion[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(2): 177–181. DOI:10.1109/LGRS.2015.2504449 |
| [15] | SAMAT A, DU Peijun, LIU Sicong, et al. E2LMs:Ensemble Extreme Learning Machines for Hyperspectral Image Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(4): 1060–1069. DOI:10.1109/JSTARS.4609443 |
| [16] | LI Wei, WU Guodong, ZHANG Fan, et al. Hyperspectral Image Classification Using Deep Pixel-pair Features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 844–853. DOI:10.1109/TGRS.2016.2616355 |
| [17] | HUANG Gao, HUANG Guangbin, SONG Shiji, et al. Trends in Extreme Learning Machines:A Review[J]. Neural Networks, 2015, 61: 32–48. DOI:10.1016/j.neunet.2014.10.001 |
| [18] | LI Jiaojiao, DU Qian, LI Wei, et al. Optimizing Extreme Learning Machine for Hyperspectral Image Classification[J]. Journal of Applied Remote Sensing, 2015, 9(1): 097296. DOI:10.1117/1.JRS.9.097296 |
| [19] | ZHOU Yicong, PENG Jiangtao, CHEN C L P. Extreme Learning Machine With Composite Kernels for Hyperspectral Image Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2351–2360. DOI:10.1109/JSTARS.2014.2359965 |
| [20] |
张春霞, 张讲社.
选择性集成学习算法综述[J]. 计算机学报, 2011, 34(8): 1399–1410.
ZHANG Chunxia, ZHANG Jiangshe. A Survey of Selective Ensemble Learning Algorithms[J]. Chinese Journal of Computers, 2011, 34(8): 1399–1410. |
| [21] | BREIMAN L. Bagging Predictors[J]. Machine Learning, 1996, 24(2): 123–140. |
| [22] | BREIMAN L. Random Forests[J]. Machine Learning, 2001, 45(1): 5–32. |
| [23] |
张春森, 郑艺惟, 黄小兵, 等.
高光谱影像光谱-空间多特征加权概率融合分类[J]. 测绘学报, 2015, 44(8): 909–918.
ZHANG Chunsen, ZHENG Yiwei, HUANG Xiaobing, et al. Hyperspectral Image Classification Based on the Weighted Probabilistic Fusion of Multiple Spectral-spatial Features[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 909–918. DOI:10.11947/j.AGCS.2015.20140544 |
| [24] | MAIRAL J, BACH F, PONCE J, et al. Online Learning for Matrix Factorization and Sparse Coding[J]. Journal of Machine Learning Research, 2010, 11: 19–60. |
| [25] | MAIRAL J, BACH F, PONCE J. Sparse Modeling for Image and Vision Processing[J]. Foundations and Trends in Computer Graphics and Vision, 2014, 8(2-3): 85–283. DOI:10.1561/0600000058 |
| [26] | ZHANG Erlei, JIAO Licheng, ZHANG Xiangrong, et al. Class-level Joint Sparse Representation for Multifeature-based Hyperspectral Image Classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(9): 4160–4177. DOI:10.1109/JSTARS.2016.2522182 |
| [27] | FANG Leyuan, WANG Cheng, LI Shutao, et al. Hyperspectral Image Classification via Multiple-feature-based Adaptive Sparse Representation[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(7): 1646–1657. DOI:10.1109/TIM.2017.2664480 |


