2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 国家测绘地理信息局第一地形测量队, 陕西 西安 710054
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. The First Topographic Surveying Brigade of National Administration of Surveying, Mapping and Geoinformation of China, Xi'an 710054, China
地基GNSS水汽层析技术是获取中小尺度三维水汽时空分布的重要方法之一,对于水汽的变化,特别是垂向水汽的流动具有重要的指示作用[1-2]。文献[3]首次提出了利用区域观测网中20个GPS观测站数据重构对流层水汽结构的概念。文献[4]实现了基于GPS层析技术的区域三维水汽信息获取。
在国内,文献[5]率先对三维水汽层析问题进行了详细、系统的介绍,并联合数值模式的预报湿度场作为背景场对上海区域的三维水汽进行反演。文献[6]提出了将高斯约束作为Kalman滤波解算初始状态变量,用于反演湿折射率廓线的方法。文献[1]对水汽层析中各种约束条件进行分析,发现水平约束方程的权阵和测站高差在不同情况下对层析结果影响不同。文献[7]发展了基于Kalman滤波的水汽层析算法,该方法能够高效、稳定地层析出大气水汽的垂直结构,使得层析结果更加忠实于实际的水汽分布。文献[8]通过结合数值积分参数化方法,发展了一种顾及地球曲率的三维水汽层析方法。文献[2]对代数重构算法在水汽层析中的应用问题进行了详细讨论,并给出了最优松弛因子的黄金分割搜索法和确定终止条件的NCP规则。文献[9]提出了基于代数重构算法的GNSS水汽层析方法,该方法能够节省计算机内存且稳定度高。文献[10]针对常规层析方程系数计算求交运算量大的缺点,提出了一种提高运算速度和反演精度的投影面算法。
上述研究是利用完整穿过研究区域倾斜路径上的水汽含量(slant water vapor, SWV)构建层析模型的观测方程,然而对于在层析区域侧面穿出的射线,由于在组成观测方程时并不能完全包含射线上的水汽信息,通常将该部分射线剔除。上述做法浪费了宝贵的GNSS观测资源,也降低了观测数据的利用率[11-12]。文献[11]通过引入水汽密度比例因子的方法提高观测数据的利用率,但该方法在计算水汽密度比例因子时需要探空数据提供的水汽密度参数作为支持。当研究区域存在探空数据时,该方法有效可行;但若研究区域无探空数据时,则该方法会受到限制,因此,难以广泛应用。
针对传统水汽层析方法在区域侧面穿出射线无法利用的问题以及已有的侧面射线利用方法中存在的缺陷,本文提出了利用ECMWF产品改善观测数据利用率的方法,通过引入比例因子,使得在研究区域侧面穿出的所有射线都能参与层析观测方程的建立,大大提高了射线利用率和网格覆盖率。此外,利用的ECMWF格网数据是全球分布的,能够适用于全球任何区域。
1 利用ECMWF改善射线利用率的三维水汽层析算法 1.1 层析原理GNSS卫星信号穿过低空大气层时,受到的斜路径湿延迟(slant wet delay, SWD)可以表达成如下形式
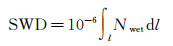 (1)
(1)
利用式(2)即可得到斜路径上的SWV
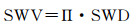 (2)
(2)
式中,Π表示转换因子,Π=106/((k2′+k3/Tm)·Rv·ρw)为无纲量转换因子。其中,Rv=461.495 J·kg-1·K-1,表示水汽气体常数,k3=373 900±0.001 2 K2·mb-1和k2′=22.1±2.2 K·mb-1为大气折射常数[13-15]。最终,得到SWV与水汽之间的积分关系
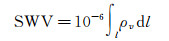 (3)
(3)
式中,ρv表示水汽密度,单位为g/m3。根据地基GNSS对流层层析原理,将层析区域离散化成若干个独立的三维单元网格,则卫星信号路径上的水汽含量可离散化成如下[4]
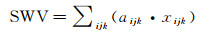 (4)
(4)
式中,aijk表示射线在(i, j, k)网格内的截距;xijk表示(i, j, k)网格内的待估水汽密度值。
由于缺乏足够的观测数据以及层析区域位置的特定性,组成层析观测方程的卫星信号并非空间最优分布,导致观测方程的设计矩阵病态,致使三维水汽反演结果精度较差[4]。为了解决该问题,通常需要加入一些约束信息[2, 4, 16]。在水平方向上,本文根据水汽在空间上连续变化的特点引入水平约束[16];在垂直方向上根据水汽随高度的变化,利用负指数函数建立相邻网格内水汽的函数关系[17-18]。因此,传统层析方法的模型可表示为
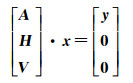 (5)
(5)
式中,A、H和V分别表示观测方程、水平约束方程和垂直约束方程的系数矩阵。
1.2 利用ECMWF改善三维水汽层析射线利用率的方法针对传统水汽层析方法无法利用在研究区域侧面穿出射线的缺陷,提出了利用ECMWF ERA-interim格网产品改善射线利用率的三维水汽反演算法。该方法首先利用ECMWF ERA-interim提供的分辨率为0.125°×0.125°的格网气象资料,计算层析区域每个网格内的水汽密度初值,然后通过引入比例因子(表示一条射线在层析区域内部分的水汽含量与该射线路径上总水汽含量的比值),得到在侧面穿出射线和侧面交点的高与比例因子之间的关系,进而通过该比例因子关系得到在层析区域侧面穿出射线在层析区域内部分的水汽含量,进一步参与观测方程的建立。该方法的优点是能够利用所有在层析区域侧面穿出的射线参与层析模型中观测方程的建立,大大改善了射线利用率和网格覆盖度。
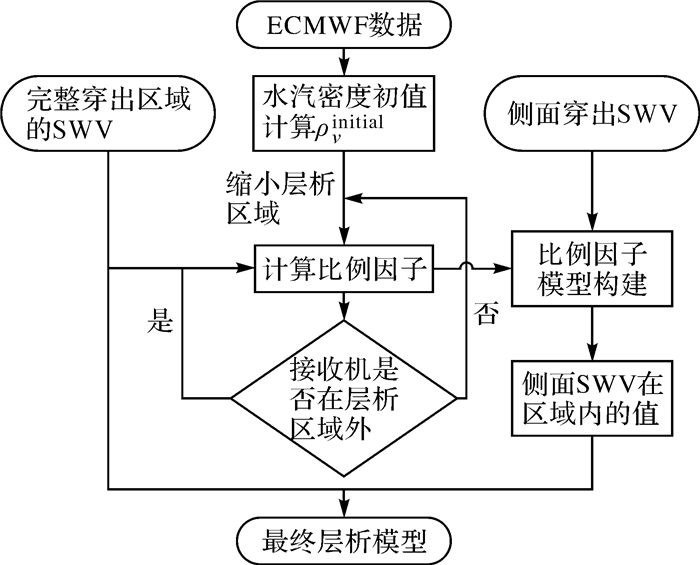
下面给出该方法的具体实现过程,具体流程见图 1。
|
| 图 1 利用ECMWF改善三维水汽反演射线利用率流程 Fig. 1 Flow chart of improving the utilization rate of satellite ray for three-dimensional water vapor tomography using ECMWF |
(1) 利用ECMWF ERA-interim格网数据计算并插值出层析区域每个网格内的水汽密度初值。由水汽状态方程可得出[19]
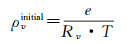 (6)
(6)
式中,e表示水汽分压,单位为hPa;T表示温度,单位为K。
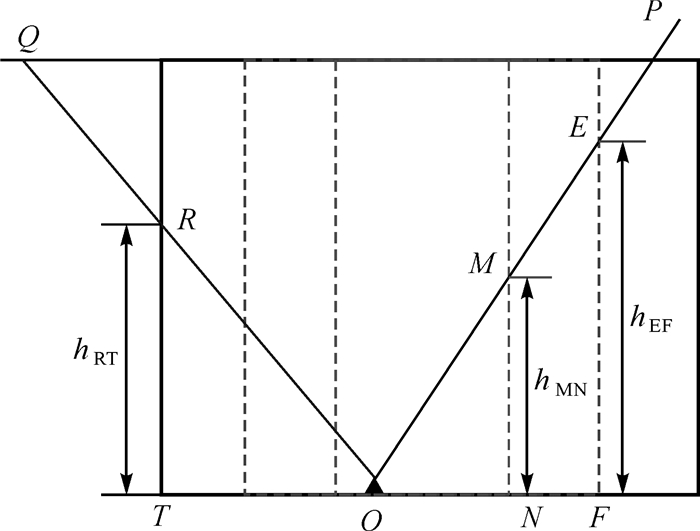
(2) 在水平方向上缩小层析区域,使原来在层析区域顶部穿出的射线在侧面穿出。如图 2所示。
|
| 图 2 改善三维水汽层析射线利用率原理 Fig. 2 Schematic diagram of improving the utilization rate of satellite ray for three-dimensional water vapor tomography |
(3) 计算比例因子。如图 2所示,射线OP的水汽含量值SWVOE可表示为如下形式
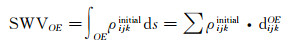 (7)
(7)
式中,dijkOE表示射线OP在网格(i, j, k)内的截距。因此,射线OP对应高度为hEF的一个比例因子λEFOP可通过如下方法计算得到
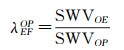 (8)
(8)
式中,SWVOP表示射线OP路径上的总水汽含量值。同理,计算射线OP对应高度为hMN的比例因子λMNOP
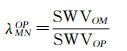 (9)
(9)
依次缩小层析区域,直到接收机位于缩小的层析区域之外为止。通过该方法,可以得到射线OP上多个高度对应的比例因子。
(4) 对某一测站重复步骤(1)—(3),直至该测站上所有在层析区域顶部穿出的射线对应不同高度上的比例因子全部求出。
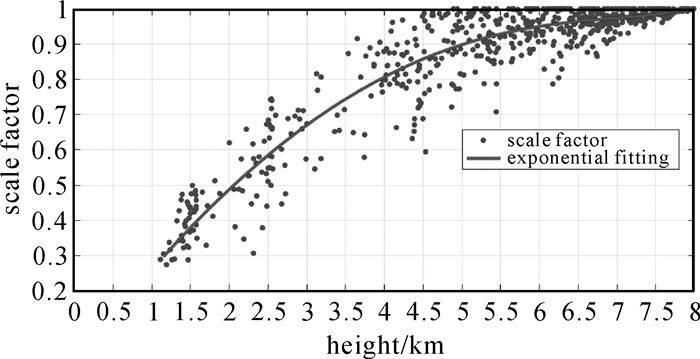
(5) 对层析区域内的所有测站重复步骤(1)—(4)。通过分析比例因子和射线与侧面交点的高之间的关系(如图 3所示),建立如下比例因子模型
|
| 图 3 比例因子与高程之间的关系 Fig. 3 Relationship between the scale factor and height |
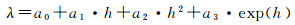 (10)
(10)
式中,a0-a3表示比例因子模型的系数,可以通过最小二乘方法求得;h为射线与侧面交点的高程。需要说明,上述模型表达式是根据试验时段内每天UTC 00:00, 06:00, 12:00和18:00的数据通过拟合得到,后面将会详细介绍。
(6) 计算在层析区域侧面穿出射线在区域内的水汽含量。根据侧面穿出射线与侧面交点的高程,利用步骤(5)中建立的比例因子模型可求得对应高度上的比例因子。如图 2所示,与侧面交点的高为hRT,因此可以求得该射线对应高程的比例因子λRTOQ
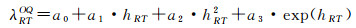 (11)
(11)
进一步可以求出射线OQ在层析区域内上的水汽含量SWVOR
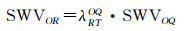 (12)
(12)
式中,SWVOQ表示射线OQ上总的水汽含量值。
(7) 利用侧面穿出射线构建观测方程,最终得到本文提出方法的层析模型
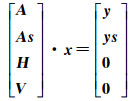 (13)
(13)
式中,As表示侧面穿出射线在研究区域网格内的截距组成的系数矩阵;ys表示侧面穿出射线在层析区域内的水汽含量组成的列向量。
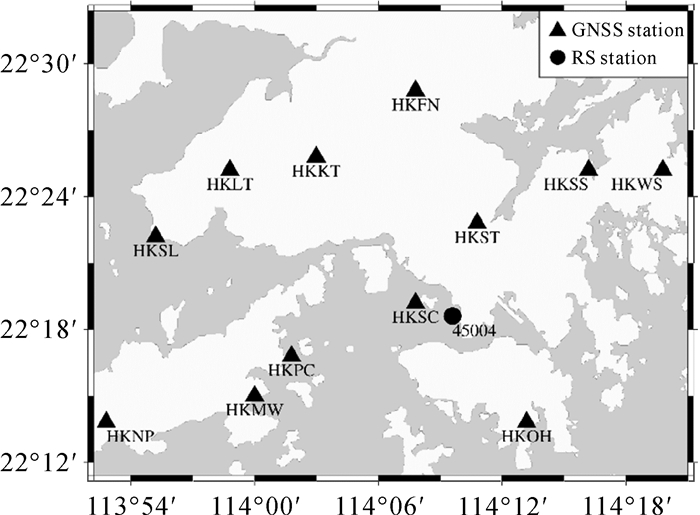
2 层析策略 2.1 试验介绍选取香港卫星定位参考站网(satellite positioning reference station network, SatRef)中12个测站的数据为例进行分析,时间为2013年5月4日至5月21日共18 d的数据,各测站的地理位置如图 4所示。选取该时段数据进行试验是因为该时段内香港对应着晴天、多云、阵雨、中雨和大雨等天气情况,能够很好地反映不同天气下水汽的变化,具有一定的代表性。表 1给出了试验时段内对应的天气状况。
|
| 图 4 香港SatRef中GPS测站和无线电探空站地理位置分布 Fig. 4 Geographic distribution of GPS stations and Radiosonde station in Hong Kong SatRef |
| 日期 | 5.04 | 5.05 | 5.06 | 5.07 | 5.08 | 5.09 | 5.10 | 5.11 | 5.12 | 5.13 | 5.14 | 5.15 | 5.16 | 5.17 | 5.18 | 5.19 | 5.20 | 5.21 |
| 天气状况 | 阵雨 | 多云 | 阵雨 | 阵雨 | 阵雨 | 阵雨 | 中雨 | 中雨 | 多云 | 晴 | 阵雨 | 大雨 | 大雨 | 中雨 | 晴 | 多云 | 大雨 | 暴雨 |
层析区域范围:纬度22.19°N—22.54°N,经度113.87°E—114.35°E,高度0~10 km;在纬向和经向上的水平分辨率分别为0.05°和0.06°,垂直分辨率采用非等间距划分方法[20],从地面到层析顶部分别为0.5 km、0.5 km、0.7 km、0.7 km、0.7 km、0.9 km、0.9 km、0.9 km、1.1 km、1.1 km。因此,层析区域共有7×8×10个网格。此外,在研究区域内还有一无线电探空站45004,如图 4中●所示。探空站每天在UTC00:00和12:00发射探空气球,能够观测得到不同高度上的气象数据,可作为本文水汽反演结果的检验。利用GAMIT软件对采样率为30 s的观测数据进行处理,然后结合气象数据得到各测站不同高度上的SWV[4, 11]。
为了验证本文方法,设计两种方案进行层析试验。方法1:利用传统方法组成的层析模型反演水汽,如式(5)所示;方法2:利用本文方法组成的层析模型反演水汽,如式(13)所示。
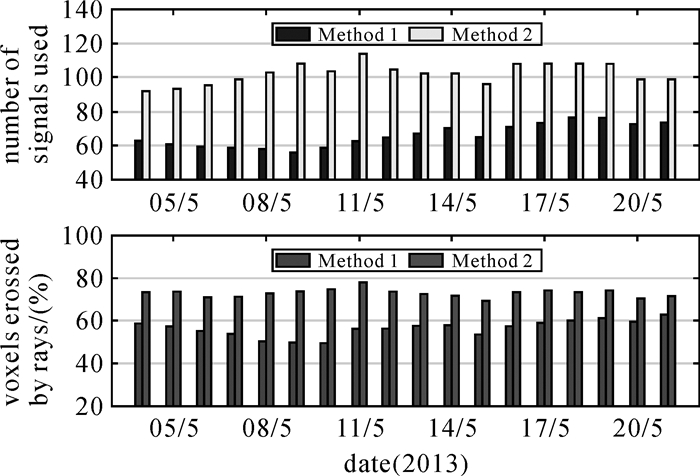
2.2 射线利用率及网格覆盖率对比本文首先对层析时段2013-05-04—2013-05-21共18 d的每天射线利用情况以及网格覆盖率进行对比,如图 5所示。由图可以明显看出,利用本文方法(方法2)后,层析时段内每天的射线利用率有了很大的提高,此外,网格覆盖率也均有不同程度的提高。表 2给出了18 d的平均射线利用率和有射线穿过的网格数的统计情况。通过计算可得,射线利用率平均提高了约54.55%,有射线穿过的网格数平均提高了16.43%,由原来的56.25%提高到72.68%。
|
| 图 5 试验时段内不同方法每天射线利用率及网格覆盖率对比 Fig. 5 Comparison of utilization rate of satellite ray and coverage rate of voxels of each day derived from two method for the experimental period |
| 方法 | 射线利用情况 | 射线穿过网格数 | |||||
| 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | ||
| 方法1 | 66 | 77 | 56 | 315 | 350 | 277 | |
| 方法2 | 102 | 114 | 92 | 407 | 436 | 387 | |
2.3 比例因子模型可靠性分析
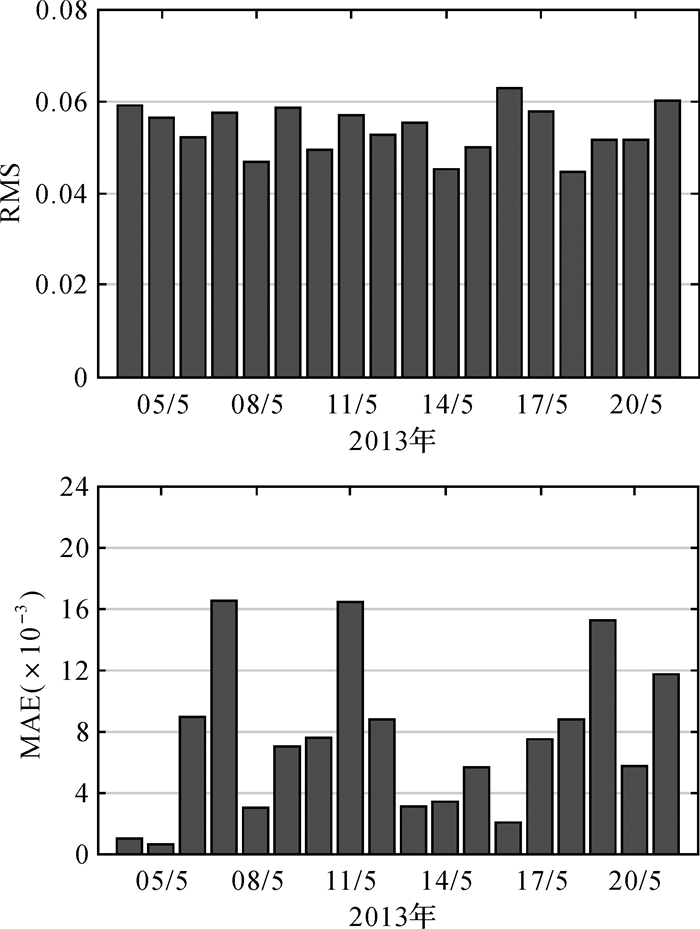
由式(12)可以看出,层析区域侧面穿出的射线在区域内部分的水汽含量的精度依赖于比例因子模型的精度。因此,首先对试验时段内本文方法建立的比例因子模型的精度进行检验和可靠性分析。利用实测数据计算得到的比例因子与利用模型计算的比例因子进行对比,图 6分别给出了18 d比例因子模型的RMS和MAE。通过计算可得,层析时段内比例因子模型的平均MAE为-0.007,这说明建立的模型系统误差很小;该模型的平均RMS为0.054,通过统计,在研究区域侧面穿出射线的SWV的均值约为110 mm,因此,由比例因子模型引起的误差仅有6 mm左右,进一步验证了建立的比例因子模型具有很高的精度。
|
| 图 6 试验时段内比例因子模型每天的RMS和MAE分布情况 Fig. 6 The RMS and MAE of scale factor model for the experimental period |
3 试验分析 3.1 内符合精度检验
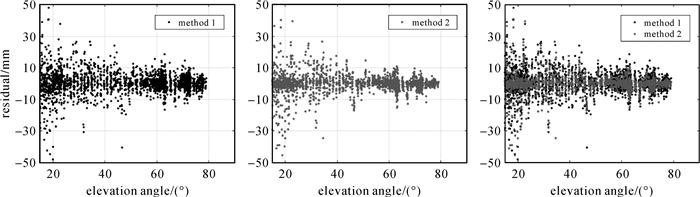
层析结果的质量是检验建立层析模型精度的关键。因此,本文首先对上述两种层析方法进行内符合精度验证。图 7给出了两种层析方法计算得到的SWV残差随高度角变化的对比情况。由图可以看出,两种方法的SWV残差随高度角总体呈现递减的趋势,且方法2的SWV残差波动比方法1的要小,这说明本文方法(方法2)其内符合精度优于传统方法。通过计算,发现两种方法的标准差(STD)和MAE分别为11.4/5.8 mm和10.6/4.4 mm,相对于传统方法,本文方法的内符合精度提高了约7.5%。
|
| 图 7 层析时段内两种层析方法计算得到的SWV残差随高度角变化对比图 Fig. 7 The SWV residuals change with elevation derived from two tomographic method for the experimental period |
3.2 外符合精度检验
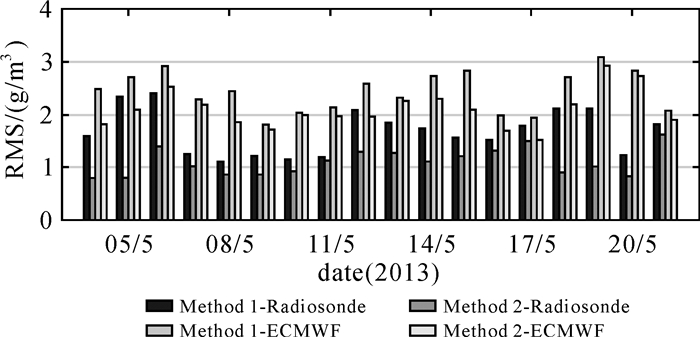
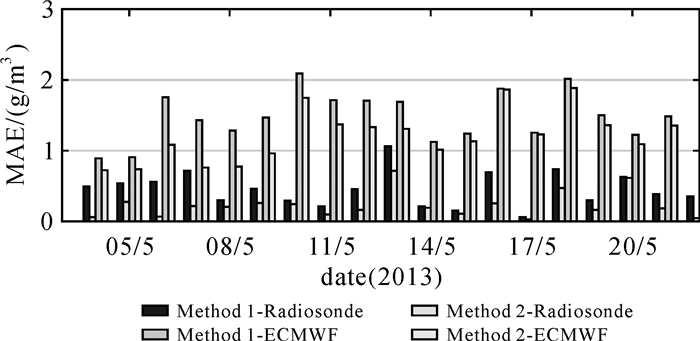
前已述及,探空数据能够提供精确的水汽密度廓线信息。此外,ECMWF ERA-interim也能够提供高精度的分层气象参数,因此,本文将这两种不同来源数据计算的结果作为标准对水汽反演结果进行检验。首先利用不同水汽反演方法得到探空站所在位置上UTC00:00和12:00的水汽密度信息,然后分别与探空数据与ECMWF计算结果进行对比。图 8和9分别给出了试验时段内每天不同方法层析结果与探空数据和ECMWF对比的平均RMS和MAE。由两图可以看出,无论是与探空数据还是ECMWF对比,本文方法(方法2)得到的水汽质量均优于传统方法(方法1)。表 3给出了试验时段内不同方法层析结果与探空数据和ECMWF数据对比信息。由表可得,与探空数据对比,方法2的RMS和MAE分别为1.2 g/m3和0.3 g/m3,优于方法1的1.7 g/m3和0.5 g/m3,其RMS的精度提高了29.4%;与ECMWF数据对比,方法2的RMS和MAE分别为2.1 g/m3和1.4 g/m3,优于方法1的2.4 g/m3和1.6 g/m3,其RMS的精度提高了12.5%。
|
| 图 8 试验时段内不同方法层析结果与探空数据对比每天的平均RMS Fig. 8 Comparison of average RMS of each day of water vapor density between Radiosonde, ECMWF and different tomographic result for the experimental period |
|
| 图 9 试验时段内每天不同方法层析结果与探空数据对比的平均MAE Fig. 9 Comparison of average MAE of each day of water vapor density between Radiosonde, ECMWF and different tomographic result for the experimental period |
| data comparison | RMS | MAE | maximum | minimum |
| Method 1 VS Radiosonde | 1.7 | 0.5 | 2.4 | 1.1 |
| Method 2 VS Radiosonde | 1.2 | 0.3 | 1.8 | 0.7 |
| Method 1 VS ECMWF | 2.4 | 1.6 | 3.1 | 1.8 |
| Method 2 VS ECMWF | 2.1 | 1.4 | 2.9 | 1.5 |
| Radiosonde VS ECMWF | 2.1 | 1.7 | 2.9 | 1.6 |
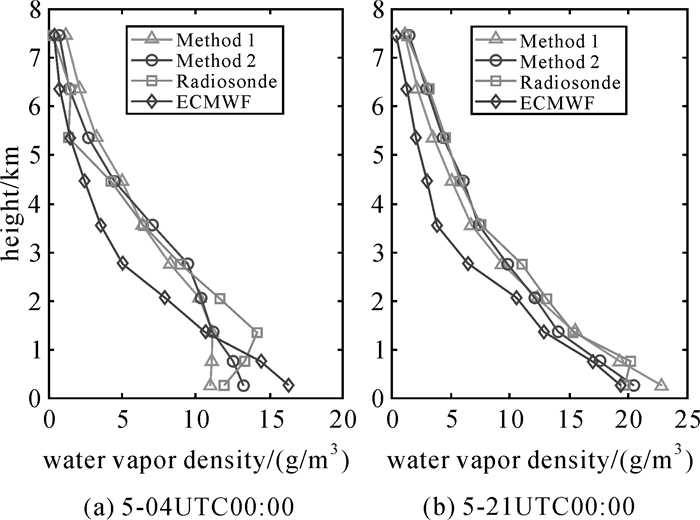
此外,对两个特殊历元(5-04UTC 00:00和5-21UTC 00:00)上的水汽廓线进行对比,选取该两个历元是因为它们对应着试验时段内最小和最大的RMS值。图 10给出了两个历元上不同方法反演得到的水汽廓线与探空数据和ECMWF数据对比图。由图可以看出,两种层析模型反演得到的水汽廓线与探空数据均有很好的一致性,ECMWF数据计算得到的水汽廓线精度稍差。通过计算,与探空数据、ECMWF数据对比,两个历元上方法1和方法2反演水汽密度的RMS分别为1.6/0.5 g/m3和1.9/1.5 g/m3。
|
| 图 10 两个历元不同方法反演得到的水汽廓线与探空数据和ECMWF数据对比 Fig. 10 Comparison of water vapor profile between Radiosonde, ECMWF and different tomographic result for two specific epochs |
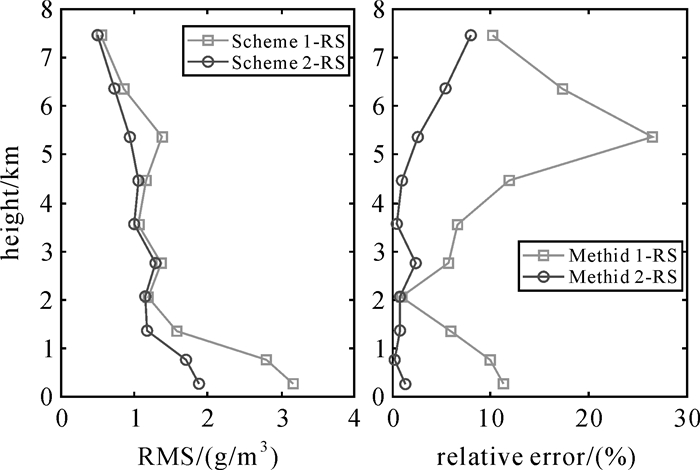
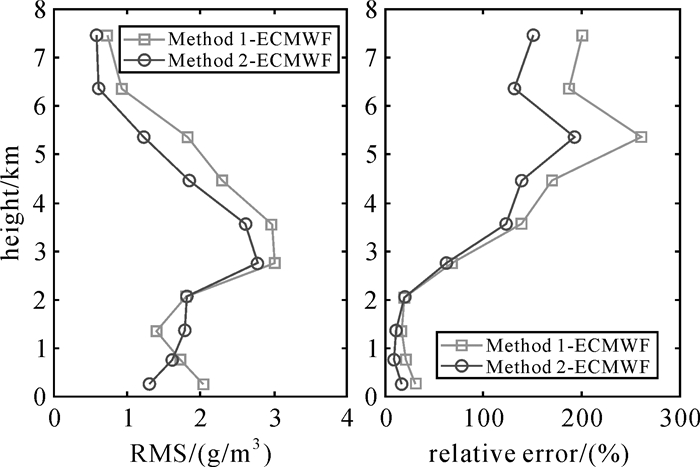
为了进一步对比不同方法反演的水汽密度与高程的关系,对层析时段内不同高程上的水汽进行对比。图 11和图 12分别给出了两种层析方法水汽结果在不同高度上与探空数据和ECMWF数据对比的RMS及相对误差(relative error)。由两图可以看出,无论与探空数据还是ECMWF数据对比,在绝大多数高度上,方法2反演得到的水汽密度廓线的RMS和相对误差均优于方法1,这进一步证明了本文方法的优越性。综上对比可得,本文提出的三维水汽反演方法在香港区域不同天气情况下均适用,因此,可以推断该方法具有较好的实用性。
|
| 图 11 两种层析方法水汽结果在不同高度上与探空数据对比的RMS和相对误差 Fig. 11 RMS and Relative error changes with height derived from two tomographic result when compared with Radiosonde |
|
| 图 12 两种层析方法水汽结果在不同高度上与ECMWF数据对比的RMS和相对误差 Fig. 12 RMS and Relative error changes with height derived from two tomographic result when compared with ECMWF |
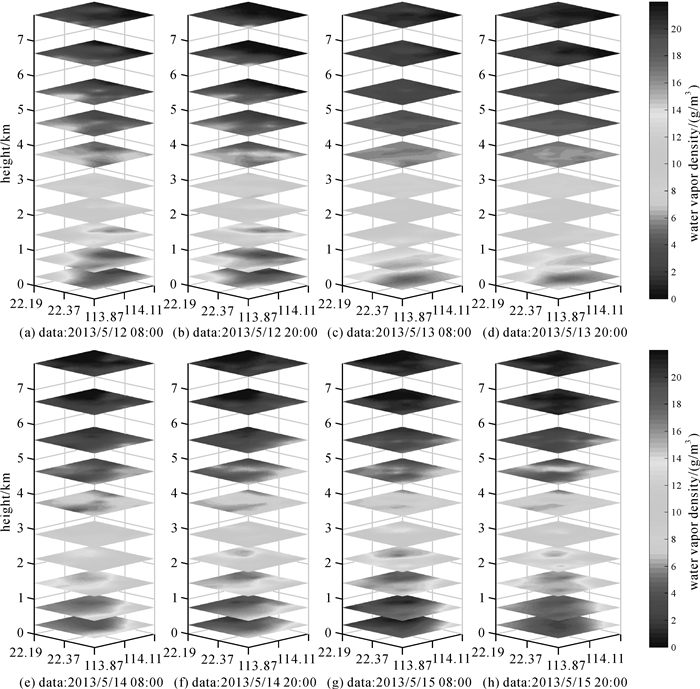
最后,图 13给出了2013年5月12日至14日对应多云、晴、阵雨和大雨天气的三维水汽层析结果。由上图可以看出,在12日多云天气下,水汽密度在不同层上分布,尤其是底层均多于13日的晴天天气。而在13日和14日的阵雨和大雨天气下,该地区在各层上的水汽密度值明显高于多云和晴天天气下的水汽分布,并且在14日大雨天气下各层上的水汽密度值均大于13日的水汽反演结果,在给出的4 d中最大。综合上述4 d不同天气下不同层上的水汽密度分析可以看出,三维水汽密度值大小可依次排序为大雨>阵雨>阴天>晴天,这也与不同天气下实际的水汽分布相符合。
|
| 图 13 2013年5月12日至14日水汽层析结果的三维分布图 Fig. 13 Three-distribution of water vapor tomographic result during the May 12 to 14, 2013 |
此外,本试验选取的实验时段(共18 d)对应着晴天、多云、阵雨、中雨和大雨等多种天气情况,在上述不同气象条件下,水汽的垂直结构分布有时并不符合负指数分布规律,但通过与探空数据对比以及对水汽的三维分布进行分析,发现本文方法仍然适用,均能取得可靠的反演结果。这是因为本文算法只是利用负指数分布函数对垂直方向上的网格进行约束,并不能决定最终的水汽反演结果。
4 结论本文提出了基于ECMWF产品改善三维水汽反演射线利用率的方法,通过引入比例因子,计算得到在层析区域侧面穿出射线在层析区域内部分的水汽含量,然后将其作为观测方程输入值参与水汽层析模型的建立。
利用香港SatRef中2013-05-04—2013-05-21共18 d的实测GPS和气象数据对提出的方法进行验证,通过对建立的比例因子模型进行分析,发现该模型计算SWV时的误差仅为6 mm左右。本文方法能够大大改善观测数据的利用率以及射线穿过网格的覆盖率,分别将探空数据和ECMWF数据计算结果作为标准对水汽反演结果精度及有效性进行验证。试验结果表明:本文方法能有效提高水汽反演结果的精度(分别提高了29.4%和12.5%)。此外,通过对不同高度上反演的水汽廓线进行对比,发现本文方法反演的水汽廓线的RMS和相对误差在绝大多数层上均优于传统方法。
致谢: 感谢IGRA和ECMWF提供的气象数据,感谢香港SatRef提供的试验数据。
| [1] |
于胜杰, 柳林涛, 梁星辉.
约束条件对GPS水汽层析解算的影响分析[J]. 测绘学报, 2010, 39(5): 491–496.
YU Shengjie, LIU Lintao, LIANG Xinghui. Influence Analysis of Constraint Conditions on GPS Water Vapor Tomography[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 491–496. |
| [2] |
何林, 柳林涛, 苏晓庆, 等.
水汽层析代数重构算法[J]. 测绘学报, 2015, 44(1): 32–38.
HE Lin, LIU Lintao, SU Xiaoqing, et al. Algebraic Reconstruction Algorithm of Vapor Tomography[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 32–38. DOI:10.11947/j.AGCS.2015.20130308 |
| [3] | BRAUN J, ROCKEN C, MEERTENS C, et al. Development of A Water Vapor Tomography System Using Low Cost L1 GPS Receivers[C]//Proceedings of the 9th ARM Science Team Meeting. San Antonio, Texas: [s. n. ], 1999: 22-26. |
| [4] | FLORES A, RUFFINI G, RIUS A. 4D Tropospheric Tomography Using GPS Slant Wet Delays[M]//Annales Geophysicae. [S. l. ]: Springer-Verlag, 2000, 18(2): 223-234. |
| [5] |
宋淑丽. 地基GPS网对水汽三维分布的监测及其在气象学中的应用[D]. 上海: 中国科学院上海天文台, 2004. SONG Shuli. Sensing Three Dimensional Water Vapor Structure with Ground-Based GPS Network and the Application in Meteorology[D]. Shanghai: Shanghai Astrono-mical Observatory, Chinese Academy of Sciences, 2004. |
| [6] | CAO Yunchang, CHEN Yongqi, LI Pinghua. Wet Refractivity Tomography with an Improved Kalman-filter Method[J]. Advances in Atmospheric Sciences, 2006, 23(5): 693–699. DOI:10.1007/s00376-006-0693-y |
| [7] |
毕研盟, 杨光林, 聂晶.
基于Kalman滤波的GPS水汽层析方法及其应用[J]. 高原气象, 2011, 30(1): 109–114.
BI Yanmeng, YANG Guanglin, NIE Jing. Method of GPS Water Vapor Tomography Based on Kalman Filter and Its Application[J]. Plateau Meteorology, 2011, 30(1): 109–114. |
| [8] |
叶世榕, 江鹏, 刘炎炎.
地基GPS网层析水汽三维分布数值积分方法[J]. 测绘学报, 2013, 42(5): 654–660.
YE Shirong, JIANG Peng, LIU Yanyan. A Water Vapor Tomographic Numerical Quadrature Approach with Ground-based GPS Network[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 654–660. |
| [9] |
于胜杰, 万蓉, 付志康.
代数重构算法在GNSS水汽层析解算中的应用[J]. 武汉大学学报(信息科学版), 2016, 41(8): 1113–1117, 1124.
YU Shengjie, WAN Rong, FU Zhikang. Application of Algebraic Reconstruction Technique on the GNSS Water Vapor Tomography[J]. Geomatics and Information Science of Wuhan University, 2016, 41(8): 1113–1117, 1124. |
| [10] |
丁楠, 张书毕.
地基GPS水汽层析的投影面算法[J]. 测绘学报, 2016, 45(8): 895–903.
DING Nan, ZHANG Shubi. Land-based GPS Water Vapor Tomography with Projection Plane Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 895–903. DOI:10.11947/j.AGCS.2016.20160010 |
| [11] |
姚宜斌, 赵庆志, 何亚东, 等.
基于水汽密度比例因子的三维水汽层析算法[J]. 测绘学报, 2016, 45(3): 260–266.
YAO Yibin, ZHAO Qingzhi, HE Yadong, et al. A Three-dimensional Water Vapor Tomography Algorithm Based on the Water Vapor Density Scale Factor[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 260–266. DOI:10.11947/j.AGCS.2015.20150205 |
| [12] | YAO Y B, ZHAO Q Z, ZHANG B. A Method to Improve the Utilization of GNSS Observation for Water Vapor Tomography[J]. Annales Geophysicae, 2016, 34(1): 143–152. DOI:10.5194/angeo-34-143-2016 |
| [13] | ASKNE J, NORDIUS H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data[J]. Radio Science, 1987, 22(3): 379–386. DOI:10.1029/RS022i003p00379 |
| [14] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS Meteorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15787–15801. DOI:10.1029/92JD01517 |
| [15] | BEVIS M, BUSINGER S, CHISWELL S, et al. GPS Meteorology:Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Applied Meteorology, 1994, 33(3): 379–386. DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2 |
| [16] | ROHM W. The Ground GNSS Tomography-unconstrained Approach[J]. Advances in Space Research, 2013, 51(3): 501–513. DOI:10.1016/j.asr.2012.09.021 |
| [17] | ELÓSEGUI P, RUIS A, DAVIS J L, et al. An Experiment for Estimation of the Spatial and Temporal Variations of Water Vapor Using GPS Data[J]. Physics and Chemistry of the Earth, 1998, 23(1): 125–130. DOI:10.1016/S0079-1946(97)00254-1 |
| [18] |
段虎荣, 郭新成, 丁宁.
最小二乘预估法在GPS高程转换中的应用[J]. 西安科技大学学报, 2006, 26(1): 62–64, 69.
DUAN Hurong, GUO Xincheng, DING Ning. The Least Squares Estimation Used in Model of GPS Altitude Transformation[J]. Journal of Xi'an University of Science and Technology, 2006, 26(1): 62–64, 69. DOI:10.3969/j.issn.1672-9315.2006.01.016 |
| [19] |
盛裴轩, 毛节泰, 李建国, 等. 大气物理学[M]. 2版. 北京: 北京大学出版社, 2013. SHENG Peixuan, MAO Jietai, LI Jianguo, et al. Atmospheric Physics[M]. 2nd ed. Beijing: Peking University Press, 2013. |
| [20] | YAO Yibin, ZHAO Qingzhi. A Novel, Optimized Approach of Voxel Division for Water Vapor Tomography[J]. Meteorology and Atmospheric Physics, 2017, 129(1): 57–70. DOI:10.1007/s00703-016-0450-4 |


