2. 中南大学地球信息科学与物理学院, 湖南 长沙 410083
2. School of Geosciences and Info-physic, Central South University, Changsha 410083, China
在测绘数据获取过程中,不可避免的误差来源使观测数据与真值间存在差异,人们认为数据具有不确定性,其实质是指数据的误差[1]。不确定性是不精确性、模糊性、不明确性等概念的一个总称,它与误差的意义相近。但前者指一种广义的误差,它包含可度量的数值误差和难以度量的概念误差。很多时候测量数据的不确定性不再是一个具体数值,它们可能各自在一定的实数区间内变动,或者仅是一个模糊数,此时沿用随机误差的分布限定会使测量平差数据处理效果受到影响[2]。为抑制观测不确定性因素的影响,很多学者做了相关的研究。如运用整体平差算法[3-5]来进行数据处理,它总体上考虑了观测向量L和系数矩阵A的误差,但容易出现对A的过度校正,从而影响状态参数估计的可提出给这种校正加上先验上界。后续研究包括应用不确定度理论研究不确定性评定方法[7-11],寻找抑制不确定性影响的算法[8, 12-13],针对不确定性建立新的平差准则[14]等。
不确定度是不确定性的一种度量指标体系,它与测量界的精度度量方式几乎一致,所有不确定度均可以用方差、均方差、误差区间、误差椭圆、误差椭球表示[15]。在测绘数据处理领域,应用先验信息和不确定度理论进行抑制观测不确定性影响的相关研究已成为热点。文献[2]、[6]和[14]直接将不确定度作为一个参数融入函数模型中,建立不确定性平差模型,依据不确定性min-max平差准则,利用奇异值分解,而后迭代求解该问题。文献[16]针对不确定性min-max平差准则等价转换后的形式,提出了一种可行的加权方法,增加了参数估计的可靠性。文献[17]将文献[6]提出的不确定性度量方法融入不确定性平差模型中,并给出了新的参数求解算法。
本文在文献[17]方法的基础上,将随机误差和有界不确定性误差平方和最小的新平差准则运用到不确定性混合平差模型求解中,提出了一种新的迭代求解算法,并证明了该算法的收敛性,简化了文献[2, 14]中的算法,同时其应用范围更广。
1 系数矩阵中部分有界不确定性的混合平差模型建立如下不确定性混合平差模型
 (1)
(1)
式中,L为n×1维观测变量;A1是n×p维系数矩阵;A2是n×q维系数矩阵;ΔL和ΔA2分别是L和A2的有界不确定性误差,p+q=m,
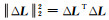
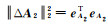

关于平差模型的误差设立,文献[18]研究的污染误差模型仅考虑模型误差和随机误差,未对模型误差作约束。文献[19]研究的总体平差模型考虑了随机误差和系数矩阵误差,未对系数矩阵误差作约束。文献[2]在文献[14]的基础上引入了观测变量和系数矩阵的有界不确定性误差,但未考虑随机误差。文献[17]在文献[2]的基础上考虑了随机误差,也做了不确定性误差有界约束。在测量实践中,会遇到方程式系数矩阵部分有误差的情况,诸如曲面拟合、GPS伪距单点定位、坐标转换模型等[20]。因此,本文将系数矩阵A分割为A1和A2,提出不确定性平差模型(1)。
模型(1)中的不确定性误差的有界性约束可看成是A2和L的先验信息[2]。文献[2]对所建立的平差模型采用的min-max准则进行参数解算,但该准则无法利用观测信息和先验有界信息估计不确定误差ΔL和ΔA2。另外,未知参数X的估计结果中不含不确定度β,这导致不确定性误差ΔL对平差解算结果没有影响。鉴于此,本文基于模型式(1),在式(1)的不确定性误差有界约束下,提出了随机误差和不确定性误差平方和最小准则
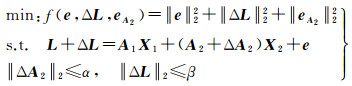 (2)
(2)
关于带约束的最小二乘问题,文献[21]提出了一种线性不等式约束平差模型算法,文献[22—24]针对总体最小二乘模型中附加等式约束给出了Euler-Lagrange逼近解算方法。对上述参数带有约束的最小二乘问题,本文参照前述文献的方法,引入Lagrange乘子,结合Kuhn-Tucker条件求得参数最小二乘估计的一般形式。
根据Euler-Lagrange求极值方法,构造如下目标函数
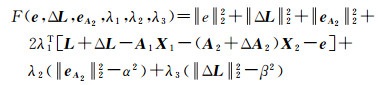 (3)
(3)
式中,λ1为n×1维Lagrange乘子;λ2、λ3为1×1维Lagrange乘子,均非负。运用Kuhn-Tucker条件得到
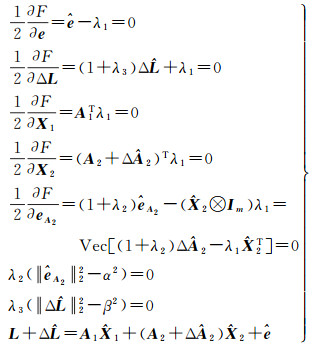 (4)
(4)
其中,⊗表示Kronecker积。由式(4)可得
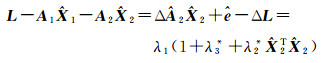 (5)
(5)
其中,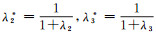
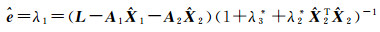 (6)
(6)
对式(5)两边分别同乘-A1T和-A2T,结合式(4)得
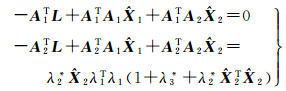 (7)
(7)
将式(6)代入式(7)得
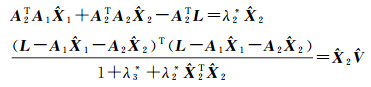 (8)
(8)
其中,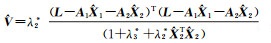
对式(8)进行整理推得
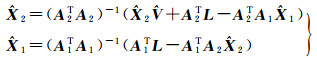 (9)
(9)
将式(6)代入式(4)得
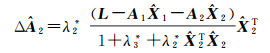 (10)
(10)
将式(6)代入式(4)得
 (11)
(11)
根据式(10)和式(11),不确定性ΔL和ΔA2在给定解
(1) λ2>0,λ3>0。据式(4)可知
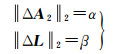 (12)
(12)
将式(10)和式(11)代入式(12)解方程组得到
 (13)
(13)
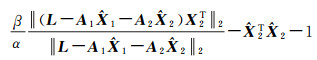 (14)
(14)
将式(13)和式(14)代入式(10)和式(11)即得不确定性ΔL和ΔA2。
(2) λ2=0(λ2<0视为λ2=0),λ3>0。据式(4)有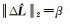
 (15)
(15)
故而不确定性可分别表示为
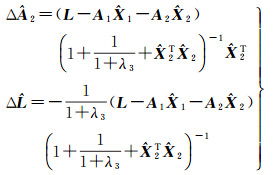 (16)
(16)
(3) λ2>0,λ3=0(λ3<0视为λ3=0)。据式(4)有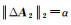
 (17)
(17)
从而不确定性可以表示为
 (18)
(18)
(4) λ2=λ3=0(λ2<0视为λ2=0,λ3<0视为λ3=0)。此时,不确定性分别为
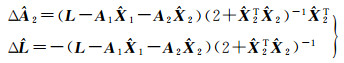 (19)
(19)
利用式(9)求解X1和X2非常复杂,考虑用迭代法求解。下面讨论迭代过程的收敛性问题。
由式(9)得
 (20)
(20)
将式(20)代入式(9)并令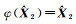
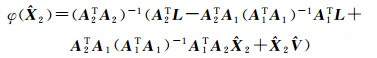 (21)
(21)
其中,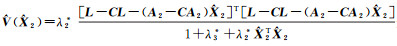
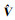
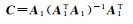
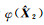
 (22)
(22)
其中,
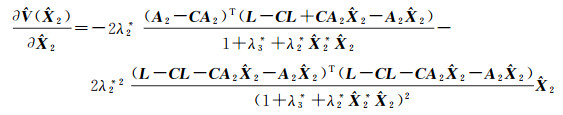 (23)
(23)
利用式(4)和式(5),式(21)可简化为
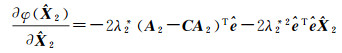 (24)
(24)
同时代入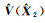
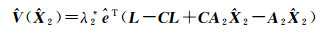 (25)
(25)
将式(24)和式(25)代入式(22),利用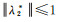
 (26)
(26)
因目标函数式(3)是凸规划问题,其最小二乘解



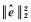
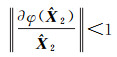 (27)
(27)
该算法收敛。
在上述不确定性混合平差模型中,若令α→+∞,β=0。则根据式(4)可知λ2=0,如此λ2*=1,对应于Lagrange乘子分类讨论的情况(2),则由式(15)可得λ3=+∞,从而λ3*=0。将之代入式(8)得到
 (28)
(28)
此与文献[23]中公式一致,即混合总体最小二乘模型。因此,本文的不确定性混合平差模型可认为是更广的混合平差模型。
2 不确定性混合平差模型解算方法根据上述推导可归纳迭代计算步骤如下:
(1) λ2(0)=0,λ3(0)=0。
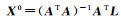
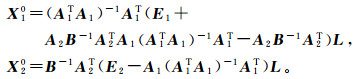
其中,E1、E2分别为对应维度的单位阵。
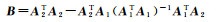
(2) 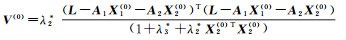
(3) 计算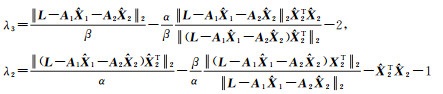
令λ2=max(0, λ2),λ3=max(0, λ3)。
(4) 若λ2>0,λ3>0,则令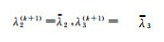
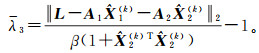
令λ2(k+1)=0,λ3(k+1)=max(0, λ3);若λ2>0,λ3=0,则计算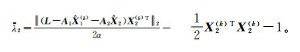
(5) 计算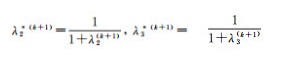
令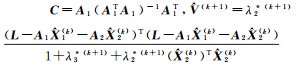
(6) 计算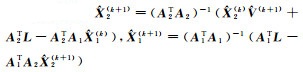
(7) 当
(8) 令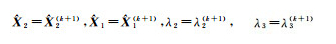
在应用包括GPS在内的空间定位技术进行测量时, 往往还需要进行不同基准间的转换。进行基准转换的模型很多, 较为常用的有布尔沙-沃尔夫(Bursa-Wolf)模型和莫洛金斯基(Molodensky)模型[25]。本文将文献[25]中的Bursa-Wolf模型改写为不确定性混合平差模型。基于空间坐标采样数据,分析比较了该模型min-max准则下的算法(ULS1)和本文提出的算法(ULS2)的解算优劣。数据见表 1。该数据共19个观测点,57条数据。其中前16个观测点用于建立转换模型,并进行参数估计,后3个观测点用于预测和比较。
| m | |||||||
| 编号 | 坐标系A | 坐标系B | |||||
| XA | YA | ZA | XA | YA | ZA | ||
| 1 | 342 978.367 5 | 524 439.014 4 | 532 144.829 5 | 343 259.664 2 | 524 871.780 7 | 532 584.028 0 | |
| 2 | 337 243.729 9 | 515 675.553 2 | 523 252.022 7 | 337 529.991 5 | 516 113.098 5 | 523 696.091 6 | |
| 3 | 331 518.006 8 | 506 920.331 0 | 514 368.328 1 | 331 804.195 3 | 507 358.090 4 | 514 812.426 4 | |
| 4 | 325 792.242 9 | 498 165.458 5 | 505 484.368 6 | 326 078.591 7 | 498 603.547 9 | 505 929.071 4 | |
| 5 | 320 066.574 2 | 489 410.113 4 | 496 600.727 2 | 320 352.807 3 | 489 847.577 3 | 497 044.885 1 | |
| 6 | 314 340.867 7 | 480 654.879 9 | 487 717.072 7 | 314 627.184 8 | 481 092.699 8 | 488 161.259 4 | |
| 7 | 308 615.197 1 | 471 900.297 7 | 478 833.284 7 | 308 901.477 8 | 472 338.202 2 | 479 277.870 7 | |
| 8 | 302 893.730 6 | 463 162.909 7 | 469 946.730 6 | 303 179.197 9 | 463 602.110 3 | 470 391.459 5 | |
| 9 | 297 174.847 5 | 454 438.906 4 | 461 058.280 9 | 297 461.138 2 | 454 841.305 4 | 461 502.843 6 | |
| 10 | 291 529.080 7 | 449 917.035 4 | 452 109.183 7 | 291 798.726 6 | 450 169.321 2 | 452 564.603 6 | |
| 11 | 286 228.038 3 | 439 369.637 4 | 442 979.475 5 | 286 499.677 1 | 440 076.878 4 | 443 430.529 5 | |
| 12 | 280 783.920 3 | 425 828.302 6 | 433 960.731 6 | 281 056.576 1 | 426 473.233 4 | 434 411.537 0 | |
| 13 | 275 355.550 5 | 413 165.794 5 | 424 923.984 7 | 275 625.698 2 | 413 787.093 9 | 425 377.315 8 | |
| 14 | 269 979.527 7 | 401 066.999 8 | 415 845.838 6 | 270 250.047 0 | 401 694.093 6 | 416 298.311 4 | |
| 15 | 264 529.918 3 | 388 252.881 6 | 406 821.319 9 | 264 804.570 2 | 388 897.333 4 | 407 271.082 6 | |
| 16 | 258 982.888 3 | 375 362.878 4 | 397 861.133 5 | 259 261.518 1 | 376 018.055 4 | 398 308.863 0 | |
| 17 | 253 419.284 5 | 362 129.102 6 | 388 912.670 8 | 253 697.957 5 | 362 779.431 1 | 389 359.793 1 | |
| 18 | 247 854.028 5 | 349 421.683 0 | 379 960.068 9 | 248 131.962 0 | 350 046.836 0 | 380 408.162 0 | |
| 19 | 242 299.447 2 | 337 089.413 7 | 370 997.052 1 | 242 577.174 6 | 337 696.959 9 | 371 445.651 3 | |
对文献[25]中的Bursa-Wolf模型进行适当变形得到
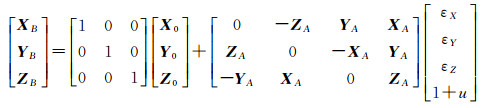 (29)
(29)
式中,[XA YA ZA]T和[XB YB ZB]T分别代表空间中某点在不同系统下的坐标观测值;[X0 Y0 Z0]T是模型的平移参数向量;u是模型的尺度参数;εX、εY、εZ为模型的旋转参数。设有n个空间观测点,令

则有
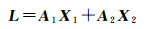 (30)
(30)
式中,X1=[X0 Y0 Z0]T,X2=[εX、εY、εZ1+u]T。系数矩阵A1为常数矩阵,不存在误差;系数矩阵A2含有观测坐标,存在误差,因此该模型可用不确定性混合平差模型式(1)来刻画。
首先算法的实现需要确定不确定度,而不确定性是未知的。文献[6]假设真实的系数矩阵为A2+ΔA2,真实的观测向量为L+ΔL。其中ΔA2和ΔL分别为不确定性误差,并假设仅知道它们的2范数上界,即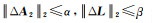
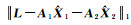
| δ | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 | 0.000 5 | 0.000 1 |
| 残差(ULS1) | 128 731.95 | 2 068.777 7 | 1 190.304 8 | 1 139.157 3 | 1 126.156 5 | 1 125.506 7 | 1 125.204 0 |
| 残差(ULS2) | 1 125.214 4 | 1 125.214 4 | 1 125.214 4 | 1 125.214 4 | 1 125.214 4 | 1 125.214 4 | 1 125.209 0 |
| p | 1.000 0 | 0.875 0 | 0.562 5 | 0.500 0 | 0.500 0 | 0.500 0 | 0.437 5 |
本文将最后3个未参与建模的观测作为度量算法外符合精度的检验点。由表 2可知,当不确定性被设置的越来越小时,两种算法关于前16个观测的预测残差均逐渐变小。在δ取0.000 1时,ULS1的预测残差值最小,但通过计算发现ULS2算法对3个检验点的预测效果依然优于ULS1算法,具体精度见表 3,计算方式为
| 观测序号 | 17 | 18 | 19 |
| ULS1 | 40.210 5 | 87.445 0 | 126.943 3 |
| ULS2 | 7.468 3 | 50.655 0 | 86.149 9 |
为了进一步比较两种算法的有效性,本文参照文献[14],利用不同的平差准则下的目标函数,将δ=0.000 1时的算法解回代,以比较两种算法的优劣。结果见表 4。这里,笔者设定a(A,L
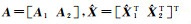
| 方法 | R(A, L, X) | a(A, L, X) | r(A, L, X, α, β) |
| ULS1 | 364.874 6 | 0.240 5 | 12 549 555.93 |
| ULS2 | 364.874 5 | 0.240 7 | 1 253 502.36 |
在实际情况中,由于模型误差、人为误差、仪器误差以及样本影响等,同一控制点在两套坐标系下的坐标量测值均包含了误差,这使得观测向量L和系数矩阵A2都需要修正。本文运用混合不确定性模型来解决该数据误差问题,最终使得新旧坐标系下的坐标测量值都能够平等、匀称地进行改正。
4 结论目前的测量平差理论大多是基于“观测值的不确定性就是随机性”的假设进行的研究。但在实际测量工程中,有许多不确定因素是不同于传统的随机性误差的,它们没有分布规律,因而无法进行统计描述。所以有文献将观测中的不确定性因素进行数值化、参数化后融入平差模型中。本文沿用以上思路,提出了基于混合不确定性模型的参数求解算法。主要有以下结论:
(1) 结合部分系数矩阵A2和观测向量L存在一定的误差的事实,本文将平差模型扩展到混合不确定性平差模型,该模型在某些应用领域更加切合实际。
(2) 本文将不确定信息转化为先验信息,以参数的形式融入模型,建立有界不确定性约束下随机误差和不确定性误差平方和最小的平差准则,最后对该优化问题进行迭代求解。从参数估计的残差角度考虑,min-max准则下的算法所得残差取值几乎总是大于本文算法,说明本文所提算法精度更高。
(3) 本文算法利用了有界不确定性误差的先验信息-不确定度β,而文献[2]的参数估计结果中没有β,这样的结果未体现不确定度β作为参数融入模型的意义。
(4) 在本文算例中,当不确定性设定在一定范围内时,本文所提算法所得结果变化不太大。说明在坐标转换中,转换参数对系数矩阵的有界不确定性误差不十分敏感,也有可能是测量不确定性过大淹没了矩阵的有界不确定性。
| [1] |
陶本藻.
GIS质量控制中不确定度理论[J]. 测绘学院学报, 2000, 17(4): 235–238.
TAO Benzao. Basic Theory of Uncertainty of Quality Control in GIS[J]. Journal of Institute of Surveying and Mapping, 2000, 17(4): 235–238. DOI:10.3969/j.issn.1673-6338.2000.04.001 |
| [2] |
宋迎春, 谢雪梅, 陈晓林.
不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135–141.
SONG Yingchun, XIE Xuemei, CHEN Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertain[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135–141. DOI:10.11947/j.AGCS.2015.20130213 |
| [3] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883–893. DOI:10.1137/0717073 |
| [4] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem:Computational Aspects and Analysis[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1991. |
| [5] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415–421. DOI:10.1007/s00190-007-0190-9 |
| [6] | CHANDRASEKARAN S, GOLUB G H, GU M, et al. Parameter Estimation in the Presence of Bounded Data Uncertainties[J]. SIAM Journal on Matrix Analysis and Applications, 1998, 19(1): 235–252. DOI:10.1137/S0895479896301674 |
| [7] |
杨元喜.
关于"新的点位误差度量"的讨论[J]. 测绘学报, 2009, 38(3): 280–282.
YANG Yuanxi. Discussion on "A New Measure of Positional Error"[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 280–282. DOI:10.3321/j.issn:1001-1595.2009.03.015 |
| [8] |
史玉峰, 史文中, 靳奉祥.
GIS中空间数据不确定性的混合熵模型研究[J]. 武汉大学学报(信息科学版), 2006, 31(1): 82–85.
SHI Yufeng, SHI Wenzhong, JIN Fengxiang. Hybrid Entropy Model of Spatial Data Uncertainty in GIS[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 82–85. |
| [9] |
陈伟. 最小不确定度估计理论及其应用[D]. 武汉: 武汉大学, 2005. CHEN Wei. Least Uncertainty Estimation Theory with Applications[D]. Wuhan: Wuhan University, 2005. |
| [10] |
陈伟, 王新洲.
最小不确定度估计原理及其病态问题解法研究[J]. 武汉大学学报(信息科学版), 2008, 33(7): 752–754.
CHEN Wei, WANG Xinzhou. Least Uncertainty Estimation Theory and Its Applications to Resolving Morbid Problems[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 752–754. |
| [11] |
王新洲.
最小不确定度约束下的极大可能性估计[J]. 测绘工程, 2003, 12(1): 5–8.
WANG Xinzhou. Maximum Possibility Estimation Restricted by Least Uncertainty[J]. Engineering of Surveying and Mapping, 2003, 12(1): 5–8. DOI:10.3969/j.issn.1006-7949.2003.01.002 |
| [12] |
张正禄, 范国庆, 张松林, 等.
测量的广义可靠性研究[J]. 武汉大学学报(信息科学版), 2012, 37(5): 577–581.
ZHANG Zhenglu, FAN Guoqing, ZHANG Songlin, et al. General Reliability of Measurement[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 577–581. |
| [13] |
贾帅东, 张立华, 宋国大, 等.
基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3): 454–460.
JIA Shuaidong, ZHANG Lihua, SONG Guoda, et al. A Method for Constructing an Adaptive Grid Digital Depth Model Based on Mean Vertical Uncertainty of Area[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 454–460. |
| [14] |
宋迎春, 金昊, 崔先强.
带有不确定性的观测数据平差解算方法[J]. 武汉大学学报(信息科学版), 2014, 39(7): 788–792.
SONG Yingchun, JIN Hao, CUI Xianqiang. Adjustment Algorithm about Observation Data with Uncertain[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 788–792. |
| [15] |
杨元喜.
卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646–650.
YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646–650. |
| [16] |
朱国红, 鲁铁定.
有界不确定性平差模型的迭代算法[J]. 测绘科学, 2017, 42(6): 41–45.
ZHU Guohong, LU Tieding. Iterative Algorithm for Adjustment Model with Bounded Data Uncertainties[J]. Science of Surveying and Mapping, 2017, 42(6): 41–45. |
| [17] |
王志忠, 陈丹华, 宋迎春.
具有不确定性平差算法[J]. 测绘学报, 2017, 46(7): 834–840.
WANG Zhizhong, CHEN Danhua, SONG Yingchun. An Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(7): 834–840. DOI:10.11947/j.AGCS.2017.20160522 |
| [18] |
王志忠, 朱建军.
污染模型下的最优估计[J]. 测绘学报, 1999, 28(1): 51–56.
WANG Zhizhong, ZHU Jianjun. Optimal Estimation Under Contaminated Error Model[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1): 51–56. DOI:10.3321/j.issn:1001-1595.1999.01.010 |
| [19] |
鲁铁定, 周世健.
总体最小二乘的迭代解法[J]. 武汉大学学报(信息科学版), 2010, 35(11): 1351–1354.
LU Tieding, ZHOU Shijian. An Iterative Algorithm for Total Least Squares Estimation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1351–1354. |
| [20] |
鲁铁定. 总体最小二乘平差理论及其在测绘数据处理中的应用[D]. 武汉: 武汉大学, 2010. LU Tieding. Research on the Total Least Squares and Its Applications in Surveying Data Processing[D]. Wuhan: Wuhan University, 2010. |
| [21] |
宋迎春, 左廷英, 朱建军.
带有线性不等式约束平差模型的算法研究[J]. 测绘学报, 2008, 37(4): 433–437.
SONG Yingchun, ZUO Tingying, ZHU Jianjun. Research on Algorithm of Adjustment Model with Linear Inequality Constrained Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 433–437. DOI:10.3321/j.issn:1001-1595.2008.04.006 |
| [22] | SCHAFFRIN B, FELUS Y A. On Total Least-squares Adjustment with Constraints[M]//SANSò F. A Window on the Future of Geodesy. Berlin, Heidelberg: Springer, 2005: 417-421. |
| [23] | SCHAFFRIN B, LEE I, FELUS Y A, et al. Total Least-squares (TLS) for Geodetic Straight-line and Plane Adjustment[J]. Bollettino di Geodesia e Scienze Affini, 2006, 65(3): 141–168. |
| [24] | SCHAFFRIN B. A Note on Constrained Total Least-squares Estimation[J]. Linear Algebra and its Applications, 2006, 417(1): 245–258. DOI:10.1016/j.laa.2006.03.044 |
| [25] |
李征航, 黄劲松.
GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005.
LI Zhenghang, HUANG Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2005. |



