2. 中南大学地球科学与信息物理学院, 湖南 长沙 410083;
3. 中南林业科技大学土木工程学院, 湖南 长沙 410004
2. School of Geosciences and Info-physics, Central South University, Changsha 410083, China;
3. School of Civil Engineering, Central South University of Forestry and Technology, Changsha 410004, China
大地测量实际问题中,除了观测信息,还有参数本身或者前期研究中得到一些附加的有用信息或者先验约束信息[1-3]。这些附加信息虽然没有实际观测值的绝对精度或可靠性,但可以降低模型的不适定性,选择合适的解空间,保持参数先验值和验后估值的统计、几何或物理意义,它们在平差模型中的重要体现就是约束条件[4-5]。通过附加约束条件,补充(先验)信息,可以充分利用参数附加信息或先验信息(参数内在的相关性、精度、几何或物理信息),对部分参数进行约束,可以很好地保证参数解的唯一性和稳定性。有许多的学者,对带有等式或不等式约束的平差模型进行了大量的研究,提出了许多有效的算法[6-11]。然而,在测绘数据处理中,还有一些复杂的先验信息用等式或不等式来表示比较困难,只能用参数的可行区间、噪声范围等来描述[12]。利用区间约束或集合方法来描述复杂先验信息,可以简化平差模型。区间约束平差模型还很少在测量数据处理中应用,仅有少数数学研究学者对它们进行了研究。他们给出的算法非常复杂,强调的是最优解的解算方法[13-18],并不关心解的精度评估,不适合测量工作中的应用。在测量数据处理中,针对区间约束平差模型,常用的方法是将其转化为不等式约束平差。但这种转换增加了不等式约束的个数,而不等式约束的解算本身就是一件困难的事[8-11]。区间约束是一种简单界约束,又称为框约束或箱形约束[14-17],在二次规划理论中有大量的研究,如投影梯度方法[14]、分枝定界法[16]、内点算法[18-19]、积极集法[20-21]等。但这些方法非常复杂,不能直接应用于测量数据的处理,需要进行改进和简化。本文将针对区间约束的特点,研究参数带有区间约束的平差模型解算方法,利用矩阵正则分裂方法[22-23],将平差问题转化成一个简单的二次规划问题,探索一种新的参数估计迭代算法,并针对病态问题,对算法进行验证,证实了将区间约束加入到平差解算中,可以有效提高解的可靠性。本文利用最优估计理论拓展了现有的误差理论与测量平差方法。
1 参变量带有区间约束的平差模型当参数向量的不确定性用一个区间来描述时,可以建立如下的平差模型
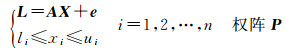 (1)
(1)
式中,A为m×n(m≥n)维设计矩阵;L为m维观测向量;e为m维随机误差向量;X=(x1, x2, …, xn)T为n维参数向量,X的不确定性可以用一个有界向量来进行描述,记为l≤X≤u,此处,l=(l1, l2, …, ln)T,u=(u1, u2, …, un)T分别为X的下界和上界向量。本文定义模型(1)为参变量带有区间约束的平差模型。模型(1)中,考虑约束条件进行最小二乘平差,即解||L-AX||P2的最小值问题,可以等价为求解下面的二次规划问题
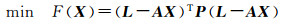 (2a)
(2a)
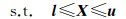 (2b)
(2b)
由于目标函数F(X)=(L-AX)TP(L-AX)=XT(ATPA)X-2LTPAX+LTPL中,LTPL为一个常量,若设N=ATPA、c=-ATPL,则二次规划问题(2),可以转化为如下的二次规划问题
 (3a)
(3a)
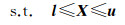 (3b)
(3b)
已有学者研究了带有不等式约束的平差模型,提出了有效约束的思想[9]。利用这一思想,设L={i:xi=li}、U={i:xi=ui}、E={1, 2, …, n},可以找到E的子集S=L∪U,则区间约束平差模型(3),等同于具有等式约束的平差模型
 (4)
(4)
式中,BS为对角矩阵,当i∈S时,对角元素bii=1,当i∉S时,对角元素bii=0;dS为向量,当i∈S时,第i分量di=li,或di=ui。由文献[24-25]可知,其参数估计
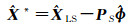 (5)
(5)
式中,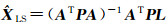
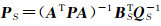
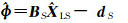
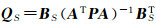

式中,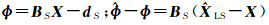
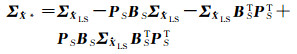 (6)
(6)
此处
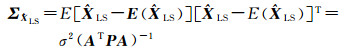
因此有
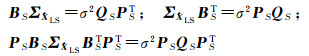
故
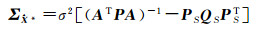 (7)
(7)
由此可知,参数具有线性区间约束的平差模型的参数估计的精度评估可归结为无约束或具有等式约束的平差模型参数估计问题来讨论。寻找有效约束的方法非常复杂,在数据处理中直接利用式(5)来进行参数估计是不可行的, 下面介绍一种利用矩阵正则分裂方法,把平差问题转化成一个简单的二次规划问题,建立一种新的参数估计迭代算法。
2 区间不确定性的平差模型的解算方法假设(M, H)是N的一个正则分裂,即,N=M+H,并且(M-H)是对称正定矩阵[26],对于任意可行解X(满足(式(3b))的任意X)有
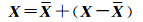
这时
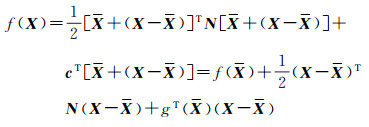
式中,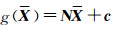

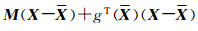
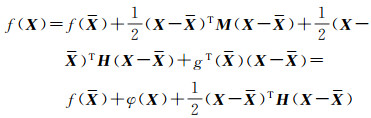 (8)
(8)
式中
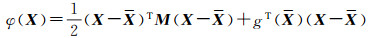
为了求解二次规划问题式(3),可以先求解
 (9a)
(9a)
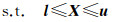 (9b)
(9b)
若X1是式(8)的最优解,令X=X1,重新代入式(9)又可以得到最优解X2、…。设第k次的最优解为Xk,再令X=Xk代入式(9)求得的最优解为Xk+1。任意给定X∈Ω,利用Ω是凸集的特性,对于任意的0≤λ<1,有Xk+1+λ(X-Xk+1)∈Ω。这时
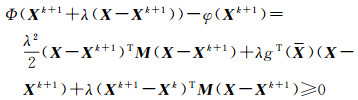
上式两边除以λ,并令λ→0,可以得到

注意到X=Xk,由式(8)有
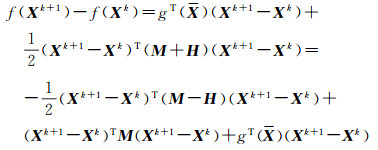
由上式,顾及(M-H)的正定性,可知,f(Xk+1)<f(Xk),即f(Xk)是单调递减有界序列,它是收敛的。
要解决带有区间不确定性平差模型,只要解决二次规划问题式(3),现设X*是式(3)的最优解,{Xk}是用上面方法得到的二次规划问题式(9)的迭代最优解序列,有f(Xk+1)-f(X*)>0,f(Xk)-f(X*)>0,由于f(Xk)是单调递减,有
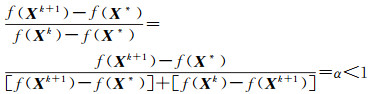
即有
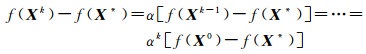 (10)
(10)
这说明limk→∞f(Xk)=f(X*),即,规划问题(9)得到的迭代最优解序列可以收敛到规划问题(3)的最优解。已有许多文献给出了正则分裂的方法[22-23]。下面是本文给出的一个简单的正则分裂方法:设N的特征值从小到大排列为:λ1、λ2、…、λn,如令M=dI,(M, H)是N的一个正则分裂,即N=H+M,因此,H=N-M,容易计算出M-H=2M-N的特征值为2d-λi,i=1, 2, …, n。为了保证M-H的正定性,d只要满足:2d-λn>0,即d>λn/2。
3 区间约束平差模型算法若平差问题式(1)的系数矩阵A是列满秩的,则N=ATPA是一个正定矩阵,取

step1:令X=Xk、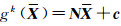

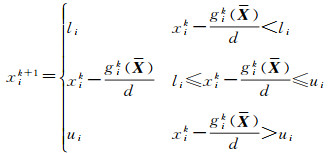 (11)
(11)
式中,d为M的对角元素。
step2:若||Xk+1-Xk||<ε,算法终止,此时,Xk+1就是带有区间约束平差模型(1)的解,否则转step1继续迭代。
由φ(X)可知

这说明,h(X)是单调递增的。h(Xk+1)的第i个分量为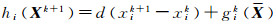
(1) 当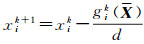
(2) 当

(3) 当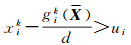
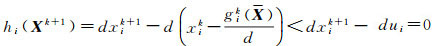
以上3项正好说明Xk+1满足最优解的K-T条件,所以Xk+1是式(9)的最优解,利用前面的推导可以证明此算法的收敛性。注意到式(11)中,xik+1=li或xik+1=ui它就是式(4)中提到的有效约束,因此可以利用式(7)来计算解的协方差。
4 算例及分析算例1:如图 1所示的测边网,P1、P2为已知点,其坐标分别为(48 580.285, 600 500.496)和(47 943.013, 66 225.845)。为了便于分析比较,算例中的点P3、P4、P5、P6的真实坐标假设已知(表 1),边长的观测值利用真实坐标计算,再加上误差得到的,观测边长视为同精度(表 2)。为了便于分析,假设由前期的观测得到了P3、P4、P5、P6的近似坐标(表 1),以及它们相应的点位精度。先验约束区间D1是通过点位精度进行推算的,D2、D3是放大2倍和3倍的约束区间,以便分析算法。迭代的终止条件设置为||Xk+1-Xk||<10-10。
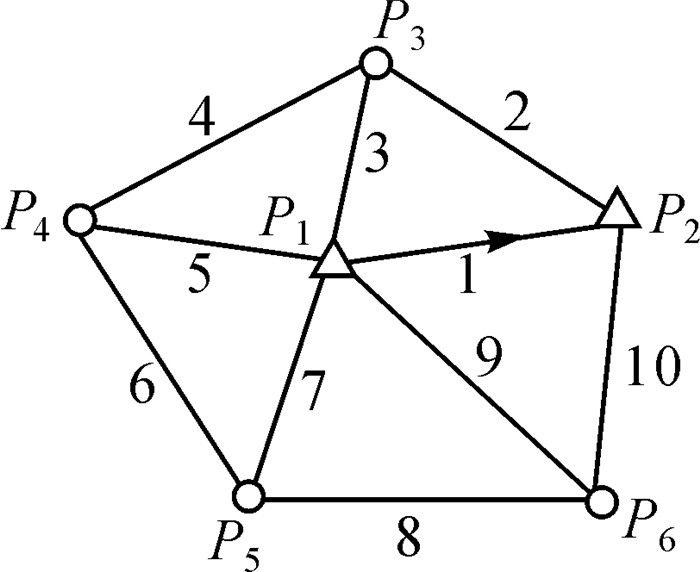
|
| 图 1 测边三角网 Fig. 1 Distance-measuring triangulation network |
| 点名 | 真实坐标 | 近似坐标 | |||||||
| P3 | P4 | P5 | P6 | P3 | P4 | P5 | P6 | ||
| x/m | 53 743.151 | 48 681.398 | 43 767.234 | 40 843.239 | 53 743.674 | 48 680.496 | 43 768.794 | 40 840.905 | |
| y/m | 61 003.810 | 55 018.270 | 57 968.590 | 64 867.876 | 61 006.568 | 55 018.806 | 57 966.087 | 64 870.541 | |
| 边号 | 观测边长/m |
| 1 | 5 760.706 |
| 2 | 7 804.611 |
| 3 | 5 187.314 |
| 4 | 7 838.890 |
| 5 | 5 483.157 |
| 6 | 5 731.827 |
| 7 | 5 438.409 |
| 8 | 7 493.319 |
| 9 | 8 884.539 |
| 10 | 7 228.509 |
设τ=[1, 1, 1, 1, 1, 1, 1, 1]T,约束区间D1={X:-3τ≤X≤3τ}、D2={X:-6τ≤X≤6τ}、D3={X:-9τ≤X≤9τ}, 目标函数为F(X)=(L-AX)TP(L-AX), 误差平方和的计算公式为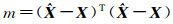

算例1说明,算法收敛的速度与可行域的大小有关,对于系数矩阵列满秩;因为目标函数是凸函数,最优解是唯一的。从表 3可以看出针对不同的区间约束,本文算法与最小二乘算法一致,最优解与真值非常接近,说明对于正常的法矩阵。因为观测信息充分,不需要补充先验信息。但是,最优解是在可行域上求得的,当最小二乘解的最优解在可行域(约束区间)D上,由唯一性可知算法得到的解与最小二乘是一致的(先验信息没有起作用)。当最小二乘解的最优解不在可行域D上,说明最小二乘解不符合先验信息,应选择符合先验约束的解。
| 真值 | 最小二乘算法 | 本文算法 | |||
| D1 | D2 | D3 | |||
| 迭代957次 | 迭代1076次 | 迭代1076次 | |||
 |
-0.523 0 | -0.516 0 | -0.516 0 | -0.516 0 | -0.516 0 |
| -2.758 0 | -2.786 0 | -2.786 0 | -2.786 0 | -2.786 0 | |
| 0.902 0 | 0.923 3 | 0.923 3 | 0.923 3 | 0.923 3 | |
| -0.536 0 | -0.560 6 | -0.560 6 | -0.560 6 | -0.560 6 | |
| -1.560 0 | -1.577 4 | -1.577 4 | -1.577 4 | -1.577 4 | |
| 2.503 0 | 2.456 2 | 2.456 2 | 2.456 2 | 2.456 2 | |
| 2.334 0 | 2.327 0 | 2.327 0 | 2.327 0 | 2.327 0 | |
| -2.665 0 | -2.728 6 | -2.728 6 | -2.728 6 | -2.728 6 | |
 |
0.008 5 | 0.004 0 | 0.004 0 | 0.004 0 | 0.004 0 |
| m | 0 | 0.008 5 | 0.008 5 | 0.008 5 | 0.008 5 |
算例2:修改算例1中已知点P2的坐标为(48 570.013, 60 555.845),让它非常靠近P1点,导致算法1中的系数矩阵病态,用来分析病态问题中算法的性能。此时相应的边长观测也会发生变化,见表 4,相应的平差模型的系数矩阵和观测向量为
| 边号 | 观测边长/m |
| 1 | 45.075 |
| 2 | 5 222.056 |
| 3 | 5 187.391 |
| 4 | 7 838.867 |
| 5 | 5 483.162 |
| 6 | 5 731.756 |
| 7 | 5 438.383 |
| 8 | 7 493.316 |
| 9 | 8 884.603 |
| 10 | 8 839.687 |
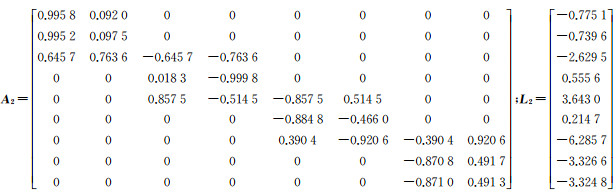
算例2中,迭代的终止条件设置为||Xk+1-Xk||<10-10,虽然N=ATPA是一个正定矩阵(此例中P为单位矩阵),但有一特征值接近0,N的条件数为1.353 3×106属于法方程病态。这时最小二乘解偏离真值较大,其估计值不在约束区间内,与先验信息明显不符,严重失真。加入一些先验信息可以显著改善其病态性,如表 5中基于不同区间约束D1、D2和D3的参数解。N病态时,算法的收敛速度较正常矩阵的收敛速度慢,可行域增大(如D3),目标函数值的最优值通常会下降,直至接近最小二乘的最优值,但解失真的程度也会增大。这正好说明,对于较小的可行域,可以对参数进行约束,从而可以改善病态性。因此,在建立平差模型时充分利用参数的先验信息,可以弥补观测不充分导致的病态问题。
| 真值 | 最小二乘算法 | 本文算法2 | |||
| D1 | D2 | D3 | |||
| 迭代7302次 | 迭代155 028次 | 迭代391 691次 | |||
 |
-0.523 0 | -1.347 3 | -0.510 5 | -0.700 5 | -0.890 4 |
| -2.758 0 | 6.162 5 | -2.630 5 | -0.634 2 | 1.362 0 | |
| 0.902 0 | 10.443 9 | 1.084 3 | 3.209 2 | 5.334 1 | |
| -0.536 0 | -0.364 5 | -0.535 7 | -0.496 8 | -0.458 0 | |
| -1.560 0 | 2.869 2 | -1.458 1 | -0.475 7 | 0.506 7 | |
| 2.503 0 | -5.908 4 | 2.307 9 | 0.442 6 | -1.422 8 | |
| 2.334 0 | -5.331 9 | 2.125 6 | 0.432 6 | -1.260 5 | |
| -2.665 0 | -16.214 1 | -3.000 0 | -6.000 0 | -9.000 0 | |
 |
0.004 3 | 1.686 1×10-5 | 0.001 2 | 7.439 4×10-4 | 3.795 6×10-4 |
| m | 0 | 504.044 1 | 0.253 7 | 30.025 3 | 109.495 1 |
5 结束语
大地测量平差模型中的参数通常存在一些不确定的附加信息或先验信息(参数内在的相关性、精度、几何或物理信息),充分利用它们可以对部分参数进行约束,从而保证参数解的唯一性和稳定性。这些附加信息虽然没有实际观测值的绝对精度或可靠性,但可以降低模型的不适定性,选择合适的解空间,保持参数先验值和验后估值的统计、几何或物理意义,有效提高参数估计的效率。本文针对参数的区间约束信息,提供了一种新的平差方法,其算法简单,可以很好地应用于测量数据处理,提供参数估计的准确率。
| [1] |
朱建军, 丁晓利, 陈永奇.
集成地质、力学信息和监测数据的滑坡动态模型[J]. 测绘学报, 2003, 32(3): 261–266.
ZHU Jianjun, DING Xiaoli, CHEN Yongqi. Dynamic Landsliding Model with Integration of Monitoring Information and Mechanic Information[J]. Acta Geodaetica et Cartographica Sinca, 2003, 32(3): 261–266. DOI:10.3321/j.issn:1001-1595.2003.03.015 |
| [2] |
张勤, 黄观文, 王利, 等.
附有系统参数和附加约束条件的GPS城市沉降监测网数据处理方法研究[J]. 武汉大学学报(信息科学版), 2009, 34(3): 269–272.
ZHANG Qin, HUANG Guanwen, WANG Li, et al. Datum Design Study of GPS Height Monitoring Network with Systematic Parameters and Constraints[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 269–272. |
| [3] |
赵少荣, 陶本藻, 于正林.
论变形测量数据的反演[J]. 测绘学报, 1992, 21(3): 161–172.
ZHAO Shaorong, TAO Benzao, YU Zhenglin. On the Inversion of Deformation Survey Data[J]. Acta Geodaetica et Cartographica Sinica, 1992, 21(3): 161–172. |
| [4] |
曾安敏, 杨元喜, 欧阳桂崇.
附加约束条件的序贯平差[J]. 武汉大学学报(信息科学版), 2008, 33(2): 183–186.
ZENG Anmin, YANG Yuanxi, OUYANG Guichong. Sequential Adjustment with Constraints Among Parameters[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 183–186. |
| [5] |
王乐洋, 许才军, 汪建军.
附有病态约束矩阵的等式约束反演问题研究[J]. 测绘学报, 2009, 38(5): 397–401.
WANG Leyang, XU Caijun, WANG Jianjun. Research on Equality Constraint Inversion with Ill-posed Constraint Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 397–401. DOI:10.3321/j.issn:1001-1595.2009.05.004 |
| [6] |
宋迎春, 左廷英, 朱建军.
带有线性不等式约束平差模型的算法研究[J]. 测绘学报, 2008, 37(4): 433–437.
SONG Yingchun, ZUO Tingying, ZHU Jianjun. Research on Algorithm of Adjustment Model with Linear Inequality Constrained Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 433–437. DOI:10.3321/j.issn:1001-1595.2008.04.006 |
| [7] |
谢建, 朱建军.
等式约束对病态问题的影响及约束正则化方法[J]. 武汉大学学报(信息科学版), 2015, 40(10): 1344–1348.
XIE Jian, ZHU Jianjun. Influence of Equality Constraints on Ill-conditioned Problems and Constrained Regularization Method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(10): 1344–1348. DOI:10.13203/j.whugis20130764 |
| [8] | PENG J H, ZHANG H P, SHONG S, et al. An Aggregate Constraint Method for Inequality-constrained Least Squares Problem[J]. Journal of Geodesy, 2006, 79(12): 705–713. DOI:10.1007/s00190-006-0026-z |
| [9] |
冯光财, 朱建军, 陈正阳, 等.
基于有效约束的附不等式约束平差的一种新算法[J]. 测绘学报, 2007, 36(2): 119–123.
FENG Guangcai, ZHU Jianjun, CHEN Zhengyang, et al. A New Approach to Inequality Constrained Least-squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 119–123. DOI:10.3321/j.issn:1001-1595.2007.02.001 |
| [10] | SONG Yingchun, ZHU Jianjun, LI Zhiwei. The Least-squares Estimation of Adjustment Model Constrained by Some Non-negative Parameters[J]. Survey Review, 2010, 42(315): 62–71. DOI:10.1179/003962610X12572516251367 |
| [11] |
朱建军, 谢建.
附不等式约束平差的一种简单迭代算法[J]. 测绘学报, 2011, 40(2): 209–212.
ZHU Jianjun, XIE Jian. A Simple Iterative Algorithm for Inequality Constrained Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 209–212. |
| [12] |
宋迎春, 谢雪梅, 陈晓林.
不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135–141.
SONG Yingchun, XIE Xuemei, CHEN Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 135–141. DOI:10.11947/j.AGCS.2015.20130213 |
| [13] |
肖运海. 求解大规模优化问题的几种方法[D]. 长沙: 湖南大学, 2007. XIAO Yunhai. Research on the Iteration Method for Several Kinds of Consistent and Inconsistent Constrained Matrix Equation[D]. Changsha: Hunan University, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1209515 |
| [14] |
周斌, 高立, 戴彧虹.
求解大规模带边界约束二次规划问题的单调投影梯度法[J]. 中国科学(A辑):数学, 2006, 36(5): 556–570.
ZHOU Bin, GAO Li, DAI Yuhong. A Monotonic Ciadient Rrojection Method in Large-scale Quadratic Programming with Boundary Constraints[J]. Scientia Sinica Mathematica, 2006, 36(5): 556–570. |
| [15] | GAO Yuelin, XU Chengxian, YANG Chuansheng. A Global Optimality Method for Solving the Nonconvex Quadratic Programming Problem with Additional Box Constraints[J]. Chinese Journal of Engineering Mathematics, 2002, 19(1): 99–103. |
| [16] |
付文龙, 杜廷松, 翟军臣.
基于D. C.分解的一类箱型约束的非凸二次规划的新型分支定界算法[J]. 数学研究, 2013, 46(3): 311–318.
FU Wenlong, DU Tingsong, ZHAI Junchen. A New Branch and Bound Algorithm Based on D. C. Decomposition about Nonconvex Quadratic Programming with Box Constrained[J]. Journal of Mathematical Study, 2013, 46(3): 311–318. DOI:10.3969/j.issn.1006-6837.2013.03.013 |
| [17] |
朱克强, 贺力群.
大规模简单界约束的凸二次规划新算法[J]. 北方交通大学学报, 1998, 22(3): 98–103.
ZHU Keqian, HE Liqun. New Algorithm of Large Scale Convex Quadratic Programs with Simple Bound Constraints[J]. Journal of Northern Jiaotong University, 1998, 22(3): 98–103. |
| [18] | LIN C J, MORÉ J J. Newton's Method for Large Bound-constrained Optimization Problem[J]. SIAM Journal on Optimization, 1999, 9(4): 1100–1127. DOI:10.1137/S1052623498345075 |
| [19] |
张艺.
框式约束凸二次规划问题的内点算法[J]. 高等学校计算数学学报, 2002, 24(2): 163–168.
ZHANG Yi. An Interior Point Algorithm for Convex Quadratic Programming Problem with Box Constraints[J]. Numerical Mathematics A:Journal of Chinese Universities, 2002, 24(2): 163–168. |
| [20] |
王晓.
求解一般界约束优化问题的积极集信赖域方法[J]. 中国科学:数学, 2011, 41(4): 377–391.
WANG Xiao. An Active Set Trust Region Method for General Bound Constrained Optimization[J]. Scientia Sinica Mathematica, 2011, 41(4): 377–391. |
| [21] | HAGER W W, ZHANG Hongchao. A New Active Set Algorithm for Box Constrained Optimization[J]. SIAM Journal on Optimization, 2006, 17(2): 526–557. DOI:10.1137/050635225 |
| [22] |
卢战杰, 魏紫銮.
边界约束二次规划问题的分解方法[J]. 计算数学, 1999, 21(4): 475–482.
LU Zhanjie, WEI Ziluan. Decomposition Method for Quadratic Programming Problem with Box Constrains[J]. Mathematica Numerica Sinica, 1999, 21(4): 475–482. |
| [23] |
于绍慧. 边界约束凸二次规划的求解[D]. 南京: 南京航空航天大学, 2005. YU Shaohui. Algorithms for Bound Constrained Convex Quadratic Programming[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y697011 |
| [24] | RAO C R. Linear Statistical Inference and Its Applications[M]. New York: John Wiley and Sons, 1973. |
| [25] |
谢建, 朱建军.
等式约束病态模型的正则化解及其统计性质[J]. 武汉大学学报(信息科学版), 2013, 38(12): 1440–1444.
XIE Jian, ZHU Jianjun. A Regularized Solution and Statistical Properties of Ill-posed Problem with Equality Constraints[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1440–1444. |



