2. 国家测绘地理信息局卫星测绘应用中心, 北京 100048
2. Satellite Surveying and Mapping Application Center, NASG, Beijing 100048, China
合成孔径雷达(synthetic aperture radar,SAR)具有高精度几何定位能力。然而,由于卫星轨道参数和成像参数等存在测量误差,制约着SAR影像的几何定位精度。几何定标技术是实现SAR影像高精度定位的关键,也是提升SAR系统在无控制点情况下几何定位精度的主要途径之一。
国外对几何定标的研究已经比较成熟。ERS发射后,欧盟成立相关部门利用地面检校场对ERS影像进行几何定标处理,最终达到20 m单景无控几何定位精度[1]。意大利的COSMO-SKYMED利用检校场进行几何定标后,可实现无控条件下15 m的几何定位精度。日本ALOS卫星上的PALSAR载荷经地面几何定标后,条带模式的几何定位精度为9.7 m,扫描模式的几何定位精度为70 m[2]。Radarsat-2利用角反射器进行几何定标后,距离向定位精度为5.68 m,方位向为0.85 m[3]。德国利用角反射器完成了TerraSAR系列卫星的高精度几何定标,可实现厘米级定位精度[4-6]。其中TerraSAR-X是当前在轨运行分辨率最高的一颗民用卫星,文献[7-8]总结了TerraSAR-X的几何定标精度,方位向为0.5 m,距离向为0.3 m。我国最早的民用SAR卫星是HJ-1C,由于卫星很快发生了故障,所以其几何定位精度的研究较少。高分三号发射之后,文献[9-10]总结了其定位误差,并验证了定标后的高分三号系统级几何定位精度可达到3 m左右。
在SAR影像几何定位中,几何定位模型是实现高精度定位的关键和核心问题[11]。SAR定位模型主要包括距离-多普勒(range-Doppler,R-D)模型[12]、Leberl雷达共线模型[13]、Konecny投影模型[14]、有理多项式模型[15]和距离-共面模型[16]等。其中,R-D模型对于SAR成像几何的描述最为直观和准确,是目前应用最为广泛的模型[17]。由于存在测量误差,导致使用R-D模型反算得到的地物点坐标与真实地物点之间仍存在偏差。解决方法一般利用数据较多、良好分布的地面控制点来精确轨道参数和成像参数,进而提高影像的几何定位精度。但在广域范围内,特别是高山地区域,控制点往往极难获取。传统几何定标方法通常基于单景影像进行误差参数标定,然后利用参数改正量标定同平台下的其他影像。但由于平台间性能差异,不同平台下SAR影像的定标参数改正量也不尽相同,因此传统方法无法实现多平台下SAR影像的几何定标。
基于上述分析,使用尽可能少的控制点实现多景、多平台影像的几何定标是本文研究的重点,为此本文提出了一种稀少控制的多平台星载SAR联合几何定标方法。首先选取SAR主影像,并基于稀少控制点对该影像进行几何定标,然后利用主影像与从影像之间的连接点逐级传递标定其他SAR影像。该方法突破传统几何定标方法只能标定单一平台SAR影像的限制,可同时实现多平台下星载SAR影像的几何定标。通过对3景TerraSAR-X、3景TanDEM-X、5景高分三号影像进行联合定标,并利用SF-3050星站差分GNSS接收机实测地面GPS点进行精度评价,验证了本文方法的有效性和正确性。
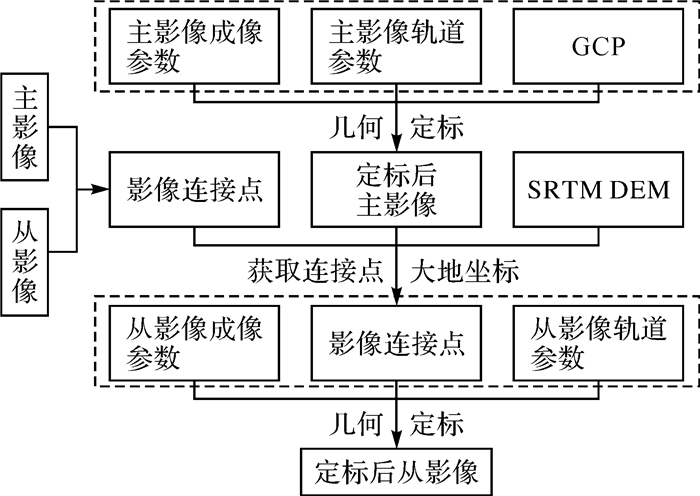
1 稀少控制的多平台星载SAR联合几何定标本文方法主要体现了传递式几何定标的思想,其流程如图 1所示。首先,选定包含实测控制点的SAR影像(主影像),基于R-D模型使用非线性最小二乘原理对模型参数进行精细化估计,确定定标参数改正量,完成主影像的几何定标;然后,使用几何参数计算与主影像具有重叠区域的邻接影像(从影像),利用点位追踪算法提取主、从影像连接点,并使用定标后主影像和SRTM DEM解算连接点的大地坐标;最后,基于连接点完成从影像的几何定标。
1.1 星载SAR几何定标R-D模型作为目前SAR几何处理主流的定位模型,是一种符合SAR成像机理的严密模型,描述了卫星传感器与地物点在地心坐标系下的几何关系[18]。R-D模型是由距离方程式(1)、多普勒方程式(2)和地球椭球方程式(3)组成的非线性方程组[19]。
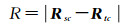 (1)
(1)
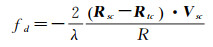 (2)
(2)
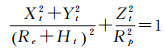 (3)
(3)
式中,R为卫星传感器与地物点之间的距离;Rsc=[XsYsZs]T为卫星传感器的位置矢量;Rtc=[XtYtZt]T为地物点的位置矢量;fd为多普勒频率;λ为雷达波长;Vsc=[VxVyVz]T为卫星传感器的速度矢量;Re和Rp分别为地球参考椭球的长半轴和短半轴;Ht为地物点的高程。
|
| 图 1 星载SAR联合几何定标流程 Fig. 1 Flowchart of hybrid geometric calibration for spaceborne SAR image |
卫星传感器位置矢量、速度矢量可用三次多项式描述为时间的函数如下
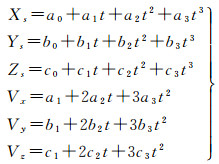 (4)
(4)
由R-D定位模型可知,几何定位的必要变量包括斜距R、卫星传感器位置矢量[XsYsZs]T、卫星传感器速度矢量[VxVyVz]T、多普勒频率fd、雷达波长λ、椭球参数Re/Rp。其中,雷达波长是已知值,可根据公式λ=c/f(c为光速,f为雷达载荷频率)求得;椭球参数在选定椭球模型后也为已知值。
斜距R是通过测量雷达脉冲收发时间差来获得的,斜距误差将引起目标的视场位置沿着多普勒线移动从而产生定位误差。对于斜距成像SAR影像,其斜距可表示为影像列号的线性函数
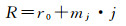 (5)
(5)
式中,r0为初始斜距;mj为距离向像元分辨率;j为从近距端到远距端逐渐增大的影像列号。一般认为头文件中提供的距离向像元分辨率是准确的,前期试验也发现改正距离向像元分辨率对最终定位结果产生的影响很小,可忽略不计,因此这里只考虑初始斜距误差对距离向定位所产生的影响。
由式(4)可知,卫星传感器的位置和速度状态矢量误差与方位向时间t密切相关。方位向时间t可表示为影像行号的线性函数
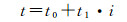 (6)
(6)
式中,t0为影像起始成像时间;t1为方位向时间分辨率;i为沿方位向逐渐增大的影像行号。经试验表明,方位向时间分辨率误差对最终定位结果产生的影响也可忽略不计,因此这里只考虑起始成像时间误差对方位向定位所产生的影响。
在星载SAR的成像过程中,需要对卫星进行偏航导引,从而确保多普勒值在零附近,并在影像聚焦阶段完成零多普勒成像,确保所有像点方位向多普勒参数为零。因此本文对多普勒参数不再进行额外的标定[20]。
综上所述,本文中只考虑初始斜距r0和影像起始成像时间t0的测量误差对几何定位精度的影响,故定标参数向量Σ=[r0t0]T。接下来根据R-D定位模型建立条件方程,进行模型参数估计。
基于距离方程式(式(1))的条件方程为
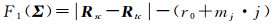 (7)
(7)
对于多普勒归零的数据产品,基于多普勒频率方程式(式(2))的条件方程为
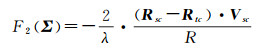 (8)
(8)
由于地球椭球方程式(式(3))中不涉及成像参数,因此无须对其建立条件方程。
由条件方程,利用若干个定标控制点能够对模型参数进行非线性最小二乘估计。以定标参数向量Σ作为未知观测值,对观测值求导进行线性化得到误差方程式为
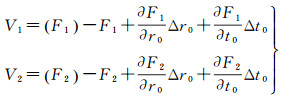 (9)
(9)
式中,观测值误差(F1)、(F2)可通过各待定参数Σ的近似值代入式(7)、(8)计算得到,观测值真值F1=F2=0。利用若干个定标控制点对模型进行参数优化时,误差方程式可写为矩阵形式
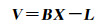 (10)
(10)
式中
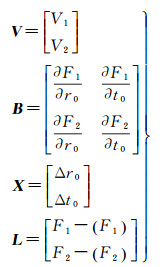
矩阵B由方程F1、F2对定标参数集Σ中的元素的偏微分构成。对矩阵B中的元素进行求解则有如下表示形式
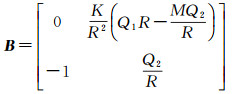 (11)
(11)
式中,K=-2/λ;M=Xv(Xs-Xt)+Yv(Ys-Yt)+Zv(Zs-Zt);Q1=Xv(a1+2a2t+3a3t2)+(Xs-Xt)·(2a2+6a3t)+Yv(b1+2b2t+3b3t2)+(Ys-Yt)·(2b2+6b3t)+Zv(c1+2c2t+3c3t2)+(Zs-Zt)·(2c2+6c3t),Q2=(Xs-Xt)·(a1+2a2t+3a3t2)+(Ys-Yt)·(b1+2b2t+3b3t2)+(Zs-Zt)·(c1+2c2t+3c3t2)。
给定参数初始值X0,构建法方程式BTBX-BTL=0,求解法方程,解算未知数改正量X=(BTB)-1BTL,即可得到定标参数的第一次校正值
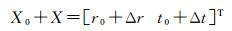 (12)
(12)
定标参数的求解过程是一个逐步迭代趋近的过程。其基本思路为:首先给定定标参数r0、t0的初始值;其次按照初始值构造误差方程式,由法方程式求解定标参数的改正量,从而求得定标参数的第一次趋近值;最后以此趋近值作为下一次迭代的初始值,多次迭代后定标参数逐渐稳定,当参数改正量小于指定阈值(本文取ε=10-6)时,迭代收敛,则此时参数改正量的累加结果即为最终定标参数改正值。
1.2 连接点点位追踪算法从影像的几何定标依赖主影像的定标成果,故需先找到主、从影像之间的某种关系,才能借助已定标影像改正待定标影像。本文通过在重叠影像之间寻找连接点来建立这种联系,连接点体现了主影像像点与从影像像点之间的映射关系。连接点在从影像的定标过程中起到了控制点的作用,但相比于控制点主要有两方面优势。其一,点位追踪算法能够达到亚像素级匹配精度,可降低人工选点误差;其二,点位追踪算法能够通过程序实现自动化,可降低人工测点成本。
不同平台下SAR影像的分辨率存在差异,为保证后续连接点的匹配精度,需对影像进行过采样预处理,使影像的分辨率保持一致,进而使用点位追踪算法实现连接点的定位与匹配。首先,按照均匀分布的原则在主影像上选择若干个具有强后向散射系数的点,作为初始连接点;其次,利用点位追踪算法获取从影像上对应的连接点点位坐标;最后,对所有连接点进行多项式拟合,剔除残差较大的误匹配连接点。借鉴SAR影像配准的相关算法,点位自动追踪的核心算法主要包括连接点粗定位和精匹配两部分。
1.2.1 连接点粗定位连接点粗定位的目的是为精匹配算法提供初始偏移量以及搜索窗口。粗定位基于R-D定位模型和主、从影像轨道参数进行快速解算,其几何定位精度在10个像素以内。
粗定位算法的核心包括两个方面,即直接几何定位算法和间接几何定位算法[21]。其中,前者实现由主影像中心点M(i, j)到地物点P(x, y, z)之间的转换,后者实现由地物点P(x, y, z)到从影像对应的匹配点S(i', j')之间的转换。这两个转换过程,基于一个相同的前提条件,即SAR影像的每个像点均对应一个单独的成像时间以及特定的斜距值(式(5)、(6))。通过上述过程获取的连接点初始偏移量Δ可由式(13)得出。
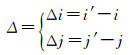 (13)
(13)
归一化互相关系数(normalized cross correlation,NCC)匹配方法可根据两幅影像上匹配窗口内的灰度信息进行匹配,具有一定的抗噪声能力,NCC计算公式如下[22]
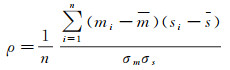 (14)
(14)
式中,mi表示主影像窗口内的像素值;si表示从影像的像素值;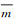
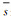
连接点精匹配将在初始偏移量的基础上进行偏移量的精细化,以达到亚像素级的匹配精度。首先,根据粗定位得到的偏移量和搜索窗口,分别在主、从影像上以初始连接点为中心选取一个含L×L个像点的窗口,并根据式(14)计算窗口内各像点的NCC值,可得到一个含L×L个NCC值的窗口;然后,对窗口内的NCC值进行曲面拟合,得到NCC曲面的函数表达式
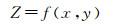 (15)
(15)
式中,(x, y)为像点的坐标,Z为该像点的NCC值;最后,根据拟合得到的NCC曲面函数表达式,以亚像素的间距插值NCC值,此时最大NCC值所对应的位置即为所求的连接点精匹配位置。
1.2.3 误匹配点剔除在连接点精匹配阶段,采用连接点粗定位结果并结合连接点全局残差进行约束匹配,能剔除存在明显错误的匹配点。但由于多源SAR影像的雷达波段、成像视角和地物散射特性等不尽相同,使得点位追踪算法的提取结果中仍然存在一些误匹配连接点。
SAR相邻影像的几何畸变较小,一般表现为平移、拉伸以及极小的旋转。这种类似刚性形变的畸变特性可采用一次多项式结合部分二次项进行修正。较为常用的拟合多项式可表达为式(16)[23]
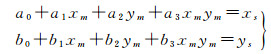 (16)
(16)
式中,(xm, ym)、(xs, ys)分别为连接点在主影像和从影像上的像点坐标;ai、bi为多项式拟合系数,i=0,1,2,3。
误匹配点剔除分为两步:首先,根据连接点求解一次多项式模型参数并计算残差,当残差大于1个像素时,剔除误差最大的连接点,并重新计算多项式模型参数和残差,直至残差小于1个像素。然后,计算水平和垂直方向上的均方差σx和σy,并剔除水平垂直方向上的位置偏差大于阈值Tx和Ty的连接点(本文取Tx=3σx、Ty=3σy)。值得注意的是,随着不断迭代剔除误匹配点,连接点数量也会逐渐下降,当连接点的个数不足以解算多项式模型时,则连接点点位追踪算法判定为失败。此时,可通过扩大搜索窗口和增大阈值设定来重新执行点位追踪算法,直至产生足够数量且满足亚像素级精度要求的连接点。
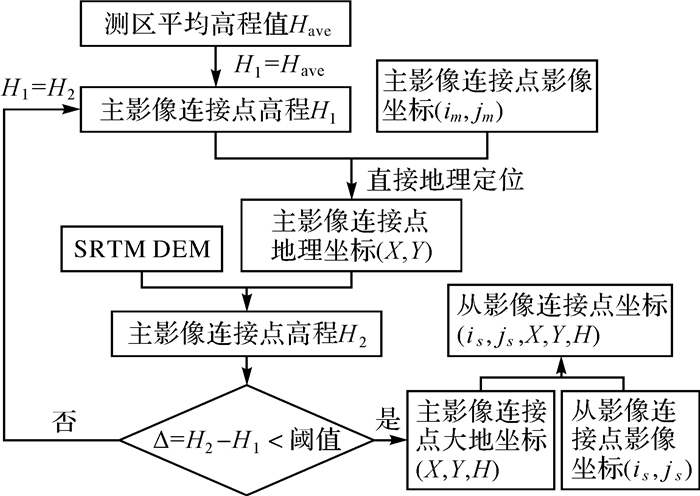
1.3 基于SRTM的连接点大地坐标获取影像连接点都是成对存在的,且主、从影像上的同一对连接点应具有相同的大地坐标。主影像定标完成后,从影像需要借助连接点实现其自身的几何定标,因此影像连接点还需带有地理坐标和高程信息。而通过点位追踪算法获取的连接点只含有影像坐标系下的行列号信息,因此本文借助SRTM数据迭代获取连接点的大地坐标,实现流程如图 2所示。首先,获取测区平均高程值并将该值作为所有连接点的高程初始值,基于主影像连接点的影像坐标和高程值H1,利用直接几何定位算法,得到主影像连接点对应的地理坐标;然后,在SRTM数据中获取该地理坐标处的高程值H2,判断前后两次高程差是否小于设定的阈值(本文取ε=10-6),若不满足条件则对高程值进行修正并执行下一次迭代;最后,综合主影像连接点的大地坐标和从影像连接点的影像坐标,得到从影像连接点的完整坐标信息。
|
| 图 2 基于SRTM获取连接点大地坐标流程 Fig. 2 Flowchart of obtaining TP's geodetic coordinate based on SRTM DEM |
2 试验与结果分析 2.1 试验数据
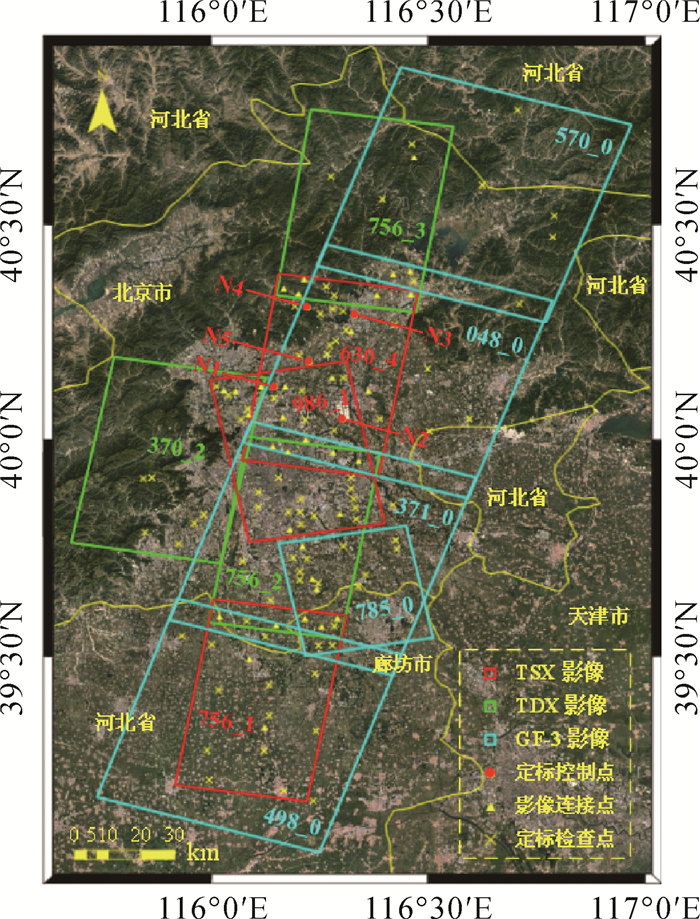
试验数据中心区域位于北京市,中心经纬度为116°28′E、39°55′N,南北向分布达235 km,区域内兼有平原和山区,海拔为16~1588 m,其地理位置如图 3所示。首先,结合光学影像在SAR影像上选取196个备选点,主要分布于宽度适宜、在SAR影像上易于辨认的道路交叉口;然后,实地调整、确认备选点位置,并根据实际情况舍弃部分测量困难(如道路车流量较大、附近有高大建筑遮挡等)的备选点,对筛选后的87个备选点进行GPS测量;最后,内业整理野外实测的所有GPS点,并将GPS点转刺到SAR影像上。在测得的GPS点中选定控制点5个、检查点82个。此外,使用点位追踪算法提取的影像连接点34个,详细点位分布如图 3所示。
|
| 图 3 试验区域地理位置及点位分布 Fig. 3 Geographical position and point's distribution of study region |
试验数据包括3景TSX、3景TDX和5景GF-3数据,获取时间为2013年11月20日—2016年08月16日。选择90 m分辨率SRTM作为外部DEM数据。试验影像基本参数见表 1。
| 影像编号 | 平台 | 成像时间 | 升降轨 | 平均高程/m | 方位向分辨率/m | 距离向分辨率/m | 方位向起始时间/ms | 近地点斜距/m |
| 630_4 | TSX | 20140316 | 降 | 221.598 | 2.00 | 1.36 | 80 266 935.211 | 690 732.087 |
| 756_1 | TSX | 20140316 | 降 | 9.464 | 2.00 | 1.36 | 80 280 935.395 | 691 168.601 |
| 986_1 | TSX | 20151119 | 升 | 31.420 | 1.85 | 0.91 | 36 266 414.462 | 595 457.579 |
| 756_3 | TDX | 20140316 | 降 | 488.793 | 2.00 | 1.36 | 80 259 935.119 | 690 208.271 |
| 756_2 | TDX | 20140316 | 降 | 32.110 | 2.00 | 1.36 | 80 273 935.299 | 691 243.627 |
| 370_2 | TDX | 20131120 | 降 | 282.103 | 1.97 | 1.36 | 80 787 910.594 | 597 318.189 |
| 785_0 | GF-3 | 20160908 | 升 | 21.529 | 5.29 | 2.25 | 36 515 935.223 | 903 671.719 |
| 570_0 | GF-3 | 20160816 | 降 | 489.643 | 3.14 | 2.25 | 83 209 554.134 | 919 669.644 |
| 048_0 | GF-3 | 20160816 | 降 | 38.271 | 3.14 | 2.25 | 83 217 764.984 | 920 101.346 |
| 371_0 | GF-3 | 20160816 | 降 | 32.089 | 3.14 | 2.25 | 83 225 975.835 | 919 977.681 |
| 498_0 | GF-3 | 20160816 | 降 | 14.751 | 3.14 | 2.25 | 83 234 186.686 | 919 869.756 |
2.2 结果与分析
采用间接几何定位算法对试验影像进行定标前的几何精度评价。首先,进行人工刺点,将GPS点转刺到影像上,获取GPS点对应的像点坐标P1;然后,利用GPS点的大地坐标,采用间接几何定位算法解算GPS点对应的像点坐标P2;最后,将P2与P1相减得到该点的几何定位误差Δ,并分别统计所有点在方位向和距离向的像点中误差(RMS,式(17)),以此评价影像的几何定位精度。使用82个检查点对11景试验影像进行定标前的几何精度评价见表 2。
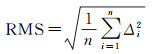 (17)
(17)
式中,n为GPS点的个数,Δi为第i个GPS点的几何定位误差,i=1, 2, …, n。
| 影像编号 | 检查点个数 | 定标前几何精度/m | ||
| 距离向 | 方位向 | 平面 | ||
| 630_4 | 11 | 3.967 | 2.686 | 4.791 |
| 756_1 | 6 | 6.899 | 1.693 | 7.104 |
| 986_1 | 7 | 20.400 | 381.378 | 381.923 |
| 756_3 | 5 | 71.151 | 464.520 | 469.938 |
| 756_2 | 9 | 69.840 | 463.826 | 469.055 |
| 370_2 | 7 | 5.705 | 2.240 | 6.129 |
| 785_0 | 7 | 26.172 | 6.173 | 26.890 |
| 570_0 | 5 | 19.931 | 114.569 | 116.290 |
| 048_0 | 8 | 20.969 | 113.488 | 115.409 |
| 371_0 | 11 | 24.561 | 109.149 | 111.878 |
| 498_0 | 6 | 22.997 | 106.984 | 109.428 |
由表 1、表 2可知,不同平台下数据产品的几何定位精度存在较大差异,例如630_4景TSX影像的几何定位精度为4.791 m,而570_0景GF-3影像的几何定位精度为116.290 m。且同平台下数据产品的几何定位精度也有较大差异,例如756_1景TSX影像的几何定位精度为7.104 m,而986_1景TSX影像的几何定位精度为381.923 m。传统几何定标方法通常基于单景影像进行参数标定,然后利用参数改正量标定同平台下的其他影像,但本文试验中对于同平台、不同平台的数据产品,参数改正量均不具备继承性,此时传统定标方法将不再适用。
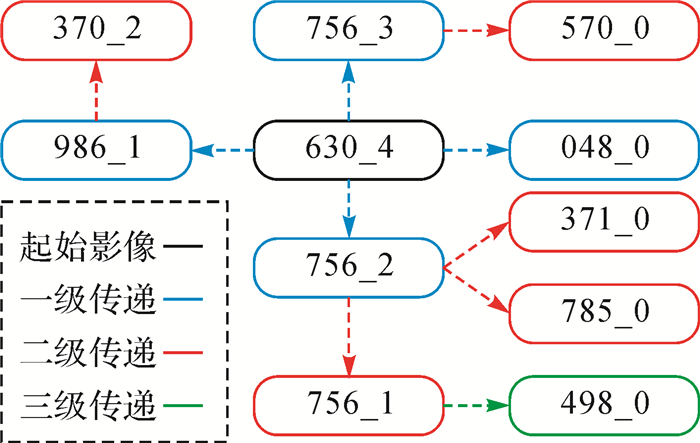
2.2.1 试验1:稀少控制的多平台星载SAR联合几何定标根据本文方法对11景SAR影像进行联合几何定标试验。选择630_4景影像为起始主影像,并从中选取5个GPS点作为控制点,从该景影像出发提取主、从影像之间的连接点,利用连接点对从影像进行几何定标,定标后的从影像将作为下一级传递的主影像,以此类推,逐级传递标定每景影像Δt、Δr两个定标参数的改正量。影像之间的传递关系如图 4所示。当全部影像定标完成后,再次使用间接几何定位算法对定标后的SAR影像进行几何精度评价,见表 3。
|
| 图 4 影像传递关系 Fig. 4 Transfer relation of images |
| 影像编号 | 检查点个数 | 定标参数改正量 | 定标后几何精度/m | ||||
| Δt/ms | Δr/m | 距离向 | 方位向 | 平面 | |||
| 630_4 | 11 | -0.435 | -3.527 | 0.958 | 1.908 | 2.135 | |
| 756_1 | 6 | -0.548 | -7.664 | 1.605 | 2.388 | 2.877 | |
| 986_1 | 7 | 53.901 | -21.190 | 1.343 | 1.951 | 2.369 | |
| 756_3 | 5 | -65.919 | 71.004 | 1.159 | 2.280 | 2.558 | |
| 756_2 | 9 | -66.004 | 69.955 | 1.237 | 2.137 | 2.469 | |
| 370_2 | 7 | -0.444 | -6.792 | 1.370 | 2.148 | 2.548 | |
| 785_0 | 7 | -0.030 | -25.189 | 3.524 | 6.319 | 7.235 | |
| 570_0 | 5 | -17.582 | -20.827 | 2.673 | 5.479 | 6.096 | |
| 048_0 | 8 | -17.349 | -19.092 | 2.717 | 5.581 | 6.207 | |
| 371_0 | 11 | -16.069 | -20.954 | 4.371 | 4.091 | 5.987 | |
| 498_0 | 6 | -16.438 | -19.268 | 4.143 | 5.767 | 7.101 | |
由表 3可知,几何定标后TSX/TDX影像的几何定位精度优于3 m,GF-3影像的几何定位精度优于7.5 m,SAR影像在定标后可实现高精度几何定位。在暂不考虑几何定标精度的情况下,传统几何定标方法每景SAR影像至少需要1个控制点才能完成几何定标,而本文的11景影像只采用了5个控制点即实现了高精度几何定标,控制点数量极少,属于“稀少控制”,且控制点集中分布于同一景SAR影像(630_4)中,避免了大范围的野外测量作业。整体来看,除起始主影像外,其他影像的几何定标过程均未使用控制点,这为实现SAR影像在无控制点或稀少控制点情况下的大范围、多场景几何定标提供了思路。此外,试验数据的几何定位精度在定标前存在较大差异,传统的几何定标方法将不再适用,而本文方法可最大限度地屏蔽不同卫星平台的影响,因此该方法具有较好的通用性。
几何定标后不同平台下SAR影像的几何定位精度仍存在一定的差距,GF-3平台下的几何定位精度明显低于TSX/TDX平台。对不同平台下影像的几何定位精度进行统计并求均值,可知TSX、TDX和GF-3影像对应的几何定位精度均值分别为2.460 m、2.525 m和6.525 m,其中TSX与TDX影像的几何定位精度相差不大,而GF-3影像相比于二者则有较大差距。造成这种差距的原因主要有两方面:其一,GF-3影像的分辨率低于TSX和TDX影像,这对影像刺点和连接点匹配的精度均有一定的影响。一般来说,分辨率较高的影像更有利于实现高精度的几何定标;其二,TDX作为TSX的姊妹星,二者在系统参数和成像等方面都比较相近,其几何定位精度也大致相当。但由于我国SAR卫星起步相对较晚,GF-3卫星的几何定位精度与TSX、TDX相比仍有一定差距,虽然几何定标技术可以大幅度提高影像的几何定位精度,但仍受限于平台自身的性能。
由于几何定标后TSX和TDX影像的几何定位精度相差不大,现结合二者分析不同级传递对几何定标结果的影响。按照传递关系选取两组数据:第一组,依次选取影像630_4、986_1、370_2,其几何定标后的几何定位精度分别为2.135 m、2.369 m、2.548 m;第二组,依次选取影像630_4、756_2、756_1,其几何定标后的几何定位精度分别为2.135 m、2.469 m、2.877 m。可以看出,影像的几何定位精度随着逐级传递而依次降低,这是由于每一级影像的几何定标都必然存在一定的误差,而逐级定标的过程使得误差不断的传播和累积,导致定标后影像的几何定位精度逐渐降低。因此,当影像数量较多时,应合理地设计影像之间的传递关系,尽量使传递级别处于相对较低的水平,以确保整体可以达到较好的几何定标精度。
试验区域内兼有平原和高山地,为了分析不同高程对几何定标结果的影响,现统计3组定标后影像的几何定位精度。同时,考虑到不同级传递对几何定标精度会有影响,因此每组影像需保证处于相同的传递级别。第1组,选取一级传递TSX/TDX影像756_2、756_3,其平均高程分别为32.110 m、448.793 m,几何定位精度分别为2.469 m、2.558 m;第2组,选取二级传递GF-3影像371_0、570_0,其平均高程分别为32.089 m、489.643 m,几何定位精度分别为5.987 m、6.096 m;第3组,选取二级传递TSX/TDX影像756_1、370_2,其平均高程分别为9.464 m、282.103 m,几何定位精度分别为2.877 m、2.548 m。可以看出,每组数据中的平均高程相差较大,但定标后的几何定位精度相差较小,差值均小于0.5 m。就本文而言,不同地形条件对几何定标结果的影响主要归因于STRM在不同地形条件下的高程精度差异,SRTM的高程精度越高,则连接点的大地坐标越精确,对应的几何定标精度也会相应提高。一般而言,高山地条件下的SRTM高程精度低于平原地区,但由图 3可知在高山地条件下包含分布于较平坦区域的影像连接点,在平原条件下也包含分布于较陡峭地区的连接点,这在一定程度上抵消了SRTM在不同地形条件下的高程精度差异,因此不同地形条件对几何定标结果的影响不大。
传统几何定标方法一般选取角反射器作为参考控制目标。角反射器具有极强的后向散射能量,从而可被准确地识别出来,其识别精度一般可达到亚像素级。而试验中所有GPS点的影像坐标均通过人工转刺得到,该过程存在刺点误差,这对SAR影像的几何定标以及精度评价都有一定的消极影响。此外,试验所采用的外部DEM分辨率较低,对几何定标也存在一定影响(将在试验2中进行讨论),但并不影响采用相同DEM进行多景SAR影像几何定标的结果比较。
2.2.2 试验2:外部数据对几何定标精度的影响在获取连接点大地坐标的过程中需要使用到外部DEM数据,DEM质量的好坏决定了连接点大地坐标的精度,这对后续几何定标的精度也会产生影响。为确保本文方法的通用性,DEM选用了获取免费、覆盖范围广、精度较高的SRTM数据。如果使用更高精度、更高分辨率的DEM数据,则本文的几何定标精度可能会进一步提高。为对该问题进行研究,试验过程中使用TanDEM-XCoSSC数据生产了三景高精度DEM(TanDEM DEM),其分辨率为12 m,覆盖范围分别对应影像756_2、756_1和370_2。使用GPS点对三景TanDEMDEM和对应区域SRTM进行精度评价。经比较,TanDEM DEM的高程精度(≈2 m)比SRTM高约30%。使用TanDEM DEM作为外部DEM数据进行几何定标,定标后的精度评价见表 4。
| 影像编号 | 检查点个数 | 定标后几何精度/m | ||
| 距离向 | 方位向 | 平面 | ||
| 756_2 | 9 | 1.348 | 1.524 | 2.035 |
| 756_1 | 6 | 1.333 | 2.151 | 2.531 |
| 370_2 | 7 | 1.458 | 1.943 | 2.429 |
由表 4可知,采用更高精度、更高分辨率的TanDEM DEM数据进行几何定标,756_2、756_1和370_2景影像的几何定位精度分别提高了0.434 m、0.346 m和0.119 m。证明高精度、高分辨率的DEM数据有利于实现更高的几何定标精度。
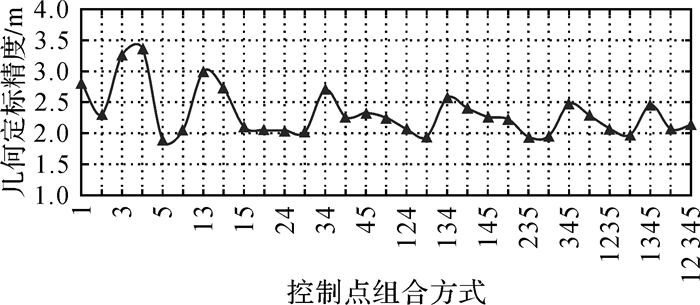
另一方面,本文基于5个控制点对多景SAR影像进行几何定标,这5个控制点大致分布于630_4景影像的4个角点(N1~N4)和中心点(N5),点位分布及编号如图 3所示。控制点的数量可能会对几何定标精度产生影响,现对该问题进行研究。首先,从5个控制点中依次选取1~5个控制点进行组合,共有31种组合方式(C51+C52+C53+C54+C55);然后,使用组合后的控制点对630_4景影像进行几何定标;最后,使用11个GPS检查点进行几何定标精度评价,如图 5所示。
|
| 图 5 不同控制点组合方式下的几何精度评价 Fig. 5 Accuracy evaluation of different GCP combinations |
由图 5可知,当使用N3或N4号单个控制点进行几何定标时定标精度较低,而后续几何定标精度相对较差的控制点组合方式(如13、14、34、134、345、1345)均与N3或N4号控制点相关,说明精度较差的控制点不利于实现高精度的几何定标。同时也应注意到,控制点组合方式下的几何定标精度优于单独使用N3或N4号控制点,说明当多个控制点进行组合时,高精度的控制点会在一定程度上弥补低精度的控制点,从而降低个别精度较低的控制点对最终几何定标结果的干扰。当使用1~2个控制点时,几何定标精度变化较大,精度差值最大可达到1.5 m左右;当使用3~5个控制点时,几何定标精度趋于稳定,精度差值可控制在0.5 m左右。因此,建议使用3~5个控制点进行几何定标,通过增加多余观测以降低低精度控制点的干扰,保证几何定标精度的稳定性和可靠性。
3 结论随着国产SAR卫星的陆续发射,迫切需要对星载SAR几何定标技术进行深入研究,实现国产星载SAR影像的高精度几何定位,推进国产星载SAR的实用化。本文基于R-D几何定位模型,分析了几何定位精度的影响因素,建立了几何定标模型。在此基础上,提出了一种稀少控制的多平台星载SAR联合几何定标方法,使用3景TerraSAR-X、3景TanDEM-X、5景高分三号影像进行几何定标试验,并利用82个GPS点进行精度评价。结果表明定标后TSX/TDX影像的几何定位精度优于3 m,GF-3影像的几何定位精度优于7.5 m,提高了多源SAR影像的几何定位能力,在实际数据处理和应用中具有参考价值,尤其是对后续做多场景的DOM或DEM融合等都具有实际意义。此外,本文依然有诸多问题有待进一步研究,例如在逐级定标过程中如何对传播误差进行约束和改正;由于卫星左右视角不同,导致升降轨影像之间存在一定的几何畸变,特别是在山区,如何减小畸变对连接点匹配所造成的影响。后续研究工作将主要从这两方面展开,为本文的多平台联合几何定标研究提供更有利的支撑。
致谢: 特别感谢德国宇航中心提供的TerraSAR-X、TanDEM-X数据(CAL_VAL6993)。
| [1] | MOHR J J, MADSEN S N. Geometric Calibration of ERS Satellite SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(4): 842–850. DOI:10.1109/36.917909 |
| [2] | SHIMADA M, ISOGUCHI O, TADONO T, et al. PALSAR Radiometric and Geometric Calibration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 3915–3932. DOI:10.1109/TGRS.2009.2023909 |
| [3] | ZHOU Xiao, ZENG Qiming, JIAO Jian, et al. Field Calibration and Validation of Radarsat-2[C]//Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium. Melbourne, VIC, Australia: IEEE, 2013: 4451-4454. |
| [4] | EINEDER M, MINET C, STEIGENBERGER P, et al. Imaging Geodesy:Toward Centimeter-level Ranging Accuracy with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 661–671. DOI:10.1109/TGRS.2010.2060264 |
| [5] | CONG Xiaoying, BALSS U, EINEDER M, et al. Imaging Geodesy:Centimeter-level Ranging Accuracy with TerraSAR-X:An Update[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 948–952. DOI:10.1109/LGRS.2012.2187042 |
| [6] |
周晓, 曾琪明, 焦健.
TerraSAR-X传感器定标精度及其应用分析[J]. 遥感信息, 2014, 29(2): 33–37.
ZHOU Xiao, ZENG Qiming, JIAO Jian. Analysis of TerraSAR-X Sensor Calibration Accuracy and Its Application[J]. Remote Sensing Information, 2014, 29(2): 33–37. |
| [7] | SCHWERDT M, BRÄUTIGAM B, BACHMANN M, et al. Efficient Calibration and First Results of TerraSAR-X[C]//Proceedings of the Advanced SAR Workshop. Vancouver, Canada: CSA, 2007. |
| [8] | SCHWERDT M, BRAUTIGAM B, BACHMANN M, et al. Final TerraSAR-X Calibration Results Based on Novel Efficient Methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 677–689. DOI:10.1109/TGRS.2009.2035308 |
| [9] |
张庆君.
高分三号卫星总体设计与关键技术[J]. 测绘学报, 2017, 46(3): 269–277.
ZHANG Qingjun. System Design and Key Technologies of the GF-3 Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 269–277. DOI:10.11947/j.AGCS.2017.20170049 |
| [10] |
丁赤飚, 刘佳音, 雷斌, 等.
高分三号SAR卫星系统级几何定位精度初探[J]. 雷达学报, 2017, 6(1): 11–16.
DING Chibiao, LIU Jiayin, LEI Bin, et al. Preliminary Exploration of Systematic Geolocation Accuracy of GF-3 SAR Satellite System[J]. Journal of Radars, 2017, 6(1): 11–16. |
| [11] |
张红敏, 靳国旺, 徐青, 等.
利用单个地面控制点的SAR图像高精度立体定位[J]. 雷达学报, 2014, 3(1): 85–91.
ZHANG Hongmin, JIN Guowang, XU Qing, et al. Accurate Positioning with Stereo SAR Images and One Ground Control Point[J]. Journal of Radars, 2014, 3(1): 85–91. |
| [12] | BROWN W M. Synthetic Aperture Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1967, AES-3(2): 217–229. DOI:10.1109/TAES.1967.5408745 |
| [13] | LEBERL F. Radargrammetry for Image Interpretation[M]. Enschede: ITC, 1978. |
| [14] | WU S S C, SCHAFER F J, HOWINGTON-KRAUS A. Mapping Accuracy Using Side-looking Radar Images on the Analytical Stereoplotter[C]//Proceedings of the 16th International Society for Photogrammetry and Remote Sensing Conference. Kyoto: ISPRS, 1988: 474-480. |
| [15] |
张过, 费文波, 李贞, 等.
用RPC替代星载SAR严密成像几何模型的试验与分析[J]. 测绘学报, 2010, 39(3): 264–270.
ZHANG Guo, FEI Wenbo, LI Zhen, et al. Analysis and Test of the Substitutability of the RPC Model for the Rigorous Sensor Model of Spaceborne SAR Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 264–270. |
| [16] |
程春泉, 张继贤, 邓喀中, 等.
雷达影像几何构像距离-共面方程[J]. 遥感学报, 2012, 16(1): 38–49.
CHENG Chunquan, ZHANG Jixian, DENG Kazhong, et al. Range-coplanarity Equation for Radar Geometric Imaging[J]. Journal of Remote Sensing, 2012, 16(1): 38–49. |
| [17] |
陈继伟, 曾琪明, 焦健, 等.
利用轨道参数修正的无控制点星载SAR图像几何校正方法[J]. 测绘学报, 2016, 45(12): 1434–1440.
CHEN Jiwei, ZENG Qiming, JIAO Jian, et al. Spaceborne SAR Image Geometric Rectification Method without Ground Control Points Using Orbit Parameters Modulation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1434–1440. DOI:10.11947/j.AGCS.2016.20160182 |
| [18] |
杨书成. 合成孔径雷达立体测图技术与方法[D]. 武汉: 武汉大学, 2006. YANG Shucheng. Technique and Method on Synthetic Aperture Radar Stereoplotting[D]. Wuhan: Wuhan University, 2006. |
| [19] | CURLANDER J C, MCDONOUGH R N. Synthetic Aperture Radar:Systems and Signal Processing[M]. New York, NY: John Wiley & Sons, 1991. |
| [20] |
曹鹏志, 顾建政, 许荣庆, 等.
星载SAR姿态误差及偏航调整对多普勒特性的影响[J]. 哈尔滨工业大学学报, 1999, 31(1): 39–42.
CAO Pengzhi, GU Jianzheng, XU Rongqing, et al. Effect of Spaceborne SAR Attitude Errors and Yaw Steering on the Doppler Characteristics[J]. Journal of Harbin Institute of Technology, 1999, 31(1): 39–42. |
| [21] |
陈尔学. 星载合成孔径雷达影像正射校正方法研究[D]. 北京: 中国林业科学研究院, 2004. CHEN Erxue. Study on Ortho-rectification Methodology of Space-Borne Synthetic Aperture Radar Imagery[D]. Beijing: Chinese Academy of Forestry, 2004. http://cdmd.cnki.com.cn/Article/CDMD-82201-2005030713.htm |
| [22] | OLLER G, ROGNANT L, MARTHON P. Correlation and Similarity Measures for SAR Image Matching[C]//Proceedings of the SPIE SAR Image Analysis, Modeling, and Techniques Ⅵ. Barcelona, Spain: SPIE, 2004, 5236(2): 182-190. |
| [23] | HANSSEN R F. Radar Interferometry:Data Interpretation and Error Analysis[M]. Kluwer: Springer, 2001. |



