2. 西安测绘研究所, 陕西 西安 710054
2. Xi'an Institute of Surveying and Mapping, Xi'an 710054, China
卫星摄影测量中,利用星敏感器和Global Navigation Satellite System测定的外方位元素初值(位置和姿态数据),是影响卫星影像几何定位精度的重要因素[1-6]。外方位元素的精度, 不仅取决于姿态和轨道测定系统的精度, 在实际卫星工程中, 还与卫星平台稳定度密不可分。因此,地面数据处理所使用的外方位元素数据中也含有随卫星平台稳定度变化的误差项,共同影响卫星影像的上下视差和定位精度[7-8]。光束法平差是实现线阵卫星影像无控定位的有效途径之一[9-11],对于线阵影像而言,精确求解每一线阵影像对应的外方位元素是难以实现的。卫星在轨飞行中,平台通常具有较好的稳定性,可将平差航线离散为若干摄影时刻,平差时只求解一定时刻的外方位元素,如定向片法或等效框幅相片(简称EFP)法[12-13]。定向时刻(或EFP时刻)之间的外方位元素,采用多项式内插获得[14]。为了加强平差中各三角锁的连接条件,文献[13]提出外方位元素平滑条件,带权参与EFP光束法平差计算,其权值根据理论分析和经验确定后,固定在平差模型中。
通常,外方位元素观测值变化较为平稳, 可用特定的样条函数拟合[15]。在实际卫星工程中,外方位元素观测值会发生突变现象,且无规律性。如对天绘一号卫星在轨数据分析发现,处理航线中存在同名像点上下视差突变现象。立体影像上下视差主要由外方位元素高频误差及像点量测误差引起[16]。当卫星姿态测定系统发生突然较大变化时,会使外方位元素的观测值发生与整体变化趋势不一致的跳变,直接导致该拐点附近的立体影像上下视差存在突变现象。本文根据天绘一号卫星在轨实际运行状况,在全三线交会EFP光束法平差理论基础上[17],提出外方位元素自适应分段平滑策略及其数学模型。首先,根据平差航线立体影像的上下视差变化情况,对平差航线的立体影像进行自动分段;在此基础上,对不同段的平滑条件赋予不同权值,共同参与全三线交会EFP光束法平差。为了验证本文提出方法的正确性和可行性,利用天绘一号卫星影像进行了相关试验。
1 EFP光束法平差数学模型全三线交会EFP光束法平差的基本思路是根据EFP时刻,建立一系列空中三角锁,采用后方交会与前方交会交替迭代计算的方式。在全三线交会EFP光束法平差中, 正视影像上像点按一定规则分布, 即垂直于飞行方向按上、中、下三排分布[18],平行于飞行方向定向点和连结点间距离约10 km,如图 1所示(为了显示方便,将航线逆时针旋转90°)。根据平差航线立体影像的上下视差差分情况,对平差航线的立体影像进行自动分段,对不同段的外方位元素平滑条件方程赋予不同权值,将离散的各条空中三角锁的外方位元素联系为整体,进行外方位元素整体求解。

|
| 图 1 定向点和联结点分布 Fig. 1 Distribution of orientation points and tie points |
1.1 上下视差一阶差分
由于外方位元素观测值受星敏感器、GNSS及卫星平台稳定度等多种因素制约,单独分析星敏感器数据或GNSS数据,无法有效确定引起变化的误差源和变化时间段,但这些误差数据最终反映在立体影像的上下视差变化中。在EFP光束法平差中,定向点(或连接点)上、中、下3点并不要求严格在同一摄影时刻,即同一条线阵影像上。但参与平差的像点需等效到EFP时刻的框幅坐标,上、中、下3点的等效像点上下视差,反映了在该EFP时刻外方位元素的变化情况。因此,以上下视差数据为依据,分析外方位元素变化情况。对立体影像的上下视差进行一阶差分,其数学模型如下
 (1)
(1)
式中, Dpyi为上下视差一阶差分值;n为同名像点的个数;pyi为根据初始外方位元素观测值计算出的上下视差。根据式(1)可计算出平差航线中上下视差一阶差分值。当在某段影像上下视差一阶差分值变化较大时(大于均值的3倍),光束法平差中对该段外方位元素平滑方程的权值应有所调整。
1.2 外方位元素分段平滑模型在卫星平台平稳运行时,外方位元素变化比较小,此时赋予统一权值的外方位元素平滑方程参与平差计算,能较大改善三角锁间的连接条件[13]。当卫星平台稳定度发生较大变化时,直接反映在外方位元素变化趋势中。此时,平差航线中不同段的平滑方程应赋于不同权值。若通过上下视差一阶差分得出,m至m+1段差分值变化较大时,可将整条航线分段为3段,建立平滑条件并赋于不同权值,如下式
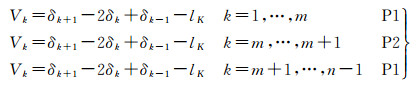 (2)
(2)
式中,Vk为外方位元素余差;δk为外方位元素改正值,lk=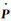
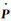
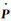
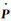
试验数据采用天绘一号03星2015年12月18日和2016年4月3日摄影数据,包括上下视差变化平稳和发生突变两种情况。2015年12月18日摄影影像长度约220 km,2016年4月3日摄影影像长度约170 km。通过对立体影像同名像点的上下视差数据差分计算,其统计结果如表 1所示,分布如图 2所示。
| 像素 | ||||||||||||||||
| 摄影时间 | Dpyi | |||||||||||||||
| 2015-12-18 | 0.3 | -0.7 | 0.3 | -0.5 | -0.07 | -0.6 | 0.09 | 3 | 0.08 | 0.1 | 0.4 | 1 | 0.07 | 0.9 | 0.1 | -0.5 |
| 2016-04-03 | -0.1 | -0.6 | 0.6 | 0.7 | -0.7 | -1 | -0.8 | 0.7 | 0.2 | -0.9 | 1 | -0.6 | -0.005 | 0.1 | -0.5 | 0.9 |
| 注:表中每隔10 km统计。 | ||||||||||||||||
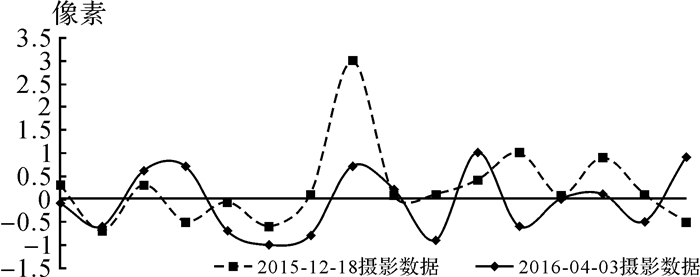
|
| 图 2 上下视差一阶差分分布 Fig. 2 Distribution of first-order difference of vertical parallax |
从表 1和图 2看出,上下视差经一阶差分后,总体变化比较平稳。其中,2016年4月3日影像上下视差差分数据变化均在-1和1范围内,2015年12月18日影像数据中大部分变化也在-1和1间,但该航线段中出现上下视差变化异常情况,一阶差分达到3个像素,超出了正常变化值的3倍。上下视差主要由外方位元素高频误差及像点量测误差引起,一阶差分值达到3个像素,主要系该时间段的外方位元素发生突变造成。外方位元素变化是由定轨、定姿数据及卫星平台稳定度等综合因素影响的结果,对于此类异常航线数据,在全三线交会EFP光束法平差中对外方位元素平滑方程中权值进行调整。为此,研发具有外方位元素平滑方程权值自适应调整功能的全三线交会EFP光束法平差软件(以下简称自适应EFP光束法平差软件),实现对外方位元素突变数据的特殊处理。
2.2 分段平差后的精度检测为了验证本文提出外方位元素平滑方程自适应EFP光束法平差理论的正确性,利用天绘一号03星2015年12月18日和2016年4月3日摄影数据进行无地面控制点条件下两种方式的EFP光束法平差,即外方位元素平滑方程中固定权值和自适应权值调整。最后利用已知地面控制点作为检查点,对平差后影像的定位精度进行分析,其统计结果如表 2所示。
| 摄影时间 | 权值固定/m | 权值自适应调整/m | 检查点数量 | |||||||
| μX | μY | μh | μp | μX | μY | μh | μp | |||
| 2015-12-18 | 6.7 | 5.7 | 6.1 | 8.7 | 6.2 | 5.6 | 4.3 | 7.8 | 30 | |
| 2016-04-03 | 3.5 | 3.8 | 2.6 | 5.2 | 3.5 | 3.8 | 2.6 | 5.2 | 30 | |
表 2中,μX为X方向的均方根误差;μY为Y方向的均方根误差;μp为水平位置的均方根误差;μh为垂直高程的均方根误差[19]。
从表 1看出,2016年4月3日数据上下视差一阶差分变化较小,在光束法平差中,外方位元素平滑方程固定权值和自适应权值调整两种方式定位精度相同,表明在自适应权值调整中,权值未发生变化,即权值固定。当上下视差一阶差分发生突变时(如2015年12月18日摄影数据),在光束法平差中外方位元素平滑方程权值自适应调整后,定位精度有明显提高,其中高程精度从6.1 m提高至4.3 m,验证了自适应EFP光束法平差软件功能的正确性。
2.3 分段平差方法的适应性检测天绘一号03星地面影像全三线交会EFP平差中,已增加外方位元素平滑方程权值自适应调整功能。在相机参数在轨标定数据基础上[20],对03星获取的国内外5条航线进行无地面控制点条件下新全三线交会EFP光束法平差,平差后定位精度如表 3所示。
| 摄影时间 | 全三线交会EFP平差后/m | 检查点数量 | |||
| μX | μY | μh | μp | ||
| 2015-10-30(国外地区) | 1.4 | 6.5 | 1.9 | 6.7 | 7 |
| 2015-11-08(国外地区) | 4.4 | 4.8 | 2.5 | 6.5 | 24 |
| 2015-11-12(国外地区) | 3.8 | 4.2 | 2.4 | 5.7 | 8 |
| 2015-12-18(国外地区) | 6.2 | 5.6 | 4.3 | 7.8 | 30 |
| 2016-02-14(国内地区) | 5.8 | 4.9 | 2.6 | 7.5 | 5 |
| 5个区平均值 | 4.3 | 5.2 | 2.7 | 6.9 | |
天绘一号01、02星定位精度达到平面10.3 m、高程5.7 m[21]。利用外方位元素平滑方程权值固定的光束法平差对2015年12月18日摄影数据处理后,高程精度为6.1 m(表 2),其高程精度对于5.7 m高程中误差是可以接受的。即上下视差一阶差分突变情况,对6 m精度要求的高程影响有限,其值在误差统计范围内。但随着03星采用双频GPS接收机、光束法平差软件适应性改造后,定位精度有较大改善。初步定位精度检测,平面精度为7.2 m,高程精度为2.6 m[22]。当要求高程精度在3 m时,上下视差一阶差分突变现象需引起重视,并加以处理。5条摄影数据中,仅2015年12月18日摄影数据上下视差发生突变,经过权值调整后,其高程精度为4.3 m。从误差统计区间分析,对于高程精度3 m中误差而言,其最大误差应为4.9 m(90%置信区间)[23],4.3 m在最大误差范围内。因此,03星定位精度统计中,即使该摄影航线定位精度不佳,仍应参与最终的误差统计。
3 结论摄影测量卫星工程是系统且复杂的工程,卫星平台及各类有效载荷的误差最终反映在外方位元素和影像中[24-25],地面影像处理中要针对卫星在轨运行状况,分析异常数据的处理。通过对天绘一号在轨数据分析表明,卫星在轨飞行中,姿态测定系统受平台稳定度影响会发生突变。虽然出现频率低(约占5%),但无规律可循,影响无控定位精度。因此,本文提出光束法平差中外方位元素自适应分段平滑策略及其处理方法,根据航线段内上下视差变化情况,对平差航线进行自动分段,对不同段的外方位元素平滑方程赋予不同权值,共同参与光束法平差,有效保证了影像的定位精度及其精度的一致性。
| [1] |
王之卓.
摄影测量原理[M]. 北京: 测绘出版社, 1990.
WANG Zhizhuo. Principle of Photogrammetry[M]. Beijing: Publishing House of Surveying and Mapping, 1990. |
| [2] |
唐新明, 张过, 祝小勇, 等.
资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191–198.
TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191–198. |
| [3] | KOCAMAN S, WOLFF K, GRUEN A, et al. Geometric Validation of Cartosat-1 Imagery[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: ISPRS, 2008: 1363-1368. |
| [4] | TADONO T, SHIMADA M, HASHIMOTO T, et al. Results of Calibration and Validation of Alos Optical Sensors, and Their Accuracy Assesments[C]//Proceedings of 2007 IEEE International Geoscience and Remote Sensing Symposium. Barcelona: IEEE, 2007: 3602-3605. |
| [5] | BOUILLON A, BRETON E, DE LUSSY F, et al. SPOT5 Geometric Image Quality[C]//Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium. Toulouse: IEEE, 2003: 303-305. |
| [6] | GRUEN A, KOCAMAN S. Optical Sensors High Resolution: Geometry Validation Methodology[R]. RFQ/3-11780/06/I-OL, Zurich, Switzerland: Institute of Geodesy and Photogrammetry, 2008. |
| [7] |
王任享, 王建荣, 胡莘.
光学卫星摄影无控定位精度分析[J]. 测绘学报, 2017, 46(3): 332–337.
WANG Renxiang, WANG Jianrong, HU Xin. Analysis of Location Accuracy Without Ground Control Points of Optical Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 332–337. DOI:10.11947/j.AGCS.2017.20160650 |
| [8] |
王任享, 王建荣.
无地面控制点卫星摄影测量探讨[J]. 测绘科学, 2015, 40(2): 3–12.
WANG Renxiang, WANG Jianrong. Discussion on Satellite Photogrammetry Without Ground Control Point[J]. Science of Surveying and Mapping, 2015, 40(2): 3–12. DOI:10.16251/j.cnki.1009-2307.2015.02.001 |
| [9] | EBNER H, KORNUS W, OHLHOF T, et al. Orientation of MOMS-02/D2 and MOMS-2P/PRIRODA Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(5-6): 332–341. DOI:10.1016/S0924-2716(99)00034-9 |
| [10] |
王任享.
卫星三线阵CCD影像光束法平差研究[J]. 武汉大学学报(信息科学版), 2003, 28(4): 379–385.
WANG Renxiang. Bundle Adjustment of Satellite Borne Three-line Array CCD Image[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 379–385. |
| [11] |
张永军, 郑茂腾, 王新义, 等.
"天绘一号"卫星三线阵影像条带式区域网平差[J]. 遥感学报, 2012, 16(S1): 84–89.
ZHANG Yongjun, ZHENG Maoteng, WANG Xinyi, et al. Strip-based Bundle Adjustment of Mapping Satellite-1 Three-line Array Imagery[J]. Journal of Remote Sensing, 2012, 16(S1): 84–89. DOI:10.11834/jrs.20120017 |
| [12] | HOFMANN O. The Stereo-push-broom Scanner System DPS and Its Accuracy[C]//International Geoscience and Remote Sensing Symposium. Rovaniemi: IEEE, 1986: 21-28. |
| [13] |
王任享.
三线阵CCD影像卫星摄影测量原理[M]. 北京: 测绘出版社, 2016.
WANG Renxiang. Satellite Photogrammetric Principle for Three-line-array CCD Imagery[M]. Beijing: Publishing House of Surveying and Mapping, 2016. |
| [14] |
王兴涛, 李迎春, 李晓燕.
"天绘一号"卫星星敏感器精度分析[J]. 遥感学报, 2012, 16(S1): 90–93.
WANG Xingtao, LI Yingchun, LI Xiaoyan. Mapping Satellite-1 Star Sensor Accuracy Analysis[J]. Journal of Remote Sensing, 2012, 16(S1): 90–93. DOI:10.11834/jrs.20120018 |
| [15] | SULTAN K. Sensor Modeling and Validation for Linear Array Aerial and Satellite Imagery[D]. Istanbul: Middle East Technical University, 2008. http://dx.doi.org/10.3929/ethz-a-005780510 |
| [16] | POLI D. Modelling of Spaceborne Linear Array Sensors[D]. Zurich: Switzerland: Swiss Federal Institute of Technology, 2005. http://ci.nii.ac.jp/naid/10024353493 |
| [17] |
王任享, 王建荣, 胡莘.
EFP全三线交会光束法平差[J]. 武汉大学学报(信息科学版), 2014, 39(7): 757–761.
WANG Renxiang, WANG Jianrong, HU Xin. The EFP Bundle Adjustment of All Three Line Intersection[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 757–761. |
| [18] | WANG Jianrong, WANG Renxiang, HU Xin, et al. The On-orbit Calibration of Geometric Parameters of the Tian-Hui 1(TH-1) Satellite[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 124(1): 144–151. |
| [19] |
杨元喜.
卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646–650.
YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646–650. |
| [20] |
王任享, 王建荣, 胡莘.
LMCCD相机影像摄影测量首次实践[J]. 测绘学报, 2014, 43(3): 221–225.
WANG Renxiang, WANG Jianrong, HU Xin. Photogrammetry Practice for the First Time of LMCCD Camera Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 221–225. DOI:10.13485/j.cnki.11-2089.2014.0032 |
| [21] |
王任享, 胡莘, 王建荣.
天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42(1): 1–5.
WANG Renxiang, HU Xin, WANG Jianrong. Photogrammetry of Mapping Satellite-1 Without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 1–5. |
| [22] |
王任享, 王建荣, 胡莘.
天绘一号03星定位精度初步评估[J]. 测绘学报, 2016, 45(10): 1135–1139.
WANG Renxiang, WANG Jianrong, HU Xin. Preliminary Location Accuracy Assessments of 3rd Satellite of TH-1[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1135–1139. DOI:10.11947/j.AGCS.2016.20160373 |
| [23] | DOWMAN I, JACOBSEN K, KONECNY G, et al. High Resolution Optical Satellite Imagery[M]. Dunbeath: Whittles Publishing, 2012. |
| [24] |
王任享, 王建荣, 胡莘.
卫星摄影姿态测定系统低频误差补偿[J]. 测绘学报, 2016, 45(2): 127–130.
WANG Renxiang, WANG Jianrong, HU Xin. Low-Frequency Errors Compensation of Attitude Determination System in Satellite Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 127–130. DOI:10.11947/j.AGCS.2016.20150167 |
| [25] |
李德仁, 王密.
"资源三号"卫星在轨几何定标及精度评估[J]. 航天返回与遥感, 2012, 33(3): 1–6.
LI Deren, WANG Mi. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 1–6. |


