2. 中国科学院光电研究院, 北京 100094
2. Academy of Opto-electronics, Academy of Sciences, Beijing 100094, China
全球卫星导航系统(global navigation satellite system,GNSS)已开始播发多频信号,这为提升模糊度解算性能提供了契机。目前,围绕是否利用卫星几何信息,多频模糊度解算(multi-carrier ambiguity resolution,MCAR)方法[1-4]可以划分两种模型:几何无关(geometry-free,GF)模型与几何相关(geometry-based,GB)模型[5-6]。传统GF模型通过测距一致性原则消除了几何距离、对流层延迟等影响,但并未顾及电离层延迟影响,使得该模型仅能适用于电离层活动平静的短基线领域[7-8]。为了削弱电离层延迟影响,出现了几何无关-弱电离层(geometry-free and ionosphere-reduced,GF-IR)与几何无关-消电离层(geometry-free and ionosphere-free,GF-IF)模型的研究[9-11]。这两种模型在超宽巷/宽巷组合中,凭借波长噪声比的优势,取得较高的模糊度解算可靠性[12]。但对于窄巷组合而言,存在波长较短以及误差抑制能力弱等不利因素,使得现有的两种模型方法还不能很好地处理电离层延迟对窄巷模糊度解算可靠性的影响[4-5]。另外,GF模型没有充分利用几何约束信息,也是导致该模型的模糊度解算可靠性不高的主要因素之一[12]。
充分利用几何约束信息的GB模型在MCAR中得到了广泛的研究[4]。与GF模型相类似,电离层延迟依然是影响GB模型的主要误差源之一。为此,文献[4]提出通过构造几何相关-弱电离层(geometry-based and ionosphere-reduced,GB-IR)模型来削弱电离层延迟的影响,但是模型所残余的电离层延迟分量将会成为影响模糊度解算可靠性的潜在威胁。文献[12-13]开展了基于GB模型的倾斜电离层延迟估计算法研究,其目的是补偿电离层延迟分量。但考虑到电离层具有时空不规律特性[14],使得电离层随机模型的先验参数难以准确描述,导致参数估计性能降低,从而直接影响模糊度解算与定位性能。目前看来,在解决电离层延迟方面,考虑到弱电离层或者电离层延迟估计方法所受到的限制,一种可行的手段是构造几何相关-消电离层(geometry-based and ionosphere-free,GBIF)组合,直接消除电离层延迟影响[15]。因此,基于以上分析,本文提出一种新的MCAR方法,利用模型等价性原理构建GBIF模型,消除电离层延迟影响;同时凭借能够可靠解算的超宽巷/宽巷模糊度形成线性约束,形成窄巷模糊度解算模型,从而求解窄巷模糊度及精密定位结果。
本文直接描述所提MCAR方法的理论推导,通过试验验证算法的正确性,最后得出结论。
1 方法现有的MCAR方法在超宽巷与宽巷模糊度解算方面已取得较高的模糊度解算可靠性[4, 13, 16-17]。所以,本文所提的MCAR方法将重点关注于如何构建窄巷模糊度解算模型。为便于方法理论描述,本文仅以一组卫星对的观测量模型进行理论推导,最后解算模型是将所有卫星对联立求解的。考虑到残余双差电离层与对流层等大气延迟影响,双差伪距与载波相位多频非组合模型表示为[18]
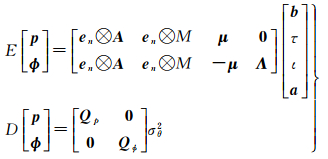 (1)
(1)
式中,E与D分别表示期望与方差;p=[p1,p2, …, pn]T、ϕ=[ϕ1,ϕ2, …, ϕn]T分别表示双差伪距与载波相位观测量向量;pi、ϕi表示第i频点(fi)的伪距与相位观测量;n表示总的可用频率数目;en表示1n×1列向量;A是基线向量b的设计矩阵;M代表经Saastamoinen对流层模型修正的相对天顶对流层分量τ所对应的Neill模型映射系数;μ=[u1, u2, …, un]T,ui=f12/fi2表示对应fi相对f1的电离层比例系数,ι表示基于f1的双差倾斜电离层分量;Λ=diag{[λ1, λ2, …, λn]},λi表示对应fi的相位波长;a=[a1, a2, …, an]T表示在n个频率上的窄巷双差模糊度值;Qp=diagσ2p1, σ2p2, …, σ2pn、Qϕ=diagσ2ϕ1, σ2ϕ2, …, σ2ϕn,σ2pi、σ2ϕi分别对应fi的非差伪距与相位观测量的方差;σθ2表示双差操作后的高度角加权系数。
为了使得窄巷模糊度解算模型免受电离层延迟影响,根据文献[18]与[19]所提的等价性原理设计变换矩阵C,消除式(1)中的倾斜电离层延迟参数ι,建立基于GBIF的窄巷模糊度解算模型。为了便于理论推导,将式(1)变换成
 (2)
(2)
式中,l=[p, ϕ];x=[b, τ, a];A为相应的设计矩阵;y=ι;B为相应的设计矩阵。
为了等价消除电离层延迟分量,变换矩阵C应满足如下条件
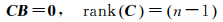 (3)
(3)
根据式(3)的约束条件可知,变换矩阵C属于B的左零空间,即C∈null(B)。根据文献[20]提出的定理2可知
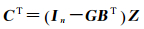 (4)
(4)
式中,G是BT的一个广义逆矩阵GT=(BTB)-1BT;Z为任意满足rank(C)=(n-1)约束的n×(n-1)矩阵。通过变换矩阵C得GBIF模型及相应的协方差有
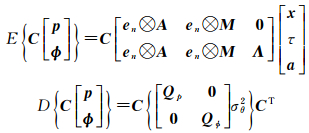 (5)
(5)
从式(5)的推导过程中发现,GBIF组合模型在非组合模型基础上等价地消除了电离层参数项,从而避免了描述电离层相关的状态信息。
考虑到超宽巷/宽巷组合具有可靠解算模糊度的优势,本文利用超宽巷/宽巷模糊度与窄巷模糊度间的线性关联,构造最终的窄巷模糊度解算模型。假设多频观测量能够构造m组线性无关的超宽巷/宽巷组合,其中m≤n,而且此m组超宽巷/宽巷组合均具有较高的模糊度解算性能。将m组正确解算的组合模糊度整理可得
 (6)
(6)
式中,

将式(6)中的矩阵Tc进行列初等变换,使得列变换矩阵Qn满足rank(Rm)=m,有
 (7)
(7)
利用变换矩阵Qn将式(5)中模糊度向量a拆分成
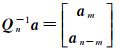 (8)
(8)
需要说明的是,为了保证模糊度的整周特性,列变换矩阵Qn除满足rank(Rm)=m约束之外,还应保证Qn-1所有元素为整数。
将式(7)、(8)代入式(6)中,整理有
 (9)
(9)
利用变换矩阵Qn将式(5)中的波长矩阵Λ变换为ΛQn=[ΛmΛn-m],这样结合式(9)可将式(5)变换为
 (10)
(10)
其中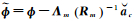

相比于式(5),式(10)的模糊度估计状态减少了m个,正好等于所构造的m组线性无关的超宽巷/宽巷组合线性约束,而且式(5)的观测量个数并未发生改变。因此,利用超宽巷/宽巷模糊度形成的线性约束,构造了最终的窄巷模糊度解算模型。
本文所提的MCAR方法以消除电离层延迟影响为出发点,通过等价性原理设计变换矩阵C用于消除窄巷模糊解算模型中的电离层参数,从而构建了GBIF组合模型。从理论推导说明了GBIF组合模型的本质与非组合模型具有等价关系,但GBIF模型相比于非组合模型的优势在于避免了因电离层随机模型先验参数难以准确描述其时空变化特性,影响模糊度解算及定位精度的弊端。同时,所提方法挖掘了可靠解算的超宽巷/宽巷模糊度间的线性关联,构建了最终的窄巷模糊度解算模型,从而解算出了窄巷模糊度及精密定位结果。
2 试验为了有效评估所提MCAR方法的模糊度解算性能,本文采用北斗三频信号,即f1=1 561.098 MHz、f2=1 207.14 MHz、f3=1 268.52 MHz;并通过3组测试基线分别为22.4 km、42.5 km及68.8 km对所提方法进行验证分析;根据文献[5, 10, 17]的试验条件设置,选取24 h时长数据,综合测试所提方法性能,其测试数据的详细信息见表 1。为了后续评估模糊度解算性能,试验前已经利用全部的观测数据正确解算窄巷模糊度参考值,方便后续超宽巷、宽巷及窄巷的模糊度解算性能的评估。
| 序号 | 基线/km | 接收机类型 | UTC时间 | 时长/h | 间隔/s | 站名 |
| 1 | 22.4 | TRIMBLE NETR9 | 2015-10-27 | 24 | 30 | CUT0-PERT |
| 2 | 42.5 | TRIMBLE NETR9 | 2014-02-26 | 24 | 30 | JENG-WHHP |
| 3 | 68.8 | TRIMBLE NETR9 | 2014-02-26 | 24 | 30 | WHHP-WHHN |
首先,本文利用模糊度正确解算的双差载波相位观测量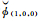

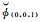
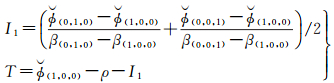 (11)
(11)
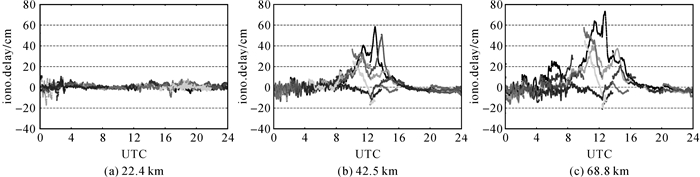
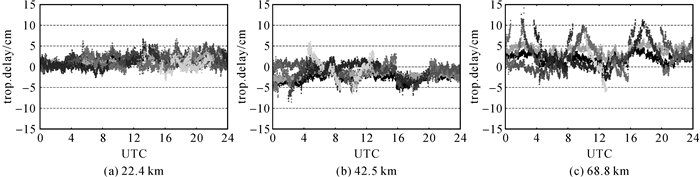
式中,I1表示频率f1的一阶双差电离层延迟量;T表示双差对流层延迟量;一阶电离层组合系数β(i,j,k)=f12·(i/f1+j/f2+k/f3)/(i·f1+j·f2+k·f3);ρ为利用基站真实位置计算的卫星与接收机间双差距离量。提取结果分别如图 1与图 2所示,其目的在于展现不同基线情况下双差电离层与对流层延迟的变化趋势。从图中可以定性看出,随基线长度增加,相应的双差电离层与对流层延迟均具有增大趋势。其中,双差电离层最大延迟达73.2 cm,双差对流层最大延迟达14.3 cm。如此大的延迟分量如果不能对其进行合理补偿,将会严重影响模糊度解算的正确性。
|
| 图 1 各基线提取的双差电离层延迟 Fig. 1 Double-differenced ionospheric delays from different baselines |
|
| 图 2 各基线提取的双差对流层延迟 Fig. 2 Double-differenced tropospheric delays from different baselines |
2.1 超宽巷/宽巷模糊度解算模型
对于本文所提的MCAR方法而言,可靠解算超宽巷/宽巷模糊度是执行窄巷模糊度解算的前提。因此,构建基于北斗三频信号的超宽巷/宽巷组合是十分必要的。众多学者推荐的适用于北斗三频信号的基于GF模型的超宽巷/宽巷组合策略见表 2,它们能够在获得满意模糊度解算可靠性的同时,具有较好的解算效率。在表 1中,(i,j,k)与(l,m,n)分别表示三频组合系数;组合波长λ(i,j,k)=c/(i·f1+j·f2+k·f3);组合噪声系数γ(i,j,k)=sqrt((i·f1)2+(j·f2)2+(k·f3)2)/(i·f1+j·f2+k·f3)。
| 序号 | ϕ(i, j, k)-p(l, m, n) | λ(i,j,k)/m | β(i,j,k)+β(l,m,n) | γ(i,j,k) | γ(l, m, n) |
| 1 | ϕ(0, -1, 1)-p(0, 1, 1) | 4.884 | 0 | 28.529 | 0.707 |
| 2 | ϕ(1,4, -5)-p(1, 1, 0) | 6.371 | 1.945 | 172.614 | 0.713 |
| 3 | ϕ(1,3, -4)-p(1, 1, 1) | 2.765 | 0.745 | 59.263 | 0.581 |
| 4 | ϕ(1,0,-1)-p(1, 0, 1) | 1.025 | 0 | 6.875 | 0.711 |
| 5 | ϕ(1,-1,0)-p(1, 1, 0) | 0.847 | 0 | 5.575 | 0.713 |
需要说明的是,尽管相比于Rounding与Bootstrapping搜索算法,LAMBDA搜索算法被证明是最优的[21],但是考虑到上述所选GF模型具有较好的波长噪声比,即使采用Rounding算法也可获得较高的解算成功率,而且执行效率优于LAMBDA搜索算法[8]。因此,在本文中,基于GF模型的超宽巷/宽巷组合策略的模糊度搜索算法采用Rounding算法。
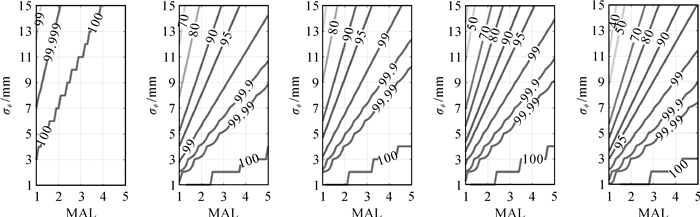
为评估上述5种基于GF模型的超宽巷/宽巷模糊度解算性能,假设GF模型引起偏差的主要误差来源于电离层延迟,根据图 1提取的电离层延迟分量等级,本文取双差电离层延迟为ι=100 cm。伪距与载波相位观测量标准差的比值设为σp:σϕ=100:1。考虑到影响Rounding算法解算可靠性的主要因素除了电离层偏差还包含组合观测精度,而多历元移动平滑方法能够有效提升组合观测精度[8],因此,5种基于GF模型的超宽巷/宽巷模糊度解算的理论成功率随原始观测量精度与移动平滑长度(moving average length,MAL)的变化关系如图 3所示。
从图 3中可以看出,ϕ(0, (1, 1)-p(0, 1, 1)组合策略具有最优的模糊度解算性能,ϕ(1,3, -4)-p(1, 1, 1)与ϕ(1,4, -5)-p(1, 1, 0)次之,在σϕ≤3 mm时,单历元模式下即可实现高于99%的解算成功率,随着移动平滑长度增加,解算成功率还将进一步提升,可容纳的观测量精度范围也同步得到提升。相比而言,ϕ(1,0,-1)-p(1, 0, 1)与ϕ(1,-1,0)-p(1, 1, 0)组合策略的模糊度解算性能稍有降低,但是在σϕ≤3 mm时,单历元模式下仍然可以获得高于95%的解算成功率,而且在两历元平滑长度下可实现高于99%的解算成功率。另外,这两组组合策略还可用于双频信号处理中,避免依赖于三频甚至多频接收机的严苛条件限制。
从理论分析,上述5种基于GF模型的超宽巷/宽巷组合策略中,仅有两组模糊度是线性无关的,其余均可由这两组模糊度线性表征[13]。因此,基于模糊度线性无关特性及解算成功率最优的考虑,本文在MCAR方法中,选择ϕ(0, -1, 1)-p(0, 1, 1)与ϕ(1,3, -4)-p(1, 1, 1)两组超宽巷组合来解算模糊度a(0, -1, 1)与a(1,3, -4)。
所选超宽巷组合策略在单历元模式下模糊度浮点解与真值差值的柱状图如图 4所示,对应的统计结果见表 3。从图 4可以看出,所选的两组超宽巷组合模糊度浮点解与真值的差值均被有效控制在0.5 cycles以内,从表 3中反映出所有测试数据的最大偏差都不超过0.4 cycles。由此可见,利用Rounding搜索算法进行超宽巷模糊度解算,在单历元模式下即可实现100%的解算成功率。
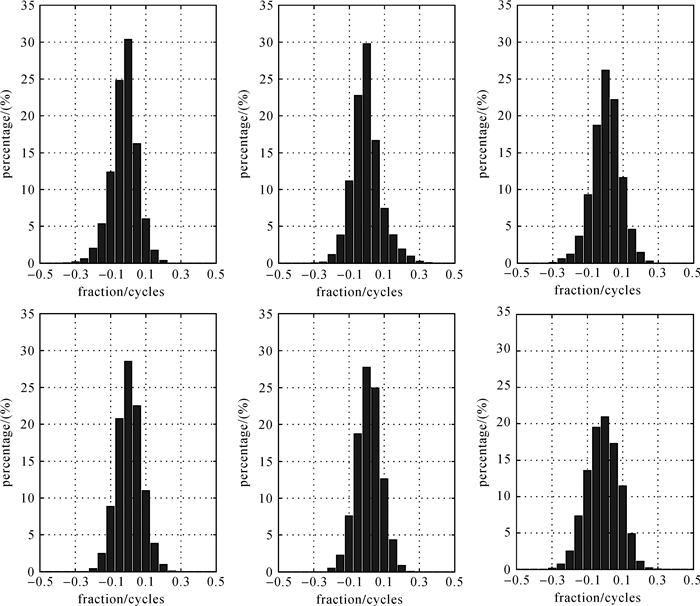
|
| 图 4 超宽巷模糊度浮点解与模糊度真值差值的统计柱状图 Fig. 4 Histogram of difference between extra wide-lane ambiguity-float and ambiguity-true value 从左至右:22.4 km、42.5 km、68.8 km;从上至下:a(0, -1, 1)与a(1,3,-4) |
| 基线 /km |
a(0, -1, 1) | a(1,3,-4) | |||||
| MEAN | STD | MAX | MEAN | STD | MAX | ||
| 22.4 | -0.002 | 0.073 | 0.362 | 0.006 | 0.071 | 0.316 | |
| 42.5 | -0.002 | 0.081 | 0.375 | 0.012 | 0.070 | 0.281 | |
| 68.8 | 0.005 | 0.081 | 0.325 | -0.012 | 0.091 | 0.387 | |
2.2 窄巷模糊度解算模型
在超宽巷/宽巷模糊度被正确解算后,窄巷模糊度正确解算是实现高精度定位的关键。本文所提方法通过北斗三频的非组合模型,根据式(4)设计变换矩阵C消除模型中的电离层延迟参数ι,构建如式(5)的基于GBIF组合的窄巷模糊度解算模型。同时利用上述两组正确解算的超宽巷模糊度值,形成的模糊度线性约束如下
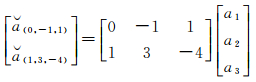 (12)
(12)
利用式(12)的模糊度线性约束,通过式(7)、(8)可以构建变换矩阵Qn为
 (13)
(13)
根据式(10)的理论推导,最终形成基于模糊度线性约束的GBIF的窄巷模糊度解算模型,利用模糊度线性约束,从模糊度估计状态量中消除了a1与a2,仅余下窄巷模糊度a3需要解算,这有助于改善窄巷模糊度解算模型的强度。
为了综合评估所提方法(GBIF)的模糊度解算及定位性能,3种解算窄巷模糊度的典型方法被采用,分别是:①文献[5]的消几何-消电离层方法(geometry-free and ionosphere-free,GFIF);②文献[4]的几何相关-弱电离层方法(geometry-based and ionosphere-reduced,GBIR);③文献[13]的几何相关-估计电离层方法(geometry-based and ionosphere-estimated,GBIE)。为了保证试验验证的一致性,以上4种方法的截止高度角均设为15°;观测量随机模型采用高度角加权模型σθ=σo(1+1/sin θ),其中θ表示卫星高度角,σo表示对应非差伪距与相位观测量标准差,分别取30 cm与3 mm[25-26];参数估计算法采用序贯最小二乘滤波算法[13];整周模糊度搜索算法采用性能最优的LAMBDA算法;由于后3种方法在窄巷解算环节采用了GB模型,包含有未被组合消除的对流层延迟,因而必须对对流层延迟进行合理补偿。本文采用Saastamoinen模型修正各倾斜对流层延迟干分量[22],通过Niell函数映射估计的天顶湿分量对各倾斜对流层湿分量进行补偿,其中估计参量建模为随机游走模型[23, 24]。相邻历元间的对流层湿分量状态变换关系为τk=τk-1+ω,ω表示过程噪声,相应的状态方差为σω2=qτΔt,其中qτ表示谱密度,本试验采用qτ=3 cm2/h,Δt表示采样间隔。需要说明的是,GBIE方法的模糊度解算性能依赖于电离层随机模型的准确描述,因此本文试验针对GBIE采用了不同先验参数的电离层随机模型:σI=0.3 mm/km与σI=3 mm/km,其系数选择参考了文献[27],用于反映单差天顶电离层随机特性随基线长度的变化程度。
在评估模糊度解算性能方面,本文采用统计量模糊度解算成功率Ps,即模糊度解算正确数与全部解算历元数之比[6, 13]。在评估定位精度方面,本文采用统计量标准差(standard deviation,STD)与95%的球概率(spherical error probability,SEP 95%)[25]。在模糊度解算实时性方面,本文采用统计量初始解算时间TTFF(time to first fix),即从算法初始化后,某一时间点模糊度解算正确且后续连续9个历元也全部解算正确,将此时间点定义为TTFF[6]。为了统计准确性,本文将24 h测试数据每隔3 h进行算法初始化,利用统计的TTFF序列完成性能评估。
不同定位模式在多组测试基线下的模糊度解算结果见表 4。不同定位模式在多组测试基线下的浮点解及模糊度正确解算解的误差曲线如图 5所示,相应的定位误差统计见表 5。不同定位模式在不同测试基线下的TTFF结果如图 6所示。基于弱电离层的GBIR与所提GBIF方法对比,从表 4可以看出,随着测试基线增加,GBIR的解算成功率呈现大幅度降低趋势,甚至在68.8 km测试基线下,仅实现了15.0%的解算成功率,在图 5中的相应的定位误差也已超过了70 cm,表现了GBIR在基线长度较长或双差电离层较为活跃的情况下的弊端,相比而言,GBIF几乎不受基线长度变化影响,均实现了96.0%以上的模糊度解算成功率,相应的定位误差优于15 cm。同为消电离层组合的GFIF与GBIF进行对比,从表 4中可以看出,GFIF的解算成功率与GBIF相当,但GFIF的TTFF值相比于GBIF的略大,随基线长度增加其差异性越大,在68.8 km测试基线下相差12.0%,其原因在于GFIF未充分利用其几何约束信息且组合观测量噪声较大,所以需要更长时间的历元平滑,才能可靠地解算模糊度。
| 基线/km | 定位模式/(%) | ||||
| GFIF | GBIR | GBIE(σI=0.3 mm/km) | GBIE(σI=3 mm/km) | GBIF | |
| 22.4 | 98.72 | 100 | 100 | 98.78 | 99.03 |
| 42.5 | 99.55 | 60.76 | 100 | 99.58 | 100 |
| 68.8 | 94.06 | 15.48 | 95.76 | 94.55 | 96.43 |

|
| 图 5 不同定位模式下在不同测试基线下的定位误差曲线 Fig. 5 Graphs of positioning errors in different positioning modes for different baselines 对应基线从左到右分别为:22.4 km、42.5 km与68.8 km;对应定位模式从上到下分别为:GFIF、GBIR、GBIE(σI=0.3 mm/km)、GBIE(σI=3 mm/km)与GBIF |
| 定位模式 | float/cm | fix/cm | ||||||
| STD | SEP 95% |
STD | SEP 95% |
|||||
| E | N | U | E | N | U | |||
| 基线距离:22.4 km | ||||||||
| GFIF | 3.4 | 1.6 | 6.3 | 10.7 | 0.2 | 0.1 | 1.3 | 4.2 |
| GBIR | 0.8 | 0.9 | 2.3 | 6.3 | 0.2 | 0.7 | 3.1 | 6.1 |
| GBIE(σI=0.3 mm/km) | 0.8 | 0.4 | 2.0 | 5.5 | 0.2 | 0.2 | 1.8 | 4.5 |
| GBIE(σI=3 mm/km) | 3.1 | 1.2 | 4.9 | 12.9 | 0.2 | 0.2 | 1.8 | 4.5 |
| GBIF | 3.0 | 2.0 | 3.8 | 5.8 | 0.2 | 0.1 | 1.8 | 4.7 |
| 基线距离:42.5 km | ||||||||
| GFIF | 3.2 | 1.5 | 4.6 | 4.1 | 0.5 | 0.4 | 3.4 | 6.1 |
| GBIR | 0.3 | 4.8 | 14.1 | 32.1 | 0.7 | 3.7 | 7.0 | 14.1 |
| GBIE(σI=0.3 mm/km) | 1.0 | 0.5 | 3.3 | 4.6 | 0.6 | 0.4 | 3.5 | 6.4 |
| GBIE(σI=3 mm/km) | 2.9 | 1.3 | 4.5 | 4.9 | 0.6 | 0.4 | 3.5 | 6.4 |
| GBIF | 1.7 | 0.7 | 6.3 | 7.6 | 0.5 | 0.4 | 3.5 | 6.3 |
| 基线距离:68.8 km | ||||||||
| GFIF | 4.6 | 1.9 | 3.4 | 12.1 | 0.7 | 0.4 | 2.7 | 10.3 |
| GBIR | 2.4 | 8.5 | 24.4 | 70.3 | 3.2 | 4.2 | 3.3 | 14.7 |
| GBIE(σI=0.3 mm/km) | 1.7 | 1.1 | 2.6 | 9.8 | 0.8 | 0.4 | 2.7 | 11.0 |
| GBIE(σI=3 mm/km) | 4.2 | 1.8 | 3.3 | 12.2 | 0.8 | 0.4 | 2.6 | 10.8 |
| GBIF | 1.7 | 0.6 | 3.3 | 4.1 | 0.8 | 0.4 | 3.1 | 13.0 |

|
| 图 6 不同定位模式下在不同测试基线下的TTFF值统计 Fig. 6 Statistics of TTFF in different positioning modes for different baselines |
基于电离层估计的GBIE与GBIF对比,从表 4中可以看出两种方法的模糊度解算成功率相当,其中结果比较呈现出GBIE(σI=0.3 mm/km)≥GBIF≥GBIE(σI=3mm/km)。从图 6的TTFF值比较中也可以得到相似的结果,GBIE(σI=0.3 mm/km)≥GBIF≥GBIE(σI=3 mm/km)。通过分析可知,对于GBIE而言,选取不同的电离层随机模型将会产生不同解算性能,所以说GBIE的模糊度解算性能与电离层随机模型精度有关,如果电离层随机模型参数选取过大,将达不到GBIE的理想性能,但如果电离层随机模型参数选取过小,将可能会导致GBIE的状态估计精度描述虚高,造成滤波算法发散或模糊度解算错误的情况出现。
因此,针对电离层的时空不规律特性,GBIE难以根据实际环境实时准确地获取电离层随机特性描述,使得本文所提出的GBIF在模糊度解算性能及定位性能上更具有实用性。另外,需要说明的是,从表 5统计的不同定位模式的浮点解与固定解精度来看,除了GBIR在68.8 km的情况下,浮点解精度差于固定解精度,其余定位模式均表现浮点解与固定解精度相当,但从图 5中可以明显看出,在达到相同的定位精度时,固定解需要更短的收敛时间,表现了模糊度正确解算的优势。
3 结论与展望本文提出一种用于MCAR方法的基于模糊度线性约束的几何相关-消电离层窄巷模糊度解算模型,有效地解决了电离层延迟造成窄巷模糊度解算可靠性降低的问题。所提方法采用等价性原理,设计变换矩阵C,构造GBIF组合模型,避免了非组合模型难以准确描述电离层随机模型及弱电离层模型受残余电离层延迟影响的弊端。与此同时,本文方法充分挖掘了超宽巷/宽巷模糊度值的线性约束,构造了窄巷模糊度解算模型。所提方法通过3组测试基线进行性能测试,表现了该方法在模糊度解算与定位的优越性能,即使在双差电离层延迟达73.2 cm的68.8 km基线测试中,仍表现了优于96%的解算成功率以及优于15 cm的定位精度。从而证明,所提MCAR方法能够可靠地解算窄巷模糊度。
本文所提的MCAR理论推导具有通用性,适用于双频、三频乃至多频信号处理中,而且不只针对于北斗系统,对GPS、GLONASS、Galileo等具有多频信号播发的系统也同样适用,只需根据不同频率使用情况调整消电离层变换矩阵C与模糊度线性约束条件即可。特别说明的是,所提方法采用几何相关-消电离层模型消除了双差电离层延迟对模糊度解算性能的影响,理论上可推广到中-长基线应用领域。
| [1] | FORSSELL B, MARTÍN-NEIRA M, HARRIS R. Carrier Phase Ambiguity Resolution in GNSS-2[C]//Proceedings of ION GPS. Kansas City, MO: [s. n. ], 1997: 1727-1736. |
| [2] | VOLLATH U, BIRNBACH S, LANDAU L, et al. Analysis of Three-carrier Ambiguity Resolution Technique for Precise Relative Positioning in GNSS-2[J]. Navigation, 1999, 46(1): 13–23. DOI:10.1002/navi.1999.46.issue-1 |
| [3] | WERNER W, WINKEL J. TCAR and MCAR Options with Galileo and GPS[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation. Portland, OR: [s. n. ], 2003: 790-800. |
| [4] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847–862. DOI:10.1007/s00190-008-0209-x |
| [5] | LI Bofeng, FENG Yanming, SHEN Yunzhong. Three Carrier Ambiguity Resolution:Distance-independent Performance Demonstrated Using Semi-generated Triple Frequency GPS Signals[J]. GPS Solutions, 2010, 14(2): 177–184. DOI:10.1007/s10291-009-0131-6 |
| [6] | ZHANG Xiaohong, HE Xiyang. Performance Analysis of Triple-frequency Ambiguity Resolution with BeiDou Observations[J]. GPS Solutions, 2016, 20(2): 269–281. DOI:10.1007/s10291-014-0434-0 |
| [7] | ZHAO Dongsheng, ROBERTS G W, LAU L, et al. A Theoretical and Empirical Integrated Method to Select the Optimal Combined Signals for Geometry-free and Geometry-based Three-carrier Ambiguity Resolution[J]. Sensors, 2016, 16(11): 1929. DOI:10.3390/s16111929 |
| [8] | LI Liang, JIA Chun, ZHAO Lin, et al. Integrity Monitoring-based Ambiguity Validation for Triple-carrier Ambiguity Resolution[J]. GPS Solutions, 2017, 21(2): 797–810. DOI:10.1007/s10291-016-0570-9 |
| [9] | FENG Yanming, RIZOS C. Three Carrier Approaches for Future Global, Regional and Local GNSS Positioning Services: Concepts and Performance Perspectives[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation. Long Beach, CA: [s. n. ], 2005: 2277-2278. |
| [10] | CHEN Dezhong, YE Shirong, XIA Jinchao, et al. A Geometry-free and Ionosphere-free Multipath Mitigation Method for BDS Three-frequency Ambiguity Resolution[J]. Journal of Geodesy, 2016, 90(8): 703–714. DOI:10.1007/s00190-016-0903-z |
| [11] | ZHAO Qile, DAI Zhiqiang, HU Zhiguang, et al. Three-carrier Ambiguity Resolution Using the Modified TCAR Method[J]. GPS Solutions, 2015, 19(4): 589–599. DOI:10.1007/s10291-014-0421-5 |
| [12] | LI Bofeng, FENG Yanming, GAO Weiguang, et al. Real-time Kinematic Positioning over Long Baselines Using Triple-frequency BeiDou Signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3254–3269. DOI:10.1109/TAES.2015.140643 |
| [13] | TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency Carrier Ambiguity Resolution for BeiDou Navigation Satellite System[J]. GPS solutions, 2014, 18(3): 335–344. DOI:10.1007/s10291-013-0333-9 |
| [14] | LIU Libo, WAN Weixing, NING Baiqi, et al. Solar Activity Variations of the Ionospheric Peak Electron Density[J]. Journal of Geophysical Research:Space Physics, 2006, 111(A8): A011598. |
| [15] | GENG Jianghui, BOCK Y. Triple-frequency GPS Precise Point Positioning with Rapid Ambiguity Resolution[J]. Journal of Geodesy, 2013, 87(5): 449–460. DOI:10.1007/s00190-013-0619-2 |
| [16] |
李博峰, 沈云中, 冯延明.
利用三频GNSS进行长距离实时精密导航[J]. 武汉大学学报(信息科学版), 2009, 34(7): 782–786.
LI Bofeng, SHEN Yunzhong, FENG Yanming. Long-range Real-time Precise Navigation with Three Fequency GNSS[J]. Geomatics and Information Science of Wuhan University, 2009, 34(7): 782–786. |
| [17] | LI Bofeng, LI Zhen, ZHANG Zhiteng, et al. ERTK:Extra-wide-lane RTK of Triple-frequency GNSS Signals[J]. Journal of Geodesy, 2017, 91(9): 1031–1047. DOI:10.1007/s00190-017-1006-1 |
| [18] | SHEN Yunzhong, Xu Guochang. Simplified Equivalent Representation of GPS Observation Equations[J]. GPS Solutions, 2008, 12(2): 99–108. DOI:10.1007/s10291-007-0070-z |
| [19] |
李博峰, 葛海波, 沈云中.
无电离层组合、Uofc和非组合精密单点定位观测模型比较[J]. 测绘学报, 2015, 44(7): 734–740.
LI Bofeng, GE Haibo, SHEN Yunzhong. Comparison of Ionosphere-free, Uofc and Uncombined PPP Observation Models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 734–740. |
| [20] |
吴永康.
矩阵方程的通解及其结构[J]. 工科数学, 2002, 18(1): 102–104.
WU Yongkang. The General Solutions and Its Structure of Matrix Equation[J]. Journal of Mathematics for Technology, 2002, 18(1): 102–104. |
| [21] | TEUNISSEN P J G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606–612. DOI:10.1007/s001900050199 |
| [22] | SAASTAMOINEN J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1973, 105(1): 279–298. |
| [23] | WIELGOSZ P, PAZIEWSKI J, BARYŁA R. On Constraining Zenith Tropospheric Delays inProcessing of Local GPS Networks with Bernese Software[J]. Survey Review, 2011, 43(323): 472–483. DOI:10.1179/003962611X13117748891877 |
| [24] | TAKASU T, YASUDA A. Kalman-filter-based Integer Ambiguity Resolution Strategy for Long-baseline RTK with Ionosphere and Troposphere Estimation[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR: [s. n. ], 2010: 161-171. |
| [25] | LI Liang, LI Zishen, YUAN Hong, et al. Integrity Monitoring-based Ratio Test for GNSS Integer Ambiguity Validation[J]. GPS Solutions, 2016, 20(3): 573–585. DOI:10.1007/s10291-015-0468-y |
| [26] |
高成发, 赵毅, 万德钧.
GPS载波定位中双差观测值权的合理确定[J]. 测绘科学, 2005, 30(3): 28–32.
GAO Chengfa, ZHAO Yi, WAN Dejun. The Weight Determination of the Double Difference Observation in GPS Carrier Phase Positioning[J]. Science of Surveying and Mapping, 2005, 30(3): 28–32. |
| [27] | LI Bofeng, VERHAGEN S, TEUNISSEN P J G. Robustness of GNSS Integer Ambiguity Resolution in the Presence of Atmospheric Biases[J]. GPS Solutions, 2014, 18(2): 283–296. DOI:10.1007/s10291-013-0329-5 |