高精度的海域重力场对水下潜器的导航、飞行器的轨道确定及海洋航空重力测量的检核有重要作用。随着海洋地质调查资料的增多,不同测高卫星的数据积累,建立更高精度和分辨率的重力场模型的需求也越来越迫切。融合船载重力数据与卫星测高数据既可以充分发挥船载数据精度高,还可以利用卫星测高反演的重力场分布均匀的优点。对于多源重力数据融合问题,常见的方法有最小二乘配置法,也可采用文献[1]中的方法,即先利用残差重力异常修正重力位模型系数,进而融合卫星、航空、地面(海面)重力数据的迭代计算。其他的方法还有泊松小波径向基函数[2]、点质量方法[3]及小波分解的数据融合方法[4]。点质量方法理论模型直接由反映重力场性质的模型推导而来。在众多的利用点质量法研究中,研究重点通常是在讨论如何克服法方程矩阵求逆导致数值解算过程失稳的问题[5-8]。
本文不研究点质量方法的稳定性问题,主要利用点质量法对于重力场的解析表达形式,借鉴移去-恢复技术的思路,通过点质量法拟合船载重力测量数据的中低频信号,将测高重力数据中的高频信号与船载重力数据中的高频信号使用加权最小曲率方法进行格网化,然后采用点质量模型恢复其中重力数据的中低频信号,实现船载重力数据与卫星测高数据的融合,最后使用国际船载重力数据进行检核。
1 计算模型与融合方法 1.1 计算模型点质量模型是
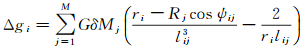
式中, ri、φi、λi表示第i个重力异常;Δgi为观测点的球面三维坐标;Rj、φj、λj表示第j个质量源的球面三维坐标;M是质量源的总数;lij、ψij分别是第i个重力异常观测点与第j个质量源之间的空间距离及其与地心连线的夹角;G是万有引力常数;δMj是第j个质量源的质量;Rj是Bjerhammar球半径。点质量模型是基于重力场等效原理而建立的,拟合重力异常数据时对重力场物理属性表征更多一些,有别于纯数学模型的拟合。
点质量模型的最小二乘解为
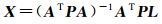
式中,P为观测值向量L的权矩阵;L由不同类型的观测量组成,按定权公式确定它们的权比。本文仅使用船载重力数据,故P为单位矩阵。
1.2 测高重力异常与船载重力异常融合方法为了实现测高重力异常与船载重力异常融合,本文设计了如下的步骤:
第1步:考虑到船载重力数据的精度比测高的重力异常精度要高,用点质量法对收集到的全部船载重力测量数据(61 226个点值)进行拟合。
第2步:利用得到的质量源三维坐标位置及质量大小计算船载重力测线上重力数据重力异常gship,并与船载重力异常求差,得到残差rgs。
第3步:同样利用得到的质量源三维坐标位置及质量大小计算测高重力格网模型处的重力异常galt,并计算残差rga。
第4步:分别计算rgs与rga在重合点处的方差,取船载重力残差方差作为单位权中误差,计算测高重力残差的权因子。
第5步:对rgs与rga利用加权最小曲率方法进行格网化,得到残差重力异常模型g1。1974年,文献[9]首次提出最小曲率网格化方法。经过前人的对比分析[10-12],认为该方法的优点是所需参数少、计算工作量小、有利于稀疏数据的网格化,且插值结果能够保证二阶导数连续。因此,本文采用加权最小曲率方法对离散数据进行格网化。
第6步:利用得到的质量源三维坐标位置及质量大小计算格网点处的重力异常g2。
第7步:将g1与g2相加即为融合的重力异常模型。
第8步:利用船载重力测量数据对模型进行检核。
从公开发表的文献来看,对于重力场量进行融合通常是基于不同重力场量(如重力异常、高程异常和垂线偏差等),采用点质量模型,解算出点质量的三维坐标位置及质量大小来实现的。本文对此步骤进行了改进,即在第2步至第7步之间借鉴移去-恢复的思路,利用点质量模型计算测高与船载重力中所包含的相同的中低频信号,仅对测高与船载重力异常的高频信号进行融合。在移去-恢复的过程中,未采用全球重力场模型移去-恢复中低频的重力场信号,而是基于点质量模型反映出的局部重力场的中低频信号来进行移去-恢复运算。这在一定的程度上可避免全球重力场模型在拟合局部重力数据时存在系统偏差的影响。
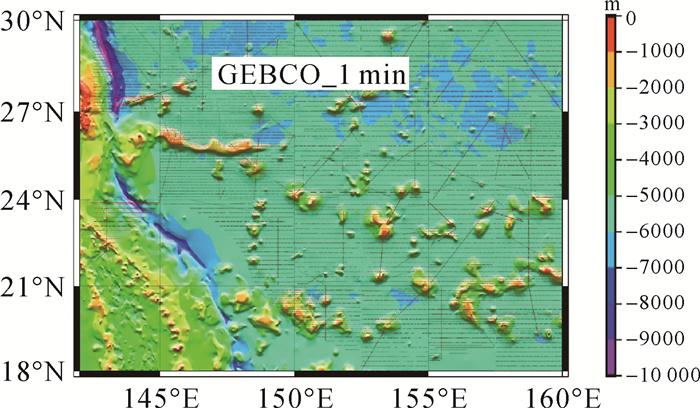
2 实测数值计算与结果分析 2.1 船载重力数据收集的船载重力测量数据分布如图 1中点线所示,由国内不同部门,在不同年代进行测量得到,空间分辨率约10′。考虑到船载重力测量数据处理不是本文的重点,对其精细处理主要借鉴了文献[13-17]等提供的方法。该区域内的船载重力数据有3种不同分辨率。分别是:测线间距约20 km,测点之间的间距约为3 km;测线间距约11 km,测点之间的间距约为3.7 km;测线间距约6 km,测点之间的间距约为4 km;主要以第1种与第2种数据为主。第3种主要分布在海底地形起伏较大区域。整个研究范围内数据分为50个测区,编号分别为100—149。
|
| 图 1 研究区内船载重力数据的分布 Fig. 1 The distribution of shipborne gravity anomaly |
采用美国地球物理数据中心NGDC(National Geophysical Data Center)网站提供的数据作为第三方检核数据,用来对本文融合后的重力异常模型进行检核。其分布情况如图 2中红色点线所示。有关NGDC数据的介绍可以参考文献[18-19]。

|
| 图 2 NGDC国际船载重力测量数据分布及检核区的分布 Fig. 2 The distribution of the trackline gravity anomaly of NGDC and the validation regions |
2.2 点质量源的数量与位置的探讨
尽管本文讨论的重点不是点质量法的稳定性问题,但有必要讨论点质量源的数量、位置(平面坐标与埋深)与原始观测值偏离情况。为此,根据GEBCO海底地形模型(general bathymetric chart of the oceans,分辨率为1′)依据点质量法的正演模型,讨论点质量源的平面位置、埋深以及质量源的数量。
一般而言,点质量反演方法的埋深初值可以根据数据的地球物理先验信息给定,在反演过程进行精化。本文根据可用的数据情况,假定点质量源分布于海底,即依据GEBCO海底地形模型内插测线上各点重力异常数据的水深值,将该值作为对应点处的质量埋深初值。
本文在任意测区的测线方向,按照10、15和20 km的分辨率对测线数据进行了重采样。将重采样的数据,反演对应测区的点质量模型,进而由点质量模型计算的重力异常与全部测线上重力异常的差异来比较,不同分辨率数据的差别。为了文章的简洁,表 1列举部分测区采用不同分辨率的数据与原始数据的差异。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |
| region | 原始数据集 | 重采样的数据集(空间分辨率10 km) | |||||||||
| max | min | mean | STD | 数据点数 | max | min | mean | STD | 数据点数 | ||
| 100 | 47.543 | -23.594 | 0.035 | 6.903 | 1020 | 45.348 | -21.239 | 0.117 | 6.568 | 246 | |
| 101 | 49.989 | -34.348 | 1.209 | 13.054 | 1526 | 49.121 | -29.825 | 1.504 | 13.035 | 371 | |
| 102 | 49.930 | -49.262 | 1.822 | 15.942 | 787 | 49.447 | -48.203 | 2.349 | 16.250 | 228 | |
| 103 | 49.570 | -16.089 | 0.813 | 9.462 | 140 | 46.955 | -12.419 | 0.741 | 8.350 | 37 | |
| 110 | 49.735 | -19.932 | 0.481 | 6.988 | 803 | 49.951 | -19.269 | 0.179 | 6.907 | 213 | |
| 120 | 9.469 | -10.498 | 0.067 | 2.336 | 1594 | 9.567 | -10.550 | 0.118 | 2.386 | 345 | |
| 130 | 49.969 | -22.052 | 2.120 | 12.006 | 636 | 49.966 | -25.357 | 1.651 | 11.641 | 174 | |
| 140 | 49.523 | -15.168 | 1.015 | 8.513 | 1313 | 49.959 | -19.724 | 0.710 | 8.253 | 280 | |
| 149 | 49.748 | -18.726 | 1.025 | 8.728 | 2790 | 49.872 | -13.904 | 1.769 | 9.437 | 600 | |
| (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | (22) | |
| region | 重采样的数据集(空间分辨率15 km) | 重采样的数据集(空间分辨率20 km) | |||||||||
| max | min | mean | STD | 数据点数 | max | min | mean | STD | 数据点数 | ||
| 100 | 49.814 | -32.721 | 0.129 | 7.396 | 168 | 49.722 | -41.588 | -0.185 | 7.525 | 126 | |
| 101 | 49.969 | -42.927 | 1.284 | 13.302 | 278 | 49.879 | -47.076 | 0.920 | 13.898 | 198 | |
| 102 | 48.757 | -49.006 | 2.690 | 16.693 | 167 | 49.845 | -44.203 | 2.855 | 16.371 | 129 | |
| 103 | 48.118 | -7.692 | 1.293 | 8.435 | 29 | 45.310 | -9.655 | 1.198 | 8.836 | 21 | |
| 110 | 49.868 | -22.257 | 0.315 | 7.071 | 162 | 46.197 | -21.524 | 0.110 | 7.103 | 116 | |
| 120 | 10.813 | -10.893 | 0.077 | 2.563 | 241 | 10.291 | -12.022 | 0.070 | 2.701 | 184 | |
| 130 | 48.378 | -39.253 | 0.918 | 11.470 | 121 | 49.637 | -27.651 | 1.544 | 11.740 | 93 | |
| 140 | 49.408 | -18.176 | 0.229 | 7.931 | 197 | 49.240 | -29.668 | 0.523 | 8.874 | 151 | |
| 149 | 49.975 | -13.866 | 1.837 | 9.512 | 426 | 49.771 | -16.872 | 1.317 | 8.992 | 309 | |
表 1中,(1)、(12)列是研究区内数据的分区编号;(2)—(6)列为各分区采用该区内全部的数据作为初始数据(第(6)列为该区内的数据总数)反演点质量模型,然后利用点质量模型计算测线上重力异常,并将原始值与其求差,对差值进行统计((2)—(5)列);(7)—(11)列为各分区按照10 km的空间分辨率重采样后(第(11)列为该区内的数据点数)反演点质量模型,然后利用点质量模型计算测线(第(6)列)上重力异常,并将原始值与其求差,对差值进行统计((7)—(10)列);(12)—(17)列为各分区按照15 km的空间分辨率重采样后(第(17)列为该区内的数据点数)反演点质量模型,然后利用点质量模型计算测线(第(6)列)上重力异常,并将原始值与其求差,对差值进行统计((13)—(17)列);(18)—(22)列为各分区按照20 km的空间分辨率重采样后(第(22)列为该区内的数据点数)反演点质量模型,然后利用点质量模型计算测线(第(6)列)上重力异常,并将原始值与其求差,对差值进行统计((18)—(22)列)。
从表 1可以看出,采用不同分辨率的采样数据,反演的结果相差不大,也说明点质量法模型对数据的质量不敏感。需要说明的是,采样数据需要包含测线上重力异常的基本特征(最大值、最小值以及变化趋势),即数据分布不能太稀疏。
为此,本文采用了20 km的分辨率对所有的测线数据进行重采样,依据GEBCO模型的深度值,以及测线的平面坐标反演点质量源大小,作为后文研究的基础。
2.3 已有海洋重力场模型的比较目前,国际上发布的两个重力场模型分别是Sandwell v23.1和DTU13模型。Sandwell v23.1模型于2014年发布,其中采用部分Cryosat-2及Jason-1的大地测量周期内的数据,精度达到了1~2 mGal(文献[20])。DTU13模型由DTU08逐渐发展而来,在世界范围内得到了广泛应用,该模型仍在持续更新中,具体细节可见文献[21]。在部分区域Sandwell v23.1精度要高于DTU13模型,但Sandwell v23.1与DTU13模型均不同程度地融入了船载重力数据。为了客观评价卫星测高重力场数据与船载重力数据融合后构建的新重力场模型的精度,本文采用中国测绘科学研究院研制的纯卫星测高重力场模型(CASM-ALT)。该模型与本文中研究区域内收集的船载重力异常(非NGDC数据)的差异如表 2中第2行所示。表 2第3行为Sandwell v23.1模型与船载数据的差异,第4行为DTU13模型与船载数据的差异。从表中可以看出,CASM-ALT精度略低于Sandwell v23.1、DTU13模型重力异常。在后文中主要以NGDC数据作为检核。表 2中也给出了NGDC船载重力数据与各模型的差异。
| mGal | |||||
| 船载重力数据 | 模型 | 最大值 | 最小值 | 平均值 | 标准差 |
| 本文收集的数据 | CASM-ALT | 49.59 | -49.73 | -4.00 | 5.51 |
| Sandwell v23.1 | 49.96 | -45.61 | -4.16 | 3.72 | |
| DTU13 | 49.29 | -49.85 | -4.19 | 4.04 | |
| NGDC重力数据 | CASM-ALT | 49.99 | -49.90 | -1.15 | 7.47 |
| Sandwell v23.1 | 49.96 | -49.99 | -1.36 | 6.94 | |
| DTU13 | 49.98 | -49.94 | -1.22 | 7.32 | |
从表 2可以看出,本文收集的数据与NGDC的数据有一定的系统差。另外由于研究区域位于马里亚纳海沟东侧,该处海底地形起伏较为剧烈(图 1中的背景),且NGDC数据的标准差也比本文收集的数据标准差要大。
2.4 融合的重力异常模型检核基于上节的步骤,得到融合卫星测高与船载重力数据的重力异常模型。图 2中红线表示NGDC的国际船载重力测量数据。考虑到区域A、区域B和区域C的海底有起伏的海山,高频信号丰富,选择这几个区域作为检核区域更能反映融合后重力场模型的精度。
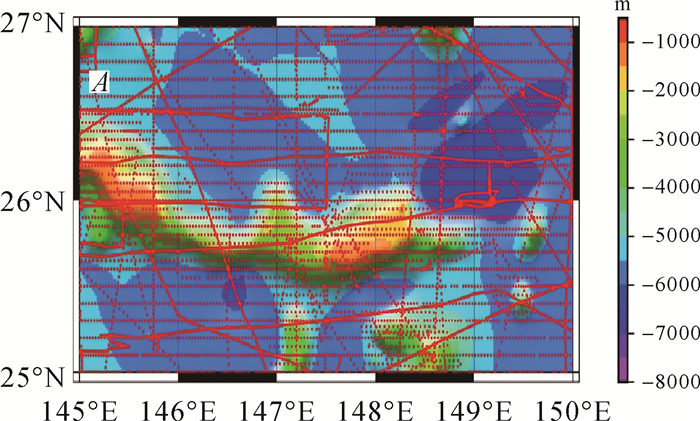
检核区域A、B、C的海底地形及NGDC船载重力检核数据的分布如图 3—图 5所示。相对于整个研究区域而言,所选的检核区域是海底地形起伏较大的区域。对融合后的重力异常检核结果如表 3所示。标准差在4 mGal左右,但仍然有1~2 mGal的整体偏差。相比于纯卫星测高的重力异常模型,精度有一定的提升,平均偏差的绝对值有一定增大,标准差也有一定的改善。
|
| 图 3 检核区A的海底地形及船载重力数据分布 Fig. 3 Bathymetry and shipborne gravity data distribution of region A |
|
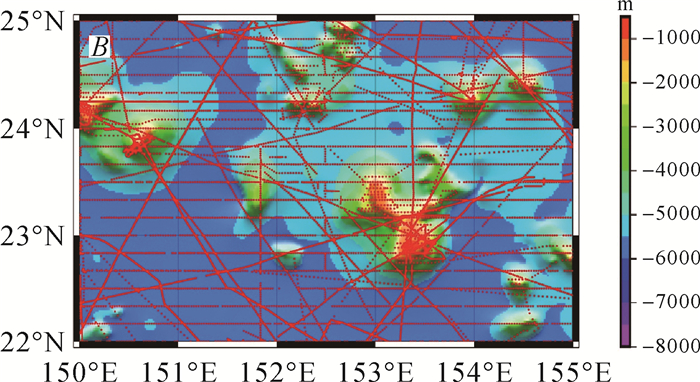
| 图 4 检核区B的海底地形及船载重力数据分布 Fig. 4 Bathymetry and shipborne gravity data distribution of region B |

|
| 图 5 检核区C的海底地形及船载重力数据分布 Fig. 5 Bathymetry and shipborne gravity data distribution of region C |
| mGal | |||||
| 区域 | 检核数据点值个数 | 最大值 | 最小值 | 平均值 | 标准差 |
| A | 8310 | 49.96 | -49.93 | -2.11 | 4.06 |
| B | 14 889 | 49.24 | -50.00 | -2.20 | 4.02 |
| C | 15 569 | 40.35 | -45.34 | -1.65 | 4.09 |
3 结论
基于点质量法拟合船载重力异常数据的中、低频信号,在卫星测高重力异常中将其移去。对船载重力数据的高频信号及卫星测高的高频信号进行加权最小曲率格网化,基于点质量模型恢复中低频信号,实现二者的融合。经国际船载重力测量数据检核,研究结果表明:
(1) 文中采用的融合步骤相比以往常用的数据融合步骤进行了改进,即引进了基于点质量模型移去-恢复技术的融合方法。
(2) 采用GEBCO的海底地形先验模型,指定点质量的平面坐标位置,减少反演参数,回避了点质量模型法方程求逆失稳的问题。
(3) 在移去-恢复的过程中,没有使用全球重力场模型作为参考,而是依据点质量模型参数所具有的局部重力场特征,计算区域重力异常的中低频分量,这有助于避免引入全球重力场模型的误差。
(4) 对不同平台下获取的重力异常的高频信息进行融合,所得的融合后重力场模型的精度有一定提高,成果标准差约为4 mGal,反映了本文的技术思路及方法具有一定的可行性与可靠性。
(5) 构建的融合重力场模型依然与NGDC重力异常数据存在1~2 mGal平均偏差,可能是因为重力数据之间的系统偏差或者由于不同年代进行重力测量时测量仪器之间存在偏差造成的,其实际成因拟在后续研究做进一步分析。
| [1] |
黄谟涛, 欧阳永忠, 翟国君, 等.
海域多源重力数据融合处理的解析方法[J]. 武汉大学学报(信息科学版), 2013, 38(11): 1261–1265.
HUANG Motao, OUYANG Yongzhong, ZHAI Guojun, et al. Analytical Methods of Multi-source Gravity Data Fusion Processing in the Sea Area[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11): 1261–1265. |
| [2] |
吴怿昊, 罗志才, 周波阳.
基于泊松小波径向基函数融合多源数据的局部重力场建模[J]. 地球物理学报, 2016, 59(3): 852–864.
WU Yihao, LUO Zhicai, ZHOU Boyang. Regional Gravity Modeling Based on Heterogeneous Data Sets by Using Poisson Wavelets Radial Basis Functions[J]. Chinese Journal of Geophysics, 2016, 59(3): 852–864. |
| [3] |
黄谟涛, 欧阳永忠, 刘敏, 等.
融合海域多源重力数据的正则化点质量方法[J]. 武汉大学学报(信息科学版), 2015, 40(2): 170–175.
HUANG Motao, OUYANG Yongzhong, LIU Min, et al. Regularization of Point-mass Model for Multi-source Gravity Data Fusion Processing[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 170–175. |
| [4] |
吴健生, 刘苗.
基于小波的位场数据融合[J]. 同济大学学报(自然科学版), 2008, 36(8): 1133–1137.
WU Jiansheng, LIU Miao. Potential Field Data Fusion Based on Wavelet Multi-resolution Decomposition[J]. Journal of Tongji University (Natural Science), 2008, 36(8): 1133–1137. |
| [5] | SUNKEL H. The Generation of a Mass Point Model from Surface Gravity Data[M]. Ohio: Ohio State University, 1983. |
| [6] |
吴晓平.
局部重力场的点质量模型[J]. 测绘学报, 1984, 13(4): 249–258.
WU Xiaoping. Point-mass Model of Local Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 1984, 13(4): 249–258. |
| [7] |
陆仲连.
地球重力场理论与方法[M]. 北京: 解放军出版社, 1996.
LU Zhonglian. Theory and Method of Earth's Gravity Field[M]. Beijing: Liberation Army Press, 1996. |
| [8] |
高新兵, 李姗姗, 李海, 等.
点质量模型与最小二乘配置在多源重力数据融合中的应用[J]. 大地测量与地球动力学, 2013, 33(1): 145–149.
GAO Xinbing, LI Shanshan, LI Hai, et al. Application of Point Mass Model and Least Square Collocation in Multi-source Gravity Data Fusion[J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 145–149. |
| [9] | BRIGGS I C. Machine Contouring Using Minimum Curvature[J]. Geophysics, 1974, 39(1): 39–48. DOI:10.1190/1.1440410 |
| [10] |
庞振兴, 张传定, 叶修松.
Surfer8.0在重力异常数据格网化中的应用[J]. 海洋测绘, 2008, 28(1): 43–45, 51.
PANG Zhenxing, ZHANG Chuanding, YE Xiusong. Application Surfer8.0 in the Gridding of Gravity Anomaly Data[J]. Hydrographic Surveying and Charting, 2008, 28(1): 43–45, 51. |
| [11] |
王万银, 邱之云.
一种稳定的位场数据最小曲率网格化方法研究[J]. 地球物理学进展, 2011, 26(6): 2003–2010.
WANG Wanyin, QIU Zhiyun. The Research to a Stable Minimum Curvature Gridding Method in Potential Data Processing[J]. Progress in Geophysics, 2011, 26(6): 2003–2010. |
| [12] |
骆遥, 吴美平.
位场向下延拓的最小曲率方法[J]. 地球物理学报, 2016, 59(1): 240–251.
LUO Yao, WU Meiping. Minimum Curvature Method for Downward Continuation of Potential Field Data[J]. Chinese Journal of Geophysics, 2016, 59(1): 240–251. |
| [13] |
黄谟涛.
海洋重力测量半系统差检验、调整及精度计算[J]. 海洋通报, 1990, 9(4): 81–86.
HUANG Motao. Examination, Adjustment and Precision Estimation of Half-systematic Error in Marine Gravity Surveying[J]. Marine Science Bulletin, 1990, 9(4): 81–86. |
| [14] |
黄谟涛.
海洋重力测线网平差[J]. 测绘学报, 1993, 22(2): 103–110.
HUANG Motao. Marine Gravity Survey Line Network Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 1993, 22(2): 103–110. |
| [15] |
李明叁, 刘雁春, 黄谟涛, 等.
海洋测线网系统误差确定的3种模型[J]. 测绘学院学报, 2002, 19(3): 157–161.
LI Mingsan, LIU Yanchun, HUANG Motao, et al. Three Models for Determination of Survey-line Systematic Errors in Marine Survey Net[J]. Journal of Institute of Surveying and Mapping, 2002, 19(3): 157–161. |
| [16] |
刘雁春, 李明叁, 黄谟涛.
海洋测线网系统误差调整的秩亏网平差模型[J]. 武汉大学学报(信息科学版), 2012, 26(6): 533–538.
LIU Yanchun, LI Mingsan, HUANG Motao. The Rank-defect Adjustment Model for Survey-line Systematic Errors in Marine Survey Net[J]. Geomatics and Information Science of Wuhan University, 2012, 26(6): 533–538. |
| [17] |
柯宝贵, 章传银, 郭春喜, 等.
船载重力测量数据不同测区系统偏差纠正方法研究[J]. 武汉大学学报(信息科学版), 2015, 40(3): 417–421.
KE Baogui, ZHANG Chuanyin, GUO Chunxi, et al. Research on the System Error Correction for Shipborne Gravimetric Data of Different Region in China Offshore[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 417–421. |
| [18] | HWANG C, PARSONS B. Gravity Anomalies Derived from Seasat, Geosat, ERS-1 and TOPEX/Poseidon Altimetry and Ship Gravity:A Case Study over the Reykjanes Ridge[J]. Geophysical Journal International, 1995, 122(2): 551–568. DOI:10.1111/gji.1995.122.issue-2 |
| [19] | WESSL P, WATTS A B. On the Accuracy of Marine Gravity Measurements[J]. Journal of Geophysical Research, 1988, 93(B1): 393–413. DOI:10.1029/JB093iB01p00393 |
| [20] | SANDWELL D T, MVLLER R D, SMITH W H F, et al. New Global Marine Gravity Model from Cryosat-2 and Jason-1 Reveals Buried Tectonic Structure[J]. Science, 2014, 346(6): 65–67. |
| [21] | ANDERSEN O B, KNUDSEN P, BERRY P A M. The DNSC08GRA Global Marine Gravity Field from Double Retracked Satellite Altimetry[J]. Journal of Geodesy, 2010, 84(3): 191–199. DOI:10.1007/s00190-009-0355-9 |


