2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
整数模糊度解算是利用GNSS载波相位进行精密定位等各类应用的性能倍增器。因为差分能够消除接收机或卫星端公共的非整数偏差项,在相当长的一段时间内,人们一度只能对双差模糊度进行固定。在过去的10余年里,针对单台接收机的整数模糊度解算,国内外学者提出了多种方法,以期提高精密单点定位(precise point positioning, PPP)的精度、稳定性和缩短收敛时间。概括起来可以分为以下3种[1]:①提供卫星端的非整数偏差改正数,即小数周偏差(fractional cycle bias, FCB[1-2])(在不同文献中,尽管名词不同,如fractional phase offset[3],uncalibrated phase delay[4],uncalibrated fractional offsets[5-6]等,但其内涵均相同);②提供基于非差整数模糊度固定得到的卫星钟差[1],包括“整数”钟差[7-8](integer clock)和解耦钟差[9-10](decoupled clock);③提供网解时的宽巷和消电离层组合模糊度列表(wide-lane phase bias list, WLPBLIST)[11]。文献[1]通过公式推导和数值试验证明了途径①和途径②在理论上和应用效果上都是等效的。已有文献表明,不同条件下的FCB解算及PPP应用研究已取得不少成果[2, 5-6, 12-17],而“整数”钟差(包括解耦钟差)的解算似乎还没有得到广泛关注。其中原因大概与下述情况不无关系,即现有文献详尽地给出了FCB解算的关键算法,且其所需要的观测量——宽巷和消电离层组合非差模糊度——可以方便地通过PPP处理得到;而“整数”钟差解算采用的观测模型在形式上与传统钟差解算算法截然不同,且其关键技术——非差模糊度基准[9]或参考模糊度[8]的固定——在现有文献却少见清晰的描述。卫星钟差产品,除了支持单台接收机的精密定位之外,在时间频率传递、卫星钟性能评估方面也有重要意义[18]。有鉴于此,笔者对卫星钟差解算进行了较深入的研究,提出通过星间单差模糊度固定恢复出卫星钟差的方法。
基于上述研究背景,本文第1节从消除秩亏的角度分析传统钟差解算方法与“整数”钟差解算方法的区别,指出“整数”钟差解算的关键在于建立整数模糊度基准。第2节阐述实现“整数”卫星钟差解算的关键过程——星间单差模糊度固定。第3节采用IGS测站数据进行GPS卫星钟差解算试验,证明获得的卫星钟差及宽巷FCB产品具备分离出单台接收机的星间单差整数模糊度的能力,并通过试验展示进行模拟动态PPP定位的效果。
1 观测模型假设接收机r在频点i观测到卫星s的伪距Pr, is和载波相位Lr, is,观测方程表示如下[9]
 (1)
(1)
式中,θi*=cdt*+αi*和δi*=cdt*+βi*分别为伪距和相位钟差,它们分别包含了各自的设备时延αi*和βi*,dt*为卫星钟或接收机本地钟与系统时的偏差;上标r和s分别代表接收机和卫星;下标i表示信号频点;λi为载波波长;ρrs为信号传播路径延迟,包括对流层延迟和相对论效应;c为光速;wr,s i为相位缠绕效应;Ir, is为电离层延迟;Nr,s i为整数相位模糊度;ξi和εi分别为伪距和相位的测量误差及模型化误差。如果同时观测到两个频点(i和j)的数据,可利用电离层延迟与频率的平方成反比的性质,构造出双频消电离层组合观测量
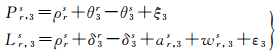 (2)
(2)
式中,
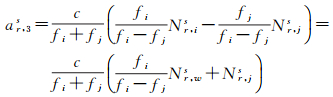 (3)
(3)
式中,Nr, ws=Nr, is-Nr, js称为宽巷模糊度,对应波长为

在式(2)中,接收机钟差与卫星钟差无法分离,钟差参数与模糊度参数也不可分离。这导致在没有其他约束的情况下得到的法方程是奇异的。对于前者导致的秩亏问题,在网解中可以通过选择一台接收机或一颗卫星的时钟作为基准钟得以解决[8, 9];在仅用单站数据的(精密)单点定位中,则可以通过固定卫星钟差而消除。由于设备时延通常是长期稳定的,对于后一原因导致的秩亏问题,可以采用以下两种方法进行处理。
方法1:也是最传统的方法,利用伪距钟差对相位钟差进行约束,将式(2)改写为
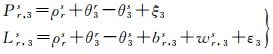 (4)
(4)
式中
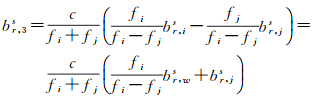 (5)
(5)
式中,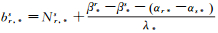
方法2:通过对模糊度参数进行先验约束或者确定S基准[20]消除模糊度参数引起的秩亏。特别地,为了获得整数钟差或解耦钟差[1],文献[8-9]通过选择和固定非差模糊度基准(reference ambiguity[8]或ambiguity datum[9]),进而实现非差宽巷和窄巷模糊度固定,得到基于非差模糊度固定解的钟差产品。当然,二者在细节上还是有明显区别的,前者单独解算的伪距钟差被后者忽略;前者将宽巷小数偏差作为时变参数处理,而后者将其作为分段常数处理。它们所采用的观测方程也与式(2)或式(4)有明显的差异,前者在式(2)两个观测量的基础上还加入了MW组合观测量,后者先利用MW组合解算出非差宽巷整数模糊度,然后将式(2)的载波观测方程表示为仅含窄巷模糊度的无电离层组合相位。
由平差理论可知,求解观测方程式(2)是个秩亏自由网平差问题[21]。不论是方法1还是方法2,本质上只是提供了平差的必要基准以达到消除秩亏的目的。在方法1中,伪距钟差为相位钟差和非差模糊度提供了平差基准,也使得非差整数模糊度参数受到设备时延的“污染”而失去整数性质。文献[8-9]的特别和关键之处是通过选择并固定非差模糊度基准,建立其余非差模糊度参数的整数性质。由此可知,模糊度参数或其线性组合是否具有整数性质,取决于平差解算时被选作用于消除秩亏的基准。
由于载波相位的测量精度通常是伪码测量精度的100倍甚至更高,在以式(4)为观测方程的传统钟差解算方法中,伪距与相位的权比通常是1:10 000,甚至更低,因此伪距只是为模糊度参数提供了松弛的基准。如果能够像文献[8-9]那样选出并固定模糊度基准(更强的基准),则同样有望恢复出模糊度参数的整数性质。考虑到PPP用户只需要卫星的钟差,因此可以通过星间单差消除包含在模糊度参数中的接收机端的非整数偏差,然后通过星间单差模糊度固定将卫星钟差与具有整数性质的星间单差模糊度组合(下文简称为单差模糊度)分离,其中模糊度基准的选择与固定是这一过程的关键。
2 星间单差模糊度固定星间单差模糊度固定是在获得非差模糊度实数解的基础上进行的。由于消电离层组合模糊度的波长通常很短,例如对于GPS,L1和L2的消电离层组合的波长约为6 mm,直接固定消电离层模糊度非常困难[9]。一种有效的方法是将其分解为宽巷模糊度和窄巷模糊度,然后分别进行宽巷和窄巷模糊度固定[22-24]。与双差模糊度不同,单差模糊度并不天然地具有整数性质,因此固定单差模糊度的方法也与固定双差模糊度有很大区别:需要分离出卫星端的小数偏差和选择模糊度基准。本文通过以下3个步骤实现单差模糊度固定:
(1) 卫星端宽巷FCB解算。利用MW组合计算宽巷非差模糊度及其标准差的估值[28]:


(2) 宽巷单差模糊度固定。对于任意两颗卫星(s和l)间理论存在(被同一测站同步观测)的单差模糊度,利用式(6)计算其宽巷的估值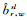
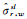
 (6)
(6)
然后,按照式(7)计算宽巷的固定成功概率。
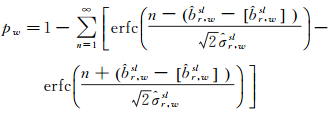 (7)
(7)
式中,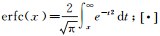
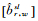
(3) 消电离层组合单差模糊度固定。消电离层组合单差模糊度固定按照以下3个步骤进行:
① 构造窄巷单差模糊度。对于所有固定了宽巷的单差模糊度,由式(8)计算与之对应的消电离层组合单差模糊度的估值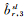
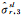
 (8)
(8)
式中,

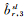
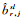
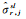
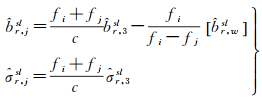 (9)
(9)
注意,至此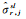
② 单差模糊度基准选择和固定。为了固定单差窄巷模糊度,需要为每个卫星钟差选择一个单差模糊度基准,并将其固定到最近的整数。需要强调的是,单差模糊度基准的选择非常关键,因为它们为其余的单差模糊度提供整数基准,是后续单差模糊度固定的基础。为了选出可靠的单差模糊度基准,本文先从每一对卫星中选出一个标准差最小的作为候选单差模糊度基准,然后将它们按照标准差的升序进行排列,采用最小生成树算法(如Kruskal算法)选出所有独立的卫星对(以GPS星座为例,卫星数为32颗,独立的卫星对有31对),将所对应的候选窄巷单差模糊度固定到最近的整数,进而对消电离层组合单差模糊度进行固定。
③ 独立单差模糊度固定。在完成了单差模糊度基准的选择与固定之后,剩余的单差模糊度就恢复了整数性质,就可以采用类似于双差模糊度固定的方法进行独立单差模糊度的序贯固定:基于已有的单差模糊度固定解对所有候选的未固定的单差模糊度按照式(7)重新计算其窄巷的固定成功概率,每次固定综合成功率最大的且与已固定的单差模糊度相互独立的消电离层组合单差模糊度,直到没有可固定的独立的单差模糊度为止。这一过程中采用Kruskal算法进行独立性判断。
在步骤②和③中,对消电离层组合单差模糊度(包括单差模糊度基准)进行“固定”是指按照式(10)利用固定了的宽巷和窄巷计算消电离层组合的整数解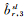
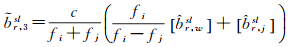 (10)
(10)
式中,
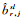
这样,本文进行卫星钟差解算的观测方程可等效地表示如下
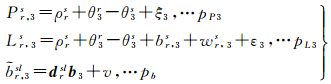 (11)
(11)
式中,p*为3类(虚拟)观测量的权,一般地,pL3/pP3≈104,而pb≫pL3。
3 验证本文提出的“整数”卫星钟差解算方法所采用的观测模型与传统的GNSS非差数据处理完全一致,数据处理时只需要在获得非差消电离层组合模糊度的实数解之后,增加星间单差模糊度固定过程。以上方法已经很方便地应用于西安测绘研究所研制的多功能GNSS数据处理软件SPODS[25]当中。
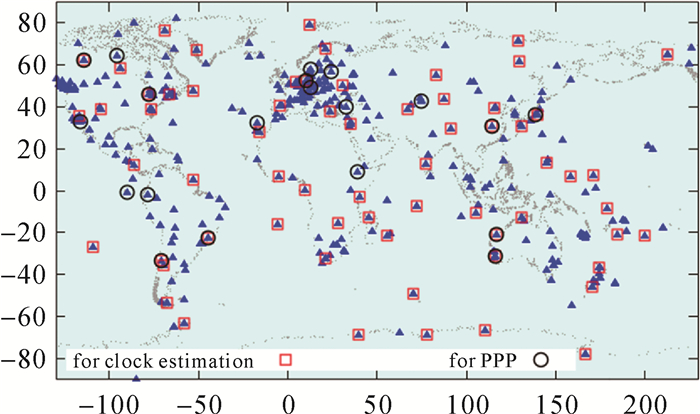
为了验证本文方法,笔者收集2015年DOY 243—261期间的IGS监测站的GPS数据进行钟差解算试验。测站分布如图 1所示,测站总数约为450个,其中66个测站(红色方形)用于解算钟差。在进行钟差解算时,将测站坐标和GPS卫星轨道固定到IGS最终轨道和站坐标产品,EOP参数采用IERS提供的最终产品;卫星和接收机的天线相位中心改正信息来自igs08.atx,测站的潮汐形变采用IERS2003协议,日月历表采用JPL DE405,对流层天顶延迟先验值采用Saastamoinen模型计算,映射函数采用GMF模型计算[26],天顶延迟采用分段常数模型模拟,每2 h解算一个参数,每24 h估计一组水平梯度参数。GPS卫星的姿态模型采用文献[27]提出的简化模型。数据处理弧长为24 h,数据采样间隔为300 s,采用文献[28]的方法将钟差加密到30 s。消电离组合伪距和相位的先验精度设为2 m和2 cm,并根据高度角e按照函数sin2e进行降权。在星间单差模糊度固定过程中,仅对固定成功概率大于99%且小数部分绝对值小于0.15周的单差模糊度进行固定,约束权pb取1010。
|
| 图 1 IGS测站分布 Fig. 1 Distribution of IGS stations |
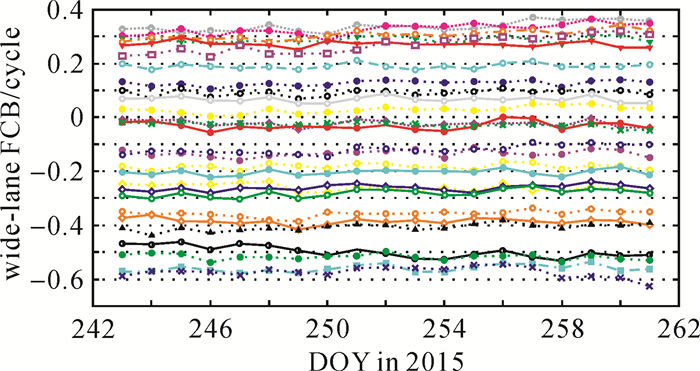
图 2绘出了各颗卫星的宽巷FCB(相对于PRN01)序列。可以看出,FCB的估值相当地稳定,统计表明重复精度在0.009周(PRN02)~0.031周(PRN04)之间。
|
| 图 2 GPS卫星星端宽巷FCB序列 Fig. 2 Estimated wide-lane FCBs for GPS satellites |
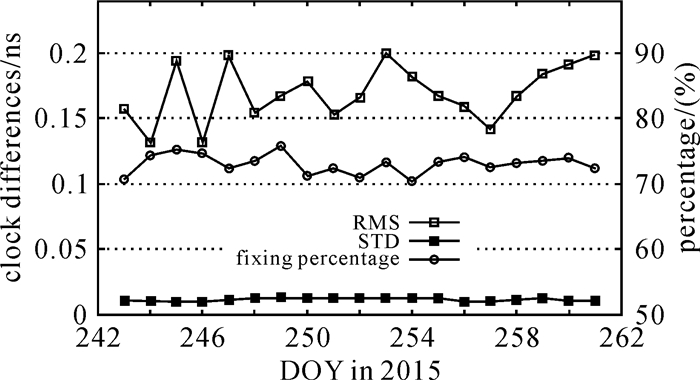
图 3按天统计了单差模糊度成功固定的比例及解算得到的卫星钟差与IGS最终钟差之差的RMS和STD。可以看出,模糊度固定的成功率稳定在70%~75%,平均固定成功率为73%。钟差的RMS为0.13~0.2 ns,STD都小于0.014 ns,平均的RMS和STD分别为0.17 ns和0.012 ns。
|
| 图 3 单差模糊度固定的比例和卫星钟差的精度 Fig. 3 Percentage of fixed BSSD ambiguities and the RMS and STD difference between the estimated satellite clocks and the IGS final clocks |
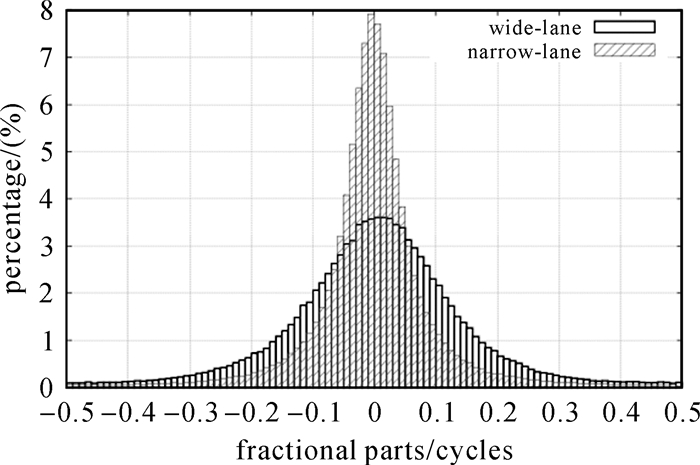
为了证明本文的钟差(和宽巷FCB)具备恢复出单台接收机的单差整数模糊度的能力,笔者利用所获得的DOY 250的宽巷FCB和卫星钟差对当天所有IGS测站(共448个)的观测数据进行PPP处理,得到非差消电离层组合模糊度的实数解之后,构造出所有可能的单差模糊度并进行宽巷FCB改正,而后进行宽巷单差模糊度固定,输出所有宽巷和固定了宽巷的窄巷单差模糊度,总个数分别为228 958和174 894,图 4统计了它们小数部分的分布。可以看出,宽巷和窄巷的小数部分均呈现出以0为均值的近似正态分布,其中,宽巷的小数部分绝对值小于0.2周的比例达到了85.8%,窄巷的这一比例达到了94.6%。这可说明宽巷和窄巷单差模糊度数学期望是整数,因此可以采用已有的模糊度固定方法对单差模糊度进行固定。
|
| 图 4 448个IGS测站宽巷和窄巷单差模糊度小数部分的分布 Fig. 4 Distribution of the fractional parts of wide-/narrow-lane BSSD ambiguities from 448 IGS stations |
为了展示利用本文的钟差(和宽巷FCB)进行PPP定位模糊度固定的效果。采用DOY 250共20个测站(图 1中圆圈表示的点)的数据进行模拟动态PPP试验。将每个测站的24 h rinex数据文件切分为12个2 h弧长的独立文件分别进行处理。卫星轨道固定到IGS最终轨道,采用不同的钟差产品或模糊度解算策略进行以下3组试验:
(1) 试验1(EXP1):采用IGS最终钟差产品,模糊度采用浮点解;
(2) 试验2(EXP2):采用本文的钟差产品,模糊度采用浮点解;
(3) 试验3(EXP3):采用本文的钟差产品并进行单差模糊度固定。模糊度固定采用序贯取整方法,具体方法见文献[22], 同样仅对固定成功概率大于99%且小数部分的绝对值小于0.15周的单差模糊度进行固定。
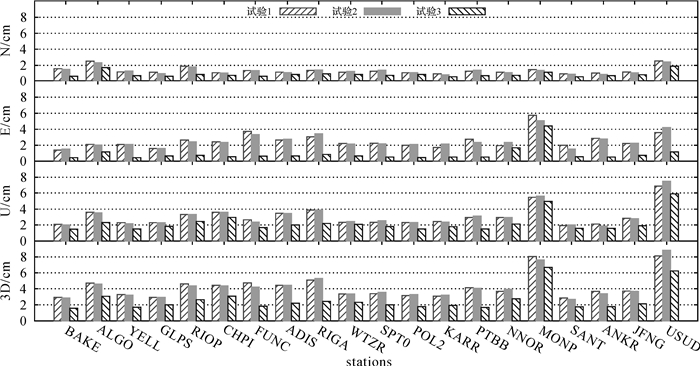
将定位结果与IGS天解的站坐标进行比较评估定位精度。图 5统计了3组PPP试验各测站N、E、U方向和三维位置(3D)误差的RMS。可以看出,试验2和试验1的结果在不同测站的RMS统计中互有优劣,但都相差不大;试验3各测站各方向坐标误差的RMS普遍地较试验1和试验2有明显减小,其中在E方向的改进尤为明显。统计表明,相比于试验1,试验3各测站N方向的改善幅度在14%~63%;E方向的改善幅度在10%~86%;U方向的改善幅度在4%~48%;3D定位精度的改善幅度在18%~60%。表 1给出了20个测站定位结果的平均RMS统计值。可以看出,相比于试验1,试验2的结果在毫米量级上没有差异;而试验3则在3个方向都有明显的提高,N、E、U和3D误差的RMS分别达到了0.009、0.010、0.023和0.027 m,比试验1分别提高了30.8%、61.5%、23.3%和37.2%。这说明模糊度固定有效提高了PPP的定位精度,再次证明了本文解算的钟差具有支持PPP模糊度固定的能力。需要说明的是,以上PPP试验仅是为了验证本文的整数钟差产品,所用的模糊度固定方法仍有改进余地。
|
| 图 5 3组试验各测站动态PPP定位误差的RMS Fig. 5 RMS of the kinematic PPP for each station |
| m | ||||
| 试验 | N | E | U | 3D |
| 试验1 | 0.013 | 0.025 | 0.031 | 0.042 |
| 试验2 | 0.013 | 0.025 | 0.031 | 0.042 |
| 试验3 | 0.009 | 0.010 | 0.023 | 0.027 |
4 总结
本文提出一种基于星间单差模糊度固定的卫星钟差解算方法,所得到的卫星钟差能够支持PPP用户进行整数模糊度解算。为了验证本文方法,采用IGS测站的GPS数据进行了钟差解算试验,结果表明星间单差模糊度固定的成功率约为73%,得到的卫星钟差与IGS最终钟差产品相比,平均的RMS差和STD分别为0.17 ns和0.012 ns。分析448个IGS测站的星间单差模糊度小数部分的分布表明,本文得到的卫星钟差和宽巷FCB产品能够恢复出单台接收机星间单差模糊度的整数性质。20个测站的模拟动态PPP定位结果表明,模糊度固定后,N、E、U和3D误差的RMS分别达到了0.009、0.010、0.023和0.027 m,相比于不固定模糊度或采用IGS最终钟差产品的结果,改进幅度分别为30.8%、61.5%、23.3%和37.2%,有力证明了本文方法的正确性和有效性。
本文实现星间单差模糊度解算固定的核心思想是通过选择和固定模糊度基准,恢复星间单差模糊度的整数性质,这一思想也可以应用于Galileo、BDS等其他GNSS系统的“整数”卫星钟差解算。
| [1] | GENG Jianghui, MENG Xiaolin, DODSON A H, et al. Integer Ambiguity Resolution in Precise Point Positioning:Method Comparison[J]. Journal of Geodesy, 2010, 84(9): 569–581. DOI:10.1007/s00190-010-0399-x |
| [2] | GENG Jianghui, SHI Chuang, GE Maorong, et al. Improving the Estimation of Fractional-cycle Biases for Ambiguity Resolution in Precise Point Positioning[J]. Journal of Geodesy, 2012, 86(8): 579–589. DOI:10.1007/s00190-011-0537-0 |
| [3] | GABOR M J, NEREM R S. GPS Carrier Phase Ambiguity Resolution Using Satellite-satellite Single Differences[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1999). Nashville, TN: Institute of Navigation, 1999: 1569-1578. |
| [4] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [5] | ZHANG Xiaohong, LI Pan, GUO Fei. Ambiguity Resolution in Precise Point Positioning with Hourly Data for Global Single Receiver[J]. Advances in Space Research, 2013, 51(1): 153–161. DOI:10.1016/j.asr.2012.08.008 |
| [6] | LI Xingxing, ZHANG Xiaohong. Improving the Estimation of Uncalibrated Fractional Phase Offsets for PPP Ambiguity Resolution[J]. Journal of Navigation, 2012, 65(3): 513–529. DOI:10.1017/S0373463312000112 |
| [7] | LAURICHESSE D, MERCIER F. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation. Fort Worth, TX: Institute of Navigation, 2007: 839-847. |
| [8] | LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS Ambiguity Resolution at CNES-CLS IGS Analysis Center[J]. Journal of Geodesy, 2012, 86(11): 991–1003. DOI:10.1007/s00190-012-0559-2 |
| [9] | COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 2010, 57(2): 123–135. DOI:10.1002/navi.2010.57.issue-2 |
| [10] | COLLINS P, LAHAYE F, HÉROUX P, et al. Precise Point Positioning with Ambiguity Resolution Using the Decoupled Clock Model[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation. Savannah: Institute of Navigation, 2008: 1315-1322. |
| [11] | BERTIGER W, DESAI S D, HAINES B, et al. Single Receiver Phase Ambiguity Resolution with GPS Data[J]. Journal of Geodesy, 2010, 84(5): 327–337. DOI:10.1007/s00190-010-0371-9 |
| [12] | LI Xingxing, GE Maorong, ZHANG Hongping, et al. A Method for Improving Uncalibrated Phase Delay Estimation and Ambiguity-fixing in Real-time Precise Point Positioning[J]. Journal of Geodesy, 2013, 87(5): 405–416. DOI:10.1007/s00190-013-0611-x |
| [13] | LI Pan, ZHANG Xiaohong, REN Xiaodong, et al. Generating GPS Satellite Fractional Cycle Bias for Ambiguity-fixed Precise Point Positioning[J]. GPS Solutions, 2016, 20(4): 771–782. DOI:10.1007/s10291-015-0483-z |
| [14] | GENG Jianghui, BOCK Y. GLONASS Fractional-cycle Bias Estimation Across Inhomogeneous Receivers for PPP Ambiguity Resolution[J]. Journal of Geodesy, 2016, 90(4): 379–396. DOI:10.1007/s00190-015-0879-0 |
| [15] |
潘宗鹏, 柴洪洲, 刘军, 等.
基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210–1218.
PAN Zongpeng, CHAI Hongzhou, LIU Jun, et al. Partial Ambiguity Resolution Method for Zero-difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210–1218. DOI:10.11947/j.AGCS.2015.20150056 |
| [16] | GENG Jianghui, SHI Chuang. Rapid Initialization of Real-time PPP by Resolving Undifferenced GPS and GLONASS Ambiguities Simultaneously[J]. Journal of Geodesy, 2017, 91(4): 361–374. DOI:10.1007/s00190-016-0969-7 |
| [17] | LI Pan, ZHANG Xiaohong, GUO Fei. Ambiguity Resolved Precise Point Positioning with GPS and BeiDou[J]. Journal of Geodesy, 2017, 91(1): 25–40. DOI:10.1007/s00190-016-0935-4 |
| [18] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211–225. DOI:10.1007/s10291-008-0089-9 |
| [19] | GENG Jianghui, TEFERLE F N, SHI C, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solutions, 2009, 13(4): 263–270. DOI:10.1007/s10291-009-0119-2 |
| [20] | JONGE P J. A Processing Strategy for the Application of the GPS in Networks[D]. Delft: Delft University of Technology, 1998: 238. |
| [21] |
黄维彬.
近代平差理论及其应用[M]. 北京: 解放军出版社, 1990: 525.
HUANG Weibin. Modern Adjustment Theory and Applications[M]. Beijing: The People's Liberation Army Press, 1990: 525. |
| [22] |
阮仁桂.
SPODS软件GPS/GNSS网解的模糊度解算方法[J]. 测绘学报, 2015, 44(2): 128–134.
RUAN Rengui. Ambiguity Resolution for GPS/GNSS Network Solution with SPODS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 128–134. DOI:10.11947/j.AGCS.2015.20130461 |
| [23] | GE Maorong, GENDT G, DICK G, et al. Improving Carrier-phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy, 2005, 79(1-3): 103–110. DOI:10.1007/s00190-005-0447-0 |
| [24] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km[J]. Journal of Geophysical Research, 1989, 94(B8): 10187–10203. DOI:10.1029/JB094iB08p10187 |
| [25] | RUAN Rengui, JIA Xiaolin, WU Xianbing, et al. SPODS Software and Its Result of Precise Orbit Determination for GNSS Satellites[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2014 Proceedings: Volume Ⅲ. Berlin: Springer, 2014: 301-312. |
| [26] | BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF):A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7): L07304. |
| [27] | KOUBA J. A Simplified Yaw-Attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1–12. DOI:10.1007/s10291-008-0092-1 |
| [28] | RUAN Rengui, WEI Ziqing, JIA Xiaolin. Estimation, Validation, and Application of 30-s GNSS Clock Corrections[M]//SUN Jiadong, LIU Jingnan, YANG Yuanxi, et al. Proceedings of China Satellite Navigation Conference (CSNC) 2017 Proceedings: Volume Ⅲ. Singapore: Springer, 2017: 21-36. |


