惯性导航系统(inertial navigation system,INS)是室外和室内导航定位系统的重要组成部分,具有自主性好、隐蔽性高、抗干扰强、导航信息丰富、短期导航定位精度高等优点[1-3]。受惯性元件误差和环境等因素的影响,INS导航解算误差随时间累积。惯性元件误差包括确定性误差和随机误差。确定性误差可以通过标定进行补偿消除,而随机误差由随机干扰引起,不具有明显的规律性,很难通过准确的函数模型表示,由于加速度计精度较高,因此陀螺随机误差是影响INS精度的主要因素[4-6]。故对INS输出信号进行降噪处理,能降低陀螺随机误差的影响,从而提高INS导航系统的精度。
小波分析具有良好的时频局部性和多分辨分析能力,通过小波变换对信号不同频率的成分进行分解,为噪声消除提供了有效的途径[7]。INS中陀螺随机误差表现为高频特性,真实信号大多集中在低频部分,故利用小波阈值降噪能削弱陀螺中的随机误差,提高导航精度[8, 9]。然而小波阈值降噪方法不能抑制异常噪声的干扰,且需事先确定基函数和分解层数,不具有自适应能力,同时降噪结果受阈值和阈值函数的影响较大[10]。
文献[11]针对非线性、非平稳信号提出了一种自适应的时频分析方法——经验模态分解(empirical mode decomposition,EMD),将原始信号自适应地分解成多个从高频到低频的本征模态函数(intrinsic mode function,IMF)分量和1个残余分量。由于EMD分解非常有效,受测不准误差影响较小,且不需要指定基函数和分解层数,广泛应用于陀螺信号降噪[12-14]、振动信号分析[15]、电磁信号降噪[16]等领域。当信号的信噪较低且存在脉冲干扰或异常噪声时,信号的极值点分布不均匀,从而产生模态混叠现象,导致相邻2个IMF分量混叠,难以区分[17-18]。文献[19]提出了集合经验模态分解(ensemble empirical mode decomposition,EEMD)方法,在原始信号中多次加入高斯白噪声进行EMD分解,然后对多次EMD分解的结果进行均值化处理,进而达到信号分解的目的,其利用高斯白噪声频率均匀分布的特征,有效抑制甚至消除模态混叠效应,从而获得更好的分解效果。
分解得到的多个IMF分量中,将纯噪声的IMF分量丢弃,对其余的IMF分量进行阈值降噪处理,然后进行信号重构得到降噪后的信号[13, 20]。文献[10]利用2σ准则剔除异常噪声,依据每个残余分量与原始信号的相关系数确定噪声IMF分量,将其余的IMF分量进行信号重构获得降噪信号,但未考虑噪声和信号共存的IMF分量的降噪过程,且相关系数确定噪声IMF分量的方法不具通用性。文献[12]在考虑惯性元件随机误差中分形高斯噪声的情况下,利用IMF分量间功率谱密度关系确定各IMF分量的噪声标准差,然后利用硬阈值方法进行阈值降噪处理。该方法降噪效果明显,但降噪后信号存在不连续问题。文献[13]利用EEMD对信号进行分解,并利用区间硬阈值和均值滤波方法对除第一阶以外的IMF分量进行降噪处理,利用静态陀螺数据和Allan方差进行了分析验证,但未给出纯噪声IMF分量的确定方法。
文献[21]提出了一种IMF分量与原始信号的概率密度函数(probability density function,PDF)之间的相似性度量方法。多次试验结果表明,基于2范数的几何相似性度量方法能获得较高精度。文献[22]对信号进行EMD分解,利用各IMF分量与原始信号PDF间的2范数距离的最大值确定噪声IMF分量,然后进行阈值降噪。当IMF分量中不存在噪声时,会出现后几个2范数距离高于噪声部分的情况,导致噪声IMF分量判断错误。针对上述问题,本文提出了一种基于EEMD的区间阈值降噪方法。该方法针对陀螺信号中的随机误差,首先对INS输出信号进行EEMD分解,将噪声和有用信号更好地分解在不同的IMF分量中;然后利用各IMF分量与原始信号PDF的2范数距离值确定噪声IMF分量;最后利用区间阈值降噪方法获得连续的降噪信号,提高INS导航精度。
1 EMD与EEMD算法EMD方法将信号自适应分解成多个具有不同特征尺度的IMF分量和1个残余分量,每个IMF分量既可以是线性的,也可以是非线性,其极值点个数和过零点个数相等或最多相差1个,且极值点构成的局部上下包络线的均值为零。对信号x(t)进行EMD分解的流程为[11]:
(1) 依据信号x(t)的极大值和极小值点,利用三次样条函数插值构造上下包络线并得到上下包络线的均值m1(t),用x(t)减去m1(t)得到消除低频部分的信号h1(t)。如果h1(t)满足IMF分量条件,则h1(t)则为第1个IMF分量c1(t),否则重复上述流程直到满足IMF分量条件为止。
(2) 用x(t)减去c1(t)得到第1个残余分量r1(t),将r1(t)按照流程(1)进行分解得到第2个IMF分量c2(t)。重复这一过程直到第n个残余分量rn(t)为单调函数时,EMD分解结束。
经过上述流程,信号x(t)分解为n个IMF分量和1个残余分量之和,即
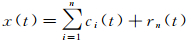 (1)
(1)
在实际信号分解中,IMF分量很难严格满足极值点构成的局部上下包络线的均值为零的条件,一般利用两个消除低频部分的信号hk-1(t)和hk(t)间的标准差代替上下包络线的均值为零的条件[18],即
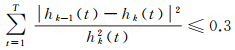 (2)
(2)
在EMD分解过程中,当信号的信噪较低且存在脉冲干扰或异常噪声时,将导致信号的极值点分布不均匀,从而出现模态混叠现象。即1个IMF分量中包含差异较大的特征尺度,或者相同特征尺度出现在不同的IMF分量中[17],导致相邻2个IMF分量混叠,相互影响,难以区分。为了解决模态混叠问题,文献[19]在EMD的基础上提出了EEMD方法。这是一种噪声辅助的信号分解方法,将高斯白噪声加入待分解的信号中补充缺失的特征尺度,进行多次EMD分解,对得到的IMF分量和残余分量进行总体平均得到最终的IMF分量和残余分量。由于其利用高斯白噪声频率均匀分布的特征,避免了模态混叠的问题,文献[17-19]给出了大量的仿真信号和实际信号的EMD与EEMD分解方法对比说明。对信号x(t)进行EEMD分解的流程为[17-19]:
(1) 设置总体平均次数M以及白噪声的幅值系数k,一般M取100,k取0.01~0.5倍信号标准差,当噪声太大可能淹没信号的本质特征,而噪声太小则不足以引起信号极值点的变化。通过多次试验,本文中k取0.2倍信号标准差。
(2) 在信号x(t)中加入随机的高斯白噪声序列得到新的信号,xm(t)=x(t)+knm(t),对信号xm(t)进行EMD分解得到n个IMF分量ci, m(t)和1个残余分量rn, m(t),i=1, 2, …, n。
(3) 重复流程(2)进行M次EMD分解,即m=1, 2, …, M。计算所有IMF分量和残余分量的均值,从而得到EEMD分解的结果为
 (3)
(3)
EEMD方法将信号分解成多个由高频到低频的IMF分量和1个残余分量,由于真实信号通常表现为低频部分,噪声信号表现为高频部分,因此剔除纯噪声的IMF分量,对其余的IMF分量进行阈值降噪处理,再与1个残余分量进行信号重构可得到降噪后的信号[20]。降噪后的信号可表示为
式中,
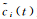
在纯噪声分量确定中,一般利用n个残余分量与原始信号的相关系数确定两个信号相似程度,然后利用经验阈值确定纯噪声IMF分量个数[10, 11],即
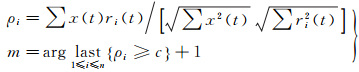 (5)
(5)
式中,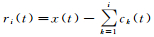
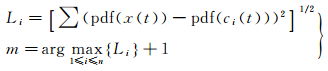 (6)
(6)
式中,pdf(x)为信号x的概率密度函数;Li为基于PDF的2范数距离。随着IMF分量的频率不断降低,纯噪声逐渐降到最低,下一阶IMF分量中真实信号最多,之后真实信号逐渐减少,Li整体呈现先增大再减小最后再增大的趋势;因而式(6)会存在后几个IMF分量的Li值高于噪声IMF分量的情况,从而出现噪声IMF分量判断错误。本文认为Li中第1个极大值为最后一个纯噪声IMF分量,下一阶则为噪声信号共存的IMF分量,即
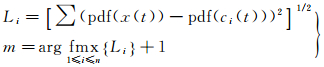 (7)
(7)
式中,fmx·为Li中第一个极大值,若Li单调减小且不存在局部极大值,则原始信号中没有噪声,若Li单调增加且不存在局部极大值,则残余分量为有用信号。
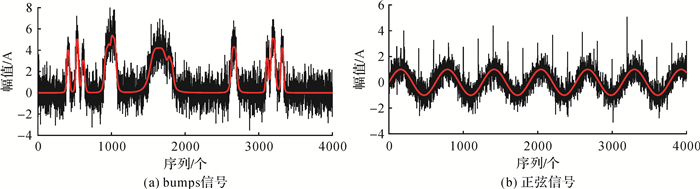
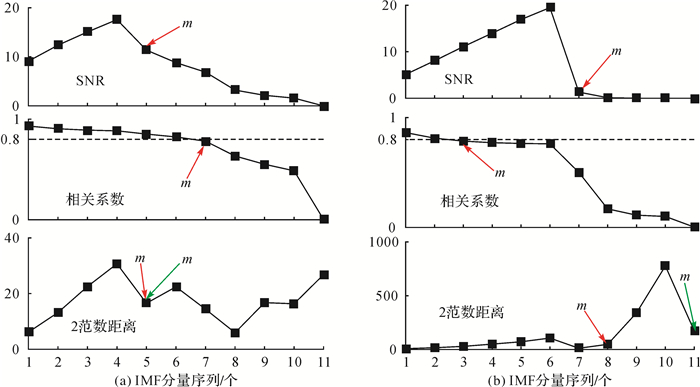
针对式(5)—式(7)的3种纯噪声IMF分量确定方法,利用仿真信号进行说明比较。仿真信号设置为:共两组信号,信号长度均为4000,第一组为bumps信号,第二组信号为正弦信号,两组信号中均添加信噪比为5 dB的高斯白噪声,第二组信号中每隔200个序列额外添加一个异常噪声,两组信号如图 1所示,其中红线为真实信号,黑线为含噪声信号。对两组信号进行EEMD分解均得到10个IMF分量和1个残余分量,利用式(5)—式(7)进行噪声分量的确定,m值的真实值由真实信号和n个残余分量计算的信噪比中最大值的下一阶得到。
|
| 图 1 Bumps和正弦仿真信号 Fig. 1 Bumps signal and sine signal |
图 2给出式(5)—式(7)3种方法确定m情况,其中“SNR”为真实信号和残余分量计算的信噪比,“相关系数”为残余分量与原始信号的相关系数,“2范数距离”为IMF分量(包括残余分量)与原始信号PDF的2范数距离,图中红色箭头为所确定的m值,“2范数距离”中红色箭头为式(7)得到的结果,绿色箭头为式(6)得到的结果。可以看出无论是bumps信号还是正弦信号,式(5)和式(6)两种方法存在m参数计算出错的情况,而式(7)中利用IMF分量与原始信号PDF的2范数距离方法能准确地确定纯噪声IMF分量的个数,得到更准确的m参数估值。
|
| 图 2 Bumps和正弦信号中m参数的确定 Fig. 2 Determine parametric m of bumps and sine signal |
2.2 区间阈值降噪
阈值降噪方法是建立在信号大于噪声的基础上,当纯噪声IMF分量的个数大于IMF分量总个数一半时,即m-1>n/2,此时信号中噪声较多,利用阈值降噪方法很难将噪声和有用信号有效分离。故当m-1>n/2时,不对信号进行降噪处理;当m-1≤n/2时,剔除纯噪声IMF分量进行降噪处理。
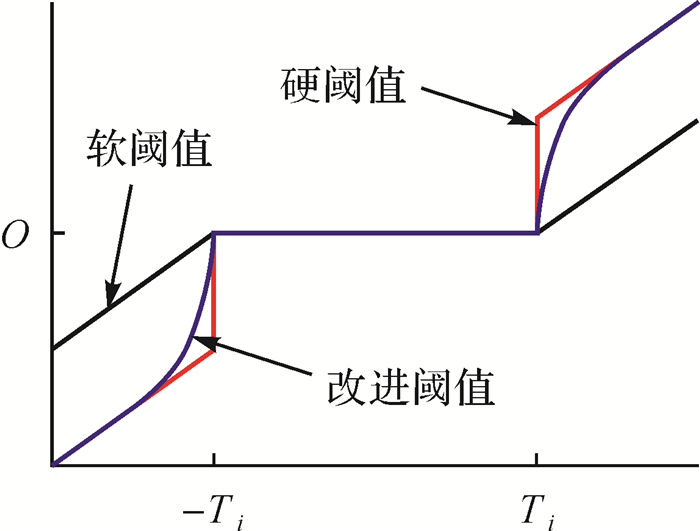
对于剔除纯噪声分量的IMF分量进行阈值降噪,将幅值低于设定阈值的部分置零,将高于阈值的部分进行保留或缩放处理,然后进行信号重构得到降噪后信号。硬阈值会导致信号在阈值处的不连续,软阈值对大于阈值的部分进行缩放会导致处理后的信号存在恒定的偏差[9, 22]。针对这一问题,本文提出一种改进的阈值函数。从图 3可以看出,改进的阈值函数既能保持信号在阈值处的连续性,又能保持信号不失真;同时结合区间阈值降噪方法进行处理,既保证降噪后信号的连续性又保证降噪后信号的不失真。
|
| 图 3 改进的阈值函数 Fig. 3 Improved threshold function |
区间硬阈值降噪方法为
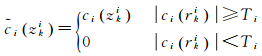 (8)
(8)
区间软阈值降噪方法为
 (9)
(9)
改进的区间阈值降噪方法为
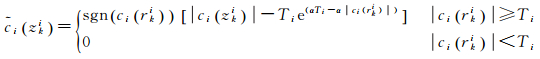 (10)
(10)
式中,sgn·为符号函数;zki=[zki, zk+1i]为第i个IMF分量中相邻两个过零点构成的区间;ci(zki)为区间zki内所有的值;rki为区间zki内的极值点;Ti为第i个IMF分量的阈值;α为调节因子,当α取0时,改进的阈值函数变为软阈值函数,当α趋于无穷大时,改进的阈值函数变为硬阈值函数,合理选择α能兼顾硬阈值和软阈值函数的优点,调节因子α≥100。通过区间内的极值点对整个区间进行统一的降噪处理。
由于第1阶IMF分量频率远高于有用信号的频率范围,其为纯噪声分量,文献[11]在此基础上推导了各个IMF分量与第1阶IMF分量噪声能量的关系
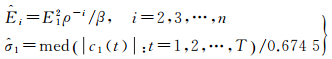 (11)
(11)
式中,
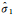
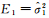
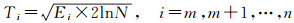 (12)
(12)
综上,利用EEMD区间阈值降噪的一般流程为:
(1) 对原始信号进行EEMD分解得到多个IMF分量和1个残余分量;(2)在多个IMF分量中,利用式(7)对纯噪声IMF分量进行判断并丢弃;
(3) 余下的IMF分量中,利用式(11)、式(12)得到各IMF分量的噪声阈值;
(4) 利用式(10)得到降噪后的IMF分量,最后通过式(4)得到降噪后的信号。
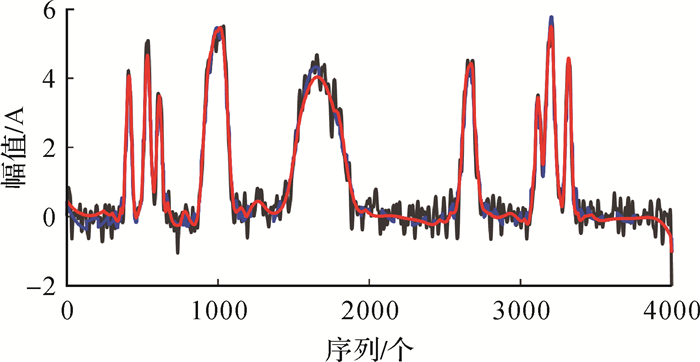
针对文中所提出的方法,采用3种方案(方案1:直接剔除纯噪声IMF分量;方案2:利用软阈值降噪方法;方案3:利用改进的区间阈值降噪方法)对2.1节中的bumps信号进行降噪处理。降噪结果如图 4所示,图中黑线为方案1结果,蓝线为方案2结果,红线为方案3结果。表 1给出了3种方案的信噪比和均方根误差。
|
| 图 4 Bumps信号的3种降噪结果 Fig. 4 Three de-noising methods of bumps signal |
| 参数 | 原始信号 | 方案1 | 方案2 | 方案3 |
| SNR/dB | 5.11 | 15.09 | 17.42 | 18.64 |
| RMS/A | 1.02 | 0.33 | 0.25 | 0.19 |
通过图 4和表 1可以看出,由于EEMD分解方法能较好地将噪声和有用信号分解到不同的IMF分量中,故3种方案均能降低原始信号中的噪声,提高信号的信噪比。相较于方案1和方案2,所提出的方案3能更有效地去除噪声,具有更高的信噪比和更低的均方根误差,在保留有用信号的同时保持降噪后信号的连续性。
3 试验与分析试验数据由惯性测量单元(inertial measurement unit,IMU)采集,其陀螺漂移和加速度计偏置分别为0.1°/h和0.06 mg,数据采样率为200 Hz,分别进行动态定位试验和静态测姿试验,并采用4种方案对IMU数据进行纯惯性导航解算:
方案1:利用原始的IMU数据进行解算。
方案2:利用去除EMD分解后的纯噪声IMF分量后的IMU数据进行解算。
方案3:利用去除EEMD分解后的纯噪声IMF分量后的IMU数据进行解算。
方案4:利用EEMD区间阈值降噪后的IMU数据进行解算。
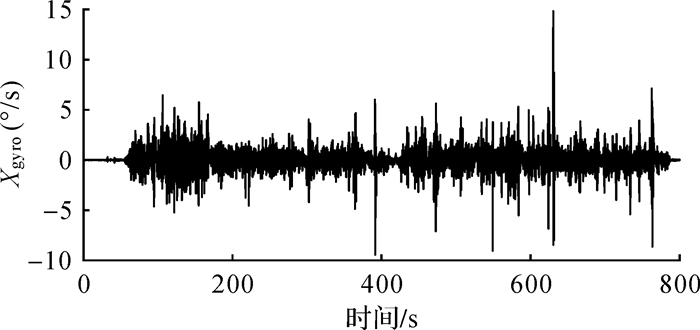
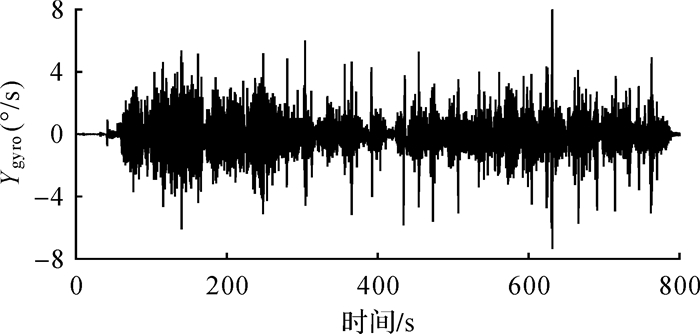
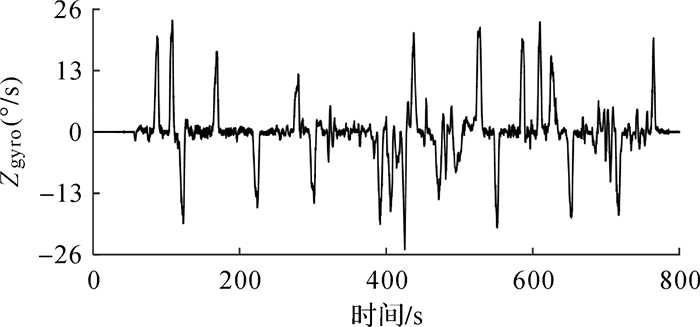
在动态定位中,将GPS和INS固定汽车顶部,在城市区域进行跑车试验。数据总长1200 s,前400 s为静态数据用于初始对准,后800 s为动态数据,用差分GPS与INS组合的结果作为参考真值,利用差分GPS的结果作为初始位置,利用上述4种方案进行定位解算。由于INS中加速度计精度较高,因此方案2—4只对陀螺数据进行处理,其中陀螺X轴、陀螺Y轴和Z轴的原始动态数据如图 5—图 7所示。
|
| 图 5 陀螺X轴原始信号 Fig. 5 Original signal of X gyro |
|
| 图 6 陀螺Y轴原始信号 Fig. 6 Original signal of Y gyro |
|
| 图 7 陀螺Z轴原始信号 Fig. 7 Original signal of Z gyro |
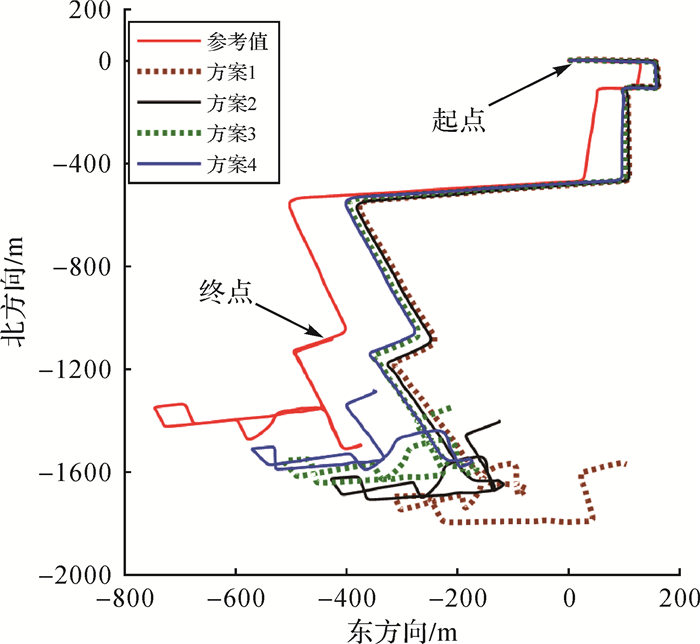
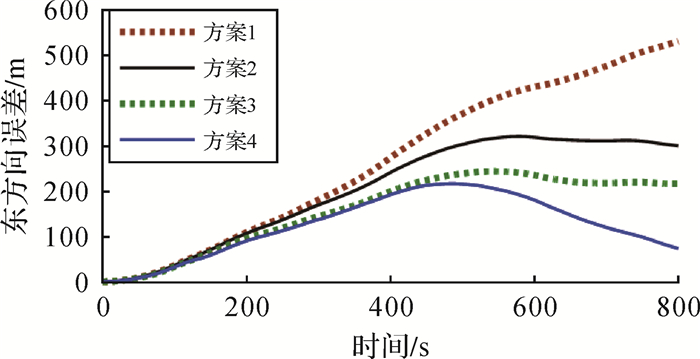
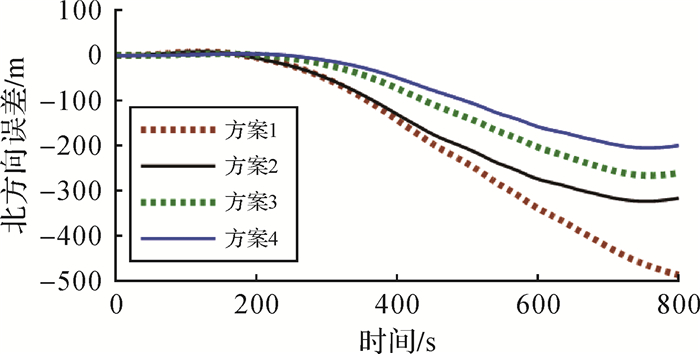
试验中,陀螺X轴、Y轴和Z轴的数据经EMD和EEMD分解后均为16个IMF分量和1个残余分量,利用式(7)计算纯噪声IMF分量个数。陀螺X轴的EMD分解和EEMD分解中的纯噪声IMF分量分别为前13个和前11个,由于均超过IMF分量总个数的一半,故不对陀螺X轴信号进行降噪处理;陀螺Y轴的EMD分解和EEMD分解中的纯噪声IMF分量分别为前2个和前3个;陀螺Z轴的EMD分解和EEMD分解中的纯噪声IMF分量分别为前2个和前3个。图 8为4种方案解算结果经高斯投影到平面中的轨迹,由于投影后坐标数值较大,故在横纵坐标上分别减去一个常值;图 9和图 10分别为4种方案在东方向和北方向上的误差,表 2为4种方案的最大误差和均方根误差。
|
| 图 8 4种方案解算的平面轨迹 Fig. 8 Plane trajectories of 4 schemes |
|
| 图 9 4种方案在东方向的误差 Fig. 9 East errors of 4 schemes |
|
| 图 10 4种方案在北方向的误差 Fig. 10 North errors of 4 schemes |
| m | |||||
| 误差 | 方案1 | 方案2 | 方案3 | 方案4 | |
| RMS | 东方向 | 317.38 | 233.30 | 177.91 | 141.85 |
| 北方向 | 247.80 | 189.49 | 141.61 | 109.79 | |
| MAX | 东方向 | 530.62 | 320.57 | 243.39 | 216.51 |
| 北方向 | 486.27 | 323.12 | 265.90 | 205.06 | |
动态试验中难以得到精确的姿态角信息。为进一步验证本文方法,利用一组静态IMU数据进行姿态解算,数据总长500 s,利用差分GPS的结果作为初始位置,通过初始对准确定初始姿态信息,并将初始对准的结果作为参考值,并利用上述4种方案进行姿态解算。由于加速度计精度较高,故对陀螺3轴的数据进行处理。
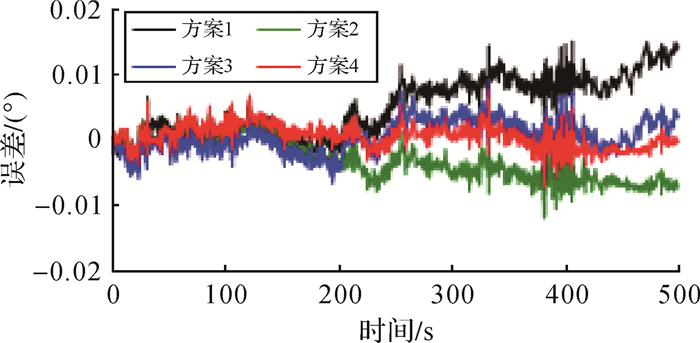
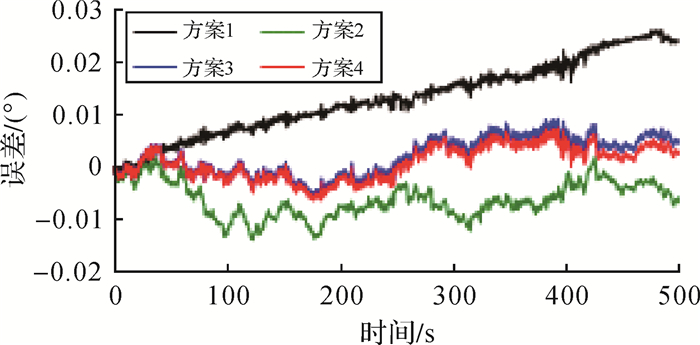
经EMD和EEMD分解后,陀螺X轴、Y轴和Z轴的数据均分解为15个IMF分量和1个残余分量,利用式(7)计算纯噪声IMF分量个数,其中Y轴和Z轴的前3个IMF分量均为纯噪声分量,X轴的前2个IMF分量为纯噪声分量。图 11—图 13分别为4种方案解算的横滚角误差、俯仰角误差和航向角误差,表 3为4种方案姿态解算的误差统计。
|
| 图 11 4种方案的横滚角误差 Fig. 11 Roll errors of 4 schemes |
|
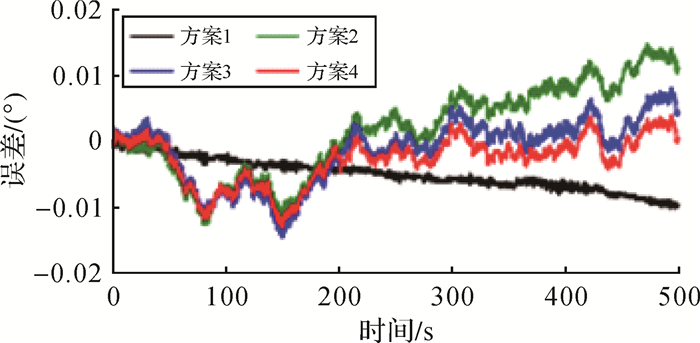
| 图 12 4种方案的俯仰角角误差 Fig. 12 Pitch errors of schemes |
|
| 图 13 4种方案的航向角误差 Fig. 13 Yaw errors of 4 schemes |
| (°) | |||||||
| 方案 | RMS | MAX | |||||
| 横滚角 | 俯仰角 | 航向角 | 横滚角 | 俯仰角 | 航向角 | ||
| 方案1 | 0.006 8 | 0.014 9 | 0.005 4 | 0.015 2 | 0.026 1 | 0.010 2 | |
| 方案2 | 0.004 3 | 0.007 2 | 0.007 1 | 0.011 9 | 0.014 1 | 0.014 8 | |
| 方案3 | 0.002 4 | 0.004 1 | 0.005 0 | 0.009 3 | 0.009 2 | 0.014 6 | |
| 方案4 | 0.001 7 | 0.003 3 | 0.004 5 | 0.007 8 | 0.007 5 | 0.013 2 | |
分析以上试验结果,可以得出:
(1) 对比方案1,方案2和方案3定位解算和姿态解算的精度更高、误差更小,说明EMD分解和EEMD分解能有效分离陀螺信号的随机噪声,在剔除纯噪声IMF分量后能提高INS导航精度;由于EMD分解中存在模态混叠问题,无法更好地将噪声和有用信号分离,甚至会消除部分有用信号,而EEMD分解能有效抑制模态混叠问题,能更好地将噪声和有用信号分离,从而能获得更高的导航精度。
(2) 对比方案3,方案4能更有效分离陀螺信号中随机噪声,在此基础上进一步提高INS姿态解算和定位解算的精度,说明区间阈值降噪方法能进一步将IMF分量中的随机噪声有效剔除,并保持降噪后信号的连续性,进一步提高INS导航精度。
(3) 在姿态解算中,方案2—方案4能有效抑制姿态角误差累积的速度,得到精度更高姿态信息;当信号中有用信号的细节部分与噪声特性相似时,EMD和EEMD分解会将部分有用信号当成噪声消除,导致方案2—方案4的航向角在50~180 s期间的误差比方案1误差更大;在动态定位中,受到陀螺X轴噪声和加速度计误差的影响,且EMD和EEMD方法均很难将混在噪声中的信号分离,4种方案解算的误差都会随时间的增加而不断积累,对陀螺Y轴和Z轴的数据进行降噪处理,能有效抑制误差累积的速度。
4 结论在惯性导航中,加速度计精度较高,陀螺随机噪声是影响惯性导航系统精度的主要因素,在针对EMD分解中存在模态混叠问题的基础上,本文利用EEMD分解方法进行陀螺数据处理,并提出了一种改进的区间阈值降噪方法。在仿真的信号中利用信噪比和均方根误差进行了分析验证,在动态定位和静态试验中通过纯INS解算进行了分析验证,试验结果表明本文方法能有效削弱陀螺随机噪声,从而提高INS精度和可靠性。当有用信号淹没在噪声中时,利用EEMD区间阈值降噪方法不能有效分离出信号;当有用信号的细节部分与噪声特性相似时,EMD和EEMD方法很难将部分有用信号和噪声进行分离,针对这两种情况下的信号降噪将是下一步的研究重点。
| [1] |
王巍.
惯性技术研究现状及发展趋势[J]. 自动化学报, 2013, 39(6): 723–729.
WANG Wei. Status and Development Trend of Inertial Technology[J]. Acta Automatica Sinica, 2013, 39(6): 723–729. |
| [2] |
甘雨. GNSS/INS组合系统模型精化及载波相位定位测姿[D]. 郑州: 信息工程大学, 2015. GAN Yu. GNSS/INS Integrated System Model Refining and Position and Attitude Determination Using Carrier Phase[D]. Zhengzhou: Information Engineering University, 2015. |
| [3] | HARLE R. A Survey of Indoor Inertial Positioning Systems for Pedestrians[J]. IEEE Communications Surveys & Tutorials, 2013, 15(3): 1281–1293. |
| [4] |
吴富梅. GNSS/INS组合导航误差补偿与自适应滤波理论的拓展[D]. 郑州: 信息工程大学, 2010. WU Fumei. Error Compensation and Extension of Adaptive Filtering Theory in GNSS/INS Integrated Navigation[D]. Zhengzhou: Information Engineering University, 2010. |
| [5] | STEBLER Y, GUERRIER S, SKALOUD J, et al. Generalized Method of Wavelet Moments for Inertial Navigation Filter Design[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 2269–2283. DOI:10.1109/TAES.2014.120751 |
| [6] |
张玉莲, 储海荣, 张宏巍, 等.
MEMS陀螺随机误差特性研究及补偿[J]. 中国光学, 2016, 9(4): 501–510.
ZHANG Yulian, CHU Hairong, ZHANG Hongwei, et al. Characteristics and Compensation Method of MEMS Gyroscope Random Error[J]. Chinese Optics, 2016, 9(4): 501–510. |
| [7] | DONOHO D L. De-noising by Soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613–627. DOI:10.1109/18.382009 |
| [8] |
吴富梅, 杨元喜.
基于小波阈值消噪自适应滤波的GPS/INS组合导航[J]. 测绘学报, 2007, 36(2): 124–128.
WU Fumei, YANG Yuanxi. GPS/INS Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold De-noising[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 124–128. |
| [9] |
刘晓光, 胡静涛, 高雷, 等.
基于改进小波阈值的微机械陀螺去噪方法[J]. 中国惯性技术学报, 2014, 22(2): 233–236.
LIU Xiaoguang, HU Jingtao, GAO Lei, et al. Micro Mechanical Gyro Denoising Method Based on Improved Wavelet Threshold[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 233–236. |
| [10] |
甘雨, 隋立芬.
基于经验模分解的陀螺信号消噪[J]. 测绘学报, 2011, 40(6): 745–750.
GAN Yu, SUI Lifen. De-noising Method for Gyro Signal Based on EMD[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 745–750. |
| [11] | HUANG N E, SHEN Zheng, LONG S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995. DOI:10.1098/rspa.1998.0193 |
| [12] | GAN Yu, SUI Lifen, WU Jiangfei, et al. An EMD Threshold De-noising Method for Inertial Sensors[J]. Measurement, 2014, 49: 34–41. DOI:10.1016/j.measurement.2013.11.030 |
| [13] |
崔冰波, 陈熙源, 宋锐.
EMD阈值滤波在光纤陀螺漂移信号去噪中的应用[J]. 光学学报, 2015, 35(2): 53–58.
CUI Bingbo, CHEN Xiyuan, SONG Rui. Application of EMD Threshold Filtering for Fiber Optical Gyro Drift Signal De-noising[J]. Acta Optica Sinica, 2015, 35(2): 53–58. |
| [14] |
刘晓光, 郝沙沙, 王光磊, 等.
基于自相关特性的经验模态分解微机械陀螺去噪方法[J]. 中国惯性技术学报, 2016, 24(4): 537–541.
LIU Xiaoguang, HAO Shasha, WANG Guanglei, et al. Micro Mechanical Gyro Denoising Method Based on EMD Autocorrelation[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 537–541. |
| [15] |
孙一航, 武建文, 廉世军, 等.
结合经验模态分解能量总量法的断路器振动信号特征向量提取[J]. 电工技术学报, 2014, 29(3): 228–236.
SUN Yihang, WU Jianwen, LIAN Shijun, et al. Extraction of Vibration Signal Feature Vector of Circuit Breaker Based on Empirical Mode Decomposition Amount of Energy[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 228–236. |
| [16] |
王金贵, 张苏.
基于频域约束独立成分分析的经验模态分解去噪方法[J]. 煤炭学报, 2017, 42(3): 621–629.
WANG Jingui, ZHANG Su. EMD Denoising Method Based on Frequency Domain Constrained Independent Component Analysis[J]. Journal of China Coal Society, 2017, 42(3): 621–629. |
| [17] |
窦东阳, 赵英凯.
集合经验模式分解在旋转机械故障诊断中的应用[J]. 农业工程学报, 2010, 26(2): 190–196.
DOU Dongyang, ZHAO Yingkai. Application of Ensemble Empirical Mode Decomposition in Failure Analysis of Rotating Machinery[J]. Transactions of the CSAE, 2010, 26(2): 190–196. |
| [18] |
李利品, 党瑞荣, 樊养余.
改进的EEMD算法及其在多相流检测中的应用[J]. 仪器仪表学报, 2014, 35(10): 2365–2371.
LI Lipin, DANG Ruirong, FAN Yangyu. Modified EEMD De-noising Method and Its Application in Multiphase Flow Measurement[J]. Chinese Journal of Scientific Instrument, 2014, 35(10): 2365–2371. |
| [19] | WU Zhaohua, HUANG N E. Ensemble Empirical Mode Decomposition:A Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1–41. DOI:10.1142/S1793536909000047 |
| [20] | KOPSINIS Y, MCLAUGHLIN S. Development of EMD-based Denoising Methods Inspired by Wavelet Thresholding[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1351–1362. DOI:10.1109/TSP.2009.2013885 |
| [21] | KOMATY A, BOUDRAA A O, AUGIER B, et al. EMD-based Filtering Using Similarity Measure Between Probability Density Functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27–34. DOI:10.1109/TIM.2013.2275243 |
| [22] | YANG Gongliu, LIU Yuanyuan, WANG Yanyong, et al. EMD Interval Thresholding Denoising Based on Similarity Measure to Select Relevant Modes[J]. Signal Processing, 2015, 109(1): 95–109. |
| [23] | SHIN, HWAN E. Estimation Techniques for Low-cost Inertial Navigation[D]. Calgary: University of Calgary, 2005. |
| [24] | SAVAGE P G. Strapdown Inertial Navigation Integration Algorithm Design Part 1:Attitude Algorithms[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(1): 19–28. DOI:10.2514/2.4228 |
| [25] | SAVAGE P G. Strapdown Inertial Navigation Integration Algorithm Design Part 2:Velocity and Position Algorithms[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 208–221. DOI:10.2514/2.4242 |



