现有卫星定位导航系统如GPS、GLONASS、BeiDou、Galileo和QZSS(日本准天顶卫星导航系统)及IRNSS(印度区域卫星导航系统), 以及相应的地基和星基增强系统,构建了全球定位、导航和授时(PNT)服务的基础设施。但是,卫星导航信号微弱,易被干扰和欺骗,地基增强和星基增强无线电导航定位信号也容易被干扰,而且所有无线电信号的穿透性能均较差,不能惠及地下、水下及其他被遮蔽区域的导航定位。于是多源PNT信息源的集成与融合应用将成为未来PNT服务的主要发展方向,即综合PNT服务体系[1-3];相应地,多传感器集成PNT服务也将成为PNT应用端的主流方向,而且多传感器集成必须小型化且低功耗,于是微型PNT将是综合PNT终端的核心技术[4-6]。随着未来综合PNT体系的建设以及微型PNT核心技术的突破,多源PNT组件的弹性集成、多源PNT函数模型的弹性调整和随机模型的弹性优化,即弹性PNT服务体系建设将成为研究热点。
所谓弹性PNT(resilient PNT,RPNT)体系是相对于固定PNT体系来说的。弹性PNT至今没有明确的定义,而且学术论文也不多。笔者仅基于综合PNT体系的服务或应用模式来描述弹性PNT,类似于组合PNT体系,但有区别。
弹性PNT定义:以综合PNT信息为基础,以多源PNT传感器优化集成为平台,以函数模型弹性调整和随机模型弹性优化为手段,融合生成适应多种复杂环境的PNT信息,使其具备高可用性、高连续性和高可靠性。
弹性PNT是近几年提出的PNT服务模式[7-10]。一般侧重讨论舰船多传感器的弹性集成应用,以增强PNT服务的可用性和安全性。已有公司开发出能用于舰船的定位、导航、授时的初步产品,目前在航海导航领域讨论较多。Gregory等[10]研究将多GNSS差分信息与AIS(automatic identification system)信息以及eLoran信息集成,构建测距模式(ranging-mode或R-Mode)PNT服务系统。
笔者认为,弹性PNT首先必须有冗余信息,否则不可能有“弹性”选择。弹性PNT的基本出发点是,任何一种单一的PNT信息源都可能存在风险,如GNSS提供的PNT服务尽管具有全天候、全天时和全球覆盖的特点,但GNSS存在明显的弱点,如信号易被遮蔽、易被干扰、易被欺骗,于是PNT服务的安全性、完好性得不到保障。凡涉及人身安全的PNT服务,必须确保安全可靠。于是,其他手段的“冗余”PNT信息源的利用就显得十分重要。弹性PNT是一种新型的PNT聚合,通过聚合冗余PNT信息源,改进陆、海、空、天动态载体导航定位的可靠性、安全性和稳健性。
RPNT与Parkinson[11]及美国国防部提出的“安全的PNT”(assured PNT,简称AsPNT)与美国联邦航空局(FAA)提出的“可选择的PNT”(alternative PNT, 简称AlPNT)[12, 13]意义相近。笔者认为,用“柔性PNT”(flexible PNT,简称FPNT)或笔者搭建的自适应导航定位理论[14-17],简称“自适应PNT”(adaptive PNT,简称AdPNT)也能表达实际含义。
本文所定义的新型弹性PNT是指,利用一切可利用的PNT信息源,生成连续、可用、可靠、稳健的PNT应用信息,其中“连续”、“稳健”和“可靠”的PNT信息生成是弹性PNT的核心。于是,弹性PNT必须包含硬件的弹性优化集成、函数模型的弹性优化改进、随机模型的弹性实时估计,以及多源PNT信息的弹性融合。
弹性技术方法已经广泛应用于风险管理与控制,其方法与智能学习与优化控制方法关系密切,如神经网络计算法、模糊计算法和遗传算法等。
1 多PNT传感器弹性集成复杂环境下,单一PNT服务体系存在不连续、不可用或不可靠风险,甚至完全失去服务能力。充分利用多传感器获取多源PNT信息是合理的选择,于是,需要多传感器的有效集成。
多传感器弹性集成指的是,多传感器分享共性组件,弹性优化集成满足兼容性的传感器组件,形成适应多种复杂环境的多功能PNT服务终端。见图 1。
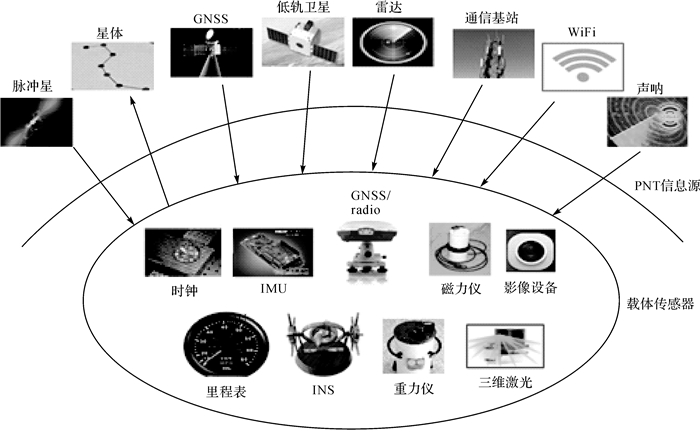
|
| 图 1 PNT信息源及多传感器集成 Fig. 1 PNT information sources and integration of sensors |
多传感器弹性集成强调:在优化集成的基础上,特殊场景采用特殊组合模式,确保复杂环境下的PNT终端的适应性。所有能接收到GNSS信号的地域或空域,都应该首先选用多源GNSS信号进行优化组合,并采取防欺骗、防干扰措施。其他复杂区域则应该采用不同的传感器集成方式。
室内PNT服务,可采用惯性传感器、磁力传感器以及室内无线电信标接收组件等进行优化组合。
水下PNT服务,尤其是深海水下PNT服务,可采用高精度惯性传感器、水下声呐信标接收传感器[18]、物理场匹配传感器、微型原子钟传感器等进行优化组合。
深空PNT服务,可采用脉冲星信号接收传感器、GNSS主瓣或旁瓣信号接收设备、惯性传感器、星敏感器等进行综合集成。
无论何种应用场景,多种不同物理原理PNT传感器都不能简单捆绑集成。简单捆绑集成的终端必然存在互相干扰、终端体积大、功耗高、可携带性差、实用性差等问题。为了实现多源传感器的“弹性集成”,多类微型化PNT(micro-PNT)传感器组件整体优化设计十分重要。
首先,各类传感器的集成必须一体化设计,如伺服组件和数据处理单元等能共用的组件必须共用;凡不能共用的,要确保互相兼容;各传感器相位中心的几何和物理关系应尽量保持固化,并具有精确的标校参数,以便实现归一化处理。
其次,各传感器的功能组合应该具备智能化,具备在特定场景根据PNT的感知能力进行优选组合,确保复杂场景PNT服务的连续性。
第三,弹性PNT终端的各类组件及其接口必须标准化,便于组件弹性组合和弹性替换。非标准化PNT传感器组件容易造成通联难,替换难,非标准化组件优化集成也十分困难,容易造成各类传感器的硬性捆绑,不利于集成后的传感器的小型化,不利于集成传感器的低功耗。
2 弹性函数模型观测函数模型及动态载体的动力学模型是多源PNT传感器信息融合的基础。通常情况下,观测函数模型及动力学模型在数据融合之前即已经确定,在数据融合过程中一般不作调整。实际上,任何观测函数模型都是在某种意义上的近似,如非线性函数模型的一阶近似,载体运动模型常采用简化的常速度模型或常加速度模型,载体偏离假设模型的任何变化都视为扰动,凡此种种,都会造成函数模型本身的误差。
一般情况下,函数模型误差与观测误差同等看待,即在最小二乘准则下进行误差补偿,求得待估参数的最优估计值。为了补偿函数模型误差,尤其是非线性模型线性化带来的误差,有学者采用粒子滤波(particle filter)、无迹滤波(unscented Kalman filter)[19]改善函数模型输出结果的精度,减弱模型误差影响;也有通过自适应滤波法方式[14-17]降低误差较大的函数模型在参数估计中的贡献,进而削弱其对状态参数估计的影响。
笔者所讨论的函数模型的弹性修正或弹性补偿,强调的是在对函数模型误差充分识别的基础上,建立函数模型误差的拟合模型,并实时或准实时地修改原有的函数模型,使其适应相应场景和相应传感器;函数模型的弹性处理还包含函数模型的弹性选择,即强调特殊的时期、特殊的场景选择备份好的特殊模型,使得模型的适应性最佳化。
观测函数模型弹性修正的概念模型如下
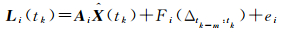 (1)
(1)
式中,Li(tk)为tk时刻第i个传感器的输出向量;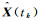
如果采用Kalman滤波,则动力学函数模型也可以附加弹性修正项
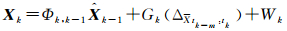 (2)
(2)
式中,Xk为tk时刻动力学模型预报参数向量;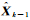
状态参数估计时,如果观测条件许可,则修正函数ΔLi(tk)和ΔXk(tk)中的未知参数可以采用增广参数向量的方法,与状态向量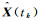
式(1)和式(2)与附加参数的观测模型有相似之处[14],利用附加待估参数来补偿模型误差计算相对简单,可以与状态参数并行计算。但是,附加参数估计法,通常只估计单历元的模型误差,不具备模型误差预报校正功能。尤其在没有外部高精度参考PNT信息的条件下,这种单历元估计的模型补偿参数,不具备多历元模型误差纠正的能力。
3 弹性随机模型随机模型表示的是随机变量之间的不确定性及其相互关系,一般以统计值给出,如随机变量的期望、方差、协方差、误差分布等。在参数估计领域,随机模型一般作为先验信息给出,在参数估计过程中一般不再变动。
弹性随机模型指的是,各PNT传感器的随机模型在状态参数估计过程中不是固定不变的,而是随着观测信息不确定度的变化而弹性变化。在数据融合领域,随机模型的弹性调整已经有很丰富的研究成果,如基于方差分量估计的参数估计[21-24],基于方差分量估计的融合导航[25, 26]和基于抗差估计准则的多传感器PNT数据融合[27]等都属于弹性随机模型范畴。
将观测函数模型式(1)和动力学模型式(2)写成误差方程
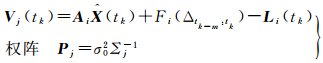 (3)
(3)
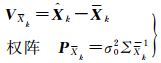 (4)
(4)
其中观测向量Li的协方差矩阵为Σj,由于考虑了函数模型的弹性调整部分,则Lj的协方差矩阵为
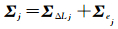 (5)
(5)
式中,Σej为观测随机噪声的协方差矩阵,ΣΔLj为弹性函数模型误差修正向量的协方差矩阵。
动力学模型预报的状态向量为Xk,相应协方差矩阵为ΣXk,相应表达式分别为
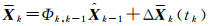 (6)
(6)
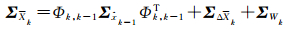 (7)
(7)
式中,ΣΔXk为动力学模型的弹性调整向量的协方差矩阵,ΣWk为动力学模型本身的随机误差协方差矩阵。
为了使不同观测在状态参数估计中对应合理的贡献,往往采用方差分量估计或方差-协方差分量估计[21-24, 27, 28],重新调整观测的权重,即随机模型弹性化调整。如果有r个传感器输出观测信息Lj(j=1, 2, …, r),假设各传感器输出信息统计不相关,先验权矩阵为Pj,若认定先验协方差矩阵能可靠反映观测向量或状态预报向量的不确定度,则基于最小二乘准则,可获得状态向量的最小二乘估计式
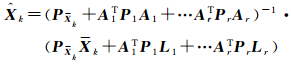 (8)
(8)
式(8)给出的状态参数估计为非弹性估计向量,如果各协方差矩阵不能可靠地表征相应随机向量的不确定度,则可以利用各随机向量的残差向量及方差分量估计方法重新求得相应的方差因子σ0j2(包括σXk2),并重新求得相应协方差矩阵。假设,经过N次迭代计算,各随机向量的方差因子趋于一致,都约等于σ02,再重新确定各随机向量的权矩阵[23, 25, 28],迭代模型如下
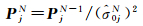 (9)
(9)
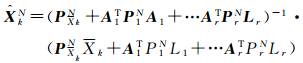 (10)
(10)
为了控制异常误差对随机模型估计的影响,也可在进行方差分量估计时,采用抗差估计准则[24, 25, 27],使得随机模型的弹性调整不受个别异常误差影响。
抗差估计本身也属于基于弹性随机模型的参数估计。抗差估计采用观测残差重新确定观测等价权[29-31],残差大的相应观测方差弹性增大,或相应观测权弹性减小。相应参数估计式为
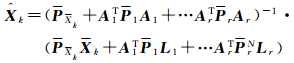 (11)
(11)
式中PXk和Pj分别为状态预报向量及观测随机向量Lj的等价权矩阵。所有等价权矩阵都是基于残差确定的,其中第j组观测Lj的第i个观测Lji的权元素为pji,可以采用IGGIII权函数[31],也可以用其他成熟的等价权函数。
若考虑动力学模型存在异常扰动,同时考虑观测信息存在异常误差,则可采用自适应抗差估计法进行多传感器PNT的弹性融合[16, 17]。
4 结论综合PNT是安全PNT应用的必然趋势,而弹性PNT又是综合PNT的重要支撑;没有弹性PNT,综合PNT很难发挥作用;弹性PNT包括信息的弹性利用,多传感器的弹性集成,弹性函数模型建立,弹性随机模型建立及弹性数据融合。弹性PNT不仅强调满足可用性的多源PNT信息的利用,更强调满足最优性的弹性优化集成、弹性函数模型优化和弹性随机模型优化等。基于最优化准则的弹性PNT才能满足综合PNT的连续性、可用性、稳健性和可靠性。
| [1] | Department of Transportation and Department of Defense of USA. National Positioning, Navigation, and Timing Architecture Implementation Plan[R]. Washington D C: [s. n. ], 2010. |
| [2] | MCNEFF J. Changing the Game Changer, The Way Ahead for Military PNT[J]. Inside GNSS, 2010: 44–45. |
| [3] |
杨元喜.
综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505–510.
YANG Yuanxi. Concepts of Comprehensive PNT and Related Key Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 505–510. DOI:10.11947/j.AGCS.2016.20160127 |
| [4] | SHKEL A M. Precision Navigation and Timing Enabled by Microtechnology: Are We There Yet?[C]//Proceedings of the SENSORS, 2010 IEEE. Kona, HI: IEEE, 2010. |
| [5] | SHKEL A M. Microtechnology Comes of Age[J]. GPS World, 2011, 22(9): 43–50. |
| [6] |
杨元喜, 李晓燕.
微PNT与综合PNT[J]. 测绘学报, 2017, 46(10): 1249–1254.
YANG Yuanxi, LI Xiaoyan. Micro-PNT and Comprehensive PNT[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1249–1254. DOI:10.11947/j.AGCS.2017.20170249 |
| [7] | ZIEBOLD R, DAI Z, LANCA L, et al. Initial Realization of a Sensor Fusion Based Onboard Maritime Integrated PNT Unit[J]. TransNav, the International Journal on Marine Navigation and Safety of Sea Transportation, 2013, 7(1): 127–134. |
| [8] | ZIEBOLD R, DAI Z, NOACK T, et al. Concept for an On-board Integrated PNT Unit[J]. TransNav, the International Journal on Marine Navigation and Safety of Sea Transportation, 2011, 5(2): 149–156. |
| [9] | ZIEBOLD R, DAI Zhen, NOACK T, et al. The On-board Maritime PNT Module-Integrity Monitoring Aspects and First Experimental Results[C]//Proceedings of the 14th International Scientific and Technical Conference on Marin Traffic Engineering. Swinouscie, Polen: [s. n. ], 2011. |
| [10] | GREGORY J, SWASZEK P, ALBERDING J, et al. The Feasibility of R-Mode to Meet Resilient PNT Requirements for E-navigation[C]//Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation. Tampa, Florida: ION, 2014: 3076-3100. |
| [11] | PARKINSON B. Assured PNT for Our Future: PTA Actions Necessary to Reduce Vulnerability and Ensure Availability[C]//Proceedings of the 25th Anniversary GNSS History Special Supplement. [S. l. ]: GPS World Staff, 2014. |
| [12] | FAA Navigation Services, AJW-91. Industry Day for Alternate, Position, Navigation and Timing[EB/OL], SatNavNews, Vol. 38, Winter 2010/2011. https://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/gnss/library/satnav/media/satnavnews_winter2011_final.pdf. |
| [13] | NARINS M. The Benefits of Alternative Positioning, Navigation, and Timing (APNT) to Aviation and Other Users: The Need for Robust Radio Navigation, in Integrated Communications[C]//Navigation and Surveillance Conference. Herndon, VA, USA: IEEE, 2012: 1-37. |
| [14] |
杨元喜.
自适应动态导航定位[M]. 北京: 测绘出版社, 2006.
YANG Yuanxi. Adaptive Dynamic Navigation and Positioning[M]. Beijing: Surveying and Mapping Press, 2006. |
| [15] |
杨元喜, 何海波, 徐天河.
论动态自适应滤波[J]. 测绘学报, 2001, 30(4): 293–298.
YANG Yuanxi, HE Haibo, XU Tianhe. Adaptive Robust Filtering for Kinematic GPS Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 293–298. |
| [16] | YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109–116. DOI:10.1007/s001900000157 |
| [17] | YANG Yuanxi, GAO Weiguang. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177–183. DOI:10.1007/s00190-006-0041-0 |
| [18] |
杨元喜, 徐天河, 薛树强.
我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1–8.
YANG Yuanxi, XU Tianhe, XUE Shuqiang. Progresses and Prospects in Developing Marine Geodetic Datum and Marine Navigation of China[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 1–8. DOI:10.11947/j.AGCS.2017.20160519 |
| [19] | YANG Cheng, SHI Wenzhong, CHEN Wu. Comparison of Unscented and Extended Kalman Filters with Application in Vehicle Navigation[J]. The Journal of Navigation, 2016, 70(2): 411–431. DOI:10.1017/S0373463316000655 |
| [20] | YANG Y, ZHANG S. Adaptive Fitting of Systematic Errors in Navigation[J]. Journal of Geodesy, 2005, 79(1-3): 43–49. DOI:10.1007/s00190-005-0441-6 |
| [21] | KOCH K R. Bayesian Inference for Variance Components[J]. Manuscripta Geodaetica, 1987, 12(2): 309–313. |
| [22] | KOCH K R. Maximum Likelihood Estimate of Variance Components[J]. Bulletin Gæodésique, 1988, 60(4): 329–338. |
| [23] |
杨元喜, 徐天河.
基于移动开窗法协方差估计和方差分量估计的自适应滤波[J]. 武汉大学学报(信息科学版), 2003, 28(6): 714–718.
YANG Yuanxi, XU Tianhe. An Adaptive Kalman Filter Combining Variance Component Estimation with Covariance Matrix Estimation Based on Moving Window[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6): 714–718. |
| [24] | WISNIEWSKI Z. Concept of Robust Estimation of Variance Coefficient (VR-estimation)[J]. Bollettino di Geodesia e Scienze Affini, 1999, 58(3): 291–310. |
| [25] |
杨元喜, 高为广.
基于方差分量估计的自适应融合导航[J]. 测绘学报, 2004, 33(1): 22–26.
YANG Yuanxi, GAO Weiguang. Integrated Navigation by Using Variance Component Estimates of Multi-sensor Measurements and Adaptive Weights of Dynamic Model Information[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 22–26. |
| [26] | YANG Yuanxi, CUI Xianqiang, GAO Weiguang. Adaptive Integrated Navigation for Multi-sensor Adjustment Outputs[J]. The Journal of Navigation, 2004, 57(2): 287–295. DOI:10.1017/S0373463304002711 |
| [27] | YANG Yuanxi, XU Tianhe, SONG Lijie. Robust Estimation of Variance Components with Application in Global Positioning System Network Adjustment[J]. Journal of Surveying Engineering, 2005, 131(4): 107–112. DOI:10.1061/(ASCE)0733-9453(2005)131:4(107) |
| [28] |
杨元喜, 张菊清, 张亮.
基于方差分量估计的拟合推估及其在GIS误差纠正的应用[J]. 测绘学报, 2008, 37(2): 152–157.
YANG Yuanxi, ZHANG Juqing, ZHANG Liang. Variance Component Estimation Based Collocation and Its Application in GIS Error Fitting[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 152–157. |
| [29] | YANG Yuanxi. Robust Bayesian Estimation[J]. Bulletin Géodésique, 1991, 65(3): 145–150. DOI:10.1007/BF00806343 |
| [30] | YANG Yuanxi. Robust Estimation for Dependent Observation[J]. Manuscripta Geodeatica, 1994, 19(1): 10–17. |
| [31] | YANG Y X, SONG L Q, XU T H. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353–358. DOI:10.1007/s00190-002-0256-7 |

