2. 河南城建学院, 河南 平顶山 467036
2. Henan University of Urban Construction, Pingdingshan 467036, China
随着传感器技术的发展,数据获取手段的不断增加,传统的二维数据已经逐渐不能满足用户的需求,LiDAR、城市模型、地下管网、空间动态目标及气象海洋等三维空间数据的研究和应用越来越多。三维空间数据具有体量大、种类多、类型复杂及尺度多样等特点,导致其组织和管理的难度越来越大,因此,如何围绕三维空间信息的管理,设计一种有效的空间索引计算方法是亟待解决的难题。
三维空间区域划分是建立空间编码与索引的基础。一般而言,三维空间索引的研究方法与二维空间索引相似,多数为二维空间向三维空间的推广,如二维空间划分索引中有规则格网、四叉树、不规则R树等,与之对应,三维空间有三维格网、八叉树、三维不规则R树等。现阶段常用的空间索引按照其对划分后空间的实现方法的不同,大致可以分成两大类:
(1) 空间树状索引。经典的空间树状索引有KD树[1-2]、八叉树[3-6]、R树及其变种树[7-12]、R树相关改进算法[13-14]和K-D-B树[15]、QR树[16-17]等组合索引方法。空间树状索引能够与对象的空间分布相适应,但是受树深的影响较大,且动态维护困难。采用空间树状索引管理不同尺度尤其是尺度差异较大的数据时存在较大的局限性,因为不同尺度对应于不同深度的数据,容易导致查询路线变长,耗时更多,且查询不平衡。R树及其改进树虽然具备比较好的多尺度信息管理能力,但是由于R树是一种平衡树,导致其更新和维护的成本较高,其索引结构本身的复杂性导致索引所占空间巨大,一定程度上影响了它的有效性,特别是在三维空间中,一些高动态的对象及其更新的处理,会直接降低R树的效率。
(2) 空间编码索引。空间编码索引是建立在空间格网划分基础上的一种顺序结构,适用于空间信息组织管理,能够快速实现对象的多尺度编码,且可以根据格网与目标之间的对应关系,实现对象的快速访问和关系计算[18]。经典的空间编码索引有规则格网[19-20]、空间填充曲线[21]、多级格网[22-23]及自适应格网[24]等。从编码的方法来看,空间编码索引主要分为两种:一种是采用变长的字符串/数组对格网进行编码。该方法中,不同位上的数/字符代表不同尺度/层级的格网,通过字符串/数组的长度来确定划分深度,在操作上需要涉及数组循环与下标操作,在海量数据计算中,存在局限性,如多级格网等。另一种是采用定长的数对格网进行编码,再通过增加额外的信息实现尺度/深度编码,如空间填充曲线或规则格网等。该方法利用空间排序确定单尺度格网的编码,并附加上尺度/深度信息,由于尺度和编码分离,因此在对空间区域进行查询时,需要同时考虑编码和尺度两个因素,运算复杂度较高。
问题:能否在现有空间编码索引的基础上,设计一种同时顾及尺度与空间的定长整数编码,使其能够有效地规避现有方法存在的问题,实现基于单整数的计算而无须多字段或者逐字段的处理。笔者所在团队于2016年针对一维的时间信息,提出了一种新型的多尺度剖分和整数编码方法[25],并提供了完全基于位操作的计算方法,极大地提升了时间信息的多尺度计算的效率。参照上述一维编码的多尺度整数化方法,本文针对三维空间提出了一种多尺度的整数编码方法,采用整数编码代替传统空间坐标来对格网进行组织和管理,目的是实现三维多尺度格网的编码及高效的空间检索和计算。
1 三维多尺度整数编码设计方案首先给出几个基本概念:
三维单尺度整数编码(three dimensions single-scale integer coding,TDSIC)指的是采用整数统一地对单一尺寸格网构成的空间区域进行编码,建立整数与格网坐标之间的一一对应关系。
三维多尺度整数编码(three dimensions multi-scale integer coding,TDMIC)指的是采用整数统一地对多种尺寸格网构成的空间区域进行编码,建立整数与格网坐标之间的一一对应关系。
三维空间整数化编码设计是在利用格网对空间区域进行剖分的基础上进行的,充分利用计算机处理的优势,采用整数对空间区域中的每一个格网进行编码,仅通过位域操作和加减运算即能实现空间数据编码与计算,既考虑了编码的可行性也兼顾了编码运算的高效性。下面主要从三维单尺度整数编码的设计和三维多尺度编码的设计两个方面进行叙述。
1.1 三维单尺度整数编码的设计对整个三维的研究空间(定义为0级空间)进行八叉划分,将空间等分成8个相同的子空间,再将每个子空间继续划分为8个相同的更高级别的子空间,如此递归下去,直到达到规定的最高层级N-1级,共N级。
常见的三维空间不同的编码方式有Z序编码、H序编码、Gray序编码等。本文方法理论上支持各种排序编码方法。在众多的编码方式中,Z序编码和H序编码的应用最为广泛,由于Z序编码可以利用Mordon码[26]的方式,快速形成行列编码,对编码在高维空间的平移计算具有较大的优势。除此之外,Z编码在维数变化、网格排序及P-赋范距离等方面性能均优于H序编码[27],这些优势也被代入多尺度化的Z序编码计算中。因此,本文采用三维的Z曲线对空间区域进行填充,每一级具体的编码规则如图 1所示,具体叙述如下。
从图 1中可以看出该编码是由一系列整数构成的一维Z形曲线。采用一个m bit的整数(在x64的机器上m=64,可以根据系统位数不同进行调整或者利用内存拼接进行扩展,本文以m=64说明编码方法)来进行编码,为了确定每一个格网对应整数的值,需要建立整数与格网局部坐标的对应关系,设格网局部坐标为(x, y, z),其中x, y, z均为不小于0的整数。为了充分使用存储空间,满足编码结构简单、高效及多尺度编码的需求,设计了格网坐标系,其坐标结构体如表 1所示。
| 含义 | X | Y | Z |
| 位数 | 21 | 21 | 21 |
| 取值范围 | 0~2 097 151 | 0~2 097 151 | 0~2 097 151 |
| 存储值 | X方向格网坐标 | Y方向格网坐标 | Z方向格网坐标 |
由于需要将64 bit的整数平均分配给X、Y、Z3个坐标轴(与编码交叉取位有关),则每一个坐标轴的取值范围为0~221-1即0~2 097 151,如表 1所示。
根据Z形编码的结构特点,在进行编码时,可以通过交叉取位的方法来获取每一个格网的整数编码,即先将十进制的X、Y、Z坐标转换成二进制编码,均为21位,不足的用0补齐,然后再按照Z、Y、X的顺序,依次取位,组成一个63位的二进制编码,最后将该编码转换成十进制的整数,即实现了单尺度整数编码。如格网坐标为(2, 0, 2)对应的编码计算步骤如下:①对应的二进制编码(10, 00, 10);②采用三维Mordon[26]交叉取位得到101000;③得到十进制整数编码40。
前文所提方法只需通过位操作就能建立三维单尺度编码,具有高效的特点,但是这种编码方法只能对一个层级的格网进行编码,格网的尺寸固定,无法同时对不同尺度的格网进行编码。而在对一个场景进行表达时,一般都需要用到多个尺度的格网信息,对于细节层次要求高的地方要采用小尺寸的格网;反之,则需要采用大尺度的格网。因此,在实际的应用过程中,需要有多个尺度的格网协同工作,这就要求编码方法具有多尺度的特性。
1.2 三维多尺度整数编码的设计为了解决单尺度整数编码存在不能表达多尺度信息的缺点,在三维单尺度整数编码的基础之上,提出了一种多尺度的编码方法。其核心思想是用一个64 bit的整数将不同尺度下的格网编码同时在空间和尺度层上进行排序,通过整数运算体现编码的层级及格网间的空间关系。
由于一个63 bit的整数就能实现单尺度编码(基础层级第21级),而多尺度编码的实质是一个八叉树金字塔结构,按照等比数列求和的原理,基础层级(第21级)之上所有层级(前20级)所有网格的总数为
(1) 不同尺度整数编码后的排序应该和单一尺度网格编码排序在空间上前后关系保持一致。
(2) 不同尺度整数编码后应该能体现不同尺度网格间的包含层级关系。例如:空间中任意一个三维网格整数编码应该能够通过运算,快速得到包含该网格内所有三维网格编码的整数区间,并且是连续的。
基于上述目标,三维多尺度整数编码TDMIC的设计采用下面的基本思路:在单尺度整数编码基础上,对单尺度的编码的整数值×2(左移1位),得到多尺度编码中最大尺度(层级最大,分辨率最高)的编码值。很明显,在这一个层级中的整数编码值均为偶数,空出了所有的奇数值,后续层级的编码都在此层的基础之上产生,并且利用的就是空出的奇数值。具体是将每相邻的8个编码值取平均,就可以得到下一个层级中的编码值,依此类推,便实现了场景的多尺度整数编码,原理如图 2所示。这样设计的目的主要是为了将尺度和空间信息同时编码,一方面顺序体现了单一尺度格网的排序,另一方面也体现了尺度间的顺序,还可以通过编码值的大小关系,保证父单元和子单元的包含关系。其产生方法如下:
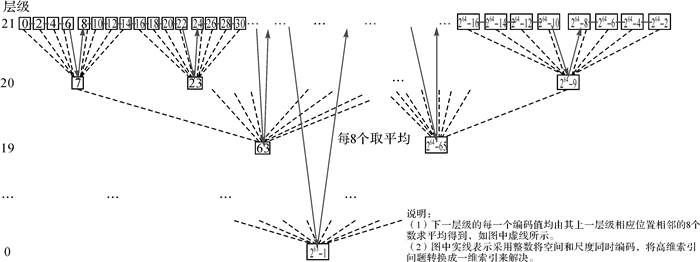
|
| 图 2 多尺度编码示意图 Fig. 2 Illustration of the formation of a multi-scalar code |
第1步:按照1.1节中方法建立三维单尺度整数编码。
第2步:将通过第1步计算得到的整数编码值都乘以2,即左移一位,得到第21层也就是基础层级的编码值。由此可见,这一个层级的编码值均为偶数,相邻编码值之差为2。
第3步:实现多尺度编码其他层级编码值的计算。以第21层为基础,每8个相邻的值为一组取平均值,得到第20层的编码值;然后以第20层为基础,每8个编码值为一组取平均值,得到第19层的编码。依次类推,便可得到每一个层级的编码值。很明显,除基础层以外,其余各层的编码值均为奇数。
根据编码原理,对多尺度编码的性质进行了归纳,约定符号如表 2所示,具体描述如下:
| 符号 | 含义 |
| TDSC | 三维单尺度整数编码集合 |
| TDSC(i) | 三维单尺度整数编码中的第i个元素 |
| TDMC | 三维多尺度整数编码集合 |
| N | 三维多尺度整数编码的层级 |
| ΔTDMC(N) | 三维多尺度整数编码第N层的编码间隔 |
| TDMC(N,i) | 三维多尺度整数编码第N层第i个格网的编码值 |
| TDMC(N) | 三维多尺度整数编码第N层的编码集合 |
三维多尺度整数编码层级范围
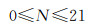 (1)
(1)
三维多尺度整数编码第N层编码间隔
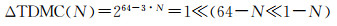 (2)
(2)
三维多尺度整数编码第N层第0个编码值
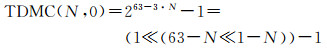 (3)
(3)
三维多尺度整数编码第N层第i个编码值
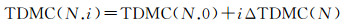 (4)
(4)
三维多尺度整数编码第N层i的取值范围
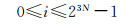 (5)
(5)
根据三维多尺度整数编码的原理及性质可知,三维多尺度整数编码方法其本质是一颗倒立的八叉树。对空间区域建立三维多尺度整数编码,所有的编码值会形成一个整数集合,将集合中的整数作为输入,建立B树、B+树索引或其他一维索引,由于整数本身就包含了空间顺序和尺度顺序,因此只需对该集合进行一维排序(从大到小或从小到大),就可以形成多尺度空间信息的存储与索引方式,将尺度三维+尺度空间的索引问题转换为一维索引进行解决,从而达到提高效率的目的。
2 三维多尺度整数编码计算方法三维多尺度整数编码计算指的是利用位域操作及加减运算实现编码的空间关系计算。本节结合三维多尺度整数编码的特点,重点研究了编码层级运算、编码与格网坐标转化运算、父单元查询及子单元查询等基础运算。其中,编码层级计算是进行编码运算的基础,编码与格网坐标转换运算是建立多尺度整数编码与三维空间联系的关键,父、子单元查询可以用于确定编码间的空间关系。
2.1 编码层级运算多尺度编码具有多个层级,不同的层级编码数值不一样,相应的格网尺寸也不一样。因此,在进行多尺度编码以后,任意给定一个编码,在使用过程中,需要确定的就是编码层级。设多尺度编码的数值为Mc,总层级为N,其算法原理描述如下[25]:
首先需要判断编码值Mc的奇偶性,如果为偶数,则位于基础层级,如果为奇数则需要进一步的计算,主要是计算Mc-1与Mc+1最近的相同父单元,即数值Mid=(Mc-1)∧(Mc+1)左边有多少位为0,从而达到计算层级的目的。
具体实现步骤叙述如下:
(1) 若Mc为偶数,则有Mc&1=0,可得层级N=21。
(2) 若Mc为奇数,通过异或运算计算整数Mid=(Mc-1)∧(Mc+1),其目的是计算Mc-1和Mc+1前面高位有多少位是相同的,找这两个多尺度整数编码最近的相同父编码。
(3) 通过分支方法确定整数Mid(64 bit)左边有多少位是0,计算多尺度整数编码Mc的层级N。首先令N=0:
① 利用0xFFFFFFFF00000000取Mid的高位,然后右移32位得到Mid0,判断Mid0是否为0。若Mid0≠0,则Mid=Mid0,N不变;否则,Mid=Mid&0x00000000FFFFFFFF,N=32。
② 利用0xFFFF0000取Mid的高位,然后右移16位得到Mid0,判断Mid0是否为0。若Mid0≠0,则Mid=Mid0,N不变;否则,Mid=Mid&0x0000FFFF,N=N+16。
③ 利用0xFF00取Mid的高位,然后右移8位得到Mid0,判断Mid0是否为0。若Mid0≠0,则Mid=Mid0,N不变;否则,Mid=Mid&0x00FF,N=N+8。
④ 利用0xF0取Mid的高位,然后右移4位得到Mid0,判断Mid0是否为0。若Mid0≠0,则Mid=Mid0,N不变;否则,Mid=Mid&0x0F,N=N+4。
⑤ 利用0xC取Mid的高位,然后右移2位得到Mid0,判断Mid0是否为0。若Mid0≠0,则Mid=Mid0,N不变;否则,Mid=Mid&0x3,N=N+2。
⑥ 利用0x2取Mid的高位,然后右移1位得到Mid0,判断Mid0是否为0。若Mid0≠0,则Mid=Mid0,N不变;否则,Mid=Mid&0x1,N=N+1。
⑦ 对按以上步骤计算得到的N进行转换得到层级n,所用公式如下
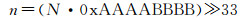 (6)
(6)
三维多尺度整数编码在格网场景应用的过程中,需要快速地进行编码与格网坐标之间的转换,即根据编码,实现格网坐标的快速计算。格网坐标的计算首先需要确定该编码所在的层级,进而确定该编码对应的基础层级子单元编码对应的体素坐标,最终根据多尺度生成的规则(8个相邻的体合并得到上一层级的单元)通过移位操作计算得到格网坐标。设多尺度编码值为Mc,则有计算方法和步骤如下:
(1) 计算编码的层级N。编码所在的层级决定了相应格网的尺寸,也是进行编码转换的基础,可以采用上述层级计算的方法快速得到给定编码的层级N。
(2) 将编码转换到基础层级编码上,并计算得到编码范围,取最小编码值Mcmin。三维多尺度整数编码由三维单尺度整数编码发展而来。因此,要实现多尺度编码与格网坐标之间的转换,首先需要找到该编码对应的基础层级编码。
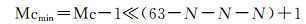 (7)
(7)
(3) 将最小编码值转换为单尺度编码。通过第二步计算得到基础层级对应的编码以后,根据式(8),可以计算得到单尺度编码的值Sc
 (8)
(8)
(4) 计算得到单尺度编码对应的格网坐标(i, j, k)。由1.1节中内容可知,根据格网的坐标,通过交叉取位的方式可以计算得到单尺度编码值。同样的,根据编码值,可以通过逆向交叉取位的方法计算得到相应的格网坐标。
(5) 计算得到第N层的格网坐标(Ni, Nj, Nk)。完成上述步骤,计算得到单尺度编码对应的格网坐标以后,只需要进行移位计算就可以得到多尺度编码对应格网的坐标,计算方法如下
 (9)
(9)
利用格网对空间区域进行多尺度表达时,需要找到与小尺寸格网位置关系相对应的大尺度格网,在不影响表达效果的前提下,用大尺度格网代替小格网,减少数据量,提高效率。
根据编码生成规则可知,父单元查询的关键在于计算查询层级的起始编码值与相对于起始编码值的编码间隔,通过这两个量即可实现父单元的查询。
已知多尺度整数编码Mc,需要查询层级为N′(N′≤N)的父单元FMc,具体步骤如下:
(1)计算第N′层编码中的第1个整数编码oTN′, 根据式(10)可以得到
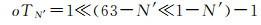 (10)
(10)
(2) 计算第N′级的父单元编码相对于第一个编码的间隔ΔFMc
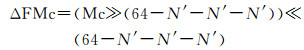 (11)
(11)
(3) 计算第N′级的父单元编码FMc
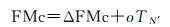 (12)
(12)
在格网的应用过程中,需要根据编码对其子单元进行查找,确定编码间对应的空间关系;在进行三维表达时,由于视点的变化,也需要用小尺度的格网,来代替大尺度的格网,使得表达效果更加的逼真。
给定一个多尺度整数编码值Mc,相应的层级为N,计算其包含所有第N′的整数编码NT, 其中N′≥N。
由于多尺度整数编码在整数排序上,满足包含关系,进行子单元查询时,只需要确定多尺度编码对应的范围即可。若层级为N的整数值,包含最小尺度的范围[A, B],则有
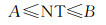 (13)
(13)
 (14)
(14)
 (15)
(15)
式中,oTN表示第N层第0个编码值,可由式(3)计算得到。
对于特定层级子单元的查询,只需在计算A和B在该层级对应的父单元即能实现。
3 试验与分析为了验证三维多尺度编码多尺度转换及区域查询的效率,本文共设计了两组试验。试验1为多尺度转换试验,通过统计编码向不同尺度转换消耗的时间,验证多尺度转换的效率;试验2为与Oracle Spatial的对比试验,从数据导入、索引建立及区域查询3个方面进行对比,验证三维多尺度整数编码在这3个方面的效率。试验环境如下:
硬件为Intel(R)Core(TM) i5-4590 CPU(3.1 GHz),8 GB,硬盘为1 TB;操作系统为Windows 7 64 bit;编译环境为Visual Studio 2013,Release版本,x64,c++,数据库版本:Oracle 11.2.0.1.0。
3.1 三维单尺度编码与三维多尺度编码转换试验三维多尺度整数编码的优势很大一部分在于其多尺度性,因此需要对单尺度到多尺度编码之间的转换效率进行测试。试验1就是为了实现这个目的而设计。试验数据采用的是模拟数据,随机生成格网坐标作为试验数据,格网坐标范围与前文设计的体素坐标范围一致,具有一般性,其试验流程如下:随机生成n个格网坐标(每一个坐标轴坐标的取值范围为0~2 097 151);对生成的n个格网坐标进行三维单尺度整数编码;分别将生成的n个三维单尺度整数编码转换为第21层、第19层、第17层以及第15层的三维多尺度整数编码,并分别统计消耗的时间;分别将上述转换结果转换为单尺度编码,并分别统计消耗的时间。
将n分别取8 000 000、27 000 000、64 000 000,分别进行10次试验,取平均值,最终统计信息如表 3所示。
| 操作 | n=8 000 000 | n=27 000 000 | n=64 000 000 | |||||
| 总耗时/s | 效率/(个/ms) | 总耗时/s | 效率/(个/ms) | 总耗时/s | 效率/(个/ms) | |||
| 转换为第21层的多尺度编码 | 0.035 000 | 228 571 | 0.117 900 | 229 007 | 0.289 000 | 221 453 | ||
| 转换为第19层的多尺度编码 | 0.034 900 | 229 226 | 0.118 200 | 228 426 | 0.287 600 | 222 531 | ||
| 转换为第17层的多尺度编码 | 0.034 300 | 233 236 | 0.118 500 | 227 848 | 0.299 100 | 213 975 | ||
| 转换为第15层的多尺度编码 | 0.035 000 | 228 571 | 0.115 700 | 233 362 | 0.296 200 | 216 070 | ||
| 第19层编码值转换为单尺度编码 | 0.071 600 | 111 731 | 0.245 500 | 109 979 | 0.633 000 | 101 105 | ||
| 第17层编码值转换为单尺度编码 | 0.073 200 | 109 289 | 0.251 500 | 107 355 | 0.637 600 | 100 376 | ||
| 第15层编码值转换为单尺度编码 | 0.072 100 | 110 957 | 0.247 700 | 109 002 | 0.634 600 | 100 850 | ||
由试验结果可知:三维多尺度整数编码每一层的转换效率是一样的,在三维单尺度整数编码与三维多尺度整数编码相互转换的过程中,与转换的层级无关,只与转换编码个数相关,其时间复杂度为O(n)。
3.2 与Oracle Spatial进行对比试验本文重点强调多尺度整数编码方法对多尺度数据的组织优势,因此,选择R树作为对比对象,一是R树着重解决的就是多种不同尺度对象的混合索引问题;二是R树是现阶段空间格网数据的管理中应用最广泛的索引,便于与其他类型的索引进行横向对比;三是R树能够有效地组织和管理不同尺度的三维空间数据[28-32],也是目前最主要的商业化三维空间数据索引代表。其中Oracle从9i开始通过Oracle Spatial组件提供了对三维R树的支持,其实质是将二维R树拓展到了三维空间,它能够很好地解决了高维空间区域查找的问题,拥有较高的查询效率。
为了验证三维多尺度编码的可靠性,设计了与Oracle Spatial的对比试验,从数据导入、索引建立及区域查询3个方面进行比较。其具体原理如下所示:
假设整个空间的尺度为0~21层,按照第21层的格网最小粒度为单位1,以此定义坐标。
(1) 根据层级要求,随机生成字符串,字符串的有效数值为0~7(按照递归八分的方式划分空间,由于每一个格网都将被划分为8份,因此只需0~7之间的整数即能实现划分后每一个格网的标识),每一个字符串对应一个格网,其中字符串中的有效数值个数n表示相应格网的层级为第n层,字符串中的第i个数j表示第i层的第j个格网。如字符串431表示的含义为:该字符串对应第3层的格网,表示的是第1层的第4个格网,第1层的第4个格网在第2层八分中的第3个格网,第2层格网基础上在第3层上八分的第1个格网,如图 3所示。由此可见,字符串唯一确定了格网的位置。

|
| 图 3 数据生成原理图 Fig. 3 The data generation scheme |
(2) 根据生成的字符,生成格网对应的多尺度整数编码值和相应的8个顶点坐标分别作为多尺度整数编码和Oracle Spatial的试验数据。其中生成跨度为3个尺度(第7层—第9层)、5个尺度(第7层—第11层)、10个尺度(第7层—第16层)、15个尺度(第7层—第21层)的数据各1000万条、15个尺度(第7层—第21层)的数据各1000万条、2000万条、5000万条、7000万条以及1亿条(每条数据对应一个格网信息,对于多尺度整数编码来说是一个编码值,对于Oracle Spatial而言指的是8个顶点坐标)。
(3) 将上述数据分别导入数据库中,并统计数据导入时间以及建立索引的时间。
(4) 任意选择1000个第n1—n2层的不同大小的格网范围作为查询区域,分别进行查询,对比Oracle Spatial和多尺度整数编码的效率,统计总时间,再求平均。
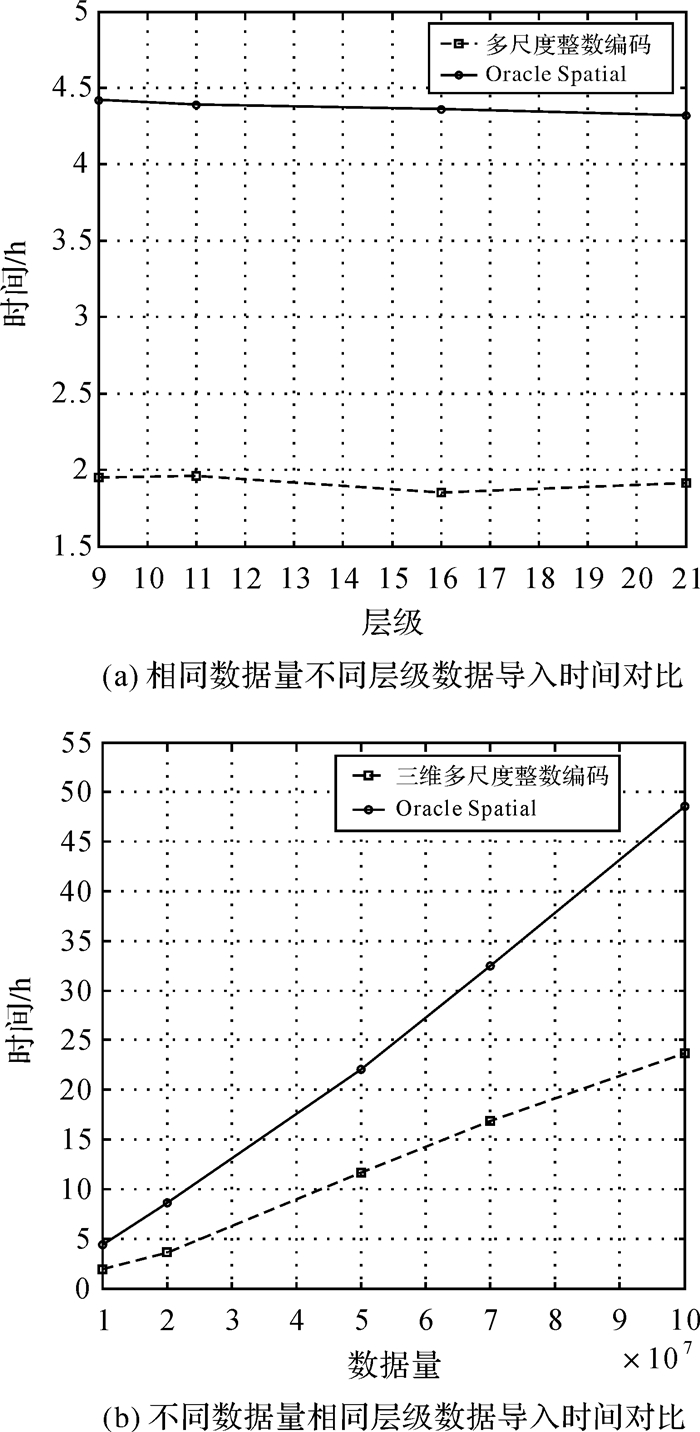
| 序号 | 层级范围 | 数据量 | 多尺度整数编码/h | Oracle Spatial/h |
| 1 | 7—9 | 10 000 000 | 1.95 | 4.42 |
| 2 | 7—11 | 10 000 000 | 1.96 | 4.39 |
| 3 | 7—16 | 10 000 000 | 1.85 | 4.36 |
| 4 | 7—21 | 10 000 000 | 1.91 | 4.32 |
| 5 | 7—21 | 20 000 000 | 3.60 | 8.61 |
| 6 | 7—21 | 50 000 000 | 11.69 | 22.01 |
| 7 | 7—21 | 70 000 000 | 16.87 | 32.42 |
| 8 | 7—21 | 100 000 000 | 23.64 | 48.52 |
|
| 图 4 数据导入时间对比 Fig. 4 Comparison of data import times |
设计对比试验导入数据时,由于多尺度整数编码导入的是一个64 bit的整数,而Oracle Spatial导入的数据为相应的格网范围,即8个顶点坐标,数据量本身就要大于多尺度整数编码,因此耗时较长,具体如表 4和图 4所示。
表 4统计了两种不同的数据导入数据库的时间信息。图 4是表 4中信息的直观表示,其中图 4(a)表示两种方式下相同数据量不同层级跨度的数据导入时间对比,对应表中1—4组试验;图 4(b)表示不同数据量,相同层级跨度的数据导入时间对比,对应表中4—8组试验。综合分析图表可知:
图 4(a)中曲线平稳,在导入数据量不变的情况下,消耗的时间基本保持不变,而图 4(b)中曲线均匀变化,在层级不变的情况下,导入数据消耗的时间随数据量的增加而增加,呈正相关,而且Oracle Spatial数据导入时间的曲线斜率大于多尺度整数编码, 约为多尺度整数编码的2倍。由此可以得出,两种方式的数据导入时间与层级无关,与数据量正相关,且Oracle Spatial方式数据导入时间长于多尺度整数编码,且随数据量增加变化更加明显。
按照设计的方案进行试验,可以得到两种方式建立oracle索引的时间对比信息,如表 5和图 5所示。
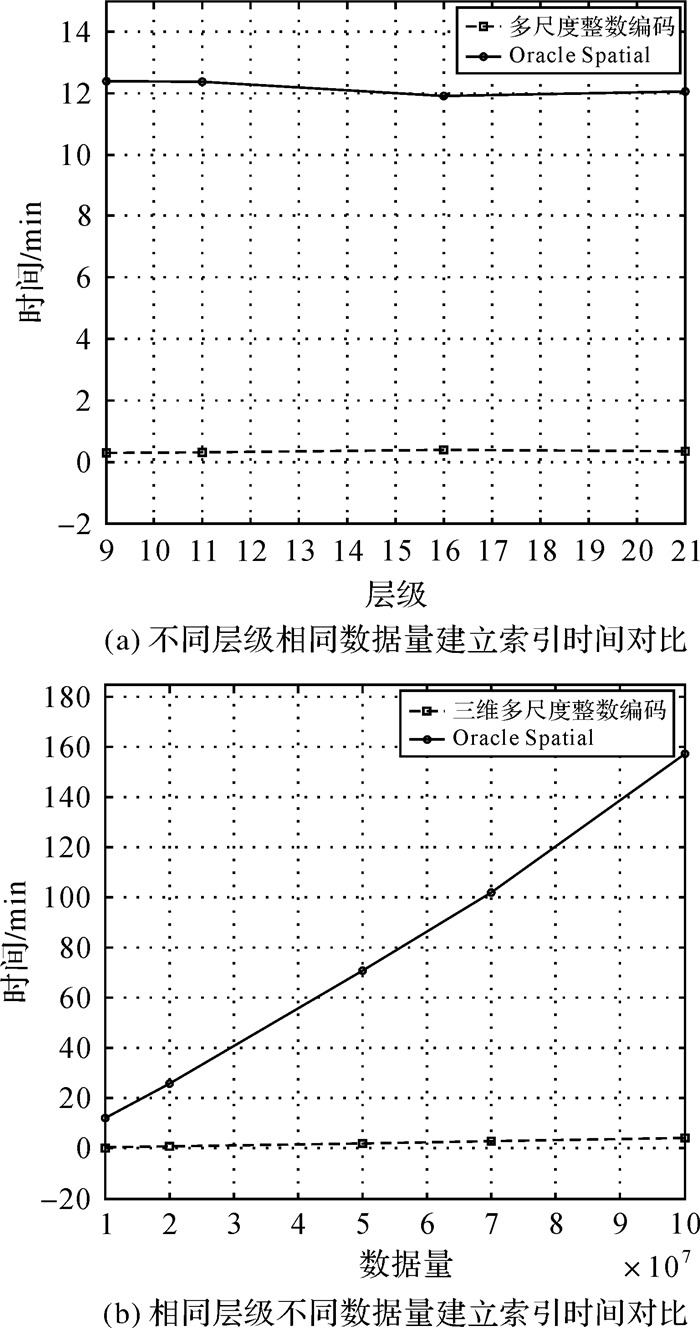
| 序号 | 层级范围 | 数据量 | 多尺度整数编码/min | Oracle Spatial/min |
| 1 | 7—9 | 10 000 000 | 0.28 | 12.38 |
| 2 | 7—11 | 10 000 000 | 0.29 | 12.37 |
| 3 | 7—16 | 10 000 000 | 0.38 | 11.90 |
| 4 | 7—21 | 10 000 000 | 0.33 | 12.04 |
| 5 | 7—21 | 20 000 000 | 0.72 | 25.80 |
| 6 | 7—21 | 50 000 000 | 1.96 | 70.80 |
| 7 | 7—21 | 70 000 000 | 2.80 | 102.01 |
| 8 | 7—21 | 100 000 000 | 4.11 | 157.20 |
|
| 图 5 建立索引时间对比 Fig. 5 Comparison between index construction times |
表 5统计了两种不同方式建立索引的时间信息。图 5是表 5中信息的直观表示,其中图 5(a)表示两种方式下相同数据量不同层级跨度建立索引的时间对比,对应表中1—4组试验;图 5(b)表示不同数据量,相同层级跨度建立索引的时间对比,对应表中4—8组试验。综合分析图表可知:
(1) 图 5(a)中曲线平稳,在数据量相同的情况下,两种方式建立索引的时间基本保持不变,而图 5(b)中两条曲线均匀变化,在层级不变的情况下,建立索引消耗的时间随数据量的增加而增加,呈正相关,且Oracle Spatial的曲线斜率大于多尺度整数编码。由此可以看出,两种方式建立索引的时间与层级无关,与数据量正相关,且Oracle Spatial随数据量的增加,建立索引消耗的时间越大,而多尺度编码建立索引时间随数据量的变化则比较平稳。
(2) 从图 5(a)和图 5(b)中两种方式建立索引的时间对比可以看出,影响多尺度整数编码与Oracle Spatial导入数据时间的因素相同,但是多尺度整数编码建立索引消耗的时间明显少于Oracle Spatial。
综合分析可以得到,在索引的建立和更新的过程中,多尺度编码要优于R树,更加适用于三维动态数据的索引。
按照上述原理进行试验,可以得到两种方式给定区域范围查询的时间对比信息,如表 6和图 6所示。
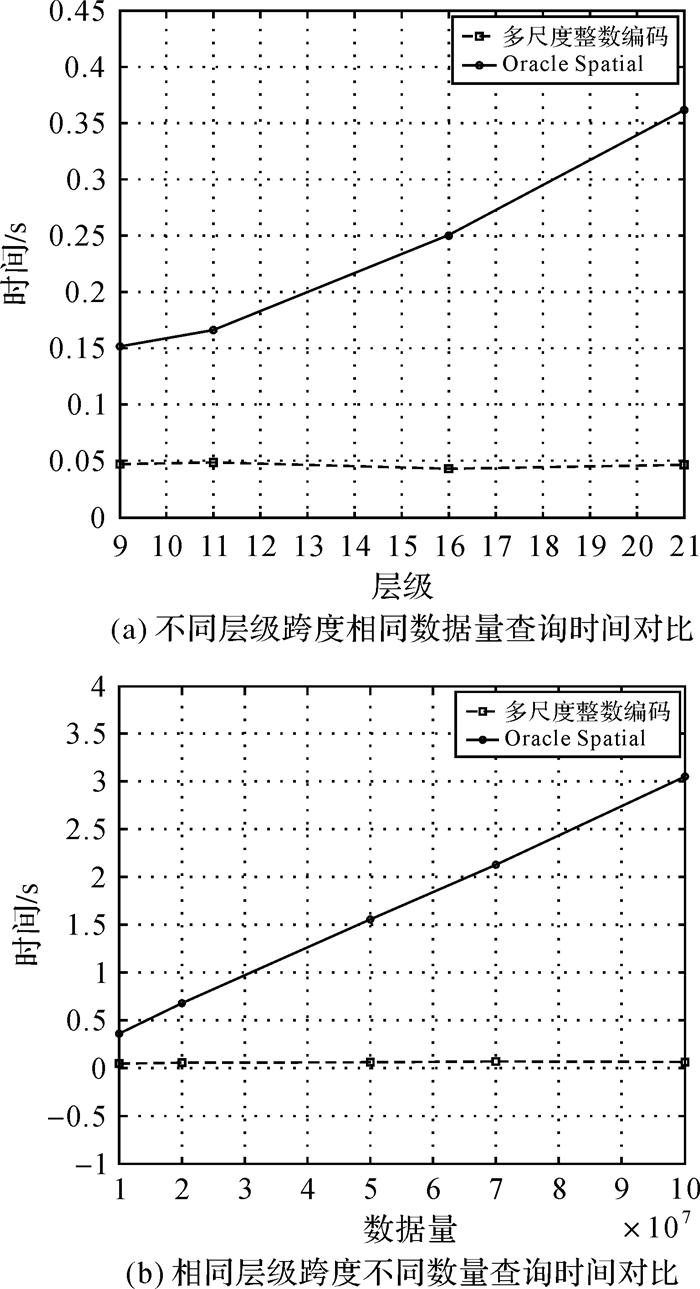
| 序号 | 层级范围 | 数据量 | 多尺度整数编码/s | Oracle Spatial/s |
| 1 | 7—9 | 10 000 000 | 0.047 214 | 0.151 219 |
| 2 | 7—11 | 10 000 000 | 0.048 436 | 0.166 442 |
| 3 | 7—16 | 10 000 000 | 0.042 864 | 0.250 155 |
| 4 | 7—21 | 10 000 000 | 0.046 318 | 0.361 664 |
| 5 | 7—21 | 20 000 000 | 0.053 333 | 0.678 587 |
| 6 | 7—21 | 50 000 000 | 0.055 456 | 1.550 572 |
| 7 | 7—21 | 70 000 000 | 0.063 991 | 2.129 624 |
| 8 | 7—21 | 100 000 000 | 0.059 889 | 3.045 037 |
|
| 图 6 查询时间对比 Fig. 6 Comparison between query times |
表 6统计了两种不同方式给定相同的区域进行查询消耗的时间信息。图 6是表 6中信息的直观表示,其中图 6(a)表示两种方式下相同数据量不同层级跨度给定区域查询消耗的时间信息对比,对应表中1—4组试验;图 6(b)表示不同数据量,相同层级跨度给定区域查询消耗的时间对比,对应表中4—8组试验。综合分析图表可知:
(1) 图 6(a)中多尺度整数编码曲线平稳,在数据量不变的情况下,多尺度整数编码查询消耗的时间基本保持不变,而Oracle Spatial曲线均匀变化,在数据量不变的情况下,Oracle Spatial查询消耗的时间随层级跨度的增大而变长。图 6(b)中Oracle Spatial对应曲线均匀变化,在层级不变的情况下,建立索引消耗的时间随数据量的增加而增加,呈正相关,而多尺度整数编码查询时间变化比较平稳,对于大数据的适应性较好。由此可以看出,多尺度整数编码查询消耗的时间与层级无关,与数据量正相关,而Oracle Spatial查询消耗的时间随层级跨度的变大而增大,且随着数据量的增加,查询消耗的时间增加较快,而多尺度编码查询消耗的时间随数据量的变化比较平稳。
(2) 从图 6(a)和图 6(b)中两种方式区域查询消耗的时间对比可以看出,多尺度整数编码区域查询的效率只与数据量相关,而Oracle Spatial区域查询的效率与层级跨度和数据量均相关,且多尺度整数编码区域查询消耗的时间明显少于Oracle Spatial。
综上所述:多尺度整数编码与Oracle Spatial中的R树索引两种方式所需要的原始数据导入时间与层级无关,与数据量正相关。由于R树进行空间查询时需要的数据为8个顶点坐标,而多尺度编码只需要一个整数值就能与其8个顶点坐标相对应,因此多尺度整数编码的数据导入时间要优于Oracle Spatial,相同数据量数据导入时间约为Oracle Spatial的1/2。随着数据量的增加,从数据导入时间的角度的来看,多尺度整数编码更加具有优越性。
将数据导入数据库以后,多尺度整数编码与R树两种方式建立索引所需要的时间与层级无关,与数据量正相关。由于多尺度整数编码将三维编码问题转换为一维编码来进行解决,而且Oracle Spatial为了实现快速查询,在建立索引的过程中进行了大量的优化,因此在建立索引的时间上多尺度整数编码要明显优于Oracle Spatial,约为Oracle Spatial的1/46,且随着数据量的增大,优势会更加突出。另外,对于高速变化的三维对象,涉及大量的数据插入和删除操作,索引的更新会非常频繁,三维多尺度编码也有着较大的优势。
给定区域进行查询,由于多尺度整数编码为一维编码,多尺度整数编码将三维数据查询问题转换为了一维数据的查询问题,而且Oracle Spatial建立R树对数据进行查询时,当层级跨度变大时,R树的深度也会变大而一维查询不存在这个问题,因此多尺度编码的查询效率要优于Oracle Spatial。在数据量为1000万,层级跨度为7~9的情况下,多尺度整数编码的查询时间约为Oracle Spatial的1/4,而且随着数据量和层级跨度的增大,多尺度编码的优势会更加明显。当数据量和层级跨度增加时,多尺度整数编码查询时间的曲线变化比较平缓,其时间复杂度为O(1),但是Oracle Spatial的增长较快,时间复杂度为O(n)。由此可见,相比于Oracle Spatial多尺度整数编码能够更加满足大数据对编码查询的需求。
4 总结本文设计了一种三维空间格网的多尺度整数编码与数据索引方法,并从编码方案设计与编码计算两个方面对该方法进行了较为详细的叙述。设计了多尺度编码转换试验,以及与Oracle Spatial的对比试验。由试验结果可以看出:多尺度整数编码方法在数据量、索引建立,以及区域查询等3个方面均有着独到的优势,相比于经典的三维R树索引,该方法更加满足空间大数据对编码与索引的需求。
最后,需要说明的是限于文章的篇幅,关于更多的改进、应用与后续研究成果,如将本文的编码与索引方法应用于空间动态目标数据的管理、点云数据的组织等方面,没有进行详细的描述。本文的编码查询范围采用的也是固定框架下的体块,针对任意的查询范围,可以通过多尺度聚合,即将查询区域拆分为固定格网进行查询,具体技术细节另文详述。
| [1] | BENTLEY J L. Multidimensional Binary Search Trees Used for Associative Searching[J]. Communications of the ACM, 1975, 18(9): 509–517. DOI:10.1145/361002.361007 |
| [2] | GAEDE V, GVNTHER O. Multidimensional Access Methods[J]. ACM Computing Surveys, 1998, 30(2): 170–231. DOI:10.1145/280277.280279 |
| [3] |
邵正伟, 席平.
基于八叉树编码的点云数据精简方法[J]. 工程图学学报, 2010, 31(4): 73–76.
SHAO Zhengwei, XI Ping. Data Reduction for Point Cloud Using Octree Coding[J]. Journal of Engineering Graphics, 2010, 31(4): 73–76. |
| [4] |
张会霞.
基于八叉树的点云数据的组织与可视化[J]. 太原师范学院学报(自然科学版), 2011, 10(3): 128–132.
ZHANG Huixia. The Organization and Visualization of Point Cloud Data Based on the Octree[J]. Journal of Taiyuan Normal University (Natural Science Edition), 2011, 10(3): 128–132. |
| [5] |
张传明, 潘懋, 徐绘宏.
基于分块混合八叉树编码的海量体视化研究[J]. 计算机工程, 2007, 33(14): 33–35, 78.
ZHANG Chuanming, PAN Mao, XU Huihong. Hybrid Blocking Octree-based Mass Volume Rendering[J]. Computer Engineering, 2007, 33(14): 33–35, 78. DOI:10.3969/j.issn.1000-3428.2007.14.011 |
| [6] |
綦科, 谢冬青, 刘洁.
基于八叉树空间分割的三维点云模型密写[J]. 计算机工程, 2011, 37(4): 7–9.
QI Ke, XIE Dongqing, LIU Jie. 3D Point Cloud Model Steganography Based on Octree Space Division[J]. Computer Engineering, 2011, 37(4): 7–9. |
| [7] |
宋扬, 潘懋, 朱雷.
三维GIS中的R树索引研究[J]. 计算机工程与应用, 2004(14): 9–10, 21.
SONG Yang, PAN Mao, ZHU Lei. Study of R-tree Spatial Access Method in Three Dimensional GIS[J]. Computer Engineering and Applications, 2004(14): 9–10, 21. DOI:10.3321/j.issn:1002-8331.2004.14.004 |
| [8] | BRAKATSOULAS S, PFOSER D, THEODORIDIS Y. Revisiting R-tree Construction Principles[C]//Proceedings of the 6th East European Conference on Advances in Databases and Information Systems. Bratislava, Slovakia: Springer, 2002: 149-162. |
| [9] |
郑坤, 朱良峰, 吴信才, 等.
3D GIS空间索引技术研究[J]. 地理与地理信息科学, 2006, 22(4): 35–39.
ZHENG Kun, ZHU Liangfeng, WU Xincai, et al. Study on Spatial Indexing Techniques for 3D GIS[J]. Geography and Geo-Information Science, 2006, 22(4): 35–39. |
| [10] | GUTTMAN A. R-trees:A Dynamic Index Structure for Spatial Searching[J]. ACM SIGMOD Record, 1984, 14(2): 47–57. DOI:10.1145/971697 |
| [11] | BECKMANN N, KRIEGEL H P, SCHNEIDER R, et al. The R-tree:An Efficient And Robust Access Method for Points and Rectangles[J]. ACM SIGMOD Record, 1990, 19(2): 322–331. DOI:10.1145/93605 |
| [12] | SELLIS T K, ROUSSOPOULOS N, FALOUTSOS C. The R+-tree: A Dynamic Index for Multi-dimensional Objects[C]//Proceedings of the 13th International Conference on Very Large Data Bases. San Francisco: Morgan Kaufmann Publishers, 1987: 507-518. |
| [13] |
邓红艳, 武芳, 翟仁健, 等.
一种用于空间数据多尺度表达的R树索引结构[J]. 计算机学报, 2009, 32(1): 177–184.
DENG Hongyan, WU Fang, ZHAI Renjian, et al. R-tree Index Structure for Multi-scale Representation of Spatial Data[J]. Chinese Journal of Computers, 2009, 32(1): 177–184. |
| [14] |
龚俊, 朱庆, 张叶廷, 等.
顾及多细节层次的三维R树索引扩展方法[J]. 测绘学报, 2011, 40(2): 249–255.
GONG Jun, ZHU Qing, ZHANG Yeting, et al. An Efficient 3D R-tree Extension Method Concerned With Levels of Detail[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 249–255. |
| [15] | ROBINSON J T. The K-D-B-tree: A Search Structure for Large Multidimensional Dynamic Indexes[C]//Proceedings of the 1981 ACM SIGMOD international conference on Management of data. New York: ACM, 1981: 10-18. |
| [16] |
张泽宝. 空间数据库的索引技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. ZHANG Zebao. Research on Spatial Index Technology for Spatial Database[D]. Harbin: Harbin Engineering University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10217-1011020990.htm |
| [17] |
张芩, 王振民.
QR-树:一种基于R-树与四叉树的空间索引结构[J]. 计算机工程与应用, 2004(9): 100–103.
ZHANG Qin, WANG Zhenmin. QR-tree:A Kind of Spatial Index Structure Based on R-tree and Quad-tree[J]. Computer Engineering and Applications, 2004(9): 100–103. |
| [18] |
童晓冲, 贲进.
空间信息剖分组织的全球离散格网理论与方法[M]. 北京: 测绘出版社, 2016.
TONG Xiaochong, BEN Jin. The Principle and Method of Discrete Global Grid Systems for Geospatial Information Subdivision Organization Principle and Method of Discrete Global Grid Systems for Geospatial Information Subdivision Organization[M]. Beijing: Surveying and Mapping Press, 2016. |
| [19] |
王晏民. 多比例尺GIS矢量空间数据组织研究[D]. 武汉: 武汉大学, 2002. WANG Yanmin. Multiscale GIS Vector Spatial Data Organization Study[D]. Wuhan: Wuhan University, 2013. |
| [20] |
夏宇, 朱欣焰, 李德仁.
空间信息多级网格索引技术研究[J]. 地理空间信息, 2006, 4(6): 4–7.
XIA Yu, ZHU Xinyan, LI Deren. Indexing Technology in Spatial Information Multi-grid[J]. Geospatial Information, 2006, 4(6): 4–7. |
| [21] | SAGAN H. Space-filling Curves[M]. New York: Springer-Verlag, 1994. |
| [22] |
史绍雨, 唐新明, 吴凡, 等.
多级格网时空索引[J]. 测绘科学, 2006, 31(3): 54–55.
SHI Shaoyu, TANG Xinming, WU Fan, et al. Multi-level Grid Spatio-temporal Index[J]. Science of Surveying and Mapping, 2006, 31(3): 54–55. |
| [23] |
张小虎, 钟耳顺, 王少华, 等.
多尺度空间格网数据的索引编码研究[J]. 测绘通报, 2014(7): 35–38.
ZHANG Xiaohu, ZHONG Ershun, WANG Shaohua, et al. Research on Index and Code For Multi-scale Grid Data[J]. Bulletin of Surveying and Mapping, 2014(7): 35–38. |
| [24] |
周勇, 何建农, 凃平.
一种改进的自适应层次网格空间索引查询算法[J]. 计算机工程与应用, 2006, 42(7): 159–161, 165.
ZHOU Yong, HE Jiannong, TU Ping. An Algorithm of Improved Auto-selection Multi-layer Grid Spatial Index[J]. Computer Engineering and Applications, 2006, 42(7): 159–161, 165. |
| [25] |
童晓冲, 王嵘, 王林, 等.
一种有效的多尺度时间段剖分方法与整数编码计算[J]. 测绘学报, 2016, 45(S1): 66–76.
TONG Xiaochong, WANG Rong, WANG Lin, et al. An Efficient Integer Coding and Computing Method for Multiscale Time Segment[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 66–76. DOI:10.11947/j.AGCS.2016.F008 |
| [26] | ORENSTEIN J A, MERRETT T H. A Class of Data Structures for Associative Searching[C]//Proceedings of the 3rd ACM SIGACT-SIGMOD Symposium on Principles of Database Systems. Waterloo, Ontario, Canada: ACM, 1984: 181-190. |
| [27] | DAI H K, SU H C. Locality and Clustering Performances of Space-filling Curves[M]. Stillwater, OK, USA: Oklahoma State University, 2003: 78-85. |
| [28] | MURRAY C. Spatial and Graph Developer's Guide[DB/OL]. https://docs. oracle.com/database/121/SPATL/, 2017-01/2017-11. |
| [29] | MURRAY C. Oracle Spatial User's Guide and Reference, Release 9. 2[DB/OL], https://docs.oracle.com/cd/B10501_01/appdev.920/a96630.pdf, 2002-03/2017-11. |
| [30] | RAVADA S, KAZAR B M, KOTHURI R. Query Processing in 3D Spatial Databases: Experiences with Oracle Spatial 11g[M]//LEE J, ZLATANOVA S. 3D Geo-information Sciences. Berlin: Springer, 2009: 153-173. |
| [31] | STOTER J E, ZLATANOVA S. 3D GIS, Where are We Standing?[C]//ISPRS Joint Workshop on 'Spatial, Temporal and Multi-dimensional Data Modelling and Analysis'. Québec: ISPRS, 2003. |
| [32] | BRAKATSOULAS S, PFOSER D, TRYFONA N. Modeling, Storing and Mining Moving Object Databases[C]//Proceedings of 2004 International Database Engineering and Applications Symposium. Coimbra: IEEE, 2004: 68-77. |




