2. 南洋理工大学机械与航天工程学院, 新加坡 639798
2. The School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798
由于传统三维成像到平面成像硬件的二维约束,而不得不采用3-2-3维信息转换模式[1],其本质是利用物体的向空间进行漫反射特性获取多个视角的影像信息,再利用光线的可逆追踪计算三维信息,而这一方法带来的劣势在于对运动目标无法进行三维信息测量。而生物信息学研究发现,生物采用复眼技术可以直接一次三维成像,即3-3维的信息直接获取,给运动目标的三维获取带来了优势。然而传统的仿生复眼结构由多相机阵列组成,在成像的同时需要考虑相机的姿态以及重叠度等信息,制造相对复杂。因此本文提出利用光场技术进行仿生三维信息获取。光场成像是一种单次三维测量[3]技术,由于其特殊的光学结构,可以在一次成像过程中完成对目标景物多个方向的光线采集。第一台手持光场相机由Ng等[4-5]利用微透镜开发。之后,商业相机由Lytro[6]和Raytrix[2]生产,可应用于近距离摄影测量[7]。
由于光场相机一般由主透镜、微透镜阵列与探测器阵列三级结构组成,因此一般视点的移动为水平方向和垂直方向,导致同名核线排列在影像数据的同一行或者同一列,这一特性为构建核线平面影像(epipolar plane image,EPI)带来了便利[8-10]。依据核线平面影像的性质即同名点在核线平面影像上成线性排列,在2004年文献[11]首先提出了利用梯度算子检测核线斜率,同时推导了光场影像中核线斜率与深度之间的关系,并成功应用到实际场景的计算中。但是通过梯度算子直接进行斜率的计算受影像的噪声影响,深度估计存在较大误差。
之后Universität Heidelberg的Wanner Seven和Bastian Goldluecke等[12-13]通过增加全局一致性检验算法,对经过梯度算子计算得到的原始信息进行了优化,提高了深度计算的准确度,但梯度算子本身对图像噪声的敏感性依然存在。此外在大视差存在的情况下,相邻两条核线的灰度分布将会出现跳变,此时进行梯度算子检测将完全失效。因此在2013年University of California,Berkeley的Michael Tao等[14]提出了对EPI影像进行裁剪的方法,只进行EPI影像垂直方向的检测,该方法有效弥补了梯度算子检测的缺点,同时Michael Tao等引入Markov Random Fields理论对深度信息结果进行了优化,优化同时考虑了两种EPI处理方式(同名点对应关系和离焦相邻点对应关系,correspondence and defocus)。由于直接利用EPI影像进行深度计算的核心在于同名点构成的直线检测,因此北京航空航天大学的Shuo Zhang等[15]利用罗盘算子对比在同名点直线两旁的像素点分布情况(进行直方图统计),计算光场数据的深度,同时利用Graph Cuts[16]对深度信息进行优化。
但是对于微透镜阵列结构相机,其获取的影像数据本身为微透镜形式影像,利用上述的方法进行计算时,需要将原始影像解析成多视几何图像,过程相对复杂而且一部分靠近微透镜边缘的有效数据被舍弃。因此针对上述的问题,本文提出利用微透镜影像直接进行三维计算的方法,利用光线传播时强度一致性原理进行影像重聚焦计算,利用最佳的重聚焦点估计目标对象的深度信息,从而避免了将光场影像进行分解。同时与现有的直接利用光场影像进行深度计算的方法相比,本文所提出的方法能够方便进行三维视觉中的代价计算,并利用图割优化手段进行深度信息的平滑与准确估计,为了验证本文方法的有效性,试验结果将与现有的方法进行比较。
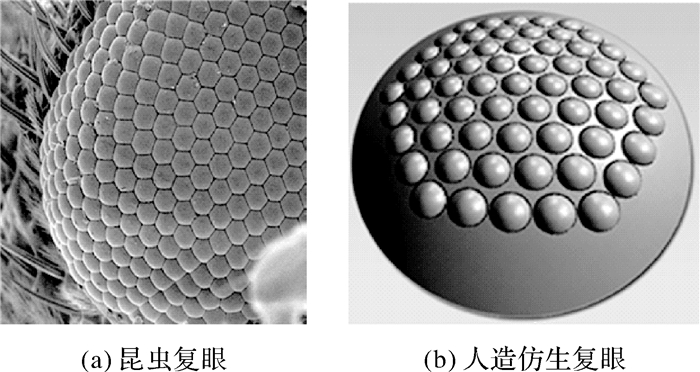
1 传统复眼结构与光场光学结构 1.1 仿生视觉结构昆虫的复眼是由许多个小眼组合而成的,小眼的个数从几百个到几万个不等,其每个小眼由1套屈光器(1个角膜和1个晶锥)、6至8个小网膜细胞及其特化产生的视杆和基细胞等构成,即每个小眼可视为一个光学系统,如图 1所示。
由于每一个小眼均可以对物体进行成像,因此一个复眼系统可以获取来自同一物体的不同的角度的信息,从而能够进行三维信息计算,然后现有的仿生复眼结构很难达到生物复眼的精细结构,因此一般而言仍然采用多相机结构组成,其体积较大且三维计算过程复杂。
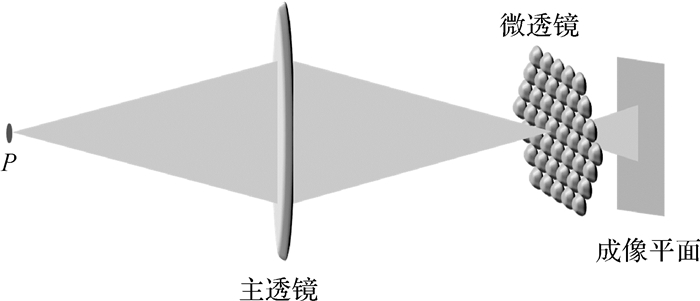
1.2 光场光学结构目前常用的光场相机采用主透镜、微透镜阵列和探测器阵列结构,其中一个微透镜阵列由上万个小微透镜组成,一个小微透镜可以覆盖100~ 1000个像素单元,因此每一个微透镜和被其覆盖的探测器可以组成一个微型相机系统,其光学结构如图 2所示。为了能够使得相机进行目标三维计算,主透镜会将物方三维信息进行压缩,在像方空间形成一定的景深。因此从光学角度来讲,光场相机的三维信息恢复是一种目标景深信息恢复的手段。
|
| 图 2 光场相机的结构 Fig. 2 The structure of the light field camera |
根据图 2所示的光学结构,笔者自主设计一款微透镜阵列的光场相机。其外观如图 3所示,相机的主体机构由板级相机、主透镜及内部的微透镜构成,相机总长度约为7 cm。

|
| 图 3 光场相机外观 Fig. 3 The appearance of light field camera |
微透镜阵列采用六角形排列,相机的参数如表 1所示。其中F#表示光场相机的F数,b是指微透镜到探测器的距离。d是指单个微透镜覆盖的像元数目;u是指像素的尺寸。
| 参数 | 值 |
| F# | 2.8 |
| b | 168 μm |
| d | 27.3像素 |
| u | 2.2 μm |
2 基于仿生视觉微透镜技术的3-3-2维向3-3维转换的光场成像新手段 2.1 重聚焦原理
对于传统相机,当物点处于景深范围内时,物点表现为清晰像点;当物点处于景深范围之外时,物点表现为模糊像点。
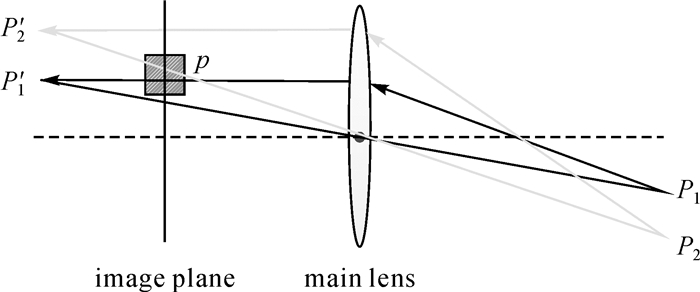
其主要原因在于,处于景深范围内的物点,其通过成像透镜聚焦时,由该物点向各个方向发射的光线聚焦于一个探测单元;而非景深范围内的点,其向各个方向发射的光线分散投影到不同的探测单元,而不同的物点的几条光线将会投影到一个探测单元。
如图 4所示,其中像点p的亮度为
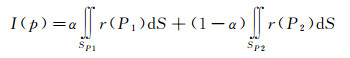 (1)
(1)
|
| 图 4 传统相机物点成像 Fig. 4 Imaging progress of traditional camera |
式中,α代表不同光线在探测单元覆盖的面积比率。
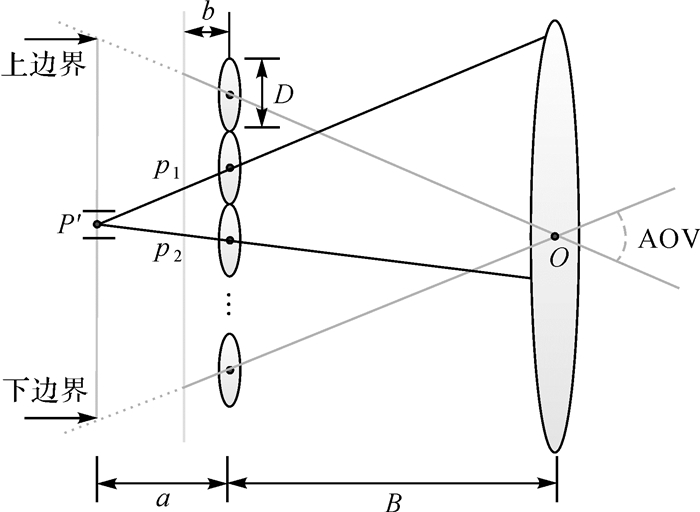
但是对于光场相机,其内部的光线的方向可以确定,因此不同像点的光线可以通过光线的筛选进行重聚焦,来实现像点的清晰成像,如图 5所示。
|
| 图 5 光场相机重聚焦的光线筛选 Fig. 5 Rays selection for the refocusing of light field camera |
重聚焦像点P′的亮度为
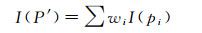 (2)
(2)
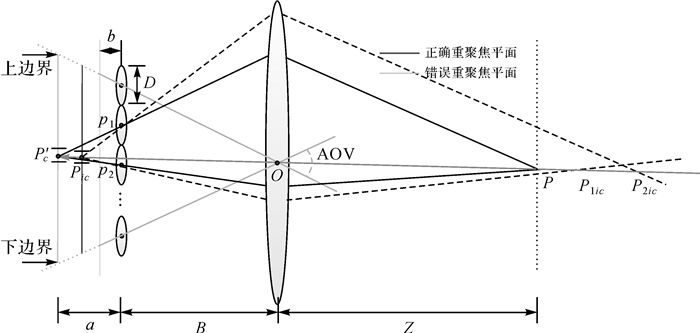
式(2)能够计算出清晰像点的亮度的前提在于pi(i=1, 2)为同名像点,即重聚焦平面距离微透镜平面为正确的像方深度z。根据同名像点亮度一致原理,各个像点的亮度的方差理想值应该为零,反之,当重聚焦平面不在正确的像方深度时,pi(i=1, 2)为非同名像点,则其方差将会变大,如图 6。因此利用重聚焦原理计算的深度信息为
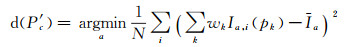 (3)
(3)
|
| 图 6 光场信息不同深度的聚焦 Fig. 6 Image refocusing on different depths in light field |
式中,k是pi邻域中的点;N为邻域中的点的数目。在重聚焦的过程中距离一般表示成微透镜与成像平面之间距离的倍数,这个距离也被称为虚拟深度v=a/b。而且P′ c与光场相机上的像点pi以及微透镜的中心点满足共线条件。
然而由于式(3)进行深度计算是需要对同一重聚焦点进行不同深度的方差信息扫描,然而同一重聚焦点在不同深度上的位置的空间位置不易计算。为解决这一问题,本文利用相机视场角信息计算出重聚焦影像的上下左右边界,通过该边界,进行重聚焦像点坐标确定
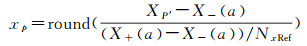 (4)
(4)
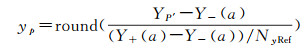 (5)
(5)
xp和yp为重聚焦影像上的像点的图像坐标;XP′和YP′为该像点在空间上的绝对坐标。X-(a)、X+(a)、Y-(a)、Y+(a)为重聚焦影像的上下边界坐标,Nx Ref和Ny Ref为预先定义的重聚焦影像的分辨率。
2.3 三维深度优化由于利用式(3)进行深度计算的结果为Winner-Take-All的结果,其深度计算出来的信息相对比较粗糙,在此基础之上,本文利用改进的自适应窗口方法[17]对利用式(3)计算出来的代价信息进行进一步的优化。因此修改后的代价信息为
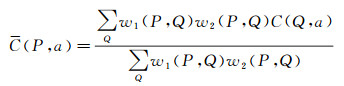 (6)
(6)
式(6)中,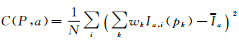
w1(P, Q)=e-(P-Q)2/rd2描述了相邻点之间的距离的相似度。针对经过自适应窗口优化之后的代价信息,本文采用Graph Cuts进行全局优化。
3 试验结果本文试验首先对本文设计的相机进行了成像特性的评估,包括重聚焦性能测试。图 7展示的是自主设计的光场相机重聚焦的实验平台,图 8显示了该相机不同虚拟深度处的影像重聚焦结果。另外三维成像算法的验证则利用Raytrix相机提供的公开数据进行试验。图 9展示了利用Raytrix光场相机拍摄出的白光影像图案,用于构建微透镜阵列的中心点。利用构建的微透镜阵列的中心点可以有效地进行影像的信息重聚焦工作,并以此进行三维重建。在试验过程中重聚焦的深度分层为80个,起始虚拟深度为v=2.0,设置每步深度间隔为0.1。而在进行深度计算时,重聚焦影像的分辨率被设置为1/4倍的原始光场影像大小。

|
| 图 7 光场相机重聚焦的实验平台 Fig. 7 The Experimental platform for refocusing of light field camera |

|
| 图 8 影像重聚焦结果 Fig. 8 The result of refocusing image |

|
| 图 9 Raytrix相机的白光光场影像 Fig. 9 White image of the Raytrix camera |
利用图 9中白光影像采集出来的图像的中心点,结合重聚焦影像的聚焦深度信息,利用式(3)和式(6)可以计算出不同深度层次聚焦点的代价信息,最终利用Graph Cuts技术对所有深度层次的代价立方体(Cost Volume)进行优化可以得到最终的深度结果。图 10和图 11分别展示了本文提出的方法与Raytrix软件计算比较(参数以达到最佳的性能)和Matthieu Hog的方法[18]。从结果来看,本文提出的方法可以提供更平滑的深度图,并保持细节。而如图 10(b)和图 11(b),从Raytrix软件获取的结果其深度信息噪声较大且边缘被侵蚀。而用文献[18]提出的方法实现的结果,可以提供平滑的深度结果,但是在水平方向具有重复纹理的地方。该方法则完全失效,如图 10(c)所示。在利用自适应窗口进行代价信息优化时, 根据试验效果窗口大小设置成7×7个像素,且rc=9、rd=23。
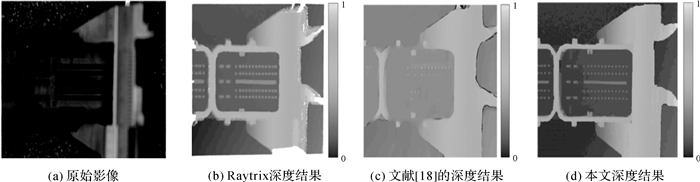
|
| 图 10 工件 Fig. 10 Workpiece |

|
| 图 11 水果堆 Fig. 11 Fruitpile |
4 结论
本文论述了利用仿生复眼进行目标三维信息获取的基本方法,提出了单次成像获取三维信息的手段来实现3维到3维的信息转换获取。因为利用传统手段构建的复眼相机为利用多个相机的组合进行多视几何三维构像,对相机的姿态信息有一定的要求,本文利用新型的光场成像相机,通过其独特的微透镜与探测器的结合可以方便地实现三维信息的三维获取,同时在本文的三维信息获取方法中利用重聚焦手段对原始光场影像数据进行直接处理,避免传统利用光场解码数据对核线影像处理,有效利用成像像素,并且通过预设重聚焦影像尺寸的方式可以极大提升计算结果的分辨率。此外本文提出的方法,利用重聚焦影像为深度信息获取的基础,可以有效地构建代价函数,因此最终深度估计的结果与现有的技术相比十分平滑而且准确。
| [1] |
高鹏骐. 无人机仿生复眼运动目标检测机理与方法研究[D]. 北京: 北京大学, 2009. GAO Pengqi. Research on UAV Moving Target Detection Inspired by Compound Eye[D]. Beijing: Peking University, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1609771 |
| [2] | RAYTRIX. "The Raytrix Camera"[EB/OL]. [2017-08-10]. https://www.raytrix.de. |
| [3] | NG R. Digital Light Field Photography[D]. Stanford, CA, USA: Stanford University, 2006. https://www.researchgate.net/publication/239510318_Digital_Light_Field_Photography |
| [4] | NG R, LEVOY M, BRÉDIF M, et al. Light Field Photography with a Hand-held Plenoptic Camera[R]. Stanford Tech Report CTSR 2005-02, 2005. https://www.researchgate.net/publication/246688556_Light_Field_Photography_with_a_Hand-held_Plenoptic_Camera |
| [5] | LYTRO. "The Lytro Camera"[EB/OL]. [2017-08-10]. https://www.lytro.com. |
| [6] | YANG Peng, WANG Zhaomin, YAN Yizhen, et al. Close-range Photogrammetry with Light Field Camera:from Disparity Map to Absolute Distance[J]. Applied Optics, 2016, 55(27): 7477–7486. DOI:10.1364/AO.55.007477 |
| [7] | DANSEREAU D G, PIZARRO O, WILLIAMS S B. Decoding, Calibration and Rectification for Lenselet-based Plenoptic Cameras[C]//Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE, 2013. |
| [8] | CRIMINISI A, KANG S B, SWAMINATHAN R, et al. Extracting Layers and Analyzing Their Specular Properties Using Epipolar-plane-image Analysis[J]. Computer Vision and Image Understanding, 2005, 97(1): 51–85. DOI:10.1016/j.cviu.2004.06.001 |
| [9] | MATOUŠEK M, WERNER T, HLAVÁČ V. Accurate Correspondences from Epipolar Plane Images[C]//Proceedings of Computer Vision Winter Workshop. Bled, Slovenia: Slovenian Pattern Recorgnition Society, 2001. |
| [10] | BOLLES R C, BAKER H H, MARIMONT D H. Epipolar-plane Image Analysis:An Approach to Determining Structure from Motion[J]. International Journal of Computer Vision, 1987, 1(1): 7–55. DOI:10.1007/BF00128525 |
| [11] | DANSEREAU D, BRUTON L. Gradient-based Depth Estimation from 4D Light Fields[C]//Proceedings of 2004 International Symposium on Circuits and Systems. Vancouver: IEEE, 2004: 23-26. |
| [12] | WANNER S, GOLDLUECKE B. Variational Light Field Analysis for Disparity Estimation and Super-resolution[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(3): 606–619. DOI:10.1109/TPAMI.2013.147 |
| [13] | WANNER S, GOLDLUECKE B. Globally Consistent Depth Labeling of 4D Light Fields[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE, 2012: 16-21. |
| [14] | TAO M W, HADAP S, MALIK J, et al. Depth From Combining Defocus and Correspondence Using Light-field Cameras[C]//Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 1-8. |
| [15] | ZHANG Shuo, SHENG Hao, LI Chao, et al. Robust Depth Estimation for Light Field via Spinning Parallelogram Operator[J]. Computer Vision and Image Understanding, 2016, 145: 148–159. DOI:10.1016/j.cviu.2015.12.007 |
| [16] | JEON H G, PARK J, CHOE G, et al. Accurate Depth Map Estimation from a Lenslet Light Field Camera[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 7-12. |
| [17] | HOG M, SABATER N, VANDAME B, et al. An Image Rendering Pipeline for Focused Plenoptic Cameras[J]. IEEE Transactions on Computational Imaging, 2016, 3(4): 811–821. |
| [18] | KANADE T, OKUTOMI M. A Stereo Matching Algorithm with An Adaptive Window:Theory and Experiment[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(9): 920–932. DOI:10.1109/34.310690 |