数字摄影测量技术经历了从半数字时代到全数字时代的变革,正在由传统光学摄影测量手段进一步转向为具有高精度、高智能化、宽内涵化的多传感器联合测量技术。现阶段,以高自动化、高精度为主的智能精密干涉测量技术,已经成为了数字摄影测量技术的必要内涵。精密干涉测量技术使用合成孔径雷达干涉(interferometric SAR,InSAR)获取地表的干涉相位,从而反演高精度高程信息,现已成为了最有效的全球测图手段之一[1]。InSAR的高自动化体现在其干涉链路处理过程中。InSAR数据处理过程中采用具备高相干性的两景单视复(single look complex,SLC)数据,完成自动化干涉、去平、解缠、编码等操作,生成具有较高精度的数字高程模型,整个链路完全无需人工参与,在多节点并行条件下,可在一分钟之内完成整个链路的处理。InSAR的高精度体现在其干涉链路之前的参数设计与检校过程,以及之后的DEM后处理过程。其中最重要的是参数的设计过程,即卫星平台与载荷稳定性设计,测量检校精度设计等。随后的DEM后处理需要采用外部数据修正基线、斜距、轨道、整周未知数等残差带来的微小的高程梯度误差及高程常数误差,修正之后的数据能够达到极高的精度要求。例如TanDEM-X的DEM数据修正完之后,其精度能够由4 m提升到1.3 m(不包含南极地区)。
由于精密干涉测量技术具有高智能化特性,因此多次被用于全球测图任务中。早在2000年,美国国家航空航天局就启动了航天飞机雷达地形测绘任务(shuttle radar topography mission,SRTM),采用C波段SAR数据获取了56°S至60°N的全球DEM数据,并于2003年发布了第一个版本,其标称格网大小为3″,约90 m,绝对高程精度优于16 m[2]。虽然已经过去十数年,但是SRTM依然是迄今为止在覆盖范围、高程精度、公开程度等各方面综合评价最好的全球DEM数据。表 1中给出了现有全球DEM的获取技术及主要参数。其中最早的是美国地质调查局(U.S.Geological Survey,USGS)于1996年发布的GTOPO30数据,其格网大小为30″,约900 m,高程精度优于30 m。其后,美国国家海洋和大气管理局在2008年发布了全球1′的地形模型ETOPO1,其中包含了冰盖及基岩数据。然而ETOPO1的数据来源更加复杂多样,无法给出具体的精度[3]。USGS随后发布了GMTED2010(global multi-resolution terrain elevation data 2010),这是由11种数据融合得到的DEM,其产品包含3种分辨率,即30″、15″及7.5″,精度优于10 m[4]。2009年ASTER GDEM发布了第一个版本,然而由于质量不佳,只能支撑部分科研应用,随后在2011年,ASTER GDEM发布了第二个版本,其标称格网大小为15 m,绝对高程精度接近像素尺寸大小[5]。2015年,JAXA发布了ALOS DSM,其标称精度为15 m。2016年,DLR获取了全球包括南极地区的DEM数据,其高程精度达到了惊人的4 m以内[6],为全球测图拉开了新的序幕,然而DLR获取的DEM数据由Airbus进行代理售卖,已经不再是完全公开的数据。
| 名称 | 发布时间 | 覆盖范围 | 网格尺寸 | 高程精度/m | 所用技术 |
| GTOPO30 | 1993 | 90°S-90°N | 30″/~900 m | 30 | 使用8种数据源进行融合 |
| SRTM-C-v1 | 2003 | 56°S-60°N | 3″/~90 m | 16 | InSAR |
| ETOPO1 | 2008 | 90°S-90°N | 1′ | 无 | 使用12种数据源进行融合 |
| GMTED2010 | 2010 | 90°S-84°N | 7.5″、15″及30″ | 10 | 使用11种数据源进行融合 |
| ASTER GDEM-v2 | 2011 | 80°S-80°N | 15 m | 15 | 光学立体摄影测量 |
| ALOS DSM | 2015 | 82°S-82°N | 1″/~30 m | 5 | 光学立体摄影测量 |
| TanDEM-X DEM | 2016 | 90°S-90°N | 0.4″/~12 m | 4 | InSAR |
从表 1可以看出,除了多数据源融合之外,获取全球DEM的技术主要包括两类,即光学立体摄影测量和InSAR。其中光学立体摄影测量技术使用具有一定视差的像对完成高程解算,其视差大小一般不小于30°,并确保基高比在1左右,从而平衡同名点匹配精度和立体几何的稳健性。现阶段,我国第一颗民用立体测绘卫星资源三号,已经完成了国内近400万平方千米的高精度DEM生产[7]。DOM更是覆盖了924万平方千米,有效覆盖率达到96%。然而在西南地区,由于全年都有云雾覆盖,始终无法获得有效数据。因此我国对干涉SAR卫星的需求日益迫切。InSAR技术使用视差极小的像对完成高程解算,其视差大小不会超过0.1°,并确保模糊高在35~55 m之间,从而平衡相位解缠精度和干涉几何的稳健性。相对于光学来说,InSAR无需进行逐像素匹配,粗差较少,不受云雾干扰,且能够直接提供逐点的高程信息,无需借助三角网构建DEM,因此有极大的测绘优势。然而其阴影、叠掩、穿透性等问题,则需要在任务设计过程中予以高度重视。现阶段,我国虽然已经先后发射了环境一号和高分三号两颗民用SAR卫星,然而受限于轨道回归过程中垂直基线的控制精度,卫星并不具备较好的业务化干涉能力。在“十三五”期间,我国规划了第一对以干涉为主要任务的民用SAR卫星,即L波段差分干涉SAR卫星。卫星拟采用双星绕飞模式获取DEM数据,为我国全球测图开启新的篇章。
InSAR获取全球DEM的技术在国内外诸多文献中已经有详细介绍。国外以NASA和DLR为主的科研团队已经公开了SRTM及TanDEM-X的精密干涉测量指标设计方法[8-10]、几何参数标定方法[8, 11-13]、数据处理方法[14-15]、精度的详细评估[2]等。国内也有学者针对精密干涉测量开展了卫星性能分析[16]、数据处理方法研究[17]等。然而SRTM的原始SLC数据并不公开发布,TanDEM-X的SLC数据也必须通过科研途径申请获取,因此数据来源的限制使得国内针对双天线及分布式SAR卫星的研究多处于模拟仿真阶段[18],或者使用机载数据替代星载数据进行先期研究[19-22]。本文从精密干涉测量的全球测图应用出发,给出了基于分布式SAR卫星的原始数据到最终DEM产品的整个技术链路,并阐述了SAR卫星的测量检校技术、数据处理技术及DEM数据后处理技术,为数字摄影测量的自动化和智能化奠定了基础,并为国产SAR卫星的全球测图任务提供技术参考。
1 测量检校技术SAR卫星参数是数据处理的必要输入,参数的精度决定了数据处理的直接精度。然而,高精度测量参数无法通过卫星直接给定。例如基线参数是干涉过程中的重要参数,毫米级的基线误差会带来米级的高程误差。卫星的基线测量设备直接给出的是设备的几何中心的位置,而并非天线相位中心的位置,天线相位中心基线参数则需要联合人工角反射器进行检校。因此,检校技术是确定星上参数误差并进行误差修正的必要途径。SAR卫星的检校链路包括内定标、天线指向标定、辐射定标、几何检校、干涉测量检校等。其中几何检校和干涉测量检校技术确定了应用过程中所能获取的干涉几何参数的精度,二者共同决定了全球DEM的直接精度水平。
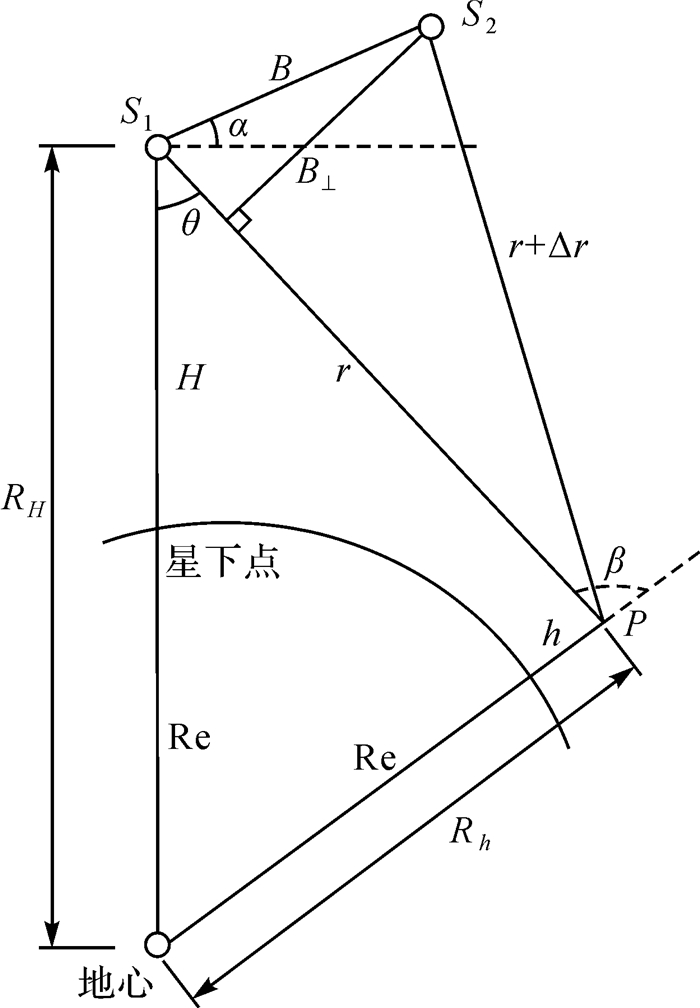
1.1 几何检校技术几何检校的目的是检验并校正与几何定位相关的SAR系统参数。图 1中给出了SAR干涉过程中的基本几何关系,其中P为地面点,S1为主影像成像时刻的相位中心位置,S2为从影像成像时刻的相位中心位置,B为双星之间的基线长度,α为基线倾角,B⊥为垂直基线长度,θ为侧视角,RH为主影像相位中心到地心的距离,H为卫星高度,r为P点对应的斜距,Re为地球曲率半径,h为P点的高程,β为本地入射角,Rh为P点到地心的距离。为了便于描述,所有的参数统一在WGS-84坐标系中进行探讨。SAR一般采用斜距-多普勒(Range-Doppler,R-D)模型完成像素坐标与地理坐标的转换,即
 (1)
(1)
|
| 图 1 干涉几何示意图 Fig. 1 Diagrammatic drawing of interferometric geometry |
式中,r0是主影像近地点斜距;Δr0是斜距分辨率;
斜距的误差来源主要包括两部分,一部分为大气误差,另一部分是距离向计时系统误差。其中大气误差包含流体静力学分量(气压)、湿分量(水汽)及流体力学分量(水滴)。对于TanDEM-X来说,三类分量在天顶方向的延迟可采用经验模型近似表达[23]
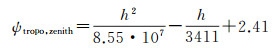 (2)
(2)
当高程小于9000 m时,经验模型与精确的大气模型之间的差异一般在0.7 m以内,对于1:50 000比例尺要求的25 m平面定位精度来说,其误差在允许的范围之内。星上距离向计时系统误差一般来说是数百ns,这会带来数十米的斜距测量误差,不过这部分误差是系统误差,可通过与式(2)类似的过程加以检校,即
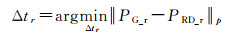 (3)
(3)
检校后的时间误差基本在1 ns左右,能够完成无控条件下的1:50 000比例尺定位要求。
SAR卫星一般需要在星上采用偏航导引,并在地面采用零多普勒成像,以确保SLC中多普勒中心频率会在0 Hz附近。实际过程中多普勒中心频率无法严格归零,其误差一般在数个赫兹,对于ScanSAR成像模式来说,中心频率误差最大,不过其限差也会控制在10 Hz以内。在实际处理过程中,多普勒中心频率误差为时间域高频分量,无法精确标定,因此一般不做过多处理。除了多普勒中心频率之外,多普勒方程中的未知参数还包括主星位置及速度矢量。它依赖于星上GPS精度,现阶段双频GPS可提供优于5 cm的事后定轨精度,以及mm/s级的速度测量精度。在这种情况下,轨道的误差大部分来源于方位向时间误差,如果轨道运行在500 km高度,那么1 ms的方位向时间误差会引入约7 m的定轨偏差,这对于精密定位来说,是不可忽略的误差源。方位向时间误差Δta一般通过地面角反射器进行修正,即
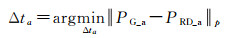 (4)
(4)
式中,PG_a为控制点在方位向的真实位置,一般采用差分GPS进行精确测量,其精度在厘米级,PRD_a为使用R-D模型解算的真实位置,‖·‖p为向量的P-范数。
几何检校过程中需要使用人工角反射器确保地面点的坐标与影像坐标严格对应,从而减少刺点误差,提高检校精度。理论上来说,一个角反射器就可以完成检校工作,但是为了减少粗差的影响,一般至少采用6个角反射器,采用两行三列的方式均匀分布在影像刈幅范围内,同时为了减小其他误差的影响,检校区域的高程变化应尽量小。几何检校之后,需要保证SAR影像在全球范围内无控定位精度达到25 m以内,且卫星参数应至少在3个月内保持极好的稳定性,从而支撑全球测图任务。
1.2 干涉测量检校技术干涉测量检校的目的是修正基线误差,确保无控条件下的高程精度满足指定标准。从资源三号的成功应用来看,卫星测绘的精度一般不低于1:50 000,即丘陵地区的高程精度优于5 m。对于InSAR全球测图来说,一般也遵循类似的标准,即SAR卫星需要在完成干涉测量检校及后处理之后,保证全球高程精度达到5 m。这对于我国InSAR全球测图来说,是极为严苛的精度水平。首先,我国民用干涉SAR卫星刚刚起步,虽然已经有了高分三号卫星,卫星成像质量也达到了极高的水平,但是高分三号尚不具备业务化干涉能力,无法用于全球测图。其次,我国L-SAR虽然是以干涉为主的卫星,但是依然是科研星,部分研制指标相比TanDEM-X依然有较大的差距,在这种情况下,进行可靠的干涉测量检校,测量和修正干涉基线误差,就显得尤为重要。
SAR卫星基线测量方式与干涉模式相关。现阶段InSAR地形测绘主要通过两种干涉模式实现,一种是以SRTM为代表的双天线干涉模式,这种情况下,基线需采用姿轨测量仪(Attitude and Orbit Determination Avoinics,AODA)进行测量,AODA提供的基线数据精度约2 mm,姿态精度约9″,能够满足DETD-2的高程精度要求(16 m)。另一种是以TanDEM-X为代表的双星编队干涉模式,这种情况下,基线需采用星间双差GPS(double differential GPS,DDGPS)进行测量,测量精度要求达到1 mm,从而满足HRTI-3的高程精度要求(4 m)。
然而值得说明的是,无论何种测量方式,获取的始终是天线的几何中心对应的基线,而并非SAR天线相位中心对应的基线。在InSAR地形测绘过程中使用的则是后者,因此在实际测绘过程中,依然需要对基线参数进行标定,消除基线参数测量和转换过程中的误差。L-SAR采用的双星编队绕飞模式,其基线测量方式与TanDEM-X相似。DDGPS直接获取的参数是基线的三维分量,即[Bx By Bz],在InSAR地形测绘过程中,一般采用更为直观的基线分量[BT B⊥ B‖],即沿轨基线、垂直基线及平行基线。其中沿轨基线并不影响InSAR交轨干涉的地形测绘精度,一般不予考虑。垂直基线误差对高程误差的传播可描述为
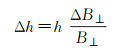 (5)
(5)
即垂直基线误差传播过程与地表高程相关。因此检校过程中应尽量选择平坦地区,以避免高程差异引入额外的误差。平行基线误差对高程误差的传播分为两个方面,一方面,平行基线会通过误差传播直观传递到高程误差中,即
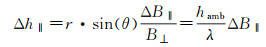 (6)
(6)
式中,hamb为InSAR地形测绘中的高程模糊度(height of ambiguity,HoA),一般在35~55 m。另一方面,平行基线带来的高程误差与入射角相关,随着入射角的增加,高程误差会随之增加,从而在较广域范围(上千千米)内形成一个高程斜坡Δh‖t,通过几何关系的简单转换,可以得到
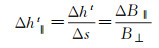 (7)
(7)
式中,Δs为地距向两点间的距离;Δht为两点间的相对高程误差,在基线倾角小于侧视角的情况下,侧视角越大,垂直基线越小,平行基线误差带来的高程误差越大。基于平行基线的这种误差特性,一般需要采用相隔上千千米的高程较为一致的区域进行平行基线误差标定。
2 数据处理技术卫星下传的数据是回波数据,数据处理系统需完成零多普勒成像及距离徙动校正等,生成经严格配准的SLC数据。同时使用SLC完成干涉链路的处理,生成高精度的经编码的DEM初始产品。干涉链路的处理过程中,严格来讲不应采用任何外部数据,即可将高程误差控制在一定精度标准以内(一般为最终产品精度的2~3倍)。这对于数据处理的精度和效率提出了极大的挑战,特别是高精度相位解缠技术及快速地理编码技术。
2.1 高精度相位解缠技术高精度相位解缠技术需要同时确保解缠结果的稳健性和可靠性。首先,算法应能够满足不同地形条件下的相位解缠精度需求,不会由于地形的变化或者解缠参数的变化出现较大的解缠精度差异。其次,算法需能够确保相位的可靠性,即解缠相位应与真实相位保持最小的L-P范数。一般来说,在工程中常采用1-P范数,即最小费用流进行相位解缠,以平衡稳健性、可靠性与解缠效率。解缠之后的相位常数需要采用雷达摄影测量的手段解算,即获取主辅影像同名点之间的雷达摄影测量时间延迟Δts和Δtm,从而用下式解算获得[15]
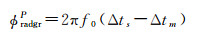 (8)
(8)
式中,f0为雷达中心频率。由于时间延迟差异为未知量,一般在配准过程中采用配准偏移量确定。推荐在整景影像中采用32×32个点进行解算,以便同时兼顾精度和效率。在获取了每个点的配准偏移量,从而解算出绝对相位常数之后,应使用稳健估计算法,获取最终的绝对相位对应的整周未知数,从而解算参考点的绝对相位。
2.2 快速地理编码技术快速地理编码技术是确保整个数据处理链路效率的重要环节。地理编码算法一般分为前向编码和后向编码。前向编码通过R-D模型将像素坐标解算到地理坐标,解算之后的DEM数据并不具备规则的格网,因此一般采用后向编码。后向编码从规则的DEM格网中获取地理坐标,通过R-D模型解算到对应的像素坐标,从而获取对应高程值,迭代优化模型参数,获取精确的点位,最后以16点sinc截断函数进行点位高程插值,获取可靠的点位高程信息。如果不进行算法优化,单线程条件下30×50 km2的范围内完成10 m格网插值会消耗长达二三十分钟的时间,这会大大降低全球测绘的效率,因此需要进行工程优化,将编码时间控制在1 min以内。编码之后的DEM为初始DEM,这些残差的大小一般不超过10 m,需要在后续的区域网平差及多数据后处理过程中进一步消除。
3 数据后处理技术初始DEM的高程精度虽然已经能够控制在较好的水平,但是对于1:50 000比例尺地形图测绘来说,需达到平地、丘陵、山地和高山地分别为3 m、5 m、8 m及14 m的高程精度水平,还需要进一步的数据处理。首先,需借助区域网平差技术消除部分卫星参数残差;其次,需使用多轨数据进行联合处理,减小低相干区域面积,提高DEM的有效覆盖范围。
3.1 DEM区域网平差技术几何和干涉测量检校并不能消除所有误差,初始DEM中将包含基线残差、斜距残差、定轨残差及绝对相位解算残差等。这些残差量呈现一定的系统性,可在镶嵌拼接过程中,通过连接点进行平差消除。为了提高DEM精度,需要采用适量的地面控制点完成区域网平差过程。一般来说,各类残差在影像中可采用一阶多项式进行拟合,其多项式表达为[24]
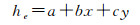 (9)
(9)
式中,a、b、c为多项式系数;x、y为距离向及方位向坐标。在平差过程中,可用的控制数据主要包括三类,即ICESat-GLAS数据、SRTM数据及资源三号控制点库数据。由于L-SAR的设计精度为1:50 000,在高山地的精度需要达到14 m,因此SRTM(16 m)并不能满足平差的参考数据精度要求。而资源三号控制点库只能覆盖国内区域,且点位密度不均,不能确保参数估计的稳健性。因此建议采用ICESat-GLAS数据完成平差处理,ICESat-GLAS的标称精度为2 m,可用于高程控制。然而ICESat-GLAS的光斑直径为70 m,L-SAR的分辨率为米级,平差过程中需要将InSAR生成的DEM对应的直径为70 m圆覆盖范围内的点的高程进行平均,以建立合理的对应关系。
3.2 长短基线组合技术长短基线组合算法的目的是提高相位解缠的可靠性[25]。相位解缠精度与相位梯度相关,按照奈奎斯特采样定律,当相位梯度超过π时无法恢复真实相位。在实际相位解缠过程中,最大可探测相位梯度(maximum detectable phase gradient,MDPG)与多视数和相干系数之间的关系可表达为[26]
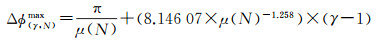 (10)
(10)
式中,Δϕ(γ, N)max是MDPG,μ(N)=min{μ(a), μ(r)},μ(a)和μ(r)分别是N倍多视之后的像素采样间隔。假设SAR影像原始分辨率为3 m,处理过程中采用2×2多视,经多视和滤波处理之后干涉图的相干性高于0.9,此时的MDPG为0.44弧度,即21°。这意味着相邻两点之间的高程梯度不超过2.0(HoA=35 m)或者3.2(HoA=55 m),相邻两点之间的高程差异分别不超过12.0 m及19.6 m。基于此点考虑,一般采用较大的HoA获取第一遍DEM数据,此时相位梯度较小,解缠精度较高。随后采用较小的HoA获取第二遍DEM数据,此时相位梯度较大,解缠精度较小,但是第一遍获取的DEM数据能够提供参考相位,这允许第二遍的干涉过程中采用去地形-相位解缠-加地形的操作,减小相位梯度,保障相位解缠精度。值得说明的是,长短基线数据的入射几何应尽量一致,以确保影像具有相似的几何畸变。
3.3 升降轨融合技术SAR卫星的侧视特性会引入其特有的阴影、叠掩等畸变,因此使用InSAR技术进行全球测图的过程中,至少需要对地面进行两次观测,以弥补测试过程中阴影和叠掩带来的信息损失。例如SRTM完成了两次对地全覆盖,TanDEM-X完成了四次对地覆盖(两次全覆盖,两次重点地区重复覆盖)。在一轨之内,获取升轨数据和降轨数据的时间各占一半。升轨数据提供指定区域由西向东的侧视信息,降轨数据提供指定区域由东向西的侧视信息。升降轨数据的阴影和叠掩区域基本互补,数据融合后可提高DEM数据的完整性。此外,对其他地区的数据来说,采用相干系数进行加权计算,能够在一定程度上剔除粗差,进一步提高DEM精度。
4 试验分析 4.1 试验数据选择试验过程中采用了德国宇航中心(German Aerospace Center,DLR)提供的陕西省的TanDEM-X数据,数据是经测量检校处理的配准的斜距复图像(coregistered single look slant range complex,CoSSC)。研究区在西安市的东北侧,涵盖了阎良区、富平县、蒲城县及白水县等。整个区域南侧地形起伏极小,属于典型的平地地形,东北侧有一定的地形起伏,符合丘陵地的特征,而西北侧地形起伏较大,符合山地的特征。试验过程中用到的数据共6景。其中成像日期为20130903(YYYYMMDD)和20130925的四景影像为降轨数据,20121021和20140402为升轨数据。影像的方位向采样间隔为2.2 m,距离向采样间隔为1.4 m,入射角为42.6°,对应地距采样间隔为2.1 m,刈幅大小为35.5×56.9 km2,其他概要信息如表 2所示。由于影像的西北侧地形起伏极其复杂,因此需联合采用升降轨融合以及长短基线组合算法进行联合解算。详细的解算过程如4.2节所示。

|
| 图 2 研究区及所用影像分布图 Fig. 2 Images distribution map of the research regions |
| m | |||
| 影像编号 | 升降轨 | 垂直基线 | HoA |
| 20140402_1 | 升轨 | -129.40 | 79.06 |
| 20121021_2 | 升轨 | -370.75 | 27.33 |
| 20130903_3 | 降轨 | 215.16 | 57.15 |
| 20130925_4 | 降轨 | 204.52 | 56.29 |
| 20130903_5 | 降轨 | 214.96 | 57.22 |
| 20130925_6 | 降轨 | 204.33 | 56.36 |
4.2 试验结果及分析
由于DLR已经对CoSSC影像进行了处理,分发的是检校之后的数据,因此研究过程中无法对结果进行进一步的检校处理。然而通过数据处理过程中可对DLR的检校结果进行侧面的验证。首先,4景影像的无控地面定位精度可通过与SRTM的配准确定。以20130903_3为例,其距离向的常数项偏移为2.65像素,方位向常数项偏移为0.12像素,处理过程中为了最大程度的抑制相干斑,采用了8×8的多视数,多视之后的像素采样间隔为16 m,这意味着影像距离向和方位向直接定位精度分别为42.4 m及1.92 m,解算得到大气的影响为5.52 m,对应的距离向定位误差为8.16 m,那么由斜距延迟带来的误差至少为34.2 m,并不能满足高精度直接定位要求。处理过程中为了获取更精确几何位置,将影像与10倍过采样之后的SRTM数据做了精配准,其配准精度为0.1像素以内,以确保平面定位精度不超过0.9 m。同时,计算过程中采用精配准之后的SRTM均匀选取了10 000个高程点进行基线的精估计,精估计后的交轨方向和垂轨方向基线变化量分别为11.9 cm和5.7 cm,这意味着采用TanDEM-X提供的CoSSC数据只能获取与定轨精度(5 cm)同数量级的基线精度,在实际的数据处理过程中,依然需要采用地面控制点完成高精度基线的估计。
CoSSC数据处理过程中采用的常规干涉处理流程,即多视、干涉、去平、滤波、相位解缠、相高转换、地理编码等。其中的关键技术之一就是无控条件下整周未知数的解算技术。论文从CoSSC中均匀选取了1024个同名点,通过配准偏移量解算时间延迟和整周未知数,并求取整周未知数的众数,以获取稳健结果。结果表明,这6景影像的整周未知数分别为π、12π、8π、11π、0π、3π弧度。在解缠结果中添加整周未知数,并进行相高转换以及地理编码,即可得到初始DEM数据。
本文采用了SRTM、ICESat-GLAS数据及资源三号控制点库数据进行了初始DEM的精度评估,不同影像的高程精度如表 2所示。其中使用SRTM及ICESat-GLAS评估的结果较为一致,精度会同步提升或下降,而控制点库数据量较少,并不能全面反映高程的精度水平,综合考虑下,推荐使用SRTM进行InSAR处理链路的精度评估(从回波数据到初始DEM数据),使用GLAS对区域网平差、升降轨融合及长短基线组合等中间结果进行精度的二次评估,而GCP适合对最终的DEM产品进行精度评估,给出最终的产品精度。图 3给出了ICESat-GLAS点及控制点库数据的分布情况。其中包含激光点17 439个,控制点58个。激光点在20130925_6中分布较少,只有411个,且集中在影像的西南方向,从分布上来看,其精度的评估并不稳健。

|
| 图 3 试验用到的矢量点数据分布情况 Fig. 3 Vector data distribution map of the experimental regions 其中深色为ICESat-GLAS点,浅色为DEM平差连接点,黑色为资三控制点库数据, 多边形选定区域为升降轨和长短基线共同覆盖的区域。 |
DEM区域网平差针对的是具有相同侧视角度、相同飞行方向的数据,因此试验过程中使用表 3中的后4景影像开展了平差试验。平差过程中所用连接点为西侧影像的最后一列(升轨情况下)或者北侧影像的最后一行(降轨情况下),首先在影像边缘均匀选取100个连接点,并使用R-D模型解算连接点的地理坐标信息,随后将地理坐标转换为邻接影像的像素坐标,最终完成像素坐标空间的平差。4景影像的平差结果如表 4所示,由于20130925_6的点位分布较为集中,出现了秩亏问题,并未解算成功。由影像的平差结果可知,DEM结果在距离向及方位向均会有2~6 m/万像素,即10~30 cm/km的高程斜坡。这种高程斜坡除了基线误差的贡献之外,还包括斜距、定轨误差、相位整周未知数估算误差等。在进行全球测绘的过程中,如果能够进行精确的斜距和轨道标定,并解决无控条件下整周未知数精估计问题,将有望进一步缩小高程斜坡对应的误差大小。4景影像平差之后,使用GLAS点进行了精度的重新评估,其高程精度分别提升到1.79 m、0.46 m、1.06 m及0.67 m,这说明平差算法有效提高了DEM的高程精度水平。
| 影像编号 | SRTM | ICESat-GLAS | 控制点库 |
| 20140402_1 | 3.12 | 5.96 | 1.28 |
| 20121021_2 | 2.42 | 4.75 | 3.44 |
| 20130903_3 | 1.39 | 4.72 | 3.75 |
| 20130925_4 | 0.98 | 3.14 | 0.74 |
| 20130903_5 | 1.03 | 1.67 | 1.80 |
| 20130925_6 | 0.65 | 1.95 | 1.36 |
| 影像编号 | a(×10-4) | b(×10-4) | c(×10-4) |
| 20130903_3 | 5.30 | -2.13 | -7.30 |
| 20130925_4 | -6.24 | -2.38 | 3.02 |
| 20130903_5 | 4.35 | -3.04 | -5.55 |
| 20130925_6 | -8.96 | -3.43 | 0.00 |
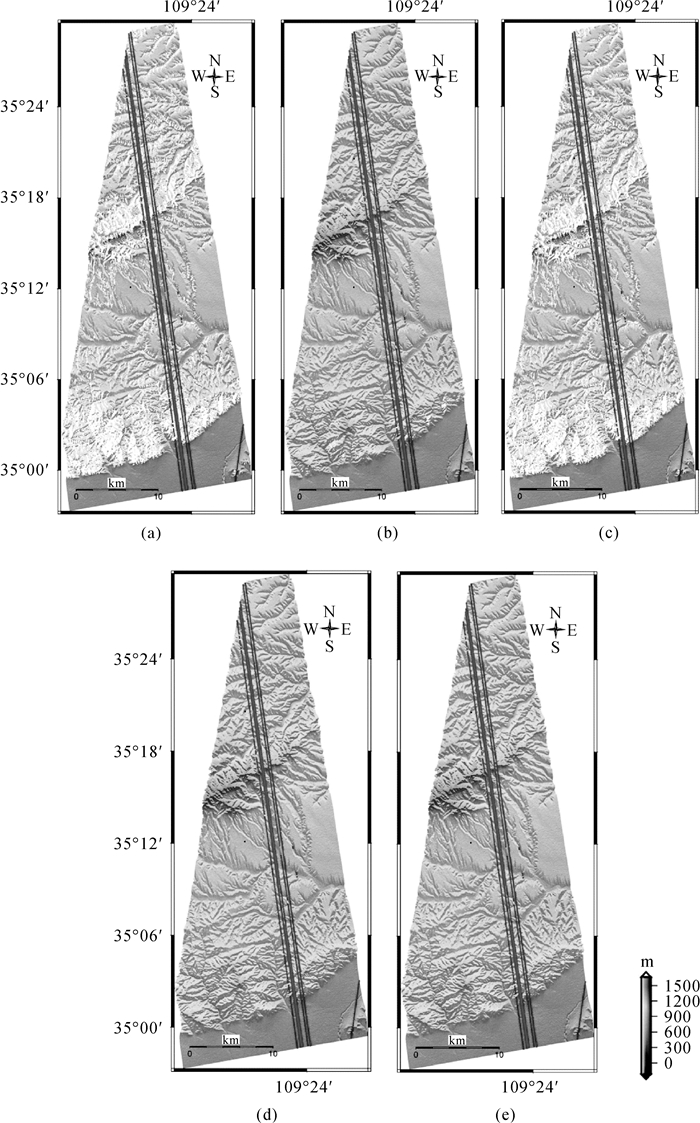
由于影像西北区域地形复杂,精度较差,多为3~5 m(表 2),因此论文针对这部分数据进行了长短基线组合及升降轨融合试验。试验结果如图 4所示。由于第一景及第二景影像的侧视几何较为一致,因此本文使用这两景影像进行长短基线组合试验。试验过程中首先完成短基线的相位解缠及相高转换,然后将短基线高程数据配准到主影像空间中,进而完成主影像干涉图的去平去地形操作,减小相位梯度,提高相位解缠精度。论文使用GLAS数据对长短基线的公共区域进行了精度评估,长基线的精度为5.90 m,短基线的精度为3.77 m,经长短基线组合之后,精度达到5.04 m,长基线精度有较为明显的提升。进一步融合降轨数据之后,精度变为5.07 m,此时精度虽然已经没有提升,但是低相干区域面积已经极大降低,统计结果表明,升轨数据经长短基线组合之后,其低相干区域(经多视及滤波之后相干性<0.9)的面积为253.6 km2,而升降轨融合之后的低相干面积仅为0.8 km2,这对于实现全球测图中DEM的全覆盖来说具有重要意义。
|
| 图 4 升降轨以及长短基线组合试验 Fig. 4 Results of the descending-and-ascending, long-and-short baseline combination experiments 其中(a)—(e)的DEM分别对应长基线、短基线、长短基线组合、降轨数据、长短基线和降轨数据融合结果。 |
5 结论与展望
本文提出了面向全球测图的智能化精密干涉测量系统技术,并采用6景覆盖陕西区域的TanDEM-X数据进行了技术的处理与验证。首先,论文对数据进行了定标精度的评估。由于缺乏角反射器数据,本文采用SRTM数据对定位精度进行了侧面验证。结果表明,TanDEM-X在距离向的误差较大,为40 m以上,而方位向能够控制在2 m以内。因此,在后续处理过程中,为了确保高程精度,采用SRTM数据为参考。其次,论文完成了数据的干涉处理,获取了初始DEM,并开展了区域网平差试验,将DEM高程精度提升了0.61~2.93 m不等。随后,本文进行了长短基线和升降轨融合的试验分析。试验表明,长短基线组合算法能够将长基线精度从5.9 m提升到5.04 m,进一步融合降轨数据之后,精度并没有明显的提升,然而低相干区域的面积已经从253.6 km2降低到0.8 km2,这极大提升了DEM数据的有效性。在数据处理及区域网平差过程中,不包含人工交互过程,这意味着使用InSAR进行全球测图时,除了DEM编辑过程之外,可极大提高整个链路的智能化水平,达到高精度、高效率、高智能化的摄影测量新要求。本文处理结果表明,TanDEM-X可提供5 m左右的高精度DEM数据,这能够满足我国1:50 000比例尺山地地形8 m的测绘精度,能够基本满足我国1:25 000比例尺山地地形5 m的测绘精度。
在使用InSAR进行全球测图的过程中,除了本文重点阐述的测绘精度之外,还需解决测绘效率问题、测绘标准问题及测绘产品生产问题。一方面,需要确保在多节点并行运算情况下,从回波数据开始,完成整个干涉链路处理,生成经编码的初始DEM数据,能够将时间控制在1 min左右。另一方面,亟需针对L波段差分干涉SAR卫星开展权威的国家标准的制定。最后,需积累测绘人才,去除房屋、植被、水体等的影响,并完成DEM空洞区域的插值,完成DEM的后期编辑,生成可靠的全球DEM产品。
本文提出的面向全球测图的精密干涉测量技术,是面向未来数字摄影测量智能化下的自动成图技术,精密干涉测量技术的高自动化、高精度化等特点,使得它能够在无人工参与的情况下,1 min内完成数千平方千米的DEM数据粗生产,并在自动化智能化筛选ICESat-GLAS点之后,完成大范围数据的后处理,生成具备极高精度的全球DEM数据。这种技术将有望打破我国全球高精度DEM长期依赖SRTM数据的现状,为我国全球测图提供大范围、高精度、高一致性的基础数据。
| [1] | MASSONNET D, ELACHI C. High-resolution Land Topography[J]. Comptes Rendus Geoscience, 2006, 338(14-15): 1029–1041. DOI:10.1016/j.crte.2006.06.001 |
| [2] | RODRIGUEZ E, MORRIS C S, BELZ J E, et al. An Assessment of the Srtm Topographic Products[R]. JPL D-31639, Pasadena, California: JPL, 2005. |
| [3] | AMANTE C, EAKINS B W. Etopo11 Arc-minute Global Relief Model: Procedures, Data Sources and Analysis[R]. NESDIS NGDC-24, NOAA, 2009. |
| [4] | DANIELSON J J, GESCH D B. Global Multi-resolution Terrain Elevation Data 2010(GMTED2010)[R]. Open-File Report 2011-1073, Reston: U. S. Department of the Interior, U. S. Geological Survey, 2011. |
| [5] | NIKOLAKOPOULOS K G, KAMARATAKIS E K, CHRY-SOULAKIS N. SRTM Vs ASTER Elevation Products. Comparison for Two Regions in Crete, Greece[J]. International Journal of Remote Sensing, 2006, 27(21): 4819–4838. DOI:10.1080/01431160600835853 |
| [6] | BUCKREU S. Terrasar-X/Tandem-X Mission Overview[C]//Proceedings of TerraSAR-X/TanDEM-X Science Meeting. München: [s. n. ], 2016. |
| [7] |
国家测绘地理信息局卫星测绘应用中心. 国家测绘地理信息局卫星测绘应用中心2010-2015科技报告[R]. 国家测绘地理信息局卫星测绘应用中心, 北京: 2016. Satellite Surveying and Mapping Application Center. National Administration of Surveying Mapping and Geoinformation, 2010-2015 Scientific and Technical Report[R]. Beijing: Satellite Surveying and Mapping Application Center. 2016. |
| [8] | FARR T G, ROSEN P A, CARO E, et al. The Shuttle Radar Topography Mission[J]. Reviews of Geophysics, 2007, 45(2): RG2004. |
| [9] | KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X:A Satellite Formation for High-resolution SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3317–3341. DOI:10.1109/TGRS.2007.900693 |
| [10] | BAMLER R. The SRTM Mission: A World-Wide 30 M Resolution DEM from Sar Interferometry in 11 Days[C]//FRITSCH D, SPILLER R. Photogrammetric Week'99. Heidelberg: Wichmann, 1999. |
| [11] | FREY O, MEIER E, NVESCH D, et al. Geometric Error Budget Analysis for Terrasar-X[C]//Proceedings of the 5th European Conference on Synthetic Aperture Radar. Ulm, Germany: EUSAR, 2004. |
| [12] | HUESO GONZÁLEZ J, WALTER ANTONY J M, BACH-MANN M, et al. Bistatic System and Baseline Calibration in TanDEM-X to Ensure the Global Digital Elevation Model Quality[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 3–11. DOI:10.1016/j.isprsjprs.2012.05.008 |
| [13] | SCHWERDT M, GONZALEZ J H, BACHMANN M, et al. In-orbit Calibration of the TanDEM-X System[C]//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver, BC, Canada: IEEE, 2011: 2420-2423. |
| [14] | DEO R, ROSSI C, EINEDER M, et al. Framework for Fusion of Ascending and Descending Pass Tandem-X Raw DEMs[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(7): 3347–3355. DOI:10.1109/JSTARS.2015.2431433 |
| [15] | ROSSI C, RODRIGUEZ GONZALEZ F, FRITZ T, et al. TanDEM-X Calibrated Raw DEM Generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 12–20. DOI:10.1016/j.isprsjprs.2012.05.014 |
| [16] |
汪丙南, 向茂生.
TanDEM-X系统相对测高性能分析[J]. 遥感学报, 2009, 13(1): 49–53.
WANG Bingnan, XIANG Maosheng. Relative Height Accuracy Analysis of TanDEM-X System[J]. Journal of Remote Sensing, 2009, 13(1): 49–53. |
| [17] |
杜亚男, 冯光财, 李志伟, 等.
Terrasar-X/Tandem-X获取高精度数字高程模型技术研究[J]. 地球物理学报, 2015, 58(9): 3089–3102.
DU Yanan, FENG Guangcai, LI Zhiwei, et al. Generation of High Precision DEM from TerraSAR-X/TanDEM-X[J]. Chinese Journal of Geophysics, 2015, 58(9): 3089–3102. DOI:10.6038/cjg20150907 |
| [18] |
张永胜, 黄海风, 梁甸农, 等.
星载分布式insar测高性能的理论及系统仿真评价方法[J]. 电子学报, 2008, 36(7): 1273–1278, 1255.
ZHANG Yongsheng, HUANG Haifeng, LIANG Diannong, et al. Theoretic and Simulation Experimental Performance Evaluation Methods of Spaceborne Distributed InSAR System[J]. Acta Electronica Sinica, 2008, 36(7): 1273–1278, 1255. |
| [19] |
靳国旺, 张薇, 向茂生, 等.
一种机载双天线inSAR干涉参数定标新方法[J]. 测绘学报, 2010, 39(1): 76–81.
JIN Guowang, ZHANG Wei, XIANG Maosheng, et al. A New Calibration Algorithm of Interferometric Parameters for Dual-antenna Airborne InSAR[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 76–81. |
| [20] |
李芳芳, 胡东辉, 丁赤飚, 等.
机载双天线inSAR对飞数据处理与分析[J]. 雷达学报, 2015, 4(1): 38–48.
LI Fangfang, HU Donghui, DING Chibiao, et al. Antiparallel Aspects of Airborne Dual-antenna InSAR Data Processing and Analysis[J]. Journal of Radars, 2015, 4(1): 38–48. |
| [21] |
王萌萌, 黄国满, 花奋奋, 等.
机载双天线inSAR联合定标算法[J]. 测绘学报, 2014, 43(12): 1259–1265.
WANG Mengmeng, HUANG Guoman, HUA Fenfen, et al. Joint Calibration Method of Airborne Dual-antenna Interferometric SAR[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1259–1265. DOI:10.13485/j.cnki.11-2089.2014.0139 |
| [22] |
张延冰, 郭华东, 韩春明.
利用机载双天线InSAR数据生成高精度DEM的试验研究——以大面积丘陵地区为例[J]. 国土资源遥感, 2014, 26(1): 97–102.
ZHANG Yanbing, GUO Huadong, HAN Chunming. High Precision DEM Generation Using Airborne Dual-antenna InSAR Data:A Case Study of Large Hilly Areas[J]. Remote Sensing for Land & Resources, 2014, 26(1): 97–102. DOI:10.6046/gtzyyg.2014.01.17 |
| [23] | JEHLE M, PERLER D, SMALL D, et al. Estimation of Atmospheric Path Delays in Terrasar-X Data Using Models Vs. Measurements[J]. Sensors, 2008, 8(12): 8479–8491. DOI:10.3390/s8128479 |
| [24] | GRUBER A, WESSEL B, HUBER M, et al. Operational Tandem-X DEM Calibration and First Validation Results[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73: 39–49. DOI:10.1016/j.isprsjprs.2012.06.002 |
| [25] | FRITZ T, BALSS U, BAMLER R, et al. Phase Unwrapping Correction with Dual-baseline Data for the TanDEM-X Mission[C]//Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich, Germany: IEEE, 2012: 5566-5569. |
| [26] | GAO Xiaoming, LIU Yaolin, LI Tao, et al. High Precision DEM Generation Algorithm Based on Insar Multi-look Iteration[J]. Remote Sensing, 2017, 9(7): 741. DOI:10.3390/rs9070741 |



