2. 伦敦大学学院土木、环境与地理工程学院, 伦敦 WCIE 6BT, 英国
2. Department of Civil, Environmental and Geomatic Engineering, University College London(UCL), London, WCIE 6BT, UK
数字摄影测量技术在各行各业中发挥着越来越重要的作用,主要包括近景摄影测量、航空摄影测量和航天摄影测量。
从我国摄影测量发展进程上看,主要有两个学术思路:一是以王之卓等为奠基的直角坐标系摄影测量理论[1],服务于现有近景和常规摄影测量有效,至今遥感测绘对地观测领域几乎全部沿用这个体系;二是基于射线角的极坐标摄影测量方法,20世纪50年代唐山铁道学院罗河[2]和中国地质大学的周卡[3],从射线角出发证实了对直角坐标系矩阵病态解算有改观,对高阶奇异的现象有所缓解,但没有成功地从数学原理上加以系统推导和证明,亦没有上升到理论创建的高度,致使其后期的逐步消沉。近10余年,本文针对直角坐标系摄影测量方法在航空航天和近景摄影测量新技术处理中遇到的解算效率降低、精度下降甚至发散等问题,基于国外仿生机器视觉原理,引入了极坐标方法,初步为构建面向航空航天的极坐标摄影测量的相关理论体系[4-7]奠定了基础。
1.1 摄影测量解算中的病态问题航天观测直角坐标系垂直参量Z相对于其他两个平面参量具有式(1)特征
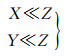 (1)
(1)
因此,当三轴具有相同量级的增量值时(例如同一相机拍摄空间影像具有三轴相同的分辨率),Z轴的相对增量远小于平面相对增量。
 (2)
(2)
这是三维影像在Z轴方向交角极小时产生病态奇异性的根源,即高程增量相对于平面增量相比非常微小。当然此时的微小值不是绝对的0值,因此三维相对误差计算矩阵尽管满秩不相关,但实质上Z轴相对增量趋于零值会导致法方程具有极弱正定性[8],成为引发计算发散的根源。
为了避免发散,有3种方法可以降低病态奇异性。
其一,可以“放大”Z轴相对增量相应量级,这样与平面相对参量相“适应”,消除奇异性;但同时把Z轴高程误差也同量级放大,“淹没”了高分辨率的精准辨识力,影像失去应有的高分辨率精度水平。
其二,布设大量地面控制点,以降低病态性,但成本巨大且违背了不要或少要地面控制点的产业发展原则,且在境外及特殊领域无法实测地面控制点。
其三,选择数学方法。首先人们尝试局部数学的改进。例如20世纪90年代提出的Inverse depth方法[9-12],即1/Z方法。实际上是它针对较复杂的近景摄影测量中无穷远特征点在XYZ坐标中Z无穷大的问题,采用特征点深度的倒数,以及相机中心到特征点观测向量的方位角与高程角,同时结合在全局坐标系中被称为“锚点”的相机中心来表达,可以实现法方程非奇异,但例如近景摄影测量中可能某个特征点离相机很近,采用此方法表示与解算会使法方程奇异,解算发散。
分析可知,直角坐标系X、Y、Z采用长度单位米(m)作为度量,相对比较会产生式(1)与式(2)的微小和极大数值的多量级差异,使得法方程病态。
由此引入极坐标。将平面ΔX、ΔY增量m的度量单位转化为弧度增量Δθ、Δφ度量单位,ΔZ以Δr表征而保留m的度量单位如下
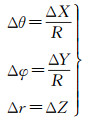 (3)
(3)
极坐标系表达方法避免了原有法方程中的微小值,从源端去除法方程的病态奇异性,根本上避免发散。例如上述1/Z方法远近特征点的表达局限性问题,避免由于过远或过近特征点的存在造成发散。
1.2 极坐标理论试验系统及分析本文基于极坐标方法,采用多种极坐标视差角空间仪器试验系统(图 1),以探索直角坐标影像处理机制面对长距离或高重叠投影等易导致交会角偏小,方程易呈病态奇异性问题;推扫式、变角摆头凝视、变焦成像、动姿态、大角度等新技术引发的更易为极坐标体系破解的问题;以及快速收敛和三维测量的需求,进而为探索空间信息极坐标方法体系奠定基础。

|
| 图 1 多种极坐标视差角(变角标定,双角推扫,高重叠4×4探测阵列)空间仪器试验系统 Fig. 1 Spatial instrument test system for different polar coordinates of parallax angle (variable angle calibration, double angle push, high overlap 4×4 detection array) |
其次,从观测过程看,空间信息以角度为特征,其来自于地球的经纬度,最终的产品也以经纬度的方式进行表达,由于历史原因,中间一般采用直角坐标系进行处理。若能直接采用极坐标系,将使得地物信息的表达更为直接。尤其是,高分辨率使得经纬直线表达的方式越来越需要以弧长来精化表征,即恰恰以矢径与微增量夹角表达更直接,从而降低由于三维直角分解原始参量而引发的计算源端误差。
其三,基于2n及整型一维数组的全球经纬度剖分网格[13-15]的“地球空间网格与编码”已被公开颁布为国家军用标准GJB 8896—2017,它是基于经纬度坐标和地心坐标体系来定义的空间信息组织、管理和存储的标准,对军民两用都具有强制性,因而可以用极坐标表达,如果再结合本文的极坐标空间信息获取和处理方法,有望为新一代空间信息获取-组织-管理-存储-处理-应用一体化的极坐标体系构建确立基础。
2 极坐标理论方法本节从数学上证明极坐标系统避免解算的非收敛性,并通过理论证明极坐标矢量系统解算能使复杂姿态和大角度场景下影像解算收敛,并达到精度-效率-抗干扰性统一。
2.1 矢量坐标体系对非收敛性破解由于二维场景中的成像原理与三维场景中类似且更易于理解分析,因此,讨论二维场景情况。为与直角坐标数据直接相连,在本文提及的极坐标系统中,表示相机姿态的外方位元素仍然沿用在地面直角坐标系统中的表达,而极坐标系的建立针对影像中的像点,确定其主锚点和副锚点,以及主副锚点间基线方向和长度后,在此极坐标系统中表达像点坐标。
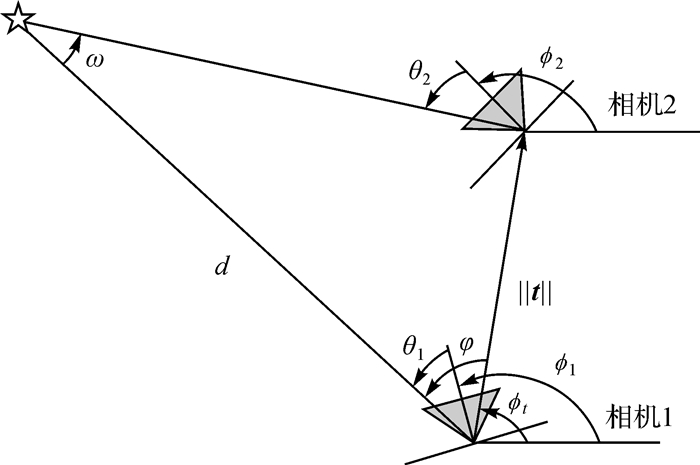
图 2[16]中,假设相机1中心为坐标系原点。2台相机间距为‖t‖常量,在局部坐标系下的方向角为ϕ1、ϕ2,相机基线的方向角为ϕt,因此,相机1的位置表示为(ϕ1, 0, 0),同理,相机2的位置为(ϕ2, ‖t‖cos ϕt, ‖t‖sin ϕt)。在二维场景下,选取第一个相机为特征点主锚点,在直角坐标系下可以表示为
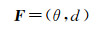 (4)
(4)
|
| 图 2 二维场景的成像原理 Fig. 2 Imaging principle of two dimensional scene |
式中,d表示特征点到主锚点的深度信息;θ表示特征点在局部坐标系下的方向角,等价于
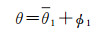 (5)
(5)
式中,θ1表示特征点在其主锚点上的观测角的真值。
在极坐标系下,特征点可以表示为
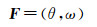 (6)
(6)
式中,ω表示主锚点和副锚点到像点光线间的夹角,称之为“视差角”。
为与三维光束法平差模型中以二维图像特征点作为观测值相区别,在二维场景中,特征点在两个相机上的观测量为两个局部观测角,即θ1、θ2,见图 2。光束法平差的数学本质为非线性最小二乘优化问题[17-19],迭代求解的公式可以表示为
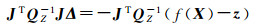 (7)
(7)
假设所有观测误差为高斯白噪声,可以认为是等权的,即Qz-1=E,式(7)可以简化为
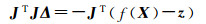 (8)
(8)
式中,JTJ为法方程,当问题收敛时,JTJ表示为信息矩阵,即变量的不确定度。式(8)表明,法方程的奇异性直接影响光束法平差的收敛性。若法方程奇异,法方程无法求逆,则利用Gauss-Newton无法进行数值计算,此时光束法平差问题发散。
直角参数空间光束法平差的观测量为θ1、θ2,变量为(θ, d),其最小二乘优化问题可以表示为
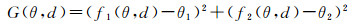 (9)
(9)
式中,f1(θ, d)和f2(θ, d)分别为特征点在两个相机上的观测方程,可以表示为式(10)、式(11)。
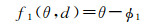 (10)
(10)
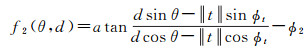 (11)
(11)
两个观测方程对变量(θ, d)的一阶导数组成了Jacobi矩阵
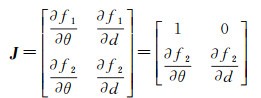 (12)
(12)
根据式(8),直角参数空间的光束法平差模型法方程可以表示为
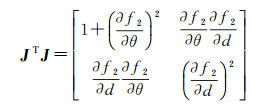 (13)
(13)
判断法方程是否奇异,可以通过行列式是否为0来计算。式(13)的行列式等于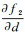
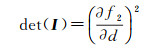 (14)
(14)
式中,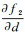
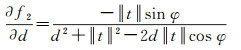 (15)
(15)
式(15)表明,直角坐标系下在两种情况下行列式为零,法方程非正定,光束法平差模型发散。情况一:特征点在相机正前方,即φ→0,此时视差角ω无穷小。情况二:特征点在无穷远位置,即d→∝,此时深度信息非常大,光束法平差方法无法准确预估深度真值,造成光束法平差问题发散。由此,从数学上解释了直角坐标发散的根源。
极坐标系中观测量仍为θ1、θ2,变量为(θ, ω),其最小二乘优化问题可以表示为公式
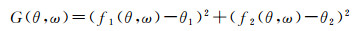 (16)
(16)
其中,f1(θ, ω)和f2(θ, ω)分别表示为
 (17)
(17)
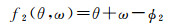 (18)
(18)
两个观测方程对变量(θ, ω)的一阶导数组成了Jacobi矩阵
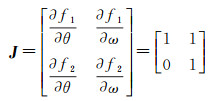 (19)
(19)
故其法方程可以表示为
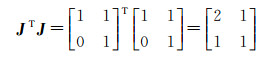 (20)
(20)
表明极坐标参数空间下的光束法平差模型在二维场景下的法方程行列式为1,即法方程正定,解算收敛。
综上,极坐标参数空间下法方程相比于直角参数空间的法方程,不受特征点深度长短和视差角大小影响,其法方程为恒正定的,避免了其奇异性风险。
参数变量对观测误差敏感度也影响着解算的收敛性。假设观测变量带有观测噪声
 (21)
(21)
式中,θ1和θ2为观测真值;θ1Δ和θ2Δ为观测噪声,假设θ1Δ和θ2Δ均满足N(0,σ2)正态分布。在直角坐标系下,假设φ和φ是相机基线到第一个相机观测方向角度的计算值和真值,因此
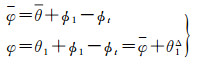 (22)
(22)
根据正弦定理,真实的深度信息可以表示为
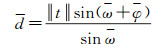 (23)
(23)
而计算的深度信息为
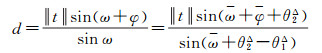 (24)
(24)
因此,深度信息对观测误差θ1Δ、θ2Δ的一阶导数为
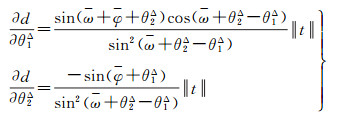 (25)
(25)
式(25)表明,θ2Δ-θ1Δ≈0,当视差角较小(ω→0)时,深度信息变量对观测误差的一阶导数无穷大,说明原函数在其定义区间不连续,在视差角无穷小的情况下迭代解算没有对应的定值。因此理论上证明,在小视差角的摄影条件下,直角坐标参数空间的深度信息对观测误差极度敏感,在直角系下解算易于发散。
极坐标参数空间的光束法平差模型中(图 2、图 3[20]),真实的视差角可以表示为
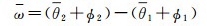 (26)
(26)
|
| 图 3 极坐标参数空间下的三维特征点参数化 Fig. 3 Parameterization of three dimensional feature points in polar coordinate parameter space |
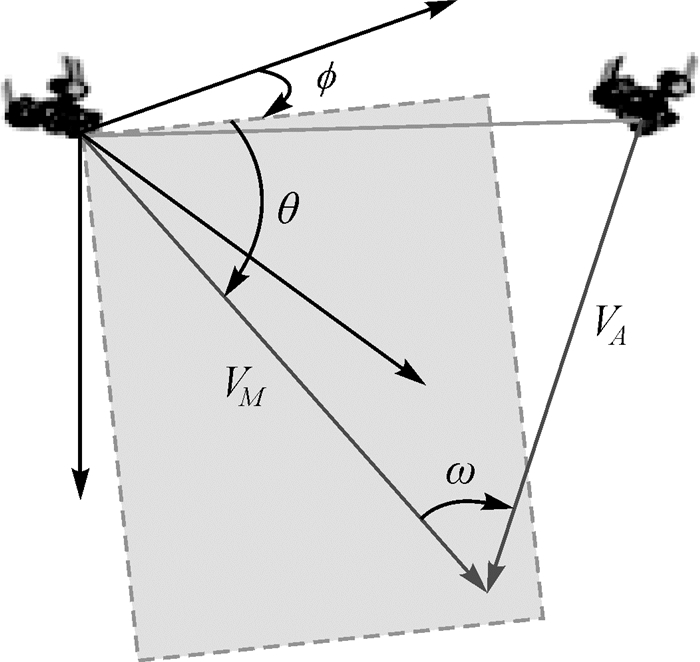
同时,计算的视差角表示为
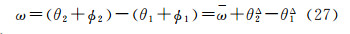 (27)
(27)
因此
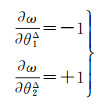 (28)
(28)
式(28)表明在极坐标系下,参数变量对观测误差的一阶导数为定值1,表明原函数在其定义空间中连续,即原图像有解,确保收敛。符号代表视差角逼近0时的方向,无论是右极限还是左极限,迭代均能很好地趋于一个定值,解算收敛。同时,正负值代表了视差角趋零的方向性,加上数值形成矢量域。
综上,直角坐标系的数值没有方向性,本质是标量参考系,是矢量系的一个特例,即没有代表方位方向选择性的数值大小。而极坐标是方向+数值要素,是矢量参考系,可以更为全面地表达地物信息。因此,极坐标系统更为先进、简洁、应用范围更加广泛。
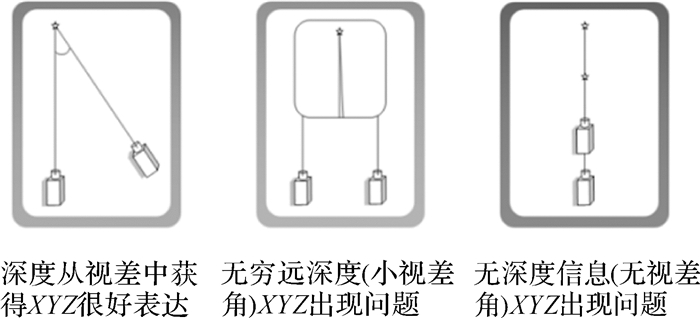
2.2 极坐标光束法平差模型经典直角坐标系(X, Y, Z)可以非常直接简单地表达三维特征点,但是这种表达方式可能会在一些特殊场景结构下失败。比如,当特征点无穷远或者视差角较小甚至接近于0的情况下,Z很难用具体数字刻画(图 4)。近景摄影测量中,对于高维非线性优化的光束法平差模型,只要存在这样的一个点,就可能会造成优化问题发散。所以经典方法并不是一个适用于所有场合的表示方法。为了从数学上完整表达所有情况下的特征点,本节采用极坐标基准下的角度参数化来表达三维特征点,即F=(φ, θ, ω),如图 3。
|
| 图 4 视差角大小对XYZ表达的影响 Fig. 4 The effect of parallax angle on the XYZ expression |
当主副锚点选定后,二维特征点坐标和三维视差角参数的变换关系(观测方程)可表示为
 (29)
(29)
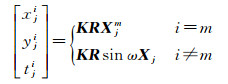 (30)
(30)
极坐标光束法平差模型的数学本质为非线性最小二乘优化,优化变量包括所有相机姿态位置和加密点的极坐标参数,即X=[α β γ XS YS ZS ϕ θ ω];优化的观测量为二维图像坐标z=[u v],且图像特征点的权重为Qz-1。在极坐标光束法平差模型中需要估算出最佳的未知参数,使得目标函数(式(31))最小。
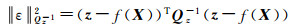 (31)
(31)
式中,f(X)表示三维点在图像上投影的观测方程,即式(29)。因观测方程为非线性,故该优化问题变成非线性优化问题。
给定所有变量的初值X0,对观测方程进行泰勒级数展开可以得到
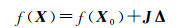 (32)
(32)
式中, J表示观测值对所有未知数的一阶导数。将式(32)代入式(31),可以得到线性最小二乘优化方程式
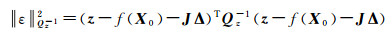 (33)
(33)
对于式(33)的极值点,其一阶导数必须为0,因此,得到下式
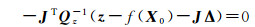 (34)
(34)
故未知数的增量可以通过式(35)求解。
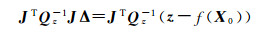 (35)
(35)
计算得到增量Δ后,新的未知参数可以更新为
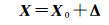 (36)
(36)
式(33)中,z-f(X0)表示误差方程,半正定矩阵JTQz-1J表示法方程。然后通过非线性最小二乘优化方法求解式(33),得到迭代结果。
3 极坐标下航空遥感影像处理试验本节通过真实的试验数据验证极坐标光束法平差模型的精度与效率。
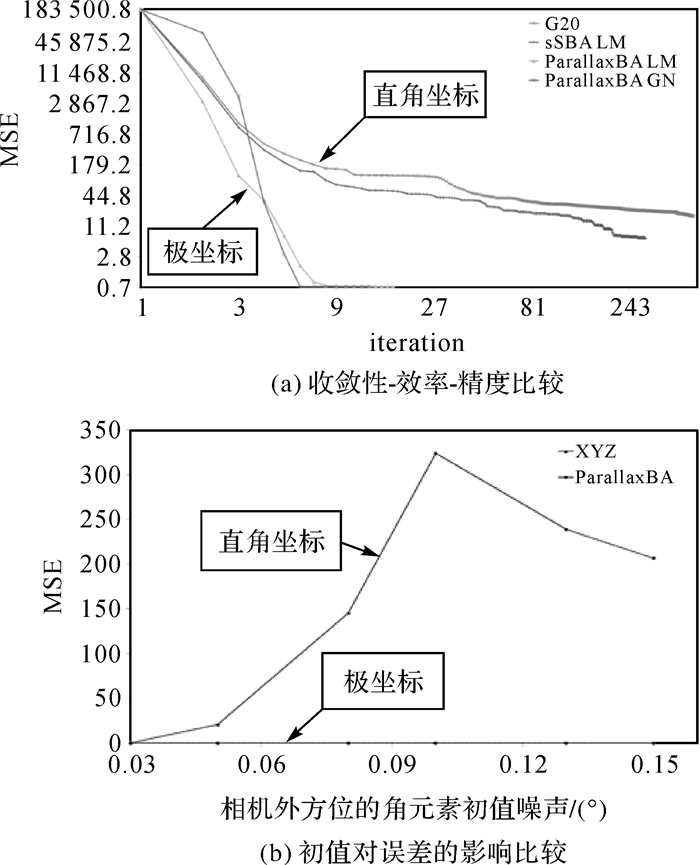
3.1 极坐标光束法平差模型收敛性与抗干扰性试验通过采用国内外现有方法开源数据解算试验,如G20, sSBA以及本团队ParallaxBA LM和ParallaxBA GN。此外,又对比了直角坐标系和极坐标系下解算结果对噪声误差的敏感度,所得结果如图 5、图 6所示[4]。
|
| 图 5 不同坐标体系的性能比较 Fig. 5 Performance comparison between Cartesian and polar coordinate systems |
|
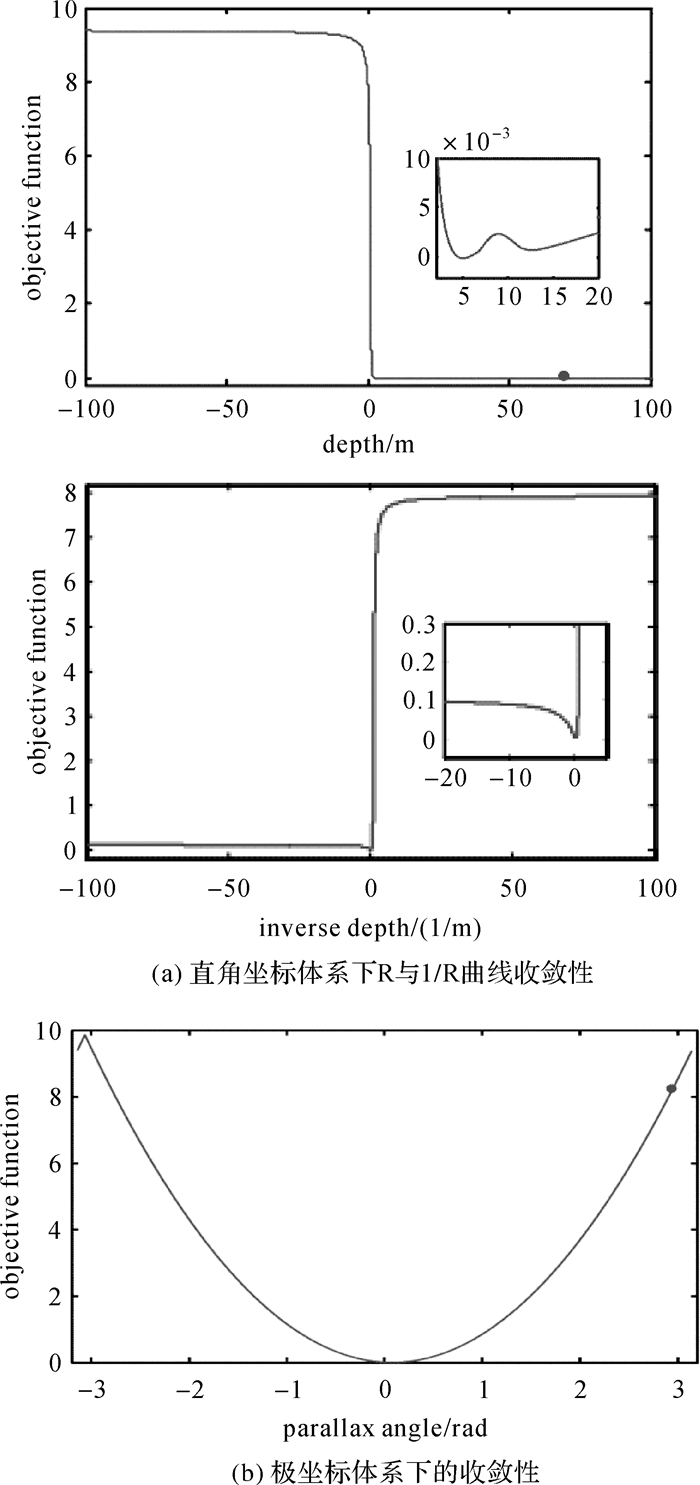
| 图 6 不同坐标体系下收敛性 Fig. 6 Convergence graph under different coordinate systems |
图 5表示极坐标方法与国际现行直角坐标方法,在采用同一数据源时,处理效率可提高2~3个数量级,结果精度可提高1个数量级,且解算结果对误差的敏感度大大降低,即在针对高分辨率遥感影像处理中,基于极坐标系统的方法能够更加快速收敛、保障精度。图 6[5]表示不同坐标体系下的收敛情况,图 6(a)勾画了深度变量从-100 m到+100 m时的目标函数值,结果表明直角坐标系下的光束法平差目标函数呈平谷状,故为找到其极值点,需要较多次数的迭代才能收敛;此外,放大的曲线局部图表明,当初值选在局部极小值右侧时,迭代结果只能取得极小值,无法获得最小值。即使针对微小量采用反向计算即倒数迭代方式,也会出现同样的现象。故直角坐标系下的解算对初始值选取具有很高的依赖性。图 6(b)勾画了在极坐标系下视差角变量从-3.14 rad到+3.14 rad的目标函数值,其目标函数呈二次曲线分布,只需要较少迭代次数便可得到收敛值,无论初始值精度如何,结果精度都能迭代至最小值,即使曲线中间存在极小值,也能够通过函数的“惯性势能”到达最小值,结果准确度提高。因此极坐标系下最优解对初值依赖性小。
抗干扰性表现为对误差的敏感度。式(21)—式(28)表明,当小视差角(ω→0)摄影条件时,直角参数空间下的光束法平差的变量对观测误差有着很强的敏感性,会造成不易收敛或者发散;但对于极坐标参数空间下的光束法平差模型,无论摄影条件如何,变量的误差和观测误差属于同一量级。因此,在极坐标系下光束法平差的抗干扰性可以得到保障。
需要强调的是,上述在极坐标系中处理获得的结果不依赖于地面控制点,从而为实现无地面控制点的高分辨率遥感影像精密处理测量提供了可能。
上述成果体现在团队2011—2015年间所发表的系列文献[4-7, 21-22]中,在OpenSLAM上公布了Parallax BA源代码,经过近3年全球应用和世界上不同用户的不断反馈意见,证明了其可用性。详细解算过程参见代码:http://openslam.org/ParallaxBA.html,欢迎本领域的中国学者支持使用并提出问题,为未来Parallax BA-2源代码发展和世界公布提供帮助。
3.2 航空摄影测量数据验证本节采用3组航空摄影测量数据,验证极坐标光束法平差模型(ParallaxBA)[14, 19-20]的性能,给定相同的初值,比较最后收敛的MSE、迭代次数和运行效率。所用到的G20和sSBA算法为直角坐标模型,ParallaxBA为本团队极坐标模型。G20和sSBA的软件包在Windows平台上解算效率非常低,但在Linux平台有着最佳效率性能。为了说明极坐标的特点,故在所有试验中只取用直角坐标平差模型最好的结果即在Linux系统中的计算结果,与本文极坐标体系方法ParallaxBA法的Windows和Linux平台的结果一一列出进行比较。此外,G20和sSBA的相机初值为四元数,而ParallaxBA的相机初值为欧拉角,因为四元数和欧拉角之间的转换存在微小的数值误差,故G20、sSBA与ParallaxBA的初值存在细微差别,但可以忽略。G20软件包中选用Gauss-Newton优化进行光束法平差的方法记为G20 GN,G20软件包中选用Levenberg-Marquardt优化进行光束法平差的方法记为G20 LM;类似的对于ParallaxBA,Gauss-Newton和Levenberg- Marquardt优化的光束法平差的方法分别记作ParallaxBA GN和ParallaxBA LM;由于sSBA只有Levenberg-Marquardt优化方法,故sSBA LM等价于sSBA[8]。
3.2.1 Vaihingen数据集参与平差的数据包括20个相机,554 914个三维特征点,故平差中的未知数为1 664 862、观测方程数为2 409 776。将上述变量和观测量输入到G20、sSBA和ParallaxBA中,在保证有相同的初值(初始MSE)时,收敛精度(收敛MSE)、迭代次数、线性方程数和运行时间见表 1;3种软件包的每次迭代的目标函数曲线见图 7。G20的GN优化的平差因法方程奇异造成平差问题发散,利用LM优化法,需要200次迭代才能收敛到135.06。sSBA、ParallaxBA GN和ParallaxBA LM均可收敛到0.126 012,且迭代次数相近,分别为8、6和20次。时间效率上,ParallaxBA GN和ParallaxBA LM版本平差的效率分别是G20效率的38.7和10倍。而ParallaxBA与sSBA的时间效率相近。平差的最终结果见图 8和图 9。图 8为重建出Vaihingen的三维点和相机姿态,其中三角锥为相机,蓝色点为重建点云。图 9为Vaihingen的三维点,颜色不具有任何实际物理意义。
| Vaihingen | G20 GN直角坐标 | G20 LM直角坐标 | sSBA直角坐标 | ParallaxBA GN极坐标 | ParallaxBA LM极坐标 | |
| 初始MSE | 144 707.21 | 144 707.21 | 144 707.21 | 144 707.18 | 144 710.18 | |
| 收敛MSE | N/A | 135.060 663 | 0.126 012 | 0.126 012 | 0.126 012 | |
| 迭代次数 | N/A | 200 | 8 | 6 | 20 | |
| 线性方程数 | N/A | 214 | 8 | 6 | 25 | |
| 单次迭代时间 | Win | N/A | N/A | N/A | 1.21 | 1.21 |
| 时间 | Linux | N/A | 1.2 | 0.8 | 1.45 | 1.45 |
| 总时间 | Win | N/A | N/A | N/A | 8.46 | 26.43 |
| Linux | N/A | 263.6 | 6.8 | 8.86 | 35.24 | |

|
| 图 7 对于Vaihingen数据,G20,sSBA和ParallaxBA的目标函数曲线变化 Fig. 7 Changes in the objective function curves for Vaihingen data, G20, sSBA, and ParallaxBA |

|
| 图 8 重建Vaihingen的地形和相机姿态 Fig. 8 Reconstruction of the terrain and camera posture of Vaihingen |

|
| 图 9 重建Vaihingen的地形 Fig. 9 Reconstructing the terrain of Vaihingen |
3.2.2 College数据集
试验采用信息工程大学提供的一组多姿态航摄影像数据进行,参与平差的数据包括468个相机,1 236 502个三维特征点,故平差中的未知数为3 712 314,观测方程数为6 215 048。将上述变量和观测量输入到G20、sSBA和ParallaxBA中,在保证有相同的初值(初始MSE)时,最后的收敛精度(收敛MSE)、迭代次数、线性方程数和运行时间见表 2;另外三种软件包的每次迭代的目标函数曲线见图 10。G20的GN优化的平差因法方程奇异造成平差问题发散,利用LM优化法,需要200次迭代才能收敛到25.723 307;sSBA需要200次迭代才能收敛到9.272 481。ParallaxBA只需要12次或17次迭代便可收敛到更小的值,即0.734 738。时间效率上,ParallaxBA GN版本平差的效率分别是G20和sSBA效率的18倍和12倍;ParallaxBA LM版本平差的效率分别是G20和sSBA效率的12和9倍。平差的最终结果见图 11、图 12。图 11为重建出College的三维点和相机姿态,其中三角锥为相机,深色点为重建点云。图 12为College的三维点,颜色不具有任何实际物理意义。
| College | G20 GN直角坐标 | G20 LM直角坐标 | sSBA直角坐标 | ParallaxBA GN极坐标 | ParallaxBA LM极坐标 | |
| 初始MSE | 202 329.64 | 202 329.64 | 202 329.64 | 202 329.44 | 202 329.44 | |
| 收敛MSE | N/A | 25.723 307 | 9.272 481 | 0.734 738 | 0.734 738 | |
| 迭代次数 | N/A | 200 | 200 | 12 | 17 | |
| 线性方程数 | N/A | 349 | 228 | 12 | 17 | |
| 单次迭代 | Win | N/A | N/A | N/A | 2.71 | 2.71 |
| 时间 | Linux | N/A | 2.51 | 2.72 | 3.85 | 3.85 |
| 总时间 | Win | N/A | N/A | N/A | 37.14 | 49.68 |
| Linux | N/A | 674.83 | 453.22 | 51.55 | 69.58 | |

|
| 图 10 对于College数据,G20,sSBA和ParallaxBA的目标函数曲线变化 Fig. 10 Changes in the objective function curves for College data, G20, sSBA, and ParallaxBA |
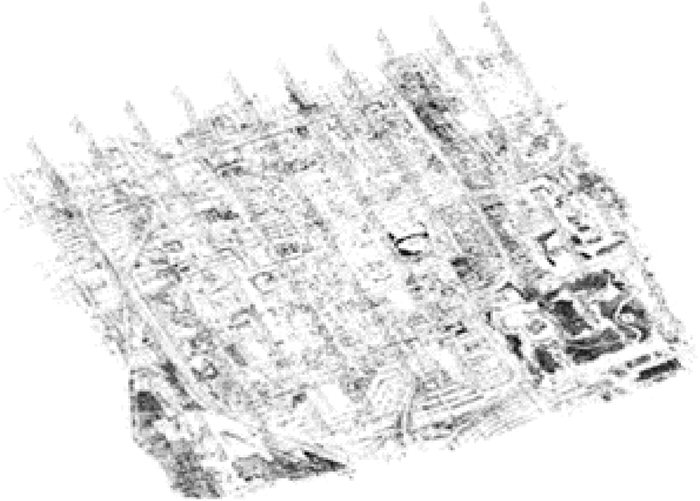
|
| 图 11 重建College的地形和相机姿态 Fig. 11 Reconstruction of the terrain and camera posture of College |

|
| 图 12 重建College的地形 Fig. 12 Reconstructing the terrain of College |
3.2.3 Village数据集
试验采用国家航空遥感数据获取与服务技术创新联盟第一届理事长单位北京星天地信息科技有限公司的数据。以长期生产作业挑选的航飞数据,检验视差角极坐标新方法;且平差过程中没有使用任何地面控制点,以检验无地面控制点时平差的精度和效率。
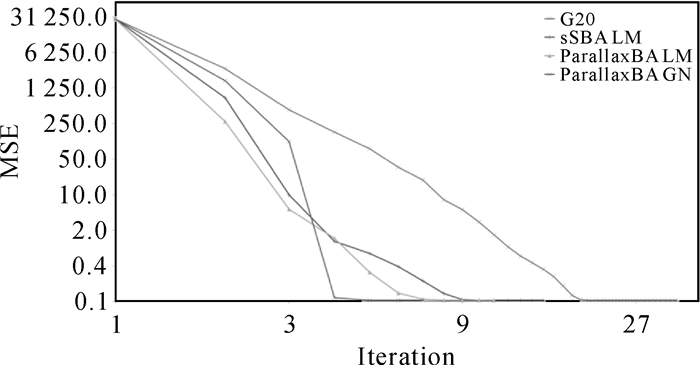
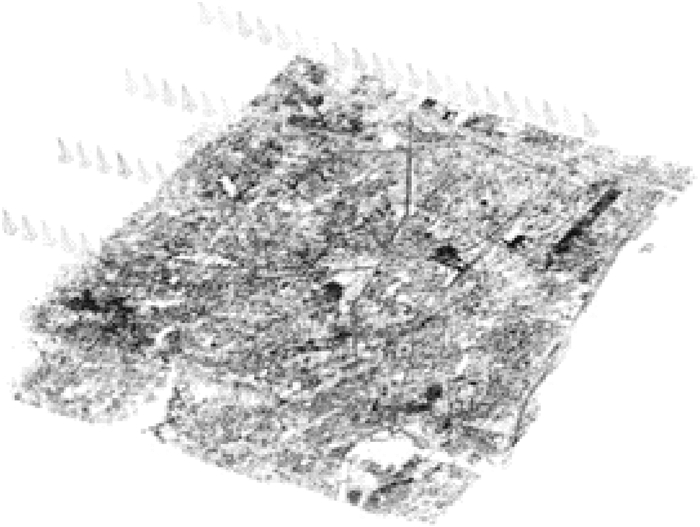
参与平差的数据包括90个相机、305 719个三维特征点,故平差中的未知数为917 697,观测方程数为1 558 536。将上述变量和观测量输入到G20、sSBA和ParallaxBA中,在保证有相同的初值(初始MSE)时,收敛精度(收敛MSE)、迭代次数、线性方程数和运行时间见表 3;另外3种软件包的每次迭代的目标函数曲线见图 13。G20的GN优化的平差因法方程奇异造成平差问题发散,利用LM优化法,需要34次迭代才能收敛到0.083 716。sSBA和ParallaxBA均可收敛到0.083 716,且迭代次数相近,时间效率相近,分别为8、6和11次。时间效率上,ParallaxBA GN和ParallaxBA LM版本平差的效率分别是G20效率的5.2和3.7倍。平差的最终结果见图 14和图 15。图 14为重建出Village的三维点和相机姿态,其中三角锥为相机,深色点为重建点云。图 15为Village的三维点,颜色不具有任何实际物理意义。
| Village | G20 GN直角坐标 | G20 LM直角坐标 | sSBA直角坐标 | ParallaxBA GN极坐标 | ParallaxBA LM极坐标 | |
| 有无地面控制点 | 有 | 有 | 有 | 无 | 无 | |
| 初始MSE | 28 174.10 | 28 174.10 | 28 968.73 | 28 170.98 | 28 170.98 | |
| 收敛MSE | N/A | 0.083 716 | 0.083 716 | 0.083 716 | 0.083 716 | |
| 迭代次数 | N/A | 34 | 8 | 6 | 11 | |
| 线性方程数 | N/A | 55 | 8 | 6 | 11 | |
| 单次迭代 | Win | N/A | N/A | N/A | 0.67 | 0.67 |
| 时间 | Linux | N/A | 0.62 | 0.56 | 0.96 | 0.96 |
| 总时间 | Win | N/A | N/A | N/A | 5.07 | 7.92 |
| Linux | N/A | 27.46 | 4.54 | 6.98 | 12.23 | |
|
| 图 13 对于Village数据,G20,sSBA和ParallaxBA的目标函数曲线变化 Fig. 13 Changes in the objective function curves for Village data, G20, sSBA, and ParallaxBA |
|
| 图 14 重建Village的地形和相机姿态 Fig. 14 Reconstruction of the terrain and camera posture of Village |

|
| 图 15 重建Village的地形 Fig. 15 Reconstructing the terrain of Village |
通过分析发现:①极坐标系光束法平差模型处理常规情况下的航空遥感影像时,在精度、效率上比直角坐标方法有数量级提高,且在不同平台下都能较好的收敛,无发散现象;②对于直角坐标系平差模型,采用了其效果较好的情况(如Linux平台),而将极坐标系光束法平差的Linux和Windows平台下的结果一一列出,说明极坐标系光束法平差模型对操作系统依赖性低,具有较好的可移植性,而直角坐标方法对平台差异较为敏感;③试验中采用的直角坐标方法是现有的成熟开源软件,而极坐标平差模型是初期的编译代码,软件的成熟程度对处理结果的质量也存在较大影响,若将此方法完善成为成熟软件,则在精度和效率上再提高数倍或一个量级是有可能的。
试验(3)采用了在实际生产作业中直角坐标体系方法无法实现拼接的航摄影像,在无地面控制点参与平差的情况下利用极坐标方法实现了影像特征提取和拼接,为实现基于极坐标的去地面控制点影像解算的产业化应用奠定基础;此方法也适应于大量航空影像数据的处理。因此极坐标自由网光束法平差模型既可以处理常规场景数据(稳定的飞行姿态及简单的几何摄影结构),也可以高稳健性处理复杂摄影场景数据(如近景拍摄影像、无人机航摄、多姿态飞行摄影等)。
4 极坐标系统绝对定向如何在现有自由网平差模型的基础上实现极坐标绝对网光束法平差,是实现极坐标摄影测量理论体系完善的重要任务之一。由于绝对网平差引入的地面控制点和极坐标表达的加密点分别在两个坐标系下,因此直角坐标系下的绝对网平差模型不能直接应用于极坐标平差模型。由此给出一种基于相似变换约束的极坐标绝对网平差优化模型,建立极坐标系中加密点坐标和直角坐标系中控制点参数化联系。
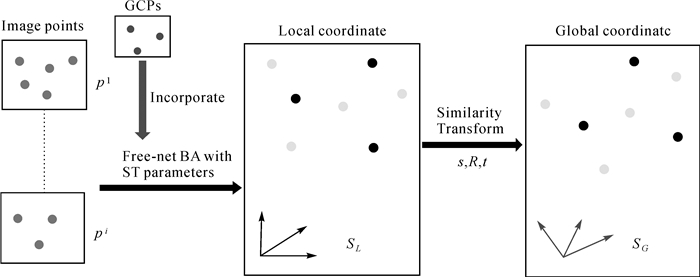
极坐标绝对网平差模型主要通过相似变换约束条件,以实现欧氏空间表征的控制点统一到角度表征的极坐标自由网中,从而实现图像误差在自由网优化中得到有效控制点,为后续相似变换提供刚体变换前提条件。其主要流程可以分为两步(图 16)。
|
| 图 16 模型主要包含步骤 Fig. 16 The main steps of the model |
本节通过两套不同尺度真实航空数据来验证极坐标绝对网平差模型对真实数据适应性。第一套数据(Village数据集)为丘陵数据,包含90张DMC影像,有4条航带,其图像几何分辨率为0.1 m;第二套数据(Taian数据集)为高山数据,包含737张DMC影像,几何分辨率为0.5 m。2套数据具体参数见表 4。
| 参数 | Village数据 | Taian数据 |
| 影像数 | 90 | 737 |
| 航带数 | 4 | 12 |
| 地形 | 丘陵 | 高山 |
| 比例尺 | 1:1000 | 1:5000 |
| 测区大小 | 2 km×3.5 km | 53 km×35 km |
| 相机 | DMC | DMC |
| 像幅 | 7680×13 824 | 7680×13 824 |
| 分辨率/m | 0.1 | 0.5 |
| 控制点 | 6 | 32 |
| 检查点 | 6 | 20 |
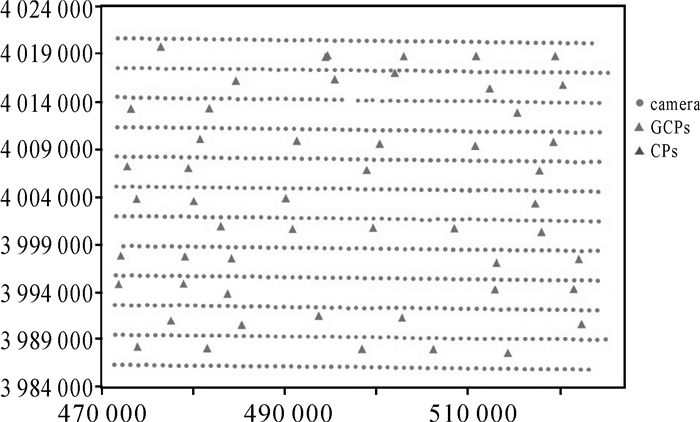
本文利用L2-SIFT算法[21, 23]从大像幅航空影像中提取并匹配高精度连接点,得到的特征像点将作为平差模型的第一类观测量。2套数据中相机、控制点和检查点在平面方向空间分布情况见图 17、图 18。

|
| 图 17 Village数据分布 Fig. 17 Village data distribution |
|
| 图 18 Taian数据分布 Fig. 18 Taian data distribution |
算法运行在i5-3210M@2.8 GHz CPU笔记本上,其运行时间及平差包含参数变量见表 5。
| 参数 | Village | Taian |
| 加密点 | 305 719 | 2 743 625 |
| 图像点 | 779 320 | 6 017 028 |
| 初始误差 | 56 432.16 | 590 764.93 |
| 收敛误差 | 0.090 13 | 0.138 706 |
| 迭代次数 | 11 | 18 |
| 总时间/s | 11.2 | 126.4 |
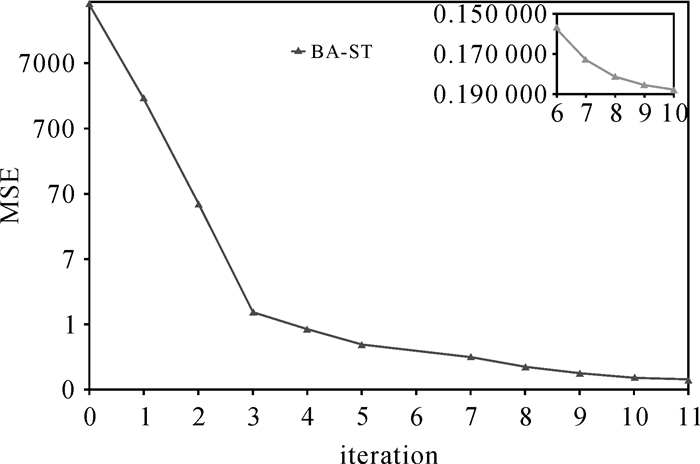
表 5表明,第1套数据经过11次迭代,在初值误差函数为56 432的前提下,可以快速收敛到0.090 13(图 19)。第2套数据,目标函数经过18次迭代可以从590 764.93收敛到0.138 706(图 20)。
|
| 图 19 第一套Village数据目标函数收敛过程 Fig. 19 The first set of Village data objective function convergence process diagram |

|
| 图 20 第2套Taian数据目标函数收敛过程 Fig. 20 Second sets of Taian data objective function convergent process diagram |
试验结果见表 6,经过极坐标绝对网平差估算出的加密点见图 21。对于第1套数据,将6个控制点引入到极坐标绝对网平差模型中,利用6个检查点来评价模型精度。平面和高程精度分别为0.16 m和0.21 m,满足国标GBT 23236—2009规定的1:1000比例尺丘陵地形空三测量平面和高程精度均小于0.35 m要求(GBT 23236—2009,2009)。对于第2套数据,将32个控制点引入平差模型,利用20个检查点来评价模型精度。其得到平面和高程精度分别为0.57 m和1.83 m,满足国标GBT 23236—2009规定的1:5000比例尺高山地形空三测量平面和高程精度均小于2.5 m要求(GBT 23236—2009,2009)。
| 参数 | Village | Taian | |
| 最大误差/m | 东向 | 0.117 8 | 0.638 7 |
| 北向 | 0.258 6 | 1.272 8 | |
| 平面 | 0.235 2 | 1.042 5 | |
| 高程 | 0.316 1 | 3.508 7 | |
| RMSE | 东向 | 0.069 0 | 0.307 3 |
| 北向 | 0.150 2 | 0.480 2 | |
| 平面 | 0.165 3 | 0.570 2 | |
| 高程 | 0.219 4 | 1.834 8 | |

|
| 图 21 极坐标绝对网平差模型重建出海量加密点 Fig. 21 Reconstruction of massive encrypted points by polar coordinate absolute network adjustment model |
因此,极坐标体系下的绝对网光束法平差仍然能解算出高精度的加密点坐标。
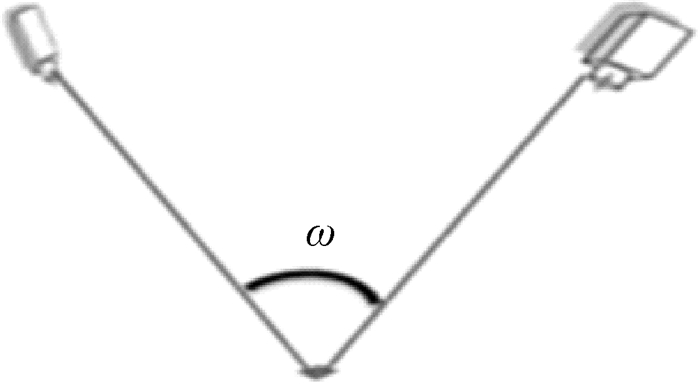
5 极坐标体系方法的应用特点 5.1 航天对地观测的极坐标应用必要性近景摄影测量通常采用两个相对静止、相距一定距离的相机对地面目标进行成像(图 22),利用立体像对对目标物进行观测,以得到其位置,形状等特征。航空摄影常将2个相机置于同一平台,这种作业模式可以保证2台相机无相对位移,不需要考虑航空平台行进的速度及加速度,此时仅存在位置(静态)误差,解算过程中也无需引入动态参量。
|
| 图 22 近景摄影测量 Fig. 22 Close range photogrammetry |
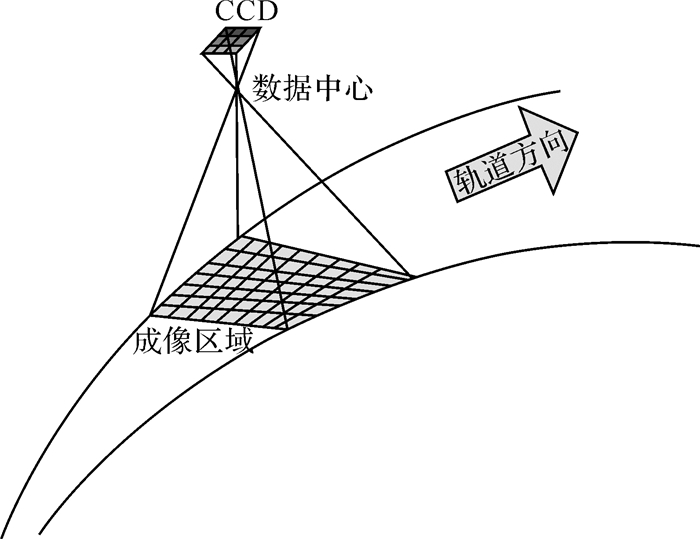
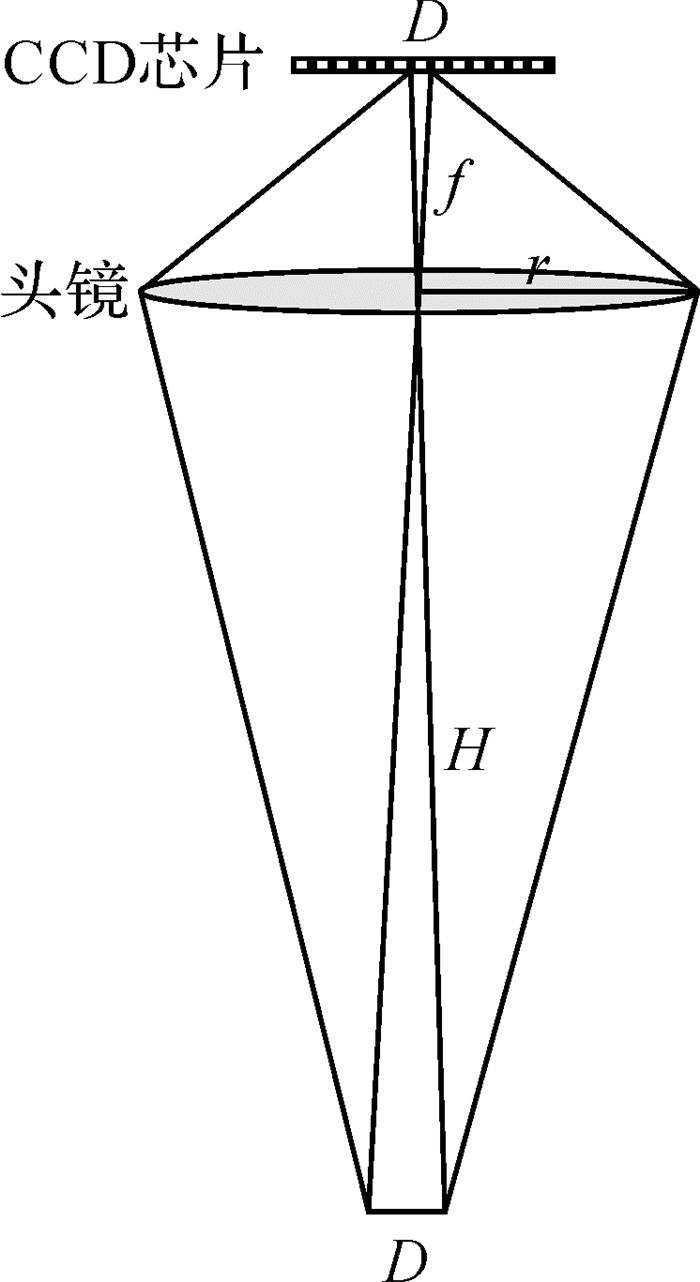
航空成像多采用面阵成像(图 23),本质为扇形-锥体成像,适应于极坐标表达,但目前主要是直角坐标表达。根据航空针孔成像模型下CCD像素与成像区域之间的对应关系(图 24)可知,随着焦距f增大,获取影像的分辨率会逐渐增高,即H高度矢径保持不变,焦距f增大,极角减小,影像分辨率增高。因此,极坐标系统的引入是必要的,它可以使航空获取-处理高分辨率影像更加高效便捷。航天成像多使用线阵推扫方式,获得的弧长目前主要用矢径乘以极角来表示;这样可以允许其视差角非常小时并不影响精度。若如此,航天线阵推扫和航空面阵成像处理,有望实现统一的极坐标数学表达。
|
| 图 23 航空面阵成像 Fig. 23 Aerial array imaging |
|
| 图 24 CCD像素与成像区域关系 Fig. 24 Relationship between CCD pixels and imaging region |
在航天摄影测量中,由于传感器距离目标较远,需要保证在摄影时有较大的视差角,避免由于视差角过小引入偏差。为避免直角坐标系下航天同一平台2台相机对地成像引起的小角度、短基线问题(式(1)),采用两种对地观测模式:模式一,同一平台2台相机不同时刻对地观测;模式二,两个平台相同时刻以一定角度对地成像。
实际上,航天平台不同时刻存在不同飞行状态,经典的处理过程中只考虑静态参量,导致解算的结果是不精确的,常只从处理模型及静态位置参量考虑误差来源,这时就不能称之为高分辨率下的高精度处理。实际情况需要考虑两个运动卫星位置(X, Y, Z)、姿态(俯仰、摇摆、滚动)6个自由度、位置及姿态的一阶导数、二阶导数和3个位置残差,形成高分辨率遥感影像21阶方程如下
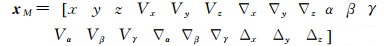 (37)
(37)
航天设备如飞船就是这样解算动态载体参数的,其实时解算非常不易。但如果对影像考虑上述21阶参量影响并解算,其计算量成数量级上升,目前条件下几乎不能实现。因此,目前航天影像只是考虑静态参量加入处理解算,但高分辨率所需要的精度在动态参量未参与计算时根本无法体现,成为一个新的较大误差源。例如,卫星振颤的消除[24],本质上是扰动力F产生的加速度a的作用
 (38)
(38)
这里m是卫星平台质量。加上速度变量v的贡献,得到位移与v和a的作用
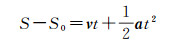 (39)
(39)
这里S-S0是成像时间t的位移增量。显然,卫星振颤产生的加速度误差是时间增量t的平方,如果不予考虑是不可能获得动态误差剔除后的高精度解算的。
进一步针对高分辨率航天影像处理,如果只考虑静态参量的解算,对于高精度参量的保障是相对困难的,也是有悖运动方程解算机理的。因此在考虑现有方法解算时,如果速度平稳,其21阶方程的6阶速度分量可以近似为常数,但与扰动振动相关的加速度分量是无法忽略也是动态误差的最大根源。
为了既保障高精度,又不引入动态变量来解算图像,唯一保障的就是两个相机没有相对位移,即同一航天平台装载两个相机实现同步观测。然而,在同一平台上必然出现视差角过小的现象,使用直角坐标系统已不能准确刻画影像信息甚至发散,而极坐标表示方法可以表达出小视差角、短基线下的影像细节信息,使解算过程变得更加便捷有效。这将是一个新课题。
要说明的是,现在航天影像处理所采用的有理多项式函数通用模型,其阶次数是对静态非线性描述,一般不高于3次,多项式的一次项的比值用来描述投影误差,二次项的比值用来描述地球曲率误差、大气折光差、镜头畸变差等;更高次项的比值用来描述其他一些未知的具有高阶分量的误差,但都不适宜对动态误差直接刻画。
因此,引入极坐标是较接近解决上述问题的方法:采用同一平台、相同时刻、2台相机对地观测,可以不考虑直角坐标系下小角度、短基线引发的奇异阵、非收敛性问题;同时避免由于航天单载荷平台在不同时刻或不同平台同一时刻观测,存在不同飞行状态所引发的高分辨率影像21阶方程解算困难,甚至不可解算的问题。
航空航天处理的极坐标应用具有巨大优越性。将极坐标体系实现硬件化装机到多类传感器上,可以有望实现星上实时解算、实时传输,由传感器平台引发的处理问题可以在线处理。
5.2 航空航天处理的极坐标应用将极坐标高分辨率观测方法扩展应用于海洋海事领域[25],本文合作团队把极坐标方法引至多角度海洋海事目标探测识别, 见图 25和表 7,可以解决拼接速度慢、对误差高敏感度等问题;在极坐标系统下可以很好地处理大角度、变姿态问题(图 15)。总之,虽然在简单摄影条件情况(例:载人航空摄影),与直角坐标性能相当,但是在其他复杂摄影条件(例:无人机摄影及高重叠近景摄影),其优势显著,见表 8。

|
| 图 25 海洋遥感影像精准拼接 Fig. 25 Accurate mosaic of ocean remote sensing |
| 比较要素 | 海洋海事 | ||
| 定量化特点 | 数据有效性 | 目标识别 | |
| 原有方法 | 相对弱 | 一般 | 弱 |
| 引入极坐标法 | 无人艇监测定标 | 极坐标变角度,好 | 识别度高 |
| 比较要素 | 满足直角坐标约束的规范影像 | 对高重叠影像 | 影像精度-效率-抗干扰性 | 大角度 | 变姿态 | 航空面阵航天线阵 | 与国军标数据组织存储比较 |
| 现有方法直角坐标 | 可处理 | 易产生奇异性,有时发散 | 可以 | 相对困难 | 相对困难 | 坐标不同 | 需直角-弧度转换 |
| 极坐标 | 可处理 | 极大去除奇异性根源,无发散 | 可数量级提高 | 方便处理 | 方便处理 | 可统一坐标 | 无需转换 |
其二,极坐标在GeoSOT剖分经纬格网也有重要的应用意义,它着眼于地球空间信息“取自经纬,归于经纬”和椎体成像的本质特征,采用极坐标系作为空间信息链条中间阶段的数据组织、管理和存储基准,为建立新型空间信息表达结构提供了新的途径。
其三,SAR图像方位向表达,LiDAR点云初始表达,都与极坐标直接相关或源自极坐标。由此,可以探索空间信息多种成像方式的统一坐标系表达,或可成为空间信息基础研究的重要探索方向。
6 结论(1) 高分辨率遥感数据处理效率低甚至发散的根源是影像处理的病态性。为此引入极坐标体系,其本质是将直角坐标同量纲几何参量转换为角度和矢径量纲,从根源上避免了病态奇异性引发的发散问题,实现高维非线性优化问题快速收敛和三维测量。
(2) 本文历经10余年初步建立了一套空间信息极坐标基准的数学模型,完善了极坐标方法体系。根据最复杂的近景摄影测量和自由网平差试验,证明了极坐标的引入使效率、精度、收敛性、抗干扰性有数量级提高。团队在参考文献[4-7, 21-22]发表过程中公布的Parallax BA源代码,经过近3年全球应用,证明了其可用性。期待本领域尤其是中国团队的广泛试用,并对本团队上述6篇文献进行批评帮助。
(3) 部分航空摄影测量和绝对网平差模型试验,初步证明了极坐标方法比直角坐标处理方法为优。对应有本团队在参考文献[8, 16, 20, 23]的详细阐述,期待批评并斧正。现正在与武汉大学等航空摄影测量团队实化软件,为在国际上推出极坐标Parallax BA-2而努力。
(4) 极坐标处理方法有利于解决变姿态影像获取及拼接问题;为航天线阵推扫和航空面阵成像的统一数学表达提供可能;并有利于传感平台引发的处理问题在线解决,为影像无地面控制点定位、大倾角或短基线观测、变焦、摆扫成像等新技术提供新手段。
(5) 将极坐标体系引入航天领域,有望实现同一平台、相同时刻、两台相机对地成像。由此可以避免直角坐标系下航天观测引发的小角度、短基线,以及高分辨率影像21阶动态方程解算方可保障精度,甚至不可解算的困难。
(6) 极坐标方法的有效获取、处理与GeoSOT剖分经纬网格结合,可望为新一代空间信息体系的源端和终端,以形成多尺度全姿态空间信息获取-组织-管理-存储-处理-应用的极坐标体系奠定基础。
(7) 如何在近景摄影测量和常规状态下充分使用普遍存在的直角坐标系软件、处理模型,发挥其工业化水平高而成熟的优势;又在航空航天新技术丰富发展需求下全面转换、努力展现极坐标体系的优势,是今后需要把握当今、迎接未来的实践过程。但空间信息逐步实现从获取到应用全部过程的极坐标基准方法,是笔者的目标,也是未来智能摄影测量无人工干预情况下自组织、自协调的数学基础。
致谢: 感谢国家基金委、科技部的长期支持。感谢本团队赵亮等毕业学生的创造性贡献,感谢悉尼科技大学Shoudong HUANG、Dissanayake G,美国普渡大学Jie SHAN及童庆禧、刘先林、杨元喜、周成虎、张祖勋、龚健雅、袁修孝、宋妍对本研究提供的帮助。
| [1] |
王之卓.
摄影测量原理[J]. 测绘通报, 1979(4): 48.
WANG Zhizhuo. The Principle of Photogrammetry[J]. Bulletin of Surveying and Mapping, 1979(4): 48. |
| [2] |
罗河.
空中三角测量的一般解析法[J]. 测量制图学报, 1958, 2(1): 1–20.
LUO He. A General Analytical Method of Aerial Triangulation[J]. Acta Geodetica et Cartographica Sinica, 1958, 2(1): 1–20. |
| [3] |
周卡.
空中三角测量[J]. 土木工程学报, 1956, 3(3): 345–354.
ZHOU Ka. Spatial Aerotriianglation[J]. China Civil Engineering Journal, 1956, 3(3): 345–354. |
| [4] | ZHAO Liang, HUANG Shoudong, SUN Yanbiao, et al. ParallaxBA:Bundle Adjustment Using Parallax Angle Feature Parametrization[J]. The International Journal of Robotics Research, 2015, 34(4-5): 493–516. DOI:10.1177/0278364914551583 |
| [5] | ZHAO Liang, HUANG Shoudong, YAN Lei, et al. Parallax Angle Parametrization for Monocular SLAM[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai: IEEE, 2011: 9-13. |
| [6] | SUN Yanbiao, SUN Huabo, YAN Lei, et al. RBA:Reduced Bundle Adjustment for Oblique Aerial Photogrammetry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 121: 128–142. DOI:10.1016/j.isprsjprs.2016.09.005 |
| [7] | ZHAO Liang, HUANG Shoudong, YAN Lei, et al. Large-scale Monocular SLAM By Local Bundle Adjustment And Map Joining[C]//Proceedings of the 11th International Conference on Control Automation Robotics & Vision. Singapore: IEEE, 2011: 7-10. |
| [8] |
孙岩标. 极坐标光束法平差模型收敛性和收敛速度研究[D]. 北京: 北京大学, 2015. SUN Yanbiao. Study on Convergence and Convergence Speed of Polar Coordinate Beam Method Adjustment Model[D]. Beijing: Peking University, 2015. |
| [9] | CIVERA J, DAVISON A J, MONTIEL J M M. Inverse Depth Parametrization for Monocular SLAM[J]. IEEE Transactions on Robotics, 2008, 24(5): 932–945. DOI:10.1109/TRO.2008.2003276 |
| [10] | SOLÀ J. Consistency of the Monocular EKF-SLAM Algorithm for Three Different Landmark Parametrizations[C]//Proceedings of 2010 IEEE International Conference on Robotics and Automation. Anchorage: IEEE, 2010: 3-7. |
| [11] | MONTIELJM M, CIVERA J, DAVISON A J. Unified Inverse Depth Parametrization for Monocular SLAM[C]//Proceedings of Robotics Science & Systems. Philadelphia: [s. n. ], 2006. |
| [12] | CIVERA J, DAVISON A J, MONTIELJM M. Inverse Depth to Depth Conversion for Monocular SLAM[C]//Proceedings of 2007 IEEE International Conference on Robotics and Automation. Roma: IEEE, 2007: 10-14. |
| [13] |
程承旗, 关丽.
基于地图分幅拓展的全球剖分模型及其地址编码研究[J]. 测绘学报, 2010, 39(3): 295–302.
CHENG Chengqi, GUAN Li. The Global Subdivision Grid Based on Extended Mapping Division and Its Address Coding[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 295–302. |
| [14] |
程承旗, 任伏虎, 濮国梁, 等.
空间信息剖分组织导论[M]. 北京: 科学出版社, 2012.
CHENG Chengqi, REN Fuhu, PU Guoliang, et al. The Spatial Information Division Organization Introduction[M]. Beijing: Science Press, 2012. |
| [15] |
程承旗, 宋树华, 濮国梁, 等.
空间信息全球惟一编码GeoID模型初探[J]. 测绘科学, 2010, 35(6): 73–75, 264.
CHENG Chengqi, SONG Shuhua, PU Guoliang, et al. Preliminary Studies on Geospatial Information Global Unique Code GeoID Model[J]. Science of Surveying and Mapping, 2010, 35(6): 73–75, 264. |
| [16] |
赵亮. MonoSLAM: 参数化、光束法平差与子图融合模型理论[D]. 北京: 北京大学, 2012. ZHAO Liang. MonoSLAM: Parameterization, Bundle Adjustment and Sub Graph Merging Model Theory[D]. Beijing: Peking University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2498852 |
| [17] | BROWN D C. The Bundle Adjustment-progress and Prospects[C]//Proceedings of the 12th Congress of the International Society for Photogrammetry Helsinki: [s. n. ], 1976, 21: 29-33. |
| [18] | SLAMA C C. Manual of Photogrammetry.4th ed[M]. Falls Church: American Society of Photogrammetry, 1980. |
| [19] | COOPER M A R, CROSS P A. Statistical Concepts and Their Application in Photogrammetry and Surveying (Continued)[J]. Photogrammetric Record, 1991, 13(77): 645–678. |
| [20] | YAN Lei, CHEN Rui, SUN Huabo, et al. A Novel Bundle Adjustment Method with Additional Ground Control Point Constraint[J]. Remote Sensing Letters, 2017, 8(1): 68–77. DOI:10.1080/2150704X.2016.1235809 |
| [21] | SUN Yanbiao, ZHAO Liang, HUANG Shoudong, et al. L2-SIFT:SIFT Feature Extraction and Matching for Large Images in Large-scale Aerial Photogrammetry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 91: 1–16. DOI:10.1016/j.isprsjprs.2014.02.001 |
| [22] | SUN Yanbiao, ZHAO Liang, HUANG Shoudong, et al. Line Matching Based on Planar Homography for Stereo Aerial Images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 104: 1–17. DOI:10.1016/j.isprsjprs.2014.12.003 |
| [23] | SUN Y, LIU X, CHEN R, et al. Application and Performance Analysis of a New Bundle Adjustment Model[J]. ISPRS Annals of Photogrammetry Remote Sensing and Spatial Information Sciences, 2017, IV-2/W4: 273–278. DOI:10.5194/isprs-annals-IV-2-W4-273-2017 |
| [24] |
童小华, 叶真, 刘世杰.
高分辨率卫星颤振探测补偿的关键技术方法与应用[J]. 测绘学报, 2017, 46(10): 1500–1508.
TONG Xiaohua, YE Zhen, LIU Shijie. Essential Technology and Application of Jitter Detection and Compensation for High Resolution Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1500–1508. DOI:10.11947/j.AGCS.2017.20170384 |
| [25] |
李颖, 朱雪瑗, 曹妍, 等.
GNSS-R海洋遥感监测技术综述[J]. 海洋通报, 2015, 34(2): 121–129.
LI Ying, ZHU Xueyuan, CAO Yan, et al. Review on GNSS-R Ocean Remote Sensing Monitoring Technique[J]. Marine Science Bulletin, 2015, 34(2): 121–129. DOI:10.11840/j.issn.1001-6392.2015.02.001 |


