摄影测量学是一门“利用光学像片研究被摄物体的形状、位置、大小、特性及相互位置关系”的学科。摄影测量诞生于19世纪早期。1838年,物理学家惠斯顿发明了实体镜,第一次发现和定义了立体视觉。1839年,法国画家达盖尔发明了银版摄影法,并制作了世界上第一台真正的照相机。在此基础上,法国测量学家Fourcade首先发现了用立体照片可重建立体视觉,从而促成了摄影测量学的诞生[1]。摄影测量的第一个也是最重要的分支是航空摄影测量。1783年,西方的Montgolfier兄弟发明热气球,并第一次载人航行。1858年,法国摄影师纳达尔乘坐气球拍摄了世界上第一张航空影像。1903,莱特兄弟发明世界上第一架螺旋桨飞机。这些飞行技术的发展促成了能够大范围测图的航空摄影测量。而此前,人们只能利用大地测量技术进行测图。例如著名的数学家高斯绘制汉诺威公国的地图就花了30年。
20世纪开始后,物理和电子技术的进步持续推动着摄影测量的发展。1957年,第一颗卫星被发射到外太空,开启了卫星摄影测量与遥感研究领域。1960年开始,迅猛发展的计算机以及专业的解析测图仪使摄影测量进入解析摄影测量时代。光线的重现和交会不再依赖于此前的光学模拟仪器(60年代之前也因此称为模拟摄影测量时代),而是以虚拟形式在计算机中实现。根据爱因斯坦的光量子假说和光电效应,1973年贝尔实验室的博伊尔和史密斯发明了电荷耦合器件(charge coupled device,CCD)[2],促成数码相机和数字摄影测量时代的诞生。90年代末,无人机航摄逐渐兴起,其便捷、廉价的特性,是传统航摄的有益补充。2000年前后,各国陆续开始深空探测项目,比如中国的嫦娥登月和美国的火星探测。此外,地面测量、地下测量、水下测量、弹道测量、工业测量等也是摄影测量常见的应用研究领域。
在研究内容上,摄影测量以二维像片和被摄三维物体的几何关系为主流方向。在理论方法上,沿用笛卡儿开辟的解析几何,用代数方程表达二维或三维笛卡儿坐标系中所描绘的几何图形。如像点、物点、投影中心三点共线由共线条件方程表达;摄影基线、同名光线共面由核线方程表达。在模型解算上,由于测量中观测值固有的误差特性,以误差处理理论为指导。代表性理论是1795年高斯发明的最小二乘法和1959年德国的Schmid提出光束法区域网平差。此外,由于重建几何关系需要提取像片上的同名点,一些图像处理的内容也因此成为摄影测量的研究领域。20世纪后期,摄影测量学者提出了相关系数匹配、最小二乘匹配等经典立体匹配方法,21世纪开始,同样关注3D几何重建的计算机视觉也更加丰富了匹配方法。
虽然基于光学像片的2D/3D几何关系是摄影测量的主流,但根据摄影测量的定义,“物体的特性及其相互关系”,即语义部分也属于摄影测量学的研究内容。语义被忽略既有历史的原因也有技术上的困难。首先,从20世纪70年代开始,随着卫星成像技术的发展,摄影测量被扩展为摄影测量与遥感,图像解译任务因之成为遥感的课题。其次,摄影测量作为应用工程学科,需要为测绘等领域提供相当精度的各类地形图和专题图。然而,传统计算机分类和模式识别的方法难以达到所谓的“摄影测量精度(photogrammetric accuracy)”,而通常采用半自动或全人工判读法,所以研究进展缓慢。幸运的是,以深度学习为主流的人工智能方法开辟了关于“学习”的新航道,并把精度提高到前所未及的高度。例如,将恰当的深度神经元网络架构应用于航空图像的道路、建筑、水体等地物的自动提取,并实现高精度语义专题图,将为摄影测量学在语义方向的拓展提供新的契机,这也是本文的一个中心议题。
1.2 深度学习的历史深度学习起源于20世纪中叶的人工智能。人工智能的两个主要流派分别是符号主义(symbolism)和联结主义(connectionism)。其中,符号主义者在1956年首次提出“人工智能”的概念,并统治了该领域近半个世纪;基于统计学习的思想被广泛应用于机器学习、计算机视觉,以及摄影测量与遥感。与此对应,联结主义起伏不定,经历了低谷,也经历了3次发展浪潮:20世纪40年代到60年代的控制论[3]、80年代到90年代的联结主义[4]及2006年之后的“深度学习”[5]。
在控制论时期,联结主义的代表性名词是“人工神经元网络”。事实上,当时这只是一个单层的线性模型:根据输入变量x、输出函数f(x,w)与已知标签y的一一对应关系,学习未知参量w。这种模型(又称为单层感知机)由于无法学习诸如XOR(异或)等非线性函数,而受到以明斯基为首的符号主义流派的批评;并造成第一次人工神经元网络的衰退。
在20世纪80年代,联结主义的概念被正式提出。当时符号主义流派依然是主流,但他们也有自己的麻烦:符号推理模型难以解释大脑神经元的工作原理。而联结主义者认为,将大量的简单计算单元连接在一起,就可以实现智能行为。并提出了“分布式表示”、“后向传播算法(back propagation)”、“长短期记忆(long short-term memory,LSTM)”等对今天的深度学习异常重要的思想和概念。然而,到了20世纪90年代中期,基于神经元网络的人工智能研究无法满足商业界的业务化需求,加上诸如SVM[6]等核方法,以及概率图模型(probabilistic graphic model,PGM)的盛行[7],神经元网络再次衰退了。
2006年,Hinton的研究表明,采用一种逐层的贪心算法可实现深度神经元网络的训练[8]。而此前,训练一个多层神经网络被认为是不现实的。深度学习的概念由此浮出水面,新旗帜是:现在已经有能力训练一个深度网络,并且这个深度将赢得人工智能方法和实践上的突破。2012年,在ImageNet挑战赛中,深度学习的方法夺得第一,并一举超过传统机器学习方法10个百分点[9];而第二至第四名相差不超过1%,显示了传统方法的天花板。随后的大量试验表明,无论在图像分类、物体识别、语音识别、遥感应用等关于学习和语义的研究领域,深度学习都占据上风。
符号主义流派的空间在缩小,但基于概率图模型[7]的方法也得到了广泛应用。此外,深度学习也有自身的缺陷。虽然理论上多层网络确实可能学习出最优的函数模型,但它无法解释该模型如何构建以及模型背后的含义,就像暗箱操作一样。目前,有些学者试图发现其背后的原理。如物理学者发现了量子力学中的重整化技术与深度学习能够精确对应[10],神经科学和计算机科学家发现深度学习符合一种瓶颈理论[11],即把大量次要信息挤出去,而留下真正有效的信息。当然,这些发现距离完整回答深度神经元网络如何学习仍处在初步阶段。
1.3 摄影测量与深度学习及计算机视觉的联系除了自然语言处理(natural language processing,NLP)[12],深度学习的最重要应用是在视觉图像上,如手写字体识别[13]、自然图像分类[9]和检索等。而摄影测量的研究对象就是视觉图像,因此深度学习的成功和蓬勃发展,使得摄影测量也成为最受益的学科之一。
在几何上,摄影测量中的研究内容包括:传感器的定位定姿、从2D像片重建3D几何。将深度学习应用于几何定位目前还未进入摄影测量研究领域,但已经出现在密切相关的计算机视觉的分支中:运动恢复结构(structure from motion,SfM),以及机器人学的分支;同时定位与地图构建(simultaneous localization and mapping,SLAM)。根据文献[14],深度学习方法的定位精度目前尚不能同传统的方法相比,相差约一个数量级。对于3D重建中的关键技术密集匹配,深度学习已经取得很好的应用效果。如在KITTI等标准数据集上[15],前10名的方法都是深度学习方法。不过,虽然SGM等经典方法已经落在30名开外,但是经典方法是通用的,既可以用在自然图像中,也可以用于航空、航天图像。而深度学习方法则依赖于高精度、可靠的相似数据集。目前,完整的3D重建解决方案依然是经典方法一统天下。
在语义上,摄影测量中的研究内容就是采用智能方法为各行业提供专题图。摄影测量的应用特性使得它并不关心诸如特征描述、上下文关系等中间结果。这种端到端的模式(end-to-end)特别适用深度学习方法。目前,深度学习已经被广泛用于遥感图像的分类、识别、检索和提取。与在几何方面的欠佳表现不同,在语义上基本全面碾压了传统的方法。
最后简要讨论摄影测量、深度学习及计算机视觉的关系。1982年,Marr发表《视觉:从计算的视角研究人的视觉信息表达与处理》,是计算机视觉的开山之作。计算机视觉的最初研究:用计算机代替人眼,从图片中重建3D世界。与摄影测量在几何方面具有很高的重叠度。20世纪90年代,在语义方面计算机视觉开始蓬勃开展。其中运用了大量的机器学习知识。有学者分析指出机器学习与计算机视觉重叠度约在60%~70%,因此是非常紧密的两门学科。随着深度学习成为机器学习的主流,深度学习在计算机视觉中得到广泛应用。将深度学习引入到摄影测量中,特别是提高摄影测量后期语义处理的智能水平,是科学研究发展的必然途径。
2 方法 2.1 深度学习基本原理深度学习是“表示学习(representation learning)”[16]的一种。表示学习的最大特点是不需要设计人工特征。它指计算机根据一套通用规则自动地学习出从输入到输出的最优特征表示的方法。表示学习可用于无监督分类,如自编码器(autoencoder)[17]。而在监督学习中,深度学习是表示学习的最佳代表。深度学习通过设定神经元网络层数、每层的参数(随机初始化)、迭代规则等,自动学习调整出最优的参数。这些参数的集合最终构成从输入到输出的特征表示。基本的多层神经元网络称为前馈神经网络(feedforward neural network)[18]。
前馈神经网络或多层感知机(multilayer perceptron,MLP)[19]是一种典型的深度学习模型。前馈网络定义一个映射y=f(x,w),以x和y为已知条件,通过学习参数w的值,得到某个最优的近似函数f*。因此,前馈是指:仅由w和f得到输出y,而y不会反作用于模型f。若y反馈于f,则称为循环神经网络(recurrent neural network,RNN)[20]。RNN很少应用于图像中,摄影测量中常用的深度学习方法几乎都是MLP。
MLP由多个函数fi复合而成:f(x)=fn…(f2(f1(x))),f1称为第一层,最后一层称为输出层,函数链的全长n称为网络的深度。在最后一层上,模型要求fn的输出接近于给定的标签y;在其他层上,训练数据〈x,y〉并未指出应该如何训练,这些层被称为隐藏层。基于深度学习的方法就是采用“表示学习”的策略去主动地学习各层的参数模型而非传统的手工设计。
当f作为一个线性模型时,它无法训练诸如XOR等非线性模型[21]。因此,在隐藏层中,需要扩展为一个非线性的函数,通常称为激活函数σ。激活的概念来自人类的神经元作用机理:将0看作不激活,1看作激活,则组成一个简单的非线性系统。目前,最常用的激活函数是整流线性单元(rectified linear unit,ReLU)[22],即x′=max(0, x)。此时,一个典型的fi就是一个线性仿射变换再加上一个激活
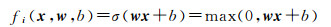
式中,w称为权重模板或核函数;b称为偏置。在加上了这个非线性激活函数后,通过二层或以上的神经元网络就可以学习出XOR等复杂的非线性模型。
输出层函数fout要保证模型的输出y′与其对应的标签y尽可能一致。在摄影测量中的光束法平差中,通常取p-范式|y-y|′p最小(通常p=2),并称之为代价函数。在深度学习中,也称为代价函数,或者损失函数(loss function)。除了最小化p-范式外,由最大似然估计导出的、给定样本与期望模型间的交叉熵也是常用的代价函数[23]。即
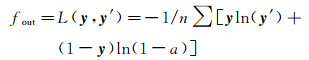
此外,和平差中的L-M算法[24]类似,对于损失函数也要考虑收敛性的问题。故常用的代价函数也包含正则化项
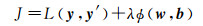
式中,y为标签;y′为模型的输出;L为损失函数;J为总代价函数;ϕ为正则化函数。
与光束法平差一样,要设定参数w和b的初始化及迭代规则。通过学者们的研究,w可初始化为随机小数。随机初值经过前馈网络传播后,得到的输出y′显然与标签y相距甚远。一个直观的想法是通过代价函数来反向逐层调整隐藏层中的参量w与b。这就是著名的梯度反向传播和链式法则[25]。标量的链式法则表达如下

式中,z=f(g(x))=f(y)。扩展到神经元网络中常用的矢量形式,即z=f(g(x))=f(y),链式法则变为
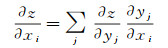
将z理解为顶层的代价函数J,将x看作隐藏层中待修正的参量w和b;则得到z相对于每个参量的梯度。用高斯-牛顿法解算光束法平差时,其迭代的步骤是x′=x+dx,即直接加上改正数。而在深度学习中,无法直接得到最优的改正数dx。通常的思路是:梯度自身反映了参量该向哪个方向修正,但并不确定具体的修正值;因此,在梯度的基础上,乘以一个很小的学习率λ,作为每次的迭代值
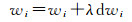
给定足够的训练样本,经过数百次乃至千万次的迭代训练(只要时间足够长),基于前馈神经元网络的深度学习期望得到一组最优参量w和b,使得代价函数最小。
以上通过摄影测量中的光束法平差为类比,简单介绍了深度神经元网络的一些本质的概念和方法。
2.2 深度卷积神经元网络2012年,Hinton课题组的一篇论文《基于卷积神经元网络的Imagenet分类》[9]引爆了整个机器学习和人工智能领域,也是至今为止深度学习中引用率最高的论文之一。卷积神经元网络(convolutional neural network,CNN)是一种特殊的前馈神经元网络,指那些至少在网络的某一层中采用卷积运算代替一般矩阵乘法的网络[26]。事实上,CNN与摄影测量的关系也同样密切。在摄影测量中,影像相关是一个入门级的概念,指判别图像间相似度的一种计算方法。相关(correlation)本质上就是卷积,或者说是卷积的一种变种,都属于线性时不变系统[27]。这两个概念的微小差异仅在于是否翻转模板。请注意,在深度学习中,常将相关也写作卷积。
除了拥有前馈神经元网络的基本特性外,卷积神经元网络包括三个明显的特征:稀疏连接、参数共享、池化。稀疏连接区别于传统神经网络的全连接。传统神经元网络采用矩阵乘法。如m个像元的图像,n个输出,则需要m×n个参数。然而,图像中兴趣特征可能只存在于图像上的一小块,而非整个图像。这与人眼看物体是一致的,眼睛(连同背后的脑处理机制)往往只专注于那些突出的特征,而选择性地忽略掉背景,称为“局部视野”。如果有k(k≪m)个像元可代表这个特征,那么,只要采用k个像元的卷积核,就能提取出该特征。同时,卷积操作的计算量仅为k×n。
参数共享对减少计算量和冗余同样具有积极的意义。以边缘特征提取为例。在深度学习中,系统需要主动去学习某个边缘特征(如水平边缘),得到某个恰当的卷积核w。显然这个卷积核不但对某个图像上方的水平边缘敏感,而且对图像任何地方的水平边缘敏感,甚至对所有的成百上千的输入图像中的水平边缘都敏感。因此,仅需要学习一个卷积核w,就可无数次重复使用,以提取出样本中所有的水平边缘特征。这就体现了卷积(相关)的作用。而在全连接中,一般不采用参数共享策略,因此参数只被使用一次。
池化是卷积神经元网络中的一个必要组成部分。池化是去冗余的一种手段,指采用某个区域的统计量去简化该区域的神经元网络输出。如在图像某处有一个2×2像素的边缘,而以此为中心的4×4窗口中不存在其他边缘。显然边缘卷积核在边缘处有最大的输出,而在窗口的其他部分输出几乎为0。若认为没有必要将背景区域传递到下层,则可采用一种“最大池化”策略[28],即取4×4窗口中的最大的响应作为该区域的输出,这时输出的大小变成2×2窗口。通常,每次池化都会使得输入图像减小,2×2池化对应图像长宽都缩小一半。
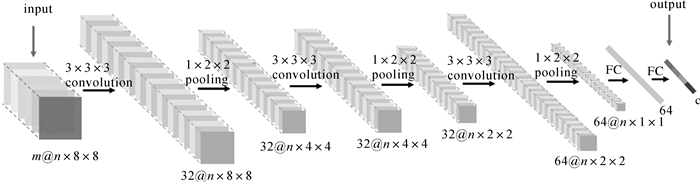
到目前为止,卷积神经元网络受到广泛研究和巨大推动。从2012年的AlexNet[9]开始,涌现了一批先进的卷积神经元网络架构,如ZFNet[29]、GoogleNet[30]、VGGNet[31]、ResNet[32]等,但CNN的本质依然是简单优雅的:卷积模板提取特征并激活、池化去除背景、前向传播计算代价、后向传播迭代收敛。图 1是一个针对遥感图像的以VGGNet为模板的CNN实例。样本大小为8×8像素,m、n分别代表遥感图像的波段和时相。首先设计卷积核(即边缘、颜色、纹理以及更抽象的待学习特征)的数量,32@8×8指从8×8的样本中提取32个特征。每一层典型的卷积网络包括3个处理流程:卷积、激活、池化。对于任意一个卷积核,在所有的图像的所有位置进行卷积操作;对于每一个卷积输出标量,选择恰当的激活函数并计算输出;最后根据池化策略,得到本卷积层的输出。图 1包括3个卷积层。经过三次池化后,图像的大小已经降低为1×1的像素,此后接2个全连接层,最后一个全连接层也是输出层。诸如图 1的看似简单的CNN有着巨大的威力,在图像分类、物体识别、检索中基本上全面超越了传统的机器学习方法。
|
| 图 1 卷积神经元网络实例 Fig. 1 An example of convolutional neural network |
2.3 深度学习在摄影测量几何方面的应用和展望
深度学习目前在几何中主要有两类应用。第一类是用于相机定位。将几何定位问题归结为深度学习,首先需要考虑:如何将一个优化问题(同时也是一个回归问题)纳入深度学习框架。2015年,PoseNet[14]第一次将CNN应用到相机的定位定姿中,可能也是迄今为止唯一较成熟的基于CNN的SLAM系统,并在2016年提出基于贝叶斯CNN的新版本[33]。PoseNet采用四元数表达角度,因此参数空间维度为7,即p=[x q]。采用二次范式(即最小二乘),损失函数表达为
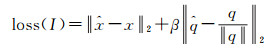
β为角度和位置参数间的量纲比例。对于一个分类问题,解空间是类别标签。可以为每个类别设定有限的离散标签。然而回归问题的解空间是无限、连续的,因此无法采用SoftMax等判决函数。PoseNet在GoogleNet基础上进行了改进。添加一个2048维度的全连接层,此后再加入一个7维全连接层,最后将SoftMax层移除并替换为以上损失函数。PoseNet利用传统的从运动恢复结构的方法(SfM)得到传感器的位置和姿态,每张图像对应一个位置(即标签)。此外,PoseNet也利用了迁移学习,将ImageNet和Places的训练结果作为初值参与后继训练,并提高了定位精度。目前,定位精度分别为户外2 m和3°,户内0.5 m和5°。距离经典的空中三角测量、SfM和SLAM所能达到的精度尚有一定的差距。
深度学习在几何上的第二个应用是3D重建。根据2D图像重建3D场景是摄影测量与计算机视觉共同的本质命题。虽然从2D到3D的重建涉及一些图像处理和特征表示知识,但是它仍属于一个几何问题。密集匹配是3D重建中的关键部分。2016年,Zbontar和LeCun的一篇文章(mc-CNN)[34]是开启深度学习进军立体匹配的代表作。mc-CNN利用CNN来学习匹配代价(matching cost)。传统的匹配代价包括亮度绝对值差异、相关系数、欧氏距离、交叉熵等,这些代价往往不是最优的,会受到亮度突变、视差突变、无纹理或重复纹理、镜面反射等影响。而深度学习方法试图通过更复杂的模式学习出对这些不利因素稳健的匹配代价。最终,这篇文章在KITTI和Middlebury数据集上得到了比绝对亮度差、census和归一化相关系数等匹配代价更低的错误率。此后,用深度学习进行立体匹配成了热门课题。许多学者纷纷提出各类匹配算法,如SGM-Net[35]、DispNetC[36]、Content-CNN[37]等。在KITTI测试集上,前30名几乎都是深度学习算法。自从1982年Marr创立计算机视觉开始[38],3D几何重建就是计算机视觉的核心。当时的想法过于浪漫:既然有了Marr理论,实现3D重建只需一个夏天。事实上,直到今天这个问题也没有完全解决。虽然计算机视觉已经开辟广阔的研究空间,但该学科的最基本问题依然望而不及。这也解释了利用深度学习进行3D重建的热度所在。除了利用深度神经元网络学习匹配代价,另外一类方法是采用端到端的策略,即从立体像对直接学习出深度图(视差图)。2017年,Kendall等提出GC-Net[39]。其核心思想是:将视差看作图像外的第三维,即处理对象变成3D张量。然后,由3D卷积学习几何与语义特征,直接得到最优的视差图(即3D张量中的一个曲面)。相对于2D图像的学习,这种3D方法需要更大的显存空间。目前,处理计算机视觉中的自然图像尚且困难,处理大视差的遥感图像目前在微机上还遥不可及。
虽然深度学习方法在有限的测试集上表现优异,但是并不能说明它的普适性。在短期内,构造性的经典方法,如多视SGM,依然是2D到3D几何重建的主流。而基于端到端的立体匹配方法具有较强的冲击力,伴随更强计算能力的GPU的普及和更多学者的参与改进,极有可能超越经典方法。
2.4 深度学习在摄影测量语义方面的应用深度学习在遥感图像语义提取方面的应用刚刚起步并逐渐普及。以下将从各类地物语义专题图出发,回顾深度学习的具体应用。
遥感图像建筑、道路网等地物的提取一直是数十年来的热门课题。虽然经典方法取得一定的效果,但距离实用、市场、商业软件尚有一定的距离。CNN目前正成为道路网提取的主流方法。文献[35]通过级联式端到端CNN同时实现了道路网提取及道路中心线提取,与其他方法比较,达到了更高的分类精度。文献[40]通过CNN结合线积分卷积克服了树木遮蔽、房屋阴影所造成的道路网残缺问题。文献[41]通过非监督学习预处理和空间相关性的应用,利用深度学习极大地提高了复杂城市场景的道路提取精度。文献[42-43]均为使用深度学习的方法进行道路提取并取得了良好的效果。
建筑物、农作物、水体等专题的提取相对道路而言较少,但预期会有许多相关文献近期发表。文献[44]采用CNN实现高分辨率多光谱卫星影像的建筑物提取。首先采用AlexNet提取特征,最后的全连接层用于训练SVM分类器并采用MRF模型精化。作物精细分类是摄影测量与遥感在农业中的重要应用。文献[45]在影像平面上进行2D卷积,在光谱方向上进行1D卷积,分别提取出影像空间特征和光谱特征,取得了比随机森林和全连接MLP更好的作物分类精度。文献[46]将CNN用于土地利用分类。文献[47]中也较全面地总结了深度学习在遥感方向的应用。
上述研究具有一定的积极意义,但目前显然还未实现遥感图像语义专题图的全自动提取。为了从本质上解决该问题,需要考虑两点。
第一点是恰当的迁移学习方法。目前ImageNet等庞大的数据库来自大众摄影图像,并不包括鸟瞰航摄图像和卫星遥感图像。照片的标注诸如人、大象或椅子;遥感图像中的标注诸如耕地、建筑、森林等。若直接将这些数据库训练得到的模型,用来进行遥感图像直接分类,就要考虑迁移学习。迁移学习是将A数据集中训练好的模型,应用在B数据集上。A与B可能是同源的,也可能存在巨大差异。这就要进一步发掘完善的迁移学习机制。以上文献几乎都存在训练集过小的问题,因此应用到其他场景可能错误率显著提高。
第二点是建立针对遥感图像的开源的、完备的标签数据库。涵盖足够多的地物类别,每个类别包括足够多的样本。这样的数据库是摄影测量与遥感走向“自动化专题制图”的必经之路。然而,实现难度要比千万图像级别的ImageNet更大。首先,由于远距成像的特性,图像受到更多电磁辐射传输的影响。经过大气传播的电磁辐射与地物间的相互作用机理更加复杂,同一标签的样本往往呈现明显的差异。这种差异不但对样本的选取造成不便,而且对深度学习模型的可区分性提出更大的挑战。第二,众包模式并不能完全起作用。普通人可能很好地辨认出诸如猫与狗的区别,因此通过互联网众包能够快速构建一个巨大的标注数据库;但是,小麦和水稻在遥感图像上的差异,则需要专业人员的目视判读。若影像分辨率较低,甚至可能需要实地调查。第三,摄影测量与遥感界的科研模式尚需向开源发展。目前,遥感学界已经开始走向开源模式,希望由公司、政府或科研机构能够在短期内建立的针对遥感图像分类的标签数据库,并实现完全开源。
有了足够的数据标签库或恰当的迁移学习方法,并借助深度学习的泛化能力,可以预期未来摄影测量与遥感专题制图的精度将比传统的特征分类方法得到明显的改进。
3 已有的研究工作本节介绍深度学习在摄影测量学中两个较有代表性的应用。一是关于立体匹配和迁移学习。如上所述,计算机视觉所面对的数据源主要是大众图像和自然图像。而摄影测量主要面对航空、航天遥感图像。将大众图像训练获得的深度学习模型,通过一定的方式应用到遥感图像中,是一个迁移学习的过程。迁移学习是深度学习在摄影测量(及其他领域)中体现泛化能力的重要概念,同时立体匹配是摄影测量以及计算机视觉的核心命题;笔者尝试将这二者结合,期望得到当前最先进的结果。
二是关于深度学习在遥感时空数据中的应用。除了运动摄影,计算机视觉中的自然图像多为静态图像。摄影测量与遥感则不然。大部分遥感图像为时空数据,即存在一个额外的时间维度,对应变化、变迁、长势、趋势、动力学等。传统的基于2D CNN的2D卷积核在理论上只能提取2D信息,因此可能无法在时空数据中取得最佳的效果。如文献[45]等作物分类方法忽略了时相信息。笔者以多时相多光谱农业遥感数据为例,引入3D卷积和3D CNN更好地提取作物生长时序特征,并得到更精细的作物分类专题图。
3.1 基于深度学习和迁移学习的立体匹配KITTI2012和KITTI2015是标准的立体匹配测试数据集[15]。数据包括纠正后的立体图像(即核线立体图像)与深度图,分别由安装在车辆上的立体相机和LIDAR获取。KITTI2012和KITTI2015各包含约200景图像。针对该数据集,目前许多立体匹配算法都公布了在该数据集上的测试结果。根据网站实时信息,深度学习的方法占据前10,SGM约排在30名左右。
如何有效地将KITTI数据集的训练模型应用于航空遥感图像密集匹配是兴趣点。数据为20幅航空图像,同时以LIDAR点云获取的深度图作为参考基准。受显卡容量限制,将航空图像裁剪到1000×300像素大小,并生成384幅立体像对用于测试。由于传统立体匹配的方法并不需要训练集,为公平起见,只在开源的KITTI数据集上训练模型,然后将模型直接应用于航空数据集上。训练和测试在Nvidia显卡Titan Xp上执行。表 1列出了SGM、SURE软件、MC-CNN[34]及GC-NET[35]的比较结果。前二者为经典的立体视觉方法,后二者是深度学习方法的代表作。其中,MC-CNN只学习匹配代价,其他代价聚合、一致性检验部分与SGM相同;而GC-NET是一种端到端的从立体像对直接获取深度图的CNN方法。表 1的结果显示,SGM的精度最低,而SURE最高。MC-CNN和GC-NET近似相等。比SGM要高出5个百分点,但比SURE低将近2个百分点。括号中的数值表示:如果采用航空影像数据自身进行训练,能达到的精度(训练集与测试集容量比例约为2:1)。图 2是较有代表性的一幅立体像对。左边是平地,右边是有层次的建筑物。图 2(c)和图 2(d)分别为SGM和深度学习的结果。这两种方法的唯一区别是代价函数的差异。绿色为正确匹配点,红色为错误点。无论是SGM还是深度学习的方法都在平地区域表现优秀。而在复杂的建筑物区,MC-CNN则更加优异。在深度急剧变化的边缘,SGM明显失误更多。虽然SURE的精度要比深度学习方法略高,但SURE用到了多视匹配的策略,而深度学习方法只利用了立体约束条件。因此,可以预见深度学习方法将会有很大的提升空间。
| 方法 | SGM | SURE | MC-CNN | GC-NET |
| 精度 | 0.900 | 0.968 | 0.948(0.953) | 0.949 |

|
| 图 2 SGM(c)与MC-CNN(d)结果比较 Fig. 2 Results comparison between SGM and MC-CNN |
3.2 基于3D卷积的时空农业数据精细分类专题图
试验数据包括两套2015年不同区域的高分2号(GF-2)数据(表 2)。数据1含4波段(红外、红、绿、蓝)4时相(6、7、8和9月)。根据目视判别的结果,影像覆盖区域内主要地物为玉米、树木、水稻和高粱。对各地物类随机选取训练样本400个,测试样本2000个。数据2含4波段(红外、红、绿、蓝)7时相(6月17日、7月8日、7月27日、9月9日、9月19日、11月7日和11月17日)。影像范围内主要地物为:道路、荒草地、居民地、空地、林带、湿地、水稻、水面、秧地和玉米。随机选取训练样本3180个,测试样本890个。以数据一为例,单通道样本窗口大小为8×8,每个样本块大小为16×8×8。其中16通道的顺序是:先红外波段的4个时相,再红波段的4个时相,以此类推。
| 数据 | 波段数 | 时相数 | 影像大小 | 分辨率/m | 地物类 | 训练样本 | 测试样本 |
| 数据1 | 4 | 4 | 1417×2652 | 4 | 4类 | 400 | 2000 |
| 数据2 | 4 | 7 | 1163×2102 | 4 | 10类 | 3180 | 890 |
本次试验的目的是为了验证在作物分类中,理论上更优秀的3D CNN是否更好地作用于多时相数据,并与2D CNN以及传统分类方法对比。
采用了图 3所示的针对多光谱多时相数据的网络架构。其中,原始输入m@n×8×8指:样本大小为n×8×8的张量,n为时相,8×8为单通道的宽和高,m为光谱段。32@则指当前层的神经元个数为32。该架构采用了3层3D卷积神经元网络和2层全连接层。

|
| 图 3 多光谱多时相遥感数据分类的3D网络架构 Fig. 3 The 3D CNN for multi-spectral multi-temporal remote sensing data classification |
表 3对比了2D CNN、3D CNN、SVM、KNN、PCA+KNN的测试精度与全图分类精度。可以看出,在两类精度上,CNN要高于SVM、KNN和PCA等方法;3D CNN略优于2D CNN。图 4为不同方法对高分2号两套数据进行全图分类的结果图。
| 数据 | 精度 | 2D CNN | 3D CNN | SVM | KNN | PCA + KNN | |
| 数据1 | 测试精度 | OA | 0.938 | 0.943 | 0.935 | 0.924 | 0.921 5 |
| 分类精度 | OA | 0.935 | 0.939 | 0.932 | 0.927 | 0.927 7 | |
| 数据2 | 测试精度 | OA | 0.961 | 0.973 | 0.785 | 0.764 | 0.745 |
| 分类精度 | OA | 0.923 | 0.932 | 0.896 | 0.889 | 0.845 |

|
| 图 4 高分2号数据1不同方法分类效果图 Fig. 4 Classification results of different methods of GF2 data1 |
本次试验与计算机视觉中的大量关于图像标签分类文献的结果相符合。在遥感图像的分类中,基于CNN的方法同样超越了传统的分类方法。在此基础上,引入了3D卷积,应对多时相多光谱数据,并得到了比2D CNN更好的分类精度。
4 结论本文首先回顾了摄影测量与深度学习的历史,并分析了二者间的紧密联系。然后,介绍了深度学习以及卷积神经元网络的基本思想;分析了摄影测量与遥感、计算机视觉、机器学习等领域的相关发展。最后,结合笔者的研究介绍了深度学习在图像立体匹配和作物分类专题图提取中的应用。
得到以下结论:第一,目前深度学习并不适合摄影测量中纯几何领域,其定位、定向精度低于光束法区域网平差、SfM、SLAM等经典方法。第二,在图像匹配和3D几何重建中,深度学习表现出色,在标准数据集上遥遥领先,但是目前的主流3D重建算法依然以多视SGM等经典方法为核心,深度学习可能需要更庞大的训练集才能做到真正的领先。第三,在图像语义提取和分类中,深度学习方法已经全面领先于传统的机器学习方法,但目前迫切需要更庞大、更专业的遥感标签数据库以训练更好的模型。最后,利用深度学习的学习和泛化能力,端到端地实现遥感图像到语义专题图的提取,将为现代摄影测量的发展提供契机。
此外,本文借鉴迁移学习的思想,研究了基于深度学习的航空图像密集匹配,并取得比SGM更好的结果。同时,首次采用3D CNN提取作物的时空生长趋势,并取得比传统分类方法和2D CNN更好的作物精细分类专题图。这两个试验作为抛砖引玉,期待相关学者发展更好的深度学习算法并自动化、智能化地应用到摄影测量领域;最终实现摄影测量定义中“几何”与“语义”的完备性。
| [1] |
龚健雅, 季顺平.
从摄影测量到计算机视觉[J]. 武汉大学学报(信息科学版), 2017, 42(11): 1518–1522.
GONG Jianya, JI Shunping. From Photogrammetry to Computer Vision[J]. Geomatics and Information Science of Wuhan University, 2017, 42(11): 1518–1522. |
| [2] | BOYLE W S, SMITH G E. Charge Coupled Semiconductor Devices[J]. The Bell System Technical Journal, 1970, 49(4): 587–593. DOI:10.1002/bltj.1970.49.issue-4 |
| [3] | ASHBY W R. An Introduction to Cybernetics[M]. London: Chapman & Hall Ltd, 1961. |
| [4] | FODOR J A, PYLYSHYN Z W. Connectionism and Cognitive Architecture:A Critical Analysis[J]. Cognition, 1988, 28(1-2): 3–71. DOI:10.1016/0010-0277(88)90031-5 |
| [5] | HINTON G E, OSINDERO S, TEH Y W. A Fast Learning Algorithm for Deep Belief Nets[J]. Neural Computation, 2006, 18(7): 1527–1554. DOI:10.1162/neco.2006.18.7.1527 |
| [6] | SUYKENS J A K, VANDERWALLE J. Least Squares Support Vector Machine Classifiers[J]. Neural Processing Letters, 1999, 9(3): 293–300. DOI:10.1023/A:1018628609742 |
| [7] | KOLLER D, FRIEDMAN N. Probabilistic Graphical Models:Principles and Techniques[M]. Cambridge: MIT Press, 2009. |
| [8] | BENGIO Y, LAMBLIN P, POPOVICI D, et al. Greedy Layer-Wise Training of Deep Networks[C]//Proceedings of the 19th International Conference on Neural Information Processing Systems. Canada: ACM, 2006: 153-160. |
| [9] | KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet Classification with Deep Convolutional Neural Networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: ACM, 2012: 1097-1105. |
| [10] | MEHTA P, SCHWAB D J. An Exact Mapping between the Variational Renormalization Group and Deep Learning[J]. arXiv Preprint arXiv: 1410. 3831, 2014. |
| [11] | TISHBY N, PEREIRA F C, BIALEK W. The Information Bottleneck Method[J]. arXiv Preprint arXiv: physics/0004057, 2000. |
| [12] | HINTON G, DENG Li, YU Dong, et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition:The Shared Views of Four Research Groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82–97. DOI:10.1109/MSP.2012.2205597 |
| [13] | LECUN Y, BOSER B, DENKER J S, et al. Backpropagation Applied to Handwritten Zip Code Recognition[J]. Neural Computation, 1989, 1(4): 541–551. DOI:10.1162/neco.1989.1.4.541 |
| [14] | KENDALL A, GRIMES M, CIPOLLA R. Posenet: A Convolutional Network for Real-time 6-dof Camera Relocalization[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 2938-2946. |
| [15] | KITTI. The KITTI Vision Benchmark Suite[DB/OL]. [2018-03-01]. http://www.cvlibs.net/datasets/kitti. |
| [16] | BENGIO Y, COURVILLE A, VINCENT P. Representation Learning:A Review and New Perspectives[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1798–1828. DOI:10.1109/TPAMI.2013.50 |
| [17] | NG A. Sparse Autoencoder[J]. CS294A Lecture Notes, 2011, 72(2011): 1–19. |
| [18] | SANGER T D. Optimal Unsupervised Learning in A Single-layer Linear Feedforward Neural Network[J]. Neural Networks, 1989, 2(6): 459–473. DOI:10.1016/0893-6080(89)90044-0 |
| [19] | RUCK D W, ROGERS S K, KABRISKY M, et al. The Multilayer Perceptron as an Approximation to ABayes Optimal Discriminant Function[J]. IEEE Transactions on Neural Networks, 1990, 1(4): 296–298. DOI:10.1109/72.80266 |
| [20] | MIKOLOV T, KARAFIÁT M, BURGET L, et al. Recurrent Neural Network Based Language Model[C]//Proceedings of the 11th Annual Conference of the International Speech Communication Association. Makuhari, Chiba, Japan: International Speech Communication Association, 2010, 2: 3. |
| [21] | MINSKY M L, PAPERT S A. Perceptrons[M]. Cambridge: MIT Press, 1969. |
| [22] | NAIR V, HINTON G E. Rectified Linear Units Improve Restricted Boltzmann Machines[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel: ACM, 2010: 807-814. |
| [23] | SHORE J, JOHNSON R. Axiomatic Derivation of the Principle of Maximum Entropy and the Principle of Minimum Cross-entropy[J]. IEEE Transactions on Information Theory, 1980, 26(1): 26–37. DOI:10.1109/TIT.1980.1056144 |
| [24] | MORÉ J J. The Levenberg-Marquardt Algorithm: Implementation and Theory[M]//WATSON G A. Numerical Analysis. Berlin, Heidelberg: Springer, 1978: 105-116. |
| [25] | LE CUN Y, BOSER B E, DENKER J S, et al. Handwritten Digit Recognition with a Back-propagation Network[M]//TOURETZKY D S. Advances in Neural Information Processing Systems. San Francisco, CA: Morgan Kaufmann Publishers Inc., 1990: 396-404. |
| [26] | GOODFELLOW I, BENGIO Y, COURVILLE A. Deep Learning[M]. Cambridge, Massachusetts: MIT Press, 2016. |
| [27] | HORN B. Robot Vision[M]. Cambridge: MIT Press, 1986. |
| [28] | GRAHAM B. Fractional Max-pooling[J]. arXiv Preprint arXiv: 1412. 6071, 2014. |
| [29] | ZEILER M D, FERGUS R. Visualizing and Understanding Convolutional Networks[C]//European Conference on Computer Vision. Zurich, Switzerland: Springer, 2014: 818-833. |
| [30] | SZEGEDY C, LIU W, JIA Y, et al. Going Deeper with Convolutions[J]. arXiv Preprint arXiv: 1409. 4842, 2014. |
| [31] | SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-scale Image Recognition[J]. arXiv Preprint arXiv: 1409. 1556, 2014. |
| [32] | HE Kaiming, ZHANG Xianyu, REN Shaoqing, et al. Deep Residual Learning for Image Recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 2016: 770-778. |
| [33] | KENDALL A, CIPOLLA R. Modelling Uncertainty in Deep Learning for Camera Relocalization[C]//Proceedings of 2016 IEEE International Conference on Robotics and Automation. Stockholm, Sweden: IEEE, 2016: 4762-4769. |
| [34] | ŽBONTAR J, LECUN Y. Computing the Stereo Matching Cost with a Convolutional Neural Network[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 1592-1599. |
| [35] | KENDALL A, MARTIROSYAN H, DASGUPTA S, et al. End-to-end Learning of Geometry and Context for Deep Stereo Regression[C]//Proceedings of the IEEE Conference on Computer Vision. Venice, Italy: IEEE, 2017: 66-75. |
| [36] | SEKI A, POLLEFEYS M. SGM-Nets: Semi-global Matching with Neural Networks[C]//Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, HI: IEEE, 2017: 21-26. |
| [37] | MAYER N, ILG E, HÄUSSER P, et al. A Large Dataset to Train Convolutional Networks for Disparity, Optical Flow, and Scene Flow Estimation[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 2016: 4040-4048. |
| [38] | LUO Wenjie, SCHWING A G, URTASUN R. Efficient Deep Learning for Stereo Matching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE, 2016: 5695-5703. |
| [39] | MARR D. Vision:A Computational Investigation into the Human Representation and Processing of Visual Information[M]. San Francisco: W.H.Freeman and Company, 1982. |
| [40] | CHENG Guangliang, WANG Ying, XU Shibiao, et al. Automatic Road Detection and Centerline Extraction via Cascaded End-to-end Convolutional Neural Network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3322–3337. DOI:10.1109/TGRS.2017.2669341 |
| [41] | LI Peikang, ZANG Yu, WANG Cheng, et al. Road Network Extraction via Deep Learning and Line Integral Convolution[C]//Proceedings of the IEEE Conference on Geoscience and Remote Sensing Symposium (IGARSS). Beijing, China: IEEE, 2016: 1599-1602. |
| [42] | MNIH V, HINTON G E. Learning to Detect Roads in High-resolution Aerial Images[C]//Proceedings of the 11th European Conference on Computer Vision. Heraklion, Crete, Greece: Springer, 2010: 210-223. |
| [43] | WANG Jun, SONG Jingwei, CHEN Mingquan, et al. Road Network Extraction:A Neural-dynamic Framework Based on Deep Learning and a Finite State Machine[J]. International Journal of Remote Sensing, 2015, 36(12): 3144–3169. DOI:10.1080/01431161.2015.1054049 |
| [44] | PANBOONYUEN T, JITKAJORNWANICH K, LAWAWIROJWONG S, et al. Road Segmentation of Remotely-sensed Images Using Deep Convolutional Neural Networks with Landscape Metrics and Conditional Random Fields[J]. Remote Sensing, 2017, 9(7): 680. DOI:10.3390/rs9070680 |
| [45] | VAKALOPOULOU M, KARANTZALOS K, KOMODAKIS N, et al. Building Detection in Very High Resolution Multispectral Data with Deep Learning Features[C]//Proceedings of the IEEE Conference on Geoscience and Remote Sensing Symposium (IGARSS). Milan, Italy: IEEE, 2015: 1873-1876. |
| [46] | KUSSUL N, LAVRENIUK M, SKAKUN S, et al. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(5): 778–782. DOI:10.1109/LGRS.2017.2681128 |
| [47] | CASTELLUCCIO M, POGGI G, SANSONE C, et al. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks[J]. arXiv Preprint arXiv: 1508. 00092, 2015. |
| [48] | ZHANG Liangpei, ZHANG Lefei, DU Bo. Deep Learning for Remote Sensing Data:A Technical Tutorial on the State of the Art[J]. IEEE Geoscience and Remote Sensing Magazine, 2016, 4(2): 22–40. DOI:10.1109/MGRS.2016.2540798 |



