2. 中国测绘科学研究院, 北京 100830;
3. 煤炭工业济南设计研究院有限公司, 山东 济南 250031
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. Coal Industry Ji'nan Design and Research Co. Ltd, Ji'nan 250031, China
资源三号系列卫星是中国首个民用三线阵立体测绘卫星系列,目前由ZY-3 01星和ZY-3 02是组成,承担了全国地理信息产品生产、地形图修测、国土资源调查等任务。资源三号卫星主要研究任务有精密定轨、姿态处理、辐射处理、几何检校等[1-5],其中,精密定轨任务是处理其他任务的重要前提条件。同时作为高精度测图卫星,资源三号系列卫星精密数据的获取应用也取决于高精度的卫星轨道。为获取资源三号卫星精密轨道,星上搭载了由中国空间技术研究院研制的双频GPS接收机,同时搭载SLR反射器以进行独立轨道检核和特殊情况下的卫星定轨。
星载GPS定轨技术首先成功用于TOPEX/Poseidon卫星[6]精密轨道确定(precision orbit determination,POD)任务,并通过国内外多颗低轨(low earth orbit,LEO)卫星,如GRACE[7]、CHAMP[8]、GOCE[9]、FY-3C[10]等多颗卫星的成功试验,因其高质量、高精度、全天候等特点,星载GPS定轨技术成为低轨卫星精密轨道确定的重要手段,因此已有学者[5, 11-12]利用星载GPS定轨方法对资源三号卫星的精密定轨展开相关研究,并取得众多成果。关于载波观测值的误差主要有电离层误差、多路径误差、观测噪声、天线相位中心误差等,电离层误差可以使用无电离层组合进行削弱,多路径误差和观测噪声很难通过明确的手段消除,而未使用或使用错误的天线相位改正模型会对POD产生重要影响。目前鲜有关于ZY-3 01星及ZY-3 02星的星载GPS天线相位中心在轨估计的研究工作,因此本文就ZY-3 01星及ZY-3 02星的天线相位中心在轨校正展开研究。
高精度的LEO轨道确定需要对定轨过程中各项误差进行精细化改正,在轨估计星载GPS天线的相位中心偏差(phase center offset,PCO)和相位中心变化(phase center variation,PCV)可以进一步提升定轨精度[13-24]。卫星入轨前可利用地面检校方法[18]得到先验PCO、PCV模型,但因卫星在轨后燃料消耗、太空环境变化、质心移动、地面测量存在误差等因素,相位中心先验模型与在轨模型往往存在较大差异。因此在轨校正PCO及PCV模型非常重要。文献[13—15]对相应LEO星载GPS天线PCO进行在轨估计,研究了PCO各个分量的在轨估计可行性以及对精密定轨的影响。文献[14]发现GRACE卫星、试验3卫星在轨PCO相比地面PCO发生了不同程度变化。文献[15]发现在如卫星调轨等特殊环境下甚至会产生PCO跳变的情况,所以必须对天线PCO进行在轨校正。关于星载GPS天线PCV的研究较多。文献[16]在Jason-1定轨过程中注意到了天线相位中心实际存在不断变化的情况,并提出利用观测值残差建立模型进行该项误差的弥补。文献[17]对地面校正和利用载波相位残差校正PCV进行详细讨论,并探讨了先验PCV模型在星载GPS天线PCV在轨估计中的作用。文献[18]则提出利用直接法和残差法估计PCV模型,利用GRACE数据估计其PCV模型,并对PCV模型在精密轨道确定、卫星基线测量、重力场恢复等方面作出详细研究。此后国内外众多学者对HY2A[15]、GRACE[19-20]、GOCE[21]、SWARM[22-23]、COSMIC[24]的PCV模型进行在轨估计,得到众多结论。
本文首先阐述了低轨卫星星载GPS天线相位中心模型及改正策略,其次,对ZY-3 01星及ZY-3 02星搭载的国产GPS接收机获取的GPS数据质量进行评估,并对定轨方案进行描述。最后对ZY-3 01星及ZY-3 02星的星载GPS接收机天线的PCO、PCV进行在轨标定,并详细分析了它们对精密定轨的影响,得到了相关结论。
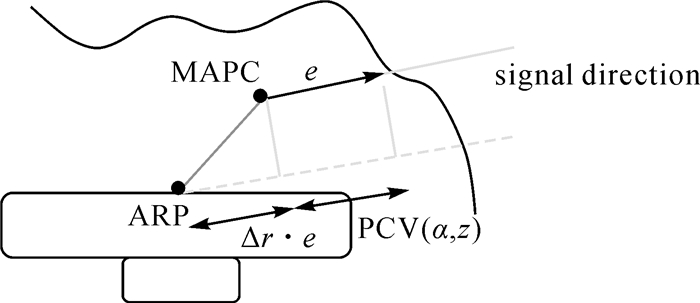
1 低轨卫星星载GPS天线相位中心模型低轨卫星最终精密轨道是以卫星质心为参考点,而用于定轨的GPS信号实际接收位置是在接收时刻下的瞬时天线相位中心,因此,需要对PCO及PCV进行改正,将瞬时相位中心改正至卫星质心上。通常平均天线相位中心(mean antenna phase center,MAPC)和天线几何参考点(antenna reference point, ARP)不重合,该项偏差即为PCO。同时由于天线制造工艺等因素,GPS信号中心会发生波动,瞬时相位中心和平均相位中心的偏差即为PCV。卫星质心与ARP的改正值由卫星制造商给出,因此,有了PCO及PCV信息,就可以将瞬时相位中心改正到卫星质心上。现对资源三号卫星相关坐标系作出简单描述。资源卫星星固系(satellite reference system, SRF)原点位于卫星质心,X轴过坐标原点,沿卫星纵轴方向指向同纵轴,Z轴指向卫星飞行对地方向,X轴和Z轴构成右手坐标系。PCO、PCV均在天线固定参考坐标系(antenna fixed system,AFS)下定义,资源三号卫星AFS原点为GPS天线参考点,x轴指向星固系X轴正向,z轴指向星固系Z轴正向,x轴和z轴构成右手坐标系。在AFS下,方位角定义为一矢量在xoy平面内+y轴旋转至+x轴的角度,高度角定义为该矢量和xoy平面的夹角。图 1为低轨卫星接收机天线相位中心改正模型。
|
| 图 1 低轨卫星接收机天线相位中心改正模型 Fig. 1 Model of LEO receiver antenna phase center correction |
PCV主要与高度角α、方位角z及信号频率有关,设PCO矢量形式为r,则由PCO及PCV导致的改正到几何参考点的距离误差为
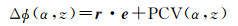 (1)
(1)
式中,e为卫星信号入射方向的单位矢量。
文献[18]指出包含PCO和PCV的天线相位中心改正具有很强的耦合性。当PCO改正矢量发生变化,PCV也会相应地发生变化,公式表示如下
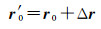 (2)
(2)
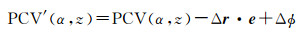 (3)
(3)
式中,r0、r′0、Δr分别为原始PCO矢量、变化后的PCO矢量以及变化值。式(2)中的PCO变化值Δr将会导致PCV发生式(3)中的变化,PCV(α, z)、PCV′(α, z)分别为原始PCV值和变化后的PCV值。式(3)中Δφ为一随机偏差,和接收机钟差等不能分离。因此,要正确估计在轨PCV值必须先估计在轨PCO,才能获得“真实的”PCV模型。PCV表示方式主要有球谐函数表示和分段线性函数[25]表示来描述,其中,球谐函数表述方法物理意义明确,但计算量大,而分段线性函数将PCV值表示与高度角、方位角相关的格网化的数值。该方法计算量小,实现容易,效果与球谐函数差异很小,所以本文采用分段线性函数模型表示PCV模型。设PCV模型由高度角和方位角组成的网格图中的不同格网点组成,利用双线性插值公式即可得到所求对应方位角和高度角的PCV值。
2 资源三号卫星GPS数据质量评估和精密轨道确定 2.1 资源三号卫星GPS数据质量评估资源三号01星及02星搭载的GPS接收机上有主天线和副天线两副天线,副天线一般在特殊情况下启用,本文所采用的数据均来自于主天线采集的数据。该GPS天线共有12个通道,数据采样率为1s,可获取C/A码伪距、L1 P码伪距、L2 P码伪距、L1载波、L2载波等观测值。为更好地分析该国产双频GPS接收机获取的GPS数据质量,本文主要从数据完备率,L1、L2频点多路径误差(MP1、MP2),周跳比,追踪卫星数目等方面进行评估。其中,数据完备率是指完整观测值占总观测值的比值;MP1、MP2分别为L1、L2频点伪距上的多路径观测误差;周跳比则是观测值总数与发生周跳的观测值数之比;卫星跟踪数量是指每个观测时刻可跟踪到的GPS卫星数目。
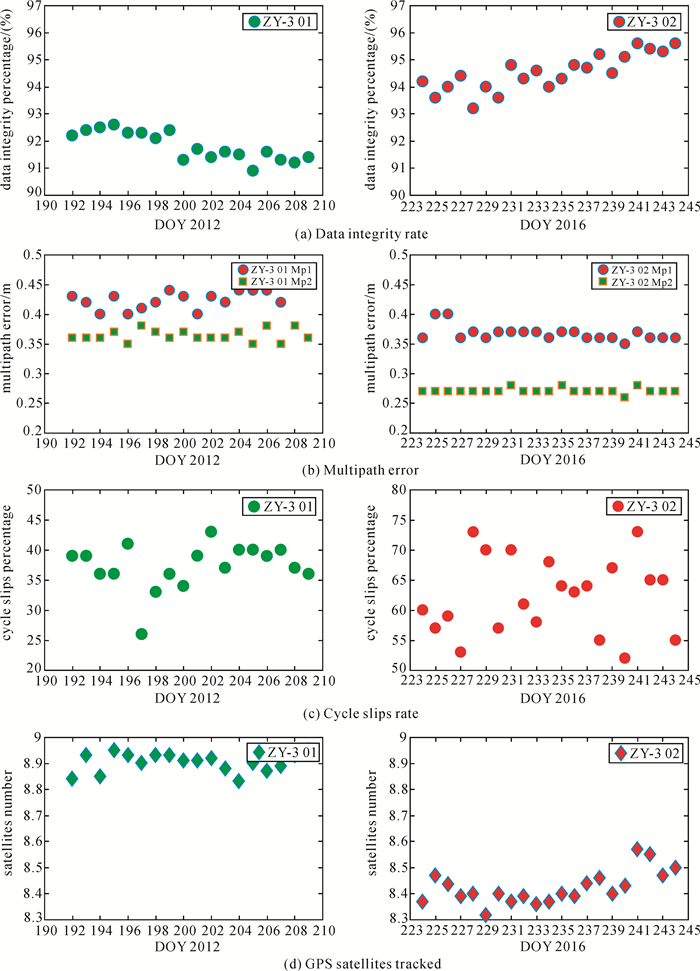
图 2统计了ZY-3 01星2012年年积日(day of year, DOY)192—209及ZY-3 02星2016年DOY 224—244内GPS数据的各个具体指标。通过分析,数据完备率方面,ZY-3 01星GPS数据平均为91.8%,低于ZY-3 02星的94.5%。多路径误差方面,两颗卫星的L1频点伪距上的多路径观测误差均高于L2频点伪距,ZY-3 01星平均L1、L2多路径误差分别为0.43 m、0.36 m,而ZY-3 02星平均L1、L2多路径误差分别为0.36 m、0.27 m。在周跳比方面,ZY-3 01星平均周跳比为32,而ZY-3 02星则为62。每时刻跟踪的GPS卫星数目方面ZY-3 01星为8.90颗,而ZY-3 02星略低,为8.42颗。各个指标均(除卫星跟踪数目)显示ZY-3 02星GPS数据质量相比01星均有不同程度的提高,这也显示我国在国产GPS接收机的硬件制造能力不断提升。
|
| 图 2 ZY-3 01星及ZY-3 02星星载GPS数据质量评估 Fig. 2 ZY-3 01 and ZY-3 02 spaceborne GPS data quality evaluation |
2.2 定轨方案描述
本文采用瑞士伯尔尼大学研制的Bernese 5.2软件进行精密定轨,定轨方法则为简化动力学定轨方法,利用简单的力学模型和伪距确定平滑轨道,将该轨道作为先验轨道引入基于相位观测值的动力学定轨中,通过添加随机脉冲参数,调节平滑的几何轨道和动力学学模型间的权重,利用过程参数来吸收卫星动力学模型误差,取得轨道最优估值[26]。
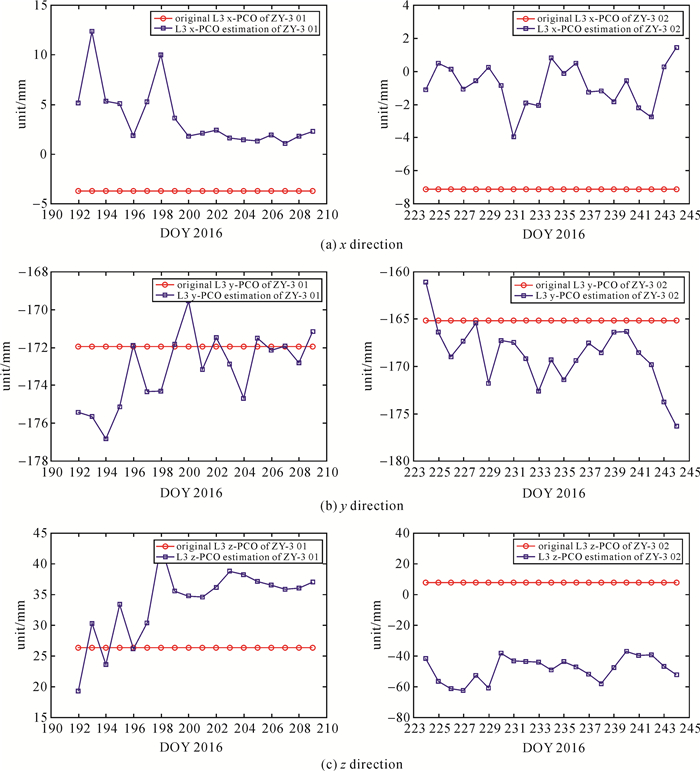
3 资源三号卫星星载GPS天线相位中心在轨估计 3.1 资源三号卫星星载GPS接收机PCO模型在轨估计根据最小二乘原理,在LEO精密定轨过程中,可将PCO参数作为未知参数引入观测方程,与轨道参数等一同估计,将定轨后包含PCO参数的法方程储存,最后通过多天法方程叠加即可求取在轨PCO最优解。本文选取多天星载GPS数据,对ZY-3 01星及ZY-3 02星的星载GPS天线PCO进行估计,相比地面获取的PCO,每天估计的无电离层组合观测值L3的PCO变化如图 3所示。
|
| 图 3 ZY-3 01星及ZY-3 02星星载GPS天线PCO估计 Fig. 3 PCO estimation for ZY-3 01 and ZY-3 02 spaceborne GPS antennas |
通过估计ZY-3 01星及ZY-3 02星星载GPS天线PCO 3个方向上的分量,发现两颗卫星的PCO变化程度并不一样,估计结果的标准差(STD)可以反映变化的稳定程度[16]。ZY-3 01星的PCO估计STD在x、y、z 3个方向分别是3.02 mm、1.86 mm、5.65 mm,而ZY-3 02星则为1.29 mm、3.11 mm、2.79 mm,可以看出整体变化结果ZY-3 02星比01星更为稳定。尽管获取了两颗卫星星载GPS天线PCO上3个方向的在轨估计值,但是根据以往学者[14-16]的研究,x及y方向上PCO分量与经验力参数等难以分离,而仅z方向PCO估计是较为可行的。此外,也为了更好地验证相对于使用地面PCO值和在轨估计PCO值对于LEO卫星精密定轨的影响,本文设计6种方案来验证PCO估计的可行性和使用在轨PCO值对精密定轨的影响。方案1不使用任何PCO信息,方案2在3个方向全部使用地面获取的PCO信息,方案3使用估计的x方向的PCO以及地面获取的y、z方向的PCO,方案4使用估计的y方向的PCO以及地面获取的x、z方向的PCO,方案5使用估计的z方向的PCO以及地面获取的x、y方向的PCO,方案6全部使用在轨估计的PCO值,其他定轨策略和数据等完全一样。利用SLR检核手段,对这6种定轨方案所获取的轨道精度进行评估。
SLR检核手段是一种高精度的LEO卫星轨道质量检核手段[27],它实际就是比较星载GPS定轨结果和SLR直接观测计算出的站星距。关于资源卫星SLR检核,ZY-3 01星加入全球激光网联测,因此获取的SLR数据较多,但个别台站整体观测资料出现粗差(残差在10m左右),因此将这些台站的观测资料剔除。而ZY-3 02星未加入全球激光网联测,仅中国境内的北京站、上海站、长春站承担了SLR观测任务,所以获取的SLR数据相对较少,ZY-3 02星的观测资料中有一定系统误差(4 cm左右),后续处理中均去除该系统误差。两颗卫星的SLR观测台站全球分布如图 4所示。在处理SLR资料时,考虑了SLR相位中心改正、潮汐改正、对流层折射改正、测站偏心改正等改正因素,其中资源卫星的SLR相位中心改正较为重要,类似于GPS天线相位中心误差,SLR观测同样存在信号参考点和卫星质心不重合的现象,通过仿真模拟和地面全站仪测量系统的到了该改正值[28]。此外,为保证数据客观性,全部SLR数据未设置截止高度角。
|
| 图 4 ZY-3 01星及ZY-3 02星星载GPS天线在轨PCV模型(10°×10°) Fig. 4 PCV model in-flight for ZY-3 01 and ZY-3 02 spaceborne GPS antennas in orbit(10°×10°) |
分析表 1可知,方案1未考虑PCO时,PCO误差对POD过程产生较大影响,ZY-3 01星SLR残差平均值为18.237 mm,RMS值为117.974 mm,02星则分别为17.111 mm和105.713 mm。方案2考虑了地面获取的PCO后,两颗卫星检核结果有极大程度的提升,其中ZY-3 01星较方案1分别提高了11.430 mm(mean),75.118 mm(RMS),02星较方案1提高了9.353 mm(mean),80.270 mm(RMS),这也说明了在精密定轨过程中,必须考虑PCO对精密定轨的影响。当方案3、4、5、6分别使用在轨估计的x、y、z方向以及全部使用3方向估计的PCO时,ZY-3 01星和02星的4种方案相比方案2,只有使用z方向的PCO估计结果的定轨精度有所提高,这也验证关于PCO在轨估计只有z方向是可行的,ZY-3 01星检核结果提高了0.674 mm(mean),0.331 mm(RMS),ZY-3 02星检核结果提高了2.060 mm(mean),0.399 mm(RMS)。因此,最终本文采用地面获取的x和y方向PCO,以及在轨估计的z方向的PCO作为最终的PCO信息。
| mm | |||
| LEO | plan | SLR mean | SLR RMS |
| ZY-3 01 | 1 | 18.237 | 117.974 |
| 2 | 6.807 | 42.856 | |
| 3 | 7.393 | 42.875 | |
| 4 | 6.917 | 42.988 | |
| 5 | 6.133 | 42.525 | |
| 6 | 10.638 | 57.847 | |
| ZY-3 02 | 1 | 17.111 | 105.713 |
| 2 | 7.758 | 25.443 | |
| 3 | 8.287 | 25.819 | |
| 4 | 8.266 | 26.550 | |
| 5 | 5.698 | 25.044 | |
| 6 | 12.863 | 36.519 | |
3.2 资源三号卫星星载GPS接收机PCV模型在轨估计
LEO星载GPS天线PCV模型在轨估计可以分为直接法和残差法。其中,直接法是将PCV参数在定轨过程中直接视为未知参数,将与其他定轨参数一同求解。该方法不易受到接收机钟差、模糊度参数等影响,但计算量大,对计算机运算和存储能力要求较高。而残差法是利用精密定轨后获取的载波相位残差,将天线空间划分为由高度角和方位角组成的格网空间,获取的载波相位残差落入格网空间后,对格网点附近小区间的残差求取平均值即为该格网点处的PCV值。该方法计算简单,容易实现,它实际属于一种后处理解算方法。该方法利用式(4)建立PCV模型
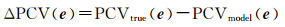 (4)
(4)
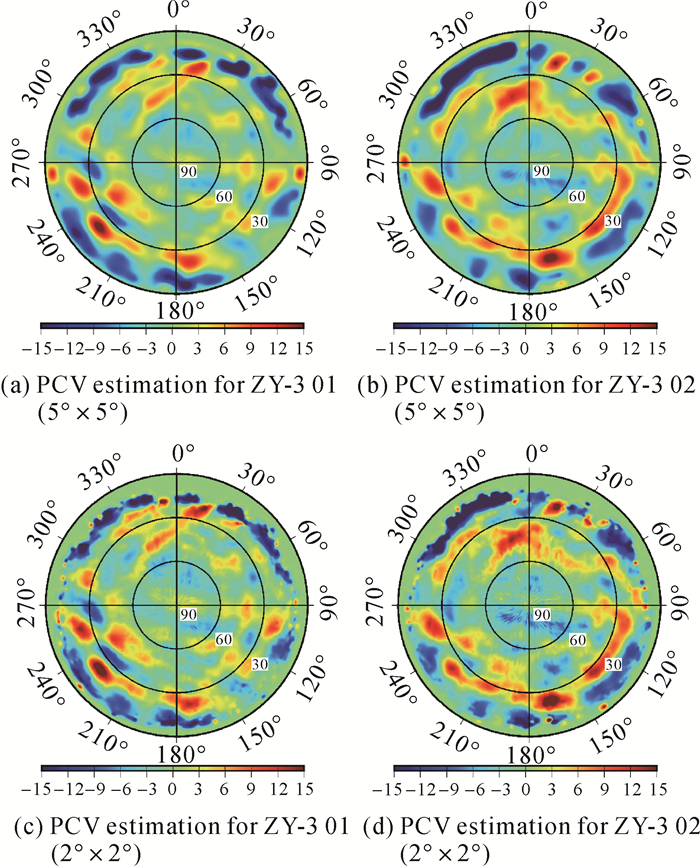
式中,PCVtrue(e)表示真实的PCV模型;PCVmodel(e)表示使用的PCV模型,其差值即为未被模型化的PCV误差,若定轨中不考虑PCV误差,则该误差在简化动力学轨道残差中分布极为明显,因此,未被模型化的PCV误差将会残留在定轨后的载波相位残差中
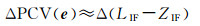 (5)
(5)
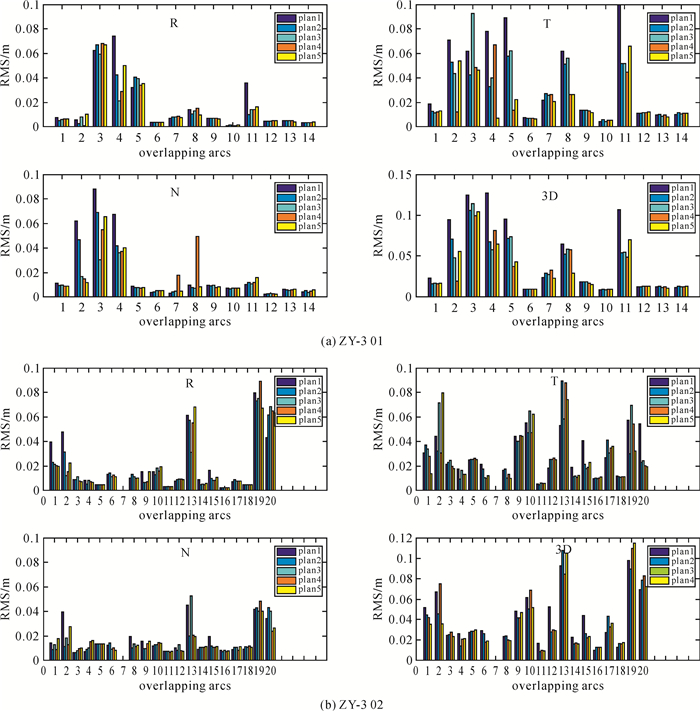
式中,LIF表示GPS观测值;ZIF表示改正其余误差(不考虑PCV)后的模型值。该方法容易受到其他轨道参数影响,故采取多次迭代处理,迭代策略如式(6)所示
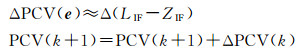 (6)
(6)
式中,k表示迭代次数,一般选取3~5次迭代,PCV即可到达足够收敛。
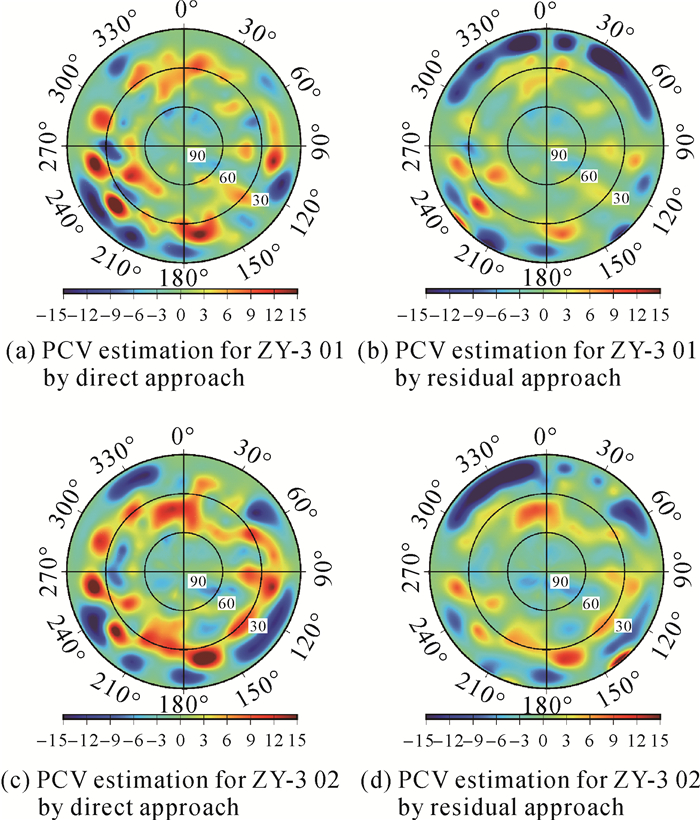
图 4展示了两种不同方法获取的天线参考坐标系下ZY-3 01星及ZY-3 02星的星载GPS天线PCV模型,分辨率为10°×10°。可以直观看出两颗卫星的星载GPS天线PCV模型都十分相似,这主要是由于接收机系统为同一制造商,而且所处太空环境相似,这种情况类似于GRACE A卫星和GRACE B卫星[14, 20]。两颗卫星的PCV整体量级均在[-15 mm 15 mm]之间,其中ZY-3 01星PCV极值为-34.42 mm和19.33 mm,ZY-3 02星PCV极值为-35.94 mm和26.41 mm。极值点以及较大的PCV值均分布在较低的高度角(低于30°),当高度角过低,观测信号强度衰减严重,且受到多路径影响更为明显,导致观测值精度较差。
对比直接法和残差法估计出的PCV模型,尽管两种方法的估计原理完全不同,但是两种方法估计出的PCV模型基本一致,这也说明了估计结果的可靠性,通过分析仍能发现两种方法估计出的PCV模型有几点不同。①直接法是将每个格网点的PCV视为未知参数进行估计,估计更为精细化,因此估计的PCV图更多地呈现斑点形状。而残差法则是将落入相应格网区间的残差求取平均值视为该格网点的PCV值,因此相邻格网的PCV估计值更为相似,估计的结果图呈现更多地条带形状。因此,使用残差法时尽量保证观测值数量较多,以更完整的覆盖天线格网空间。②为保证观测值精度,一般会设置观测值截止高度角,因此在低方位角的PCV估计上,两种方法估计出的PCV值有所差别。③在估计效率上,直接法存储一天的包含PCV信息的法方程文件大约需要4.66 MB(二进制),而残差法存储一天的残差文件仅需要774kB(二进制),当存储多天PCV信息时直接法需要远远高于残差法的存储空间。此外,由于直接法是在定轨过程中对每个格网点的PCV参数进行求解,还要对多天的法方程进行叠加以求解最终的PCV模型,计算速度较为缓慢。而残差法解算原理简单,编程容易实现,估计出的PCV模型和直接法相差无几,通过SLR检核、重叠弧段检核等发现,对于轨道精度提升效果也十分接近。所以,更推荐使用残差法解算低轨卫星星载GPS天线PCV模型。
为了进一步探讨PCV模型对低轨卫星精密定轨的影响,本文分析了不同分辨率(10°×10°、5°×5°、2°×2°)的PCV模型对精密定轨的影响,见表 2。图 5展示了由残差法获取的天线坐标系下5°×5°、2°×2°的PCV模型,联合图 5中10°×10°分辨率的PCV模型分析来看,随着分辨率的增高,PCV模型分布特征并未发生根本变化,估计的模型更为精细化,但是也带来计算效率下降的问题。
| mm | |||||||
| LEO | plan | SLR evaluation | comparison of overlapping arcs | ||||
| ZY-3 01 | mean | RMS | R | T | N | 3D | |
| 1 | 6.133 | 42.525 | 18.636 | 38.336 | 20.650 | 50.845 | |
| 2 | 3.950 | 40.382 | 14.943 | 28.971 | 16.271 | 39.468 | |
| 3 | 5.874 | 40.897 | 13.650 | 31.268 | 10.843 | 36.942 | |
| 4 | 3.655 | 40.531 | 14.164 | 21.776 | 16.443 | 32.880 | |
| 5 | 3.207 | 40.699 | 15.971 | 21.964 | 13.707 | 33.680 | |
| ZY-3 02 | 1 | 5.698 | 25.044 | 13.586 | 20.395 | 11.175 | 28.695 |
| 2 | 3.054 | 24.317 | 13.175 | 18.410 | 10.030 | 26.959 | |
| 3 | 3.804 | 24.352 | 12.353 | 18.811 | 10.065 | 27.147 | |
| 4 | 3.523 | 24.391 | 13.817 | 19.092 | 9.595 | 27.509 | |
| 5 | 2.565 | 24.453 | 14.110 | 18.096 | 9.48 | 26.863 | |
|
| 图 5 ZY-3 01星及ZY-3 02星星载GPS天线不同分辨率PCV模型 Fig. 5 Different resolutions PCV model for ZY-3 01 and ZY-3 02 spaceborne GPS antennas |
本文将仅使用PCO而未使用PCV信息的定轨方案作为方案1,将使用直接法估计的10°×10°的PCV模型,残差法估计的10°×10°的PCV模型,残差法估计的5°×5°的PCV模型,残差法估计的2°×2°的PCV模型分别作为方案2、方案3、方案4、方案5,其他定轨策略完全相同。为了更客观地评估PCV对定轨的影响,使用SLR检核作为外符合精度评估手段,使用重叠弧段对比[5]作为内符合精度评估手段。图 6反映了几种方案下,在R、T、N、3D各个方向上重叠弧段检核精度的变化情况。
|
| 图 6 ZY-3 01星及ZY-3 02星重叠弧段对比 Fig. 6 Overlapping arcs comparison for ZY-3 01 and ZY-3 02 |
从SLR检核结果来看,在仅使用在轨估计的PCO,而不使用任何PCV改正模型时,ZY-3 01星检核结果平均值为6.133 mm,RMS值为42.525 mm,ZY-3 02星检核结果则为平均值5.698 mm,RMS值为25.044 mm,已经达到较高的定轨精度。将方案2、方案3和方案1分别对比,也就是使用两种方法在轨估计的10°×10°的PCV模型时,ZY-3 01星检核结果RMS值则提高了2.143 mm(直接法)、1.628 mm(残差法)。而ZY-3 02星检核结果RMS值则提高了0.727 mm(直接法)、0.692 mm(残差法)。可以看出,当通过使用两种方法估计的PCV模型后,轨道精度都得到不同程度的提高,而且精度提升基本相当,综合考虑在计算效率,存储空间要求等方面的影响,因此也建议使用残差法估计低轨卫星星载GPS天线的在轨PCV模型。将方案3、方案4、方案5分别和方案1对比探讨PCV模型分辨率的影响时,ZY-3 01星检核结果RMS值上则分别提高了1.628 mm(10°×10°)、1.994 mm(5°×5°)、1.826 mm(2°×2°)。ZY-3 02星检核结果RMS值上则分别提高了0.692 mm(10°×10°)、0.653 mm(5°×5°)、0.591 mm(2°×2°)。SLR结果检核精度并未随着分辨率的提高而提高,因此,综合考虑计算效率和提升效果,5°×5°PCV模型是比较好的选择。
从重叠弧段对比来看,将方案2和方案1对比,即使用直接法在轨估计的10°×10°的PCV模型时,ZY-3 01星重叠弧段对比精度在R、T、N、3D分别提高了3.693 mm、9.365 mm、4.379 mm、11.377 mm,ZY-3 02星重叠弧段对比精度在R、T、N、3D分别提高了0.411 mm、1.985 mm、1.145 mm、1.736 mm。将方案3与方案1对比,即使用残差法在轨估计的10°×10°的PCV模型时,ZY-3 01星重叠弧段对比精度在R、T、N、3D分别提高了4.986 mm、7.068 mm、9.807 mm、13.903 mm,ZY-3 02星重叠弧段对比精度在R、T、N、3D分别提高了1.233 mm、1.584 mm、1.110 mm、1.548 mm。类似于SLR检核结果,当通过使用无论哪种方法估计的PCV模型后,重叠弧段对比评估轨道精度都得到不同程度的提高,而两种方法带来的精度提升基本相当。将方案3、方案4、方案5分别和方案一对比探讨PCV模型分辨率的影响时,同样类似于SLR检核结果,虽然使用不同分辨率的PCV模型都会给定轨结果带来精度提升,但是提升幅度并未随着分辨率的提高而提高,因此建议使用残差法在估计LEO卫星的PCV模型。
综合SLR检核结果和重叠弧段检核结果来看,PCV模型的使用能够进一步提升低轨卫星精密定轨精度,说明了在轨估计星载GPS天线PCV模型的重要性。文献[14]考虑GRACE卫星GPS天线PCV模型(量级:-10~10 mm),SLR检核RMS值较未考虑PCV模型提高了0.9 mm。文献[23]考虑SWARM卫星GPS天线PCV模型(量级:-20~20 mm),SLR检核RMS值较未考虑PCV模型提高了0.94 mm。文献[17]考虑TerrsSAR-X卫星GPS天线PCV模型(量级:-25~25 mm),SLR检核RMS值较未考虑PCV模型提高了1 mm。文献[21]考虑GOCE卫星GPS天线PCV模型(量级:-30~30 mm),SLR检核RMS值较未考虑PCV模型提高了1.49 cm。可以看出,PCV量级越大,对于提高轨道精度效果也更好。
4 结语随着中国越来越多低轨卫星发射升空,进一步提升LEO定轨精度成为科研人员卫星精密定轨工作的研究热点。本文对国产GPS接收机获取的星载GPS数据质量进行评估,ZY-3 02星数据质量要优于ZY-3 01星。针对低轨卫星星载GPS天线PCO及PCV误差,本文阐述了LEO卫星GPS天线相位中心改正模型及在轨估计的基本原理。基于ZY-3 01星及ZY-3 02星实测GPS数据,在轨估计了双星GPS天线PCO值,通过SLR检核,PCO在z方向分量在轨估计是可行的,且通过使用在轨估计的PCO值相比地面先验PCO值精度进一步提升。关于PCV在轨估计,本文使用残差法和直接法在轨估计双星的PCV模型,通过使用在轨PCV模型,SLR检核和重叠弧段检核精度都进一步提升。本文进一步深入比较了直接法和残差法的优缺点以及PCV模型分辨率对精密定轨的影响,通过综合考虑计算效率、存储空间、提高幅度等因素,发现使用残差法估计5°×5° PCV模型是比较好的选择,这对资源系列卫星后续的03星、04星以及我国其他低轨卫星精密定轨工作带来了有益经验。
| [1] |
李德仁.
我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317–322.
LI Deren. China's First Civilian Three-line-array Stereo Mapping Satellite:ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317–322. |
| [2] |
唐新明, 王鸿燕, 祝小勇.
资源三号卫星测绘技术与应用[J]. 测绘学报, 2017, 46(10): 1482–1491.
TANG Xinming, WANG Hongyan, ZHU Xiaoyong. Technology and Applications of Surveying and Mapping for ZY-3 Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1482–1491. DOI:10.11947/j.AGCS.2017.20170251 |
| [3] |
李德仁, 王密.
"资源三号"卫星在轨几何定标及精度评估[J]. 航天返回与遥感, 2012, 33(3): 1–6.
LI Deren, WANG Mi. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 1–6. |
| [4] |
王密, 杨博, 李德仁, 等.
资源三号全国无控制整体区域网平差关键技术及应用[J]. 武汉大学学报(信息科学版), 2017, 42(4): 427–433.
WANG Mi, YANG Bo, LI Deren, et al. Technologies and Applications of Block Adjustment without Control for ZY-3 Images Covering China[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 427–433. |
| [5] |
赵春梅, 唐新明.
基于星载GPS的资源三号卫星精密定轨[J]. 宇航学报, 2013, 34(9): 1202–1206.
ZHAO Chunmei, TANG Xinming. Precise Orbit Determination for the ZY-3 Satellite Mission Using GPS Receiver[J]. Journal of Astronautics, 2013, 34(9): 1202–1206. |
| [6] | YUNCK T P, BERTIGER W I, WU S C, et al. First Assessment of GPS-based Reduced Dynamic Orbit Determination on TOPEX/Poseidon[J]. Geophysical Research Letters, 1994, 21(7): 541–544. DOI:10.1029/94GL00010 |
| [7] | TAPLEY B D, BETTADPUR S, WATKINS M, et al. The Gravity Recovery and Climate Experiment:Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9): L09607. |
| [8] | REIGBER C, LVHR H, SCHWINTZER P. CHAMP Mission Status[J]. Advances in Space Research, 2002, 30(2): 129–134. DOI:10.1016/S0273-1177(02)00276-4 |
| [9] | BOCK H, JÄGGI A, ŠVEHLA D, et al. Precise Orbit Determination for the GOCE Satellite Using GPS[J]. Advances in Space Research, 2007, 39(10): 1638–1647. DOI:10.1016/j.asr.2007.02.053 |
| [10] | LI Min, LI Wenwen, SHI Chuang, et al. Precise Orbit Determination of the Fengyun-3C Satellite Using Onboard GPS and BDS Observations[J]. Journal of Geodesy, 2017, 91(11): 1313–1327. DOI:10.1007/s00190-017-1027-9 |
| [11] |
郭向, 张强, 赵齐乐, 等.
基于单频星载GPS数据的低轨卫星精密定轨[J]. 中国空间科学技术, 2013, 33(2): 41–46.
GUO Xiang, ZHANG Qiang, ZHAO Qile, et al. Precise Orbit Determination for LEO Satellites Using Single-frequency GPS Observations[J]. Chinese Space Science and Technology, 2013, 33(2): 41–46. |
| [12] |
龚学文, 王甫红.
海洋二号A与资源三号卫星星载GPS自主轨道确定[J]. 武汉大学学报(信息科学版), 2017, 42(3): 309–313.
GONG Xuewen, WANG Fuhong. Autonomous Orbit Determination of HY2A and ZY3 Missions Using Space-borne GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 309–313. |
| [13] | CHOI K R. Jason-1 Precision Orbit Determination Using GPS Combined with SLR and DORIS Tracking Data[D]. Austin: The University of Texas, 2003: 2917-2916. |
| [14] | GU Defeng, LAI Yuwang, LIU Junhong, et al. Spaceborne GPS Receiver Antenna Phase Center Offset and Variation Estimation for the Shiyan 3 Satellite[J]. Chinese Journal of Aeronautics, 2016, 29(5): 1335–1344. DOI:10.1016/j.cja.2016.08.016 |
| [15] | GUO Jing, ZHAO Qile, GUO Xiang, et al. Quality Assessment of Onboard GPS Receiver and Its Combination with DORIS and SLR for Haiyang 2A Precise Orbit Determination[J]. Science China Earth Sciences, 2015, 58(1): 138–150. DOI:10.1007/s11430-014-4943-z |
| [16] | LUTHCKE S B, ZELENSKY N P, ROWLANDS D D, et al. The 1-Centimeter Orbit:Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue:Jason-1 Calibration/Validation[J]. Marine Geodesy, 2003, 26(3-4): 399–421. |
| [17] | MONTENBRUCK O, GARCIA-FERNANDEZ M, YOON Y, et al. Antenna Phase Center Calibration for Precise Positioning of LEO Satellites[J]. GPS Solutions, 2009, 13: 23. DOI:10.1007/s10291-008-0094-z |
| [18] | JÄGGI A, DACH R, MONTENBRUCK O, et al. Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination[J]. Journal of Geodesy, 2009, 83(12): 1145–1162. DOI:10.1007/s00190-009-0333-2 |
| [19] |
胡志刚, 赵齐乐, 郭靖, 等.
GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(S1): 34–38.
HU Zhigang, ZHAO Qile, GUO Jing, et al. Research on Impact of GPS Phase Center Variation on Precise Orbit Determination of Low Earth Orbit Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 34–38. |
| [20] | MAO X, VISSER P N A M, VAN DEN IJSSEL J V. Impact of GPS Antenna Phase Center and Code Residual Variation Maps on Orbit and Baseline Determination of GRACE[J]. Advances in Space Research, 2017, 59(12): 2987–3002. DOI:10.1016/j.asr.2017.03.019 |
| [21] | BOCK H, JÄGGI A, MEYER U, et al. Impact of GPS Antenna Phase Center Variations on Precise Orbits of the GOCE Satellite[J]. Advances in Space Research, 2011, 47(11): 1885–1893. DOI:10.1016/j.asr.2011.01.017 |
| [22] |
田英国, 郝金明.
Swarm卫星天线相位中心校正及其对精密定轨的影响[J]. 测绘学报, 2016, 45(12): 1406–1412, 1433.
TIAN Yingguo, HAO Jinming. Swarm Satellite Antenna Phase Center Correction and Its Influence on the Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1406–1412, 1433. DOI:10.11947/j.AGCS.2016.20160132 |
| [23] | VAN DEN IJSSEL J, ENCARNAÇÃO J, DOORNBOS E, et al. Precise Science Orbits for the Swarm Satellite Constellation[J]. Advances in Space Research, 2015, 56(6): 1042–1055. DOI:10.1016/j.asr.2015.06.002 |
| [24] | HWANG C, TSENG T P, LIN T, et al. Precise Orbit Determination for the FORMOSAT-3/COSMIC Satellite Mission Using GPS[J]. Journal of Geodesy, 2009, 83(5): 477–489. DOI:10.1007/s00190-008-0256-3 |
| [25] | SCHMID R, ROTHACHER M, THALLER D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4): 283–293. DOI:10.1007/s10291-005-0134-x |
| [26] |
赵春梅, 程鹏飞, 益鹏举.
基于伪随机脉冲估计的简化动力学卫星定轨方法[J]. 宇航学报, 2011, 32(4): 762–766.
ZHAO Chunmei, CHENG Pengfei, YI Pengju. Reduced-dynamics Satellite Orbit Determination Based on Pseudo-Stochastic Pulse Estimation[J]. Journal of Astronautics, 2011, 32(4): 762–766. |
| [27] |
秦显平, 焦文海, 程芦颖, 等.
利用SLR检核CHAMP卫星轨道[J]. 武汉大学学报(信息科学版), 2005, 30(1): 38–41.
QIN Xianping, JIAO Wenhai, CHENG Luying, et al. Evaluation of CHAMP Satellite Orbit with SLR Measurements[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1): 38–41. |
| [28] |
周辉, 李松, 杨晋陵, 等. 资源三号卫星激光角反射器阵列质心改正值的解算[C]//中国测绘学会2012年学术年会论文集. 西安: 中国测绘学会, 2012. ZHOU Hui, LI Song, YANG Jinling, et al. Calculation of Centroid Correction Value of the Laser Corner Reflector Array of ZY-3[C]//Chinese Society for Geodesy Photogrammetry and Cartography 2012 Annual Conference. Xi'an: China Society of Surveying and Mapping, 2012. |


