2. 淮海工学院测绘与海洋信息学院, 江苏 连云港 222000
2. School of Geomatics and Marine Information, Huaihai Institute of Technology, Lianyungang 222000, China
在时空回归分析中,回归点与一定时空范围内的观测点有关,因此可以利用这些观测点计算回归点的拟合值[1]。时空地理加权回归是一个典型的时空回归分析方法,其步骤是先利用固定型带宽或调整型带宽准则[2]确定对回归点产生影响的观测点,再通过观测点与回归点之间的时空距离和权函数计算权重矩阵[3],最后采用加权最小二乘估计方法估算回归系数值和拟合值[4-5]。实践证明时空地理加权回归是探测时空非平稳特征的有效方法,应用广泛。文献[6]采用时空地理加权回归方法,在考虑了房价自身影响的情况下,研究了深圳市房价的时空非平稳变化情况;文献[7]利用时空地理加权回归方法建立了美国马里兰州巴尔的摩县的土地利用时空变化模型;文献[8]和[9]利用时空地理加权回归方法,研究了PM2.5、PM10的时空非平稳特征。
GTWR的加权最小二乘估计方法是在随机项方差相同且最小的假设条件下估计回归参数和拟合值,而现实中自变量的随机项方差是不相同的,因此基于加权最小二乘的GTWR估计结果会产生偏差。随机项方差不同又称异方差,它普遍存在时空分析中,例如房价变化,一线城市城区和郊区的房价差异,比二三线城市城区和郊区的波动性大,在考虑时间因素后,时空因素的变化对房价的波动影响也不相同。又例如人口变化,经济发展好的城市对人口的吸引力远大于经济条件一般的城市,随着时间的变化,这种人口增长差距更大。对于上述现象,基于加权最小二乘估计的时空地理加权回归方法分析结果会出现偏差。局部多项式估计是一种良好的非参数估计方法,可以消除异方差的影响,减小回归系数估计值偏差,提升拟合精度。文献[10]将局部多项式回归与地理加权回归(geographically weight regression,GWR)方法相结合,提出了局部线性地理加权回归方法;文献[11]在局部线性地理加权回归方法的基础上研究了回归方法的稳健性,并证明在采用局部多项式改进后,能有效消除异方差,提升估计精度。由于地理加权回归方法只涉及空间非平稳性[12],因此LGWR只能解决二维空间的异方差,而无法消除时间维度的影响,因此不能直接应用到GTWR方法估计。
为了消除时空地理加权回归中同方差假设带来的拟合偏差,本文借鉴局部线性地理加权回归方法原理,在充分考虑时间和空间的双重影响基础上,提出了局部多项式时空地理加权回归方法。重点介绍了利用三元一阶泰勒级数重构满足高斯—马尔可夫独立同分布假定要求的新时空地理加权回归方程原理,推导了新方程回归系数、拟合值与原方程回归系数、拟合值之间的关系,并给出了局部多项式时空地理加权回归方法的算法流程。此外,本文以LGWR和GTWR为对比方法,通过模拟数据和真实数据试验验证了LPGTWR在消除异方差方面的有效性。
1 GTWR原理GTWR假定回归系数是地理位置和观测时刻的任意函数[1, 13],公式如下
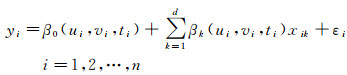 (1)
(1)
式中,(xi1, xi2, , …, xid; yi)表示观测点(ui, vi, ti), (i=1, 2, …, n)处的因变量y和自变量x1, x2, …, xd的n组观测值;βk(ui, vi, ti), (k=0, 1, …, d)是第i个数据点(ui, vi, ti)处的未知回归系数;各系数是观测点(ui, vi, ti)处的任意函数;(ε1, ε2, …, εn)为独立同分布的误差项,通常假定均值为零,方差为σ2。
根据加权最小二乘方法,第i个观测点的回归系数估计值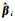
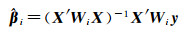 (2)
(2)
第i个观测点因变量的拟合值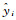
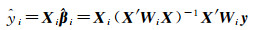 (3)
(3)
式中,Xi表示自变量X矩阵中的第i行向量Xi=(1, xi1, xi2, …, xip);Wi表示空间权重矩阵Wi= 
设定局部多项式时空地理加权回归模型的回归系数分别对横坐标u、纵坐标v和时间t存在连续的二阶偏导数。根据泰勒级数公式,回归系数βj(u, v, t)可以表示为在点(u0, v0, t0)的某邻域范围内的泰勒级数展开,表达式如下
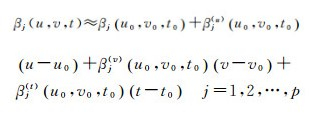 (4)
(4)
式中,βj(u)(u0, v0, t0)为回归系数βj(u0, v0, t0)在横坐标u方向的一阶偏导数;βj(v)(u0, v0, t0)为回归系数βj(u0, v0, t0)在纵坐标v方向的一阶偏导数;βj(t)(u0, v0, t0)为回归系数βj(u0, v0, t0)在时间t方向的一阶偏导数。
重新构建点(u0, v0, t0)的自变量矩阵X(u0, v0, t0)为n×4p阶矩阵
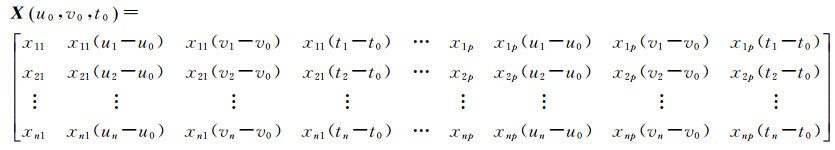 (5)
(5)
那么,回归系数列向量B(u0, v0, t0)可以表示为
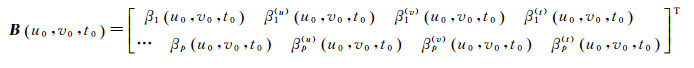 (6)
(6)
第j个回归系数、一阶偏导数和回归系数列向量B(u0, v0, t0)的关系可以表示为
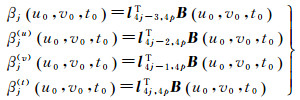 (7)
(7)
式中,l4j-3, 4pT为4p行列向量,其中第(4j-3)个元素为1,其他元素为0;l4j-2, 4pT为4p行列向量,其中第(4j-2)个元素为1,其他元素为0;l4j-1, 4pT为4p阶列向量,其中第(4j-1)个元素为1,其他元素为0;l4j, 4pT为4p行列向量,其中第4j个元素为1,其他元素为0。
因此,第i个点(ui, vi, ti)自变量和因变量的关系可以表示为
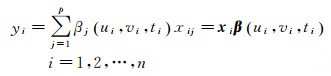 (8)
(8)
可得,
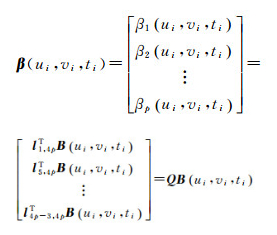 (9)
(9)
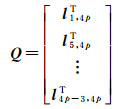 (10)
(10)
局部多项式时空地理加权回归的拟合值可以表示如下
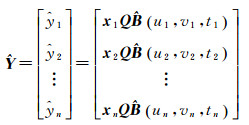 (11)
(11)
局部多项式时空地理加权回归模型基于泰勒级数展开重构自变量矩阵,利用重构的自变量矩阵和因变量建立了满足高斯-马尔可夫假定独立同分布要求的时空地理加权回归模型,新时空地理加权回归模型的拟合值可以利用加权最小二乘方法进行估计。因此,回归系数估计值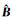
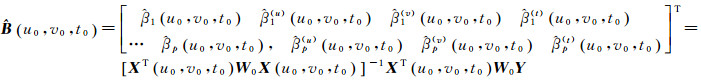 (12)
(12)
那么,第j项回归系数估计值可表示为
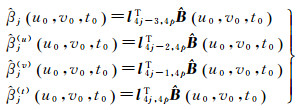 (13)
(13)
因此,回归系数估计值表达式可表示为
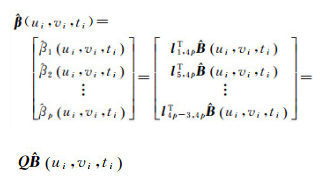 (14)
(14)
局部多项式时空地理加权回归方法因变量拟合值可以表达为
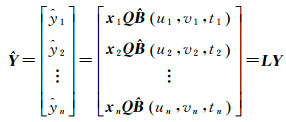 (15)
(15)
其中,L为帽子矩阵,矩阵形式如下
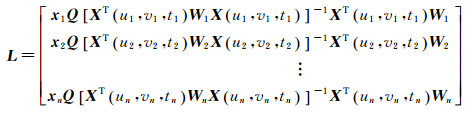 (16)
(16)
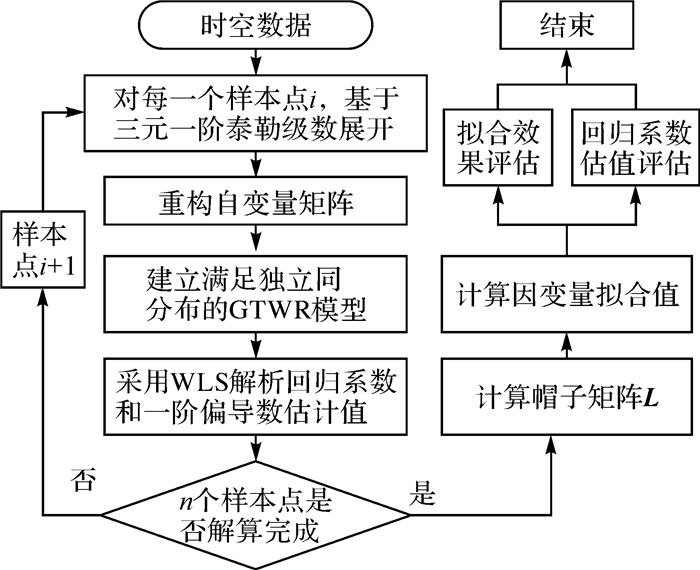
局部多项式时空地理加权回归方法的核心是将回归系数表示为其时空邻域范围内的三元一阶泰勒级数展开,通过剥离随机项方差影响,重新构建满足高斯—马尔可夫假定要求的新时空地理加权回归模型。根据泰勒级数展示式,能推导出原模型回归系数、拟合值与新模型回归系数、拟合值之间的关系,通过加权最小二乘解算出新模型回归系数和拟合值,即可估计原模型的回归系数和拟合值。为了更加清晰地阐述局部多项式时空地理加权回归方法的估计步骤,给出了算法流程如图 1所示。
|
| 图 1 LPGTWR流程图 Fig. 1 Flow chart of LPGTWR |
步骤1:对每个样本点(ui, vi, ti)第j个回归系数βj(ui, vi, ti), j=1, 2, …, p进行泰勒级数展开,表示为该点较小邻域范围内任意点(u0, v0, t0)的空间横坐标u0、纵坐标v0、时间t0一阶偏导βj(u)(u0, v0, t0)、βj(v)(u0, v0, t0)及βj(t)(u0, v0, t0)的线性组合。
步骤2:基于泰勒级数展开结果,重新设计自变量矩阵X。
步骤3:基于加权最小二乘估计方法,计算回归系数估计值,包括回归系数估计值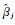
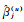
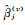
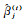
步骤4:循环完所有样本点,计算帽子矩阵L。
步骤5:求解因变量的拟合值 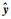
步骤6:计算拟合值评价指标和回归系数估计值评价指标,分析方法拟合精度。
算法结束。
3 试验及结果分析为了测试LPGTWR方法的性能,本文采用模拟数据和真实数据,以LGWR、GTWR作为对比方法,进行试验分析。模拟数据的回归系数和因变量的真值是已知,可以分析估计值与真实值的偏差,真实数据回归系数的真值是未知的,可以从模型估计的角度,评价LPGTWR模型的整体性能,从而多角度分析LPGTWR的性能,为方法应用提供参考和依据。
3.1 模拟数据试验 3.1.1 试验设置本文以u、v为平面坐标轴、以t为时间轴建立一个三维立体空间。设空间左下角为原点,立体空间每个坐标轴长度均为12单位长度,令u、v、t的取值分别为0,1,2,…,m-1,观测点均匀地分布在m×m×m的格点上,则空间内共有n=m3个观测点,观测点的坐标取值可以按照以式(17)计算
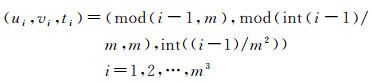 (17)
(17)
式中,mod(a, b)表示a除以b后的余数; int(a/b)表示a除以b后取整。
本文设计3组模型数据,其中自变量x1i、x2i是分布在(-4,4)之间的随机数;残差εi服从标准正态分布;回归系数β0、β1、β2与u、v、t相关,3组公式如下所示。
一组:
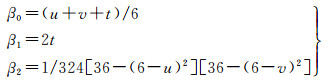
二组:
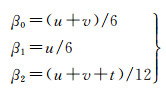
三组:
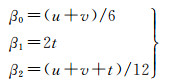
为了消除数据生成时产生的随机误差,每组数据生成10套,每个方法重复10次。本文采用Akaike信息法则(Akaike information criterion,AIC)[16]、平均均方误差(mean square error,MSE)和回归系数估计偏差作为评价指标,分析方法的适用性、整体估计效果和回归系数估计偏差。其中,回归系数估计偏差是指是回归系数的真实值和估计值之间的偏差统计量[10]。试验采用交叉验证法(cross validation,CV)确定最优带宽和时空参数[17],表 1记录了10组模拟数据在LGWR、GTWR和LPGTWR方法估计下的AIC平均值。一般地,当两个模型的AIC值相差3时,说明模型之间存在明显差异,且AIC最小值对应的模型是最优模型[18]。
| 模拟数据 | LGWR | GTWR | LPGTWR | LPGTWR与LGWR对比 | LPGTWR与GTWR对比 |
| 一组 | 5708.245 | 2981.257 | 2582.006 | 3126.239 | 399.251 |
| 二组 | 2264.925 | 2239.549 | 2231.584 | 33.341 | 7.965 |
| 三组 | 5701.105 | 2478.47 | 2218.583 | 3482.522 | 259.887 |
由表 1可知,3组模拟数据下,LPGTWR方法都取得了最小的AIC值,说明LPGTWR比LGWR和GTWR的适用性更好。对于同一个方法,二组模拟数据结果较好,一组数据结果最差,说明数据复杂程度对方法有影响,数据越简单,模拟效果越好,数据越复杂,模拟效越果差。从LPGTWR性能提升情况看,三组数据AIC值相差均大于3,且LPGTWR/LGWR性能提升幅度比LPGTWR/GTWR幅度大,说明除了异方差外,时间也是影响估计精度的重要因素。
表 2给出了10套模拟数据在LGWR、GTWR和LPGTWR下的平均MSE值。平均MSE值越小,说明估计值越接近真实值,方法的整体估计效果越好。由表 2可知:首先,LPGTWR方法在三组数据中取得了最小平均MSE,说明LPGTWR方法整体估计效果优于GTWR、GTWR。其次,二组模拟数据在3种方法下估计效果比较稳定,而一组和三组模拟数据,LGWR方法误差很大,说明数据复杂性和时间因素,给LGWR方法带来了干扰,而相对于LGWR,GTWR和LPGTWR方法考虑了时间因素,能给出较稳定的估计结果。最后,LPGTWR比LGWR和GTWR平均MSE性能提升比率大于14%,说明LPGTWR方法在处理异方差后,明显提升了整体估计精度。
| 模拟数据 | LGWR | GTWR | LPGTWR | LPGTWR与LGWR对比/(%) | LPGTWR与GTWR对比/(%) |
| 一组 | 140.4986 | 1.558552 | 1.224298 | 99.13 | 21.45 |
| 二组 | 1.256519 | 1.067717 | 0.898352 | 28.50 | 15.86 |
| 三组 | 139.8823 | 1.02706 | 0.882689 | 99.39 | 14.06 |
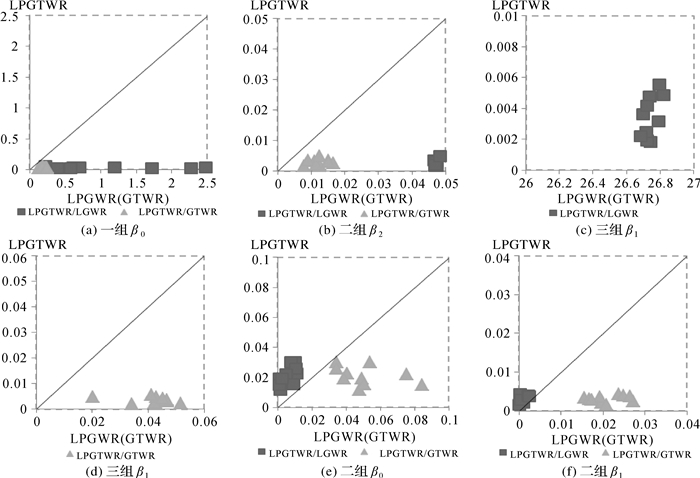
图 2绘制了3种方法的回归系数估计偏差分布图。其中,图 2(a)、图 2(b)表示局部时空变回归系数估计偏差;图 2(c)、图 2(d)表示局部时间变回归系数估计偏差; 图 2(e)、图 2(f)表示局部空间变回归系数估计偏差。图中纵轴表示LPGTWR的回归系数估计偏差,横轴表示LGWR或GTWR的回归系数估计偏差,散点表示10次试验结果。当散点靠近横标时,说明横轴的方法估计偏差大于纵轴方法的估计偏差,即纵轴方法优于横轴方法。反之,说明横轴方法优于纵轴方法。分析图 2可知,对于局部时空变回归系数和局部时间变回归系数,LPGTWR优于GTWR和LGWR方法,GTWR方法优于LGWR。对于局部空间变回归系数,LGWR方法优于LPGTWR和GTWR方法。这说明在时空回归分析中,时间对模型精度的影响比重大于异方差,在考虑时间因素的前提下,局部多项式时空地理加权回归方法能提升估计精度。
|
| 图 2 回归系数估计偏差分布图 Fig. 2 The coefficient estimation bias of simulated data |
3.2 真实数据试验及结果分析
本文以长江中下游地区人口密度分布与影响因素关系作为真实数据进行试验。研究发现人口密度分布与自然条件、土地利用以及社会经济等因素相关[19-21]。本文收集了2000年、2005年、2010年、2015年长江中下游各地市人均GDP(元/人)、年均降水量(mm)、年均气温(℃)、耕地面积(km2)、林地面积(km2)、城乡工矿居民用地面积(km2)和平原面积(km2)等7个特征变量。其中,人均GDP指区域GDP总产值除以区域常住人口数。时空因素包括空间位置坐标和时间,空间上采用WGS84坐标系,高斯克里格投影,时间设置2000年为基准年用1表示,每增加1年增加一个单位。长江中下游地区行政区划矢量数据来源于地图出版社;各地市的人口数和GDP来源于各省统计年鉴;土地利用数据来源于中国科学院资源环境科学数据中心。
为了建立可靠的人口密度分布模型,需要选择相关性强的变量。在普通线性回归分析中,一般采用逐步回归方法建立最优模型[22]。在地理加权回归分析中,文献[18]基于最小AIC准则,穷举了所有变量组合进行建模,以最小AIC值模型为最优模型。本文采用逐步回归的迭代方式,以AIC最小作为评价准则选取变量进行建模。经过多重共线性分析和变量选取,确定人均GDP、年均气温和城乡工矿居民用地面积为自变量,人口密度为因变量,分别建立LGWR、GTWR和LPGTWR模型。文本采用拟合优度(R2)、调整型拟合优度(R2adj)、MSE、误差项平方和(sum of squares for error,SSE)作为评价指标[23],结果如表 3所示。
| 方法 | R2 | R2adj | MSE | SSE |
| LGWR | 0.7114 | 0.7072 | 0.0363 | 7.5568 |
| GTWR | 0.8152 | 0.8116 | 0.0234 | 4.8396 |
| LPGTWR | 0.8828 | 0.8805 | 0.0148 | 3.0686 |
| LPGTWR/LGWR improvement/(%) | 24.09 | 24.51 | 59.23 | 59.39 |
| LPGTWR/GTWR improvement/(%) | 8.29 | 8.49 | 36.75 | 36.59 |
结果显示,3种方法R2均大于0.71,说明3种方法都能建立可靠的模型来估算人口密度。从整体建模情况看,LPGTWR方法的拟合优度达0.8828,比LGWR方法提升了24.09%,比GTWR方法提升了8.29%,调整拟合优度为0.8805,比LGWR方法提升了24.51%,比GTWR方法提升了8.49%,说明LPGTWR建立的模型最优。从估计偏差情况看,LPGTWR方法的均方差为0.0148,比LGWR方法提升了59.23%,比GTWR方法提升了36.75%,LPGTWR方法的误差项平方和为3.0686,比LGWR方法提升了59.39%,比GTWR方法提升了36.59%,上述指标均说明LPGTWR方法的整体估计偏差小,结果优于GTWR、LGWR方法。综上所述,真实数据试验说明LPGTWR方法相比GTWR和LGWR方法,能建立更优的模型,减小整体估计偏差,得到更可靠的结果。
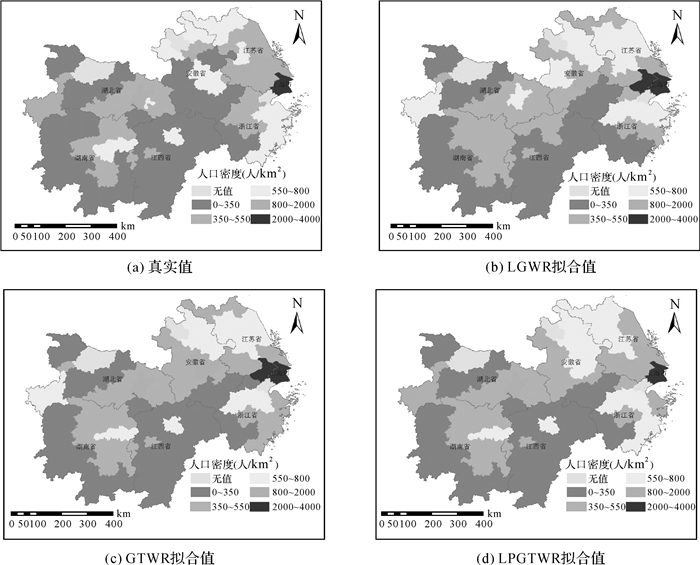
图 3绘制了2015年长江中下游地区人口密度的真值、LGWR拟合值、GTWR拟合值和LPGTWR拟合值。观察图可知,在上海、湖北西部地区,LPGTWR方法的预测结果相比LGWR和GTWR方法更接近真实情况。但3种方法在安徽西部、北部地区预测误差较大。通过进一步研究发现,安徽北部蚌埠市、宿州市和亳州市2015年人口相对2000年分别增长了14.45%、17.74%和25.01%,而15年来上海市增长了50.09%。相对上海市该地区人口的时空变化波动程度并不明显,而且该地区的时空非平稳特征也不显著,即异方差和时空非平稳性对该地区人口密度变化影响程度并不显著,因此预测结果存在偏差。
|
| 图 3 2015年长江中下游地区人口密度分布图 Fig. 3 The population distribution of middle and lower reaches of the Yangtze River |
4 结语
本文提出了一种局部多项式时空地理加权回归方法,它利用三元一阶泰勒级数展开式和加权最小二乘估计的原理,将回归系数定义为真值和在空间坐标轴和时间方向的偏差,通过剥离空间和时间维度的偏差来消除随机项方差,进而解决时空地理加权回归无法处理异方差的问题。本文介绍了局部多项式时空地理加权回归方法的原理,给出了算法流程,并通过模拟数据和真实数据对LPGTWR进行了测试。模拟数据试验从适用性、整体估计效果和回归系数估计偏差3个角度验证了LPGTWR方法优于GTWR和LGWR,特别是在时空非平稳情况下,LPGTWR能显著提升拟合精度。真实数据试验验证了LPGTWR方法的有效性,且其拟合结果在时空维度最接近真实情况。局部多项式时空地理加权回归方法是利用数学方法提升时空回归拟合精度的时空回归方法,本文在人口密度及影响因素分析中进行了验证,未来希望能在更多领域推广应用。
| [1] | HUANG Bo, WU Bo, BARRY M. Geographically and Temporally Weighted Regression for Modeling Spatio-temporal Variation in House Prices[J]. International Journal of Geographical Information Science, 2010, 24(3): 383–401. DOI:10.1080/13658810802672469 |
| [2] | BRUNSDON C, FOTHERINGHAM A S, CHARLTON M E. Geographically Weighted Regression:A Method for Exploring Spatial Nonstationarity[J]. Geographical Analysis, 1996, 28(4): 281–298. |
| [3] |
覃文忠. 地理加权回归基本理论与应用研究[D]. 上海: 同济大学, 2007. QIN Wenzhong. The Basic Theoretics and Application Research on Geographically Weighted Regression[D]. Shanghai: Tongji University, 2007. |
| [4] | BRUNSDON C, AITKIN M, FOTHERINGHAM A S, et al. A Comparison of Random Coefficient Modelling and Geographically Weighted Regression for Spatially Non-stationary Regression Problems[J]. Geographical and Environmental Modelling, 1999, 3(1): 47–62. |
| [5] | FOTHERINGHAM A S, BRUNSDON C, CHARLTON M. Geographically Weighted Regression:the Analysis of Spatially Varying Relationships[M]. New York: John Wiley & Sons, 2002: 34-45. |
| [6] | WU Bo, LI Rongrong, HUANG Bo. A Geographically and Temporally Weighted Autoregressive Model with Application to Housing Prices[J]. International Journal of Geographical Information Science, 2014, 28(5): 1186–1204. DOI:10.1080/13658816.2013.878463 |
| [7] | WRENN D H, SAM A G. Geographically and Temporally Weighted Likelihood Regression:Exploring the Spatiotemporal Determinants of Land Use Change[J]. Regional Science and Urban Economics, 2014, 44: 60–74. DOI:10.1016/j.regsciurbeco.2013.10.005 |
| [8] | BAI Yang, WU Lixin, QIN Kai, et al. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2. 5 Estimation from Satellite-derived 500 m Resolution AOD[J]. Remote Sensing, 2016, 8(3): 262. |
| [9] | CHU H J, HUANG Bo, LIN C Y. Modeling the Spatio-temporal Heterogeneity in the PM10-PM2.5 Relationship[J]. Atmospheric Environment, 2015, 102: 176–182. DOI:10.1016/j.atmosenv.2014.11.062 |
| [10] | WANG Ning, MEI Changlin, YAN Xiaodong. Local Linear Estimation of Spatially Varying Coefficient Models:An Improvement on the Geographically Weighted Regression Technique[J]. Environment and Planning A:Economy and Space, 2008, 40(4): 986–1005. DOI:10.1068/a3941 |
| [11] | ZHANG Huiguo, MEI Changlin. Local Least Absolute Deviation Estimation of Spatially Varying Coefficient Models:Robust Geographically Weighted Regression Approaches[J]. International Journal of Geographical Information Science, 2011, 25(9): 1467–1489. DOI:10.1080/13658816.2010.528420 |
| [12] | BRUNSDON C, FOTHERINGHAM A S, CHARLTON M. Some Notes on Parametric Significance Tests for Geographically Weighted Regression[J]. Journal of Regional Science, 1999, 39(3): 497–524. DOI:10.1111/0022-4146.00146 |
| [13] |
刘美玲. 时空地理加权回归模型的统计诊断[D]. 西安: 西安建筑科技大学, 2013. LIU Meiling. Statistical Diagnostics in Geographically and Temporally Weighted Regression Models[D]. Xi'an: Xi'an University of Architecture and Technology, 2013. |
| [14] |
黄砚玲. 地理加权空间经济计量模型的GMM估计及区域金融发展收敛性实证研究[D]. 广州: 华南理工大学, 2012. HUANG Yanling. GMM Estimate for SGWR Model and a Spatial Analysis of Regional Financial Convergence in China[D]. Guangzhou: South China University of Technology, 2012. |
| [15] |
杨毅. 顾及时空非平稳性的地理加权回归方法研究[D]. 武汉: 武汉大学, 2016. YANG Yi. Research on Geographically and Temporally Weighted Regression for Spatial and Temporal Nonstationarity[D]. Wuhan: Wuhan University, 2016. |
| [16] | HURVICH C M, SIMONOFF J S, TSAI C L. Smoothing Parameter Selection in Nonparametric Regression Using an Improved Akaike Information Criterion[J]. Journal of The Royal Statistical Society:Series B, 1998, 60(2): 271–293. DOI:10.1111/1467-9868.00125 |
| [17] | CLEVELAND W S. Robust Locally Weighted Regression and Smoothing Scatterplots[J]. Journal of the American Statistical Association, 1979, 74(368): 829–836. DOI:10.1080/01621459.1979.10481038 |
| [18] | LU Binbin, CHARLTON M, HARRIS P, et al. Geographically Weighted Regression with a Non-euclidean Distance Metric:A Case Study Using Hedonic House Price Data[J]. International Journal of Geographical Information Science, 2014, 28(4): 660–681. DOI:10.1080/13658816.2013.865739 |
| [19] |
柏中强, 王卷乐, 杨雅萍, 等.
基于乡镇尺度的中国25省区人口分布特征及影响因素[J]. 地理学报, 2015, 70(8): 1229–1242.
BAI Zhongqiang, WANG Juanle, YANG Yaping, et al. Characterizing Spatial Patterns of Population Distribution at Township Level across the 25 Provinces in China[J]. Acta Geographica Sinica, 2015, 70(8): 1229–1242. |
| [20] |
戚伟, 李颖, 刘盛和, 等.
城市昼夜人口空间分布的估算及其特征——以北京市海淀区为例[J]. 地理学报, 2013, 68(10): 1344–1356.
QI Wei, LI Ying, LIU Shenghe, et al. Estimation of Urban Population at Daytime and Nighttime and Analyses of Their Spatial Pattern:A Case Study of Haidian District, Beijing[J]. Acta Geographica Sinica, 2013, 68(10): 1344–1356. DOI:10.11821/dlxb201310004 |
| [21] |
鲁楠, 张委伟, 陈利军, 等.
顾及城乡差异的大区域人口密度估算——以山东省为例[J]. 测绘学报, 2015, 44(12): 1384–1391.
LU Nan, ZHANG Weiwei, CHEN Lijun, et al. Estimation of Large Regional Urban and Rural Population Density Based on the Differences of Population Distribution between Urban and Rural:Take Shandong Province as Example[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1384–1391. DOI:10.11947/j.AGCS.2015.20150005 |
| [22] |
陈彦光.
基于Matlab的地理数据分析[M]. 北京: 高等教育出版社, 2012: 34-45.
CHEN Yanguang. Geographical Data Analysis with Matlab[M]. Beijing: Higher Education Press, 2012: 34-45. |
| [23] | SONG Weize, JIA Haifeng, HUANG Jingfeng, et al. A Satellite-based Geographically Weighted Regression Model for Regional PM2.5 Estimation over the Pearl River Delta Region in China[J]. Remote Sensing of Environment, 2014, 154: 1–7. DOI:10.1016/j.rse.2014.08.008 |



