2. 武汉大学测绘学院, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
土地覆盖及其变化等地理类别信息是研究生态、环境系统变化的前提和依据,为地理国情监测中土地利用规划、资源利用政策和可持续发展等研究提供支持[1]。从遥感影像提取的土地覆盖信息,包括某时间点的静态空间分布和某时间段的动态变化特征。后者亦称为土地覆盖变化检测[2],指利用不同时期的遥感数据,定量地分析和确定地表覆盖变化的特征与过程[3]。作为地理国情监测持续生产力和长远发展的基础和保障,地理类别信息的精度验证是地理空间信息研究中不可或缺的组成部分[4-5]。从遥感影像分类得到的土地覆盖及其变化等地理类别信息的精度评估与分析,不仅能够为用户进行土地覆盖信息适用性评价提供依据,甄选出具有使用价值的信息产品和分析结果,还能为生产者进行信息提取方法和流程的优化提供参考信息,更好地服务于空间分析与应用[6]。
研究表明,地理类别(如土地覆盖与变化)的误分概率具有一定的空间分布规律和格局[7]。于是,有必要进行局域精度评估,以客观反映分类精度的空间差异性[8]。土地覆盖变化信息局域精度评估是指,将土地覆盖变化分类图与能够代表地面实况的参考数据(相对真值)进行比较,获得样本点正确分类与否的信息,以对非样本点位置的局域精度进行空间预测的过程。这里的局域精度定义为研究区影像上像元正确分类的概率。不同于总体(全局)的,或者基于特定类别的精度评估,针对特定点位的局域精度评估不仅可以描述随着空间位置变化的精度,识别特定类别中需要进行详细调查的地面区域,而且有助于改善分类器性能,提高信息融合的有效性[9]。
目前,面向单时相局域精度的评估方法主要分为生产者方法和用户方法。前者包括概率区间法[10]、最大后验概率法[11]和重采样法[12],而后者主要包括克里金插值[13]和逻辑回归分析[14]。土地覆盖变化信息的精度评估较单时相更为复杂,相关的研究相对缺乏。这是因为,单时相影像的分类精度会直接影响变化信息的精度,反映同一点位不同时相分类正确与否的二项分布的随机变量之间是相关的,无法直接以单时相正确分类概率的简单乘积作为变化检测正确分类的概率[15]。上述的概率区间法和最大后验概率法用于变化信息精度评估时,要求单时相的分类精度已经通过某种方法估算;重采样法虽然在一定程度上减轻了对验证样本的需求,但是将其扩展到变化信息精度评估时,对多时相影像和训练样本的要求较高[16]。属于用户方法的克里金插值由于过分依赖样本点本身数据质量导致其在模拟复杂景观下的土地覆盖变化检测精度时受到限制;类似的改进算法,比如指示协同克里金法,仍然无法解决该问题[17]。利用逻辑回归模型估计变化检测精度的研究,主要是基于变化检测误差发生率与影响因子(如单时相分类精度估计值、光谱数据、空间位置和景观特征等)的关系[18],这里的影响因子也称为解释变量或协变量;适于用户的逻辑回归方法可以使用的协变量是空间位置和基于待评估地图派生的景观特征等。
土地覆盖变化信息局域精度评估的核心是通过分类数据和参考数据相比较,以获取土地覆盖变化信息分类情况和地面真实情况的一致程度。一般无法对整幅分类影像进行逐像元正确分类与否的检验,而是利用一定样本对分类误差进行估计。然而,不同的抽样设计与精度评估结果的可靠性息息相关[19]。理论上来说,样本量的增加有利于提高精度评估的准确性,但是样本点自身的复杂性以及它们之间的相关性使得常用的抽样方法采集的样本存在信息冗余,使得采集的样本对精度评估结果的贡献作用无法与抽样成本相匹配。同时,常用的抽样方法在样本的确定及空间布样方面具有随机性,会影响变化信息局域精度评估的准确性[20-21]。相对于盲目地从整个研究区域搜索最优抽样点,更明智的方法是,基于现有的抽样算法,选择合适的抽样优化准则,实现提高采样效益与减小不确定性的统一[22-23]。因此,如何选择合理的抽样方案,提高面向土地覆盖变化信息局域精度评估的抽样效率是值得研究的问题。
本文的研究面向土地覆盖信息的用户,所采用的策略是直接将待研究地图上土地覆盖变化局部特征作为解释变量,以有限的样本数据建立逻辑回归模型进行局域精度预测。其中,抽样方法为重点研究对象。针对预测精度的准确性评价指标在提取预测结果可靠性有待提高的区域和样本布局中的作用,提出基于预测精度标准误差的自适应型抽样策略,在现有的样本点、增加样本点所需预算以及要求的预测精度的基础上,进行渐进式的样本采集,以提高抽样的效率,进而减少土地覆盖变化信息预测精度的不确定性。
1 研究方法 1.1 Logistic回归模型本文主要讨论表示土地覆盖变化类别正确分类与否的二值数据,对于一个类别变量C(x)来说,区域A中的指示变量I(x)可以表示为
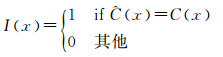 (1)
(1)
式中,C(x)和Ĉ(x)分别表示位置x(x∈A)处真实的和预测的土地覆盖变化类别。这是对样本点处正确分类与否信息的二进制编码,相应的局部均值表示像元x正确分类的概率:π(x)=prob{I(x)=1}。
作为常用的广义线性模型,Logistic回归模型是一种典型的概率和离散选择模型,能够建立二值变量(如正确分类与否)与相应的协变量之间的定量关系[24-25],从而用于在一定条件下事件发生与否的概率分析研究。其函数形式为
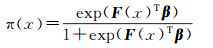 (2)
(2)
式中,β为回归系数向量;向量F(x)=(F0(x)=1, F1(x), …, FQ(x))T表示参与回归建模的协变量(F的大小为1+Q>1),Q指除了常数项之外用到的协变量总数。对于前面提到的指示变量I(x)组成的指示型随机场{I(x), x∈A},其局部均值可以通过建立一系列协变量(如局部类别发生格局指标)的组合向量F的logit模型得到。对π(x)作logit变换(用η表示),建立与协变量F的线性关系
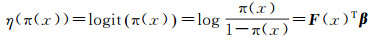 (3)
(3)
选择最大似然估计法得到回归参数的估计值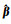

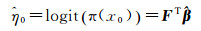 (4)
(4)
根据式(4)推导出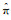
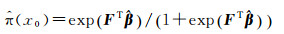 (5)
(5)
对应的估计方差为
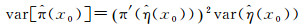 (6)
(6)
则标准误差为
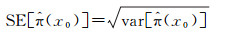 (7)
(7)
式中
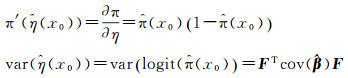
在现有的训练样本、增加采样所需预算以及要求的预测精度的基础上,基于预测精度准确性评价指标制订合理的自适应型抽样策略[28]:
(1) 基于已有的n个训练样本xi(i=1, 2, …, n),构建空间预测模型,对研究区域内的m个未知点x0j(j=1, 2, …, m)进行精度估计;
(2) 计算未知点x0j(jj=1, 2, …, m)处的估计方差σ2以及相应的标准误差SEj(j=1, 2, …, m);
(3) 按照预测精度的标准误差SEj由大到小的顺序对未知点x0j(j=1, 2, …, m)进行排序,得到集合x0j′(j′=1, 2, …, m);
(4) 选择集合x0j′(j′=1, 2, …, m)中前l个点的位置,即标准误差较大的l个点,进行增加样本的采集;
(5) 将l个增加样本加入已有的样本点xi(i=1, 2, …, n)组成新的训练样本集,重新构建空间预测模型。
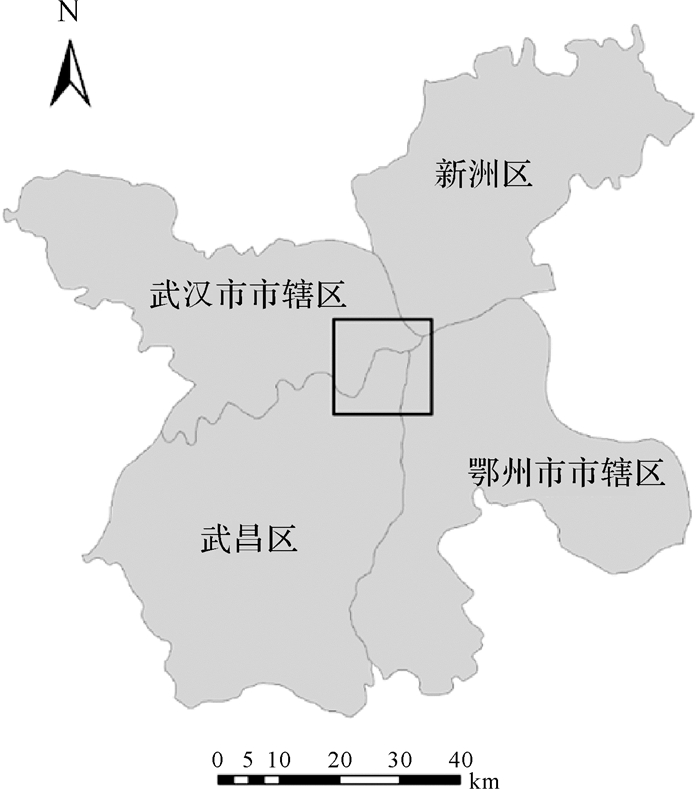
2 试验结果及分析 2.1 数据源研究区域位于湖北省武汉市与鄂州市交界处,属于武汉城市圈,地处长江中下游平原,江汉平原东部,地跨113°41′E—115°05′E,29°58′N—31°22′N。地形以建筑用地、植被和水体为主。试验采用2013年10月(Time1)和2016年10月(Time2)的空间分辨率为30m的Landsat 8 ETM+影像,选择5、4、3波段的合成影像,用于获取土地覆盖变化信息。裁剪适当大小的研究区域,如图 1中的矩形框,涵盖了281358个像素(522行×539列),每个像素大小为30m×30m。图 2(a)和2(b)分别为2013年和2016年Landsat8 ETM+影像上的裁剪区域。
|
| 图 1 研究区域位置 Fig. 1 Location of study area |

|
| 图 2 试验数据 Fig. 2 The experiment data B-建筑用地;F-森林;S-裸地;V-植被;W-水体 |
综合考虑上述研究区域信息、土地利用信息和影像有限的空间分辨率,基于局部土地覆盖及其驱动力研究,在单时相影像上选择包括以下5种土地覆盖类别的分类体系:裸地、水体、建筑用地、森林和植被。利用分类后比较法获得土地覆盖变化信息,首先对两个时相的影像分别进行分类,Time1和Time2的分类影像如图 2(c)和图 2(d)所示。然后对分类结果进行比较,判断各个像素位置对应的变化类别,创建一个特定的描述变化趋势的变化地图,如图 2(e)所示。图 2(e)中4种变化类别包括裸地到建筑用地、建筑用地到裸地、植被到裸地以及植被到建筑用地的转变。这些变化发生的主要原因是:①城市化发展,裸地和植被转变为建筑用地;②拆迁使得建筑用地转化为裸地;③城市规划中植被转变为裸地的现象,是为了城镇化建设做准备。
基于变化影像,遵循简单随机抽样原则抽取454个训练样本和446个测试样本,分别用于模型建立和局域精度预测模型的验证。此外,抽取300个备选样本,用于说明本文提出的自适应抽样方法在提高变化信息精度预测结果可靠性方面的有效性。
2.2 土地覆盖变化信息精度评估 2.2.1 解释变量研究表明,土地覆盖变化类别(Class)、斑块大小(L10B)、异质性(HET)和优势度(DMG)等景观格局指数与类别信息精度评估结果有关[7]。现直接以图 2(e)中的变化影像作为研究对象,针对描述单个像元分类正确与否信息的指示值,选择像元尺度(即中心像元3×3邻域内)景观格局指数的不同组合作为协变量,构建变化信息精度预测的Logistic回归模型。其中,Class是用二值变量表示类别[29];斑块大小(L10B)用邻域范围内与中心像元类别相同的连续像元数量表示,反映了局部斑块的破碎程度和邻域内类别纯度[30];异质性(HET)是指景观要素及其属性在空间分布上的不均匀性和复杂性,由中心像元邻域内出现的类别种类决定[31];优势度(DMG)反映区域土地覆盖中某种或某些类别支配区域土地覆盖的程度,本文将文献[29]提到的景观级别的优势度指数拓展到局部邻域尺度,并定义为异质性的对数形式与邻域内类别发生率的熵之间的差值
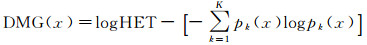 (8)
(8)
式中,pk表示像元邻域内类别k的边缘概率。
2.2.2 模型选择根据式(1)将训练样本上变化类别分类正确与否信息进行二值编码,以上述景观格局指数的不同组合作为协变量F,根据式(2)建立逐像素变化类别正确分类概率预测的逻辑回归模型。采用似然比检验法对模型进行显著性检验,选择含有最多有效解释变量的模型(α=0.01)。表 1给出增加一个额外的协变量(或一组协变量)F+1,模型显著性检验的结果。
| 卡方检验(df) | 描述:新的参数F+1对于已含有参数Fq的模型是否显著 | deviance之差 | 在α =0.01条件下是否显著 | |
| Fq | F+1 | |||
| D0-D1a(8) | 1 | Class | 167.669 | Yes |
| D0-D1b(1) | 1 | L10B | 34.351 | Yes |
| D0-D1c(1) | 1 | HET | 45.6294 | Yes |
| D0-D1d(1) | 1 | DMG | 52.122 | Yes |
| D1a-D2a(1) | 1 & Class | L10B | 3.263 | Yes |
| D1a-D2b(1) | 1 & Class | HET | 7.926 | Yes |
| D1a-D2c(1) | 1 & Class | DMG | 11.399 | Yes |
| D2c-D3a(1) | 1 & Class & DMG | L10B | 1.354 | No |
| D2c-D3b(1) | 1 & Class & DMG | HET | 1.269 | No |
| 注:Dm是模型m的deviance;模型描述见表 1;F0=1表示仅含有常数项β0。 | ||||
根据表 1,本文选择的协变量在α=0.01条件下均显著;向含有Class的模型中加入局部格局指数L10B、HET和DMG,除了模型2a(1 & Class & L10B),模型2b(1 & Class & DMG)和模型2c(1 & Class & DMG)仍然符合显著性的标准(α=0.01),但是与不含有Class的模型比较,这些变量更加显著。这是因为协变量对预测结果的驱动作用受Class的影响,其中,模型2c的结果最显著(α=0.01);为了检验含有Class和DMG的模型是否最优,向模型2c中分别增加L10B和HET,在α=0.01条件下不显著。所以模型2c(1 & Class & DMG)是含有最多显著性参数的模型,拟合优度最佳。
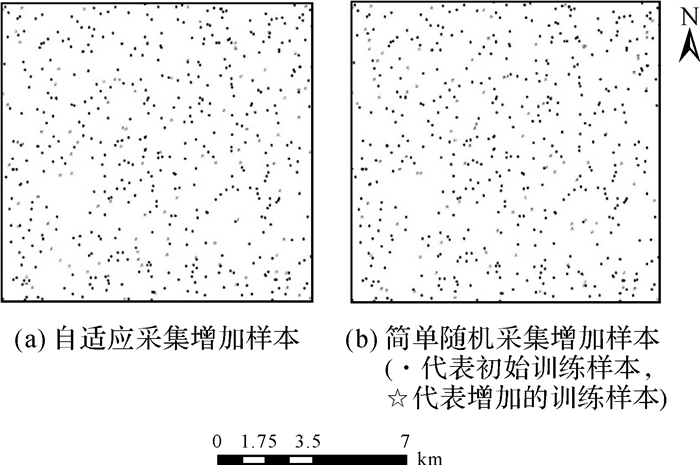
2.3 面向精度预测的自适应型抽样以Class和DMG作为协变量F,基于初始训练样本构建逻辑回归模型(式(2)),得到变化信息正确分类概率的预测表面(式(5))和回归估计的标准误差表面(式(7)),如图 4(a)和图 5(a)。之后以自适应抽样策略和简单随机抽样策略,分别从300个备选样本中抽取100个增加样本,组成新的训练样本集,如图 3(a)和3(b)。随机抽样策略下的概率预测表面和标准误差表面如图 4(b)和图 5(b),自适应抽样策略下的概率预测表面和标准误差表面如图 4(c)和图 5(c)。
|
| 图 3 初始样本和增加样本分布 Fig. 3 Location of initial samples and extra training samples |

|
| 图 4 基于不同训练样本的变化检测正确分类概率预测图 Fig. 4 The probability maps generated by different training samples |

|
| 图 5 基于不同训练样本的回归估计的标准误差图 Fig. 5 Maps of prediction standard errors by different training samples |
图 4中颜色偏浅的区域表示变化类别正确分类概率的预测精度较高,大多对应于图 2(e)中的未变化类别,而变化类别的可分性较差,预测精度较低,在图 4上颜色较深。
由图 5可以看出,对于土地覆盖变化信息精度预测的逻辑回归模型来说,增加训练样本,无论是随机抽取还是自适应抽取,预测精度的标准误差均减小,表现为图 5(b)和图 5(c)比图 5(a)暗。就子图像来说,变化类别所在区域回归估计的标准误差较大,精度预测结果的可靠性较弱,是增加面向提高精度预测抽样效率优先考虑的位置。
为了客观说明自适应抽样方法对于土地覆盖变化信息精度预测结果的影响,基于相同的测试样本,对不同抽样方法下模型的预测精度进行质量评价,结果如2.4节所示。
2.4 精度评价选择指标:平均绝对误差(MAE)、均方根误差(RMSE)和确定系数(RSS2)对预测精度进行定量评价[32],如式(9)—(11)
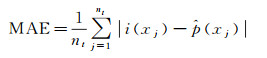 (9)
(9)
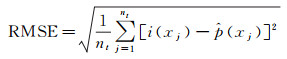 (10)
(10)
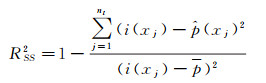 (11)
(11)
式中,i(xj)为实际观测值;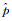
表 2为不同训练样本下预测精度的定量评价结果。
| MAE | RMSE | RSS2 | |
| 初始训练样本 | 0.335 | 0.409 | 0.302 |
| (基于额外的训练样本) | |||
| 随机抽样 | 0.329 | 0.402 | 0.354 |
| 自适应型抽样 | 0.327 | 0.400 | 0.455 |
根据表 2,得出以下结论:
(1) 相对于初始训练样本,增加额外的训练样本使得预测结果的RSS2值增大,MAE和RMSE值减小,说明变化信息正确分类概率的预测精度提高;
(2) 自适应型抽样策略比随机抽样策略的成本效益好,以RSS2指标为例,基于自适应型抽样策略增加100个训练样本使得模型预测精度的RSS2值提高了50.66%,而随机抽样策略下,增加同样大小的训练样本使得RSS2值提高了17.22%。
此外,采用Delong非参数检验法比较预测精度对应的受试者工作特征(ROC)曲线下的面积AUC,从统计学角度分析不同抽样策略对于土地覆盖变化信息精度预测结果的影响[33]。
根据表 3,两种不同方式下采集的增加样本使得预测精度的AUC值在统计意义上均显著优于初始训练样本下的结果,而自适应抽样策略下的结果显著优于随机抽样策略,这也符合表 2中的结果。
| 对比组1 | 对比组2 | p值 |
| 初始训练样本 | (基于额外的训练样本)随机抽样 | < 0.05 |
| 初始训练样本 | (基于额外的训练样本)自适应抽样 | < 0.05 |
| (基于额外的训练样本)随机抽样 | (基于额外的训练样本)自适应抽样 | < 0.05 |
综上所述,样本量的增加有利于提高预测精度的准确性,但不同抽样方法采集的增加样本对于提高模型预测精度的贡献不同。自适应型抽样策略综合考虑了估计值的不确定性与空间分布,选取具有代表性、预测精度标准误差较大的样本对模型进行训练,减小了回归估计的标准误差,提高了面向土地覆盖变化信息精度评估的抽样效率。
3 结论本文直接以待研究地图上土地覆盖变化信息局部特征作为解释变量,探讨了与土地覆盖变化信息精度预测显著相关的协变量,以有限的样本数据建立土地覆盖变化信息局域精度评估的逻辑回归模型,并提出将预测精度的标准误差作为判断标准,在初始样本数据欠采样的环境下,以自适应的方式采集增加的训练样本。试验表明,自适应型抽样策略提高了面向土地覆盖变化信息精度评估的抽样效益。同时,本文选择的景观格局指数均与土地覆盖变化信息精度预测显著相关,其中,土地覆盖变化类别(Class)和优势度指数(DMG)是“最优”的协变量组合。
| [1] |
陈军, 陈利军, 李然, 等.
基于-GlobeLand30的全球城乡建设用地空间分布与变化统计分析[J]. 测绘学报, 2015, 44(11): 1181–1188.
CHEN Jun, CHEN Lijun, LI Ran, et al. Spatial Distribution and Ten Years Change of Global Built-up Areas Derived from GlobeLand30[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1181–1188. DOI:10.11947/j.AGCS.2015.20140677 |
| [2] | FOODY G M. Assessing the Accuracy of Land Cover Change with Imperfect Ground Reference Data[J]. Remote Sensing of Environment, 2010, 114(10): 2271–2285. DOI:10.1016/j.rse.2010.05.003 |
| [3] |
明冬萍, 邱玉芳, 周文.
遥感模式分类中的空间统计学应用——以面向对象的遥感影像农田提取为例[J]. 测绘学报, 2016, 45(7): 825–833.
MING Dongping, QIU Yufang, ZHOU Wen. Applying Spatial Statistics into Remote Sensing Pattern Recognition:with Case Study of Cropland Extraction Based on GeOBIA[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 825–833. DOI:10.11947/j.AGCS.2016.20150520 |
| [4] | TSENDBAZAR N E, DE BRUIN S D, HEROLD M. Assessing Global Land Cover Reference Datasets for Different User Communities[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 103: 93–114. |
| [5] |
陈军, 陈晋, 宫鹏, 等.
全球地表覆盖高分辨率遥感制图[J]. 地理信息世界, 2011, 9(2): 12–14.
CHEN Jun, CHEN Jin, GONG Peng, et al. Higher Resolution Global Land Cover Mapping[J]. Geomatics World, 2011, 9(2): 12–14. |
| [6] | FOODY G M. Status of Land Cover Classification Accuracy Assessment[J]. Remote Sensing of Environment, 2002, 80(1): 185–201. DOI:10.1016/S0034-4257(01)00295-4 |
| [7] | SMITH J H, STEHMAN S V, WICKHAM J D, et al. Effects of Landscape Characteristics on Land-cover Class Accuracy[J]. Remote Sensing of Environment, 2003, 84(3): 342–349. DOI:10.1016/S0034-4257(02)00126-8 |
| [8] | GOODCHILD M F, GUOQING S, SHIREN Y. Development and Test of an Error Model for Categorical Data[J]. International Journal of Geographical Information Systems, 1992, 6(2): 87–103. DOI:10.1080/02693799208901898 |
| [9] | BURNICKI A C. Modeling the Probability of Misclassification in a Map of Land Cover Change[J]. Photogrammetric Engineering & Remote Sensing, 2011, 77(1): 39–49. |
| [10] | PONTIUS R G JR, LI X X. Land Transition Estimates from Erroneous Maps[J]. Journal of Land Use Science, 2010, 5(1): 31–44. DOI:10.1080/17474230903222473 |
| [11] | ZHANG Jingxiong, ATKINSON P M, GOODCHILD M F. Scale in Spatial Information and Analysis[M]. Boca Raton, FL: CRC Press, 2014. |
| [12] | STEELE B M, WINNE J C, REDMOND R L. Estimation and Mapping of Misclassification Probabilities for Thematic Land Cover Maps[J]. Remote Sensing of Environment, 1998, 66(2): 192–202. DOI:10.1016/S0034-4257(98)00061-3 |
| [13] |
陈志强, 陈健飞.
福建土地利用/覆被人为影响指数及其变化的地统计学分析[J]. 资源科学, 2008, 30(11): 1700–1705.
CHEN Zhiqiang, CHEN Jianfei. Geostatistical Analysis of Human Impact Indexes for Land Use/Cover Change in Fujian[J]. Resources Science, 2008, 30(11): 1700–1705. DOI:10.3321/j.issn:1007-7588.2008.11.012 |
| [14] |
王库.
回归克里格在土壤全氮空间预测上的应用[J]. 中国农学通报, 2013, 29(20): 142–147.
WANG Ku. Application of Regression Kriging on the Spatial Prediction of Total Soil Nitrogen[J]. Chinese Agricultural Science Bulletin, 2013, 29(20): 142–147. DOI:10.11924/j.issn.1000-6850.2012-2473 |
| [15] | CARMEL Y, FLATHER C H, DEAN D J. Combining Location and Classification Error Sources for Estimating Multi-Temporal Database Accuracy[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67(7): 865–872. |
| [16] | KEMPEN B, BRUS D J, HEUVELINK G B M. Soil Type Mapping Using the Generalised Linear Geostatistical Model:A Case Study in a Dutch Cultivated Peatland[J]. Geoderma, 2012, 189-190: 540–553. DOI:10.1016/j.geoderma.2012.05.028 |
| [17] | EMERY X. A Disjunctive Kriging Program for Assessing Point-Support Conditional Distributions[J]. Computers & Geosciences, 2006, 32(7): 965–983. |
| [18] | BURNICKI A C. Impact of Error on Landscape Pattern Analyses Performed on Land-cover Change Maps[J]. Landscape Ecology, 2012, 27(5): 713–729. DOI:10.1007/s10980-012-9719-2 |
| [19] |
孟雯, 童小华, 谢欢, 等.
基于空间抽样的区域地表覆盖遥感制图产品精度评估——以中国陕西省为例[J]. 地球信息科学学报, 2015, 17(6): 742–749.
MENG Wen, TONG Xiaohua, XIE Huan, et al. Accuracy Assessment for Regional Land Cover Remote Sensing Mapping Product Based on Spatial Sampling:A Case Study of Shaanxi Province, China[J]. Journal of Geo-Information Science, 2015, 17(6): 742–749. |
| [20] | LECHNER A M, LANGFORD W T, BEKESSY S A, et al. Are Landscape Ecologists Addressing Uncertainty in Their Remote Sensing Data?[J]. Landscape Ecology, 2012, 27(9): 1249–1261. DOI:10.1007/s10980-012-9791-7 |
| [21] |
柏延臣, 王劲峰.
遥感数据专题分类不确定性评价研究:进展、问题与展望[J]. 地球科学进展, 2005, 20(11): 1218–1225.
BO Yanchen, WANG Jinfeng. Assessment on Uncertainty in Remotely Sensed Data Classification:Progresses, Problems and Prospects[J]. Advances in Earth Science, 2005, 20(11): 1218–1225. |
| [22] |
张景雄, GOODCHILDM F.
野外空间采样的渐进式策略[J]. 武汉大学学报(信息科学版), 2008, 33(5): 441–445.
ZHANG Jingxiong, GOODCHILD M F. Towards Progressive Strategies for Spatial Sampling in the Field[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 441–445. |
| [23] | MODIS K, PAPAODYSSEUS K. Theoretical Estimation of the Critical Sampling Size for Homogeneous Ore Bodies with Small Nugget Effect[J]. Mathematical Geology, 2006, 38(4): 489–501. DOI:10.1007/s11004-005-9020-x |
| [24] |
农宇, 王坤, 杜清运.
利用多分类Logistic回归进行土地利用变化模拟——以湖北省嘉鱼县为例[J]. 武汉大学学报(信息科学版), 2011, 36(6): 743–746.
NONG Yu, WANG Kun, DU Qingyun. Modeling Land Use Change Using Multinomial Logistic Regression[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6): 743–746. |
| [25] | HENGL T, HEUVELINK G B M, ROSSITER D G. About Regression-Kriging:from Equations to Case Studies[J]. Computers & Geosciences, 2007, 33(10): 1301–1315. |
| [26] | AGRESTI A. Categorical Data Analysis[M]. 3rd ed. Hoboken, NJ: Wiley, 2013: 58-65. |
| [27] | GOTWAY C A, STROUP W W. A Generalized Linear Model Approach to Spatial Data Analysis and Prediction[J]. Journal of Agricultural, Biological, and Environmental Statistics, 1997, 2(2): 157–178. DOI:10.2307/1400401 |
| [28] | ZHANG Jingxiong, MEI Yingying. Integrating Logistic Regression and Geostatistics for User-oriented and Uncertainty-Informed Accuracy Characterization in Remotely-Sensed Land Cover Change Information[J]. ISPRS International Journal of Geo-Information, 2016, 5(7): 113. DOI:10.3390/ijgi5070113 |
| [29] | VAN OORT P A J, BREGT A K, DE BRUIN S, et al. Spatial Variability in Classification Accuracy of Agricultural Crops in the Dutch National Land-cover Database[J]. International Journal of Geographical Information Science, 2004, 18(6): 611–626. DOI:10.1080/13658810410001701969 |
| [30] | SMITH J H, STEHMAN S V, WICKHAM J D. Impacts of Patch Size and Land-cover Heterogeneity on Thematic Image Classification Accuracy[J]. Photogrammetric Engineering and Remote Sensing, 2002, 68(1): 65–70. |
| [31] | LU Dengsheng, BATISTELLA M, MORAN E, et al. Fractional Forest Cover Mapping in the Brazilian Amazon with a Combination of MODIS and TM Images[J]. International Journal of Remote Sensing, 2011, 32(22): 7131–7149. DOI:10.1080/01431161.2010.519004 |
| [32] |
马京振, 孙群, 肖强, 等.
河南省GlobeLand30数据精度评价及对比分析[J]. 地球信息科学学报, 2016, 18(11): 1563–1572.
MA Jingzhen, SUN Qun, XIAO Qiang, et al. Accuracy Assessment and Comparative Analysis of GlobeLand30 Dataset in Henan Province[J]. Journal of Geo-Information Science, 2016, 18(11): 1563–1572. |
| [33] |
杨波, 程泽凯, 秦锋.
用AUC评估分类器的预测性能[J]. 情报学报, 2007, 26(2): 275–279.
YANG Bo, CHENG Zekai, QIN Feng. Using AUC to Evaluate Predictive Performance of Classifiers[J]. Journal of the China Society for Scientific and Technical Information, 2007, 26(2): 275–279. |



