2. 北京卫星导航中心, 北京 100094;
3. 中国科学院大学地球科学学院, 北京 100049;
4. 总装备部工程设计研究总院, 北京 100028
2. Beijing Satellite Navigation Center, Beijing 100049, China;
3. College of Earth Science, University of Chinese Academy of Sciences, Beijing 100049, China;
4. Center for Engineering Design and Research under the Headquarter of General Equipment, Beijing 100028, China
为了描述电离层的特性和变化规律,自20世纪60年代开始不断有电离层全球经验模型产生。IRI(international reference ionosphere)模型是IRI工作组基于非相干散射雷达、卫星观测、探空火箭和大量的地面观测资料给出的,该模型描述了地磁活动平稳情况下的电离层变化规律[1-3]。Bent模型则是根据卫星测量数据、测站坐标、F2层峰值模型等统计出的一种经验模型,可以描述电离层不同剖面的电子密度变化情况[1-3]。自20世纪80年代以来,随着GNSS电离层实测数据的广泛使用,美国GPS采用Klobuchar提出的全球电离层模型进行电离层修正。该模型具有系数简单便于应用的优点,但只能反映电离层变化的大趋势,对于中纬度地区修正效果较差,只能达到50%左右[1-2]。2006年,文献[2]提出了一种改进Klobuchar模型,将8参数模型改为14参数模型,提高了中纬度地区的修正精度,然而由于模型本身的建模特点,改进Klobuchar模型也并不能提供高精度的电离层修正[2]。
球谐函数可用于全球的电离层模型化研究,避免了以往多项式模型的“边缘效应”。文献[3]使用4阶球谐函数模型在局部地区精度可以达到3 TECU以下[3]。CODE(Center for Orbit Determina-tion in Europe)采用15阶球谐函数构建全球电离层模型,对外发布谱系数和电离层格网数据,但并没有详细阐述电离层球谐模型高阶变化的量级和规律[1]。文献[4]针对BDS系统的特点,以中国区测站为主、境外站为辅的原则,基于2002—2007年全球GPS观测数据建立了全球电离层TEC球谐模型,并进行了相关论证与分析,构建了适用中国区域的球谐模型[4]。
电离层预报问题也是电离层研究的重要方向。文献[5-6]基于ARMA模型进行了电离层预报研究,其方法可以归结为直接法和间接法两种,在12 d内,两种方法的预报效果相差不大[7-8],但是如果作为卫星导航系统发播参数,间接法形成的模型预报系数则有很好的参数固化优势[9]。
本文将轮胎调和分析的理论与方法应用于电离层TEC的模型化,并通过分析球谐系数时间序列的变化规律,建立电离层TEC的轮胎调和分析模型并实现对电离层TEC的预报。同时利用试验验证不同模型、方法达到的应用效果,以期为BDS系统电离层产品的系统化设计提供支持。
1 全球电离层TEC的轮胎调和分析基于文献[10]提出的轮胎面调和分析方法,本文利用5°间隔的CODE格网数据,建立36阶电离层TEC的轮胎调和分析模型,并分析电离层TEC的谱变化特征与变化规律。式(1)为阶数和格网关系[11]
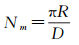 (1)
(1)
式中,Nm为阶数;D为格网间隔(km);R为地球平均半径(km)。
需要说明的是, 由于CODE格网是使用GPS全球连续测量数据进行15阶球谐分析后,再继续格网化的产物,所以格网已经丢失了15阶后的高频信息,而综合探空、GPS、雷达的原始电离层测量数据现阶段没有发布者,所以36阶球谐分析求解出的15阶后系数不具备统计意义,现阶段只有算法研究意义。
1.1 电离层TEC的球谐谱表示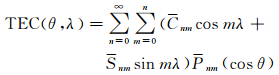 (2)
(2)
式中,Cnm和Snm为电离层TEC球谐模型的谱系数;Pnm(cos θ)为完全正常化缔合勒让德函数;θ,λ为极距和地心经度。
根据TEC单层模型的假定,本文将距地面高度350 km的球面作为边界面求解边值问题,得到电离层TEC球谐模型的谱系数Cnm和Snm,构成了基于球面的调和分析问题,具体数学流程如图 1。

|
| 图 1 电离层TEC轮胎调和分析流程 Fig. 1 Flow diagram of ionospheric TEC torus harmonic analysis |
根据文献[10, 12]关于轮胎调和分析在重力学中的使用,现推导电离层轮胎调和分析的具体公式。
由式(2),将极距θ的定义域扩充到[0, 2π],可将球面数据TEC(i, j)映射到轮胎面上的数据TECp(i, j)。原理是球面区域定义域的改变,可理解为将球面和一个180°的球面共同映射成一个轮胎面几何图形[10, 12]。TECp(i, j)的公式为
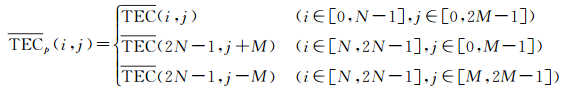 (3)
(3)
完成球面到轮胎面的转化后,再进行FFT变换,得到轮胎面上基于平均值等距B样条插值的二维Fourier谱c(k, m)。根据二维Fourier谱c(k, m),可计算实数谱[10, 12] ap(k, m)、bp(k, m),公式为
 (4)
(4)
 (5)
(5)
进而根据调和分析的原理[10, 12-14],可得谱系数(Cnm, Snm)的解算公式
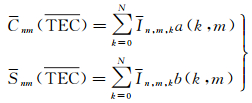 (6)
(6)
式中
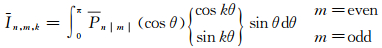
至此,给出了利用轮胎调和分析求解电离层球谐模型的实用解算式。
1.2 全球电离层TEC的谱能变化特性利用CODE发布的UTC 2011年1月1日全天共13套(每两小时发布一次)全球电离层格网数据,按照轮胎调和分析流程解算出了模型谱系数(Cnm, Snm)。由于模型谱系数(Cnm, Snm)难以直观展现,所以在之后的分析中使用阶方差来反映模型阶数与谱系数量级之间的关系[12]。公式为
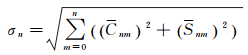 (7)
(7)
式中,Cnm和Snm即为计算所得的模型谱系数。
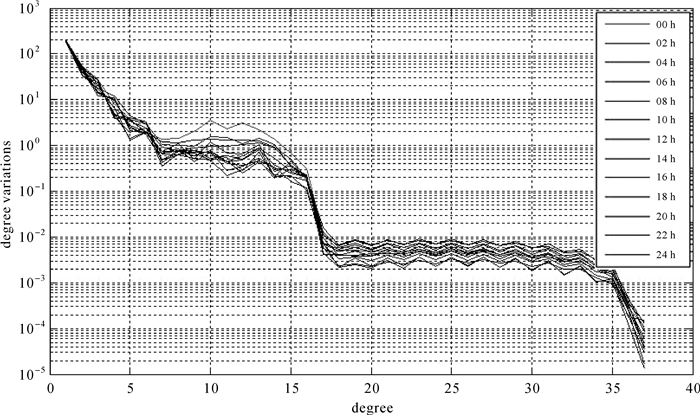
图 2为UTC 2011年1月1日13套电离层球谐模型对应的阶方差曲线图。
|
| 图 2 2011年1月1日阶方差图 Fig. 2 Degree variations to the ionospheric model on January 1, 2011 |
由图 2可知阶方差曲线的变化主要表现在5个区间:第1区间为0~7阶,此区间代表电离层的基本变化周期,阶方差量级较大达到100~102 TECU量级,为电离层变化的基本项;第2区间为7~15阶,阶方差在10-1~100 TECU的量级,此区间内日变化幅度明显较大,主要表现电离层的日变化规律。由于CODE所提供的格网数据是15阶球谐模型格网化后的产品,因此本文不再分析15阶之后的信号变化特征。通过阶方差也可知:Wilkson的低阶球谐模型取值3阶明显阶数过低,丢失了101~100 TECU量级的电离层信息。
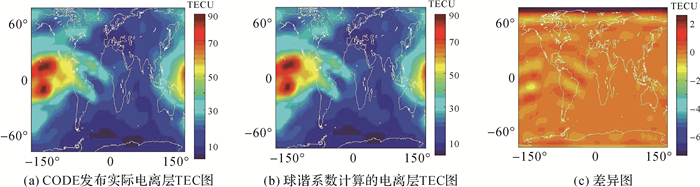
1.3 球谐系数计算格网值与实际格网值的差异根据1.2节得到的球谐系数,可由式(2)计算出格网点上的模型值。本文用UTC2011年1月1日00时对应的球谐模型值与CODE发布的格网值进行对比,见图 3。
|
| 图 3 实际电离层TEC与球谐系数计算电离层TEC的对比图 Fig. 3 Comparison chart of actual Ionospheric TEC and computational Ionospheric TEC |
由图 3可知:球谐系数计算出的电离层TEC(θ, λ)具有较高的精度,在电离层比较活跃的北纬30°至南纬30°区域内误差在1 TECU以内。总体来看,实际电离层格网图的TEC总量为52 138.4 TECU,球谐系数计算的电离层格网图TEC总量为52 542.7 TECU,相对误差为2.18%。经统计,全年电离层TEC球谐模型的相对误差小于4%。
通过图 3还可以观察在北极区域,球谐函数模型计算的TECU值和实际格网TECU值存在约-6.8 TECU的差值,这是由于北极地区存在电离层变化梯度带,球谐模型在该地区适应性差。理论上南极也应该出现类似情况,但由于南极大量海洋地区没有穿刺点,数据由插值补白得到,相关性较强而梯度较小,因此图中没有出现。
2 电离层TEC球谐系数时间序列的函数估计根据1.2节计算出的球谐系数,本文使用逐级余差的思想分别对趋势项、周期项和随机波动项进行函数估计,以期得出完整的电离层球谐系数时间序列模型[7-8, 15]。为实现电离层球谐模型系数预报的目的,需对每组球谐系数的时间序列进行函数估计。
设球谐系数的时间序列模型关系为
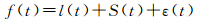 (8)
(8)
式中,f(t)为球谐系数的时间序列函数;l(t)为趋势项;S(t)为周期项;ε(t)为随机波动。
2.1 基于趋势函数特征的电离层球谐系数时间序列趋势函数估计由于趋势项l(t)具有持续向上或持续向下变动的特征,所以设l(t)的函数表达式为[7, 15]
 (9)
(9)
限于篇幅,本文仅以一年时间的电离层球谐系数C00为例。由样本序列估计出的C00趋势函数为
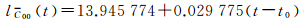 (10)
(10)
在趋势项确定后,理论上样本序列中已无趋势变化。剩余样本序列应表现以周期性为主的波动特性。这也引出了周期函数估计的问题。
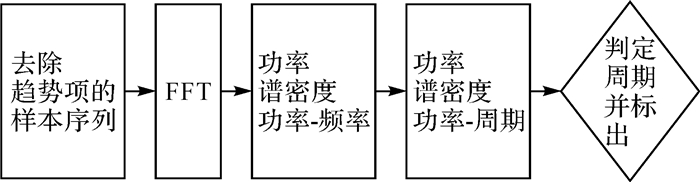
2.2 基于功率谱密度的电离层球谐系数时间序列周期函数估计周期项S(t)呈现周期性的变化特征,又因样本序列在减去趋势项后,可能包含不止一个周期的作用,所以首先要进行谱分析找出其主要周期,再利用它们各自的特点建立模型实现预报[7, 15],具体过程见图 4。
|
| 图 4 FFT周期分析流程 Fig. 4 Flow diagram of FFT periodic analysis |
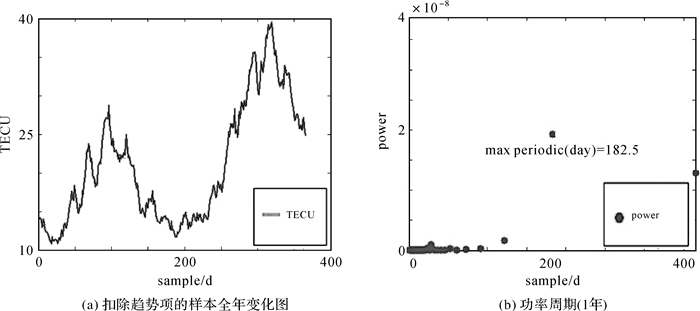
按照图 4中的流程,对每组球谐系数的周期性特征进行分析。现以C0, 0系数为例,给出扣除趋势项后的样本变化曲线、功率周期图,见图 5。
|
| 图 5 球谐系数C0, 0扣除趋势项后的功率与周期图 Fig. 5 Power and periodic diagram of C0, 0 without remove trend term |
图 6给出各阶球谐系数Cnm对应的最大周期:0~7阶可以看到365 d的年周期、182.5 d的半年周期和1 d的日周期,该区间主要受电离层的日变化影响;7~16阶可以看到除年、半年周期、日周期外,还有一个121.6 d的周期存在,该区间受年周期的影响明显变大;第3、4、5区间由于量级很小,也在数据分辨率之外,故不作具体分析。通过图 6的数据对照电离层的空间物理特性[1-4],可以得到全年电离层TEC的主要周期,见表 1。

|
| 图 6 球谐系数Cnm扣除趋势项后的最显著周期图 Fig. 6 The most prominent periodic diagram of Cnmwithout remove trend term |
| 周期/d | 周期成因 |
| 365 | 太阳的周年活动 |
| 182.502 | 4月、10月出现极值的半年变化 |
| 91.253 | 一年中四季的季节性变化 |
| 28.055 | 太阳黑子随太阳自转产生的辐射变化 |
| 14.772 | 月亮自转的影响 |
| 1 | 日变化 |
| 121.667 | 未知的变化周期 |
根据表 1中的周期建立函数模型,以三角函数表示周期项
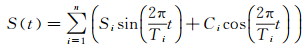 (11)
(11)
式中,S(t)为总的周期项影响;n为各种周期影响总数;Ti为周期;Ci、Si为对应的第i个周期函数系数。
依据最小二乘多余观测估计原理,可求系数Ci、Si。在解出周期性函数模型之后,电离层球谐系数时间序列中的趋势项和周期项理论上已经消除。为了更清楚地验证周期函数性能,本文利用求得的周期函数模型计算2011年全年电离层球谐系数C00消除了趋势项l(t)的时间序列,并与扣除趋势项样本值做差,残差具有随机波动特性,如图 7所示。

|
| 图 7 C0, 0项的周期函数恢复值与扣除趋势项的样本序列图 Fig. 7 Periodic function recovery value of C0, 0 and sample series to remove trend term |
由图 7可知,恢复值并不能完全与样本值吻合,因此引入对于序列中无法确定趋势项、周期项的随机波动数据的估计方法。
2.3 基于ARMA模型的电离层球谐系数时间序列随机波动估计去除趋势项、周期项后的样本数据可视为随机波动,本文使用文献[7, 16]使用的ARMA模型进行分析。在ARMA模型中,可将随机波动的数据序列看作一个随机序列ε(t),它的特性体现着ε(t)随机波动在时域上的延续。ARMA(p, q)的模型[16]为
 (12)
(12)
式中,A(q)为q阶的自回归系数多项式;C(q)为q阶的滑动平均系数多项式。
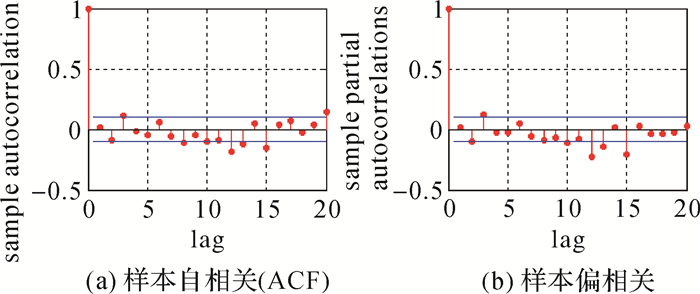
随机波动样本进行历元间差分后,需要通过自相关、偏相关函数判断模型特性,以便建立预测模型[16]。图 8是利用C00系数全年变化的ε(t)随机波动为样本序列,进行的自相关和偏相关估计。
|
| 图 8 C00差分样本序列的自相关与偏相关图 Fig. 8 Autocorrelation and partial correlation diagram of C00 |
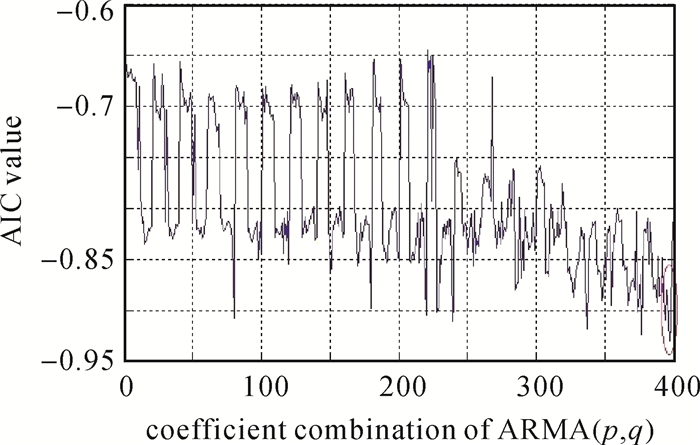
由图 8可知,样本数据自相关、偏相关自始至终表现出很强的相关性,这与ARMA模型特性相符合,所以模型可用。ARMA(p, q)的系数可利用AIC准则进行优选[16]。图 9是样本序列进行AIC选择的结果,最小的AIC值在第397个组合ARMA(20,17),所以该组合可以达到数值最优。使用该模型对随机波动进行模型化,并通过与ε(t)样本的互差检验ARMA模型的性能,精度如图 10。
|
| 图 9 C00差分样本序列的AIC值图 Fig. 9 The AIC values of C00 sample series |

|
| 图 10 ARMA恢复值和扣除趋势项、周期项的样本序列图 Fig. 10 ARMA recovery value and sample series to remove trend term and periodic terms |
2.4 电离层TEC球谐系数时间序列模型的性能分析
基于上文介绍的原理,现写出电离层TEC球谐模型系数的时间序列模型
 (13)
(13)
应用该模型分别计算2011年全年电离层球谐模型前15阶系数的间序列模型f(t),并验证模型性能,具体见图 11(以C0, 0系数为例)。

|
| 图 11 球谐系数C0, 0模型恢复值和样本值差异图 Fig. 11 The differences between model recovery values and sample values of C0, 0 |
图 11中球谐系数C0, 0模型恢复值和样本值的差异,实质上就是所建球谐模型与观测数据的差异。C0, 0的模型平均残差为2×10-1 TECU量级,其他系数的统计结果为:C1, 0、C1, 1在1×10-1 TECU量级,模型系数末端的C15, 15为1×10-3 TECU量级。这些残差表明本文构建的球谐模型反演精度较高。
3 电离层TEC球谐系数模型的预报下面通过预测的球谐模型系数和式(2)计算电离层TEC值,讨论预报TEC和实际TEC差异。
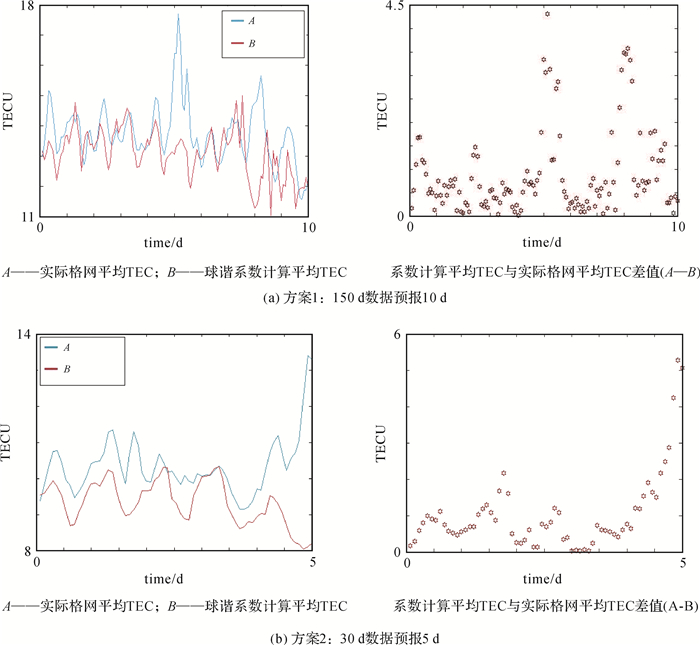
3.1 电离层TEC格网的整体预测性能试验中分别采用150 d(UTC2011-01-01—2011-05-30)预报10 d(UTC2011-05-31—2011-06-09)和30 d(UTC2011-01-01—2011-01-30)预报5 d(UTC2011-01-31—2011-02-04)两个预报方案,对全部格网点的TEC值求平均,讨论格网的整体精度,并分析所有格网点TEC预测平均值的误差变化情况,见图 12、表 2。
|
| 图 12 实际格网平均值与球谐预测系数计算格网平均值图 Fig. 12 Actual average TEC of grid data and computational TEC with spherical harmonic coefficients |
| 方案 | 预报残差/TECU | 相对误差/(%) |
| 150 d积累数据预报10 d | 0.879 6 | 6.40 |
| 30 d积累数据预报5 d | 1.012 2 | 9.79 |
150 d模型预报10 d的整体误差平均为每个格网点0.879 6 TECU,相对误差为6.40%;30 d模型预报5 d的整体误差平均为每个格网点在1.012 2 TECU,相对为9.79%。
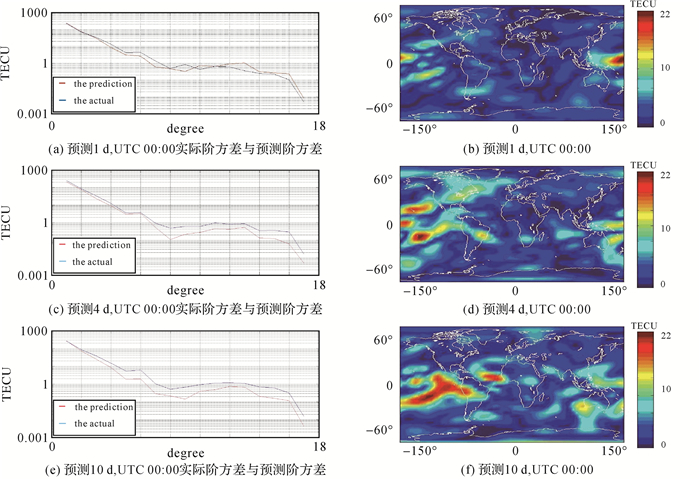
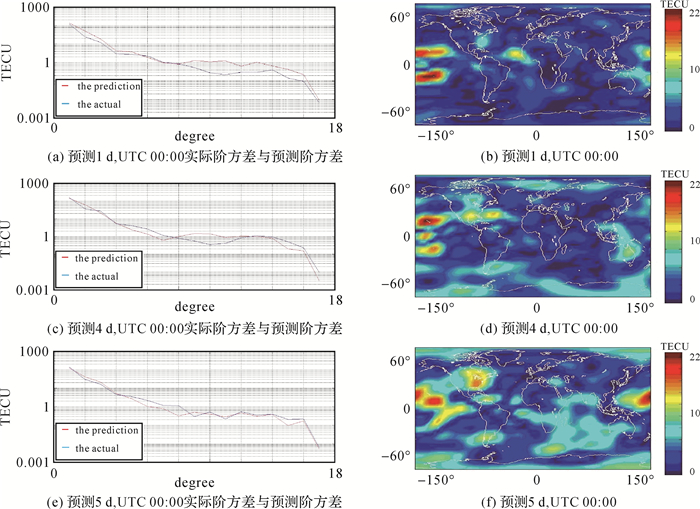
3.2 电离层TEC格网预测残差的全球分布趋势为了方便观察全球电离层的预报效果,对全球电离层的预测误差进行了计算,并且给出了相应的阶方差图,见图 13、图 14。
|
| 图 13 方案1:150 d预测1 d、4 d、10 d计算格网值与实际格网差异 Fig. 13 Scheme 1: the prediction errors of ionospheric TEC as predicting 1 days, 4 days, 10 days with 150 days |
|
| 图 14 方案2:30 d预测1 d、4 d、5 d计算格网值与实际格网差异 Fig. 14 Scheme 2: the prediction errors of ionospheric TEC as predicting 1 day, 4 days, 5 days with 30 days |
通过表 2、图 13、图 14可知两种方案相比较,方案1的主阶项整体趋势预报效果更好,且格网平均残差也更小,这是由于长时间数据构建的模型更能体现电离层活动的长期变化趋势,所以预报龄期较长。同时结合图 12、图 13、图 14可以得出结论:在数据积累时间选择上,新的时间序列模型应该考虑长期性能和短期性能,即对于长期预报用模型(如精密电离层全球模型),尽量使用长期数据进行预报;对于反映实时性的短期模型(如导航系统发播模型),应该尽量选用短期数据进行预报。
4 结论与展望本文利用轮胎面的调和分析方法建立了电离层TEC球谐模型,分析了电离层TEC的模型谱系数变化特征与变化规律,并对模型的适用性进行了探讨,结果表明除南、北极区外球谐模型有很好的适用性,模型拟合逼近精度高。此外还讨论了球谐系数时间序列的函数估计问题,对趋势项、周期项和随机波动的各自特征进行了相应的函数估计。通过对预报出的电离层格网点误差进行统计,可知150 d数据预报10 d的相对误差约为6.40%,30 d预报5 d的相对误差约为9.79%。电离层TEC格网预测误差的全球分布趋势结果还表明:在数据积累时间选择上,球谐系数类模型应该针对不同用途考虑不同的数据积累时间。精密型模型建议使用长时间的数据积累,而实时性模型则建议使用短时间数据积累进行预报。
本文使用的数据仅为一年的电离层观测数据,模型精度有一定的局限性。下一步将考虑利用一个太阳活动周期的数据来分析电离层TEC的周期特征,进一步精化电离层球谐模型参数,从而提高电离层模型的预报精度。
致谢: 感谢CODE提供的电离层格网数据。
| [1] |
袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉: 中国科学院研究生院(测量与地球物理研究所), 2002. YUAN Yunbin. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS[D]. Wuhan: Graduate University of Chinese Academy of Sciences (Institute of Surveying and Geophysics), 2002. http://cdmd.cnki.com.cn/Article/CDMD-80057-2003040660.htm |
| [2] |
章红平, 平劲松, 朱文耀, 等.
电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16–26.
ZHANG Hongping, PING Jinsong, ZHU Wenyao, et al. Brief Review of the Ionospheric Delay Models[J]. Progress in Astronomy, 2006, 24(1): 16–26. |
| [3] |
柳景斌. 基于地基GPS的区域电离层TEC球冠谐分析及预报[D]. 武汉: 武汉大学, 2008. LIU Jingbin. Modeling and Predication of Regional Ionospheric TEC based on SCHA Methodology Using Ground-based GPS[D]. Wuhan: Wuhan University, 2008. |
| [4] |
霍星亮. 基于GNSS的电离层形态监测与延迟模型研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2008. HUO Xingliang. Research on Ionospheric Morphology Monitoring and Delay Model Based on GNSS[D]. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2008. |
| [5] |
刘军, 柴洪洲, 刘先冬, 等.
基于ARIMA(p, 1, 1)的电离层预报模型[J]. 大地测量与地球动力学, 2010, 30(2): 79–82.
LIU Jun, CHAI Hongzhou, LIU Xiandong, et al. A Predicting Model of Ionospheric Based on ARIMA (p, 1, 1)[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 79–82. |
| [6] |
张小红, 任晓东, 吴风波, 等.
自回归移动平均模型的电离层总电子含量短期预报[J]. 测绘学报, 2014, 43(2): 118–124.
ZHANG Xiaohong, REN Xiaodong, WU Fengbo, et al. Short-term TEC Prediction of Ionosphere Based on ARIMA Model[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2): 118–124. DOI:10.13485/j.cnki.11-2089.2014.0018 |
| [7] |
李志刚, 程宗颐, 冯初刚, 等.
电离层预报模型研究[J]. 地球物理学报, 2007, 50(2): 327–337.
LI Zhigang, CHENG Zongyi, FENG Chugang, et al. A Study of Prediction Models for Ionosphere[J]. Chinese Journal of Geophysics, 2007, 50(2): 327–337. |
| [8] |
李志刚, 李伟超, 程宗颐, 等.
电离层TEC预报的直接法和间接法及其比较[J]. 天文学报, 2008, 49(1): 29–44.
LI Zhigang, LI Weichao, CHENG Zongyi, et al. Direct and Indirect Methods on Predicting Ionosphere and Their Compare[J]. Acta Astronomica Sinica, 2008, 49(1): 29–44. |
| [9] |
李猛. 卫星导航定位系统主控站数据处理相关问题研究[D]. 武汉: 国防科学技术大学, 2008. LI Meng. Research on Master Control Station Data Processing of Satellite Navigation System[D]. Wuhan: National University of Defense Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-90002-2009214149.htm |
| [10] |
张传定, 许厚泽, 吴星. 地球重力场调和分析中的"轮胎"问题[C]//《大地测量与地球动力学进展》论文集. [s. l. ]: 湖北省科学技术协会, 2004. ZHANG Chuanding, XU Houze, WU Xing. On the Torus Approach for Global Spherical Harmonic Computation[C]//Advances in Geodetic and Earth Dynamics. [s. l. ]: Hubei Science and Technology Association, 2004. |
| [11] |
刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州: 信息工程大学, 2011. LIU Xiaogang. Theory and Methods of the Earth's Gravity Field Model Recovery from GOCE Data[D]. Zhengzhou: Information Engineering University, 2011. http://www.cqvip.com/QK/90069X/201202/41590565.html |
| [12] |
吴星. 地球重力场调和分析方法研究[D]. 郑州: 信息工程大学, 2005. WU Xing. Research of Methods of Spherical Harmonic Analysis of the Earth's Gravity Field[D]. Zhengzhou: Information Engineering University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-90008-2006020970.htm |
| [13] |
王建强, 赵国强, 朱广彬.
常用超高阶次缔合勒让德函数计算方法对比分析[J]. 大地测量与地球动力学, 2009, 29(2): 126–130.
WANG Jianqiang, ZHAO Guoqiang, ZHU Guangbin. Contrastive Analysis of Common Computing Methods of Ultra-High Degree and Order Fully Normalized Associated Legendre Function[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 126–130. |
| [14] |
万晓云, 于锦海.
极地空白对GOCE引力场恢复的影响[J]. 测绘学报, 2013, 42(3): 317–322.
WAN Xiaoyun, YU Jinhai. Influence of Polar Gaps on Gravity Field Recovery Using GOCE Data[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 317–322. |
| [15] |
李征航, 陈锴, 刘万科, 等.
GNSS电离层延迟模型的数学统一与方法扩展[J]. 武汉大学学报(信息科学版), 2007, 32(8): 699–703.
LI Zhenghang, CHEN Kai, LIU Wanke, et al. Mathematical Unification and Method Expansion of GNSS Ionospheric Delay Model[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 699–703. |
| [16] |
武文俊, 李志刚, 杨旭海, 等.
利用时间序列模型预报电离层TEC[J]. 时间频率学报, 2008, 31(2): 141–146.
WU Wenjun, LI Zhigang, YANG Xuhai, et al. Predicting Ionospheric TEC with Time Series Model[J]. Journal of Time and Frequency, 2008, 31(2): 141–146. |
| [17] | CONTE J F, AZPILICUETA F, BRUNINI C. Accuracy Assessment of the GPS-TEC Calibration Constants by Means of a Simulation Technique[J]. Journal of Geodesy, 2011, 85(10): 707–714. DOI:10.1007/s00190-011-0477-8 |
| [18] | AZPILICUETA F, BRUNINI C. Residual Analysis of Global Ionospheric Maps Using Modip Latitude[M]//DREWES H. Geodetic Reference Frames. Berlin Heidelberg: Springer, 2009: 311-316. |
| [19] | LIU Jingbin, CHEN Ruizhi, KUUSNIEMI H, et al. Mapping the Regional Ionospheric TEC Using a Spherical Cap Harmonic Model and IGS Products in High Latitudes and the Arctic Region[C]//Proceedings of 2009 IAIN World Congress. Stockholm, Sweden: [s. n. ], 2009. |
| [20] | CHOI B, LEE W, CHO S, et al. Global GPS Ionospheric Modelling Using Spherical Harmonic Expansion Approach[J]. Journal of Astronomy and Space Sciences, 2010, 27(4): 359–366. DOI:10.5140/JASS.2010.27.4.359 |
| [21] | LI Rui, JIAO Yuanyuan, LI Yong, et al. Simulation Platform for Relative Navigation Using GPS Carrier Phase Measurements for Satellite Formation Flying Missions[C]//International Global Navigation Satellite Systems Society Symposium 2011. Sydney, NSW, Australia: IGNSS, 2011: 15-17. |
| [22] | LIU Jingbin, CHEN Ruizhi, AN Jiachun, et al. Spherical Cap Harmonic Analysis of the Arctic Ionospheric TEC for One Solar Cycle[J]. Journal of Geophysical Research:Space Physics, 2014, 119(1): 601–609. DOI:10.1002/2013JA019501 |
| [23] | ZHANG Shoujian, CHANG Xin, ZHANG Wei. Real-Time Regional Ionospheric Total Electron Content Modeling Using Spherical Harmonic Function[C]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings: BeiDou/GNSS Navigation Applications·Test & Assessment Technology·User Terminal Technology. Berlin Heidelberg: Springer, 2013: 113-123. |
| [24] |
周伟莉, 李素华, 蒋美霞.
基于球谐函数模型的电离层预报[J]. 测绘信息与工程, 2012, 37(3): 3–5.
ZHOU Weili, LI Suhua, JIANG Meixia. Ionospheric Forecast Based on Spherical Harmonic Function Model[J]. Journal of Geomatics, 2012, 37(3): 3–5. |
| [25] | ALIZADEH M M, SCHUB H, SCHMIDT M, et al. Calibrating GNSS VTEC Values by Satellite Altimetry and Formosat-3/COSMIC Data Using Parameter Estimation Technique[J]. 2011: 150-153. |



