2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054;
4. 西安测绘技术总站, 陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Xi'an Technology Station of Surveying and Mapping, Xi'an 710054, China
地球重力场及其时变效应反映了地球质量的空间分布及其迁移变化。全球性环境问题如海平面上升、冰川融化以及干旱等都与地球表层质量迁移紧密相关,研究地球表层质量迁移对监测全球环境和气候变化具有重要意义。随着GRACE卫星的成功发射,卫星重力测量技术为监测全球地表质量迁移提供了一种有效途径,目前已广泛应用于监测陆地水储量变化、冰川融化、海水质量变化等领域研究[1-4]。
当前,利用GRACE卫星测量数据反演地表质量变化的方法按照反演原理不同,主要可分为两大类:一类是文献[5]建立的球谐系数法,采用GRACE卫星Level-2时变重力场模型,通过计算时变重力场模型相对于稳态重力场模型的球谐系数改变量反演得到质量变化,该方法计算简单应用也最广泛,但是也存在着反演结果时空分辨率低、南北条带噪声显著和信号泄露等缺陷[6-8];另一类方法为Mascon方法,采用GRACE卫星Level-1B数据,将研究区域划分为规则网格,视每个网格区域内具有相同质量变化,分离不同网格区域质量变化对重力场变化的影响,建立网格区域质量变化和星间距离变率之间的直接函数关系。研究表明Mascon方法反演结果具有更高的时空分辨率[9-12],但是与球谐系数法相比,Mascon方法计算相对复杂。
为减少反演数值计算复杂程度,国外学者基于Mascon方法原理,提出了径向点质量模型方法。该方法采用Level-2时变重力场模型数据,将空间点扰动重力向下延拓,建立与地表质量变化直接关系,进而反演得到质量变化。文献[13]建立了地球表层点质量变化引起空间点扰动重力变化的数学模型;文献[14]采用径向点质量模型方法反演了格陵兰区域冰盖质量变化,反演结果空间分辨率有所提高,其中病态问题采用Tikhonov正则化求解,正则化参数通过L曲线法确定;文献[15]建立了三维点质量模型方法,并通过模拟试验验证了方法的有效性;文献[16]采用径向点质量模型方法反演了冰岛区域冰川质量变化;文献[17]采用径向点质量模型方法反演了格陵兰区域冰盖质量变化,病态问题采用截断奇异值分解方法处理,并根据反演结果统计分析了反演参数的最优选取。
径向点质量模型方法本质上是重力数据的向下延拓,属于病态问题,解算时法方程组系数矩阵奇异,采用最小二乘法无法求得稳定解,通常采用正则化方法处理[14],正则化参数一般采用L曲线或广义交叉核实法(generalized cross-validation,GCV)确定[18-20]。但是,L曲线法在解算中可能存在过度平滑问题,而GCV方法亦存在最小值点不明显的问题[21]。针对传统正则化方法存在的不足,本文利用相邻网格区域质量变化不存在阶跃变化的特性,对相邻网格区域质量变化之间引入空间约束方程条件,构建虚拟观测方程组,由于引入空间约束条件后存在两类观测方程,而两类观测方程初始权比不确定,故引入赫尔默特方差分量估计方法自适应修正两类观测方程权比,使反演结果更加稳定和符合实际。
1 径向点质量模型方法基本原理 1.1 数学模型地球重力场由正常重力场和扰动重力场两部分组成。地球表层质量变化会引起空间点的扰动重力径向分量值的改变。而扰动重力径向分量值的改变可由时变重力场模型球谐系数的改变量来表示
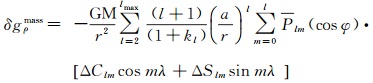 (1)
(1)
式中,G为引力常数;M为地球质量;a为地球平均半径;l和m分别为重力场模型的阶数和次数;λ、φ分别为地心经度和地心余纬;r=a+h为空间点到地心的向径,h为空间点到地面的高度;lmax是重力场球谐模型截断阶数;{ΔClm, ΔSlm}={Clm-Clm,Slm-Slm}是时变重力场模型{Clm, Slm}相对于参考重力场模型{Clm, Slm}的球谐系数改变量;kl是l阶负荷勒夫数。
如图 1所示,地球表面一点P质量变化δmj引起的空间一点S的扰动重力径向分量改变值δgρij为
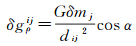 (2)
(2)
式中,dij是空间点S和地球表面点P的距离。根据图 1几何关系,可得地球表层质量变化引起的空间点S的扰动重力径向分量改变值为[12]
 (3)
(3)
|
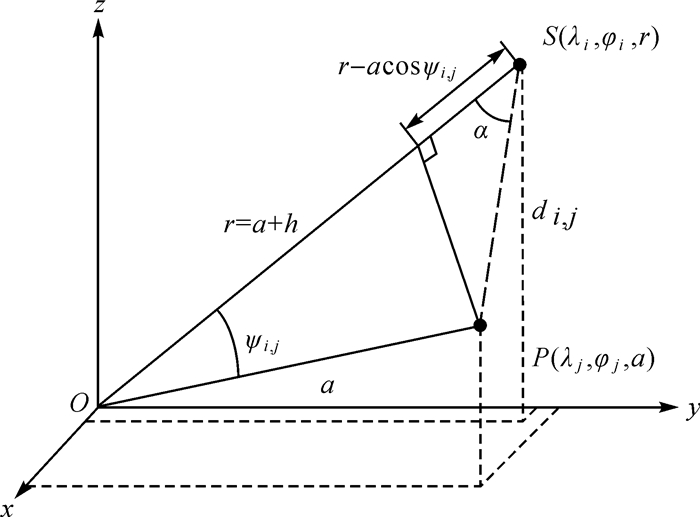
| 图 1 径向点质量模型几何示意 Fig. 1 Radial point-mass modeling geometry |
式中,n是研究区域质量异常的点的个数;ri为空间点S到地心的向径。进一步,可将待求质量变化划为等效水柱高形式。设δmj=ρ×sj×Δhj,ρ为水密度,λj1、λj2为研究区域经度范围,φj1、φj2为研究区域纬度范围,sj为研究区域面积,具体形式为
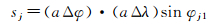 (4)
(4)
于是,可将式(3)所求区域质量变化换算成等效水柱高度Δhj形式
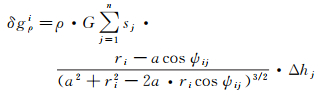 (5)
(5)
联立式(1)和式(5)即得径向点质量模型方法数学模型,其中i=1、2、…、k,为空间离散点的个数。
1.2 参数估计联立式(1)和式(5),整理后得到直接观测方程组
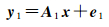 (6)
(6)
式中,e1为误差向量;y1=[δgρi]k×1为观测向量可按式(1)计算求得;x=[Δhj]n×1是待求量;矩阵A1(k×n)为线性化后系数矩阵,可按式(5)右端计算得到,权阵P1简化为单位阵I[14, 16]。由于点质量模型方法解算时法方程组系数矩阵A1TP1A1奇异[14],最小二乘解不可靠。通常采用Tikhonov正则化方法得到稳定解
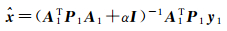 (7)
(7)
式中,α≥0是正则化参数。从式(7)可以看出,待估参数解与正则化参数密切相关,求解的关键在于如何选择合适的正则化参数。
2 附加空间约束的径向点质量模型方法 2.1 附加空间约束病态问题可通过增加约束信息得到适定的解,这类约束信息可以是待估参数的线性等式约束,也可是待估参数的二次范数约束。Tikhonov正则化方法增加待估参数间二次范数约束,通过正则化因子使观测残差和参数范数间达到平衡,从而求得稳定正则化解[20]。鉴于L曲线法在解算中可能存在过度平滑问题,而GCV方法亦存在最小值点不明显的问题。为避免此类情况发生,针对径向点质量模型方法,从实际角度考虑,空间上临近网格区域受相似环境影响,相邻网格内质量变化在数值上不应存在阶跃性变化。因此,可对不同网格间质量变化构建空间约束条件,具体形式如下[10, 22]
 (8)
(8)
即认为任意两个网格区域质量变化Δhn和Δhk(n≠k)相等,而相等的“可能性”满足一个与空间距离有关的指数函数[23],如式(9)所示,式中dnk是相应的两个网格中心的空间距离;D是相关距离,表征空间约束程度,与研究区域网格划分以及时变重力场模型数据分辨率有关,一般取值为网格宽度[10]。从式(9)可知,两网格间距离越小,其质量变化在数值上接近的可能性越大;反之差异越大。
将空间约束条件式改写成观测值为0的虚拟观测方程式(10),虚拟观测方程对应的权值为Wnk。经整理后,得到虚拟观测方程组式(11),其中y2=[0 … 0]T,e2为误差向量。系数矩阵A2具体形式如式(12)
 (9)
(9)
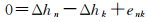 (10)
(10)
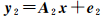 (11)
(11)
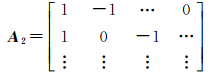 (12)
(12)
虚拟观测方程组权阵为对角阵P2,对角线元素由式(9)计算,具体形式如下
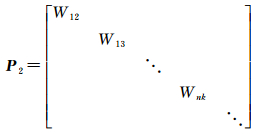 (13)
(13)
联立式(6)和式(11)即可解算得到反演结果。显然,增加空间约束条件后,反演解算实质上是联合求解两类观测方程组,但其初始权比往往不够合理,直接采用广义最小二乘准则得到的解不准确。在大地测量数据处理中,在初始权比不准确情况下,通常采用方差分量估计确定不同类型观测值的权[24]。为求得更准确和稳定的解,本文引入验后赫尔默特方差分量估计自适应确定两类观测方程组的权比,将病态问题转化为两类观测值的测量平差问题[25]。
赫尔默特方法分量估计是根据各次平差得到改正数向量估计方差分量,修正平差所用的权值,然后再以修正后的权值重新平差,直至趋近到权比合理为止。联合式(6)和式(11),即整体观测方程组式(14),设
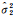
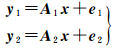 (14)
(14)
对式(14)进行赫尔默特方差分量估计,经过第J次迭代有
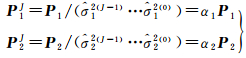 (15)
(15)
式中
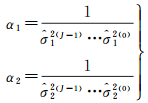 (16)
(16)
通常两类观测方程权方差初值不等,通过若干次迭代修正后可得到
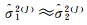 (17)
(17)
于是得到两类观测方程的权比为
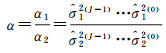 (18)
(18)
再根据广义最小二乘准则,可得待估参数解
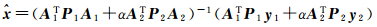 (19)
(19)
对比式(7)和式(19)可知,赫尔默特方差分量估计得到的两类观测方程权比与Tikhonov正则化因子的作用类似,都是调节最小二乘估计和稳定泛函约束间的平衡以提高待估参数解的可靠性[16]。
3 区域陆地水储量变化反演结果与分析 3.1 试验数据及处理过程由于南美大陆河流众多,水量丰富,拥有亚马孙河、巴拉那河、奥里诺科河等河流,特别是亚马孙河是世界上流域面积最广、流量最大的河流。故选择南美大陆区域(30°S—10°N,35°W—80°W)为研究区域,采用GFZ(Geo Forschungd Zentrum)发布Realease 05版本2006年1月—2008年12月共36个月的GRACE卫星时变重力场模型数据反演该区域陆地水储量变化,以验证附加空间约束的径向点质量模型方法的有效性。考虑到计算区域的边缘效应,实际选取计算区域比研究区域扩大了5°,计算时地面区域划分为边长为2°的正方形网格,空中扰动重力计算划分为边长为1°的正方形网格。GRACE时变重力场模型误差随阶数增大而增大,因此反演时球谐系数截断至60阶[26]。由于时变重力场模型C20项精度较差,反演时采用卫星激光测距(SLR)观测的C20项替换。试验中,首先对36个月的时变重力场模型求平均值作为稳态背景场,然后计算每个月时变重力场模型相对于稳态背景场的球谐系数改变量,再由每个月时变重力场模型球谐系数改变量根据第2节所述方法对研究区域陆地水储量变化进行反演计算,构造空间约束条件时只对直接相邻的不同网格之间建立空间约束方程。
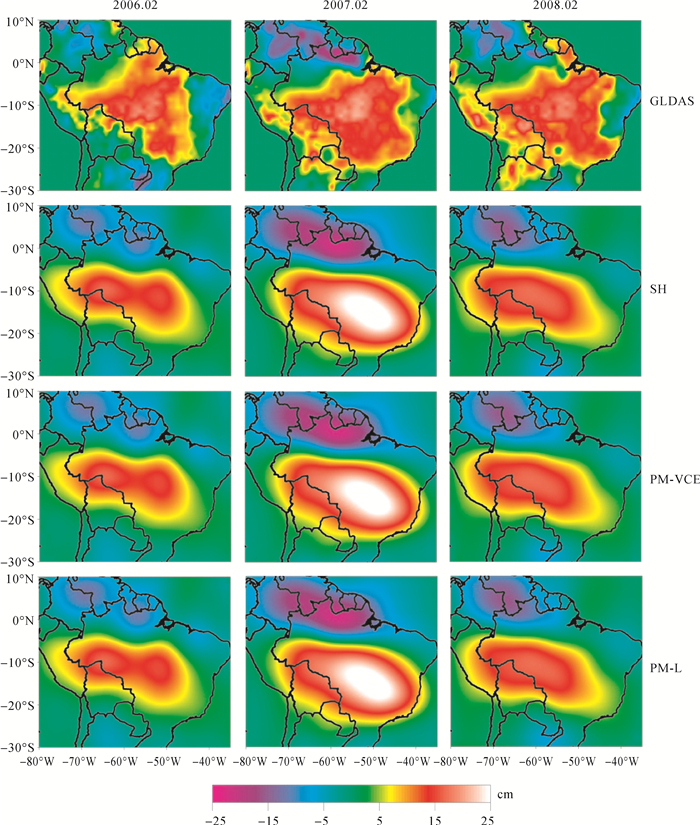
3.2 反演结果验证与分析为了方便描述,附加空间约束的径向点质量模型方法记为PM-VCE;无空间约束条件的径向点质量模型方法记为PM-L,采用Tikhonov正则化方法,其中正则化参数采用L曲线方法求解;球谐系数法记为SH,采用400 km半径的扇形滤波;GLDAS(global land data assimilation system)水文模型结果记为GLDAS。图 2所示为4种方法所得南美大陆区域陆地水储量变化反演结果,第1列至第3列分别为2006年2月、2007年2月和2008年2月反演结果。
|
| 图 2 南美大陆区域陆地水储量变化反演结果 Fig. 2 South America continent water storage variations results 注:第1行为GLDAS模型结果,第2行为SH方法结果,第3行为PM-VCE方法结果,第4行为PM-L方法结果。 |
从图 2结果可以看出,4种方法所得到的2006年2月、2007年2月以及2008年2月的南美大陆区域陆地水储量变化反演结果在整体上具有相似性。亚马孙流域的巴西中西部、玻利维亚北部以及秘鲁东部区域,陆地水储量变化呈明显增大变化;而在奥里诺科河流域的巴西北部、哥伦比亚东部和委内瑞拉南部地区陆地水储量变化呈显著减小变化。PM-VCE方法反演结果与PM-L、SH方法反演结果在空间分布和数值上具有很好的一致性,水储量变化最大和最小的区域一致。与GLDAS水文模型结果相比,PM-VCE所得结果与GLDAS模型结果在变化趋势和空间分布上也具有较好的一致性。由于GLDAS水文模型是以雷达和微波辐射计资料为主,主要反映了浅层地表土壤湿度及地表积雪随时间变化,忽略了深层土壤水、地下水和地表湖泊等影响,故GLDAS模型结果与GRACE时变重力场反演结果在数值上有所差异[27]。图 2南美大陆区域陆地水储量变化反演结果验证了PM-VCE方法的正确性。
表 1对2006年2月、2007年2月以及2008年2月的南美大陆区域陆地水储量变化PM-VCE方法反演结果进行了统计。由表 1可知,增加空间约束条件后,采用赫尔默特方差分量估计得到两类观测方程权比与Tikhonov正则化因子作用类似,调节了最小二乘和稳定泛函约束间的平衡,使得法方程组条件数明显减小、病态性减弱,进而得到待估参数的稳定解。
| 条件 | 2006年2月 | 2007年2月 | 2008年2月 |
| 两类观测方程权比 | 3.59×10-7 | 4.59×10-7 | 4.47×10-7 |
| 原法方程组条件数 | 8.34×1014 | 8.35×1014 | 8.34×1014 |
| 附加空间约束后法方程组条件数 | 2.37×1010 | 1.86×1010 | 1.91×1010 |
对2006年1月至2008年12月间南美大陆区域陆地水储量变化反演结果时间序列进行了统计分析。图 3所示为不同方法所得2006—2008年南美大陆区域陆地水储量变化反演结果时间序列。从图 3可以看出,陆地水储量变化呈现明显年周期变化,PM-VCE、PM-L和SH方法所得反演结果时间序列变化特征相符一致,并与GLDAS水文模型结果在变化整体趋势上也基本一致,其中SH方法反演结果振幅最大。

|
| 图 3 2006—2008年南美大陆区域陆地水储量变化 Fig. 3 South America continent water storage variations in the period of 2006—2008 |
表 2为4种方法所得反演结果时间序列年周期特征,可看出,GLDAS模型结果时间序列周年振幅最小,这是因为GLDAS模型是浅层土壤水含量模型结果;PM-VCE方法和PM-L方法结果时间序列周年振幅一致,SH方法结果时间序列周年振幅最大,其中PM-VCE方法结果时间序列周年振幅最接近GLDAS模型结果;并且,SH、PM-L以及PM-VCE所得时间序列周年相位结果基本一致,GLDAS模型结果相位与其他3种方法结果相差大约30°,图 3时间序列结果也反映了该相位差异。
| 方法 | 周年振幅/cm | 周年相位/(°) |
| GLDAS | 22.31 | 5.07 |
| SH | 43.72 | -27.29 |
| PM-VCE | 32.94 | -28.48 |
| PM-L | 33.37 | -28.37 |
表 3为4种方法所得反演结果时间序列信号相关性统计。从结果可见,PM-VCE方法与PM-L、SH方法时间序列结果相关系数相一致,均为0.99。而PM-VCE、PM-L以及SH方法结果与GLDAS模型结果相关性基本一致,相关系数分别为0.77、0.78和0.79。
| 方法 | GLDAS | SH | PM-VCE | PM-L |
| GLDAS | 1 | 0.79 | 0.77 | 0.78 |
| SH | 1 | 0.99 | 0.99 | |
| PM-VCE | 1 | 0.99 | ||
| PM-L | 1 |
4 结论
针对径向点质量模型方法解算中的病态问题,本文从实际角度考虑构建空间约束条件,对不同网格区域质量变化建立空间约束的虚拟观测方程组,联合原始观测方程进行反演求解,并采用赫尔默特方差分量估计自适应修正两类不同观测方程权比,使得反演结果更符合实际和稳定。根据南美大陆区域陆地水储量变化反演试验结果可知:
(1) 引入空间约束条件后,增加了待估参数的约束信息,降低了法方程组病态程度,法方程组条件数明显减小。
(2) 附加空间约束的径向点质量模型方法与球谐系数法、GLDAS模型所得南美大陆区域陆地水储量变化反演结果在空间分布、数值变化上整体相一致,验证了本文方法的正确性,表明该方法可有效应用于区域地表质量变化反演,为利用卫星重力监测地表质量变化提供了一种新途径。
(3) 针对径向点质量模型方法,考虑到Tikhonov正则化中正则化参数确定方法的不稳定性,本文通过引入空间约束条件构建虚拟观测方程组,并采用赫尔默特方差分量估计方法自适应修正虚拟观测方程组和原始观测方程组权比,避免了L曲线等方法的缺陷。
当前GRACE卫星即将结束使命任务,未来随着GRACE Follow-on计划的实施,星间测距精度将得到大幅度提高,时变重力场模型精度和空间分辨率将得到有效提升。考虑相关距离、网格划分以及平差模型等参数组合对附加空间约束的径向点质量模型方法的影响,后续将进一步研究并改进解算方法,以期提高区域地表质量变化反演结果精度和空间分辨率。
致谢: 感谢中国科学院测量与地球物理研究所冯伟副研究员、杨帆博士,德国洪堡学者陈秋杰博士对本文提出的宝贵意见。
| [1] |
文汉江, 黄振威, 王友雷, 等.
青藏高原及其周边地区水储量变化的独立成分分析[J]. 测绘学报, 2016, 45(1): 9–15.
WEN Hanjiang, HUANG Zhenwei, WANG Youlei, et al. Independent Component Analysis of Water Storage Changes Interpretation over Tibetan Plateau and Its Surrounding Areas[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 9–15. DOI:10.11947/j.AGCS.2016.20140447 |
| [2] |
高春春, 陆洋, 张子占, 等.
GRACE重力卫星探测南极冰盖质量平衡及其不确定性[J]. 地球物理学报, 2015, 58(3): 780–792.
GAO Chunchun, LU Yang, ZHANG Zizhan, et al. Ice Sheet Mass Balance in Antarctica Measured by GRACE and Its Uncertainty[J]. Chinese Journal of Geophysics, 2015, 58(3): 780–792. DOI:10.6038/cjg20150308 |
| [3] |
卢飞, 游为, 范东明, 等.
由GRACE RL05数据反演近10年中国大陆水储量及海水质量变化[J]. 测绘学报, 2015, 44(2): 160–167.
LU Fei, YOU Wei, FAN Dongming, et al. Chinese Continental Water Storage and Ocean Water Mass Variations Analysis in Recent Ten Years Based on GRACE RL05 Data[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 160–167. DOI:10.11947/j.AGCS.2015.20130753 |
| [4] |
邹正波, 罗志才, 吴海波, 等.
日本MW9.0地震前GRACE卫星重力变化[J]. 测绘学报, 2012, 41(2): 171–176.
ZOU Zhengbo, LUO Zhicai, WU Haibo, et al. Gravity Changes Observed by GRACE before the Japan MW9.0 Earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 171–176. |
| [5] | WAHR J, MOLENAAR M, BRYAN F. Time Variability of the Earth's Gravity Field:Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research, 1998, 103(B12): 30205–30209. DOI:10.1029/98JB02844 |
| [6] | SWENSON S, WAHR J. Methods for Inferring Regional Surface-mass Anomalies from Gravity Recovery and Climate Experiment (GRACE) Measurements of Time-variable Gravity[J]. Journal of Geophysical Research, 2002, 107(B9): 2193. |
| [7] | SWENSON S, WAHR J. Post-processing Removal of Correlated Errors in GRACE Data[J]. Geophysical Research Letter, 2006, 33(8): L08402. |
| [8] | HAN S C, SHUM C K, JEKELI C, et al. Non-Isotropic Filtering of GRACE Temporal Gravity for Geophysical Signal Enhancement[J]. Geophysical Journal International, 2005, 163(1): 18–25. DOI:10.1111/gji.2005.163.issue-1 |
| [9] | KLOSKO S, ROWLANDS D, LUTHCKE S, et al. Evaluation and Validation of Mascon Recovery Using GRACE KBRR Data with Independent Mass Flux Estimates in the Mississippi Basin[J]. Journal of Geodesy, 2009, 83(9): 817–827. DOI:10.1007/s00190-009-0301-x |
| [10] | ROWLANDS D D, LUTHCKE S B, MCCARTHY J J, et al. Global Mass Flux Solutions from GRACE:A Comparison of Parameter Estimation Strategies-mass Concentrations versus Stokes Coefficients[J]. Journal of Geophysical Research, 2010, 115(B1): B01403. |
| [11] | KROGH P E, ANDERSEN O B, MICHAILOVSKY C I B, et al. Evaluating Terrestrial Water Storage Variations from Regionally Constrained GRACE Mascon Data and Hydrological Models over Southern Africa-preliminary Results[J]. International Journal of Remote Sensing, 2010, 31(14): 3899–3912. DOI:10.1080/01431161.2010.483483 |
| [12] |
郭飞霄, 肖云, 汪菲菲.
利用GRACE星间距离变率数据反演地球表层质量变化的Mascon方法[J]. 地球物理学进展, 2014, 29(6): 2494–2497.
GUO Feixiao, XIAO Yun, WANG Feifei. Mascon Inversion Method of Earth Surface Mass Anomaly Using GRACE Range Rate Data[J]. Progress in Geophysics, 2014, 29(6): 2494–2497. DOI:10.6038/pg20140602 |
| [13] | FORSBERG R, REEH N. Mass Change of the Greenland Ice Sheet from GRACE[C]//Proceedings of the 1st Meeting of the International Gravity Field Service. [s. l. ]: Harita Dergisi, 2006, 18: 454-458. |
| [14] | BAUR O, SNEEUW N. Assessing Greenland Ice Mass Loss by Means of Point-mass Modeling:A Viable Methodology[J]. Journal of Geodesy, 2011, 85(9): 607–615. DOI:10.1007/s00190-011-0463-1 |
| [15] |
苏勇, 于冰, 游为, 等.
基于重力卫星数据监测地表质量变化的三维点质量模型法[J]. 地球物理学报, 2017, 60(1): 50–60.
SU Yong, YU Bing, YOU Wei, et al. Surface Mass Distribution from Gravity Satellite Observations by Using Three-dimensional Point-Mass Modeling Approach[J]. Chinese Journal of Geophysics, 2017, 60(1): 50–60. |
| [16] | SANDBERG SØRENSEN L, JAROSCH A H, ADAL-GEIRSDÓTTIR G, et al. The Effect of Signal Leakage and Glacial Isostatic Rebound on GRACE-derived Ice Mass Changes in Iceland[J]. Geophysical Journal International, 2017, 209(1): 226–233. |
| [17] | RAN J, DITMAR P, KLEES R, et al. Statistically Optimal Estimation of Greenland Ice Sheet Mass Variations from GRACE Monthly Solutions Using an Improved Mascon Approach[J]. Journal of Geodesy, 2018, 92(3): 299–319. DOI:10.1007/s00190-017-1063-5 |
| [18] |
林东方, 朱建军, 宋迎春, 等.
正则化的奇异值分解参数构造法[J]. 测绘学报, 2016, 45(8): 883–889.
LIN Dongfang, ZHU Jianjun, SONG Yingchun, et al. Construction Method of Regularization by Singular Value Decomposition of Design Matrix[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 883–889. DOI:10.11947/j.AGCS.2016.20150134 |
| [19] |
徐新禹, 李建成, 王正涛, 等.
Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J]. 测绘学报, 2010, 39(5): 465–470.
XU Xinyu, LI Jiancheng, WANG Zhengtao, et al. The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 465–470. |
| [20] |
谢建, 朱建军.
等式约束对病态问题的影响及约束正则化方法[J]. 武汉大学学报(信息科学版), 2015, 40(10): 1344–1348.
XIE Jian, ZHU Jianjun. Influence of Equality Constraints on Ill-conditioned Problems and Constrained Regularization Method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(10): 1344–1348. |
| [21] |
杨帆, 许厚泽, 钟敏, 等.
利用径向基函数RBF解算GRACE全球时变重力场[J]. 地球物理学报, 2017, 60(4): 1332–1346.
YANG Fan, XU Houze, ZHONG Min, et al. GRACE Global Temporal Gravity Recovery through the Radial Basis Function Approach[J]. Chinese Journal of Geophysics, 2017, 60(4): 1332–1346. DOI:10.6038/cjg20170409 |
| [22] | SABAKA T J, ROWLANDS D D, LUTHCKE S B, et al. Improving Global Mass Flux Solutions from Gravity Recovery and Climate Experiment (GRACE) through Forward Modeling and Continuous Time Correlation[J]. Journal of Geophysical Research:Solid Earth, 2010, 115(B11): B11403. DOI:10.1029/2010JB007533 |
| [23] |
李琼. 地表物质迁移的时变重力场反演方法及其应用研究[D]. 武汉: 武汉大学, 2014. LI Qiong. Earth's Surface Mass Transport Recovered from Temporal Gravity Field and Its Applications[D]. Wuhan: Wuhan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015528749.htm |
| [24] | KOCH K R, KUSCHE J. Regularization of Geopotential Determination from Satellite Data by Variance Components[J]. Journal of Geodesy, 2002, 76(5): 259–268. DOI:10.1007/s00190-002-0245-x |
| [25] |
徐天河. 利用CHAMP卫星轨道和加速度计数据推求地球重力场模型[D]. 郑州: 信息工程大学. XU Tianhe. Gravity Field Recovery from CHAMP Orbits and Accelerometer Data[D]. Zhengzhou: Information Engineering University, 2004. http://www.cqvip.com/QK/93330B/200503/20185368.html |
| [26] |
郑秋月, 陈石.
应用GRACE卫星重力数据计算陆地水变化的相关进展评述[J]. 地球物理学进展, 2015, 30(6): 2603–2615.
ZHENG Qiuyue, CHEN Shi. Review on the Recent Developments of Terrestrial Water Storage Variations Using GRACE Satellite-based Datum[J]. Progress in Geophysics, 2015, 30(6): 2603–2615. DOI:10.6038/pg20150619 |
| [27] |
詹金刚, 王勇.
卫星重力捕捉龙滩水库储水量变化[J]. 地球物理学报, 2011, 54(5): 1187–1192.
ZHAN Jingang, WANG Yong. Detect Water Storage Variation of Longtan Reservoir with GRACE Data[J]. Chinese Journal of Geophysics, 2011, 54(5): 1187–1192. |


