目前确定(似)大地水准面的方法主要有几何法、重力法以及组合法[1]。早期几何法主要以天文重力水准的方式确定似大地水准面[2],现在多以拟合GPS/水准点为主,虽然可以获得很高的精度,但仅限于小范围、GPS/水准点丰富的地区[3],其计算结果为区域(似)大地水准面。几何法的缺陷在于需要进行大量的水准测量,耗费巨大的人力、物力,海洋测高虽然能以很高的精度确定大地水准面,但不适用于陆地及陆海交界处[4]。重力法主要是解算物理大地测量边值问题,再由Bruns公式转换为大地水准面高或高程异常[5],计算结果为绝对大地水准面,可统一全球高程基准[6],适用范围广,但计算复杂、计算量大,需要与本国高程基准拟合。组合法则是将几何法与重力法相结合确定(似)大地水准面,其本质是将重力似大地水准面数值拟合到GPS/水准点上,与本国高程基准相统一[7-8],结合了GPS/水准精度高、重力(似)大地水准面分辨率高的优点,但其拟合过程并不严密。世界主要国家和地区如美国、欧洲、日本、加拿大及我国所建立的高精度(似)大地水准面模型多以组合法建立[4, 9-17]。由于重力场水平分量-垂线偏差对地形高频信息敏感,因此首先利用三维重力矢量-格网垂线偏差与格网重力异常,联合格网高程数据求得格网中点间相对高程异常(高程异常差),然后通过GPS/水准点的控制,构成紧密的几何条件,进行严密的平差,从而可以获得高分辨率、高精度似大地水准面的数值模型[18-19]。该方法的优点是充分吸收了高频的地形信息,弥补了我国重力场数据的不足;同时以确定相对高程异常代替以往的直接确定高程异常的方法,而且这种格网相对高程异常构成了严密的几何条件,可以通过平差消除矛盾、提高精度,比以往采用数值拟合的简单方法提高了严密度。论文基于此,展开深入研究,旨在提高我国陆海统一的似大地水准面模型的建模精度。
1 格网高程异常差及其平差模型的建立 1.1 格网垂线偏差计算高程异常差的基本原理在计算高程异常差时所用的垂线偏差数据是只包含子午方向和卯酉方向分量的格网数据,根据天文重力水准方法计算似大地水准面的原理可得高程异常差与垂线偏差的关系为[20]
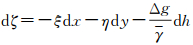 (1)
(1)
式中,ξ、η分别为子午方向和卯酉方向垂线偏差;Δg为重力异常;dh为两点间高差;Δgdh/γ为重力异常改正项;γ为平均正常重力值,可以取9.797 644 656 m/s2。
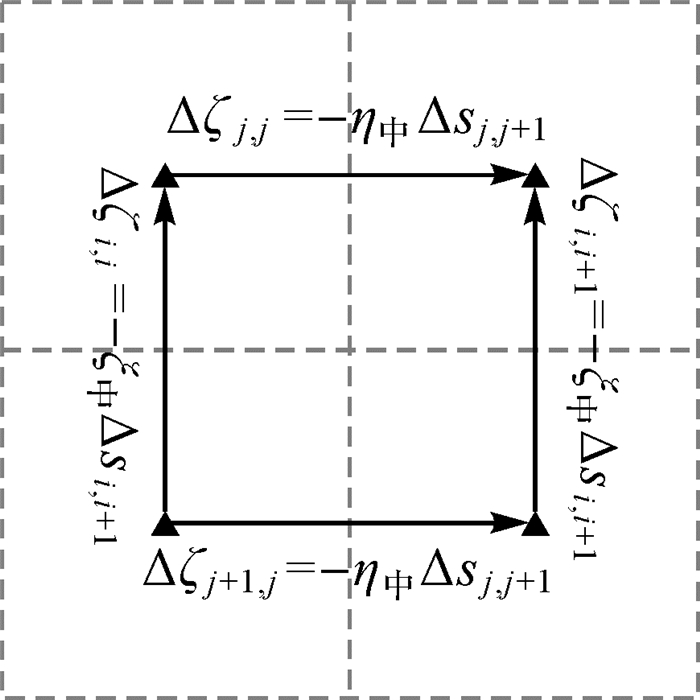
以任一格网为例说明利用垂线偏差计算相邻格网中点高程异常差的方法,如图 1所示。
|
| 图 1 垂线偏差与高程异常差的关系 Fig. 1 Using deflection of the vertical to calculate height anomaly difference |
图 1中,黑色三角形表示格网中点。考虑重力异常改正项[21],子午方向和卯酉方向相邻格网中点之间的高程异常差分别为
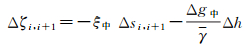 (2)
(2)
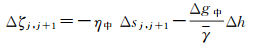 (3)
(3)
式中,ξ中、η中为相邻格网中点子午方向、卯酉方向垂线偏差的平均值;Δg中为相邻格网中点的重力异常平均值;Δh为相邻格网中点的高差;γ为平均正常重力值;i、j为中点序号。
1.2 计算高程异常差的平差模型利用式(2)与式(3)计算的高程异常差类似于水准网中的高差,施加一定的GPS/水准点作控制可以平差计算每个格网中点的高程异常。为便于编程实现,本文采用参数平差的方式。设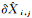
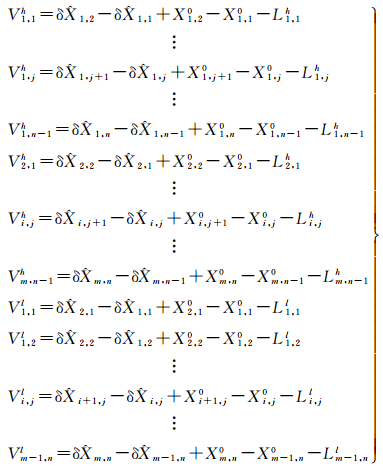 (4)
(4)
式(4)可写成矩阵形式为
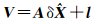 (5)
(5)
相应的法方程为
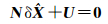 (6)
(6)
法方程的详细构建与解算过程见文献[20]。经解算后得
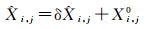 (7)
(7)
式中,N=ATPA;U=ATPl;P为观测量的权阵;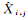
为建立我国1′×1′陆海统一的似大地水准面模型,本文采用以下数据:分辨率为1′×1′的格网垂线偏差、格网重力异常、高程数据以及全国6600多个GPS/水准数据。
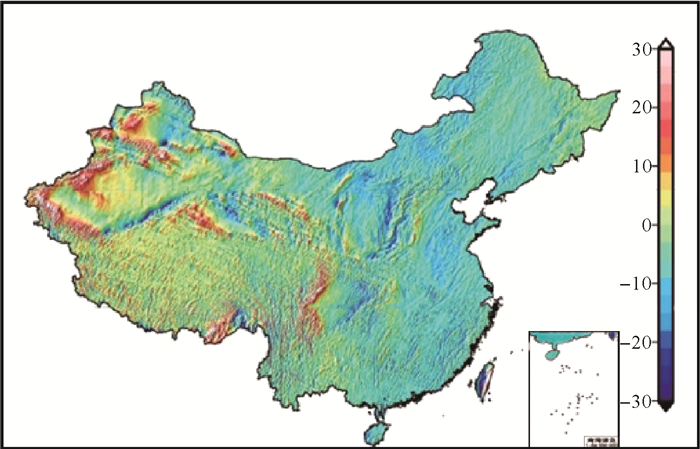
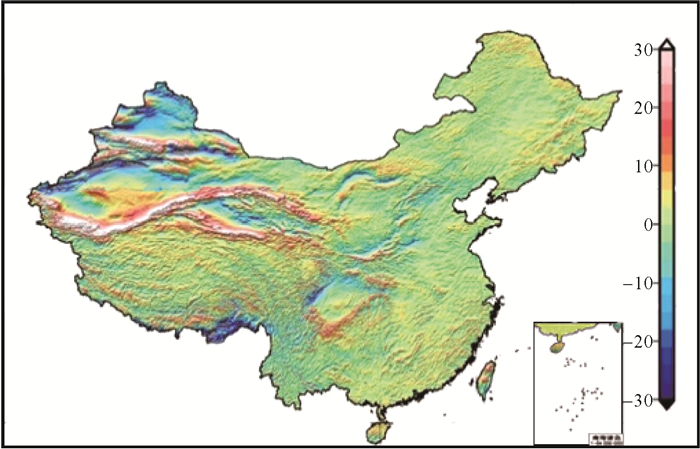
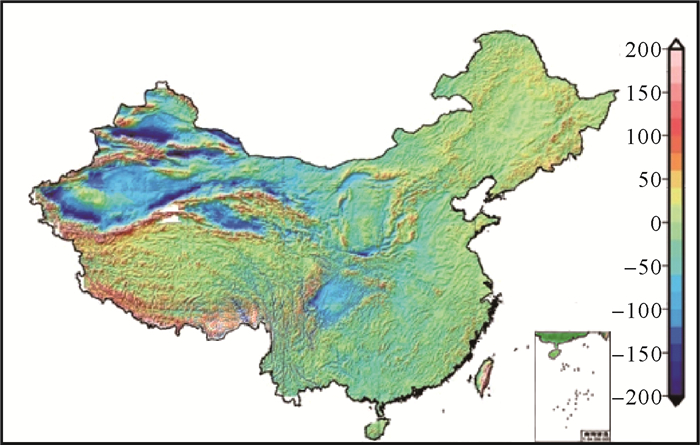
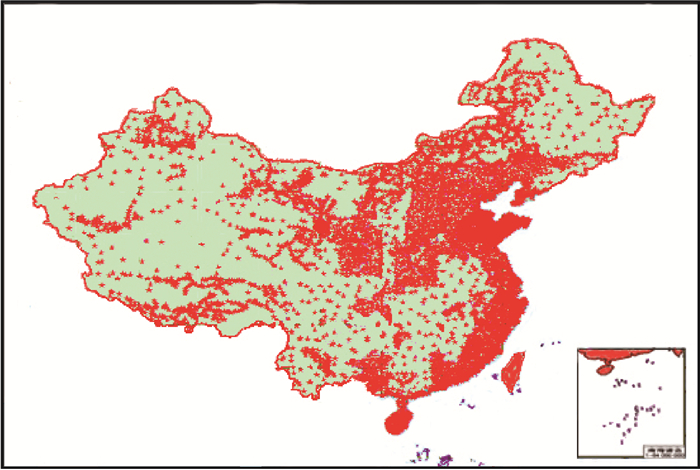
垂线偏差数据主要是采用“移去-恢复”技术[22],根据边值理论由重力、地形以及地球重力场模型确定[23-25]。垂线偏差精度优于1.5″,格网点间距以1.8 km计算,由此产生的误差低于2 cm,加入GPS/水准控制以后,可满足建立厘米级似大地水准面的要求。我国陆地子午与卯酉垂线偏差分量如图 2、图 3所示。重力异常数据主要利用我国及周边81万多个离散重力异常数据经格网化所得,如图 4所示;地形数据由分辨率3″×3″的SRTM数据取平均后处理成分辨率1′×1′的地形数据,如图 5所示。共收集包括国家GPS A、B级点、工程点,以及部分地区测量的C级网点在内的陆地GPS/水准点6700多个,如图 6所示,剔除粗差点后实际上采用了6600多个计算并检核了似大地水准面模型。
|
| 图 2 我国陆地1′×1′分辨率子午垂线偏差 Fig. 2 China land grid vertical deflections of meridian direction with a resolution of 1′×1′ |
|
| 图 3 我国陆地1′×1′分辨率卯酉垂线偏差 Fig. 3 China land grid vertical deflections of prime direction with a resolution of 1′×1′ |
|
| 图 4 我国陆地1′×1′分辨率重力异常 Fig. 4 China land grid gravity anomaly with a resolution of 1′×1′ |

|
| 图 5 我国陆地1′×1′SRTM地形数据 Fig. 5 China land SRTM terrain data with a resolution of 1′×1′ |
|
| 图 6 我国陆地GPS/水准点分布 Fig. 6 Distribution of China land GPS/leveling points |
2.2 分区似大地水准面的确定
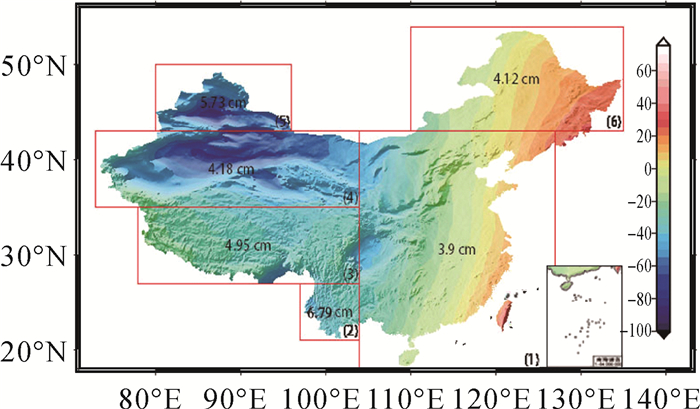
依据上述数据的质量以及分布情况,将全国分为6个区域,分区确定区域似大地水准面模型。区域1包括华东、华中、华南地区;区域2为云贵地区;区域3是藏南地区;区域4包括新疆南部及西藏北部地区;新疆北部地区作为区域5;区域6为东北地区。不同区域范围以及控制点、检核点分布如图 7—图 12所示,分区似大地水准面模型如图 13所示,检核点的残差统计如表 1、图 14所示。
|
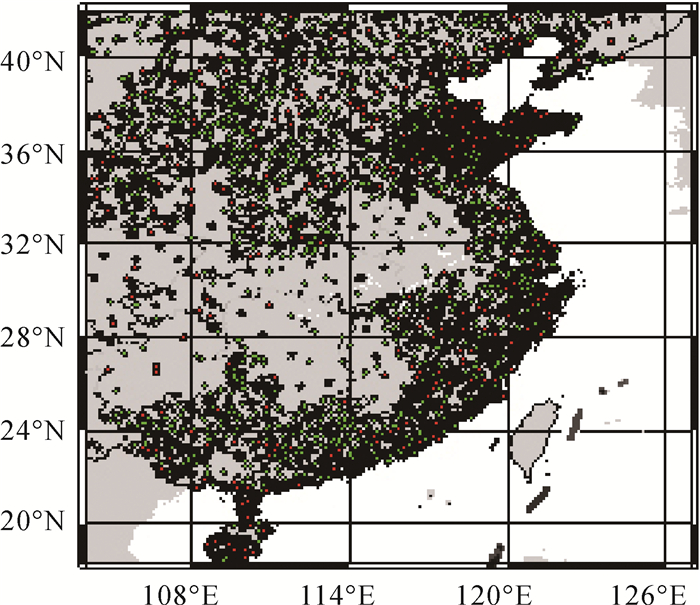
| 图 7 区域1的控制点、检核点分布 Fig. 7 Distribution of control and check points of area 1 |
|
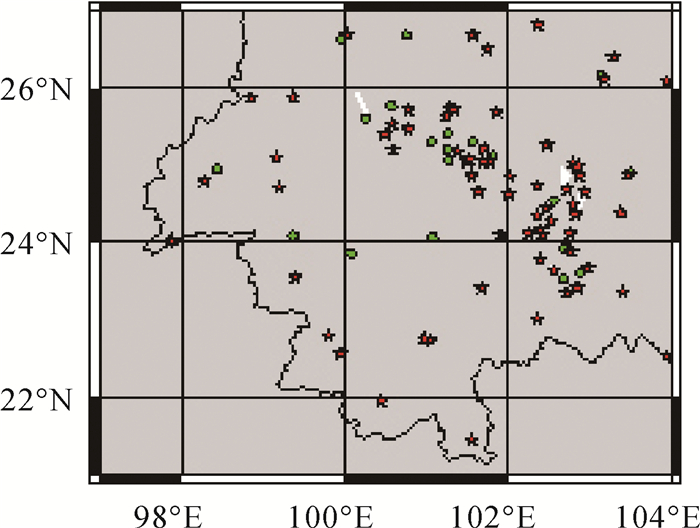
| 图 8 区域2的控制点、检核点分布 Fig. 8 Distribution of control and check points of area 2 |
|
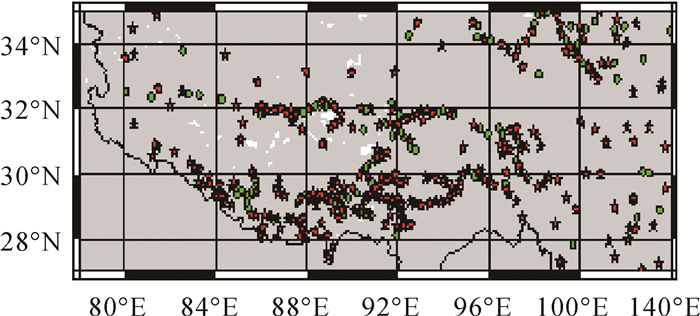
| 图 9 区域3的控制点、检核点分布 Fig. 9 Distribution of control and check points of area 3 |
|
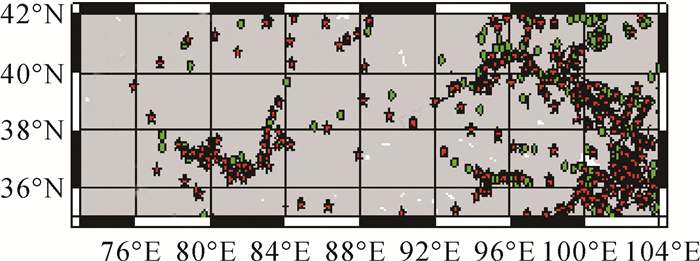
| 图 10 区域4的控制点、检核点分布 Fig. 10 Distribution of control and check points of area 4 |
|
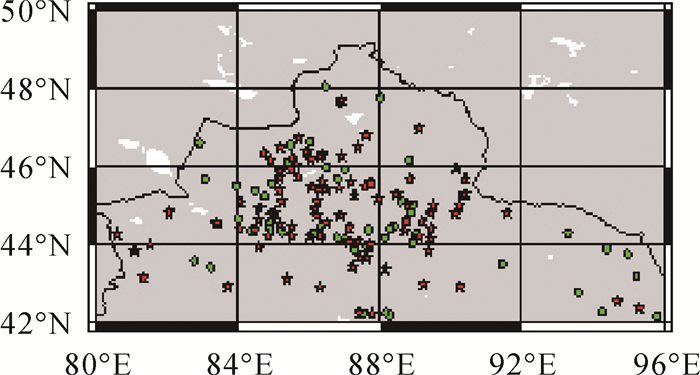
| 图 11 区域5的控制点、检核点分布 Fig. 11 Distribution of control and check points of area 5 |

|
| 图 12 区域6的控制点、检核点分布 Fig. 12 Distribution of control and check points of area 6 |
|
| 图 13 陆地分区似大地水准面模型及精度 Fig. 13 The quasi-geoid model precision of different areas |
| 区域 | 控制点数 | 检核点数 | 残差特征值/m | 残差范围/个 | ||||||
| 最大值 | 最小值 | 平均值 | RMS | < RMS | < 2×RMS | < 3×RMS | ||||
| 区域1 | 1389 | 3319 | 0.099 | -0.099 7 | 0.001 8 | 0.039 | 2223 | 3178 | 3319 | |
| 区域2 | 69 | 20 | 0.071 3 | -0.113 5 | -0.045 8 | 0.067 9 | 11 | 20 | 20 | |
| 区域3 | 266 | 114 | 0.096 1 | -0.112 | 0.002 8 | 0.049 5 | 70 | 112 | 114 | |
| 区域4 | 285 | 290 | 0.092 9 | -0.10 1 | 0.0002 7 | 0.041 8 | 187 | 281 | 290 | |
| 区域5 | 93 | 58 | 0.101 7 | -0.117 7 | -0.003 1 | 0.057 3 | 37 | 57 | 58 | |
| 区域6 | 290 | 456 | 0.097 3 | -0.099 0 | -0.003 4 | 0.041 2 | 293 | 440 | 456 | |

|
| 图 14 6个区域残差大小统计 Fig. 14 Statistic of six areas' residual |
图 7反映出区域1 GPS/水准点较多,尤其是东部沿海地区,但整体上分布不均,我国台湾地区没有任何数据,而中南部地区GPS/水准点相对匮乏,但由GPS/水准点检核后发现该地区似大地水准面的精度并没有受此影响。该区域似大地水准面的精度达到了3.9 cm。
由图 8可知,区域2 GPS/水准点较少,分布极其不均,图 5也显示该区域地势复杂,因此选择大部分的点作为控制点。边界区域都布设了控制点,个别地区控制点分布集中、距离较近,这是因为在不断选点计算时发现,这几个点单独做检核点时残差较大,但做控制点时,其对其他检核点的残差并没有大的影响,因此排除了这些点是粗差点的可能。值得注意的是沿24°N纬线分布的3个GPS/水准点附近没有任何控制点,但并没有影响似大地水准面的精度,由图 4也可以看出该地区重力场的变化并不明显。
图 9显示区域3是我国地势最高的区域,GPS/水准点的分布并不均匀,为保证精度与可靠性着重在边界地区、横断山脉附近布设较多控制点。但仍有部分地区缺少GPS/水准点,这些地区的似大地水准面模型既没有得到合理控制也没有得到有效检核,幸运的是这些地区重力异常的变化并不像喜马拉雅山脉地区变化的那么剧烈,为保证可靠性对北部山脉地区施加大量的控制点。该区域似大地水准面模型经过GPS/水准点的检核表明在GPS/水准点有效控制的区域精度达到了5 cm。
由图 10可知,区域4 GPS/水准点多集中分布在东部地区,在该区域东南角处,控制点选取较为密集,主要是因为此处是阶梯的交界处,也正是由于如此密集的选点,使得该地区的似大地水准面的精度得到了保证。经GPS/水准点检核区域4的似大地水准面模型精度达到了4 cm。
由图 11可知,区域5的GPS/水准点较少,分布多集中在中部地区,由图 4可知中部地区的重力异常变化较为剧烈,因此适度增加控制点有利于增加该区域似大地水准面的可靠性。经GPS/水准点检核区域5的似大地水准面模型精度优于6 cm。
图 12表明区域6 GPS/水准点主要集中在中西部地区,东部地区较为稀少,且重力场变化较为剧烈,因此该区域需要较多的控制点,以保证似大地水准面的可靠性,在中西部地区,控制点多为三角网的角点处。该区域似大地水准面模型的整体精度达到了4 cm,并且大部分地区选用了较少的控制点,但是在东部地区受重力场变化、地形等因素的影响,绝大部分的GPS/水准点都选作了控制点。
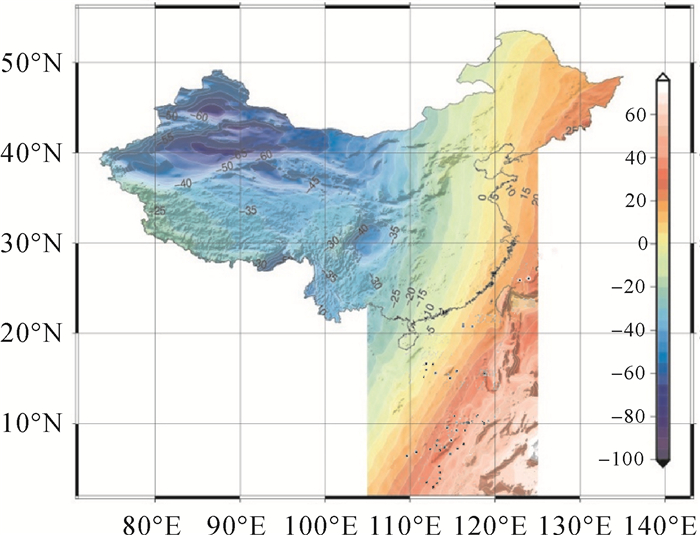
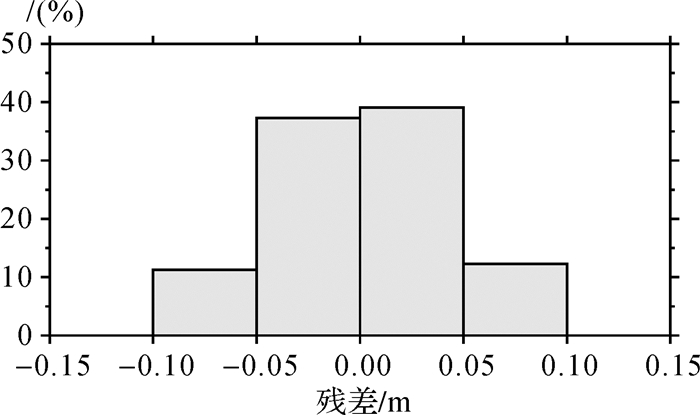
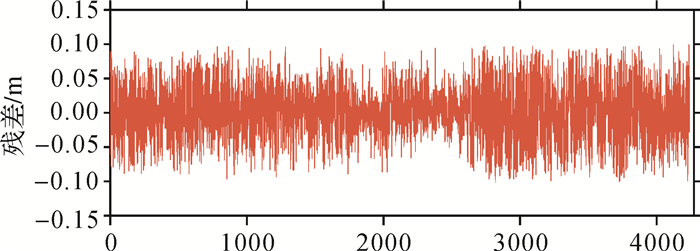
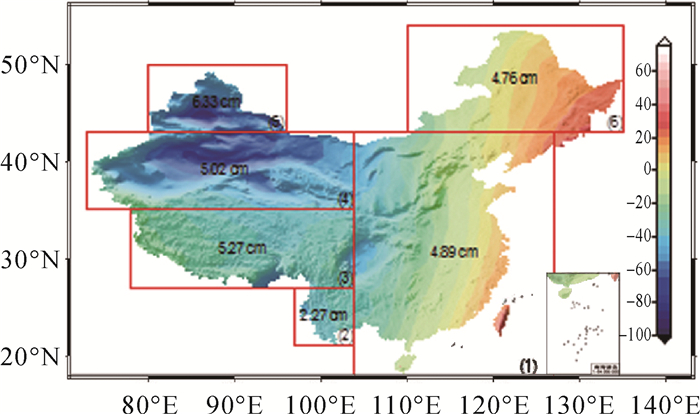
2.3 全国陆海统一似大地水准面确定综合上述陆地控制点,并联合海岛礁联测GPS/水准点进行整体平差计算,建立了我国陆海统一的似大地水准面模型,如图 15所示。其中为消除不同区域控制点对似大地水准面整体精度的影响,适当调整了部分的检核点作为控制点,最终采用共计2444个GPS/水准点做控制,经4241个GPS/水准点检核,结果表明我国似大地水准面的整体精度达到4.01 cm。检核点残差统计如图 16、图 17、表 2所示。
|
| 图 15 陆海统一的似大地水准面模型 Fig. 15 China land and ocean quasi-geoid model |
|
| 图 16 残差分布统计 Fig. 16 The distribution of residual |
|
| 图 17 残差大小统计 Fig. 17 Statistic of residual |
| 最大值 | 残差特征值/m | 残差范围/个 | |||||
| 最小值 | 平均值 | RMS | < RMS | < 2×RMS | < 3×RMS | ||
| 0.099 8 | -0.100 1 | 0.001 5 | 0.040 1 | 2822 | 4058 | 4241 | |
2.4 相对精度评定
绝对精度检核并未考虑GPS/水准点的误差累积,因此,整体上4 cm的精度只能说明所建立的似大地水准面与GPS/水准点的“吻合”情况较好。在计算过程中,地形复杂、重力场变化剧烈的地区,多是增加了GPS/水准点,增强对该区域似大地水准面的控制,考虑到绝对精度表示的是似大地水准面与本国GPS/水准点拟合以后的精度,在这种强制拟合中忽视了GPS/水准点中水准测量误差累积的影响,为此评定了似大地水准面模型的相对精度,通过做差消除了部分水准测量累积误差影响。
2.4.1 相对精度评定方法相对精度评定的具体步骤如下:
(1) 任选一检核点A,以A点为中心选择一定半径范围的检核点Bi(i=1, 2, …, n,n为以A点为中心一定半径范围内的检核点的个数)。
(2) 内插A点的高程异常得到ζ′A,内插Bi的高程异常得到ζ′i(i=1, 2, …, n),A点高程异常内插值与Bi点高程异常内插值做差,得
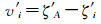
(3) A点的高程异常真值ζA与Bi点的高程异常真值ζi做差,得
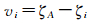
(4) 步骤(2)与步骤(3)计算所得的残差之间做差,称为相对高程异常差,得
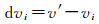
对dvi做误差统计,得到似大地水准面模型的相对精度。
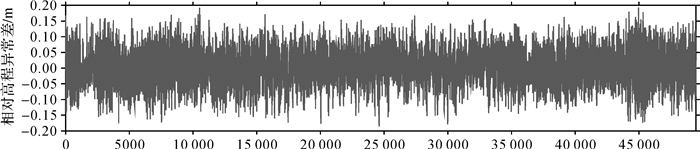
2.4.2 似大地水准面相对精度分析选择检核点0.5°半径范围的其他检核点,按照上述方法共统计了49 477组相对高程异常差,统计结果如表 3、图 18、图 19所示。不同统计半径下的分区统计如表 4所示,分区精度统计结果如图 20所示。
| 最大值 | 残差特征值/m | 残差范围/个 | |||||
| 最小值 | 平均值 | RMS | < RMS | < 2×RMS | < 3×RMS | ||
| 0.193 2 | -0.186 0 | 0.000 8 | 0.049 0 | 34 779 | 46 777 | 49 295 | |
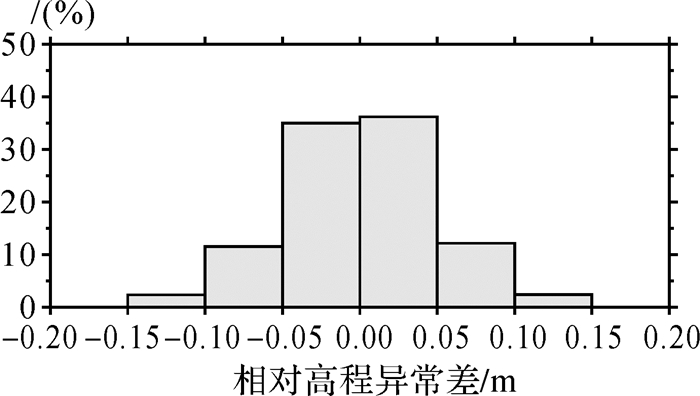
|
| 图 18 相对高程异常差分布统计 Fig. 18 Distribution of differences of relative height anomaly |
|
| 图 19 全国陆地相对精度分区统计 Fig. 19 Statistic of precision of different areas |
| 统计半径 | 区域 | 统计组数 | 残差特征值/m | 残差范围/个 | ||||||
| 最大值 | 最小值 | 平均值 | RMS | < RMS | < 2×RMS | < 3×RMS | ||||
| 0.5° | 区域1 | 46 081 | 0.193 | -0.186 | 0.000 75 | 0.049 | 32 492 | 43 540 | 45 905 | |
| 区域2 | 13 | 0.017 | -0.064 | -0.009 43 | 0.023 | 11 | 12 | 13 | ||
| 区域3 | 106 | 0.126 | -0.127 | -0.002 52 | 0.053 | 68 | 104 | 106 | ||
| 区域4 | 1898 | 0.157 | -0.153 | 0.005 57 | 0.050 | 1291 | 1808 | 1895 | ||
| 区域5 | 44 | 0.119 | -0.155 | 0.007 93 | 0.063 | 28 | 43 | 44 | ||
| 区域6 | 1335 | 0.151 | -0.140 | -0.002 10 | 0.048 | 905 | 1276 | 1333 | ||
| 1° | 区域1 | 147 926 | 0.193 | -0.193 | 0.000 5 | 0.053 | 102 121 | 140 484 | 147 632 | |
| 区域2 | 31 | 0.080 | -0.141 | -0.011 2 | 0.049 | 25 | 29 | 31 | ||
| 区域3 | 263 | 0.145 | -0.175 | -0.000 3 | 0.064 | 175 | 252 | 263 | ||
| 区域4 | 3851 | 0.179 | -0.168 | 0.005 5 | 0.052 | 2628 | 3665 | 3844 | ||
| 区域5 | 128 | 0.137 | -0.155 | 0.007 5 | 0.065 | 84 | 125 | 128 | ||
| 区域6 | 4434 | 0.177 | -0.162 | -0.000 2 | 0.052 | 3015 | 4240 | 4427 | ||
| 2° | 区域1 | 439 026 | 0.194 | -0.196 | -0.000 06 | 0.054 | 299 623 | 418 211 | 438 343 | |
| 区域2 | 95 | 0.161 | -0.183 | 0.003 5 | 0.067 | 68 | 87 | 95 | ||
| 区域3 | 805 | 0.162 | -0.178 | 0.002 0 | 0.065 | 543 | 772 | 805 | ||
| 区域4 | 7983 | 0.180 | -0.171 | 0.004 2 | 0.056 | 5409 | 7624 | 7978 | ||
| 区域5 | 418 | 0.174 | -0.184 | 0.012 6 | 0.072 | 279 | 403 | 418 | ||
| 区域6 | 13 876 | 0.186 | -0.169 | 0.001 7 | 0.055 | 9301 | 13 318 | 13 865 | ||
|
| 图 20 相对高程异常差大小统计 Fig. 20 The statistic of differences of relative height anomaly |
通过相对精度的评定,可以发现东部地区似大地水准面精度优于西部地区精度,这主要与西部地区缺少必要的观测数据有关。值得注意的是统计半径0.5°时,区域2的相对精度最高,达到了2 cm,但由于该地区GPS/水准点的数量最少,并且多数都作为控制点,造成了参与检核的相对高程异常较少,因此进一步扩大检核时选点的半径至1°、2°。由表 4可知随着选点半径的增大,区域2的精度不断降低,其他4个区域的精度基本稳定,因此可认为这4个区域先前的精度评定是可信的。考虑到区域2 GPS/水准点严重不足,可以认为统计半径为0.5°情况下得出的2 cm精度并不可信,当选点半径扩大至2°已包含了区域2绝大部分的检核点,因此认为在该选点半径情况下得出的6.7 cm的精度较为可靠。
3 结论目前似大地水准面建模的通用方法是按照Molodensky理论直接计算一点的高程异常,再用GPS/水准拟合系统差。由于大地水准面不能有效地吸收地形等高频信息并且难以利用GPS/水准数据对大地水准面做真正地实际控制,因此很难再大幅度提高似大地水准面精度。本文基于重力场水平分量-垂线偏差对地形信息敏感的特点,在根据边值理论通过重力与地形数据确定格网垂线偏差模型的基础上,利用三维重力矢量-格网垂线偏差与格网重力异常,并联合格网高程数据求得格网中点间相对高程异常,通过GPS/水准点的控制,构成紧密的几何条件,进行严密平差,从而计算得到了我国分辨率为1′×1′的陆海统一的似大地水准面模型,并进行了整体与分区的绝对精度与相对精度的评定。检核结果表明采用本文方法构建的我国似大地水准面模型的整体绝对精度达到了4 cm,相对精度优于7 cm。本文提出的基于三维重力矢量构建我国大地水准面的方法,充分利用了垂线偏差对地形信息敏感的特点,以高分辨率地形数据弥补重力场数据的不足,以确定相对高程异常代替以往的直接确定高程异常的方法,类似于GPS从直接定位到差分定位的转变,而且这种格网相对高程异常构成了严密的几何条件,可以通过平差消除矛盾提高精度,比以往采用数值拟合的简单方法提高了严密度,为我国似大地水准面模型的建立提供了一种新的思路与方法。
| [1] |
蒋光伟, 郭春喜, 田晓静, 等.
基于多种方法构建似大地水准面模型推估特性分析[J]. 地球物理学进展, 2014, 29(1): 51–56.
JIANG Guangwei, GUO Chunxi, TIAN Xiaojing, et al. The Analysis of Extrapolated Capability of Quasi-geoid Based on Muti-methods[J]. Progress in Geophysics, 2014, 29(1): 51–56. DOI:10.6038/pg20140107 |
| [2] | HOFMANN-WELLENHOF B, MORITZ H. Physical Geodesy[M]. New York: SpringerWienNewYork, 2005. |
| [3] | KAVZOGLU T, SALA M H. Modelling Local GPS/Levelling Geoid Undulations Using Artificial Neural Networks[J]. Journal of Geodesy, 2005, 78(9): 520–527. DOI:10.1007/s00190-004-0420-3 |
| [4] |
李建成, 陈俊勇, 宁津生, 等.
地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003.
LI Jiancheng, CHEN Junyong, NING Jinsheng, et al. The Theory of Earth's Gravity Field Approximation and Determination of the China Quasi-geoid 2000[M]. Wuhan: Wuhan University Press, 2003. |
| [5] | SANSÒ F, RUMMEL R. Geodetic Boundary Value Problems in View of the One Centimeter Geoid[M]. Berlin: Springer, 1997. |
| [6] | GERLACH C, RUMMEL R. Global Height System Unification with GOCE:a Simulation Study on the Indirect Bias Term in the GBVP Approach[J]. Journal of Geodesy, 2013, 87(1): 57–67. DOI:10.1007/s00190-012-0579-y |
| [7] | JIANG Ziheng, DUQUENNE H. On the Combined Adjustment of a Gravimetrically Determined Geoid and GPS Levelling Stations[J]. Journal of Geodesy, 1996, 70(8): 505–514. DOI:10.1007/BF00863623 |
| [8] | KOTSAKIS C, SIDERIS M G. On the Adjustment of Combined GPS/Levelling/Geoid Networks[J]. Journal of Geodesy, 1999, 73(8): 412–421. DOI:10.1007/s001900050261 |
| [9] | SMITH D A, ROMAN D R. GEOID99 and G99SSS:1-Arc-Minute Geoid Models for the United States[J]. Journal of Geodesy, 2001, 75(9-10): 469–490. DOI:10.1007/s001900100200 |
| [10] | ROMAN D R, WANG Yanming, HENNING W, et al. Assessment of the New National Geoid Height Model, GEOID03[J]. Surveying and Land Information Science:Journal of the American Congress on Surveying and Mapping, 2004, 64(3): 153–162. |
| [11] | WANG Y M, SALEH J, LI X, et al. The US Gravimetric Geoid of 2009(USGG2009):Model Development and Evaluation[J]. Journal of Geodesy, 2012, 86(3): 165–180. DOI:10.1007/s00190-011-0506-7 |
| [12] | DENKER H. The European Gravimetric Quasigeoid EGG2008[C]//American Geophysical Union, Spring Meeting 2009. New York: AGU, 2009. |
| [13] | ODERA P A, FUKUDA Y, KUROISHI Y. A High-resolution Gravimetric Geoid Model for Japan from EGM2008 and Local Gravity Data[J]. Earth, Planets and Space, 2012, 64(5): 361–368. DOI:10.5047/eps.2011.11.004 |
| [14] | HUANG Jianliang, VÉRONNEAU M. Canadian Gravimetric Geoid Model 2010[J]. Journal of Geodesy, 2013, 87(8): 771–790. DOI:10.1007/s00190-013-0645-0 |
| [15] | http://www.nrcan.gc.ca/earth-sciences/geomatics/geodetic-reference-systems/9054. |
| [16] |
李建成.
最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651–660, 669.
LI Jiancheng. The Recent Chinese Terrestrial Digital Height Datum Model:Gravimetric Quasi-geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651–660, 669. |
| [17] |
束蝉方, 李斐, 李明峰, 等.
应用Bjerhammar方法确定GPS重力似大地水准面[J]. 地球物理学报, 2011, 54(10): 2503–2509.
SHU Chanfang, LI Fei, LI Mingfeng, et al. Determination of GPS/gravity Quasi-geoid Using the Bjerhammar Method[J]. Chinese Journal of Geophysics, 2011, 54(10): 2503–2509. DOI:10.3969/j.issn.0001-5733.2011.10.008 |
| [18] |
朱雷鸣. 基于相对高程异常差平差法的区域似大地水准面精化[D]. 郑州: 信息工程大学, 2011. ZHU Leiming. Refining of Quasi-geoid Based on the Relative Height Anomaly Difference Adjustment[D]. Zhengzhou: Information Engineering University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-90008-1012325204.htm |
| [19] |
孙文. 我国高分辨率三维重力场与似大地水准面研究[D]. 郑州: 信息工程大学, 2014. SUN Wen. Determination of High Resolution of 3D Gravity Field and Quasi-Geoid of China[D]. Zhengzhou: Information Engineering University, 2014. |
| [20] |
邢志斌, 李姗姗, 王伟, 等.
利用垂线偏差计算高程异常差法方程的快速构建方法[J]. 武汉大学学报(信息科学版), 2016, 41(6): 778–783.
XING Zhibin, LI Shanshan, WANG Wei, et al. Fast Approach to Constructing Normal Equation during the Time of Calculating Height Anomaly Difference by Using Vertical Deflections[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 778–783. |
| [21] |
吴晓平.
似大地水准面的定义及在空中测量中涉及的问题[J]. 测绘科学, 2006, 31(6): 24–25.
WU Xiaoping. Title Definition of Quasi-geoid and Some Questions Encountered in Airborne Gravimetry[J]. Science of Surveying and Mapping, 2006, 31(6): 24–25. |
| [22] |
宁津生, 郭春喜, 王斌, 等.
我国陆地垂线偏差精化计算[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1035–1038.
NING Jinsheng, GUO Chunxi, WANG Bin, et al. Refined Determination of Vertical Deflection in China Mainland Area[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1035–1038. |
| [23] |
范昊鹏, 李姗姗.
局部区域模型重力异常快速算法研究[J]. 大地测量与地球动力学, 2013, 33(6): 28–30, 35.
FAN Haopeng, LI Shanshan. Study on a Fast Algorithm for Model Gravity Anomalies in Local Areas[J]. Journal of Geodesy and Geodynamics, 2013, 33(6): 28–30, 35. |
| [24] |
李姗姗, 吴晓平, 张传定, 等.
顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化[J]. 测绘学报, 2012, 41(4): 510–516.
LI Shanshan, WU Xiaoping, ZHANG Chuanding, et al. Regional Quasi-geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly's Gradient Term[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 510–516. |
| [25] |
边少锋, 薛芳侠.
论地形垂线偏差中央区贡献的计算[J]. 测绘学报, 1997, 26(1): 33–36, 57.
BIAN Shaofeng, XUE Fangxia. Discussion on the Calculation of Plumb Line Deviation[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(1): 33–36, 57. |


