线要素化简是自动制图综合中的重要研究内容和经典研究问题[1],当前线化简方法主要包括顶点压缩式[2-8]、弯曲化简式[9-14]、智能算法[15-17]等。海岸线要素是一种形态复杂且具有特定地理意义的线要素,通用线化简算法直接用于海岸线化简并不合适[18]。
海岸线是海图综合中重点关注的要素之一(本文海图主要指航海图),顾及相关综合原则[19],双向缓冲区算法[20-21]常用于海岸线化简应用。一般形态海岸线化简相对容易,如文献[22]改进单调链法识别弯曲,以骨架线长度作为弯曲取舍指标化简海岸线;而复杂海岸线化简往往需要多算子协同操作[23],研究难度较大。针对形态复杂的溺谷湾海岸线,文献[18]基于约束Delaunay三角网构建河口层次树模型,通过层次剪枝实现海岸线化简,但将狭长的沉溺河谷视为整体直接取舍,忽略了尺度效应影响下要素渐进变化的自然规律[5],不符合其随尺度变化的渐变过程;改进的Visvalingam算法[24]能够渐进化简狭长河谷,但该方法与比例尺间关系并不明确,且化简后容易出现尖角、锯齿等形态问题及自相交的拓扑问题。此外,以上方法都缺少视觉约束,化简结果中仍会存在人眼无法分辨[3, 27]的局部细节。
河口湾海岸线是最具代表性的复杂海岸线之一。结合现有研究不足,设计河口湾海岸线化简算法应顾及:①建立算法参数与比例尺间关系,增强算法对化简结果的可控性;②总结人工综合知识、经验,模拟人工化简过程,渐进化简河口湾海岸线;③引入视觉约束,确保化简结果符合目标尺度下视觉要求;④协调形态化简与地理特征保持[19]间关系,既要充分化简细小弯曲及局部细节,又要顾及地理要素及其对应地理特征保持,避免化简过度。
基于以上考虑,本文提出一种尺度驱动[14]的河口湾海岸线渐进化简方法:首先分析河口湾海岸线形态特征、化简约束及化简过程,然后以约束Delaunay三角网为支撑构建河口湾骨架线二叉树模型,在此模型基础上通过细小弯曲删除或弯曲细小部分删除、渐进化简、局部夸大等步骤实现河口湾海岸线渐进化简。
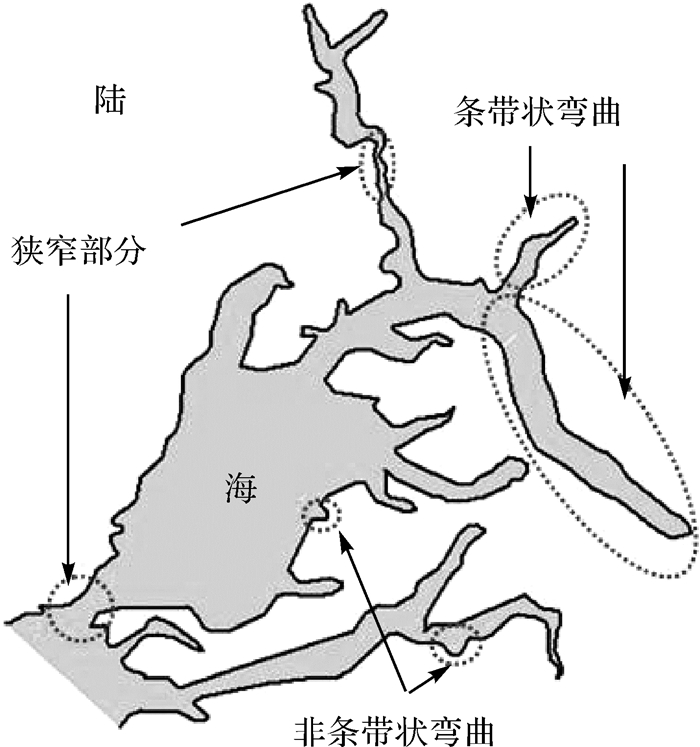
1 河口湾海岸线 1.1 表达特点存在河流注入的海湾均属河口湾范畴[25],河口湾内径流与潮流交汇,环流结构、水团组成、泥沙沉积等复杂多变[26]。受复杂地理环境影响,河口湾海岸线形态表达具有以下特点:①水流分汊是河口湾常见现象,河口湾海岸线多呈裂叶状、树枝状、喇叭状[26]。②从弯曲构成上看,河口湾海岸线主要由用于表达径流河道、沉溺河谷、峡江河槽等水流流路的明显条带状弯曲构成,也存在部分用于表达次生河口、浅湾等非条带状弯曲。蜿蜒、狭长的条带状弯曲使河口湾海岸线明显区别于其他线要素,具有更加复杂的几何形态。③河口湾海岸受侵蚀作用与沉积作用影响显著,河口湾海岸线中存在局部狭窄部分[23],如图 1所示。
|
| 图 1 河口湾海岸线表达特点 Fig. 1 Cartographic representation of estuary coastline |
1.2 化简约束
河口湾海岸线化简应遵循以下约束:
(1) 应用约束:顾及应用安全性,海图综合中海岸线化简应遵循“扩陆缩海”[19]原则。
(2) 地理约束:海岸线充分化简后应保持准确、丰富的地理特征[10, 18-19];河口湾内海水流通,海岸线化简后不能导致河口湾被“淤堵”,确保化简结果符合地理规律。
(3) 视觉约束:视觉约束是受尺度效应影响的关键约束,化简结果应符合目标尺度下视觉要求,即不存在图上不可视的细小弯曲或局部细节。结合制图经验[27],可利用以下阈值(均为图上距离)量化衡量化简后的河口湾海岸线是否符合视觉要求:①不存在小于深度阈值(thd)的条带状弯曲;②不存小于面积阈值(ths)的非条带状弯曲;③不存在小于宽度阈值(thw)的狭窄部分。
1.3 渐进化简过程河口湾海岸线化简以弯曲作为化简单元[19],其化简渐进性主要表现为两方面:
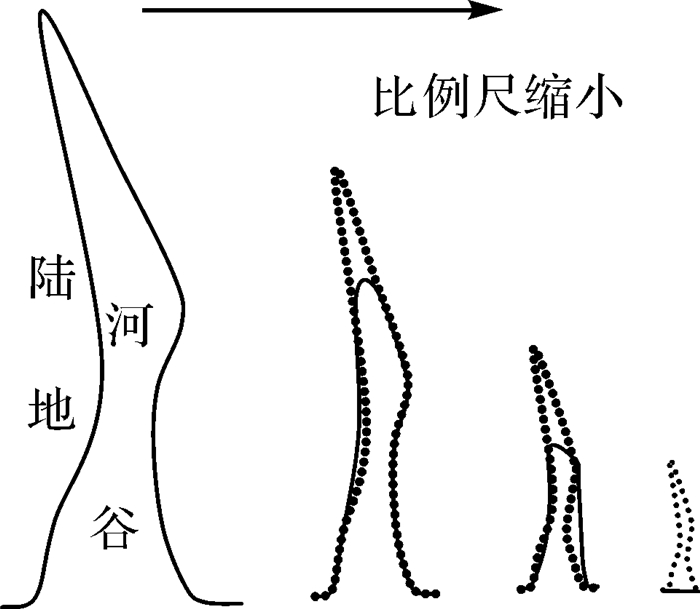
(1) 弯曲化简的渐进性。主要表现为条带状狭长河谷随尺度变化的渐变过程,如图 2所示。当条带状弯曲中既包含目标尺度下可视部分又包含不可视部分时,既不能直接保留(不符合视觉要求),也不能直接删除(导致大量地理特征丢失),往往对其中不可视部分有选择地删除或夸大,渐进化简条带状弯曲。
|
| 图 2 狭长河谷渐进化简 Fig. 2 The progressive simplification results of a narrow river valley |
(2) 化简过程的渐进性。条带状弯曲渐进化简后可能转化为非条带状弯曲,非条带状弯曲删除后也可能影响其他弯曲形态。因此,需要重复弯曲化简过程,直至充分化简为止。
河口湾海岸线渐进化简后,还需对其狭窄部分进行适当夸大以及次生冲突消除等,才得到最终化简结果。
2 河口湾海岸线结构化表达 2.1 构建Delaunay三角网利用约束Delaunay三角网[9, 18]能够较好地识别河口湾海岸线中的条带状弯曲。依文献[18]方法对河口湾海岸线加密、构建约束Delaunay三角网,提取海岸线海洋一侧三角形并构建骨架线网络。
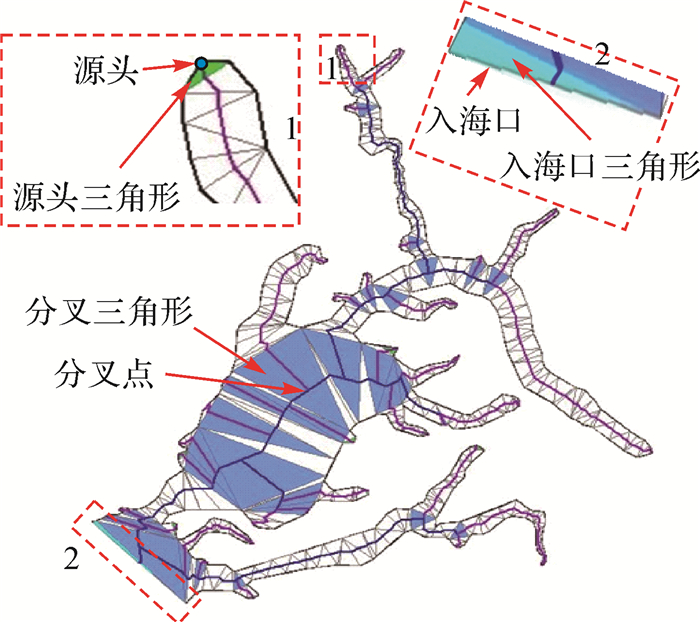
采用文献[18]中三角形分类方法,将三角形分为入海口三角形、分叉三角形、源头三角形和连接三角形4类。基于以上分类,本文将源头三角形非约束边对应的顶点称为源头,分叉三角形重心称为分叉点,入海口三角形中不与其他三角形邻接的非约束边称为入海口。对图 1中河口湾海岸线加密、构建约束Delaunay三角网、构建骨架线网络后如图 3所示,其中连接三角形、源头三角形、分叉三角形、入海口三角形分别被染为白色、绿色、蓝色、浅蓝色。
|
| 图 3 约束Delaunay三角网、骨架线网络 Fig. 3 Constrained Delaunay triangulation and skeletons network |
2.2 骨架线二叉树模型
骨架线网络是对河口湾的降维表达,能够清晰反映河口湾海岸线结构特点。文献[18]利用骨架线深度多叉树对具有明显主干特征的树枝状溺谷湾进行结构化表达;而形态多样的河口湾未必存在明显主干特征,本文提出一种骨架线二叉树模型,用于河口湾海岸线的结构化表达。按如下步骤初步构建骨架线二叉树:
步骤1:对骨架线网络进行拓扑化处理,得到所有骨架线段,且标记为0。其中,与入海口相连的骨架线段为根节点,根节点作为第i(i=1)层节点执行步骤2。
步骤2:将第i层节点骨架线段均标记为-1,若所有骨架线段都标记为-1,则二叉树构建完成;否则,将第i层所有节点依次执行步骤3,得到的所有孩子节点作为第i+1层节点,令i=i+1,重复步骤2。
步骤3:若存在与该节点骨架线段共用相同分叉点且标记为0的骨架线段(有且只有两条),则这两条骨架线段即为该节点的孩子节点;否则,该节点不存在孩子节点。
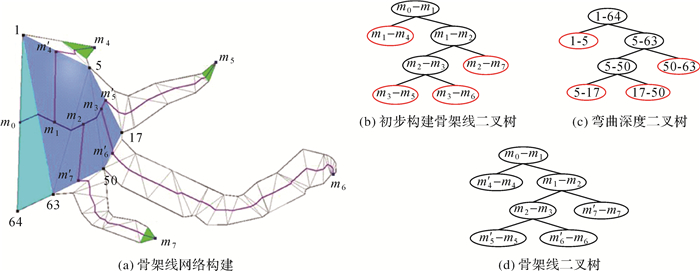
在初步构建的二叉树基础上,删除所有叶子骨架线中包含于分叉三角形内的部分,完成骨架线二叉树模型构建。骨架线二叉树与依文献[9]构建的弯曲深度二叉树结构相同,二者叶子节点间一一对应,即叶子骨架线是对应叶子弯曲的中心线。图 4(a)中河口湾海岸线初步构建的骨架线二叉树如图 4(b)所示,依文献[9]构建的弯曲深度二叉树如图 4(c)所示,最终构建的骨架线二叉树模型如图 4(d)。图 4中1—64为海岸线顶点,m0—m7为骨架线段端点,m′4—m′7为叶子弯曲对应中心线的某一端点。
|
| 图 4 河口湾海岸线骨架线二叉树模型 Fig. 4 The binary tree structure of estuary skeletons |
本文将叶子骨架线记为L0(j),L0(j)贯穿的三角形集合称为叶子流路,记为{T(j)};将非叶子骨架线记为L1(k),L1(k)贯穿的三角形集合称为过渡流路,记为{T(k)}。叶子骨架线与叶子流路、非叶子骨架线与过渡流路一一对应,所有叶子流路与过渡流路构成河口湾。
3 河口湾海岸线渐进化简 3.1 化简过程河口湾海岸线通过删除细小弯曲、部分删除条带状弯曲、渐进化简、局部夸大等步骤实现化简。基于骨架线二叉树结构模型,具体实现步骤如下:①删除目标尺度下图上不可视的叶子流路以实现细小弯曲删除;②通过叶子流路“退化”实现条带状弯曲删除或部分删除,即从源头开始沿叶子流路向入海口追溯,追溯过程中不可视的狭窄部分随之删除,直至足够可视为止;③重复骨架线二叉树构建、叶子流路删除、退化等过程实现渐进化简;④对渐进化简后的所有叶子流路、过渡流路中狭窄部分适当拓宽,实现局部夸大。
为叙述方便,将化简前后比例尺分别记为Sa、Sf;线要素L的图上长度记为Len(L);面要素X的图上面积记为Area(X)。再定义以下两个函数:
(1) X=Union({Xi}):返回多个面要素{Xi}求并后的结果X。
(2) {Xi}=Diff(X1,X2):返回属于面要素X1却不属于X2的面要素集合{Xi}。
3.2 细小叶子流路删除首先,确定叶子流路是条带状还是非条带状。利用骨架线长度衡量叶子流路深度,再用叶子流路面积和深度反算其平均宽度,由经验可知深度是宽度2倍以上的叶子流路可以视为条带状,否则为非条带状;然后,基于各自化简阈值确定目标尺度下叶子流路是否可视。由于弯曲化简具有渐进性,本节将目标尺度下不可视的叶子流路标记为“待删除”,取舍操作将在3.4节中介绍。按以下步骤遍历所有{L0(j)}:
步骤1:若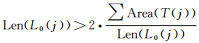
步骤2:若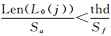
步骤3:若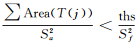
将原图上线要素L以
叶子骨架线L0(j)是叶子流路{T(j)}的中心线,Buf(L0(j))的图上覆盖范围即为目标尺度下不可视部分。条带状叶子流路退化过程如下:基于Buf(L0(j))与T(j)间关系判断三角形是否可视,进而确定条带状叶子流路中的可视部分与不可视部分;顾及最小可视距离[3](记为svo),将视觉上近似不可视的可视部分调整为不可视部分;将包含源头的不可视部分删除,实现叶子流路退化。具体步骤如下:
步骤1:遍历{T(j)},若T(j)包含于Buf(L0(j)),则T(j)标记为“待化简”;否则,T(j)标记为“保留”。邻接的待化简三角形构成待化简区域,记为{D(d)};邻接的保留三角形构成保留区域,记为{P(p)}。执行步骤2。
步骤2:保留区域P(p)中不被Buf(L0(j))覆盖的区域为目标尺度下可视部分,记为Vis(p),Vis(p)=Union(Diff(P(p), Buf(L0(j))))。包含于P(p)内的部分L0(j)记为L0(jp),若Len(L0(jp)) < thd且Area(Vis(p))/Len(L0(jp)) < svo,则P(p)近似不可视,将P(p)与相邻待化简区域合并为新的待化简区域;否则,P(p)足够可视,保持不变。遍历{P(p)},得到调整后的{D(d)},执行步骤3。
步骤3:遍历{D(d)},若{D(d)}中存在包含源头的D(d),则删除该D(d),即实现叶子流路退化;否则,不作处理。
按以上方法,图 5(a)中红边三角形即为待化简三角形,绿边为保留三角形,连续的绿边三角形构成保留区域{P(1)},连续的红边三角形构成待化简区域{D(1),D(2)},格网区域为P(1)中的可视部分Vis(1)。若P(1)足够可视,则删除D(1)即实现该叶子流路退化;若P(1)近似不可视,则P(1)与D(1)、D(2)合并成新的D(1),删除D(1)实现该叶子流路退化,如图 5(b)所示。

|
| 图 5 叶子流路“退化” Fig. 5 Partial deletion of the leaf stream |
3.4 基于骨架线二叉树的渐进化简
骨架线二叉树中互为兄弟节点的骨架线对应的叶子流路(或过渡流路)互为兄弟流路,兄弟节点的父亲节点的骨架线对应的过渡流路为父亲流路。叶子流路删除后其兄弟流路将与其父亲流路构成新叶子流路,互为兄弟的叶子流路不应同时删除。叶子流路取舍、退化后重新构建骨架线二叉树并重复此过程,直至化简结果中不存在需要删除或退化的叶子流路为止,完成渐进化简,具体步骤如下:
步骤1:按3.2节中方法遍历骨架线二叉树中所有叶子流路,若存在被标记为“待删除”的{T(j)},则执行步骤2;否则,执行步骤3。
步骤2:待删除叶子流路{T(j)}对应骨架线L0(j)的兄弟骨架线记为L0(j′),{T(j′)}为L0(j′)对应的叶子流路。当{T(j′)未被标记时,删除{T(j)}及其标记;当{T(j′)}标记为待删除时,依深度最大准则进行取舍:若Len(L0(j)) < Len(L0(j′)),则删除{T(j)}及二者标记;若Len(L0(j))≥Len(L0(j′)),则删除{T(j′)}及二者标记。遍历所有待删除叶子流路,完成叶子流路取舍,重新构建骨架线二叉树,执行步骤1。
步骤3:按3.3节方法化简叶子流路,若骨架线二叉树中所有叶子流路均未发生退化,则渐进化简结束;否则,重新构建骨架线二叉树,执行步骤1。
3.5 局部夸大骨架线也是对应叶子流路(或过渡流路)的中心线,对叶子流路与过渡流路的中心线构建视觉缓冲区,以缓冲区边界代替狭窄部分岸线实现局部夸大。具体实现步骤如下:
步骤1:遍历3.4节中的渐进化简结果,对过渡流路{T(k)},执行步骤2;对叶子流路{T(j)},执行步骤3。
步骤2:令{Xi}=Diff(Buf(L1(k)),Union({T(k)})),若{Xi}不为空,则Union({Xi},{T(k)}),实现过渡流路局部夸大;否则,无须夸大。
步骤3:令{Xi}=Diff(Buf(L0(j)),Union({T(j)})),易知{Xi}一定不为空,且至少存在包含该叶子流路源头的Xi′。将Xi′从{Xi}中剔除后,若{Xi}仍不为空,则Union({Xi},{T(k)}),实现叶子流路局部夸大;否则,无须夸大。
图 6(a)中{X1,X2}=Diff(Buf(L1(1)),Union({T(1)})),该过渡流路局部夸大为Union({X1,X2}, {T(1)}),如图 6(b)所示。图 7(a)中{X1,X2,X3}=Diff(Buf(L0(1)),Union({T(1)})),除去包含源头的X1外,该叶子流路局部夸大为Union{X1,X2},{T(1)}),如图 7(b)所示。

|
| 图 6 过渡流路局部夸大 Fig. 6 Exaggeration of the non-leaf stream |

|
| 图 7 叶子流路局部夸大 Fig. 7 Exaggeration of the leaf stream |
对夸大后的所有叶子流路及过渡流路求并后提取边界线,剔除入海口外的边界线,即为夸大后的河口湾海岸线。
河口湾海岸线渐进化简过程中不会产生自相交的拓扑问题;局部夸大能够有效消除渐进化简后河口湾内视觉冲突。通过判断夸大后的河口湾海岸线是否贯穿叶子流路、过渡流路的夸大部分{Xi},即可确定对应夸大处理是否产生拓扑问题。由于夸大程度较小,且夸大处理前河口湾海岸线已经过充分化简,一般不会产生拓扑问题。少数情况,若产生拓扑问题及其他次生冲突,可参照文献[6, 28]中的处理方法进行处理。
4 试验与分析 4.1 方法有效性验证通常认为图上最小可视距离svo为0.2 mm,海岸线线划宽度b介于0.08~0.1 mm之间[27]。本文试验令b=0.27磅(约0.094 5 mm),图上视觉指标设置如下:thw=2·b+svo;thd=2·thw;ths=thw·thd。基于ArcEngine二次开发实现本文试验。
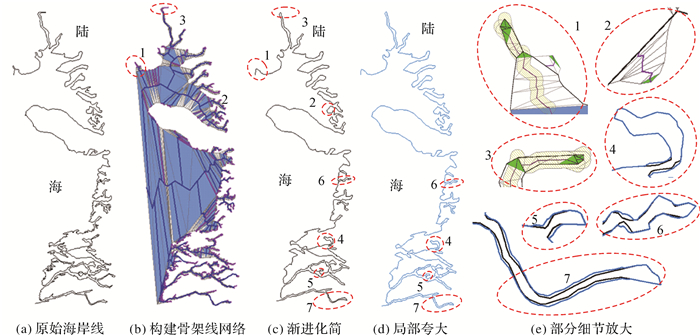
图 8为利用本文方法将1:25万河口湾海岸线化简至1:50万的主要过程:图 8(a)为裂叶状河口湾海岸线,图 8(b)为构建约束Delaunay三角网、三角形分类、构建骨架线网络的结果,图 8(c)为渐进化简后的结果,图 8(d)为局部夸大后的最终化简结果。利用本文方法化简喇叭状、树枝状河口湾海岸线,化简结果(蓝色)与原线(黑色)叠加显示分别如图 9、图 10所示。
|
| 图 8 河口湾海岸线化简过程 Fig. 8 Simplification process of the estuary coastline by the proposed method |

|
| 图 9 利用本文方法化简喇叭状河口湾海岸线结果 Fig. 9 Trumpet-like estuary coastline simplified results by the proposed method |

|
| 图 10 利用本文方法化简树枝状河口湾海岸线结果 Fig. 10 Dendritic estuary coastline simplified results by the proposed method |
参数设置上看:比例尺是本文方法参数中的唯一变量,调整目标比例尺即可得到满足该尺度视觉要求的化简结果,符合尺度驱动的制图规律,方法可控性强。
化简过程上看:重复叶子流路退化、取舍的渐进化简过程能够充分化简细小弯曲或弯曲细小部分,如图 8(e)中1—3处所示;通过局部夸大,消除河口湾内视觉冲突,如图 8(e)中4—7处所示。多算子协调下由局部向整体的渐进变化过程与人工化简过程相符合。
化简结果上看:各化简结果符合目标尺度下视觉要求,且具有良好的几何相似性和地理一致性;均未产生次生冲突,各化简结果不存在自相交或视觉上的自相交,具有良好的拓扑一致性;河口湾化简后未被淤堵(或视觉上被淤堵),化简结果符合地理规律;狭长河谷渐进化简,利于地理特征保持,如图 10中区域1、2被充分化简的同时,主要地理要素及其对应地理特征得到保留;海岸线化简后(除局部夸大部分外)位于原线海洋一侧,符合应用约束。
方法适用性上看,本文方法化简裂叶状、喇叭状、树枝状河口湾海岸线均能得到良好的化简结果,分别如图 8、图 9、图 10所示。本文方法适用于不同形态河口湾海岸线多尺度化简应用。
4.2 方法优越性验证将本文方法与D-P算法[2]、双向缓冲区算法[20-21]进行对比。双向缓冲区算法能够模拟滚动圆变换[14, 20, 29],缓冲距对应滚动圆半径[20],对岸线海洋一侧进行滚动圆变换常用于海图岸线化简。采用文献[29]中滚动圆半径尺度依赖关系的分析方法:当(r-r′)/Sa < svo/Sf时,基线长度小于等于thw的海侧弯曲被近似填平。其中,r为滚动圆半径(缓冲距),r′=[r2-(thw/2)2]1/2。计算得到r>Thr,其中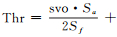
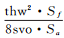
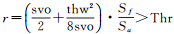
以图 8中1:25万河口湾海岸线为化简对象,对比试验结果如图 11—13所示。分析可知:
|
| 图 11 利用D-P算法化简河口湾海岸线 Fig. 11 Results simplified by D-P algorithm |
|
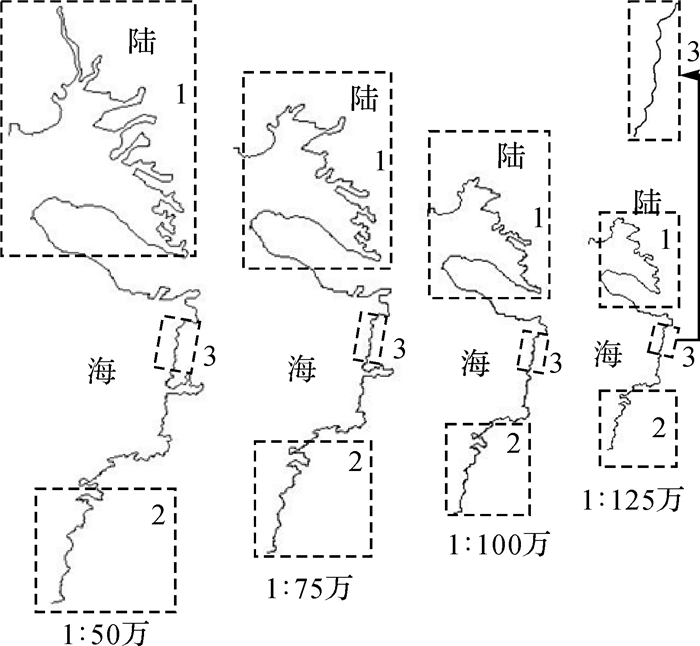
| 图 12 利用双向缓冲区算法化简河口湾海岸线 Fig. 12 Results simplified by double-buffer algorithm |
|
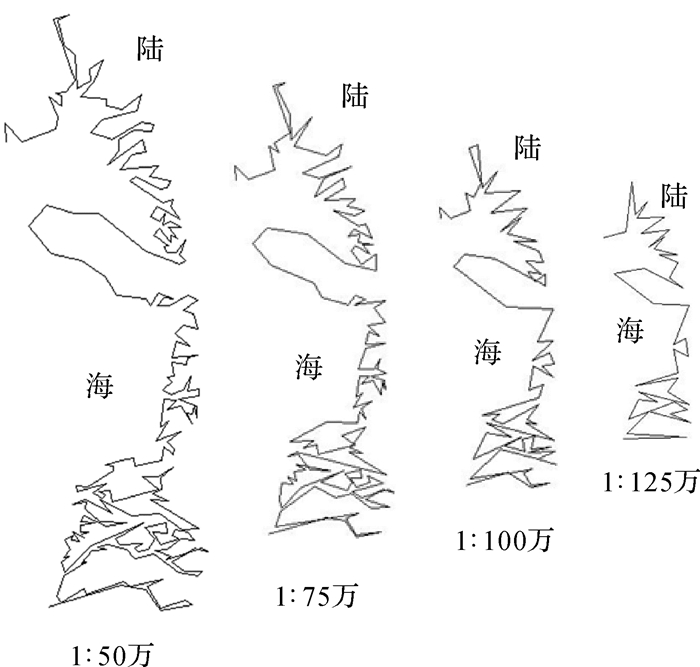
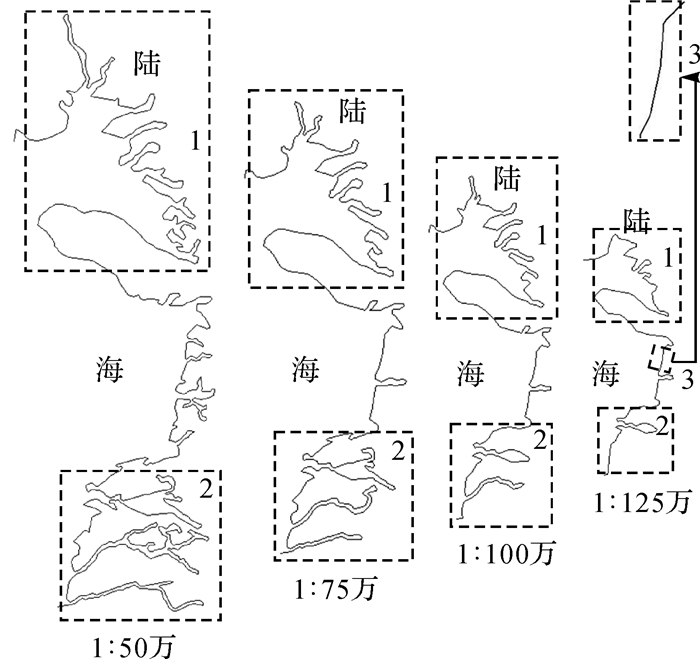
| 图 13 利用本文方法化简河口湾海岸线 Fig. 13 Results simplified by the proposed method |
D-P算法化简阈值设置繁琐,化简结果形态尖锐且存在自相交的拓扑问题,也存在目标尺度下不可视的局部细节,不符合视觉约束;此外,化简结果也不满足应用约束。D-P算法化简效果较差,不适于河口湾海岸线化简应用。
本文方法与双向缓冲区算法化简效果相对较好,都不存在自相交的拓扑问题,也都满足应用约束。几何层次上看,本文方法化简结果形态良好,较双向缓冲区算法更好地保持了原海岸线裂叶状形态特征,图 12、13中区域1对比明显;双向缓冲区算法化简结果中包含诸多连续细小弯曲构成的“锯齿”(如图 12中区域3所示),即不美观也不符合人工综合规律。地理层次上看,这些细小锯齿会引发错误地理认知,破坏化简前后地理一致性;且双向缓冲区算法较本文方法同尺度化简结果丢失了显著河谷、海湾等重要地理要素,图 12、13中区域2对比明显。
计算双向缓冲区法与本文方法化简结果的位置误差[30],用于表征线化简后的平均位移和整体变形,分别记为Eb、Em。设计参数Ebm=(Eb-Em)/Eb,若Ebm>0,则本文方法化简后产生的平均位移小于双向缓冲区法,且Ebm越大,本文方法平均位移相对越小;若Ebm < 0,则本文方法产生的平均位移大于双向缓冲区法;若Ebm=0,则两方法产生的平均位移相等。
图 8中1:25万河口湾海岸线多尺度化简结果的位置误差如表 1所示,分析可知:比例尺跨度在4倍以内时,各结果均符合目标尺度下视觉要求而本文方法产生的平均位移及整体变形更小,这是由双向缓冲区算法删除了明显海湾、溺谷等地理要素引起的,如图 12、13中1:50万~1:100万化简结果中区域2所示;随比例尺跨度增大,两方法化简结果均趋于概略,产生的平均位移与整体变形也趋于相同;当比例尺跨度较大时,可能产生本文方法的位置误差略大于双向缓冲区算法的情况,这主要是由双向缓冲区算法化简不彻底、化简后仍存在细小锯齿等引起的,如图 12、13中1:125万化简结果中区域3等所示,结合几何次、地理层次分析可知,此种情况下本文方法仍具有一定优势。
| 比例尺 | Eb/m | Em/m | Ebm/(%) |
| 1:30万 | 116.60 | 28.20 | 75.81 |
| 1:40万 | 236.72 | 73.61 | 68.90 |
| 1:50万 | 247.29 | 94.82 | 61.66 |
| 1:60万 | 262.50 | 139.69 | 46.78 |
| 1:70万 | 292.95 | 192.95 | 33.14 |
| 1:75万 | 296.14 | 207.82 | 29.82 |
| 1:80万 | 303.82 | 215.76 | 28.98 |
| 1:100万 | 359.30 | 290.72 | 19.09 |
| 1:125万 | 389.58 | 410.36 | -5.33 |
5 结论
本文基于Delaunay三角网构建骨架线二叉树模型,在此模型基础上提出一种河口湾海岸线渐进化简方法,充分化简目标尺度下不可视的细小弯曲或弯曲细小部分,保留主要弯曲及弯曲主要部分。本文方法具有以下特点:方法参数设置与比例尺间关系明确,方法可控性强;方法设计模拟人工化简的渐进过程,符合认知规律;顾及视觉约束,局部细节充分化简的同时保持了丰富、准确地理特征,化简结果符合目标尺度下视觉要求,且具有良好的几何相似性、拓扑一致性和地理一致性。本文方法可用于多种形态河口湾海岸线化简应用。
此外,如何更好地处理次生冲突及要素间冲突还有待进一步研究,海岸带多要素协同综合将作为接下来的研究重点。本文方法不局限于航海图,也可用于海底地形图等其他海图河口湾海岸线化简应用,但针对不同应用范畴,如何量化衡量、协调化简中地理约束、应用约束及视觉约束间关系仍有待进一步研究。
| [1] |
武芳, 巩现勇, 杜佳威.
地图制图综合回顾与前望[J]. 测绘学报, 2017, 46(10): 1645–1664.
WU Fang, GONG Xianyong, DU Jiawei. Overview of the Research Progress in Automated Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1645–1664. DOI:10.11947/j.AGCS.2017.20170287 |
| [2] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or its Caricature[J]. Cartographica:The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112–122. DOI:10.3138/FM57-6770-U75U-7727 |
| [3] | LI Zhilin, OPENSHAW S. A Natural Principle for the Objective Generalization of Digital Maps[J]. Cartography and Geographic Information Systems, 1993, 20(1): 19–29. DOI:10.1559/152304093782616779 |
| [4] | VISVALINGAM M, WHYATT J D. Line Generalization by Repeated Elimination of Points[J]. The Cartographic Journal, 1993, 30(1): 46–51. DOI:10.1179/caj.1993.30.1.46 |
| [5] | GUO Qingsheng, BRANDENBERGER C, HURNI L. A Progressive Line Simplification Algorithm[J]. Geo-spatial Information Science, 2002, 5(3): 41–45. DOI:10.1007/BF02826387 |
| [6] | RAPOSO P. Scale-specific Automated Line Simplification by Vertex Clustering on a Hexagonal Tessellation[J]. Cartography and Geographic Information Science, 2013, 40(5): 427–443. DOI:10.1080/15230406.2013.803707 |
| [7] | TIENAAH T, STEFANAKIS E, COLEMAN D. Contextual Douglas-Peucker Simplification[J]. Geomatica, 2015, 69(3): 327–338. DOI:10.5623/cig2015-306 |
| [8] |
李成名, 郭沛沛, 殷勇, 等.
一种顾及空间关系约束的线化简算法[J]. 测绘学报, 2017, 46(4): 498–506.
LI Chengming, GUO Peipei, YIN Yong, et al. A Line Simplification Algorithm Considering Spatial Relations between Two Lines[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(4): 498–506. DOI:10.11947/j.AGCS.2017.20160546 |
| [9] |
艾廷华, 郭仁忠, 刘耀林.
曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001, 30(4): 343–348.
AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Curve Hierarchical Structure in Depth[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 343–348. |
| [10] |
翟仁健, 武芳, 朱丽, 等.
利用地理特征约束进行曲线化简[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1021–1024, 1089.
ZHAI Renjian, WU Fang, ZHU Li, et al. Structured Representation of Curve Shape[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1021–1024, 1089. |
| [11] |
杜佳威, 武芳, 李靖涵, 等.
采用多元弯曲组划分的线要素化简方法[J]. 计算机辅助设计与图形学学报, 2017, 29(12): 2189–2196.
DU Jiawei, WU Fang, LI Jinghan, et al. Line Simplification Method Based on Multi-bends Groups Division[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(12): 2189–2196. |
| [12] |
彭东亮, 邓敏, 刘慧敏.
更充分利用独立弯曲结构的线状要素Morphing变换方法[J]. 测绘学报, 2014, 43(6): 637–644, 652.
PENG Dongliang, DENG Min, LIU Huimin. Morphing Transformation of Linear Features by Using Independent Bend Structures More Sufficiently[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 637–644, 652. DOI:10.13485/j.cnki.11-2089.2014.0100 |
| [13] | QIAN Haizhong, ZHANG Meng, WU Fang. A New Simplification Approach Based on the Oblique-dividing-curve Method for Contour Lines[J]. International Journal of Geo-Information, 2016, 5(9): 153. DOI:10.3390/ijgi5090153 |
| [14] | AI Tinghua, KE Shu, YANG Min, et al. Envelope Generation and Simplification of Polylines Using Delaunay Triangulation[J]. International Journal of Geographical Information Science, 2017, 31(2): 297–319. DOI:10.1080/13658816.2016.1197399 |
| [15] |
武芳, 邓红艳.
基于遗传算法的线要素自动化简模型[J]. 测绘学报, 2003, 32(4): 349–355.
WU Fang, DENG Hongyan. Using Genetic Algorithms for Solving Problems in Automated Line Simplification[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 349–355. |
| [16] | JIANG Bin, NAKOS B. Line Simplification Using Self-organizing Maps[C/DK]//A Working Paper Presented at ISPRS Workshop on Spatial Analysis and Decision Making. Hong Kong, China: ISPRS, 2003. |
| [17] |
郑春燕, 郭庆胜, 胡华科.
基于蚁群优化算法的线状目标简化模型[J]. 测绘学报, 2011, 40(5): 635–638.
ZHENG Chunyan, GUO Qingsheng, HU Huake. The Simplification Model of Linear Objects Based on Ant Colony Optimization Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 635–638. |
| [18] | AI Tinghua, ZHOU Qi, ZHANG Xiang, et al. A Simplification of Ria Coastline with Geomorphologic Characteristics Preserved[J]. Marine Geodesy, 2014, 37(2): 167–186. DOI:10.1080/01490419.2014.903215 |
| [19] |
王厚祥, 李进杰.
海图制图综合[M]. 北京: 测绘出版社, 1999.
WANG Houxiang, LI Jinjie. Chart Cartographic Generalization[M]. Beijing: Surveying and Mapping Press, 1999. |
| [20] | CHRISTENSEN A H J. Cartographic Line Generalization with Waterlines and Medial-axes[J]. Cartography and Geographic Information Science, 1999, 26(1): 19–32. DOI:10.1559/152304099782424893 |
| [21] |
王亮, 吴艳兰, 汤军, 等.
改进的双向缓冲海岸线综合方法研究[J]. 测绘科学, 2015, 40(1): 18–21, 13.
WANG Liang, WU Yanlan, TANG Jun, et al. A Coastline Generalization Method for Marine Delimitation[J]. Science of Surveying and Mapping, 2015, 40(1): 18–21, 13. |
| [22] |
陈惠荣, 彭认灿, 郑义东, 等.
以弯曲骨架线为化简指标的海岸线综合方法[J]. 武汉大学学报(信息科学版), 2011, 36(12): 1418–1422.
CHEN Huirong, PENG Rencan, ZHENG Yidong, et al. Coastline Generalization Based on Skeleton Line of Curve Bends[J]. Geomatics and Information Science of Wuhan University, 2011, 36(12): 1418–1422. |
| [23] | WANG Zeshen, MULLER J C. Complex Coastline Generalization[J]. Cartography and Geographic Information Systems, 1993, 20(2): 96–106. DOI:10.1559/152304093782610333 |
| [24] | VISVALINGAM M, WHELAN J C. Implications of Weighting Metrics for Line Generalization with Visvalingam's Algorithm[J]. The Cartographic Journal, 2016, 53(3): 253–267. DOI:10.1080/00087041.2016.1149906 |
| [25] |
金长茂, 眭良仁.
试论河口湾[J]. 海洋学报, 1989, 11(3): 378–384.
JIN Changmao, SUI Liangren. Discussion on the Estuary[J]. Acta Oceanologica Sinica, 1989, 11(3): 378–384. |
| [26] |
夏东兴, 边淑华, 丰爱平, 等.
海岸带地貌学[M]. 北京: 海洋出版社, 2014.
XIA Dongxing, BIAN Shuhua, FENG Aiping, et al. Coastal Zone Geomorphology[M]. Beijing: China Ocean Press, 2014. |
| [27] |
王家耀, 范亦爱, 韩同春, 等.
普通地图制图综合原理[M]. 北京: 测绘出版社, 1993.
WANG Jiayao, FAN Yiai, HAN Tongchun, et al. Cartographic Generalization Theory of General Map[M]. Beijing: Surveying and Mapping Press, 1993. |
| [28] |
李振豪, 杨春成, 魏斌, 等.
道路与建筑物空间冲突的几何相似性移位算法[J]. 测绘学报, 2016, 45(6): 747–755.
LI Zhenhao, YANG Chuncheng, WEI Bin, et al. A Displacement Algorithm Based on Geometry Similarity for Spatial Conflicts Between Roads and Buildings[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 747–755. DOI:10.11947/j.AGCS.2016.20150559 |
| [29] |
董箭, 彭认灿, 张立华, 等.
顾及"保真性"原则的双向滚动球变换DDM多尺度表达算法[J]. 测绘学报, 2017, 46(6): 789–801.
DONG Jian, PENG Rencan, ZHANG Lihua, et al. Multi-scale Representation of Digital Depth Model Based on Double Direction Rolling Ball Transform According to the Reality Principle[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 789–801. DOI:10.11947/j.AGCS.2017.20160558 |
| [30] |
朱鲲鹏, 武芳, 王辉连, 等.
Li-Openshaw算法的改进与评价[J]. 测绘学报, 2007, 36(4): 450–456.
ZHU Kunpeng, WU Fang, WANG Huilian, et al. Improvement and Assessment of Li-Openshaw Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 450–456. DOI:10.3321/j.issn:1001-1595.2007.04.015 |



