2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
河系描述了自然河流的网络连通与分布情况,是主要的基础地理信息要素之一,在地图表达时是不可或缺的骨架。河系通常包括树枝状、格状、羽毛状等类型,其中树状河系具有明显的层次结构和密度特征,主流、支流蕴含着空间上的“父子关系”,既无环路,河网密度又存在区域性差异。因此,当对树状河系进行综合选取时,必须保持这些主干河流,而且能够反映河系的空间结构特征和河网的密度差异,实际选取过程中主观经验判断处理较多,致使自动化水平不高,也直接导致了该领域的研究演变为热点和难点。
河流选取模型通常包括一元回归、多元回归、开方根等简单选取模型及模糊数学、综合指标等结构化综合模型[1]。其中,一元回归模型、多元回归模型分别依据单位面积内河流长度、河流长度与条数关联实现河流的选取;开方根模型则依据地物要素选取数量与地图比例尺之间的关系,通过计算确定新比例尺下的河流数量进行选取。简单选取模型往往缺少对于河流空间结构的考虑。结构化综合是指顾及地图要素分布特点及规律的综合[2]。河系结构化综合通常包括模糊数学模型和综合指标模型等[1]。其中,模糊数学模型考虑了河流的长度、密度、相对重要性和河网类型等因素,从而建立模糊综合评判矩阵进行河流选取;综合指标模型[1, 3-4]则分析河系简化涉及的多种因素,以河流长度为主要依据,并辅以河网密度和河流所处层次等标准,从而将河流等级、长度、层次组合起来进行河流选取。结构选取模型虽然能够顾及河系密度差异确定河流选取标准,但是处理过程复杂,过多依赖于人的主观经验,难以自动化实现。
基于层次关系的河系简化方法为综合集成应用河流选取多项指标提供了一种较好的解决思路[5],其本质是依据河系树来确定河系的层次关系,进而对其进行逐层选取。河系树结构的构建基于文献[6]提出的两个重要角度假设:“180°假设”和“锐角假设”。文献[7]较早研究了河系树结构的建立方法,并提出了河系递归特征的树结构模型,但主流干流仍靠长度识别或者人工指定;文献[8]根据子河系呈现的空间特征,提出利用空间推理的方法确定水流流向和主支流层次关系,丰富扩展了“180°假设”和“锐角假设”的应用范围;文献[9—10]提出基于知觉组织原则构建河流stroke连接方法,却仅涉及建立河系树某些环节的处理,并未形成完整的解决方案;文献[11]结合树状河系自身的结构特点和图论思想,提出了基于图论的河系结构化绘制模型,较好地解决了河系的主流和流向的自动判别问题。当前,依据河系树建立河流层次关系对河流进行选取主要采取“由上及下”(由第1层到第n层)的逐层保留选取方法[12],即通过逐层保留主干河系完成河流选取,尽管这可以较好地保留河系比较重要、层次较高的主要河流,但在选取过程中经常出现删除整条河系的情况,从而破坏了河流的空间分布形态,且无法保证河系边缘的连通性,造成河系边缘的断流。
综上所述,河系树、河系层次关系可以有效地融合河系语义、几何、拓扑等特征对河流进行选取,然而目前的选取方法对河系空间特征的保持仍存在不足。为此,本文将Gestalt认知原则中描述良好连续性的stroke特征引入选取过程中,提出一种顾及stroke特征约束的树状河系层次关系构建及简化方法,即依据树状河系有向拓扑树,综合考虑stroke对象语义、几何及拓扑等特征,构建河系层次关系,进而自动识别河流间距、河网密度等结构特征,实现河系自动简化。
1 树状河系有向拓扑树地图中河系的形态复杂多样,但大多数河系呈树状结构,即河系间具有明显的主支流层次结构,河系之间蕴含着空间上的“父子关系”。树结构是树状河系结构化表达的常用方法,然而,树状河系的内部通常蕴含着多种其他特征的河流,如辫状分支、闭合环路、与湖泊相连等,这些特征制约了河系树的建立。为此,有学者提出了基于河段的河系结构化数据模型,以图论的原理依据拓扑结构对复杂的河系实体进行描述,有效地实现了对于河流实体的一体化表达[13-14]。本文依据上述原理,将复杂河流实体打散为拓扑弧段,以有向拓扑树对河系进行结构化组织。
树状河系带有流向的拓扑结构图也称有向拓扑树(directed topology tree,DTT)[15]。DTT是节点之间弧段的集合,节点记录度、出度、入度等信息[11],弧段(边)的方向定义为从流经起始节点到终止节点时的方向。在实际地图空间数据库中,一条河流因与其他河流交汇,被打散成多条弧段,但它的图层、要素、名称等语义信息,长度、角度、流向等几何信息均融入至弧段中,如弧段的要素名称(featureID)、河流名称(nameID)、图层名称(layerID)蕴含了河流语义属性;弧段的geometry蕴含了河流的角度、长度等几何形状。河流的语义特征、几何特征、拓扑特征构成了河流的有向拓扑树,如图 1所示。
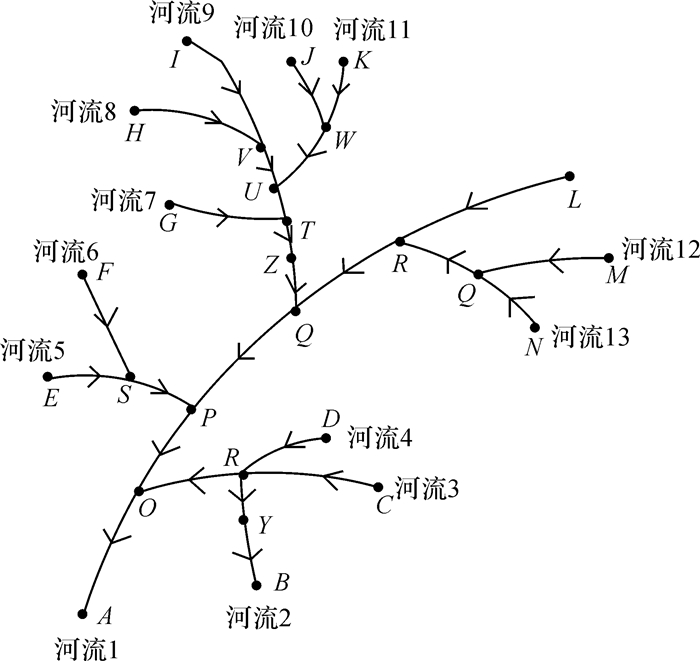
|
| 图 1 树状河系有向拓扑示意图 Fig. 1 Directed topology of tree-like river networks |
基于带有语义信息的有向拓扑树,可智能识别环状、湖泊等复杂水系特征,并建立对应的方法将复杂多样的树状河系转化为基础树状河系,如图 2所示。
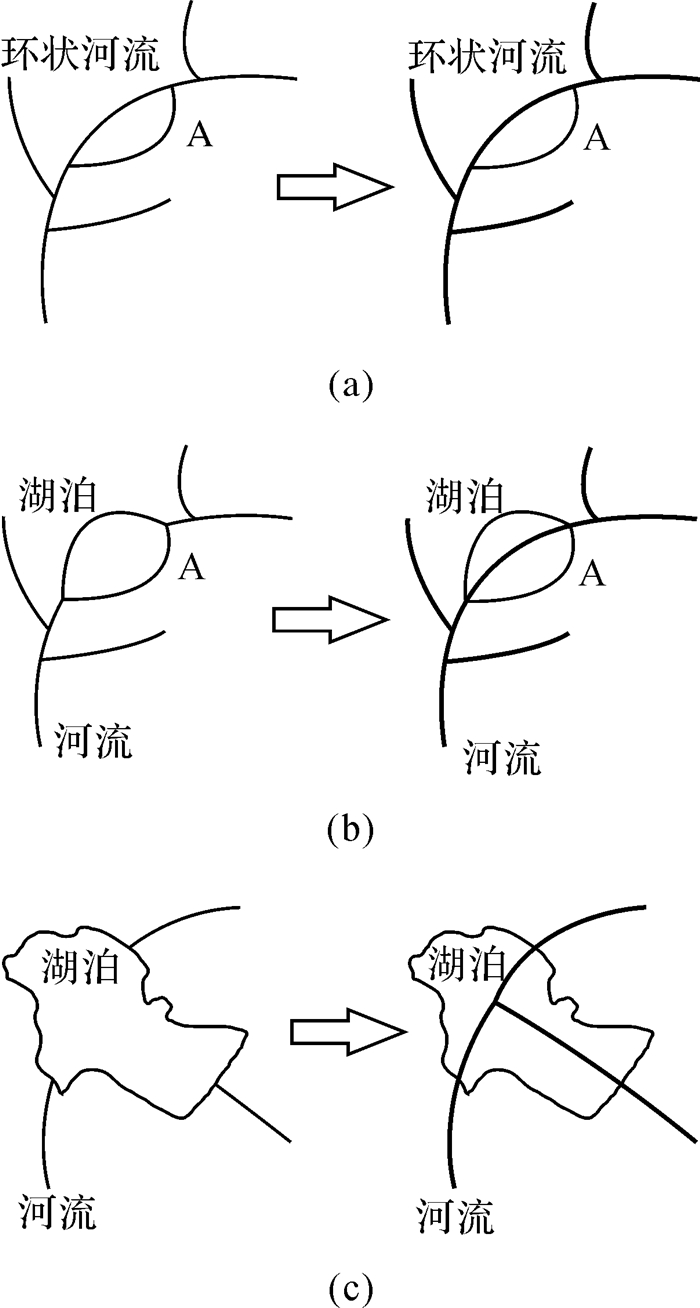
|
| 图 2 复杂树状河系向基础树状河系的转换 Fig. 2 The conversion for tree-like river from complex to simple |
在过去的研究中已完成了针对有环河系的处理[16],并以文献[17—18]所提方法完成河系结构化补偿。基础树状河系的综合是复杂树状河系综合的核心,本文重点研究基础树状河系的结构化综合方法。
2 自下而上stroke特征约束的河系层次关系构建树状河系通常具有多级“父子关系”,从而使得河系中主支流的层次关系变的难以判断。stroke源于Gestalt认知原则中好的连续律,该概念从一笔画出曲线段的思想中产生[19-20]。相较已有方法,基于stroke选取方法可以有效模拟人工选取中的视觉认知原则。本文通过顾及河流语义、长度、角度约束迭代构建树状河系stroke连接,实现河系层次关系的判断。
2.1 确定stroke连接起始节点起始节点对基于stroke连接判断河系主支流层次具有决定性影响。河源和河口是起始节点的首要选择,然而仔细探究树状水系的结构特征可以发现,上游河段通常结构较为复杂,河源众多,不同河源之间的重要性程度难以准确判断,但下游河段的河口往往只有一个。因此,本文从河口出发,采取下游向上游追踪构建stroke连接。
通常一个树状河系只有一个河口,但由于数据采集质量问题或者河系发达,致使存在多个河口,此时需要对这些河口节点进行探索计算,追踪出stroke特征约束的树状河流(简称RivStroke),以确定河系中最适宜作为河口的节点[21]。如图 3中存在A与B两个河口,从河口A、河口B分别追踪出RivStroke_A(AOPQRL)、RivStroke_B(BYR),则分别计算RivStroke_A和RivStroke_B中高等级河流数量,并选择数量多的节点作为河口;如果数量一样,则通过比较RivStroke_A和RivStroke_B的长度,选择长度较长的节点作为河系河口。
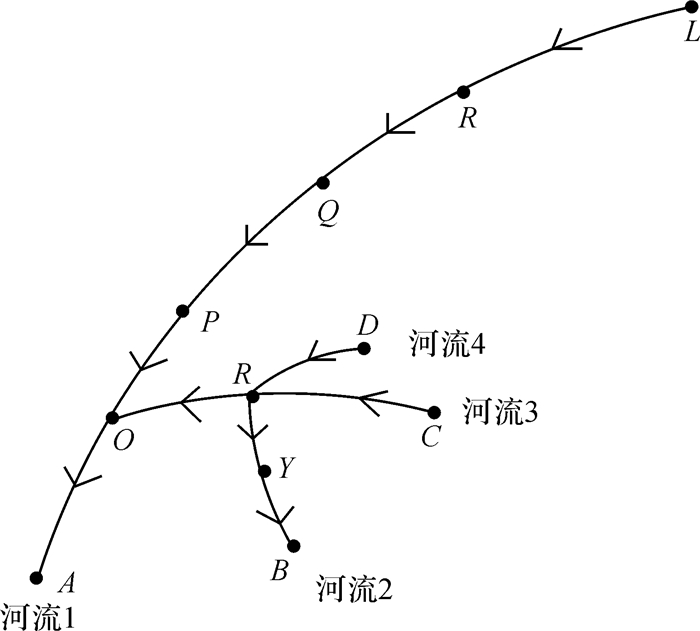
|
| 图 3 河系河口识别 Fig. 3 Identify estuary of river system |
2.2 stroke连接基本原则
stroke特征约束的树状河系(RivStroke)连接原则一般包括以下3项:
(1) 语义一致性。同属一条河流的河流弧段的要素名称(featureID)、河流名称(nameID)一致,因此,名称相同的河流弧段优先建立为同一stroke连接。常年河、干涸河、时令河等不同类别(即不同图层)的河流弧段结合下述长度优先性与方向一致性原则建立stroke连接。
(2) 长度优先性。河段的长度作为除河系语义外构建同一stroke连接的最重要因素,分叉口处长度较大的弧段优先进行stroke连接。
(3) 方向一致性。相连弧段符合良性延续性原则,连接过渡自然,同时夹角越接近180°,越可能建立为同一stroke连接;流向相反的河流不能建立为同一stroke连接。
2.3 迭代构建方法根据上述连接原则,以图 1为例,说明树状河系stroke连接的构建过程:
步骤1:河系河口作为追踪起始节点(点A),河口关联弧段作为追踪弧段(弧段AO),得到弧段的另一个节点(点O),将其作为追踪节点。
步骤2:追踪节点关联弧段作为stroke连接候选集R{AOP,AOR,…},并计算弧段夹角{∠AOP,∠AOR,…}。
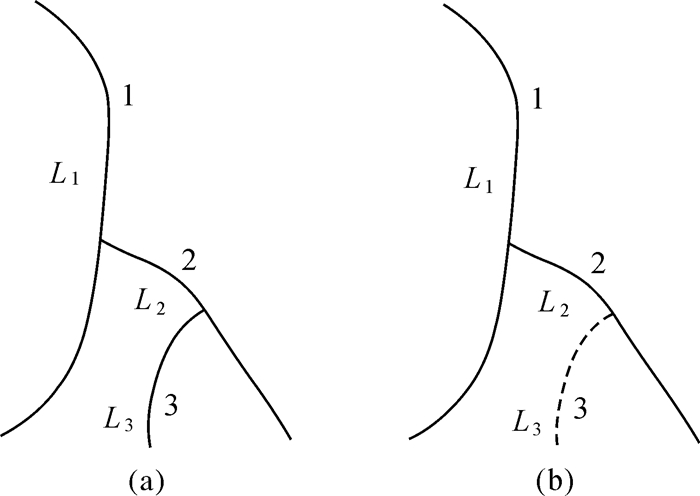
步骤3:按照河流名称、长度值、夹角值的优先级顺序依次建立stroke连接,且保证一个弧段只能在一个stroke连接中,直至R=Φ。如图 4(a)所示,当连接至弧段L1时候,后续追踪的L2、L3两条弧段为连接候选集,其中,弧段L2与L1的名称同为“小石河”,而弧段L3(“三羊河”)与L1的名称不同,此时,河流名称具有较高的连接优先级,为弧段L2与L1建立stroke连接;如图 4(b)所示,弧段L2、L3同样为L1的连接候选集,且3条弧段名称相同(均为“小石河”),但弧段L2的长度大于弧段L3,弧段L3的方向性优于弧段L2,此时,长度较大的弧段相对方向性具有较高的连接优先级,则为L2与L1建立stroke连接;如图 4(c)所示,同一条河流中存在时令河和常年河交叉出现的情况,此时仍可依据方向性为弧段建立stroke连接。
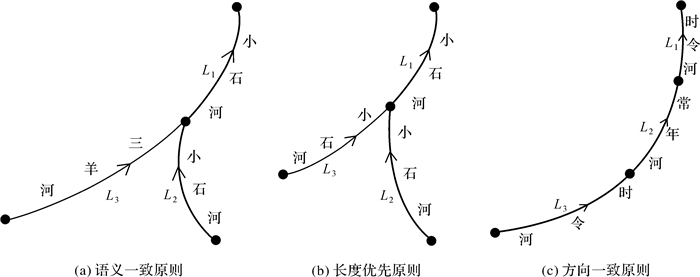
|
| 图 4 stroke构建方法 Fig. 4 Stroke construction method |
步骤4:重复步骤2、3,直至无法得到追踪弧段,追踪节点P处理完成。
步骤5:上面的追踪弧段构成节点P的RivStroke,同时记录下RivStroke中所有的追踪节点。
步骤6:依据上述过程重复迭代处理步骤5中获取的追踪节点,直到河系内所有节点处理完成。
2.4 层次关系河系层级结构隐藏在构建RivStroke的迭代过程中,所有由河系河口追踪出来的RivStroke为一级河流,一级河流的汇入点追踪出来的RivStroke为二级河流。依次类推,得到河系中各个河流的层次关系。从河流分岔点引出的河流认为是河系的一个分支,认为该出河系与分岔点其他河流同一等级。图 5中,一级河流包括河流1(L1~L5),二级河流包括河流3(L6L9)、河流5(L11L12)、河流9(L14L15L16L17L18)、河流13(L24L25)、河流2(L7L8),三级河流包括河流4(L10)、河流6(L13)、河流7(L19)、河流8(L20)、河流11(L21L22)、河流12(L26),四级河流包括河流10(L23)。
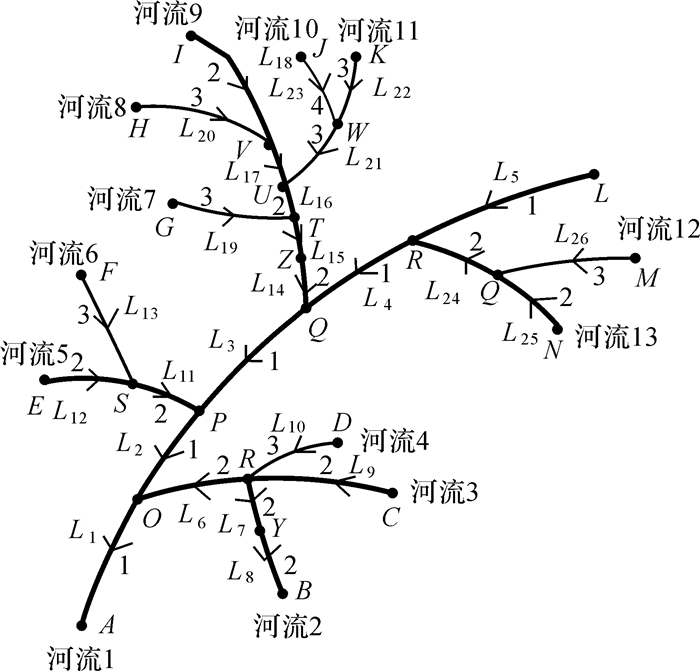
|
| 图 5 河系层次关系 Fig. 5 Hierarchical structure of river system |
3 基于层次关系的河系简化方法
河系简化过程中通常需要考虑多种因素,如河流长度、河网密度、河网类型、等级、层次等,其中河流长度是最基本的选取指标,但河流长度不能全面准确衡量河流的重要性。顾及stroke特征约束的河流层级关系综合考虑了河流的语义特征、几何特征、拓扑特征,对于判断河流的重要性具有重要意义。首先,河系层次关系反映了河系主支流的关系;其次,某一主流拥有支流数量越多,则其层级越高,在选取过程中更应得到保留;子流域的河流总数越大,则河网密度越大,空间分布特征越复杂,选取前后应保持其空间特征不发生明显变化。
3.1 确定选取数量本文采用开方根模型确定河系整体选取数量,开方根模型是德国制图学家F.Topfer根据制图经验提出的地物选取规律公式[22-23]
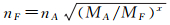 (1)
(1)
式中,nF为新编地物数量;nA为原始地物数量;MA为原始地图比例尺分母;MF为新编地图比例尺分母,x为经验系数,x的取值受河流密度、新编图的制图目的等因素影响,取值范围通常为1~5。
3.2 由外及内分层剔除简化方法河流的选取可通过“河流保留”与“河流剔除”两种方式实现。河流逐层保留选取方法关注位于河系核心位置的主干河流,分层河流剔除选取方法与此思路相反,其处理对象为河系边缘的支流。本文提出一种根据河系拓扑关系进行“由外及内”分层剔除的河流选取方法。在树状河系拓扑结构中,可将弧段分为“主干弧”和“悬挂弧”两种。主干弧指连接各个弧段的中间弧段,通常是主干河流;悬挂弧指弧段(河段)的某一端点未与其他任意一条弧段的端点相连的弧,处在河系外部边缘,主要是无支流的小河系。河系分层之后,某些悬挂弧只与其上层弧段相连,有相对低一级的重要性,这样的弧段称为上一层弧段的“子悬挂弧”,如图 6所示,图 6(a)中位于第3层的弧段L3是位于第2层的弧段L2的子悬挂弧,图 6(b)中当删除位于第3层的弧段L3后,位于第2层的弧段L2即是位于第1层的弧段L1的子悬挂弧。
|
| 图 6 子悬挂弧 Fig. 6 Sub-dangling arc |
分层河流剔除选取方法是一种循环处理子悬挂弧过程,每一次循环包括4个步骤:
步骤1:遍历整条河系,根据河系层次,统计各个层次的子悬挂弧。
步骤2:选取数量非均等分配。将剔除数量分配到各个层次,分配方式按下述公式[1]计算
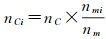 (2)
(2)
式中,nCi为第i层河流的剔除数量;nC为总的剔除数量;nmi为第i层河流数量;nm为各个层次的河流总数。子流域若是含支流少或无支流的小河系,剔除数量可能是0,为此,如果存在许多小河系,则将这些小河系进行统计相加作为一个整体进行计算。选取数量按四舍五入处理为整数。
步骤3:将各个层次的剔除数量分配到各个子流域。
步骤4:在子流域内部每一个层次上依据河流长度和河间距剔除河流。
如此循环,直至剔除的河段数量满足根据开方根模型确定的整体剔除总数,循环结束。
河流的选取需要顾及河流的空间特征,河流长度(L)和河流间距(D)是维持河流的空间密度特征的两项常用指标。为保存化简后河系的空间分布特征不变,长度更大、间隔更远的河流应该得到保留;相反长度较小、间隔较近的河流应该予以删除。但实际情况中,对于长度小、间隔大或者长度大、间隔小的河流尚无明确办法进行区别选取,为此,本文提出应用式(3)计算每一条河流的重要性指数IR
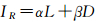 (3)
(3)
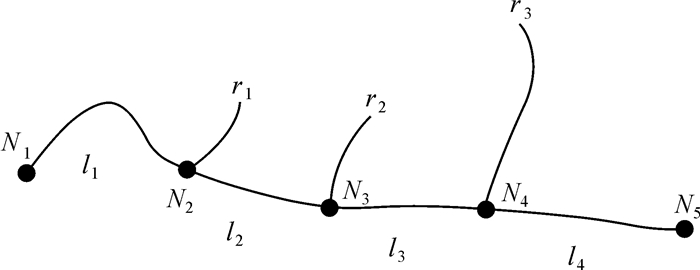
式中,α、β分别为河流长度(L)和河流间距(D)的权重系数,介于0~1之间且其和为1,其值与比例尺、河系特点相对无关,可通过足量的样本数据采用“增量法”解算。河流间距主要指某河流与其属于同一主流的同侧河流间距,本文将某一河流与主流的交点与其前后两条河流与主流的交点的距离之和作为该条的河流的间距值。如图 7所示,对于两侧均有相邻河流的r2而言,其间距值为L2(N3与N2之间的距离)与L3(N3与N4之间的距离)之和;对于只有一侧有相邻河流的r1而言,其间距值为L1(N2与之N1间的距离)与L2(N2与N3之间的距离)之和。这种方法计算河流的间距,可以充分考虑河流的上下文环境,且该值不会受河流夹角的影响。当存在两条河流的重要性指数IR相同时,则按长度指标进行选取;若长度指标也相等,说明长度、间距、长度权重系数、间距权重系数全部相等,则任选其一。
|
| 图 7 河流间距值的计算方法 Fig. 7 Computing method for river spacing |
3.3 α、β的确定
河流长度(L)和河流间距(D)权重系数α、β的确定是本文方法的关键,对于河系最终的选取结果具有决定作用,本文通过样本数据采用“增量法”进行解算。
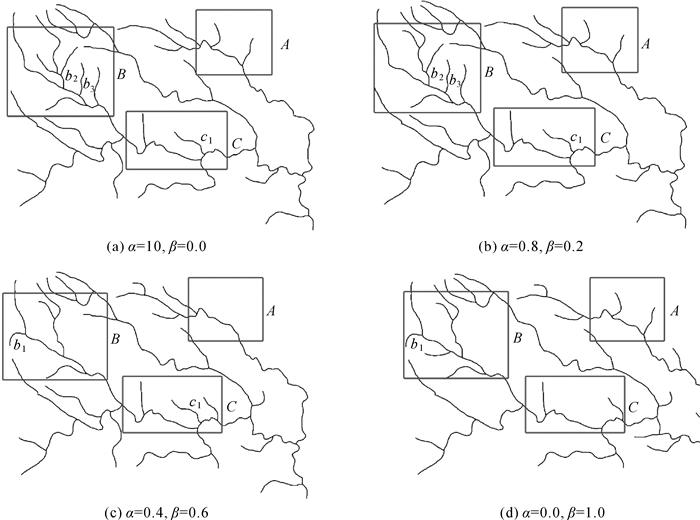
样本数据取自文献[3],为湖北省西部部分1:20万水系图,共有68条河流(图 9(a)),本文通过将其综合至1:50万说明参数α、β的确定方法。取0.1为增量,则0~1之间共有11组数据,分别应用各组数据对该水系图进行选取,部分试验结果见图 8。可以看到,当α>β时,图 8(a)、8(b)中试验数据区域B、C中选取的弧段均为长度相对较大的河流,相比图 8(c)、8(d),河系分布比较密集,河流间距较小;随着α的减小、β的增大,部分长度较短但与其他河流间距较大的弧段得到保留(如图 8(c)、8(d)的b1),河流较长但间距较近的河流被剔除(图 8(a)、8(b)中的b2、b3;图 8(a)、8(b)、8(c)中的c1)。通过将选取结果与文献[3]中的手工简化图 9(b)对照,选出最接近图 9(b)的方案是α=0.8,β=0.2(图 8(b))。
|
| 图 8 α、β部分取值及相应选取结果图 Fig. 8 Some values of α, β and the corresponding selected results |
4 试验与分析
依托中国测绘科学研究院研制的WJ-Ⅲ地图工作站,嵌入本文提出的河系简化方法,分别在少量样本数据和实际河系数据上进行试验,验证本文方法的可靠性和合理性。
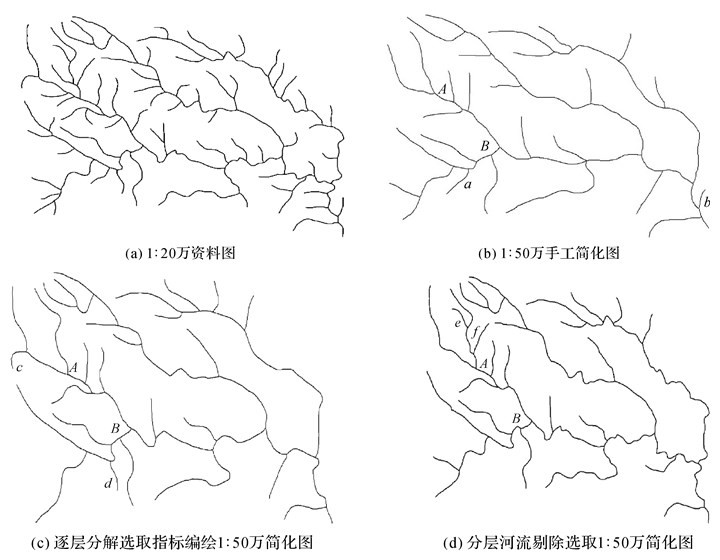
4.1 可靠性分析为了验证本文方法的可靠性,同样采用文献[3]中湖北省西部部分1:20万水系图(图 9(a))作为样本数据,简化目标比例尺为1:50万,并与手工选取方法(图 9(b),已作化简处理)、文献[1]按层次分解选取指标的方法(图 9(c),已作化简处理)进行比较。试验中相关参数设置如下:式(1)中的指数x取2,保持与文献[1]一致,α、β的值为0.8、0.2。根据上述参数,得到按照本文方法选取的1:50万水系图(图 9(d),未作化简处理)。
|
| 图 9 河系选取可靠性试验结果对比图 Fig. 9 Comparison of generalization experimental results |
采用目视比较方法评价河流选取结果,可以看出,图 9(d)选取的河流与图 9(b)、9(c)基本一致,河系中心弧段和边缘弧段的选取数量分配较为合理,河流密度的区域差异及河系的空间结构特征在综合后的图上保持得较好,选取的河流很好地照顾了河流长度和间距的平衡,不存在间隔较密、长度较短的河流,选取效果较好,证明了使用本文方法进行河流选取的可靠性。
进一步分析可以发现,图 9(d)在河系密集的子流域A中选取的河段数量比图 9(b)、9(c)多2(河段e、f),在保持河系的整体空间分布结构方面效果良好,同时图 9(d)剔除了图 9(b)、9(c)中较短的河段(河段b、c),保证了简化后图形选取均为较长的河流,子流域B中选取的河段数量比图 9(b)、9(c)少1(河段a、d),实现了河系基本轮廓的保持。
4.2 实际数据试验对湖北省某县1:1万地理国情水系数据进行试验验证本文方法的性能及有效性,试验数据的空间大小为90.91×106.56 km2,空间范围内水系发达,共有944条河流。数据预处理阶段首先去掉河网中的闭合环,使其成为树状结构;进而识别河口河段,采取“自下而上”方式迭代构建stroke特征约束的河系层次关系,如图 10所示。因试验区河段过多,图中只对1、2、3层河流进行了标注。
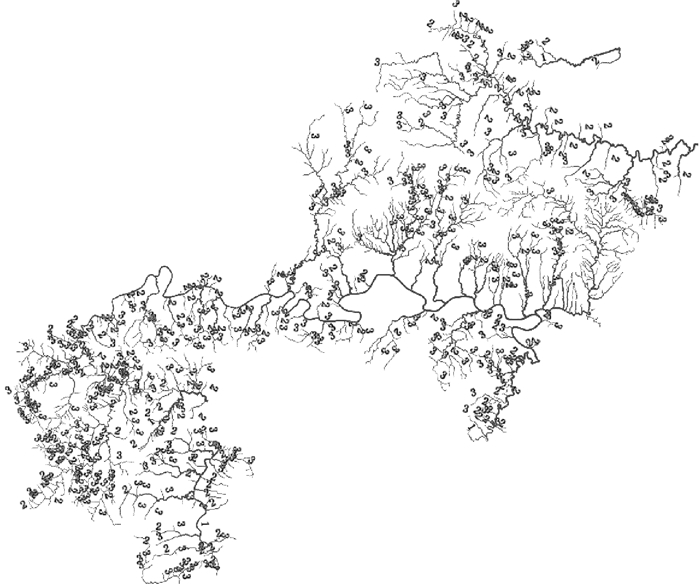
|
| 图 10 原始数据及其层次关系 Fig. 10 Original data and its hierarchical relation |
选取1:5万、1:10万、1:25万作为目标比例尺,首先采用开方根规律计算河流的整体选取数量。开方根模型计算简单,但其参数x受原比例尺与目标比例尺之间跨度影响[24-25],跨度越大,线状符号在空间中缩减的速度越快。为此,本文将各个目标比例尺中x的取值分别设为1、1、2,参数α、β的值为0.8、0.2。最后依据本文提出的河流剔除选取方法选取河流(未作河流化简),直到选取数量达到要求为止,各个目标比例尺选取结果如图 11(b)、11(c)、11(d)所示,各层次河流数量如表 1所示。
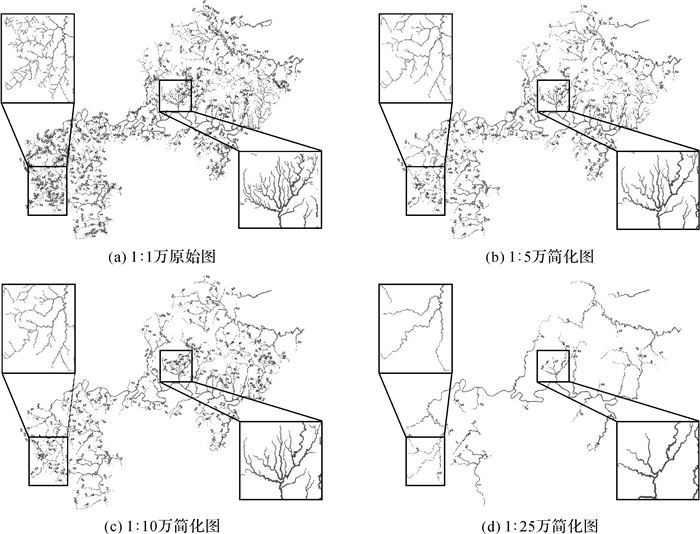
|
| 图 11 实际河系数据不同目标比例尺选取结果 Fig. 11 Selection results of different target scales for real river data |
| 比例尺 | x | 河流条数 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 | 七级 | 八级 | 九级 |
| 1:1万 | 1 | 944 | 6 | 203 | 351 | 245 | 100 | 27 | 9 | 2 | 1 |
| 1:5万 | 1 | 418 | 6 | 111 | 154 | 100 | 35 | 9 | 2 | 1 | 0 |
| 1:10万 | 1 | 296 | 6 | 90 | 107 | 66 | 20 | 5 | 1 | 1 | 0 |
| 1:25万 | 2 | 40 | 6 | 21 | 8 | 3 | 1 | 1 | 0 | 0 | 0 |
由图 11可知,采用本文方法对于多个目标比例尺进行河系选取的结果在不同尺度上较为准确地反映了河系原始的空间分布特征及不同子流域的河系密度差异,有效地避免因层级较高的河流被删除而导致与其相关的子流域全部被删除的情况,且较好地保证了河系边缘的连通性,不会出现河系边缘的断流。
由表 1可以发现,采用本文“由外及内”分层剔除选取方法较好地保留了河系主干部分,一级河流由于位于内层核心位置,在选取中一直会被保留,各个支流的取舍也较好地照顾了支流数量在河系中所占的比例,保证了河系的空间分布特征,且随着目标比例尺的逐渐缩小,层次越低的河系会优先被剔除。
此外,本文方法已在湖北、贵州等省份地理国情普查专题数据综合缩编中进行了实际应用,并取得了良好的效果,验证了本文方法的合理性和有效性。
5 结束语河系的自动简化是河系综合中的重点和难点,本文提出了一种顾及stroke特征的树状河系层次关系构建及简化方法,在考虑河系对象等级、长度、角度等因素的基础上,进一步融入河流间距、河网密度等结构特征指标进行河系“由外及内”分层剔除选取,较好地解决了传统方法中难以保持树状河系原有空间分布特征这一难题。试验结果表明,文中提出的简化方法在保留骨架河系的同时,也较好地保持了河网空间分布特征及密度差异,选取结果与人工选取结果基本一致,且选取过程易于程序实现。
目前本研究主要完成了树状河系的分层剔除选取,对于顾及居民地等其他要素对象对河系选取的约束以及本文方法对于其他类型河系(如格状、不规则状等)选取的适应性将在今后的研究中得到更深入的探讨。
| [1] |
何宗宜.
地图数据处理模型的原理与方法[M]. 武汉: 武汉大学出版社, 2004.
HE Zongyi. Elements and Methods of Model for Cartographical Data Processin[M]. Wuhan: Wuhan University Press, 2004. |
| [2] |
毋河海.
自动综合的结构化实现[J]. 武汉测绘科技大学学报, 1996, 21(3): 277–285.
WU Hehai. Structured Approach to Implementing Automatic Cartographic Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996, 21(3): 277–285. |
| [3] |
邵黎霞, 何宗宜, 艾自兴, 等.
基于BP神经网络的河系自动综合研究[J]. 武汉大学学报(信息科学版), 2004, 29(6): 555–557.
SHAO Lixia, HE Zongyi, AI Zixing, et al. Automatic Generalization of River Network Based on BP Neural Network Techniques[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 555–557. |
| [4] |
张青年.
顾及密度差异的河系简化[J]. 测绘学报, 2006, 35(2): 191–196.
ZHANG Qingnian. Generalization of Drainage Network with Density Differences[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 191–196. |
| [5] |
艾廷华, 刘耀林, 黄亚锋.
河网汇水区域的层次化剖分与地图综合[J]. 测绘学报, 2007, 36(2): 231–236, 243.
AI Tinghua, LIU Yaolin, HUANG Yafeng. The Hierarchical Watershed Partitioning and Generalization of River Network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 231–236, 243. |
| [6] | PAIVA J, EGENHOFER M J, FRANK A U. Spatial Reasoning about Flow Directions: Towards an Ontology for River Networks[C]//Proceedings of the XVⅡ International Congress for Photogrammetry and Remote Sensing. [S. l. ]: ISPRS, 1992: 224-318. |
| [7] |
毋河海.
河系树结构的自动建立[J]. 武汉测绘科技大学学报, 1995, 20(S): 7–14.
WU Hehai. Automatic Establishment of River Tree Structure[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995, 20(S): 7–14. |
| [8] |
郭庆胜, 黄远林.
树状河系主流的自动推理[J]. 武汉大学学报(信息科学版), 2008, 33(9): 978–981.
GUO Qingsheng, HUANG Yuanlin. Automatic Reasoning on Main Streams of Tree River Networks[J]. Geomatics and Information Science of Wuhan University, 2008, 33(9): 978–981. |
| [9] | THOMSON R C, BROOKS R. Exploiting Perceptual Grouping for Map Analysis, Understanding and Generalization: the Case of Road and River Networks[C]//Proceedings of the Fourth International Workshop on Graphics Recognition Algorithms and Applications. Kingston, Ontario, Canada: Springer, 2001: 148-157. |
| [10] | THOMSON R C, BROOKS R. Efficient Generalization and Abstraction of Network Data Using Perceptual Grouping[C]//Proceedings of the 5th International Conference on Geo-Computation. Greenwich, UK: Chatham, 2000: 23-25. |
| [11] |
张园玉, 李霖, 金玉平, 等.
基于图论的树状河系结构化绘制模型研究[J]. 武汉大学学报(信息科学版), 2004, 29(6): 537–539, 543.
ZHANG Yuanyu, LI Lin, JIN Yuping, et al. Structured Design of Dendritic River Networks Based on Graph[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 537–539, 543. |
| [12] |
张青年.
逐层分解选取指标的河系简化方法[J]. 地理研究, 2007, 26(2): 222–228.
ZHANG Qingnian. Drainage Generalization by Layered Division of the Number of Retained Rivers in River Trees[J]. Geographical Research, 2007, 26(2): 222–228. |
| [13] |
卢开澄, 卢华明.
图论及其应用[M]. 2版. 北京: 清华大学出版社, 1995.
LU Kaicheng, LU Huaming. Graph Theory and Its Applications[M]. 2nd ed. Beijing: Tsinghua University Press, 1995. |
| [14] |
翟仁键, 薛本新.
面向自动综合的河系结构化模型研究[J]. 测绘科学技术学报, 2007, 24(4): 294–298, 302.
ZHAI Renjian, XUE Benxin. A Structural River Network Data Model for Automated River Generalization[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2007, 24(4): 294–298, 302. |
| [15] |
吴静, 邓敏, 刘慧敏.
一种有向线间拓扑关系与方向关系的集成表达模型[J]. 武汉大学学报(信息科学版), 2013, 38(11): 1358–1363.
WU Jing, DENG Min, LIU Huimin. An Integrated Model to Represent Topological Relation and Directional Relation Between Directed Line Objects[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11): 1358–1363. |
| [16] |
郝志伟, 李成名, 殷勇, 等.
一种启发式有环河系自动分级算法[J]. 测绘通报, 2017(10): 68–73.
HAO Zhiwei, LI Chengming, YIN Yong, et al. A Heuristic Algorithm for Automatic Classification of River System with Ring[J]. Bulletin of Surveying and Mapping, 2017(10): 68–73. DOI:10.13474/j.cnki.11-2246.2017.0318 |
| [17] |
乔庆华, 吴凡.
河流中轴线提取方法研究[J]. 测绘通报, 2004(5): 14–17.
QIAO Qinghua, WU Fan. Research on Methods for Medial Axis Extraction[J]. Bulletin of Surveying and Mapping, 2004(5): 14–17. |
| [18] |
艾自兴, 毋河海, 艾廷华, 等.
河网自动综合中Delaunay三角的应用[J]. 地球信息科学, 2003, 5(2): 39–42.
AI Zixing, WU Hehai, AI Tinghua, et al. The Application of Delaunay Triangulation in River Net Automatic Generalization[J]. Geo-Information Science, 2003, 5(2): 39–42. |
| [19] | LIU Xingjian, ZHAN F B, AI Tinghua. Road Selection Based on Voronoi Diagrams and "Strokes" in Map Generalization[J]. International Journal of Applied Earth Observation and Geoinformation, 2010, 12(S2): S194–S202. |
| [20] |
杨敏, 艾廷华, 周启.
顾及道路目标stroke特征保持的路网自动综合方法[J]. 测绘学报, 2013, 42(4): 581–587, 594.
YANG Min, AI Tinghua, ZHOU Qi. A Method of Road Network Generalization Considering Stroke Properties of Road Object[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 581–587, 594. |
| [21] |
吴伟, 李成名, 殷勇, 等.
有向拓扑的河系渐变自动绘制算法[J]. 测绘科学, 2016, 41(12): 89–93.
WU Wei, LI Chengming, YIN Yong, et al. An Atomatic Plotting Algorithm of the Gradual Change of River Based on Directed Topology[J]. Science of Surveying and Mapping, 2016, 41(12): 89–93. |
| [22] | REGNAULD N. Contextual Building Typification in Automated Map Generalization[J]. Algorithmica, 2001, 30(2): 312–333. DOI:10.1007/s00453-001-0008-8 |
| [23] |
TOEPFERF.
开方根规律在制图综合中应用范围的研究[J]. 测绘译丛, 1963(2): 35–39.
TOEPFER F. Study of the Application of the Principle of Square Root in Cartographic Generalization[J]. Translated Collection of Surveying and Mapping Press, 1963(2): 35–39. |
| [24] |
王家耀, 李志林, 武芳.
数字地图综合进展[M]. 北京: 科学出版社, 2011.
WANG Jiayao, LI Zhilin, WU Fang. Advances in Digital Map Generalization[M]. Beijing: Science Press, 2011. |
| [25] |
毋河海.
地图综合基础理论与技术方法研究[M]. 北京: 测绘出版社, 2004.
WU Hehai. Research on the Basic Theory and Technology Method of Map Generalization[M]. Beijing: Surveying and Mapping Press, 2004. |



