车载激光扫描(mobile laser scanning,MLS)能快速获大场景点云数据,在道路交通领域有应用价值和潜力[1-2],如道路信息调查[3]和智能驾驶高精度三维地图制作[4]。MLS硬件系统发展很快,形成了多种类型的商业化产品,该系统必要组件包括激光扫描仪、高精度POS系统和高精度时间同步控制系统[5]。由于MLS测量存在视场限制和遮挡,需要将地面激光扫描(terrestrial laser scanning,TLS)点云数据作为补充。MLS点云位于大地坐标系,TLS点云位于局部坐标系,需要进行坐标转换。本文采用TLS与MLS点云配准以完成基准统一。
点云自动配准一般按“初始配准”和“精配准”两步进行[6]。点云精配准最著名的算法是ICP算法[7-9]。最小二乘3D(least-squares 3D,LS3D)表面配准[10]近些年也被采用。ICP和LS3D均使用局部优化算法,局部优化收敛性依赖于初始转换参数。初始配准为精配准提供初始值,研究最多的是特征匹配。特征匹配通过在重叠区自动提取特征建立对应关系,所采用的特征需要具有旋转和平移不变性,如曲率和点标签[11]、旋转图像(spin image)[12]、快速点特征直方图(FPFH)[13]。文献[14—15]对已有特征描述子进行了总结,并比较了它们的性能,结果表明特征提取方法需谨慎选择。点云特征匹配面临分布不均匀、噪声、部分重叠、数据量大、重复结构等诸多问题,加上无法准确度量同名对应关系的几何质量,特征匹配的优化往往耗时且容易失败[16]。
除两步配准外,遗传算法(genetic algorithm,GA)可一步完成配准[17]。GA是一种全局优化算法,采用在整个解空间全局自适应地搜索最优解[18]。GA很早被应用于3D医学点云配准[19]。文献[20]分析了GA应用在点云配准中的细节,提出了基于均方误差(mean square errors,MSE)的配准模型。文献[21—23]均采用基于MSE的配准模型进行GA配准。MSE度量准则源自局部优化算法,需要转化为最大化的适应度值用于评价转换参数的好坏程度。与基于特征的配准相比,GA配准不需要特征提取和描述;与ICP相比,GA配准不依赖于初始转换参数,但效率更低。论文提出一种结合GA与ICP的高效率自动配准方法。
1 GA简述GA是一种采用随机搜索机制的全局优化方法,模拟生物进化过程,即保持一个候选解组成的种群,用3个遗传操作完成进化:选择、交叉和变异[18, 24-26]。不同的优化问题,进化操作的解表达形式不同。解转化为其表达形式的过程称为编码,即将搜索空间的解表示为由多个基因组成的可遗传操作的染色体,形式上为一个向量。解码是编码的逆操作。数值优化问题采用数值编码和解码方法,常用方法为二进制和浮点编码[26]。前者是将实数解转为二进制数构成染色体,相应解码为二进制数染色体转成实数解;后者直接将实数解作为染色体,无须解码。实数编码没有转化精度损失,效率更高,也易与经典优化估计方法结合使用[18]。
标准GA包括3个主要步骤:种群初始化、适应度计算和遗传操作。在确定编码方式后,进行种群初始化生成候选解集。种群是由个体组成的集合{Pop| Ch1,Ch2,…,ChM}。M为个体数目,其经验值取几十至几百。种群初始化方法一般为均匀随机生成搜索空间内样本集合。搜索空间是优化问题的解域,定义为[-U,U],U为搜索空间上限。GA优化获得最优解的过程是种群进化的过程,适应度用于评价解的好坏,是选择操作的依据。适应度函数是非负最大的,一般由目标函数转化而来。由于搜索空间、适应度函数定义与实际问题相关,点云配准的相关定义在GA配准一章阐述。
遗传操作是模拟生物基因产生下一代的操作,包括选择、交叉和变异。选择操作是从父代总群中选择M个染色体作为子代进行进化。某一个体被选中的机会应当与适应度值成比例,适应度越高,被选中的概率越大。期望值选择[26]是一种较好的算法,可以确保适应度值较大的个体以较高的概率被选择。首先,直接复制∑Numi个个体到下一代
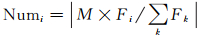 (1)
(1)
式中,Fi为第i个个体的适应度值。复制后剩余适应度值为
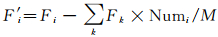 (2)
(2)
所有个体的剩余适应度值用于按适应度比例随机选择余下的M-∑Numi个个体。
交叉操作通过双亲染色体的基因值依交叉概率Pc作运算产生两个新的个体,变异操作依变异概率Pm改变染色体一个或多个基因值产生新个体。交叉与变异操作与编码方式有关。算术交叉和非均匀变异方法适用于浮点编码方法[18],在本文提出的方法中被采用。依经验,Pc取0.6~1的值,Pm不大于0.1。为了让某一代的最优解不被交叉和变异操作破坏,适应度值最高的个体直接复制到下一代群体中。
适应度值计算和遗传操作迭代进行,构成了GA进化过程。GA进化的终止条件为以下两个条件满足任意一个时:
(1) 最大代数maxgen:进化代数达到maxgen时终止;
(2) 最大适应度保持不变代数maxbest:最大适应度值已maxbest代(相邻两代最大适应度值相等)保持不变则终止。为了获得全局最优解,maxgen和maxbest不能过小。
2 配准方法 2.1 问题描述点云配准分解为两个子问题:如何建立同名对应关系(correspondences,CORRS);如何利用CORRS构造优化目标函数估计坐标转换参数。传统基于特征的配准是先提取关键点(特征明显且感兴趣的点),对关键点进行描述,再利用相似关系建立CORRS;采用RANSAC算法剔除错误CORRS,并估计最优转换参数。ICP配准利用距离最近点构造CORRS,再利用距离阈值和法向量夹角阈值剔除错误CORRS,进而估计最优转换参数。基于特征的配准和ICP配准归纳为4步[27]:点云选择、CORRS建立、错误CORRS剔除、转换参数估计。点云选择是选择部分的点用于配准,目的是提高配准效率。基于特征的配准关键点提取的过程即为点云选择。ICP配准则采用下采样完成点云选择,应用较多的方法为法线空间采样,它在法向量空间内均匀随机抽样,结果表现为地物特征变化大的地方剩余点较多,变化小的地方剩余点稀少,可有效保持地物特征[9]。
给定待配准点云S的匹配点Si,基准点云T的点Ti,点云配准首先建立S和T的对应关系(Si,Tj),再根据对应关系建立目标函数并估计最优转换参数。这里,S为TLS点云,T为MLS点云。点云配准采用的变换模型如下[27]
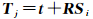 (3)
(3)
式中,S是待配准点云,Si=[Sxi Syi Szi]T为第i个配准点;基准点云T,Tj=[Txj Tyj Tzj]T为对应点;t=[tx ty tz]T为平移向量;R表示旋转矩阵,是x、y、z轴三个旋转角α、β、γ的函数。
传统配准方法的优化目标为CORRS距离平方和最小,即MSE度量
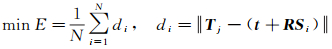 (4)
(4)
式中,N为CORRS数目。
2.2 GA配准GA本身是一种全局的启发式的优化方法,它在整个转换参数空间自适应搜索最优解。这里将GA配准概括为4个步骤(如图 1所示):总群初始化和点云选择,待配准点云转换,适应度计算,遗传操作。后3个步骤迭代计算,构成GA进化过程。总群初始化和GA进化已作了描述。在预处理后,点云数据量仍然较大,很多点位于地面,需用点云选择提高配准效率。GA配准点云选择方法与ICP配准相同,即为法线空间采样法。
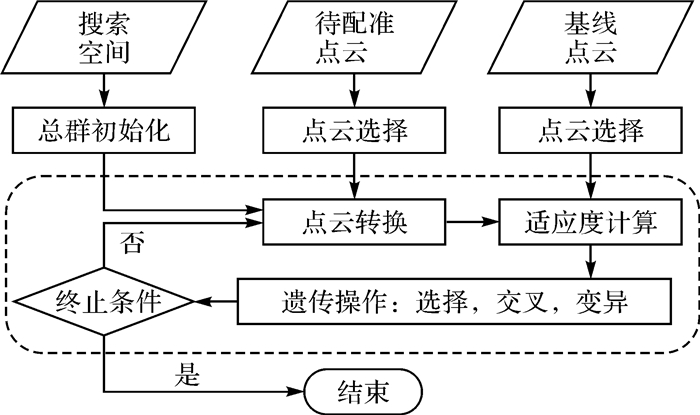
|
| 图 1 遗传算法配准流程 Fig. 1 The flow chart of the proposed GA registration 虚线框内为遗传进化过程 |
GA配准建立CORRS的方法为先对待配准点云进行转换,然后用邻近点搜索距离最近点建立CORRS。点云转换和邻近点搜索需要对总群每一个体分别进行,为计算最耗时的阶段。点云转换和适应度计算对个体的计算是独立的,可以采用多核并行运算,本文采用OpenMP编程[28]作加速。
传统配准采用最小化形式的目标函数E估计最优参数,GA配准依最大化形式的适应度F进行优化。F由E转换而来,常用方法为负指数函数作转化函数
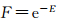 (5)
(5)
由于S和T部分重叠,文献[17, 20]提出在GA配准中使用距离截断MSE模型对式(4)作修正。距离截断函数为
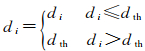 (6)
(6)
式中,dth为距离阈值,它是重叠区域CORRS的最大距离。Silva模型将CORRS分为两类:重叠区域内为内点和非重叠区域内为外点。该模型意味着通过最小化MSE同时最大化内点数目得到最优转换参数。
2.3 搜索空间GA是在整个搜索空间进化搜索最优解的过程。点云配准的搜索空间由转换参数的上界U确定,即[-U,U]。在任意情况下,α、β、γ的上界为180°,tx、ty、tz是无界的。如果搜索空间过大,GA收敛慢,或早熟(收敛至局部最优),或退化为随机搜索。搜索空间越小,GA收敛速度越快,配准效率越高。因此,确定一个有限且尽可能小的搜索空间是必要的。
本文将TLS扫描仪设站粗略位置作为先验信息限定搜索空间。扫描仪设站的粗略位置可由内置GPS获取。关于内置GPS的信息量少,可了解的是它采用单点定位方式,定位精度达分米级或米级[29]。tx、ty、tz的取值在位置误差范围内,本文将其设定为10 m。α、β与扫描平台的水平程度有关,它们的值通常很小,一般在5°以内;γ与北向对准有关,在任意设站时的范围是[-180°,180°)。因此,转换参数的搜索空间为(α,β,γ,tx,ty,tz |α,β∈ [-5°,5°],γ∈ [-180°,180°],tx,ty,tz∈ [-10 m,10 m]),即U等于[5°, 5°, 180°, 10 m, 10 m, 10 m]。
如果所采用的扫描仪不带内置GPS,可采用其他的辅助测量方式获取设站位置,如外置GPS或GPS RTK。GPS RTK采用差分GPS定位,精度达厘米级,则tx、ty、tz的搜索范围可限定在0.1 m以内,即tx,ty,tz∈ [-0.1 m,0.1 m,0.1 m]。无论采用何种辅助测量方式,平移向量的搜索范围应根据定位精度进行设置。
2.4 NSMS配准模型已有GA配准方法采用基于MSE的配准模型。MSE度量源自局部优化算法,应用于全局优化精度会受影响。对应点满足di≤dth时为内点,增加K个内点,目标函数值为
 (7)
(7)
通过作差计算,如果di≤1,则EK≤E;否则EK>E。当dth>1 m(文献[17]取值为5 m,本文取值2 m)且1 < di≤dth时EK>E,即增加内点目标函值增大,与内点增加目标函数减小的期望相反。
这里则提出了NSMS配准模型,该模型直接依距离映射函数计算F,并将法向量约束引入配准模型进行优化。NSMS配准模型的形式如下
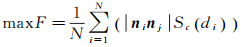 (8)
(8)
式中,ni和nj为对应点的归一化法向量;Sc为距离映射函数,其值称为匹配分数。Sc需要满足:0 < Sc≤1,单调递增。第1个条件使得F是归一化的,不会随CORRS数目增大而无限增大;第2个条件使距离越大,分数越小,即对F贡献越小。
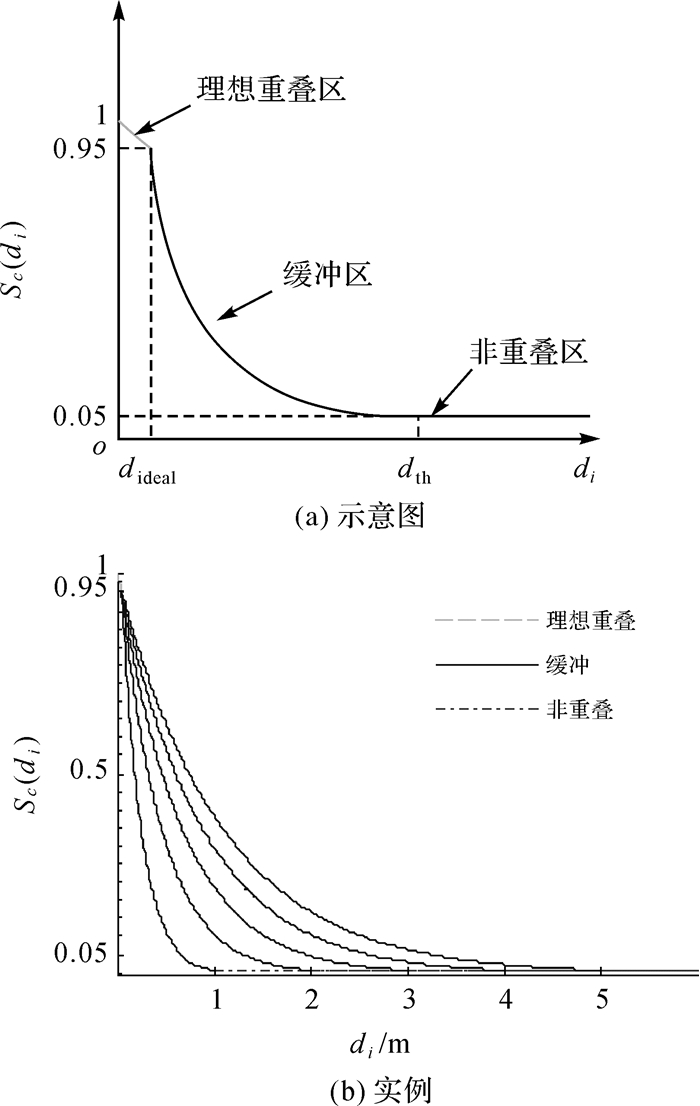
同Silva模型一样,这里将整个匹配区域也分为重叠区域和非重叠区域。为了保证距离较近的CORRS获得高的分数,重叠区域又分为理想重叠区域和缓冲区域。重叠区域内两个区域分段处的距离阈值称为理想距离dideal。在dideal处,匹配点被赋予分数高置信度0.95;在dth处,被赋予分数低置信度0.05。利用负指数函数定义连续的匹配分数函数(如图 2所示)。
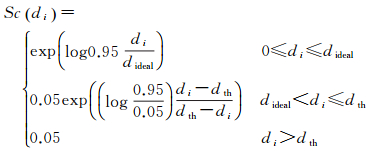 (9)
(9)
|
| 图 2 NSMS模型的匹配分数函数 Fig. 2 The matching score function of the proposed NSMS model |
NSMS模型带两个参数dideal和dth。dideal一般较小,本文取0.05 m。如果dth较小,则内点较少,总群的整体适应度值较小,不利于遗传进化,即很难搜索到最优解;其值较大,总群的整体适应度值较大,容易搜索到最优解,但分数函数变化较缓(图 2(b)),个体差异变小,所获解的精度较低。由于搜索空间已经限定,本文取适当值dth=2 m。
2.5 GA与ICP融合策略由于GA采用全局搜索策略,其收敛性不依赖于初始值,但计算效率低,局部收敛慢,因此进一步提出采用GA与ICP相结合的配准策略以提高配准效率。结合方式为:先采用GA配准,当进化到一定代数时,GA已经趋于局部搜索,其获得的解已接近于最优化解,此时改用ICP进行局部优化。由于局部范围内的GA适应度比较接近,为控制GA的终止精度,可将GA第2个终止条件中的“相邻两代最大适应度相等”改为“相邻两代最大适应度之差的绝对值小于e″。e是微小正数,一般取10-3~10-2。
3 试验与分析为验证GA配准的有效性,NSMS配准模型的优越性以及GA与ICP融合配准策略的高效性,采用两组实测数据进行了试验。图 3(a)所示为数据1,待配准点云S约1.3千万点,基准点云T约1.1千万点;图 3(b)所示为数据2,待配准点云S约5.2千万点,基准点云T含1千万点。两组数据重叠度均约为50%;使用的地面激光扫描仪为Riegl VZ400,设站粗略位置均通过扫描仪内置GPS获得。

|
| 图 3 试验点云 Fig. 3 The test point clouds 蓝色为待配准点云; 红色为基准点云 |
点云数据量大、含噪声,且配准需要法向量,因此对点云进行了预处理。预处理过程为:剔除扫描距离较大的点,这里距离阈值根据扫描仪的有效距离设置为100 m;进行均匀间隔下采样,采样间隔为2.5 cm;根据邻域局部协方差矩阵估计法向量与曲率估计[30];树叶易随风飘动,树叶点对配准有影响,其呈散状分布,曲率大,通过曲率阈值0.05可予剔除,如图 4所示。预处理后,数据1中S的点约占原始的19%,T的点约占原始的58%,效果见图 3(c);数据2中S的点约占原始的9.5%,T的点约占原始的45%,效果见图 3(d)。可见,预处理后点云数据量明显减小,但原有特征信息仍然保留。

|
| 图 4 散状点剔除 Fig. 4 The removal of scattered points 点云按高程值渲染 |
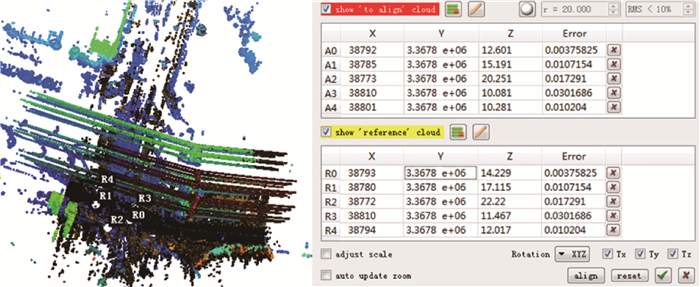
为定量评价GA配准精度,将待配准点云S与其参照点云Sref的距离均方根误差RMSE作为衡量指标。Sref是S的理论值。理论值是未知的,这里通过人工选择特征点进行粗配准(如图 5),再采用ICP精配准获得S和T之间的转换参数,将S转换点云近似作为Sref。为剔除错误的对应关系,ICP配准的对应点距离阈值设为0.2 m,法向量夹角阈值为10°。
|
| 图 5 人工选择特征点进行粗配准 Fig. 5 Coarse registration by manually selected eigen points |
因用于配准的点云是依法向量空间随机选择且GA采用随机搜索机制,各组配准试验均独立进行了50次,以统计结果进行评估。为剔除错误的对应关系,ICP算法的对应点距离阈值设为0.2 m,法向量夹角阈值为10°。试验运行环境为:Intel Core i7-4790 CPU @ 3.60 GHz,4核心处理器和8 G内存。详细的GA配准参数见表 1,计算机线程数目等于8。
| 名称 | 符号 | 数值 |
| S选择比例 | PS | 0.5% |
| T选择比例 | PT | 5% |
| 总群大小 | M | 100 |
| 理想距离/cm | dideal | 5 |
| 距离阈值/m | dth | 2 |
| 最大进化代数 | maxgen | 300 |
| 最优个体不变代数 | maxbest | 20 |
| GA+ICP终止进化精度 | e | 10-3 |
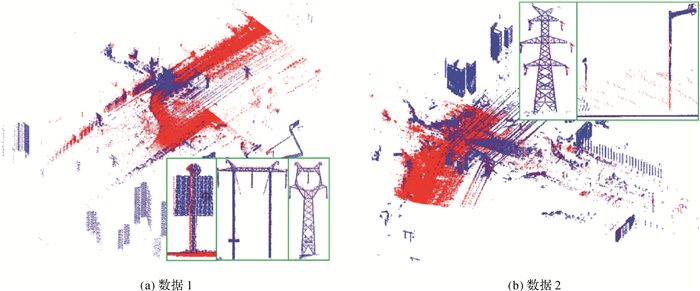
采用NSMS模型与Silva模型的GA配准对比试验结果如表 2所示。NSMS模型的精度和效率均优于Silva模型,平均优化时间高于Silva模型20%左右,RMSE在1至5 cm之间。采用NSMS模型的GA配准效果如图 6所示。在具有任意北偏角和较大平移值的情况下GA仍然能完成匹配,验证了方法有效。
| 数据 | 配准 模型 |
RMSE/cm | GA进化代数 | 平均运 行时间/s |
|||||
| 最小 | 最大 | 平均 | 最小 | 最大 | 平均 | ||||
| 数据1 | NSMS | 1.4 | 3.9 | 2.8 | 93 | 279 | 159 | 160 | |
| Silva | 6.3 | 9.3 | 7.6 | 101 | 232 | 168 | 208 | ||
| 数据2 | NSMS | 2.7 | 5.4 | 4.3 | 89 | 247 | 151 | 506 | |
| Silva | 29.2 | 16.4 | 20.7 | 103 | 251 | 173 | 590 | ||
|
| 图 6 GA配准后点云 Fig. 6 The point cloud after GA registration 蓝色为待配准点云;红色为基准点云;绿线框内为局部地物放大 |
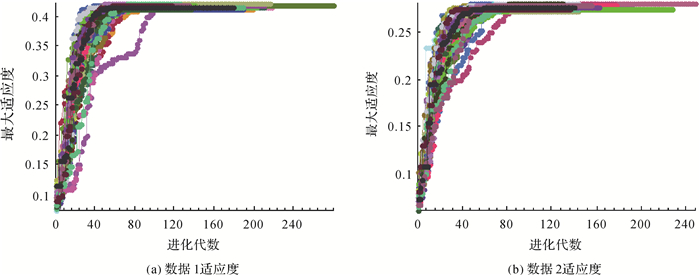
GA最大适应度变化曲线如图 7所示,在进化初期,适应度变化较快,GA表现全局搜索;当进化至一定阶段时,适应度变化缓慢并趋于成熟,GA表现局部搜索。GA配准50%以上迭代位于变化平缓区域,表明局部收敛速度慢。数据1和数据2的GA与ICP融合策略平均运行时间分别为98 s、217 s;平均进化代数为76、67。融合GA和ICP的配准策略效率比GA配准提高了50%左右。
|
| 图 7 GA配准最大适应度 Fig. 7 The max fitness of GA registration 1条折线表示1次试验 |
4 结论
为统一地面激光扫描与车载激光扫描点云坐标基准,提出了一种结合遗传算法GA与ICP的高效率自动配准方法:当GA配准趋于局部搜索时,改用ICP完成配准。本文重点研究了GA配准,其归结为4步:①总群初始化和点云选择;②匹配点云转换;③适应度计算;④遗传操作。GA配准以地面激光扫描仪内置GPS测量粗略位置作为先验信息限定优化搜索空间。笔者提出了最大化的归一化匹配分数之和(normalized sum of matching scores,NSMS)配准模型以提高全局配准精度。通过实测点云数据进行试验,结果表明:GA配准是有效的,基于NSMS模型的均方根误差(root mean square error,RMSE)为1~5 cm;NSMS模型的精度和效率均优于已有的基于均方误差(mean square errors,MSE)的Silva模型;融合配准策略可将效率提高50%左右。GA配准可以达到很高的配准精度,可一步完成点云配准;也可以作为初始配准,与精配准结合以提高效率。
| [1] | WILLIAMS K, OLSEN M J, ROE G V, et al. Synthesis of Transportation Applications of Mobile LiDAR[J]. Remote Sensing, 2013, 5(9): 4652–4692. DOI:10.3390/rs5094652 |
| [2] |
方莉娜, 杨必胜.
车载激光扫描数据的结构化道路自动提取方法[J]. 测绘学报, 2013, 42(2): 260–267.
FANG Li'na, YANG Bisheng. Automated Extracting Structural Roads from Mobile Laser Scanning Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 260–267. |
| [3] | GUAN Haiyan, LI J, CAO Shuang, et al. Use of Mobile LiDAR in Road Information Inventory:A Review[J]. International Journal of Image and Data Fusion, 2016, 7(3): 219–242. DOI:10.1080/19479832.2016.1188860 |
| [4] | YANG Bisheng, LIU Yuan, LIANG Fuxun, et al. Using Mobile Laser Scanning Data for Features Extraction of High Accuracy Driving Maps[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Prague, Czech Republic: ISPRS, 2016: 433-439. |
| [5] | BARBER D, MILLS J, SMITH-VOYSEY S. Geometric Validation of a Ground-based Mobile Laser Scanning System[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(1): 128–141. DOI:10.1016/j.isprsjprs.2007.07.005 |
| [6] | SALVI J, MATABOSCH C, FOFI D, et al. A Review of Recent Range Image Registration Methods with Accuracy Evaluation[J]. Image and Vision Computing, 2007, 25(5): 578–596. DOI:10.1016/j.imavis.2006.05.012 |
| [7] | BESL P J, MCKAY N D. A Method for Registration of 3D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239–256. DOI:10.1109/34.121791 |
| [8] | CHEN Yang, MEDIONI G. Object Modelling by Registration of Multiple Range Images[J]. Image and Vision Computing, 1992, 10(3): 145–155. DOI:10.1016/0262-8856(92)90066-C |
| [9] | RUSINKIEWICZ S, LEVOY M. Efficient Variants of the ICP Algorithm[C]//Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling. Quebec City, Quebec, Canada: IEEE, 2001: 145-152. |
| [10] | AKCA D, GRVN A. Least Squares 3D Surface Matching[M]. Zürich: Institut für Geodäsie und Photogrammetrie, 2007. |
| [11] | SEEGER S, LABOUREUX X. Feature Extraction and Registration: An Overview[M]//GIROD B, GREINER G, NIEMANN H. Principles of 3D Image Analysis and Synthesis. Kluwer: Academic Publishers, 2002: 153-166. |
| [12] | JOHNSON A E, HEBERT M. Using Spin Images for Efficient Object Recognition in Cluttered 3D Scenes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5): 433–449. DOI:10.1109/34.765655 |
| [13] | RUSU R B, BLODOW N, BEETZ M. Fast Point Feature Histograms (FPFH) for 3D Registration[C]//Proceedings of 2009 IEEE International Conference on Robotics and Automation. Kobe, Japan: IEEE, 2009: 3212-3217. |
| [14] | TOMBARI F, SALTI S, DI STEFANO L. Performance Evaluation of 3D Keypoint Detectors[J]. International Journal of Computer Vision, 2013, 102(1-3): 198–220. DOI:10.1007/s11263-012-0545-4 |
| [15] | HÄNSCH R, WEBER T, HELLWICH O. Comparison of 3D Interest Point Detectors and Descriptors for Point Cloud Fusion[C]//Proceedings of the ISPRS Technical Commission Ⅲ Symposium. Zurich, Switzerland: ISPRS, 2014: 57-64. |
| [16] | THEILER P W, WEGNER J D, SCHINDLER K. Keypoint-based 4-points Congruent Sets-automated Marker-less Registration of Laser Scans[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 96(2): 149–163. |
| [17] | SILVA L, BELLON O R P, BOYER K L. Precision Range Image Registration Using a Robust Surface Interpenetration Measure and Enhanced Genetic Algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 762–776. DOI:10.1109/TPAMI.2005.108 |
| [18] |
朱灿. 实数编码遗传算法机理分析及算法改进研究[D]. 长沙: 中南大学, 2009. ZHU Can. The Study on Mechanism and Improvement of Real-coded Genetic Algorithms[D]. Changsha: Central South University, 2009. |
| [19] | JACQ J J, ROUX C. Registration of 3-D Images by Genetic Optimization[J]. Pattern Recognition Letters, 1995, 16(8): 823–841. DOI:10.1016/0167-8655(95)00051-H |
| [20] | SILVA L, BELLON O R P, BOYER K L. Enhanced, Robust Genetic Algorithms for Multiview Range Image Registration[C]//Proceedings of the Fourth International Conference on 3D Digital Imaging and Modeling. Banff, Alta., Canada: IEEE, 2003: 268-275. |
| [21] | SCHENK S, HANKE K. Genetic Algorithms for Automatic Registration of Laser Scans with Imperfect and Subdivided Features (GAReg-ISF)[J]. Photogrammetrie-Fernerkundung-Geoinformation, 2009, 2009(1): 23–32. DOI:10.1127/0935-1221/2009/0003 |
| [22] | LOMONOSOV E, CHETVERIKOV D, EKÁRT A. Pre-Registration of Arbitrarily Oriented 3D Surfaces Using a Genetic Algorithm[J]. Pattern Recognition Letters, 2006, 27(11): 1201–1208. DOI:10.1016/j.patrec.2005.07.018 |
| [23] | ZHU Jihua, MENG Deyu, LI Zhongyu, et al. Robust Registration of Partially Overlapping Point Sets via Genetic Algorithm with Growth Operator[J]. IET Image Processing, 2014, 8(10): 582–590. DOI:10.1049/iet-ipr.2013.0545 |
| [24] | BRINDLE A. Genetic Algorithms for Function Optimization[D]. Alberta: University of Alberta, 1981. |
| [25] | MAN K F, TANG K S, KWONG S. Genetic Algorithms:Concepts and Applications[J]. IEEE Transactions on Industrial Electronics, 1996, 43(5): 519–534. DOI:10.1109/41.538609 |
| [26] |
周明, 孙树栋.
遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999.
ZHOU Ming, SUN Shudong. Genetic Algorithms:Theory and Applications[M]. Beijing: National Defense Industry Press, 1999. |
| [27] | HOLZ D, ICHIM A E, TOMBARI F, et al. Registration with the Point Cloud Library:A Modular Framework for Aligning in 3-D[J]. IEEE Robotics & Automation Magazine, 2015, 22(4): 110–124. |
| [28] | VAN DER PAS R. An Introduction into OpenMP[EB/OL]. http://www.nic.uoregon.edu/iwomp2005/iwomp2005_tutorial_openmp_rvdp.pdf. |
| [29] | COLOMINA I C. On Trajectory Determination for Photogrammetry and Remote Sensing: Sensors, Models and Exploitation[C]//Proceedings of the Photogrammetric Week. Stuttgart, Germany: [s. n. ], 2015: 131-142. |
| [30] | PAULY M, KEISER R, GROSS M. Multi-scale Feature Extraction on Point-sampled Surfaces[J]. Computer Graphics Forum, 2003, 22(3): 281–289. DOI:10.1111/cgf.2003.22.issue-3 |



