2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 武汉大学国家领土主权与海洋权益协同创新中心, 湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center for Territorial Sovereignty and Maritime Rights, Wuhan University, Wuhan 430079, China
湖泊对气候变化和人类活动较为敏感,它的任何变化都会对自然生态系统及社会经济系统产生影响。水位是反映湖泊变化的一项重要指标,传统水位测量主要由水文站完成,其测量精度高,可以连续获取湖泊水位,但不足之处也很明显,水文站维护成本高,偏远欠发达地区的水文站还不能实现全覆盖,各个地区数据难以共享,给相关科学研究带来了一定的障碍[1]。近年来,卫星测高技术成为监测湖泊水位变化的一种新手段,是湖泊水位持续监测的潜在重要数据源。
由于卫星测高技术最初是为海洋任务设计的[2],多采用雷达高度计[3],故其波束较宽,地表覆盖面积大,所测高度为卫星至该区域的平均高度。海面相对平坦,采用雷达高度计是合适的,并且雷达高度计可提供额外的信息,计算海面有效波高、后向散射系数、风场等[4, 5]。但是,将其应用于内陆湖泊时可能会产生一些问题。内陆湖泊面积普遍较小,雷达波可能会触及湖泊以外的地物,接收到的雷达回波会受到污染,导致距离跟踪错误。在计算湖泊水位时有这样一种现象,湖泊水位沿卫星轨迹呈如下分布:从湖边到湖中心降低,再从湖中心到湖边升高,最低点和最高点高程之差最大可超过10 m,水位沿卫星轨迹呈“V”字形分布。由于水位并非在某一高程上下波动,数据编辑、粗差剔除等策略无法使用[6-8],直接利用现有波形重定算法也无法得到较好结果[9-11]。有文献对这种情况进行了分析,认为这种现象是由卫星指向角偏差造成的,并利用抛物线拟合的方式对水位进行改正[12, 13],虽然其做法能够较好地对数据进行改正,但并未从波形形成的机制解释这种现象形成的原因。为了能从实质上解决该问题,需要从波形形成机制出发,探究水位沿卫星轨迹呈“V”字形分布的原因及解决方案。
为了突出“V”字形分布特征,本文以洪泽湖为研究对象,利用Jason-2雷达测高数据计算其水位。首先对洪泽湖的Jason-2测高数据进行处理,展示水位沿卫星轨迹呈“V”字形分布的现象,然后解释陆地对测高波形的影响及其导致测高波形跟踪错误的原因,指出由水面和陆地反射分别造成的上升前缘在波形中的位置,并结合Landsat影像从波形形成机制证明解释的正确性。由此设计波形重定算法,从复杂的波形中提取出正确的波形前缘中点,得到正确的湖泊水位。
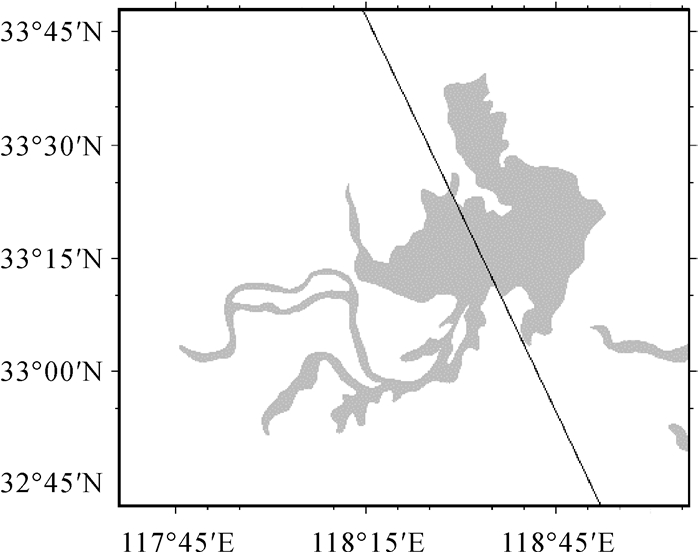
1 湖泊水位计算洪泽湖(32°45′N—33°45′N,117°45′E—119°00′E)为中国第四大淡水湖,位于江苏省西部淮河中下游,湖面面积约2000 km2。Jason-2卫星于2008年6月发射,工作至今,其搭载的雷达高度计的轨迹正好穿越该湖泊(图 1),轨迹长度为12 km。Jason-2标称轨道高为1336 km,轨道倾角66°,轨道重复周期约10 d(文献[14])。Jason-2数据来自于法国海洋卫星归档、验证及解释数据中心(Archivage,Validation et Interprétation des données des Satellites Océanographiques,AVISO)发布的SGDR数据集。
|
| 图 1 Jason-2经过洪泽湖的地面轨迹 Fig. 1 The track of Jason-2 over Hongze lake |
由测高数据计算湖泊水位高的公式如下
 (1)
(1)
式中,H为湖面相对于大地水准面的高程,即水位;Alt为卫星轨道的参考椭球高(WGS-84);R为卫星至湖面的距离(测距值);G为大地水准面相对于参考椭球高,由重力场模型EGM96得到;V为各项改正值之和,包括电离层改正、对流层干分量和湿分量改正、固体潮改正以及极潮改正等。Jason-2搭载Poseidon-3双频高度计,两种频率分别为Ku波段(13.575 GHz)和C波段(5.3 GHz),通常Ku波段测距精度高于C波段,故Ku波段测距值使用较多[15]。SGDR数据集的测距值有两种采样频率,分别为1 Hz和20 Hz,1 Hz的测距值由20 Hz的测距值线性回归得到,本文使用20 Hz的Ku波段测距值计算湖泊水位。
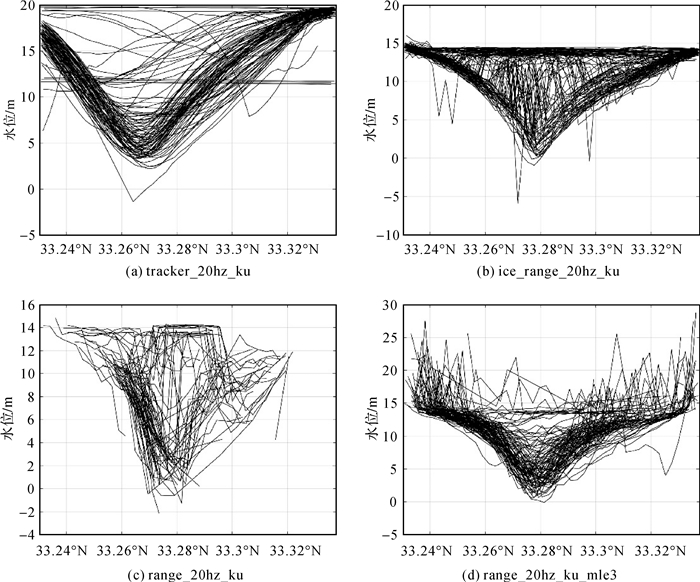
卫星接收雷达回波后对波形进行跟踪获得测距值,使用不同的跟踪算法得到的测距值可能会有差异。Jason-2在获取波形后使用默认跟踪算法即可解算出测距值,该测距值在数据中对应的字段名为tracker_20hz_ku。卫星将数据传输至地面站后对波形进行重新处理,该过程称为波形重定,用户获取卫星SGDR数据后也可进行波形重定以获取精度更高的测距值。SGDR数据中提供了3种不同波形重定算法得到的测距值,字段名称分别为:range_20hz_ku、ice_range_20hz_ku、range_20hz_ku_mle3。利用以上不同测距值进行计算将得到不同的湖泊水位,本文计算了cycle0-300的沿卫星轨迹水位,但为了便于观察,只显示叠加cycle0-100的结果,图 2展示了不同测距值得到的洪泽湖水位沿卫星轨迹的分布。可以看出,不同测距值计算得到的水位各有不同,但都有同样一个现象:大多数沿卫星轨迹水位从低纬度到高纬度(从湖边到湖中心再到湖边)先下降再上升,水位沿卫星轨迹呈“V”字形分布,最低点和最高点的差值可以超过10 m。实际上,同一条沿卫星轨迹的湖泊水位应该基本一致,而此处的水位变化明显与常理不符。需要说明的是,纬度范围两端数据的波形中水面和陆地反射信号夹杂在一起无法分离,在实际的计算中会被舍弃,但为了完整地展示水位分布特征,此处给出了整个范围内的水位分布。
|
| 图 2 不同跟踪方法的测距值计算得到的洪泽湖水位沿卫星轨迹分布 Fig. 2 Water level of Hongze Lake along the satellite track by different tracking methods |
2 湖泊沿轨水位呈“V”字形原因分析
卫星自带的波形跟踪器是针对海洋波形设计的,当雷达波照射区域为海洋或者大型水域时,测高回波波形类似海洋波形,跟踪器能够较好地跟踪波形。由于湖泊面积较小,测高波形易受地形和地物的影响,回波波形不再与海洋波形类似,原有跟踪器无法准确跟踪,从而导致水位计算错误。尽管地面处理中心给出了几种不同波形重定算法跟踪得到的测距值,当实际回波类型与算法对应的回波类型不符时仍无法有效跟踪波形。
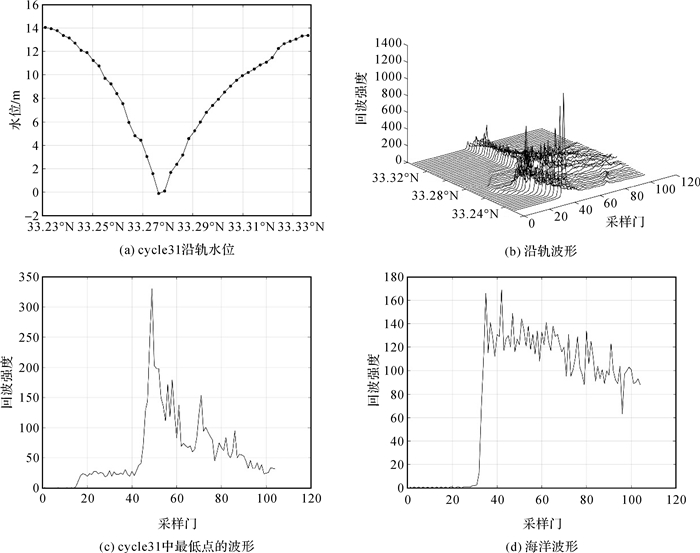
为了说明波形跟踪错误的成因,以Jason-2 cycle31在洪泽湖上的数据为例,用ice_range_20hz_ku测距值进行水位的计算,其水位沿卫星轨迹分布如图 3(a)所示。此时水位有明显的“V”字形现象,其对应的回波波形(图 3(b))与海洋波形(图 3(d))明显不同,海洋波形只有一个明显的上升前缘,且波形后缘下降缓慢。将水位最低点的波形单独取出(图 3(c)),可以看出随着采样门的增加,该波形先产生一个小的上升前缘,随后产生一个大的上升前缘,波形后缘迅速下降。基于实测数据比较,可以看出先产生的小上升前缘由水面反射导致,大上升前缘主要由陆地反射导致,波形重定时跟踪小上升前缘才能得到正确的测距值。需要说明的是,小上升前缘极易被当作热噪声剔除,传统算法错误地跟踪大上升前缘将使跟踪到的波形前缘中点靠后,因此计算的测距值偏大,导致水位偏低。
|
| 图 3 Jason-2 cycle31沿卫星轨迹水位及波形 Fig. 3 Water level and waveform along satellite track of Jason-2 at cycle31 |
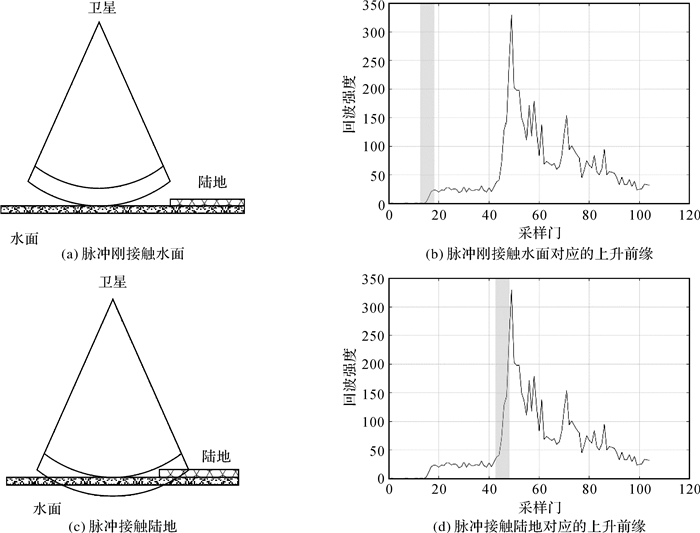
雷达高度计波束宽度为1°左右,测量时发射一束脉冲宽度为3.125 ns的脉冲[16]。脉冲发出后向下传播首先接触水面(图 4(a)),对应图 4(b)中波形的小上升前缘(灰色区域),随后脉冲在水面均匀扩散,波形基本平稳。随着脉冲的继续扩散,接触到陆地(图 4(c)),对应图 4(d)中波形的大上升前缘(灰色区域),随后脉冲继续扩散,接收到的能量减弱,波形后缘呈下降趋势。
|
| 图 4 小前缘波形形成机制 Fig. 4 Mechanism of small front edge waveform formation |
上述波形形成过程有一个特点,水面返回能量导致的波形上升量明显小于夹杂陆地信号的波形上升量。为解释此现象,图 5给出完全由水面和完全由陆地反射的波形,其中,图 5(a)为一段海洋波形,完全由水面反射;图 5(b)为洪泽湖附近完全由陆地反射的波形。可以看出,海洋波形的最大回波强度不超过300,多数在150~300之间。洪泽湖附近的陆地因地物复杂,波形回波能量峰值波动较大,但多数波形回波能量峰值接近1400,远大于海洋波形。正因如此,在水陆信号混合的波形中,水面反射形成的上升前缘峰值小,陆地反射形成的上升前缘峰值大,最终产生了具有小前缘的波形。
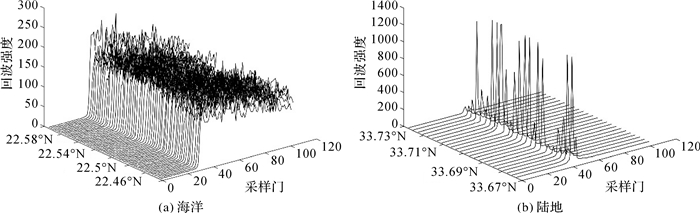
|
| 图 5 海洋和陆地波形 Fig. 5 Wave of ocean and land |
如果将波形中小上升前缘当作热噪声去除,则极易跟踪陆地反射形成的上升前缘,由此计算水位的方式如图 6所示。卫星距离水面的实际距离为R,波形跟踪时将陆地反射信号误以为水面跟踪得到距离R′,将其反算星下点水位时会产生大小为Δh的偏差,Δh=R′-R。可以看出,当星下点离陆地越远时,产生的水位偏差越大,计算得到的水位越低,与前述湖泊水位沿卫星轨迹呈“V”字形分布现象相符。

|
| 图 6 水位计算错误示意图 Fig. 6 Schematic diagram of wrong calculation of water level |
为验证本文分析的正确性,计算卫星星下点与陆地反射点的距离,并利用Landsat影像做验证。有小上升前缘的波形中,认为小上升前缘由星下点水面反射,随后的大上升前缘主要由陆地反射,那么跟踪两处上升前缘得到的前缘中点做差,即得到脉冲接触水面和陆地的时间差Δt,由此可计算Δh=Δt·c,其中c为光速,再由式(2)计算星下点与陆地反射点的距离r
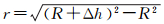 (2)
(2)
Landsat影像由美国地质勘探局(United States Geological Survey,USGS)免费提供,下载一幅与Jason-2 cycle31时间最接近的影像,时间相差5 d,以影像为背景,以卫星星下点为圆心,星下点与陆地反射点的距离r为半径作圆,结果如图 7所示。
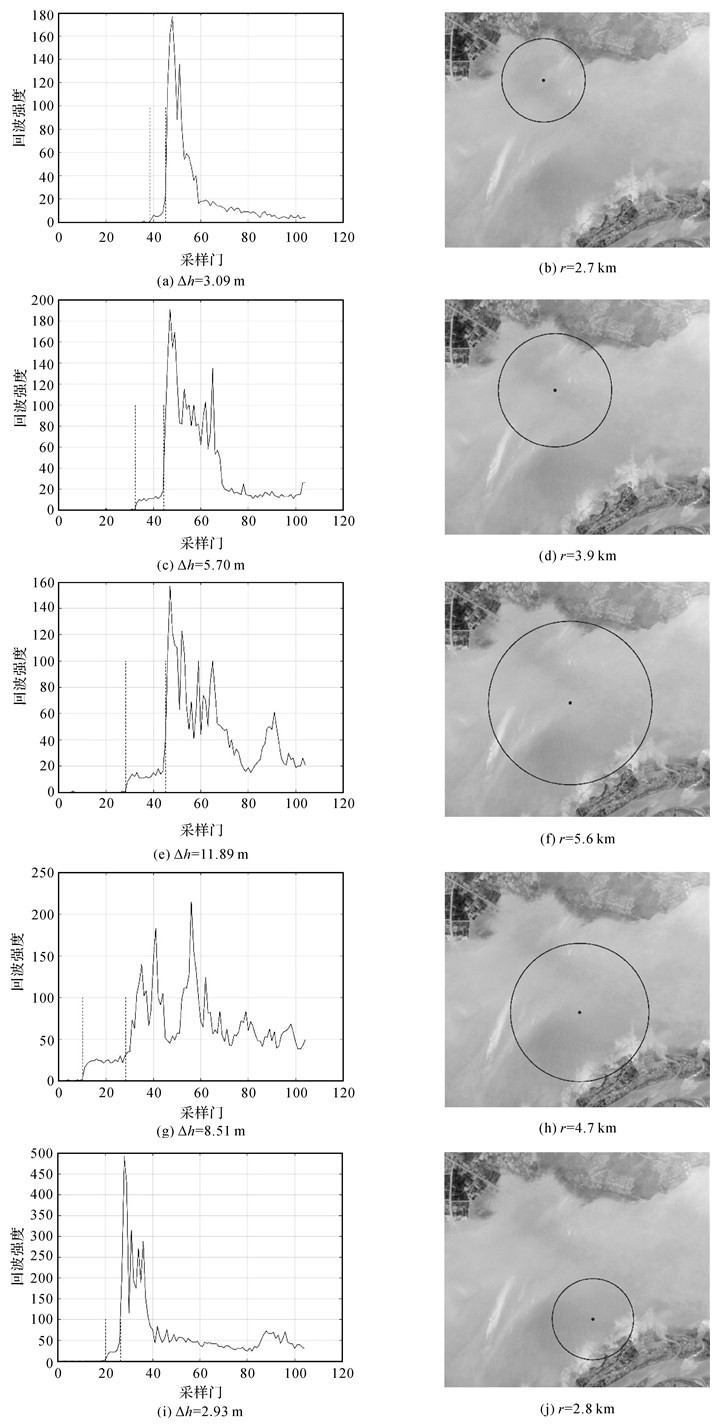
|
| 图 7 Landsat影像验证结果 Fig. 7 Results of Landsat image validation |
Jason-2 cycle31卫星轨迹方向为从北到南,刚进入湖泊时星下点离陆地较近,此时的波形如图 7(a)所示,虚线为跟踪两处上升前缘得到的前缘中点位置,可以看出小上升前缘与大上升前缘相隔较近,对应的圆半径也较小。图 7(b)中角点圆圈代表了可能引起大上升前缘的地方,可以知道当圆圈还未到达陆地时(也即脉冲未到达陆地)波形没有上升趋势,当圆圈正好与陆地相接触时,波形产生了一个大的上升前缘,故可以认为大的上升前缘由陆地反射造成。当卫星向南移动时,波形中的大、小上升前缘间隔增大(图 7(c)),对应的圆圈半径也增大(图 7(d)),但圆圈始终与陆地相接。当卫星移动至湖泊中心时,波形的大、小上升前缘间隔达到最大(图 7(e)),对应角点圆圈半径也达到最大(图 7(f)),此时圆圈与南北两岸相接,说明波形中大上升前缘可能受南北两岸陆地的共同影响。卫星越过湖泊中心继续向南移动时,波形中大上升前缘主要受南面陆地反射的影响,波形中大、小上升前缘间隔减小(图 7(g)),对应的圆圈半径也减小,只与南面陆地边界相接(图 7(h))。卫星不断向南移动的过程中,波形中大、小上升前缘间隔不断减小(图 7(i)),圆圈半径也不断减小(图 7(j)),但圆圈边界始终与陆地相接。
由上述分析可以看出,洪泽湖的测高波形受陆地影响,波形复杂,与海洋波形相差较大。由于陆地反射信号较强,使得波形中陆地反射造成的上升前缘明显,而水面反射造成的上升前缘不明显。由于水面反射的信号仍然存在于波形中,设计对应的波形重定算法,即可跟踪正确的波形前缘中点,得到正确水位。
3 波形重定现有波形重定算法主要有两类:①考虑整体波形的重定算法,如重心偏移法(OCOG)[17]、阈值法[18]、β参数法[19]等,由于陆地反射的信号在波形中占主导地位,重定后的波形前缘中点偏离真值较远;②考虑局部波形的重定算法,如子波形重定算法[20],由于不考虑整体波形,只顾及子波形,算法会检测所有有明显上升的前缘,故有可能将水面反射形成的上升前缘检测到,但无法说明提取的上升前缘是否由水面反射产生,只能通过先验信息加以判断,如模型值、已有测量值,此方法有很大的局限性。综上分析,无法直接利用现有波形重定算法进行跟踪,需要根据波形特征设计新的波形重定算法。
受陆地影响的波形有这样一个特征:波形中先有一个小的上升前缘,随后有一个大的上升前缘,小的由水面反射,大的受陆地影响较大。设计波形重定算法时,先采用子波形[20]的思想,提取小的上升前缘,再使用阈值法[18]确定子波形前缘中点。使用阈值法时,根据文献[18]的建议,并在试验中多次尝试,阈值取50%为最优。由于离岸太近时水面和陆地反射信号夹杂在一起无法分离,故此处将数据范围缩小一定程度,以有效跟踪波形前缘中点。利用上述思想计算得到洪泽湖水位,如果水位结果中存在异常值则需要进行异常值剔除。常用异常值剔除方法有剔除偏离均值3倍中误差的异常值[21]、将水位可视化后人工剔除[22]、使用四分位数间距剔除[23]等,本文使用3倍中误差的方法进行异常值剔除。将cycle0-100沿卫星轨迹水位叠加,结果如图 8所示,可以清晰地看到,水位沿卫星轨迹呈“V”字形分布现象消失。

|
| 图 8 经本文波形重定后的水位叠加图(cycle0-100) Fig. 8 The overlay of water level after waveform retracking presented by this paper (cycle0-100) |
为进一步验证波形重定结果的质量,选取了部分洪泽湖水文站水位的观测数据,该数据为2009年每个月中Jason-2通过湖面时的瞬时水位,每月取一个与卫星轨迹同步的水位观测值。水文站水位与波形重定后水位对比如图 9(a)所示。由于两种水位的高程基准不同,故存在一定的系统偏差,两者的相关系数为0.99,为强相关。逐月作差得到的水位变化可以消除基准不一致的影响,如图 9(b)所示,通过两种手段得到的逐月水位变化的互差的绝对值最大为9 cm,最小为1 cm,标准差为5 cm,说明波形重定算法效果较好,可以用于一般的水位监测。
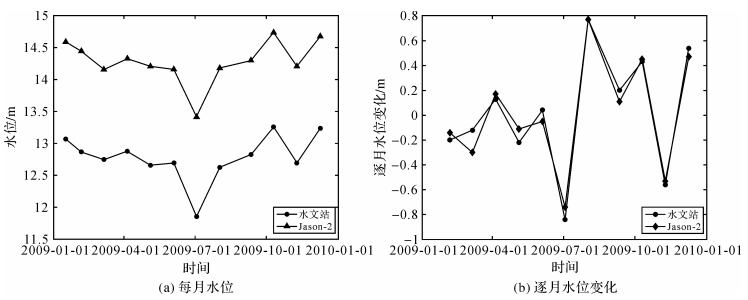
|
| 图 9 水文站水位与波形重定后水位对比 Fig. 9 Water level contrast of hydrologic station and waveform retracking |
4 试验分析与讨论
目前波形重定算法繁多,定量分析这些波形重定算法能否处理本文所提取的波形数据,同时将本文提出的波形重定算法与目前常用的波形重定算法进行比较。常见的波形重定算法有β参数法[19]、重心偏移法(OCOG)[17]、阈值法(threshold)[18]、改进后的阈值法[24, 25]、子波形阈值法[20]等,Jason-2的SGDR数据集中自带了Ice、Ocean、MLE3几种重定算法重定后的测距值[15]。将几种常用波形重定算法分别应用于处理洪泽湖区的测高数据,并用IMP(the improvement percentage)[20]描述波形重定后的改善度,IMP的定义如下
 (3)
(3)
式中,σraw、σre分别为波形重定前、后水位的标准差;IMP越高表明波形重定算法的改善效果越好。对洪泽湖Jason-2cycle0-300的测高数据进行波形重定,各个波形重定算法结果如表 1所示。可以看出,本文设计的波形重定算法表现最好,剔除异常值后水位平均标准差为0.09 m,IMP为95%。阈值法、改进后的阈值法、重心偏移法等优于未重定(tracker)的结果,可见其对本文的波形数据有一定的效果,但改善效果不如本文的波形重定算法好。SGDR数据中自带的3种波形重定算法Ice、Ocean、MLE3的结果比未重定的结果差,说明其方法不适用于本文的波形数据。值得注意的是文献[20]的波形重定算法结果最不乐观,虽本文的波形重定思想与其相似,表现却差异很大,主要原因在于,如果上升前缘中有一个点突然下降,那么这个前缘基本不会被文献[20]的波形重定算法跟踪到,而本文的数据恰在较多的上升前缘中有一个下降的点,所以该算法表现差。
5 结论
本文以Jason-2雷达测高数据计算洪泽湖水位为例,探讨了湖泊水位沿卫星轨迹呈“V”字形分布的原因。该现象对应的测高波形先有一小上升前缘随后有一大上升前缘,波形中小上升前缘由水面反射,大上升前缘主要由陆地反射,结合Landsat影像从波形形成机制证实了解释的正确性。正是由于水面反射形成的上升前缘很小,数据自带以及常用的波形重定算法很难有效跟踪正确的波形前缘中点,导致水位计算错误。针对此种波形设计了重定算法,结果显示本文的波形重定算法优于数据自带以及常用的波形重定算法,水位标准差达0.09 m,可用于一般的水位监测。
本文指出的水位沿卫星轨迹呈“V”字形分布现象不局限于Jason-2和洪泽湖,搭载雷达高度计的卫星获取的数据如果有相似特征,则可以使用本文的分析方法和波形重定算法。特别是卫星离岸较近时,如果陆地反射信号较强,则此区域测高波形中陆地反射信号占主导地位,常用的波形重定算法不适用,如不对其进行分析和波形重定将得到错误的水位。
需要说明的是,并不是所有的湖面测高波形都有小前缘并且小前缘是水面反射的,这取决于波形是否受陆地影响以及陆地反射信号的强弱、地形分布等诸多因素,需要综合分析。本文的波形重定算法表现良好,前提是波形中小上升前缘由水面反射形成,如果波形有小上升前缘但却是噪声,则此算法不再适用。
| [1] | CRÉTAUX J F, BIRKETT C. Lake Studies from Satellite Radar Altimetry[J]. Comptes Rendus Geoscience, 2006, 338(14-15): 1098–1112. DOI:10.1016/j.crte.2006.08.002 |
| [2] | BROWN O B, CHENEY R E. Advances in Satellite Oceanography[J]. Reviews of Geophysics, 1983, 21(5): 1216–1230. DOI:10.1029/RG021i005p01216 |
| [3] |
金涛勇, 李建成, 姜卫平, 等.
基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报, 2011, 40(6): 723–729.
JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-altimetric Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 723–729. |
| [4] | SHANAS P R, KUMAR V S, HITHIN N K. Comparison of Gridded Multi-mission and Along-track Mono-mission Satellite Altimetry Wave Heights with in Situ Near-shore Buoy Data[J]. Ocean Engineering, 2014, 83(1): 24–35. |
| [5] | REMY F, FLAMENT T, BLAREL F, et al. Radar Altimetry Measurements over Antarctic Ice Sheet:A Focus on Antenna Polarization and Change in Backscatter Problems[J]. Advances in Space Research, 2012, 50(8): 998–1006. DOI:10.1016/j.asr.2012.04.003 |
| [6] |
郭金运, 孙佳龙, 常晓涛, 等.
TOPEX/Poseidon卫星监测博斯腾湖水位变化及其与NINO3 SST的相关性分析[J]. 测绘学报, 2010, 39(3): 221–226.
GUO Jinyun, SUN Jialong, CHANG Xiaotao, et al. Water Level Variation of Bosten Lake Monitored with TOPEX/Poseidon and Its Correlation with NINO3 SST[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 221–226. |
| [7] | ZHANG Guoqing, XIE Hongjie, KANG Shichang, et al. Monitoring Lake Level Changes on the Tibetan Plateau Using ICESat Altimetry Data (2003-2009)[J]. Remote Sensing of Environment, 2011, 115(7): 1733–1742. DOI:10.1016/j.rse.2011.03.005 |
| [8] | GAO Le, LIAO Jingjuan, SHEN Guozhuang. Monitoring Lake-level Changes in the Qinghai-Tibetan Plateau Using Radar Altimeter Data (2002-2012)[J]. Journal of Applied Remote Sensing, 2013, 7(1): 073470. DOI:10.1117/1.JRS.7.073470 |
| [9] |
汪海洪, 罗志才, 杨元德, 等.
基于波形分类的近海卫星测高数据自适应重跟踪方法[J]. 测绘学报, 2012, 41(5): 729–734.
WANG Haihong, LUO Zhicai, YANG Yuande, et al. An Adaptive Retracking Method for Coastal Altimeter Data Based on Waveform Classification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 729–734. |
| [10] |
彭福凯, 沈云中.
长江口Envisat测高数据的波形分类重构分析[J]. 测绘学报, 2015, 44(6): 616–624.
PENG Fukai, SHEN Yunzhong. Analysis of Envisat Altimetric Data around Yangtze Estuary by Waveform Retracking[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6): 616–624. DOI:10.11947/j.AGCS.2015.20140374 |
| [11] | IDRIS N H, DENG X. The Retracking Technique on Multi-peak and Quasi-specular Waveforms for Jason-1 and Jason-2 Missions near the Coast[J]. Marine Geodesy, 2012, 35(S1): 217–237. |
| [12] | DA SANTOS J S, CALMANT S, SEYLER F, et al. Water Levels in the Amazon Basin Derived from the ERS 2 and Envisat Radar Altimetry Missions[J]. Remote Sensing of Environment, 2010, 114(10): 2160–2181. DOI:10.1016/j.rse.2010.04.020 |
| [13] | FRAPPART F, CALMANT S, CAUHOPÉ M, et al. Preliminary Results of Envisat RA-2-derived Water Levels Validation over the Amazon Basin[J]. Remote Sensing of Environment, 2006, 100(2): 252–264. DOI:10.1016/j.rse.2005.10.027 |
| [14] |
盛传贞, 甘卫军, 赵春梅, 等.
不同观测技术的Jason-2卫星精密定轨评估[J]. 测绘学报, 2014, 43(8): 796–802.
SHENG Chuanzhen, GAN Weijun, ZHAO Chunmei, et al. Assessment of Precise Orbit Determination of Jason-2 Satellite Using Different Observation Technologies[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 796–802. DOI:10.13485/j.cnki.11-2089.2014.0133 |
| [15] | SCHARROO R. OSTM/Jason-2 Products Handbook[M]. [S.l.]: NOAA, 2009. |
| [16] |
杨元德. 应用卫星测高技术确定南极海域重力场研究[D]. 武汉: 武汉大学, 2010. YANG Yuande. The Determination of Marine Gravity Anomalies over Antarctic Oceans from Satellite Altimetry[D]. Wuhan: Wuhan University, 2010. |
| [17] | WINGHAM D J, RAPLEY C G, GRIFFITHS H D. New Techniques in Satellite Altimeter Tracking Systems[C]//IGARSS 86 Symposium. Zurich: EAS, 1986. |
| [18] | DAVIS C H. A Robust Threshold Retracking Algorithm for Measuring Ice-sheet Surface Elevation Change from Satellite Radar Altimeters[J]. IEEE Transactions on Geoscience & Remote Sensing, 1997, 35(4): 974–979. |
| [19] | MARTIN T V, ZWALLY H J, BRENNER A C, et al. Analysis and Retracking of Continental Ice Sheet Radar Altimeter Waveforms[J]. Journal of Geophysical Research, 1983, 88(C3): 1608–1616. DOI:10.1029/JC088iC03p01608 |
| [20] | HWANG C, GUO Jinyun, DENG Xiaoli, et al. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry:Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006, 80(4): 204–216. DOI:10.1007/s00190-006-0052-x |
| [21] | HWANG C, CHENG Yungsheng, HAN Jiancheng, et al. Multi-decadal Monitoring of Lake Level Changes in the Qinghai-Tibet Plateau by the TOPEX/Poseidon-family Altimeters:Climate Implication[J]. Remote Sensing, 2016, 8(6): 446. DOI:10.3390/rs8060446 |
| [22] | DUAN Zheng, BASTIAANSSEN W G M. Estimating Water Volume Variations in Lakes and Reservoirs from Four Operational Satellite Altimetry Databases and Satellite Imagery Data[J]. Remote Sensing of Environment, 2013, 134: 403–416. DOI:10.1016/j.rse.2013.03.010 |
| [23] | SULISTIOADI Y B, TSENG K H, SHUM C K, et al. Satellite Radar Altimetry for Monitoring Small Rivers and Lakes in Indonesia[J]. Hydrology and Earth System Sciences, 2015, 19(1): 341–359. DOI:10.5194/hess-19-341-2015 |
| [24] | LEE H, SHUM C K, YI Yuchan, et al. Laurentia Crustal Motion Observed Using TOPEX/Poseidon Radar Altimetry over Land[J]. Journal of Geodynamics, 2008, 46(3-5): 182–193. DOI:10.1016/j.jog.2008.05.001 |
| [25] | DENG X, FEATHERSTONE W E, HWANG C, et al. Estimation of Contamination of ERS-2 and Poseidon Satellite Radar Altimetry Close to the Coasts of Australia[J]. Marine Geodesy, 2002, 25(4): 249–271. DOI:10.1080/01490410214990 |



