2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
传统的地震仪在地震监测和研究中发挥着重要作用[1-3]。但在大地震发生时,震源附近的地震仪可能会受到地震波冲击导致振幅满格而难以完整地记录地震波信号。同时,大地震造成的近场地表永久性变形及地面倾斜会导致地震仪记录的地震波信号产生扭曲、变形。而高频GPS观测资料具有能够获取宽频带信号、可以直接获取高精度水平位移信息、不会出现限幅现象以及对地面倾斜不敏感等优势。因此,充分利用高频GPS观测资料中记录的地震信息已被越来越多的学者所重视,GPS地震学[4]随之应运而生。
文献[5]利用1 Hz的GPS观测数据获取了FAIR测站记录到的2002年的Denali地震波形,并与地震仪积分结果比较,两者具有较好的一致性。此后,越来越多的学者将高频GPS技术广泛应用于其他地震的研究,并取得了大量的研究成果[6-8]。由GPS获得的同震静态永久变形信息(static offset)可用于约束震源参数如震级、震源深度等的反演,地震波信息可作为地震仪、强震仪等观测数据的重要补充,用于反演地震断层破裂过程。但是,震后的高频GPS观测资料包含了由地震引起的静态永久变形和地震波的详细信息。当需要永久性变形信息反演震源参数时,地震波信息会影响准确的获得永久性变形,反之,当需要地震波信息反演断层破裂过程时,永久性变形信息也会对地震波信息的准确性产生影响。因此,实现两者的有效分离是准确获取两种信息进而反演地震参数的关键因素。以往为了从GPS观测资料中获取同震静态永久变形,通常采用震前和震后一段时间的资料进行计算,并需要剔除地震发生或以后一段时间的数据以避免地震波位移影响。文献[9]利用卡尔曼滤波方法估计了2003年日本Tokachi-Oki地震主震和震后静态永久性变形效应,但是在应用该方法时,为了避免动态位移对滤波结果的影响,在估计中必须剔除地震发生时的观测数据,这样不仅增加了数据处理的工作量,而且也会丢失地震波信息。文献[10]利用小波分解重构方法提取高频GPS数据静态永久性变形信息,但是在利用小波分层技术时,无法完整保存地震波到时及振幅等信息,而到时和振幅信息对于准确确定震中和震级等参数具有重要意义。
为充分发挥高频GPS资料的优势,本文旨在研究在快速获取高频GPS数据静态永久变形信息的同时,如何有效分离并完整保存高频GPS资料中记录的地震波信息。本文选用平滑先验信息方法(SPM)[11-14]来实现地震引起的高频GPS观测结果中静态形变和地震波信息的分离。该方法是一种高通滤波器,对具有周期特性的高频信号最为敏感,能够有效地识别具有周期特性的高频周期信息,从而实现周期信号与非周期信号的有效分离,并且不需要剔除数据。由于地震波具有一定周期或准周期性而表现为高频信息,永久性变形则不具有周期性,正是针对高频GPS资料中地震波与永久性变形的这一特点,本文将SPM方法引入高频GPS数据后处理中,分别获取了静态永久性变形信息和地震波信息。
1 数据处理与方法 1.1 数据及地震位置本文采用的1 Hz的GPS观测数据由美国地学研究组织UNAVCO网站提供(http://www.unavco.org/data/data.html)。本文选取了近几年的3次地震,地震的详细信息见表 1。本文依照两个原则,每个地震对应选取了两个观测站:①测站到震中的距离;②在地震发生前后,观测站的数据记录是否完整。测站分布与震中位置分布情况如图 1所示。
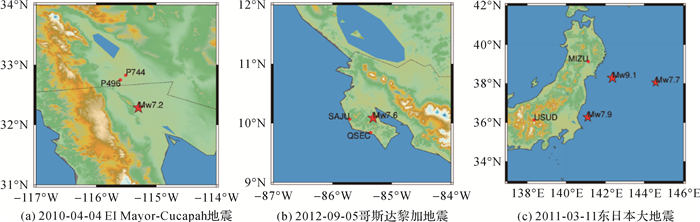
|
| 图 1 测站分布与震中位置 Fig. 1 The locations of the stations and the epicenters |
| 地震名称 | 时间/UTC | 震中位置 | 震源深度/km | 震级 | 所选测站 | 震中距/km |
| 2010-04-04 EI Mayor-Cucapah地震 |
22:40:42 | 32.286°N, 115.295°W | 10.0 | 7.2 | P496 P744 |
58.8 63.6 |
| 2012-09-05 哥斯达黎加地震 |
14:42:07 | 10.085°N, 85.315°W | 35.0 | 7.6 | QSEC SAJU |
27.6 43.3 |
| 2011-03-11 东日本大地震 |
主震05:46:24 | 38.297°N, 142.373°E | 29.0 | 9.1 | MIZU USUD |
142.4 428.9 |
| 余震06:15:40 | 36.281°N, 141.111°E | 42.6 | 7.9 | |||
| 余震06:25:50 | 38.058°N, 144.590°E | 18.6 | 7.7 |
1.2 高频GPS数据处理
本文采用Bernese 5.2软件进行动态精密单点定位,卫星轨道及钟差采用欧洲定轨中心(CODE)提供的15 min间隔的精密星历与5 s间隔的精密卫星钟差[15],并且采用IERS推荐的最新的天线相位中心模型、大气潮汐及海潮模型,卫星截止高度角设置为3°。同时,估计了载波相位模糊度、卫星钟差及接收机钟差。电离层误差通过采用双频电离层无关组合消除,天顶对流层延迟采用WET_GMF模型估计。计算得到的动态位移解仍然受多路径效应等周期性噪声的影响,本文采用改进的恒星日滤波(modified sidereal filtering, MSF)方法[16]进行处理。对P496和P744测站选用震前2 d(P496和P744测站震前只有2 d的数据),QSEC、SAJU、MIZU和USUD测站选用震前4 d相同恒星日段的时间序列进行加权平均,得到背景噪声。图 2以MIZU测站N方向为例,对比了分别采用震前2 d和震前4 d的观测数据计算得到的背景噪声。其中绿色曲线分别对应2011-03-07(年积日066)到2011-03-10(年积日069)动态位移时间序列,红色曲线为滑动平均后的结果,消除了高频噪声。蓝色曲线即为所得的背景噪声。两组背景噪声的相关系数达到了90.4%,从图中也可以看出,在震前4 d该台站周围环境稳定,没有受到明显的噪声事件干扰。从图 2结果来看,由于背景噪声只与观测台站质量和周围环境的噪声影响有关,在没有突然噪声的干扰下,选用震前2~4 d的数据处理的结果是基本相同的。从地震当天的动态位移时间序列中扣除背景噪声,扣除后的坐标时间序列基本上不再含有多路径效应等周期性噪声的影响。
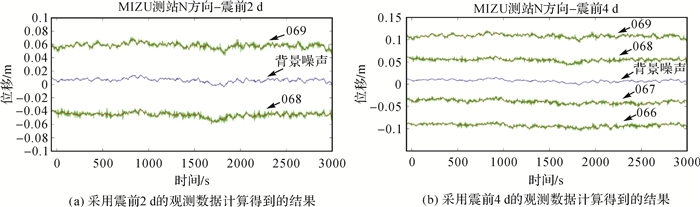
|
| 图 2 MSF恒星日滤波背景噪声分析(以MIZU测站N方向为例) Fig. 2 The background noise analysis of MSF method (taking the north component of MIZU station as an example) |
1.3 信号分离 1.3.1 SPM方法
对于任意时间序列z,均可表示为z=[z1 z2 … zn]T。其中,n为采样点个数。z可看作近似稳态的周期分量和非周期趋势项之和
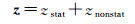 (1)
(1)
式中,zstat表示近似稳态的周期分量(即地震波);znonstat表示非周期趋势分量(即静态永久变形),可表示为
 (2)
(2)
式中,H∈Rn×m为观测矩阵;θ∈Rm为回归参数;m是回归参数的个数;ε为观测误差。求解回归参数的估计值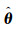
 (3)
(3)
式中,λ是正则化参数; Dd为第d次导数操作的离散逼近。显然,式(3)是在普通最小二乘方法的基础上增加了一个条件,属于条件极值问题。极值条件的目的是使式(3)的解在满足‖Hθ-z‖取得极小值的同时,使得‖Dd(Hθ)‖取值也尽可能小。这样就可以在推估线性项Hθ的过程中,加入一些已知的先验信息。式(3)的解可表示为
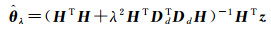 (4)
(4)
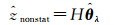 (5)
(5)
式中,
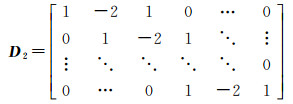 (6)
(6)
有了这些特殊选择后,该方法称为平滑先验信息方法(smoothness priors method, SPM)[11-14]。这样,周期信号可以表示为
 (7)
(7)
式(7)可以写为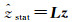
对于地震波来说,体波的频率范围约为0.02~100 Hz[17],一般地震波首波都是高频信号。为了进一步验证,笔者对P744测站E-W方向分量作了功率谱分析,结果如图 4所示。从图中可以看出,高频地震波的能量主要集中在0.05~0.40 Hz频段上,在一般理论地震波中的体波频率范围之内,因此本文假设频率大于0.04 Hz的信号是所需要保留的高频地震波信号,则所设计滤波器的截止频率为0.04 Hz。对应频率响应关系,本文选取λ=30。在一般的正则化方法中,正则化参数的选择是难点,而本文根据实际物理问题本身的特点(地震波传播频率固定,与震级大小、震中距远近无关)选取了截止频率,进而确定正则化参数。这也解决了应用正则化方法时平滑因子的选取往往会受到人为因素影响的问题。根据地震波的频率范围,同时结合FFT结果,笔者认为在以后使用SPM方法处理1 Hz的GPS数据时,可选取30作为滤波参数的经验值。
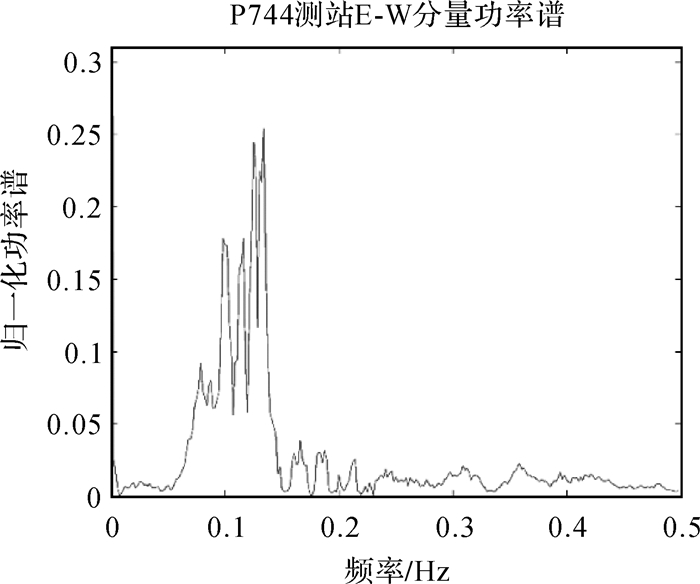
|
| 图 4 测站P744在E-W方向动态位移序列功率谱图 Fig. 4 The power spectrum of dynamic displacement sequence of station P744 in E-W direction |
2 结果
图 5是3次地震前后相应测站高频GPS动态位移时间序列。从图中结果可以明显看出,高频GPS动态位移记录了地震导致的地壳永久变形和地震波,但两种信号是混叠在一起的。在利用GPS资料反演地震参数或地震破裂过程时,通常需要永久性变形信息或地震波信息作为约束条件。如果参数不够准确,势必会导致反演结果存在一定的偏差,因此,在实际应用中,需要将永久性变形信息和高频地震波信息精确分离。
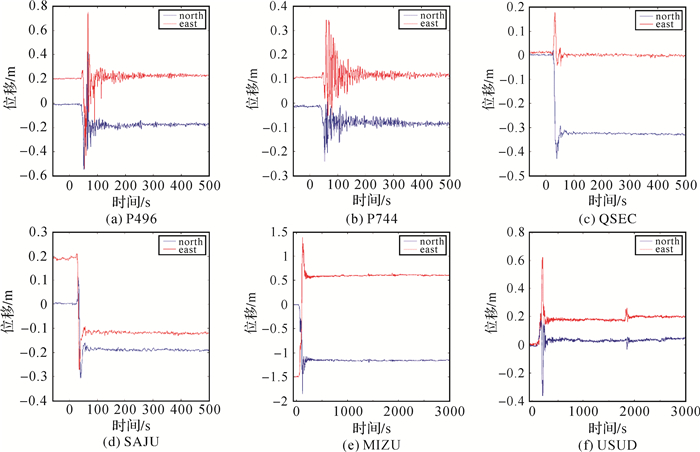
|
| 图 5 各测站高频GPS动态位移时间序列 Fig. 5 Time series of high-rate GPS dynamic displacement of each station 注:(a)、(b)对应2010-04-04 EI Mayor-Cucapah地震;(c)、(d)对应2012-09-05哥斯达黎加地震;(e)、(f)对应2011-03-11东日本大地震 |
图 6至图 8分别给出了3次地震前后相应测站高频GPS动态位移的SPM信号分离结果。从图中可以看出,地震引起的永久变形和地震波得到了有效分离。将SPM方法获取的静态永久变形与用地震前后静态天解计算的结果进行了比较,结果见表 2和表 3。从表中的结果可以看出,SPM分离结果与GPS静态天解结果有一些差异。产生该差异的原因有二。一是在地震发生后,震中距较近的GPS站产生较大的静态永久变形,震后一段时间由于断层余滑的影响,在静态天解的静态永久变形结果中包含了主震与震后余滑的共同效应。因此SPM结果与GPS静态天解结果具有差异。如2010-04-04 EI Mayor-Cucapah地震P496和P744测站南北分量,2012-09-05哥斯达黎加地震QSEC和SAJU测站东西分量及南北分量。二是在主震发生后,强余震也可能会进一步引起震中距较近的GPS站产生较大的静态永久变形。因此,在静态天解结果中包含了主、余震引起的静态永久变形的共同效应,使得SPM结果与GPS静态天解结果具有差异。例如2011-03-11东日本大地震在Mw 9.1级主震发生后约30 min又发生了Mw 7.9级强余震,此后约10 min,Mw 9.1震中东部外海又发生了一次Mw 7.7级强余震。由图 8和表 3可以看出,Mw 7.9级强余震发生后,分别引起MIZU和USUD有2.3 cm和2.0 cm的东西向永久性变形。由于Mw 7.7级强余震距离陆地较远,两个测站都没有观测到明显的静态永久变形。
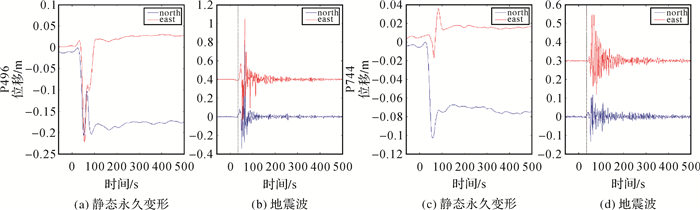
|
| 图 6 2010-04-04 EI Mayor-Cucapah地震P496和P744测站SPM滤波的结果 Fig. 6 The results of SPM filtering at P496 and P744 station |
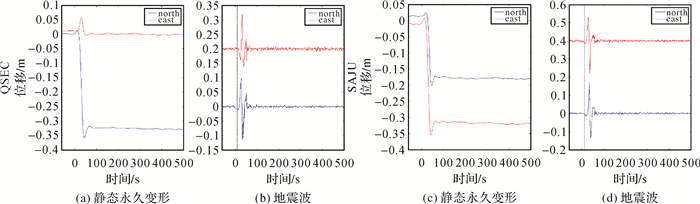
|
| 图 7 2012-09-05哥斯达黎加地震QSEC和SAJU测站SPM滤波的结果 Fig. 7 The results of SPM filtering at QSEC and SAJU station |
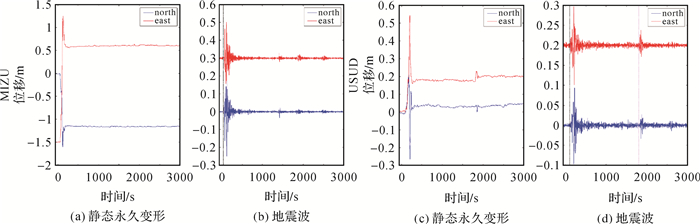
|
| 图 8 2011-03-11东日本大地震MIZU和USUD测站SPM信号分离的结果 Fig. 8 The results of SPM method at MIZU and USUD station |
| cm | |||||||
| 测站名称 | SPM方法解算1 Hz静态永久变形 | GPS静态天解解算永久变形 | UNAVCO网站结果 | ||||
| 东西 估值/中误差 |
南北 估值/中误差 |
东西 估值/中误差 |
南北 估值/中误差 |
东西/南北 | |||
| P496 | 2.55/0.18 | -16.42/0.22 | 2.44/0.20 | -18.01/0.10 | 2.40/-18.11 | ||
| P744 | 1.10/0.13 | -6.79/0.17 | 1.33/0.11 | -8.05/0.04 | 1.01/-8.08 | ||
| QSEC | -1.14/0.14 | -32.97/0.14 | -5.70/0.69 | -39.92/0.59 | -5.91/-39.94 | ||
| SAJU | -31.29/0.23 | -19.30/0.12 | -34.61/0.44 | -26.00/0.53 | — | ||
| cm | ||||||
| 测站 名称 |
SPM方法解算1 Hz静态永久变形 | GPS静态天解 解算永久变形 |
文献[18] | |||
| Mw 9.1主震后 | Mw 7.9余震后 | |||||
| 东西 估值/中误差 |
南北 估值/中误差 |
东西 估值/中误差 |
南北 估值/中误差 |
东西/南北 | 东西/南北 | |
| MIZU | 208.32/0.35 | -114.41/0.25 | 210.63/0.25 | -115.26/0.21 | 230.06/-123.36 | 204.9/-125.0 |
| USUD | 17.67/0.17 | 4.25/0.28 | 19.69/0.23 | 4.37/0.24 | 22.45/5.37 | 22.7/5.3 |
从图 6-图 8中可以看到,利用SPM方法不仅能够准确获得主、余震引起的静态永久变形,同时,得到的高频地震波信号(图 6(b)、6(d),图 7(b)、7(d),图 8(b)、8(d))比未分离前(图 5(a)-(f))更加清晰。
如图 8(b)和图 8(d)给出的2011-03-11东日本大地震经过SPM信号分离得到的MIZU和USUD测站高频地震波信号。其中黑色虚线对应的时间为Mw 9.1级主震P波到时,紫色虚线对应的时间为Mw 7.9级强余震P波到时。从图中可知,MIZU测站在Mw 9.1级主震发生后约40 s记录到了地震波信号,在Mw 7.9和Mw 7.7级余震发生后并没有记录到地震波信号;USUD测站在Mw 9.1级主震发生后约105 s记录到了地震波信号,在Mw 7.9级余震发生后约50 s记录到了地震波信号,而在Mw 7.7级余震发生后没有记录到地震波信号。
从以上的分析结果可以得出,利用SPM方法,在完整、清楚地获取地震波信息的同时,还可以清晰地分离主震引起的静态永久变形、余震引起的静态永久变形和震后断层余滑量。
3 结论(1) 利用GPS静态天解解算地震引起的静态永久变形,不仅需要几天时间才可获得稳定解,而且解算结果包含了主震、余震及震后断层余滑位移,仅靠GPS静态天解结果是难以区分的。而高频GPS数据可以清晰地记录地震引起的静态永久变形和高频地震波信息,采用SPM方法,无须剔除地震时段的数据,因而在完整保留地震波信号的同时,还可以迅速提取静态永久变形信息。分离得到的静态永久变形信息可用于震源参数如震级、震源深度等的反演,而高频地震波信息可以结合地震仪、强震仪等观测资料反演断层破裂过程,为震后快速反应及灾后评估提供保障。
(2) 相比于小波等其他信号分离的方法,SPM滤波方法最大优点是其频率响应的调整仅依赖于一个平滑参数λ,使用起来非常方便简单。当利用SPM方法分离高频GPS动态位移中的静态永久变形和高频地震波信息时,不必对其做频谱分析,λ=30可作为经验值直接使用。
(3) 本文选取的3次地震均为大地震,从分离效果来看,能够实现快速、准确地分离,与前人结果也比较一致。对于小地震引起的静态永久变形和地震波信息,只要高频地震波信号能量在噪声水平以上,也可采用SPM方法快速分离。
| [1] |
刘启元, 陈九辉, 李顺成, 等.
新疆伽师强震群区三维地壳上地幔S波速度结构及其地震成因的探讨[J]. 地球物理学报, 2000, 43(3): 356–365.
LIU Qiyuan, CHEN Jiuhui, LI Shuncheng, et al. Passive Seismic Experiment in Xinjiang-Jiashi Strong Earthquake Region and Discussion on Its Seismic Genesis[J]. Chinese Journal of Geophysics, 2000, 43(3): 356–365. |
| [2] |
陈九辉, 刘启元, 李顺成, 等.
青藏高原东北缘-鄂尔多斯地块地壳上地幔S波速度结构[J]. 地球物理学报, 2005, 48(2): 333–342.
CHEN Jiuhui, LIU Qiyuan, LI Shuncheng, et al. Crust and Upper Mantle S-wave Velocity Structure Across Northeastern Tibetan Plateau and Ordos Block[J]. Chinese Journal of Geophysics, 2005, 48(2): 333–342. |
| [3] |
刘瑞丰, 党京平, 陈培善.
利用速度型数字地震仪记录测定面波震级[J]. 地震地磁观测与研究, 1996, 17(2): 1–4.
LIU Ruifeng, DANG Jingping, CHEN Peishan. Determination or Surface Wave Magnitude by Using Velocity Type Digital Seimograph Recordings[J]. Seismological and Geomagnetic Observation and Research, 1996, 17(2): 1–4. |
| [4] | LARSON K M. GPS Seismology[J]. Journal of Geodesy, 2009, 83(3-4): 227–233. DOI:10.1007/s00190-008-0233-x |
| [5] | LARSON K M, BODIN P, GOMBERG J. Using 1-Hz GPS Data to Measure Deformations Caused by the Denali Fault Earthquake[J]. Science, 2003, 300(5624): 1421–1424. DOI:10.1126/science.1084531 |
| [6] | JI Chen, LARSON K M, TAN Ying, et al. Slip History of the 2003 San Simeon Earthquake Constrained by Combining 1 Hz GPS, Strong Motion, and Teleseismic Data[J]. Geophysical Research Letters, 2004, 31(17): L17608. |
| [7] | ANZIDEI M, BOSCHI E, CANNELLI V, et al. Coseismic Deformation of the Destructive April 6, 2009 L'Aquila Earthquake (Central Italy) from GPS Data[J]. Geophysical Research Letters, 2009, 36(17): L17307. DOI:10.1029/2009GL039145 |
| [8] |
李志才, 张鹏, 金双根, 等.
基于GPS观测数据的汶川地震断层形变反演分析[J]. 测绘学报, 2009, 38(2): 108–113, 119.
LI Zhicai, ZHANG Peng, JIN Shuanggen, et al. Wenchuan Earthquake Deformation Fault Inversion and Analysis Based on GPS Observations[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 108–113, 119. |
| [9] | LARSON K M, MIYAZAKI S. Resolving Static Offsets from High-rate GPS Data:the 2003 Tokachi-Oki Earthquake[J]. Earth, Planets and Space, 2008, 60(8): 801–808. DOI:10.1186/BF03352831 |
| [10] |
郭爱智, 王勇, 苏晓庆, 等.
利用小波分解重构提取高频GPS数据静态永久性变形[J]. 武汉大学学报(信息科学版), 2013, 38(10): 1192–1195.
GUO Aizhi, WANG Yong, SU Xiaoqing, et al. Resolving Static Offset from High-rate GPS Data by Wavelet Decomposition-reconstruction Algorithm[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1192–1195. |
| [11] | TARVAINEN M P, RANTA-AHO P O, KARJALAINEN P A. An Advanced Detrending Method with Application to HRV Analysis[J]. IEEE Transactions on Biomedical Engineering, 2002, 49(2): 172–175. DOI:10.1109/10.979357 |
| [12] | GERSCH W. Smoothness Priors[M]//BRILLINGER D, CAINES P, GEWEKE J, et al. New Directions in Time Series Analysis. New York:Springer, 1993. |
| [13] | KARJALAINEN P A. Regularization and Bayesian Methods for Evoked Potential Estimation[D]. Kuopio:University of Kuopio, 1997. |
| [14] |
詹金刚, 王勇, 史红岭, 等.
应用平滑先验信息方法移除GRACE数据中相关误差[J]. 地球物理学报, 2015, 58(4): 1135–1144.
ZHAN Jingang, WANG Yong, SHI Hongling, et al. Removing Correlative Errors in GRACE Data by the Smoothness Priors Method[J]. Chinese Journal of Geophysics, 2015, 58(4): 1135–1144. DOI:10.6038/cjg20150404 |
| [15] | BOCK H, DACH R, JÄGGI A, et al. High-rate GPS Clock Corrections from CODE:Support of 1 Hz Applications[J]. Journal of Geodesy, 2009, 83(11): 1083–1094. DOI:10.1007/s00190-009-0326-1 |
| [16] | CHOI K, BILICH A, LARSON K M, et al. Modified Sidereal Filtering:Implications for High-rate GPS Positioning[J]. Geophysical Research Letters, 2004, 31(22): L22608. |
| [17] | LAY T, WALLACE T C. Modern Global Seismology[M]. San Diego, California: Academic Press, 1995. |
| [18] |
杨少敏, 聂兆生, 贾志革, 等.
GPS解算的日本Mw 9.0级地震的远场同震地表位移[J]. 武汉大学学报(信息科学版), 2011, 36(11): 1336–1339.
YANG Shaomin, NIE Zhaosheng, JIA Zhige, et al. Far-field Coseismic Surface Displacement Caused by the Mw 9.0 Tohoku Earthquake[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1336–1339. |
| [19] |
许才军, 刘洋, 温扬茂.
利用GPS资料反演汶川Mw 7.9级地震滑动分布[J]. 测绘学报, 2009, 38(3): 195–201, 215.
XU Caijun, LIU Yang, WEN Yangmao. Mw 7.9 Wenchuan Earthquake Slip Distribution Inversion from GPS Measurements[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 195–201, 215. |
| [20] |
吴继忠, 吴文坛.
利用高频GPS进行地震动态变形分析及地震定位[J]. 大地测量与地球动力学, 2012, 32(2): 20–23.
WU Jizhong, WU Wentan. Kinematic Analysis of Coseismic Deformation and Seismic Location Using High-rate GPS[J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 20–23. |
| [21] | JIANG Zaisen, WANG Min, WANG Yanzhao, et al. GPS Constrained Coseismic Source and Slip Distribution of the 2013Mw 6.6 Lushan, China, Earthquake and Its Tectonic Implications[J]. Geophysical Research Letters, 2014, 41(2): 407–413. DOI:10.1002/2013GL058812 |
| [22] |
谭凯, 乔学军, 杨少敏, 等.
汶川地震GPS形变约束的破裂分段特征及滑移[J]. 测绘学报, 2011, 40(6): 703–709.
TAN Kai, QIAO Xuejun, YANG Shaomin, et al. Rupture Characteristic and Slip Constrained by GPS Coseismic Deformation Induced by the Wenchuan Earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 703–709. |
| [23] | WANG Qi, ZHANG Peizhen, FREYMUELLER J T, et al. Present-day Crustal Deformation in China Constrained by Global Positioning System Measurements[J]. Science, 2001, 294(5542): 574–577. DOI:10.1126/science.1063647 |
| [24] |
李萌, 黄丁发, 严丽, 等.
汶川地震前后四川盆地CORS站运动特性分析[J]. 测绘学报, 2014, 43(6): 582–589.
LI Meng, HUANG Dingfa, YAN Li, et al. Characteristics of Position Time Series at CORS Stations in Sichuan Basin before and after Wenchuan Earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 582–589. DOI:10.13485/j.cnki.11-2089.2014.0107 |
| [25] |
王敏, 李强, 王凡, 等.
全球定位系统测定的2011年日本宫城Mw 9.0级地震远场同震位移[J]. 科学通报, 2011, 56(20): 1593–1596.
WANG Min, LI Qiang, WANG Fan, et al. Far-field Coseismic Displacements Associated with the 2011 Tohoku-Oki Earthquake in Japan Observed by Global Positioning System[J]. Chinese Science Bulletin, 2011, 56(20): 1593–1596. |
| [26] |
徐韶光, 熊永良, 廖华, 等.
汶川地震同震形变的静态和动态分析[J]. 大地测量与地球动力学, 2010, 30(3): 27–30, 54.
XU Shaoguang, XIONG Yongliang, LIAO Hua, et al. Static and Kinematic Analysis of Coseismic Deformation of Wenchuan Ms 8.0 Earthquake[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 27–30, 54. |




