2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
GPS、BDS和Galileo等GNSS系统采用码分多址(CDMA)技术,观测值站间和星间双差组合能够消除卫星端和接收机端硬件延迟。GLONASS采用频分多址技术(FDMA),导致观测信号在卫星端和接收机端均存在频间偏差(inter frequency bias,IFB), 根据观测值类型可分为频间相位偏差(inter frequency phase bias, IFPB)和频间码偏差(inter frequency code bias,IFCB)[1]。站间单差观测值组合可消除卫星端IFB,由于不同GLONASS卫星的接收机通道延迟不同,星间单差无法消除接收机端IFB。GLONASS接收机端IFPB与接收机厂商相关,长期稳定,受温度、湿度等环境的影响很小,且与卫星通道号线性相关。国内外许多学者计算了不同品牌接收机的IFPB变化率用于IFPB改正,精度可达毫米级[2-4]。然而,GLONASS接收机端IFCB变化规律十分复杂,难以进行模型化或制表化。一些学者基于非差消电离层组合观测值,对IFCB进行了研究,论证了IFCB的长期稳定以及与接收机类型、固件版本和天线类型相关的特性,并应用于提高GPS/GLONASS组合精密单点定位收敛速度和定位精度[5-6]。然而,非差消电离层组合观测IFCB估值受接收机钟差等因素的影响,精度不高,无法应用于GLONASS载波相位模糊度固定。
宽巷模糊度固定是中长基线GLONASS模糊度固定的前提条件。宽巷模糊度固定后,窄巷模糊度估计主要依靠载波相位观测值,可忽略IFCB的影响。鉴于GLONASS IFCB与固件设备相关,本文将两端测站接收机固件版本和天线类型完全相同的基线称为同质基线,其他类型基线统称为异质基线。HMW(Hatch-Melbourne-Wübbena)观测值线性组合是无电离层无几何距离观测值组合,能够消除卫星钟差、接收机钟差以及大气延迟等因素的影响,且与基线长度无关。对于GPS等采用CDMA技术的GNSS系统,多历元HMW组合观测值平滑可快速实现宽巷模糊度固定[7-10]。而GLONASS双差HMW组合包含系统性偏差IFCB,尤其对于异质基线其偏差可达数米,导致HMW组合无法用于宽巷模糊度固定。GLONASS模糊度固定通常采用纯载波组合观测值,由于波长太短导致模糊度固定解易受观测噪声的影响[11-12]。一些学者提出引入外部信息辅助模糊度固定,如大气延迟信息,削弱伪距观测量在模糊度固定中的作用,但是该方法需要高精度的外部信息作为支撑[13-14]。当前中长基线GLONASS事后模糊度固定,通常采用载波观测值组合[4]。而实时模糊度固定仍局限在同质基线且忽略IFCB的影响,采用类似GPS宽巷模糊度固定的方法进行GLONASS宽巷模糊度固定[15-16]。关于异质基线实时宽巷模糊度固定的研究较少。不少学者发现,同质基线也可能存在量级较大的站间IFCB[5-6],即HMW组合并非对所有同质基线均可用,且无法预测HMW组合对目标基线是否可用。另外,实际应用中,异质基线GLONASS实时模糊度固定也是无法回避的问题。因此需要对GLONASS IFCB特性进行深入研究,探寻适用于所有类型基线的GLONASS模糊度固定策略,改善GLONASS模糊度固定效率。
本文利用事后处理软件求取宽巷模糊度,获得GLONASS双差HMW组合残差,进行整体平差,估计GLONASS各颗卫星每天的站间IFCB,并对其量级和变化规律进行了深入研究。然后,利用基于历史历元求得的站间IFCB补偿GLONASS HMW组合观测值,实现GLONASS宽巷模糊度实时固定。本文主要对GLONASS IFCB特性进行研究,IFPB利用相关学者发布的先验值进行改正[2-4]。
1 数学模型 1.1 GLONASS站间IFCB估计方法双差HMW组合可分解为一个双差伪距组合(NL)和一个双差宽巷载波组合(WL),顾及GLONASS IFB的影响,观测值组合可模型化为[17-18]
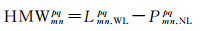 (1)
(1)
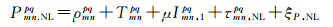 (2)
(2)
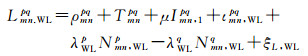 (3)
(3)
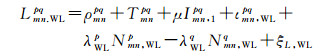 (4)
(4)
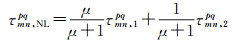 (5)
(5)
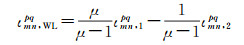 (6)
(6)
式中,P和L分别代表以米为单位的伪距和载波相位观测值;p和q为GLONASS卫星PRN,上标pq表示星间单差,q为参考星;m和n为基线测站编号,下标mn表示站间单差;ρ为卫星到接收机的几何距离;T为对流层延迟;I为频率L1上的电离层延迟;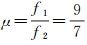
综合式(1)-(6),GLONASS双差HMW组合可表示为
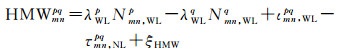 (7)
(7)
式中,IFPB可用先验值修正并利用事后处理软件求取GLONASS宽巷模糊度,未知量包括双差IFCB、观测值噪声和多路径效应。假设24 h内GLONASS IFCB为一个常数,将一天的HMW观测值残差构成方程,可表示为式(8),采用一个低通滤波剔除式(8)中包含粗差的观测量[19]
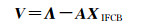 (8)
(8)
式中,V为观测方程残差向量;Λ为除IFCB外式(7)中的剩余部分向量;A为站间IFCB的系数阵;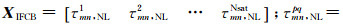
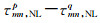
式(8)中未知参数为每颗卫星的站间单差IFCB,观测方程秩亏,需添加一个“零基准”。本文设定GLONASS R01的IFCB为0,如式(9)。式(8)与式(9)联立进行整体最小二乘平差,可获得每颗卫星的站间单差IFCB
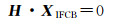 (9)
(9)
式中,H=[1 0 … … 0]Nsat。
1.2 GLONASS宽巷模糊度固定策略式(7)中两个单差模糊度转换为一个双差模糊度和一个单差模糊度[20-21],HMW组合可变换为式(10)
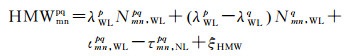 (10)
(10)
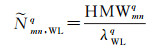 (11)
(11)
参考星单差模糊度的粗略值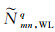
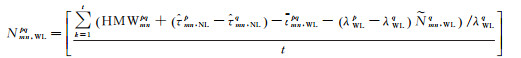 (12)
(12)
式中,[·]为取整符号;t双差HMW组合观测值个数;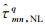
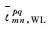
为排除多路径效应干扰,验证GLONASS IFCB稳定性,本文选择位于澳大利亚Curtin大学的两条零基线,处理2016年全年的观测数据,每天每颗卫星估计一个GLONASS站间IFCB,测站信息见表 1。
| 基线名 | 测站1 | 接收机类型 | 天线类型 | 测站2 | 接收机类型 | 天线类型 |
| CUT2-CUT0 | CUT2 | TRIMBLE NETR9 | TRM59800.00 SCIS | CUT0 | TRIMBLE NETR9 | TRM59800.00 SCIS |
| CUT2-CUT3 | CUT2 | TRIMBLE NETR9 | TRM59800.00 SCIS | CUT3 | JAVAD TRE_G3T DELTA | TRM59800.00 SCIS |
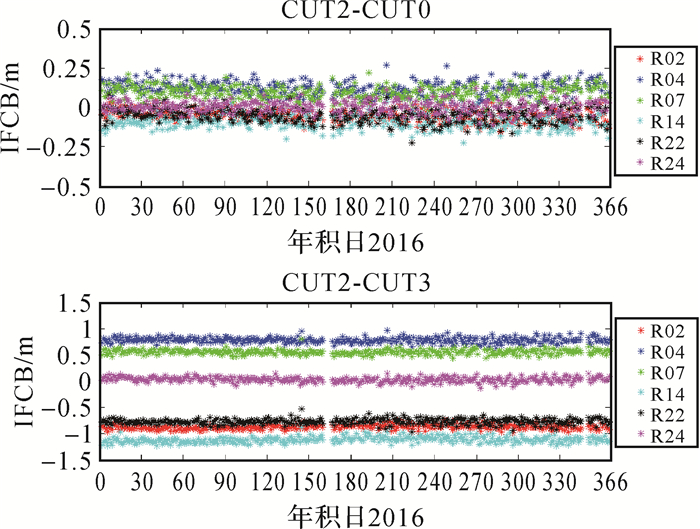
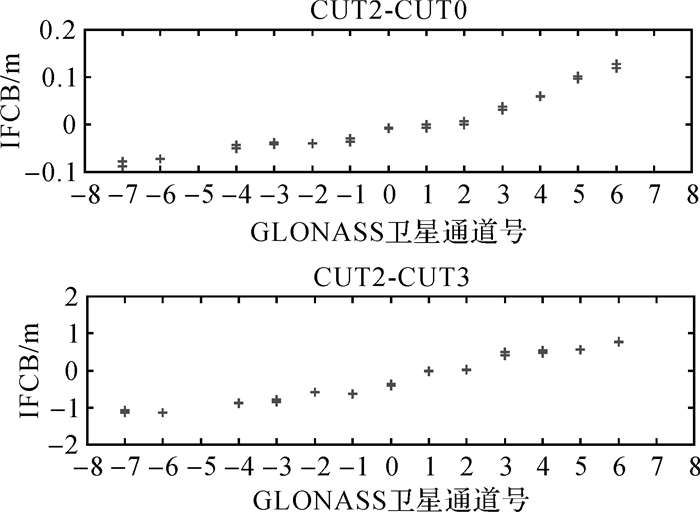
图 1给出了6颗GLONASS卫星站间IFCB估值天变化序列,同质和异质基线求得的GLONASS站间IFCB均长期稳定。同质基线CUT2-CUT0,不同卫星站间IFCB分布范围[-0.25, 0.25],单位为米(m)。例如R14的站间IFCB始终小于0而R04的站间IFCB估值始终大于0.1 m,可知相同固件版本的不同接收机个体间也存在IFCB,当站间IFCB过大时,有可能导致HMW组合无法用于GLONASS宽巷模糊度固定。异质基线CUT2-CUT3,站间IFCB变化范围[-1.2,1],单位为米(m)。不同卫星的站间单差IFCB存在明显差异,R04和R14之间的差异可达2 m以上。
|
| 图 1 两条零基线IFCB估值时间序列 Fig. 1 Time series of DS-IFCB estimates on the two zero-baselines |
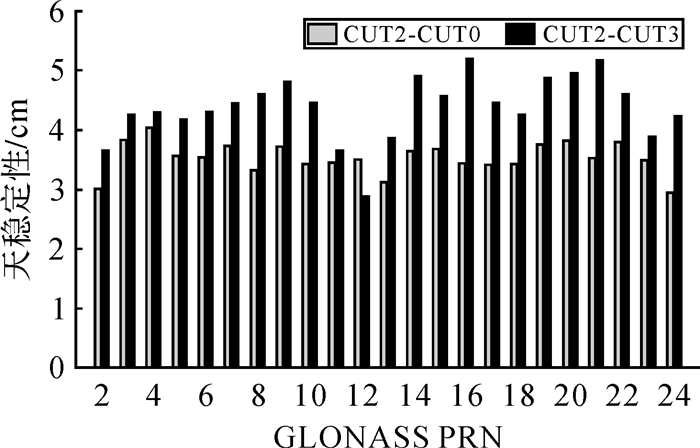
所有天解的标准差作为IFCB估值天稳定性指标,图 2为所有GLONASS卫星站间IFCB估值的天稳定性,所有卫星均优于6 cm。由于CUT3测站观测量数据质量略差,基线CUT2-CUT0大多数卫星站间IFCB天稳定性优于基线CUT2-CUT3。由图 1和图 2可知,各卫星的站间IFCB长时间十分稳定。
|
| 图 2 两条零基线每颗卫星站间IFCB估值的天稳定性 Fig. 2 Daily stability of DS-IFCB estimates on two zero-baselines |
将每颗卫星所有站间IFCB天解取平均,研究站间IFCB与GLONASS卫星通道号相关性,如图 3所示。两条基线相同通道号的两颗卫星站间IFCB十分接近,差异小于3 cm。两条基线的站间IFCB的变化规律存在明显差异,因此不能用类似IFPB的线性函数模型进行修正。
|
| 图 3 零基线站间IFCB与GLONASS卫星通道号相关性 Fig. 3 Relationship between DS-IFCB and GLONASS satellite channel number for two selected zero-baselines |
2.2 同质基线GLONASS站间IFCB
由上文可知,同质基线也存在站间IFCB,基线CUT2-CUT0中任意两颗GLONASS卫星站间IFCB小于30 cm。在站间IFCB较小时,恰当的参考星选择策略可以削弱IFCB的影响。当前,通常忽略同质基线站间IFCB,直接采用HMW组合固定宽巷模糊度。但站间IFCB较大时,HMW组合将存在明显的系统性偏差,有可能导致宽巷模糊度固定失败。为进一步研究HMW组合对于GLONASS同质基线模糊度固定的普适性,笔者选择USA CORS基准站构成的多条同质基线并估计其站间IFCB,发现大多数同质基线站间IFCB分布区间为[-0.15,0.15],单位为米(m),可直接使用HMW组合进行宽巷模糊度固定,而少数基线站间IFCB较大且不可忽略,例如基线TN26-TN29和基线NJI2-NJMT,其测站接收机和天线信息如表 2所示[22]。基线TN26-TN29为22.5 km;基线NJI2-NJMT约26.5 km。
| 基线名 | 测站1 | 接收机 | 天线 | 测站2 | 接收机 | 天线 |
| NJI2-NJMT | NJI2 | LEICA GR10 | LEIAR10 NONE | NJI2 | LEICA GR10 | LEIAR10 NONE |
| TN26-TN29 | TN26 | TPS NETG3 | TPSG3_A1 NONE | TN29 | TPS NETG3 | TPSG3_A1 NONE |
图 4中给出两条同质基线的部分GLONASS卫星在2016年全年的站间IFCB单天解时间序列,部分时段观测值缺失。两条基线各颗卫星站间IFCB估值长期稳定,且不同卫星间差异明显。基线NJI2-NJMT站间IFCB估值变化区间[-0.4, 0.5],单位为米(m),其中R02和R19之间相差0.5 m左右;基线TN26-TN29站间IFCB估值变化区间[-1, 1],单位为米(m),其中R02和R03(或R14)之间的相差约1.4 m。不同卫星站间IFCB差异导致HMW组合存在明显系统偏差,无法用于宽巷模糊度固定。

|
| 图 4 两条同质基线站间IFCB时间序列 Fig. 4 Time series of DS-IFCB for two homogeneous baselines |
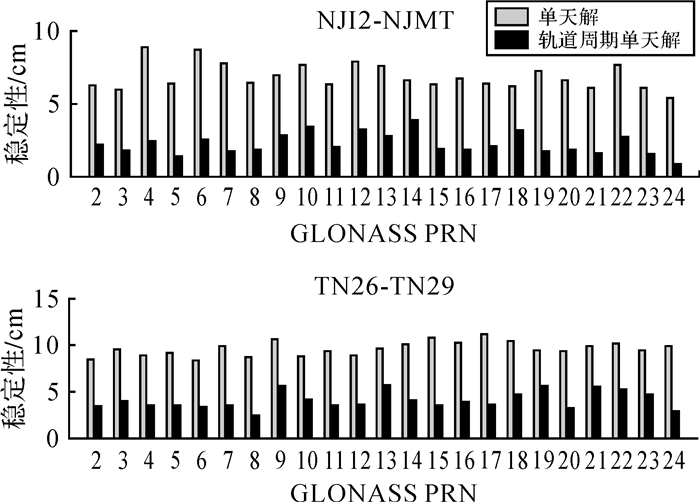
观测值多路径效应导致非零基线天稳定性较零基线变差,如图 5所示,两条非零同质基线中天稳定性最差的卫星可达12 cm。图 4中多颗卫星站间IFCB估值存在周期性变化,变化周期为8 d与GLONASS卫星轨道重复周期吻合。该现象主要是由于多路径效应的影响,而多路径与基准站和卫星相对位置相关,因此考虑轨道重复周期可获取更加稳定的卫星站间IFCB。图 5给出两条基线每颗卫星站间IFCB的单天解和轨道周期单天解的天稳定性。卫星轨道周期单天解稳定性的计算方法为,首先分别计算每颗卫星15个轨道重复周期内第n(n[1, 8],n为整数)天站间IFCB估值的标准差,然后对8个标准差值求平均。轨道重复周期单天解天稳定性明显优于单天解天稳定性,基线NJI2-NJMT和基线TN26-TN29分别平均有45%和38%的改善。
|
| 图 5 基线NJI2-NJMT和TN26-TN29站间IFCB估值的轨道重复周期单天解稳定性和天稳定性 Fig. 5 Daily stability and satellite orbit repeat cycle daily stability of DS-IFCB for two homogeneous baselines |
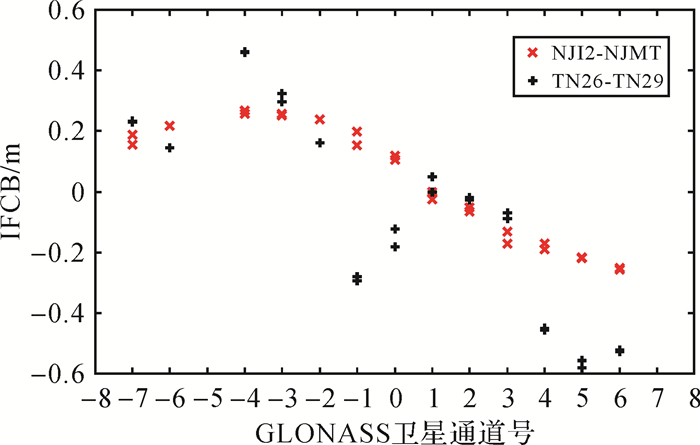
图 6为基线NJI2-NJMT和TN26-TN29站间IFCB与GLONASS卫星通道号的相关性。任一条基线中,通道号相同的两颗卫星的站间IFCB估值十分接近,差异小于5 cm。不同基线卫星通道号和站间IFCB的相关性存在明显差异。
|
| 图 6 两条同质基线间站间IFCB与卫星通道号相关性 Fig. 6 Relationship between DS-IFCB and GLONASS satellite channel number for two selected homogeneous baselines |
3 GLONASS站间IFCB实时双差宽巷模糊度固定示例
由上文章可知,GLONASS站间IFCB具有长期稳定性,基于历史观测数据求得GLONASS站间IFCB可作为先验值补偿HMW组合观测值,用于GLONASS实时双差宽巷模糊度固定。伪距多路径效应的影响和GLONASS卫星每天可见时长不同,本文基于一个轨道重复周期观测数据求得的站间IFCB估值作为改正数。本文选取USA CORS和欧洲EPN基准站网络中10条长度在20~100 km的基线[23],利用2016年第140-147 d的站间IFCB估值作为先验值,补偿改正第148-155 d HMW组合观测值。本文所选10条基线中,除了上文中提到的基线NJI2-NJMT和TN26-TN29外,剩余8条基线是由EPN的基准站构成,测站接收机和天线信息如表 3所示。
| 基线名 | 测站1 | 接收机类型 | 天线类型 | 测站2 | 接收机类型 | 天线类型 |
| BS1 | BUTE | LEICA GR25 | LEIAR25.R4 LEIT | PENC | LEICA GRX1200GGPRO | LEIAT504GG LEIS |
| BS2 | CFRM | LEICA GRX1200+GNSS | LEIAR25.R4 LEIT | KATO | TRIMBLE NETR5 | TRM57971.00 TZGD |
| BS3 | GOPE | TPS NETG3 | TPSCR.G3 TPSH | CLIB | LEICA GRX1200+GNSS | LEIAR25.R4 LEIT |
| BS4 | IGMI | TPS ODYSSEY_E | TPSCR.G3 TPSH | PRAT | LEICA GR10 | LEIAR10 NONE |
| BS5 | LINZ | TRIMBLE NETR9 | TRM59900.00 SCIS | VACO | TPS NETG3 | ASH701946.2 SNOW |
| BS6 | SFER | LEICA GR25 | LEIAR20 NONE | CEU1 | TRIMBLE NETR9 | TRM59900.00 SCIS |
| BS7 | LIL2 | LEICA GR25 | TRM57971.00 NONE | DENT | SEPT POLARX4 | TRM59800.00 NONE |
| BS8 | VILL | SEPT POLARX4 | SEPCHOKE_MC NONE | CEBR | SEPT POLARX4 | SEPCHOKE_MC NONE |
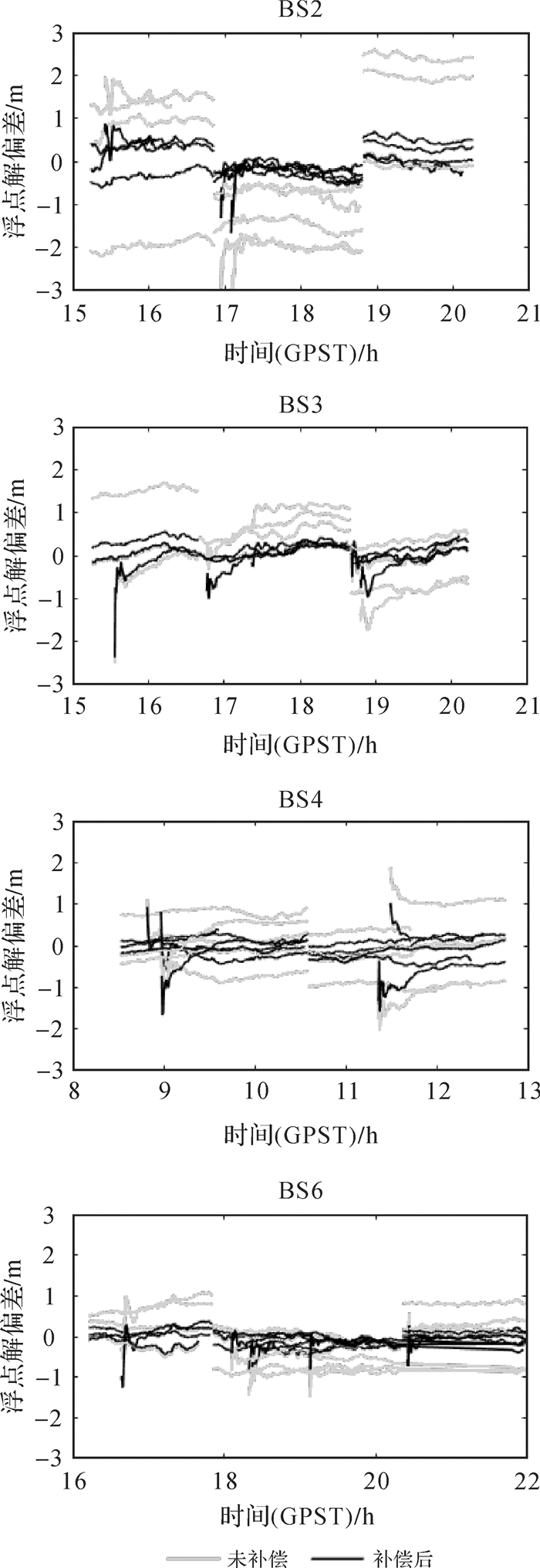
图 7给出2016年第148 d 4条基线利用先验站间IFCB补偿前后,部分GLONASS卫星HMW组合平滑序列宽巷模糊度浮点解的偏差,宽巷整周模糊度真值由事后处理软件求取。补偿前,浮点解偏差达3 m,明显无法用于宽巷模糊度固定。先验站间IFCB能够对宽巷模糊度浮点解进行有效补偿修正,补偿后,浮点解偏差明显变小,偏差在0.3 m以内,取整后可得到准确的宽巷整周模糊度。
|
| 图 7 HMW组合求得的宽巷模糊度浮点解偏差 Fig. 7 Float solution bias of HMW combination |
以浮点解统计成功率大于99.99%[24]和小数偏差小于0.3作为宽巷模糊度浮点解取整阈值,对10条基线连续7 d模糊度固定率Ps和正确率Pc进行统计。每天0点0分0秒进行重新初始化,并采用轨道重复周期内对应天数的先验站间IFCB进行补偿。模糊度固定成功率和正确率采用式(13)和式(14)进行统计
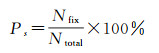 (13)
(13)
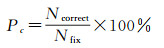 (14)
(14)
式中,Ntotal为模糊度总数;Nfix为固定的模糊度个数;Ncorrect为正确固定的模糊度个数。
表 4为利用先验站间IFCB改正后10条基线模糊度固定率和正确率。站间IFCB补偿后,所有基线模糊度固定率均在85%~90%,由于先验站间IFCB估值的误差以及GLONASS伪距观测值精度略差,补偿后GLONASS宽巷模糊度固定率仍然无法达到与GPS相当的固定率。模糊度固定正确率是评估模糊度固定可靠性的重要参数,只有在模糊度正确固定的前提下才能够实现高精度定位或生成高精度差分信息。如表 4所示,采用先验站间IFCB补偿HMW组合后,所有基线正确率均在98%以上。
| (%) | ||||||||||
| 基线名 | BS1 | BS2 | BS3 | BS4 | BS5 | BS6 | BS7 | BS8 | BS9 | BS10 |
| 固定率 | 87.08 | 86.59 | 88.22 | 85.68 | 90.30 | 88.17 | 90.65 | 89.97 | 89.57 | 91.56 |
| 成功率 | 99.42 | 97.99 | 98.94 | 98.38 | 99.17 | 98.08 | 99.94 | 98.87 | 99.54 | 99.82 |
4 结论
GLONASS IFCB无法进行精确的模型化改正,导致HMW组合观测值存在系统性偏差。本文对GLONASS双差HMW组合观测值的残差进行最小二乘平差,获得高精度的HMW组合站间IFCB单天解。通过处理2016年多条基线的观测数据,验证了站间IFCB的量级和长期稳定的特性。大多数同质基线站间IFCB小于0.15 m,恰当的参考星选择策略可以有效减小HMW组合中站间IFCB;但少数同质基线站间IFCB大于0.5 m;异质基线站间IFCB量级可达2 m以上。零基线站间IFCB估值天稳定性优于5 cm;多路径效应导致非零基线站间IFCB估值天稳定性略差,考虑GLONASS卫星轨道重复周期后其单天解稳定性优于8 cm。本文详细分析的4条基线显示,站间IFCB与卫星通道号相关,相同通道号卫星间的站间IFCB差异很小;然而,本文分析数据量有限,且有学者指出存在相同通道号卫星的IFCB量级差异明显的接收机,本文建议在GLONASS双差模糊度固定时,每颗GLONASS卫星估计一个站间IFCB参数。
无论同质基线或异质基线,IFCB均有可能导致HMW组合无法用于GLONASS宽巷模糊度固定。利用GLONASS IFCB长期稳定的特性,将基于历史历元求得的站间IFCB作为先验值,实现GLONASS双差宽巷实时模糊度固定。试验表明,补偿站间IFCB后,浮点解偏差明显变小,模糊度固定率高于85%,正确率在98%以上。本文方法不受基线长度限制且适用于所有类型基线,可显著改善GLONASS实时高精度定位性能。
| [1] | YAMADA H, TAKASU T, KUBO N, et al. Evaluation and Calibration of Receiver Inter-channel Biases for RTK-GPS/GLONASS[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR:Oregon Convention Center, 2010:1580-1587. |
| [2] | WANNINGER L, WALLSTAB-FREITAG S. Combined Processing of GPS, GLONASS, and SBAS Code Phase and Carrier Phase Measurements[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation. Fort Worth, TX:Fort Worth Convention Center, 2007:866-875. |
| [3] | WANNINGER L. Carrier-phase Inter-frequency Biases of GLONASS Receivers[J]. Journal of Geodesy, 2012, 86(2): 139–148. DOI:10.1007/s00190-011-0502-y |
| [4] |
安向东. GLONASS模糊度固定方法研究[D]. 武汉: 武汉大学, 2016. AN Xiangdong. The Research of GLONASS Integer Ambiguity Resolution[D]. Wuhan:Wuhan University. 2016. |
| [5] | SHI Chuang, YI Wenting, SONG Weiwei, et al. GLONASS Pseudorange Inter-channel Biases and Their Effects on Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(4): 439–451. DOI:10.1007/s10291-013-0332-x |
| [6] |
刘志强, 王解先, 段兵兵.
单站多参数GLONASS码频间偏差估计及其对组合精密单点定位的影响[J]. 测绘学报, 2015, 44(2): 150–159.
LIU Zhiqiang, WANG Jiexian, DUAN Bingbing. Estimation of GLONASS Code Inter-frequency Biases with Multiple Parameters Based on a Single Station and Its Impact on Combined Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 150–159. DOI:10.11947/j.AGCS.2015.20130800 |
| [7] | MERVART L, BEUTLER G, ROTHACHER M, et al. Ambiguity Resolution Strategies Using the Results of the International GPS Geodynamics Service (IGS)[J]. Bulletin Géodésique, 1994, 68(1): 29–38. DOI:10.1007/BF00806750 |
| [8] | HATCH R. The Synergism of GPS Code and Carrier Measurements[C]//Proceedings of the 3rd International Geodetic Symposium on Satellite Doppler Positioning.[S.l.]:Bulletin Géodésique, 1983:1213-1231. |
| [9] | MELBOURNE W G. The Case for Ranging in GPS-based Geodetic Systems[C]//Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System. Maryland:[s.n.], 1985:1519. |
| [10] | WVBBENA G. Software Developments for Geodetic Positioning with GPS Using TI-4100 Code and Carrier Measurements[C]//Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System. Rockville, Maryland:[s.n.], 1985:19. |
| [11] | REUSSNER N, WANNINGER L. GLONASS Inter-frequency Biases and Their Effects on RTK and PPP Carrier-phase Ambiguity Resolution[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation. Portland, OR:Fort Worth Convention Center, 2011:712-716. |
| [12] | LIU Yang, GE Maorong, SHI Chuang, et al. Improving Integer Ambiguity Resolution for GLONASS Precise Orbit Determination[J]. Journal of Geodesy, 2016, 90(8): 715–726. DOI:10.1007/s00190-016-0904-y |
| [13] | REUβNER N, WANNINGER L. GLONASS Inter-frequency Code Biases and PPP Carrier-phase Ambiguity Resolution[J]. Journal of Geodesy, 2012, 86(2): 139–148. DOI:10.1007/s00190-011-0502-y |
| [14] | GENG Jianghui, BOCK Y. GLONASS Fractional-cycle Bias Estimation across Inhomogeneous Receivers for PPP Ambiguity Resolution[J]. Journal of Geodesy, 2016, 90(4): 379–396. DOI:10.1007/s00190-015-0879-0 |
| [15] |
姚宜斌, 胡明贤, 许超钤.
基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK定位性能分析[J]. 测绘学报, 2016, 45(9): 1009–1018.
YAO Yibin, HU Mingxian, XU Chaoqian. Positioning Accuracy Analysis of GPS/BDS/GLONASS Network RTK Based on DREAMNET[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1009–1018. DOI:10.11947/j.AGCS.2016.20160133 |
| [16] |
张绍成. 基于GPS/GLONASS集成的CORS网络大气建模与RTK算法实现[D]. 武汉: 武汉大学, 2010. ZHANG Shaocheng. The GPS/GLONASS Integrated CORS Network Atmosphere Modeling and RTK Algorithm Implementation[D]. Wuhan:Wuhan University, 2010. |
| [17] | ZHANG Xiaohong, HE Xiyang, LIU Wanke. Characteristics of Systematic Errors in the BDS Hatch-Melbourne-Wübbena Combination and Its Influence on Wide-lane Ambiguity Resolution[J]. GPS Solutions, 2017, 21(1): 265–277. DOI:10.1007/s10291-016-0520-6 |
| [18] | AL-SHAERY A, ZHANG S, RIZOS C. An Enhanced Calibration Method of GLONASS Inter-channel Bias for GNSS RTK[J]. GPS Solutions, 2013, 17(2): 165–173. DOI:10.1007/s10291-012-0269-5 |
| [19] | GE Linlin, HAN Shaowei, RIZOS C. Multipath Mitigation of Continuous GPS Measurements Using an Adaptive Filter[J]. GPS Solutions, 2000, 4(2): 19–30. DOI:10.1007/PL00012838 |
| [20] | WANG J. An Approach to GLONASS Ambiguity Resolution[J]. Journal of Geodesy, 2013, 74(5): 421–430. |
| [21] |
段举举, 沈云中.
GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报, 2012, 41(6): 825–830.
DUAN Juju, SHEN Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 825–830. |
| [22] | SNAY R A, SOLER T. Continuously Operating Reference Station (CORS):History, Applications, and Future Enhancements[J]. Journal of Surveying Engineering, 2013, 134(4): 95–104. |
| [23] | BRUYNINX C, BECKER M, STANGL G. Regional Densification of the IGS in Europe Using the EUREF Permanent GPS Network (EPN)[J]. Physics and Chemistry of the Earth, Part A:Solid Earth and Geodesy, 2000, 26(6-8): 531–538. |
| [24] | TEUNISSEN P J G. An Optimality Property of the Integer Least-squares Estimator[J]. Journal of Geodesy, 1999, 73(11): 587–593. DOI:10.1007/s001900050269 |



